From Wikipedia, the free encyclopedia
Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can predict or explain many of a molecule's chemical properties, such as its dipole moment and its allowed spectroscopic transitions (based on selection rules such as the Laporte rule). Many university level textbooks on physical chemistry, quantum chemistry, and inorganic chemistry devote a chapter to symmetry.[1][2][3][4][5]
While various frameworks for the study of molecular symmetry exist, group theory is the predominant one. This framework is also useful in studying the symmetry of molecular orbitals, with applications such as the Hückel method, ligand field theory, and the Woodward-Hoffmann rules. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials.
Many techniques for the practical assessment of molecular symmetry exist, including X-ray crystallography and various forms of spectroscopy, for example infrared spectroscopy of metal carbonyls. Spectroscopic notation is based on symmetry considerations.
The 5 symmetry elements have associated with them 5 types of symmetry operations, which leave the molecule in a state indistinguishable from the starting state. They are sometimes distinguished from symmetry elements by a caret or circumflex. Thus, Ĉn is the rotation of a molecule around an axis and Ê is the identity operation. A symmetry element can have more than one symmetry operation associated with it. For example, the C4 axis of the square xenon tetrafluoride (XeF4) molecule is associated with two Ĉ4 rotations (90°) in opposite directions and a Ĉ2 rotation (180°). Since Ĉ1 is equivalent to Ê, Ŝ1 to σ and Ŝ2 to î, all symmetry operations can be classified as either proper or improper rotations.
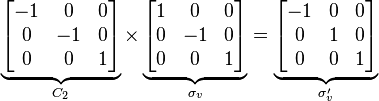
In a molecular symmetry group, the group elements are the symmetry operations (not the symmetry elements), and the binary combination consists of applying first one symmetry operation and then the other. An example is the sequence of a C4 rotation about the z-axis and a reflection in the xy-plane, denoted σ(xy)C4. By convention the order of operations is from right to left.
A molecular symmetry group obeys the defining properties of any group.
(1) closure property:
For every pair of elements x and y in G, the product x*y is also in G.
( in symbols, for every two elements x, y∈G, x*y is also in G ).
This means that the group is closed so that combining two elements produces no new elements. Symmetry operations have this property because a sequence of two operations will produce a third state indistinguishable from the second and therefore from the first, so that the net effect on the molecule is still a symmetry operation.
(2) associative property:
For every x and y and z in G, both (x*y)*z and x*(y*z) result with the same element in G.
( in symbols, (x*y)*z = x*(y*z ) for every x, y, and z ∈ G)
(3) existence of identity property:
There must be an element ( say e ) in G such that product any element of G with e make no change to the element.
( in symbols, x*e=e*x= x for every x∈ G )
(4) existence of inverse property:
For each element ( x ) in G, there must be an element y in G such that product of x and y is the identity element e.
( in symbols, for each x∈G there is a y ∈ G such that x*y=y*x= e for every x∈G )
The order of a group is the number of elements in the group. For groups of small orders, the group properties can be easily verified by considering its composition table, a table whose rows and columns correspond to elements of the group and whose entries correspond to their products.
The symmetry of a crystal, however, is described by a space group of symmetry operations, which includes translations in space.
(2) Another example is the ammonia molecule, which is pyramidal and contains a three-fold rotation axis as well as three mirror planes at an angle of 120° to each other. Each mirror plane contains an N-H bond and bisects the H-N-H bond angle opposite to that bond. Thus ammonia molecule belongs to the C3v point group that has order 6: an identity element E, two rotation operations C3 and C32, and three mirror reflections σv, σv' and σv".
The table itself consists of characters that represent how a particular irreducible representation transforms when a particular symmetry operation is applied. Any symmetry operation in a molecule's point group acting on the molecule itself will leave it unchanged. But, for acting on a general entity, such as a vector or an orbital, this need not be the case. The vector could change sign or direction, and the orbital could change type. For simple point groups, the values are either 1 or −1: 1 means that the sign or phase (of the vector or orbital) is unchanged by the symmetry operation (symmetric) and −1 denotes a sign change (asymmetric).
The representations are labeled according to a set of conventions:
The character table for the C2v symmetry point group is given below:
Consider the example of water (H2O), which has the C2v symmetry described above. The 2px orbital of oxygen is oriented perpendicular to the plane of the molecule and switches sign with a C2 and a σv'(yz) operation, but remains unchanged with the other two operations (obviously, the character for the identity operation is always +1). This orbital's character set is thus {1, −1, 1, −1}, corresponding to the B1 irreducible representation. Likewise, the 2pz orbital is seen to have the symmetry of the A1 irreducible representation, 2py B2, and the 3dxy orbital A2. These assignments and others are noted in the rightmost two columns of the table.
These groups are known as permutation-inversion groups, because a symmetry operation may be an energetically feasible permutation of equivalent nuclei, or an inversion with respect to the centre of mass, or a combination of the two.
For example, ethane (C2H6) has three equivalent staggered conformations. Conversion of one conformation to another occurs at ordinary temperature by internal rotation of one methyl group relative to the other. This is not a rotation of the entire molecule about the C3 axis, but can be described as a permutation of the three identical hydrogens of one methyl group. Although each conformation has D3d symmetry as in the table above, description of the internal rotation and associated quantum states and energy levels requires the more complete permutation-inversion group.
Similarly, ammonia (NH3) has two equivalent pyramidal (C3v) conformations which are interconverted by the process known as nitrogen inversion. This is not an inversion in the sense used for symmetry operations of rigid molecules, since NH3 has no inversion center. Rather it is a reflection of all atoms about the centre of mass (close to the nitrogen), which happens to be energetically feasible for this molecule. Again the permutation-inversion group is used to describe the interaction of the two geometries.
A second and similar approach to the symmetry of nonrigid molecules is due to Altmann.[12][13] In this approach the symmetry groups are known as Schrödinger supergroups and consist of two types of operations (and their combinations): (1) the geometric symmetry operations (rotations, reflections, inversions) of rigid molecules, and (2) isodynamic operations which take a nonrigid molecule into an energetically equivalent form by a physically reasonable process such as rotation about a single bond (as in ethane) or a molecular inversion (as in ammonia).[13]
While various frameworks for the study of molecular symmetry exist, group theory is the predominant one. This framework is also useful in studying the symmetry of molecular orbitals, with applications such as the Hückel method, ligand field theory, and the Woodward-Hoffmann rules. Another framework on a larger scale is the use of crystal systems to describe crystallographic symmetry in bulk materials.
Many techniques for the practical assessment of molecular symmetry exist, including X-ray crystallography and various forms of spectroscopy, for example infrared spectroscopy of metal carbonyls. Spectroscopic notation is based on symmetry considerations.
Symmetry concepts
The study of symmetry in molecules is an adaptation of mathematical group theory.Elements
The symmetry of a molecule can be described by 5 types of symmetry elements.- Symmetry axis: an axis around which a rotation by
 results in a molecule indistinguishable from the original. This is also called an n-fold rotational axis and abbreviated Cn. Examples are the C2 in water and the C3 in ammonia. A molecule can have more than one symmetry axis; the one with the highest n is called the principal axis, and by convention is assigned the z-axis in a Cartesian coordinate system.
results in a molecule indistinguishable from the original. This is also called an n-fold rotational axis and abbreviated Cn. Examples are the C2 in water and the C3 in ammonia. A molecule can have more than one symmetry axis; the one with the highest n is called the principal axis, and by convention is assigned the z-axis in a Cartesian coordinate system. - Plane of symmetry: a plane of reflection through which an identical copy of the original molecule is given. This is also called a mirror plane and abbreviated σ. Water has two of them: one in the plane of the molecule itself and one perpendicular to it. A symmetry plane parallel with the principal axis is dubbed vertical (σv) and one perpendicular to it horizontal (σh). A third type of symmetry plane exists: If a vertical symmetry plane additionally bisects the angle between two 2-fold rotation axes perpendicular to the principal axis, the plane is dubbed dihedral (σd). A symmetry plane can also be identified by its Cartesian orientation, e.g., (xz) or (yz).
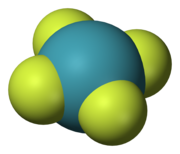
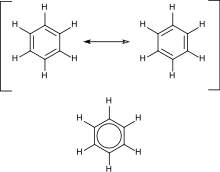
- Center of symmetry or inversion center, abbreviated i. A molecule has a center of symmetry when, for any atom in the molecule, an identical atom exists diametrically opposite this center an equal distance from it. There may or may not be an atom at the center. Examples are xenon tetrafluoride where the inversion center is at the Xe atom, and benzene (C6H6) where the inversion center is at the center of the ring.
- Rotation-reflection axis: an axis around which a rotation by
 , followed by a reflection in a plane perpendicular to it, leaves the molecule unchanged. Also called an n-fold improper rotation axis, it is abbreviated Sn. Examples are present in tetrahedral silicon tetrafluoride, with three S4 axes, and the staggered conformation of ethane with one S6 axis.
, followed by a reflection in a plane perpendicular to it, leaves the molecule unchanged. Also called an n-fold improper rotation axis, it is abbreviated Sn. Examples are present in tetrahedral silicon tetrafluoride, with three S4 axes, and the staggered conformation of ethane with one S6 axis. - Identity, abbreviated to E, from the German 'Einheit' meaning unity.[6] This symmetry element simply consists of no change: every molecule has this element. While this element seems physically trivial, it must be included in the list of symmetry elements so that they form a mathematical group, whose definition requires inclusion of the identity element. It is so called because it is analogous to multiplying by one (unity).
Operations
The 5 symmetry elements have associated with them 5 types of symmetry operations, which leave the molecule in a state indistinguishable from the starting state. They are sometimes distinguished from symmetry elements by a caret or circumflex. Thus, Ĉn is the rotation of a molecule around an axis and Ê is the identity operation. A symmetry element can have more than one symmetry operation associated with it. For example, the C4 axis of the square xenon tetrafluoride (XeF4) molecule is associated with two Ĉ4 rotations (90°) in opposite directions and a Ĉ2 rotation (180°). Since Ĉ1 is equivalent to Ê, Ŝ1 to σ and Ŝ2 to î, all symmetry operations can be classified as either proper or improper rotations.
Molecular symmetry groups
Groups
The symmetry operations of a molecule (or other object) form a group, which is a mathematical structure usually denoted in the form (G,*)) consisting of a set G and a binary combination operation say '*' satisfying certain properties listed below.In a molecular symmetry group, the group elements are the symmetry operations (not the symmetry elements), and the binary combination consists of applying first one symmetry operation and then the other. An example is the sequence of a C4 rotation about the z-axis and a reflection in the xy-plane, denoted σ(xy)C4. By convention the order of operations is from right to left.
A molecular symmetry group obeys the defining properties of any group.
(1) closure property:
For every pair of elements x and y in G, the product x*y is also in G.
( in symbols, for every two elements x, y∈G, x*y is also in G ).
This means that the group is closed so that combining two elements produces no new elements. Symmetry operations have this property because a sequence of two operations will produce a third state indistinguishable from the second and therefore from the first, so that the net effect on the molecule is still a symmetry operation.
(2) associative property:
For every x and y and z in G, both (x*y)*z and x*(y*z) result with the same element in G.
( in symbols, (x*y)*z = x*(y*z ) for every x, y, and z ∈ G)
(3) existence of identity property:
There must be an element ( say e ) in G such that product any element of G with e make no change to the element.
( in symbols, x*e=e*x= x for every x∈ G )
(4) existence of inverse property:
For each element ( x ) in G, there must be an element y in G such that product of x and y is the identity element e.
( in symbols, for each x∈G there is a y ∈ G such that x*y=y*x= e for every x∈G )
The order of a group is the number of elements in the group. For groups of small orders, the group properties can be easily verified by considering its composition table, a table whose rows and columns correspond to elements of the group and whose entries correspond to their products.
Point group
The successive application (or composition) of one or more symmetry operations of a molecule has an effect equivalent to that of some single symmetry operation of the molecule. Moreover the set of all symmetry operations including this composition operation obeys all the properties of a group, given above. So (S,*) is a group where S is the set of all symmetry operations of some molecule, and * denotes the composition (repeated application) of symmetry operations. This group is called the point group of that molecule, because the set of symmetry operations leave at least one point fixed. For some symmetries, an entire axis or an entire plane are fixed.The symmetry of a crystal, however, is described by a space group of symmetry operations, which includes translations in space.
Examples
(1) The point group for the water molecule is C2v, consisting of the symmetry operations E, C2, σv and σv'. Its order is thus 4. Each operation is its own inverse. As an example of closure, a C2 rotation followed by a σv reflection is seen to be a σv' symmetry operation: σv*C2 = σv'. (Note that "Operation A followed by B to form C" is written BA = C).(2) Another example is the ammonia molecule, which is pyramidal and contains a three-fold rotation axis as well as three mirror planes at an angle of 120° to each other. Each mirror plane contains an N-H bond and bisects the H-N-H bond angle opposite to that bond. Thus ammonia molecule belongs to the C3v point group that has order 6: an identity element E, two rotation operations C3 and C32, and three mirror reflections σv, σv' and σv".
Common point groups
The following table contains a list of point groups with representative molecules. The description of structure includes common shapes of molecules based on VSEPR theory.| Point group | Symmetry operations | Simple description of typical geometry | Example 1 | Example 2 | Example 3 |
| C1 | E | no symmetry, chiral |  bromochlorofluoromethane |
 lysergic acid |
|
| Cs | E σh | mirror plane, no other symmetry |  thionyl chloride |
 hypochlorous acid |
 chloroiodomethane |
| Ci | E i | inversion center | (R,R) 1,2-dichloro-1,2-dibromoethane (anti conformer) | ||
| C∞v | E 2C∞ ∞σv | linear |  Hydrogen fluoride |
 nitrous oxide (dinitrogen monoxide) |
|
| D∞h | E 2C∞ ∞σi i 2S∞ ∞C2 | linear with inversion center |  oxygen |
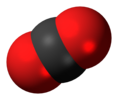 carbon dioxide |
|
| C2 | E C2 | "open book geometry," chiral |  hydrogen peroxide |
||
| C3 | E C3 | propeller, chiral |  triphenylphosphine |
||
| C2h | E C2 i σh | planar with inversion center |  trans-1,2-dichloroethylene |
||
| C3h | E C3 C32 σh S3 S35 | propeller |  boric acid |
||
| C2v | E C2 σv(xz) σv'(yz) | angular (H2O) or see-saw (SF4) |  water |
 sulfur tetrafluoride |
 sulfuryl fluoride |
| C3v | E 2C3 3σv | trigonal pyramidal |  ammonia |
 phosphorus oxychloride |
|
| C4v | E 2C4 C2 2σv 2σd | square pyramidal |  xenon oxytetrafluoride |
||
| D2 | E C2(x) C2(y) C2(z) | twist, chiral | cyclohexane twist conformation | ||
| D3 | E C3(z) 3C2 | triple helix, chiral |  Tris(ethylenediamine)cobalt(III) cation |
||
| D2h | E C2(z) C2(y) C2(x) i σ(xy) σ(xz) σ(yz) | planar with inversion center |  ethylene |
 dinitrogen tetroxide |
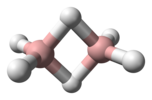 diborane |
| D3h | E 2C3 3C2 σh 2S3 3σv | trigonal planar or trigonal bipyramidal |  boron trifluoride |
 phosphorus pentachloride |
|
| D4h | E 2C4 C2 2C2' 2C2 i 2S4 σh 2σv 2σd | square planar |  xenon tetrafluoride |
 octachlorodimolybdate(III) anion |
|
| D5h | E 2C5 2C52 5C2 σh 2S5 2S53 5σv | pentagonal |  ruthenocene |
 C70 |
|
| D6h | E 2C6 2C3 C2 3C2' 3C2‘’ i 2S3 2S6 σh 3σd 3σv | hexagonal | 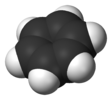 benzene |
 bis(benzene)chromium |
|
| D2d | E 2S4 C2 2C2' 2σd | 90° twist |  allene |
 tetrasulfur tetranitride |
|
| D3d | E C3 3C2 i 2S6 3σd | 60° twist |  ethane (staggered rotamer) |
 cyclohexane chair conformation |
|
| D4d | E 2S8 2C4 2S83 C2 4C2' 4σd | 45° twist |  dimanganese decacarbonyl (staggered rotamer) |
||
| D5d | E 2C5 2C52 5C2 i 3S103 2S10 5σd | 36° twist |  ferrocene (staggered rotamer) |
||
| Td | E 8C3 3C2 6S4 6σd | tetrahedral |  methane |
 phosphorus pentoxide |
 adamantane |
| Oh | E 8C3 6C2 6C4 3C2 i 6S4 8S6 3σh 6σd | octahedral or cubic |  cubane |
 sulfur hexafluoride |
|
| Ih | E 12C5 12C52 20C3 15C2 i 12S10 12S103 20S6 15σ | icosahedral or dodecahedral |  Buckminsterfullerene |
 dodecaborate anion |
 dodecahedrane |
Representations
The symmetry operations can be represented in many ways. A convenient representation is by matrices. For any vector representing a point in Cartesian coordinates, left-multiplying it gives the new location of the point transformed by the symmetry operation. Composition of operations corresponds to matrix multiplication. In the C2v example this is:Character tables
For each point group, a character table summarizes information on its symmetry operations and on its irreducible representations. As there are always equal numbers of irreducible representations and classes of symmetry operations, the tables are square.The table itself consists of characters that represent how a particular irreducible representation transforms when a particular symmetry operation is applied. Any symmetry operation in a molecule's point group acting on the molecule itself will leave it unchanged. But, for acting on a general entity, such as a vector or an orbital, this need not be the case. The vector could change sign or direction, and the orbital could change type. For simple point groups, the values are either 1 or −1: 1 means that the sign or phase (of the vector or orbital) is unchanged by the symmetry operation (symmetric) and −1 denotes a sign change (asymmetric).
The representations are labeled according to a set of conventions:
- A, when rotation around the principal axis is symmetrical
- B, when rotation around the principal axis is asymmetrical
- E and T are doubly and triply degenerate representations, respectively
- when the point group has an inversion center, the subscript g (German: gerade or even) signals no change in sign, and the subscript u (ungerade or uneven) a change in sign, with respect to inversion.
- with point groups C∞v and D∞h the symbols are borrowed from angular momentum description: Σ, Π, Δ.
The character table for the C2v symmetry point group is given below:
| C2v | E | C2 | σv(xz) | σv'(yz) | ||
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | −1 | −1 | Rz | xy |
| B1 | 1 | −1 | 1 | −1 | x, Ry | xz |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
Consider the example of water (H2O), which has the C2v symmetry described above. The 2px orbital of oxygen is oriented perpendicular to the plane of the molecule and switches sign with a C2 and a σv'(yz) operation, but remains unchanged with the other two operations (obviously, the character for the identity operation is always +1). This orbital's character set is thus {1, −1, 1, −1}, corresponding to the B1 irreducible representation. Likewise, the 2pz orbital is seen to have the symmetry of the A1 irreducible representation, 2py B2, and the 3dxy orbital A2. These assignments and others are noted in the rightmost two columns of the table.
Historical background
Hans Bethe used characters of point group operations in his study of ligand field theory in 1929, and Eugene Wigner used group theory to explain the selection rules of atomic spectroscopy.[7] The first character tables were compiled by László Tisza (1933), in connection to vibrational spectra. Robert Mulliken was the first to publish character tables in English (1933), and E. Bright Wilson used them in 1934 to predict the symmetry of vibrational normal modes.[8] The complete set of 32 crystallographic point groups was published in 1936 by Rosenthal and Murphy.[9]Nonrigid molecules
The symmetry groups described above are useful for describing rigid molecules which undergo only small oscillations about a single equilibrium geometry, so that the symmetry operations all correspond to simple geometrical operations. However Longuet-Higgins has proposed a more general type of symmetry groups suitable for non-rigid molecules with multiple equivalent geometries.[10][11]These groups are known as permutation-inversion groups, because a symmetry operation may be an energetically feasible permutation of equivalent nuclei, or an inversion with respect to the centre of mass, or a combination of the two.
For example, ethane (C2H6) has three equivalent staggered conformations. Conversion of one conformation to another occurs at ordinary temperature by internal rotation of one methyl group relative to the other. This is not a rotation of the entire molecule about the C3 axis, but can be described as a permutation of the three identical hydrogens of one methyl group. Although each conformation has D3d symmetry as in the table above, description of the internal rotation and associated quantum states and energy levels requires the more complete permutation-inversion group.
Similarly, ammonia (NH3) has two equivalent pyramidal (C3v) conformations which are interconverted by the process known as nitrogen inversion. This is not an inversion in the sense used for symmetry operations of rigid molecules, since NH3 has no inversion center. Rather it is a reflection of all atoms about the centre of mass (close to the nitrogen), which happens to be energetically feasible for this molecule. Again the permutation-inversion group is used to describe the interaction of the two geometries.
A second and similar approach to the symmetry of nonrigid molecules is due to Altmann.[12][13] In this approach the symmetry groups are known as Schrödinger supergroups and consist of two types of operations (and their combinations): (1) the geometric symmetry operations (rotations, reflections, inversions) of rigid molecules, and (2) isodynamic operations which take a nonrigid molecule into an energetically equivalent form by a physically reasonable process such as rotation about a single bond (as in ethane) or a molecular inversion (as in ammonia).[13]
 results in a molecule indistinguishable from the original. This is also called an n-fold rotational axis and abbreviated Cn. Examples are the C2 in
results in a molecule indistinguishable from the original. This is also called an n-fold rotational axis and abbreviated Cn. Examples are the C2 in