Plasma (physics)

From Wikipedia, the free encyclopedia

  (Redirected from Plasma physics)

Plasma

Top row: both lightning and electric sparks are everyday examples of phenomena made from plasma. Neon lights could more accurately be called "plasma lights", because the light comes from the plasma inside of them. Bottom row: A plasma globe, illustrating some of the more complex phenomena of a plasma, including filamentation. The colors are a result of relaxation of electrons in excited states to lower energy states after they have recombined with ions. These processes emit light in a spectrum characteristic of the gas being excited. The second image is of a plasma trail from Space Shuttle Atlantis during re-entry into Earth's atmosphere, as seen from the International Space Station.

Plasma (from Greek πλάσμα, "anything formed"^[1]) is one of the four fundamental states of matter, the others being solid, liquid, and gas. A plasma has properties unlike those of the other states.
A plasma can be created by heating a gas or subjecting it to a strong electromagnetic field applied with a laser or microwave generator. This decreases or increases the number of electrons, creating positive or negative charged particles called ions,^[2] and is accompanied by the dissociation of molecular bonds, if present.^[3]

The presence of a non-negligible number of charge carriers makes plasma electrically conductive so that it responds strongly to electromagnetic fields. Like gas, plasma does not have a definite shape or a definite volume unless enclosed in a container. Unlike gas, under the influence of a magnetic field, it may form structures such as filaments, beams and double layers.

Plasma is the most abundant form of ordinary matter in the Universe, most of which is in the rarefied intergalactic regions, particularly the intracluster medium, and in stars, including the Sun.^[4][5] A common form of plasmas on Earth is seen in neon signs.

Much of the understanding of plasmas has come from the pursuit of controlled nuclear fusion and fusion power, for which plasma physics provides the scientific basis.

Properties and parameters

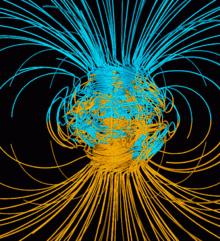
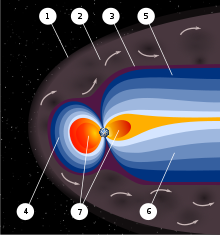
Artist's rendition of the Earth's plasma fountain, showing oxygen, helium, and hydrogen ions that gush into space from regions near the Earth's poles. The faint yellow area shown above the north pole represents gas lost from Earth into space; the green area is the aurora borealis, where plasma energy pours back into the atmosphere.^[6]

Definition

Plasma is loosely described as an electrically neutral medium of unbound positive and negative particles (i.e. the overall charge of a plasma is roughly zero). It is important to note that although they are unbound, these particles are not ‘free’ in the sense of not experiencing forces. When the charges move, they generate electrical currents with magnetic fields, and as a result, they are affected by each other’s fields. This governs their collective behavior with many degrees of freedom.^[3][7] A definition can have three criteria:^{[clarification needed][8][9]}

1. The plasma approximation: Charged particles must be close enough together that each particle influences many nearby charged particles, rather than just interacting with the closest particle (these collective effects are a distinguishing feature of a plasma). The plasma approximation is valid when the number of charge carriers within the sphere of influence (called the Debye sphere whose radius is the Debye screening length) of a particular particle is higher than unity to provide collective behavior of the charged particles. The average number of particles in the Debye sphere is given by the plasma parameter,^[ambiguous] "Λ" (the Greek letter Lambda).
2. Bulk interactions: The Debye screening length (defined above) is short compared to the physical size of the plasma. This criterion means that interactions in the bulk of the plasma are more important than those at its edges, where boundary effects may take place. When this criterion is satisfied, the plasma is quasineutral.
3. Plasma frequency: The electron plasma frequency (measuring plasma oscillations of the electrons) is large compared to the electron-neutral collision frequency (measuring frequency of collisions between electrons and neutral particles). When this condition is valid, electrostatic interactions dominate over the processes of ordinary gas kinetics.

Ranges of parameters

Plasma parameters^[ambiguous] can take on values varying by many orders of magnitude, but the properties of plasmas with apparently disparate parameters may be very similar (see plasma scaling). The following chart considers only conventional atomic plasmas and not exotic phenomena like quark gluon plasmas:

Range of plasmas. Density increases upwards, temperature increases towards the right. The free electrons in a metal may be considered an electron plasma.^[10]

Typical ranges of plasma parameters: orders of magnitude (OOM)

Characteristic	Terrestrial plasmas	Cosmic plasmas
Size in meters	10−6 m (lab plasmas) to 102 m (lightning) (~8 OOM)	10−6 m (spacecraft sheath) to 1025 m (intergalactic nebula) (~31 OOM)
Lifetime in seconds	10−12 s (laser-produced plasma) to 107 s (fluorescent lights) (~19 OOM)	101 s (solar flares) to 1017 s (intergalactic plasma) (~16 OOM)
Density in particles per cubic meter	107 m−3 to 1032 m−3 (inertial confinement plasma)	1 m−3 (intergalactic medium) to 1030 m−3 (stellar core)
Temperature in Kelvin	~0 K (crystalline non-neutral plasma[11]) to 108 K (magnetic fusion plasma)	102 K (aurora) to 107 K (solar core)
Magnetic fields in teslas	10−4 T (lab plasma) to 103 T (pulsed-power plasma)	10−12 T (intergalactic medium) to 1011 T (near neutron stars)

Degree of ionization

For plasma to exist, ionization is necessary. The term "plasma density" by itself usually refers to the "electron density", that is, the number of free electrons per unit volume. The degree of ionization of a plasma is the proportion of atoms that have lost or gained electrons, and is controlled mostly by the temperature. Even a partially ionized gas in which as little as 1% of the particles are ionized can have the characteristics of a plasma (i.e., response to magnetic fields and high electrical conductivity). The degree of ionization, $\alpha$, is defined as $\alpha ={\frac {n_{i}}{n_{i}+n_{n}}}$, where $n_{i}$ is the number density of ions and $n_{n}$ is the number density of neutral atoms. The electron density is related to this by the average charge state $\langle Z\rangle$ of the ions through $n_{e}=\langle Z\rangle n_{i}$, where $n_{e}$ is the number density of electrons.

Temperatures

Plasma temperature is commonly measured in Kelvins or electronvolts and is, informally, a measure of the thermal kinetic energy per particle. Very high temperatures are usually needed to sustain ionization, which is a defining feature of a plasma. The degree of plasma ionization is determined by the electron temperature relative to the ionization energy (and more weakly by the density), in a relationship called the Saha equation. At low temperatures, ions and electrons tend to recombine into bound states—atoms^[12]—and the plasma will eventually become a gas.
In most cases the electrons are close enough to thermal equilibrium that their temperature is relatively well-defined, even when there is a significant deviation from a Maxwellian energy distribution function, for example, due to UV radiation, energetic particles, or strong electric fields. Because of the large difference in mass, the electrons come to thermodynamic equilibrium amongst themselves much faster than they come into equilibrium with the ions or neutral atoms. For this reason, the ion temperature may be very different from (usually lower than) the electron temperature. This is especially common in weakly ionized technological plasmas, where the ions are often near the ambient temperature.

Thermal vs. non-thermal plasmas

Based on the relative temperatures of the electrons, ions and neutrals, plasmas are classified as "thermal" or "non-thermal". Thermal plasmas have electrons and the heavy particles at the same temperature, i.e., they are in thermal equilibrium with each other. Non-thermal plasmas on the other hand have the ions and neutrals at a much lower temperature (sometimes room temperature), whereas electrons are much "hotter" ($T_{e}\gg T_{n}$).

A plasma is sometimes referred to as being "hot" if it is nearly fully ionized, or "cold" if only a small fraction (for example 1%) of the gas molecules are ionized, but other definitions of the terms "hot plasma" and "cold plasma" are common. Even in a "cold" plasma, the electron temperature is still typically several thousand degrees Celsius. Plasmas utilized in "plasma technology" ("technological plasmas") are usually cold plasmas in the sense that only a small fraction of the gas molecules are ionized.

Plasma potential

Lightning is an example of plasma present at Earth's surface. Typically, lightning discharges 30,000 amperes at up to 100 million volts, and emits light, radio waves, X-rays and even gamma rays.^[13] Plasma temperatures in lightning can approach 28,000 K (28,000 °C; 50,000 °F) and electron densities may exceed 10²⁴ m⁻³.

Since plasmas are very good electrical conductors, electric potentials play an important role. The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the "plasma potential", or the "space potential". If an electrode is inserted into a plasma, its potential will generally lie considerably below the plasma potential due to what is termed a Debye sheath. The good electrical conductivity of plasmas makes their electric fields very small. This results in the important concept of "quasineutrality", which says the density of negative charges is approximately equal to the density of positive charges over large volumes of the plasma ($n_{e}=\langle Z\rangle n_{i}$), but on the scale of the Debye length there can be charge imbalance. In the special case that double layers are formed, the charge separation can extend some tens of Debye lengths.

The magnitude of the potentials and electric fields must be determined by means other than simply finding the net charge density. A common example is to assume that the electrons satisfy the Boltzmann relation:

$n_{e}\propto e^{{e\Phi /k_{B}T_{e}}}.$

Differentiating this relation provides a means to calculate the electric field from the density:

${\vec {E}}=(k_{B}T_{e}/e)(\nabla n_{e}/n_{e}).$

It is possible to produce a plasma that is not quasineutral. An electron beam, for example, has only negative charges. The density of a non-neutral plasma must generally be very low, or it must be very small, otherwise it will be dissipated by the repulsive electrostatic force.

In astrophysical plasmas, Debye screening prevents electric fields from directly affecting the plasma over large distances, i.e., greater than the Debye length. However, the existence of charged particles causes the plasma to generate, and be affected by, magnetic fields. This can and does cause extremely complex behavior, such as the generation of plasma double layers, an object that separates charge over a few tens of Debye lengths. The dynamics of plasmas interacting with external and self-generated magnetic fields are studied in the academic discipline of magnetohydrodynamics.

Magnetization

Plasma with a magnetic field strong enough to influence the motion of the charged particles is said to be magnetized. A common quantitative criterion is that a particle on average completes at least one gyration around the magnetic field before making a collision, i.e., $\omega _{{{\mathrm {ce}}}}/v_{{{\mathrm {coll}}}}>1$, where $\omega _{{{\mathrm {ce}}}}$ is the "electron gyrofrequency" and $v_{{{\mathrm {coll}}}}$ is the "electron collision rate". It is often the case that the electrons are magnetized while the ions are not. Magnetized plasmas are anisotropic, meaning that their properties in the direction parallel to the magnetic field are different from those perpendicular to it. While electric fields in plasmas are usually small due to the high conductivity, the electric field associated with a plasma moving in a magnetic field is given by ${\mathbf {E}}=-v\times {\mathbf {B}}$ (where ${\mathbf {E}}$ is the electric field, ${\mathbf {v}}$ is the velocity, and ${\mathbf {B}}$ is the magnetic field), and is not affected by Debye shielding.^[14]

Comparison of plasma and gas phases

Plasma is often called the fourth state of matter after solid, liquids and gases.^[15][16] It is distinct from these and other lower-energy states of matter. Although it is closely related to the gas phase in that it also has no definite form or volume, it differs in a number of ways, including the following:

Property	Gas	Plasma
Electrical conductivity	Very low: Air is an excellent insulator until it breaks down into plasma at electric field strengths above 30 kilovolts per centimeter.[17]	Usually very high: For many purposes, the conductivity of a plasma may be treated as infinite.
Independently acting species	One: All gas particles behave in a similar way, influenced by gravity and by collisions with one another.	Two or three: Electrons, ions, protons and neutrons can be distinguished by the sign and value of their charge so that they behave independently in many circumstances, with different bulk velocities and temperatures, allowing phenomena such as new types of waves and instabilities.
Velocity distribution	Maxwellian: Collisions usually lead to a Maxwellian velocity distribution of all gas particles, with very few relatively fast particles.	Often non-Maxwellian: Collisional interactions are often weak in hot plasmas and external forcing can drive the plasma far from local equilibrium and lead to a significant population of unusually fast particles.
Interactions	Binary: Two-particle collisions are the rule, three-body collisions extremely rare.	Collective: Waves, or organized motion of plasma, are very important because the particles can interact at long ranges through the electric and magnetic forces.

Common plasmas

Plasmas are by far the most common phase of ordinary matter in the universe, both by mass and by volume.^[18] Essentially, all of the visible light from space comes from stars, which are plasmas with a temperature such that they radiate strongly at visible wavelengths. Most of the ordinary (or baryonic) matter in the universe, however, is found in the intergalactic medium, which is also a plasma, but much hotter, so that it radiates primarily as X-rays.
In 1937, Hannes Alfvén argued that if plasma pervaded the universe, it could then carry electric currents capable of generating a galactic magnetic field.^[19] After winning the Nobel Prize, he emphasized that:

In order to understand the phenomena in a certain plasma region, it is necessary to map not only the magnetic but also the electric field and the electric currents. Space is filled with a network of currents which transfer energy and momentum over large or very large distances. The currents often pinch to filamentary or surface currents. The latter are likely to give space, as also interstellar and intergalactic space, a cellular structure.^[20]

By contrast the current scientific consensus is that about 96% of the total energy density in the universe is not plasma or any other form of ordinary matter, but a combination of cold dark matter and dark energy. Our Sun, and all stars, are made of plasma, much of interstellar space is filled with a plasma, albeit a very sparse one, and intergalactic space too. Even black holes, which are not directly visible, are thought to be fuelled by accreting ionising matter (i.e. plasma),^[21] and they are associated with astrophysical jets of luminous ejected plasma,^[22] such as M87's jet that extends 5,000 light-years.^[23]

In our solar system, interplanetary space is filled with the plasma of the Solar Wind that extends from the Sun out to the heliopause. However, the density of ordinary matter is much higher than average and much higher than that of either dark matter or dark energy. The planet Jupiter accounts for most of the non-plasma, only about 0.1% of the mass and 10⁻¹⁵% of the volume within the orbit of Pluto.

Dust and small grains within a plasma will also pick up a net negative charge, so that they in turn may act like a very heavy negative ion component of the plasma (see dusty plasmas).

Common forms of plasma

Artificially produced	Terrestrial plasmas	Space and astrophysical plasmas
Those found in plasma displays, including TV screens. Inside fluorescent lamps (low energy lighting), neon signs[24] Rocket exhaust and ion thrusters The area in front of a spacecraft's heat shield during re-entry into the atmosphere Inside a corona discharge ozone generator Fusion energy research The electric arc in an arc lamp, an arc welder or plasma torch Plasma ball (sometimes called a plasma sphere or plasma globe) Arcs produced by Tesla coils (resonant air core transformer or disruptor coil that produces arcs similar to lightning, but with alternating current rather than static electricity) Plasmas used in semiconductor device fabrication including reactive-ion etching, sputtering, surface cleaning and plasma-enhanced chemical vapor deposition Laser-produced plasmas (LPP), found when high power lasers interact with materials. Inductively coupled plasmas (ICP), formed typically in argon gas for optical emission spectroscopy or mass spectrometry Magnetically induced plasmas (MIP), typically produced using microwaves as a resonant coupling method Static electric sparks	Lightning St. Elmo's fire Upper-atmospheric lightning (e.g. Blue jets, Blue starters, Gigantic jets, ELVES) Sprites The ionosphere The plasmasphere The polar aurorae Some flames[25][26] The polar wind, a plasma fountain	The Sun and other stars (plasmas heated by nuclear fusion) The solar wind The interplanetary medium (space between planets) The interstellar medium (space between star systems) The Intergalactic medium (space between galaxies) The Io-Jupiter flux tube Accretion discs Interstellar nebulae Cometary ion tail

Complex plasma phenomena

Although the underlying equations governing plasmas are relatively simple, plasma behavior is extraordinarily varied and subtle: the emergence of unexpected behavior from a simple model is a typical feature of a complex system. Such systems lie in some sense on the boundary between ordered and disordered behavior and cannot typically be described either by simple, smooth, mathematical functions, or by pure randomness. The spontaneous formation of interesting spatial features on a wide range of length scales is one manifestation of plasma complexity. The features are interesting, for example, because they are very sharp, spatially intermittent (the distance between features is much larger than the features themselves), or have a fractal form. Many of these features were first studied in the laboratory, and have subsequently been recognized throughout the universe. Examples of complexity and complex structures in plasmas include:

Filamentation

Striations or string-like structures,^[27] also known as birkeland currents, are seen in many plasmas, like the plasma ball, the aurora,^[28] lightning,^[29] electric arcs, solar flares,^[30] and supernova remnants.^[31] They are sometimes associated with larger current densities, and the interaction with the magnetic field can form a magnetic rope structure.^[32] High power microwave breakdown at atmospheric pressure also leads to the formation of filamentary structures.^[33] (See also Plasma pinch)

Filamentation also refers to the self-focusing of a high power laser pulse. At high powers, the nonlinear part of the index of refraction becomes important and causes a higher index of refraction in the center of the laser beam, where the laser is brighter than at the edges, causing a feedback that focuses the laser even more. The tighter focused laser has a higher peak brightness (irradiance) that forms a plasma. The plasma has an index of refraction lower than one, and causes a defocusing of the laser beam. The interplay of the focusing index of refraction, and the defocusing plasma makes the formation of a long filament of plasma that can be micrometers to kilometers in length.^[34] One interesting aspect of the filamentation generated plasma is the relatively low ion density due to defocusing effects of the ionized electrons.^[35] (See also Filament propagation)

Shocks or double layers

Plasma properties change rapidly (within a few Debye lengths) across a two-dimensional sheet in the presence of a (moving) shock or (stationary) double layer. Double layers involve localized charge separation, which causes a large potential difference across the layer, but does not generate an electric field outside the layer. Double layers separate adjacent plasma regions with different physical characteristics, and are often found in current carrying plasmas. They accelerate both ions and electrons.

Electric fields and circuits

Quasineutrality of a plasma requires that plasma currents close on themselves in electric circuits. Such circuits follow Kirchhoff's circuit laws and possess a resistance and inductance. These circuits must generally be treated as a strongly coupled system, with the behavior in each plasma region dependent on the entire circuit. It is this strong coupling between system elements, together with nonlinearity, which may lead to complex behavior. Electrical circuits in plasmas store inductive (magnetic) energy, and should the circuit be disrupted, for example, by a plasma instability, the inductive energy will be released as plasma heating and acceleration. This is a common explanation for the heating that takes place in the solar corona. Electric currents, and in particular, magnetic-field-aligned electric currents (which are sometimes generically referred to as "Birkeland currents"), are also observed in the Earth's aurora, and in plasma filaments.

Cellular structure

Narrow sheets with sharp gradients may separate regions with different properties such as magnetization, density and temperature, resulting in cell-like regions. Examples include the magnetosphere, heliosphere, and heliospheric current sheet. Hannes Alfvén wrote: "From the cosmological point of view, the most important new space research discovery is probably the cellular structure of space. As has been seen in every region of space accessible to in situ measurements, there are a number of 'cell walls', sheets of electric currents, which divide space into compartments with different magnetization, temperature, density, etc."^[36]

Critical ionization velocity

The critical ionization velocity is the relative velocity between an ionized plasma and a neutral gas, above which a runaway ionization process takes place. The critical ionization process is a quite general mechanism for the conversion of the kinetic energy of a rapidly streaming gas into ionization and plasma thermal energy. Critical phenomena in general are typical of complex systems, and may lead to sharp spatial or temporal features.

Ultracold plasma

Ultracold plasmas are created in a magneto-optical trap (MOT) by trapping and cooling neutral atoms, to temperatures of 1 mK or lower, and then using another laser to ionize the atoms by giving each of the outermost electrons just enough energy to escape the electrical attraction of its parent ion.
One advantage of ultracold plasmas are their well characterized and tunable initial conditions, including their size and electron temperature. By adjusting the wavelength of the ionizing laser, the kinetic energy of the liberated electrons can be tuned as low as 0.1 K, a limit set by the frequency bandwidth of the laser pulse. The ions inherit the millikelvin temperatures of the neutral atoms, but are quickly heated through a process known as disorder induced heating (DIH). This type of non-equilibrium ultracold plasma evolves rapidly, and displays many other interesting phenomena.^[37]

One of the metastable states of a strongly nonideal plasma is Rydberg matter, which forms upon condensation of excited atoms.

Non-neutral plasma

The strength and range of the electric force and the good conductivity of plasmas usually ensure that the densities of positive and negative charges in any sizeable region are equal ("quasineutrality"). A plasma with a significant excess of charge density, or, in the extreme case, is composed of a single species, is called a non-neutral plasma. In such a plasma, electric fields play a dominant role. Examples are charged particle beams, an electron cloud in a Penning trap and positron plasmas.^[38]

Dusty plasma/grain plasma

A dusty plasma contains tiny charged particles of dust (typically found in space). The dust particles acquire high charges and interact with each other. A plasma that contains larger particles is called grain plasma. Under laboratory conditions, dusty plasmas are also called complex plasmas.^[39]

Impermeable plasma

Impermeable plasma is a type of thermal plasma which acts like an impermeable solid with respect to gas or cold plasma and can be physically pushed. Interaction of cold gas and thermal plasma was briefly studied by a group led by Hannes Alfvén in 1960s and 1970s for its possible applications in insulation of fusion plasma from the reactor walls.^[40] However later it was found that the external magnetic fields in this configuration could induce kink instabilities in the plasma and subsequently lead to an unexpectedly high heat loss to the walls.^[41] In 2013, a group of materials scientists reported that they have successfully generated stable impermeable plasma with no magnetic confinement using only an ultrahigh-pressure blanket of cold gas. While spectroscopic data on the characteristics of plasma were claimed to be difficult to obtain due to the high-pressure, the passive effect of plasma on synthesis of different nanostructures clearly suggested the effective confinement.
They also showed that upon maintaining the impermeability for a few tens of seconds, screening of ions at the plasma-gas interface could give rise to a strong secondary mode of heating (known as viscous heating) leading to different kinetics of reactions and formation of complex nanomaterials.^[42]

Mathematical descriptions

The complex self-constricting magnetic field lines and current paths in a field-aligned Birkeland current that can develop in a plasma.^[43]

Main article: Plasma modeling

To completely describe the state of a plasma, we would need to write down all the particle locations and velocities and describe the electromagnetic field in the plasma region. However, it is generally not practical or necessary to keep track of all the particles in a plasma. Therefore, plasma physicists commonly use less detailed descriptions, of which there are two main types:

Fluid model

Fluid models describe plasmas in terms of smoothed quantities, like density and averaged velocity around each position (see Plasma parameters). One simple fluid model, magnetohydrodynamics, treats the plasma as a single fluid governed by a combination of Maxwell's equations and the Navier–Stokes equations. A more general description is the two-fluid plasma picture, where the ions and electrons are described separately. Fluid models are often accurate when collisionality is sufficiently high to keep the plasma velocity distribution close to a Maxwell–Boltzmann distribution. Because fluid models usually describe the plasma in terms of a single flow at a certain temperature at each spatial location, they can neither capture velocity space structures like beams or double layers, nor resolve wave-particle effects.

Kinetic model

Kinetic models describe the particle velocity distribution function at each point in the plasma and therefore do not need to assume a Maxwell–Boltzmann distribution. A kinetic description is often necessary for collisionless plasmas. There are two common approaches to kinetic description of a plasma. One is based on representing the smoothed distribution function on a grid in velocity and position. The other, known as the particle-in-cell (PIC) technique, includes kinetic information by following the trajectories of a large number of individual particles. Kinetic models are generally more computationally intensive than fluid models. The Vlasov equation may be used to describe the dynamics of a system of charged particles interacting with an electromagnetic field. In magnetized plasmas, a gyrokinetic approach can substantially reduce the computational expense of a fully kinetic simulation.

Artificial plasmas

Most artificial plasmas are generated by the application of electric and/or magnetic fields. Plasma generated in a laboratory setting and for industrial use can be generally categorized by:

• The type of power source used to generate the plasma—DC, RF and microwave
• The pressure they operate at—vacuum pressure (< 10 mTorr or 1 Pa), moderate pressure (~ 1 Torr or 100 Pa), atmospheric pressure (760 Torr or 100 kPa)
• The degree of ionization within the plasma—fully, partially, or weakly ionized
• The temperature relationships within the plasma—thermal plasma ($T_{e}=T_{i}=T_{{gas}}$), non-thermal or "cold" plasma ($T_{e}\gg T_{i}=T_{{gas}}$)
• The electrode configuration used to generate the plasma
• The magnetization of the particles within the plasma—magnetized (both ion and electrons are trapped in Larmor orbits by the magnetic field), partially magnetized (the electrons but not the ions are trapped by the magnetic field), non-magnetized (the magnetic field is too weak to trap the particles in orbits but may generate Lorentz forces)
• The application.

Generation of artificial plasma

Artificial plasma produced in air by a Jacob's Ladder

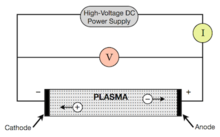
Just like the many uses of plasma, there are several means for its generation, however, one principle is common to all of them: there must be energy input to produce and sustain it.^[44] For this case, plasma is generated when an electrical current is applied across a dielectric gas or fluid (an electrically non-conducting material) as can be seen in the image to the right, which shows a discharge tube as a simple example (DC used for simplicity).

The potential difference and subsequent electric field pull the bound electrons (negative) toward the anode (positive electrode) while the cathode (negative electrode) pulls the nucleus.^[45] As the voltage increases, the current stresses the material (by electric polarization) beyond its dielectric limit (termed strength) into a stage of electrical breakdown, marked by an electric spark, where the material transforms from being an insulator into a conductor (as it becomes increasingly ionized). The underlying process is the Townsend avalanche, where collisions between electrons and neutral gas atoms create more ions and electrons (as can be seen in the figure on the right). The first impact of an electron on an atom results in one ion and two electrons. Therefore, the number of charged particles increases rapidly (in the millions) only “after about 20 successive sets of collisions”,^[46] mainly due to a small mean free path (average distance travelled between collisions).

Electric arc

Cascade process of ionization. Electrons are ‘e−’, neutral atoms ‘o’, and cations ‘+’.

Avalanche effect between two electrodes. The original ionisation event liberates one electron, and each subsequent collision liberates a further electron, so two electrons emerge from each collision: the ionising electron and the liberated electron.

With ample current density and ionization, this forms a luminous electric arc (a continuous electric discharge similar to lightning) between the electrodes.^{[Note 1]} Electrical resistance along the continuous electric arc creates heat, which dissociates more gas molecules and ionizes the resulting atoms (where degree of ionization is determined by temperature), and as per the sequence: solid-liquid-gas-plasma, the gas is gradually turned into a thermal plasma.^{[Note 2]} A thermal plasma is in thermal equilibrium, which is to say that the temperature is relatively homogeneous throughout the heavy particles (i.e. atoms, molecules and ions) and electrons. This is so because when thermal plasmas are generated, electrical energy is given to electrons, which, due to their great mobility and large numbers, are able to disperse it rapidly and by elastic collision (without energy loss) to the heavy particles.^{[47][Note 3]}

Examples of industrial/commercial plasma

Because of their sizable temperature and density ranges, plasmas find applications in many fields of research, technology and industry. For example, in: industrial and extractive metallurgy,^[47] surface treatments such as plasma spraying (coating), etching in microelectronics,^[48] metal cutting^[49] and welding; as well as in everyday vehicle exhaust cleanup and fluorescent/luminescent lamps,^[44] while even playing a part in supersonic combustion engines for aerospace engineering.^[50]

Low-pressure discharges

• Glow discharge plasmas: non-thermal plasmas generated by the application of DC or low frequency RF (<100 kHz) electric field to the gap between two metal electrodes. Probably the most common plasma; this is the type of plasma generated within fluorescent light tubes.^[51]
• Capacitively coupled plasma (CCP): similar to glow discharge plasmas, but generated with high frequency RF electric fields, typically 13.56 MHz. These differ from glow discharges in that the sheaths are much less intense. These are widely used in the microfabrication and integrated circuit manufacturing industries for plasma etching and plasma enhanced chemical vapor deposition.^[52]
• Cascaded Arc Plasma Source: a device to produce low temperature (~1eV) high density plasmas (HDP).
• Inductively coupled plasma (ICP): similar to a CCP and with similar applications but the electrode consists of a coil wrapped around the chamber where plasma is formed.^[53]
• Wave heated plasma: similar to CCP and ICP in that it is typically RF (or microwave). Examples include helicon discharge and electron cyclotron resonance (ECR).^[54]

Atmospheric pressure

• Arc discharge: this is a high power thermal discharge of very high temperature (~10,000 K). It can be generated using various power supplies. It is commonly used in metallurgical processes. For example, it is used to smelt minerals containing Al₂O₃ to produce aluminium.
• Corona discharge: this is a non-thermal discharge generated by the application of high voltage to sharp electrode tips. It is commonly used in ozone generators and particle precipitators.
• Dielectric barrier discharge (DBD): this is a non-thermal discharge generated by the application of high voltages across small gaps wherein a non-conducting coating prevents the transition of the plasma discharge into an arc. It is often mislabeled 'Corona' discharge in industry and has similar application to corona discharges. It is also widely used in the web treatment of fabrics.^[55] The application of the discharge to synthetic fabrics and plastics functionalizes the surface and allows for paints, glues and similar materials to adhere.^[56]
• Capacitive discharge: this is a nonthermal plasma generated by the application of RF power (e.g., 13.56 MHz) to one powered electrode, with a grounded electrode held at a small separation distance on the order of 1 cm. Such discharges are commonly stabilized using a noble gas such as helium or argon.^[57]
• "Piezoelectric direct discharge plasma:" is a nonthermal plasma generated at the high-side of a piezoelectric transformer (PT). This generation variant is particularly suited for high efficient and compact devices where a separate high voltage power supply is not desired.

History

Plasma was first identified in a Crookes tube, and so described by Sir William Crookes in 1879 (he called it "radiant matter").^[58] The nature of the Crookes tube "cathode ray" matter was subsequently identified by British physicist Sir J.J. Thomson in 1897.^[59] The term "plasma" was coined by Irving Langmuir in 1928,^[60] perhaps because the glowing discharge molds itself to the shape of the Crooks tube (Gr. πλάσμα – a thing moulded or formed).^[61] Langmuir described his observations as:

Except near the electrodes, where there are sheaths containing very few electrons, the ionized gas contains ions and electrons in about equal numbers so that the resultant space charge is very small. We shall use the name plasma to describe this region containing balanced charges of ions and electrons.^[60]

Fields of active research

Hall effect thruster. The electric field in a plasma double layer is so effective at accelerating ions that electric fields are used in ion drives.

This is just a partial list of topics. See list of plasma (physics) articles. A more complete and organized list can be found on the web site Plasma science and technology.^[62]

Plasma theory Plasma equilibria and stability Plasma interactions with waves and beams Guiding center Adiabatic invariant Debye sheath Coulomb collision Plasmas in nature The Earth's ionosphere Northern and southern (polar) lights Space plasmas, e.g. Earth's plasmasphere (an inner portion of the magnetosphere dense with plasma) Astrophysical plasma Interplanetary medium Industrial plasmas Plasma chemistry Plasma processing Plasma spray Plasma display Plasma sources Dusty plasmas Plasma diagnostics Thomson scattering Langmuir probe Ball-pen probe Faraday cup Spectroscopy Interferometry Ionospheric heating Incoherent scatter radar

Plasma applications Dielectric barrier discharge Enhanced Oil Recovery Fusion power Magnetic fusion energy (MFE) — tokamak, stellarator, reversed field pinch, magnetic mirror, dense plasma focus Inertial fusion energy (IFE) (also Inertial confinement fusion — ICF) Plasma-based weaponry Ion implantation Ion thruster MAGPIE (short for Mega Ampere Generator for Plasma Implosion Experiments) Plasma ashing Food processing (nonthermal plasma, aka "cold plasma") Plasma arc waste disposal, convert waste into reusable material with plasma. Plasma acceleration Plasma medicine (e. g. Dentistry[63]) Plasma window Play media Solar plasma Plasma spraying

Earth's magnetic field

From Wikipedia, the free encyclopedia

Computer simulation of the Earth's field in a period of normal polarity between reversals.^[1] The lines represent magnetic field lines, blue when the field points towards the center and yellow when away. The rotation axis of the Earth is centered and vertical. The dense clusters of lines are within the Earth's core.^[2]

Earth's magnetic field, also known as the geomagnetic field, is the magnetic field that extends from the Earth's interior to where it meets the solar wind, a stream of charged particles emanating from the Sun. Its magnitude at the Earth's surface ranges from 25 to 65 microtesla (0.25 to 0.65 gauss). Roughly speaking it is the field of a magnetic dipole currently tilted at an angle of about 10 degrees with respect to Earth's rotational axis, as if there were a bar magnet placed at that angle at the center of the Earth. Unlike a bar magnet, however, Earth's magnetic field changes over time because it is generated by a geodynamo (in Earth's case, the motion of molten iron alloys in its outer core).

The North and South magnetic poles wander widely, but sufficiently slowly for ordinary compasses to remain useful for navigation. However, at irregular intervals averaging several hundred thousand years, the Earth's field reverses and the North and South Magnetic Poles relatively abruptly switch places. These reversals of the geomagnetic poles leave a record in rocks that are of value to paleomagnetists in calculating geomagnetic fields in the past. Such information in turn is helpful in studying the motions of continents and ocean floors in the process of plate tectonics.

The magnetosphere is the region above the ionosphere and extends several tens of thousands of kilometers into space, protecting the Earth from the charged particles of the solar wind and cosmic rays that would otherwise strip away the upper atmosphere, including the ozone layer that protects the Earth from harmful ultraviolet radiation.

Importance

Earth's magnetic field serves to deflect most of the solar wind, whose charged particles would otherwise strip away the ozone layer that protects the Earth from harmful ultraviolet radiation.^[3] One stripping mechanism is for gas to be caught in bubbles of magnetic field, which are ripped off by solar winds.^[4] Calculations of the loss of carbon dioxide from the atmosphere of Mars, resulting from scavenging of ions by the solar wind, indicate that the dissipation of the magnetic field of Mars caused a near-total loss of its atmosphere.^[5][6]

The study of past magnetic field of the Earth is known as paleomagnetism.^[7] The polarity of the Earth's magnetic field is recorded in igneous rocks, and reversals of the field are thus detectable as "stripes" centered on mid-ocean ridges where the sea floor is spreading, while the stability of the geomagnetic poles between reversals has allowed paleomagnetists to track the past motion of continents. Reversals also provide the basis for magnetostratigraphy, a way of dating rocks and sediments.^[8] The field also magnetizes the crust, and magnetic anomalies can be used to search for deposits of metal ores.^[9]

Humans have used compasses for direction finding since the 11th century A.D. and for navigation since the 12th century.^[10] Although the North Magnetic Pole does shift with time, this wandering is slow enough that a simple compass remains useful for navigation. Using magnetoception various other organisms, ranging from soil bacteria to pigeons, can detect the magnetic field and use it for navigation.

Variations in the magnetic field strength have been correlated to rainfall variation within the tropics.^[11]

Main characteristics

Description

Common coordinate systems used for representing the Earth's magnetic field.

At any location, the Earth's magnetic field can be represented by a three-dimensional vector (see figure). A typical procedure for measuring its direction is to use a compass to determine the direction of magnetic North. Its angle relative to true North is the declination (D) or variation. Facing magnetic North, the angle the field makes with the horizontal is the inclination (I) or dip. The intensity (F) of the field is proportional to the force it exerts on a magnet. Another common representation is in X (North), Y (East) and Z (Down) coordinates.^[12]

Intensity

The intensity of the field is often measured in gauss (G), but is generally reported in nanotesla (nT), with 1 G = 100,000 nT. A nanotesla is also referred to as a gamma (γ).^[13] The tesla is the SI unit of the Magnetic field, B. The field ranges between approximately 25,000 and 65,000 nT (0.25–0.65 G).
By comparison, a strong refrigerator magnet has a field of about 100 gauss (0.010 T).^[14]

A map of intensity contours is called an isodynamic chart. As the 2010 World Magnetic Model shows, the intensity tends to decrease from the poles to the equator. A minimum intensity occurs over South America while there are maxima over northern Canada, Siberia, and the coast of Antarctica south of Australia.^[15]

Inclination

The inclination is given by an angle that can assume values between -90° (up) to 90° (down). In the northern hemisphere, the field points downwards. It is straight down at the North Magnetic Pole and rotates upwards as the latitude decreases until it is horizontal (0°) at the magnetic equator. It continues to rotate upwards until it is straight up at the South Magnetic Pole. Inclination can be measured with a dip circle.

An isoclinic chart (map of inclination contours) for the Earth's magnetic field is shown below.

Declination

Declination is positive for an eastward deviation of the field relative to true north. It can be estimated by comparing the magnetic north/south heading on a compass with the direction of a celestial pole. Maps typically include information on the declination as an angle or a small diagram showing the relationship between magnetic north and true north. Information on declination for a region can be represented by a chart with isogonic lines (contour lines with each line representing a fixed declination).

Geographical variation

Components of the Earth's magnetic field at the surface from the World Magnetic Model for 2010.^[15]

• 

  Intensity
• 

  Inclination
• 

  Declination

Dipolar approximation

The variation between magnetic north (N_m) and "true" north (N_g).

Near the surface of the Earth, its magnetic field can be closely approximated by the field of a magnetic dipole positioned at the center of the Earth and tilted at an angle of about 10° with respect to the rotational axis of the Earth.^[13] The dipole is roughly equivalent to a powerful bar magnet, with its south pole pointing towards the geomagnetic North Pole.^[16] This may seem surprising, but the north pole of a magnet is so defined because, if allowed to rotate freely, it points roughly northward (in the geographic sense). Since the north pole of a magnet attracts the south poles of other magnets and repels the north poles, it must be attracted to the south pole of Earth's magnet. The dipolar field accounts for 80–90% of the field in most locations.^[12]

Magnetic poles

The movement of Earth's North Magnetic Pole across the Canadian arctic, 1831–2007.

The positions of the magnetic poles can be defined in at least two ways: locally or globally.^[17]

One way to define a pole is as a point where the magnetic field is vertical.^[18] This can be determined by measuring the inclination, as described above. The inclination of the Earth's field is 90° (upwards) at the North Magnetic Pole and -90°(downwards) at the South Magnetic Pole. The two poles wander independently of each other and are not directly opposite each other on the globe. They can migrate rapidly: movements of up to 40 kilometres (25 mi) per year have been observed for the North Magnetic Pole. Over the last 180 years, the North Magnetic Pole has been migrating northwestward, from Cape Adelaide in the Boothia Peninsula in 1831 to 600 kilometres (370 mi) from Resolute Bay in 2001.^[19] The magnetic equator is the line where the inclination is zero (the magnetic field is horizontal).

The global definition of the Earth's field is based on a mathematical model. If a line is drawn through the center of the Earth, parallel to the moment of the best-fitting magnetic dipole, the two positions where it intersects the Earth's surface are called the North and South geomagnetic poles. If the Earth's magnetic field were perfectly dipolar, the geomagnetic poles and magnetic dip poles would coincide and compasses would point towards them. However, the Earth's field has a significant non-dipolar contribution, so the poles do not coincide and compasses do not generally point at either.

Magnetosphere

An artist's rendering of the structure of a magnetosphere. 1) Bow shock. 2) Magnetosheath. 3) Magnetopause. 4) Magnetosphere. 5) Northern tail lobe. 6) Southern tail lobe. 7) Plasmasphere.

Earth's magnetic field, predominantly dipolar at its surface, is distorted further out by the solar wind.
This is a stream of charged particles leaving the Sun's corona and accelerating to a speed of 200 to 1000 kilometres per second. They carry with them a magnetic field, the interplanetary magnetic field (IMF).^[20]

The solar wind exerts a pressure, and if it could reach Earth's atmosphere it would erode it. However, it is kept away by the pressure of the Earth's magnetic field. The magnetopause, the area where the pressures balance, is the boundary of the magnetosphere. Despite its name, the magnetosphere is asymmetric, with the sunward side being about 10 Earth radii out but the other side stretching out in a magnetotail that extends beyond 200 Earth radii.^[21] Sunward of the magnetopause is the bow shock, the area where the solar wind slows abruptly.^[20]

Inside the magnetosphere is the plasmasphere, a donut-shaped region containing low-energy charged particles, or plasma. This region begins at a height of 60 km, extends up to 3 or 4 Earth radii, and includes the ionosphere. This region rotates with the Earth.^[21] There are also two concentric tire-shaped regions, called the Van Allen radiation belts, with high-energy ions (energies from 0.1 to 10 million electron volts (MeV)). The inner belt is 1–2 Earth radii out while the outer belt is at 4–7 Earth radii. The plasmasphere and Van Allen belts have partial overlap, with the extent of overlap varying greatly with solar activity.^[22]

As well as deflecting the solar wind, the Earth's magnetic field deflects cosmic rays, high-energy charged particles that are mostly from outside the Solar system. (Many cosmic rays are kept out of the Solar system by the Sun's magnetosphere, or heliosphere.^[23]) By contrast, astronauts on the Moon risk exposure to radiation. Anyone who had been on the Moon's surface during a particularly violent solar eruption in 2005 would have received a lethal dose.^[20]

Some of the charged particles do get into the magnetosphere. These spiral around field lines, bouncing back and forth between the poles several times per second. In addition, positive ions slowly drift westward and negative ions drift eastward, giving rise to a ring current. This current reduces the magnetic field at the Earth's surface.^[20] Particles that penetrate the ionosphere and collide with the atoms there give rise to the lights of the aurorae and also emit X-rays.^[21]

The varying conditions in the magnetosphere, known as space weather, are largely driven by solar activity. If the solar wind is weak, the magnetosphere expands; while if it is strong, it compresses the magnetosphere and more of it gets in. Periods of particularly intense activity, called geomagnetic storms, can occur when a coronal mass ejection erupts above the Sun and sends a shock wave through the Solar System. Such a wave can take just two days to reach the Earth. Geomagnetic storms can cause a lot of disruption; the "Halloween" storm of 2003 damaged more than a third of NASA's satellites. The largest documented storm occurred in 1859. It induced currents strong enough to short out telegraph lines, and aurorae were reported as far south as Hawaii.^[20][24]

Time dependence

Short-term variations

Background: a set of traces from magnetic observatories showing a magnetic storm in 2000.
Globe: map showing locations of observatories and contour lines giving horizontal magnetic intensity in μ T.

The geomagnetic field changes on time scales from milliseconds to millions of years. Shorter time scales mostly arise from currents in the ionosphere (ionospheric dynamo region) and magnetosphere, and some changes can be traced to geomagnetic storms or daily variations in currents. Changes over time scales of a year or more mostly reflect changes in the Earth's interior, particularly the iron-rich core.^[12]

Frequently, the Earth's magnetosphere is hit by solar flares causing geomagnetic storms, provoking displays of aurorae. The short-term instability of the magnetic field is measured with the K-index.^[25]

Data from THEMIS show that the magnetic field, which interacts with the solar wind, is reduced when the magnetic orientation is aligned between Sun and Earth - opposite to the previous hypothesis. During forthcoming solar storms, this could result in blackouts and disruptions in artificial satellites.^[26]

Secular variation

Estimated declination contours by year, 1590 to 1990 (click to see variation).

Changes in Earth's magnetic field on a time scale of a year or more are referred to as secular variation. Over hundreds of years, magnetic declination is observed to vary over tens of degrees.^[12]
A movie on the right shows how global declinations have changed over the last few centuries.^[27]
The direction and intensity of the dipole change over time. Over the last two centuries the dipole strength has been decreasing at a rate of about 6.3% per century.^[12] At this rate of decrease, the field would be negligible in about 1600 years.^[28] However, this strength is about average for the last 7 thousand years, and the current rate of change is not unusual.^[29]

A prominent feature in the non-dipolar part of the secular variation is a westward drift at a rate of about 0.2 degrees per year.^[28] This drift is not the same everywhere and has varied over time. The globally averaged drift has been westward since about 1400 AD but eastward between about 1000 AD and 1400 AD.^[30]

Changes that predate magnetic observatories are recorded in archaeological and geological materials. Such changes are referred to as paleomagnetic secular variation or paleosecular variation (PSV). The records typically include long periods of small change with occasional large changes reflecting geomagnetic excursions and reversals.^[31]

Magnetic field reversal

Geomagnetic polarity during the late Cenozoic Era. Dark areas denote periods where the polarity matches today's polarity, light areas denote periods where that polarity is reversed.

Although the Earth's field is generally well approximated by a magnetic dipole with its axis near the rotational axis, there are occasional dramatic events where the North and South geomagnetic poles trade places. Evidence for these geomagnetic reversals can be found worldwide in basalts, sediment cores taken from the ocean floors, and seafloor magnetic anomalies.^[32] Reversals occur at apparently random intervals ranging from less than 0.1 million years to as much as 50 million years. The most recent geomagnetic reversal, called the Brunhes–Matuyama reversal, occurred about 780,000 years ago.^[19][33] Another global reversal of the Earth's field, called the Laschamp event, occurred during the last ice age (41,000 years ago). However, because of its brief duration it is labelled an excursion.^[34][35]

The past magnetic field is recorded mostly by iron oxides, such as magnetite, that have some form of ferrimagnetism or other magnetic ordering that allows the Earth's field to magnetize them. This remanent magnetization, or remanence, can be acquired in more than one way. In lava flows, the direction of the field is "frozen" in small magnetic particles as they cool, giving rise to a thermoremanent magnetization. In sediments, the orientation of magnetic particles acquires a slight bias towards the magnetic field as they are deposited on an ocean floor or lake bottom. This is called detrital remanent magnetization.^[7]

Thermoremanent magnetization is the form of remanence that gives rise to the magnetic anomalies around ocean ridges. As the seafloor spreads, magma wells up from the mantle and cools to form new basaltic crust. During the cooling, the basalt records the direction of the Earth's field. This new basalt forms on both sides of the ridge and moves away from it. When the Earth's field reverses, new basalt records the reversed direction. The result is a series of stripes that are symmetric about the ridge. A ship towing a magnetometer on the surface of the ocean can detect these stripes and infer the age of the ocean floor below. This provides information on the rate at which seafloor has spread in the past.^[7]

Radiometric dating of lava flows has been used to establish a geomagnetic polarity time scale, part of which is shown in the image. This forms the basis of magnetostratigraphy, a geophysical correlation technique that can be used to date both sedimentary and volcanic sequences as well as the seafloor magnetic anomalies.^[7]

Studies of lava flows on Steens Mountain, Oregon, indicate that the magnetic field could have shifted at a rate of up to 6 degrees per day at some time in Earth's history, which significantly challenges the popular understanding of how the Earth's magnetic field works.^[36]

Temporary dipole tilt variations that take the dipole axis across the equator and then back to the original polarity are known as excursions.^[35]

Earliest appearance

A paleomagnetic study of Australian red dacite and pillow basalt has estimated the magnetic field to have been present since at least 3,450 million years ago.^[37][38][39]

Future

Variations in virtual axial dipole moment since the last reversal.

At present, the overall geomagnetic field is becoming weaker; the present strong deterioration corresponds to a 10–15% decline over the last 150 years and has accelerated in the past several years; geomagnetic intensity has declined almost continuously from a maximum 35% above the modern value achieved approximately 2,000 years ago. The rate of decrease and the current strength are within the normal range of variation, as shown by the record of past magnetic fields recorded in rocks (figure on right).

The nature of Earth's magnetic field is one of heteroscedastic fluctuation. An instantaneous measurement of it, or several measurements of it across the span of decades or centuries, are not sufficient to extrapolate an overall trend in the field strength. It has gone up and down in the past for no apparent reason. Also, noting the local intensity of the dipole field (or its fluctuation) is insufficient to characterize Earth's magnetic field as a whole, as it is not strictly a dipole field. The dipole component of Earth's field can diminish even while the total magnetic field remains the same or increases.

The Earth's magnetic north pole is drifting from northern Canada towards Siberia with a presently accelerating rate—10 kilometres (6.2 mi) per year at the beginning of the 20th century, up to 40 kilometres (25 mi) per year in 2003,^[19] and since then has only accelerated.^[40]

Physical origin

The Earth's magnetic field is believed to be generated by electric currents in the conductive material of its core, created by convection currents due to heat escaping from the core. However the process is complex, and computer models that reproduce some of its features have only been developed in the last few decades.

Earth's core and the geodynamo

A schematic illustrating the relationship between motion of conducting fluid, organized into rolls by the Coriolis force, and the magnetic field the motion generates.^[41]

The Earth and most of the planets in the Solar System, as well as the Sun and other stars, all generate magnetic fields through the motion of highly conductive fluids.^[42] The Earth's field originates in its core. This is a region of iron alloys extending to about 3400 km (the radius of the Earth is 6370 km). It is divided into a solid inner core, with a radius of 1220 km, and a liquid outer core.^[43] The motion of the liquid in the outer core is driven by heat flow from the inner core, which is about 6,000 K (5,730 °C; 10,340 °F), to the core-mantle boundary, which is about 3,800 K (3,530 °C; 6,380 °F).^[44] The pattern of flow is organized by the rotation of the Earth and the presence of the solid inner core.^[45]

The mechanism by which the Earth generates a magnetic field is known as a dynamo.^[42] A magnetic field is generated by a feedback loop: current loops generate magnetic fields (Ampère's circuital law); a changing magnetic field generates an electric field (Faraday's law); and the electric and magnetic fields exert a force on the charges that are flowing in currents (the Lorentz force).^[46] These effects can be combined in a partial differential equation for the magnetic field called the magnetic induction equation:

${\frac {\partial {\mathbf {B}}}{\partial t}}=\eta \nabla ^{2}{\mathbf {B}}+\nabla \times ({\mathbf {u}}\times {\mathbf {B}})$

...where u is the velocity of the fluid; B is the magnetic B-field; and η=1/σμ is the magnetic diffusivity, a product of the electrical conductivity σ and the permeability μ .^[47] The term ∂B/∂t is the time derivative of the field; ∇² is the Laplace operator and ∇× is the curl operator.

The first term on the right hand side of the induction equation is a diffusion term. In a stationary fluid, the magnetic field declines and any concentrations of field spread out. If the Earth's dynamo shut off, the dipole part would disappear in a few tens of thousands of years.^[47]

In a perfect conductor (σ=∞), there would be no diffusion. By Lenz's law, any change in the magnetic field would be immediately opposed by currents, so the flux through a given volume of fluid could not change. As the fluid moved, the magnetic field would go with it. The theorem describing this effect is called the frozen-in-field theorem. Even in a fluid with a finite conductivity, new field is generated by stretching field lines as the fluid moves in ways that deform it. This process could go on generating new field indefinitely, were it not that as the magnetic field increases in strength, it resists fluid motion.^[47]

The motion of the fluid is sustained by convection, motion driven by buoyancy. The temperature increases towards the center of the Earth, and the higher temperature of the fluid lower down makes it buoyant. This buoyancy is enhanced by chemical separation: As the core cools, some of the molten iron solidifies and is plated to the inner core. In the process, lighter elements are left behind in the fluid, making it lighter. This is called compositional convection. A Coriolis effect, caused by the overall planetary rotation, tends to organize the flow into rolls aligned along the north-south polar axis.^[45][47]

The average magnetic field in the Earth's outer core was calculated to be 25 gauss, 50 times stronger than the field at the surface.^[48]

Numerical models

Simulating the geodynamo requires numerically solving a set of nonlinear partial differential equations for the magnetohydrodynamics (MHD) of the Earth's interior. Simulation of the MHD equations is performed on a 3D grid of points and the fineness of the grid, which in part determines the realism of the solutions, is limited mainly by computer power. For decades, theorists were confined to creating kinematic dynamos in which the fluid motion is chosen in advance and the effect on the magnetic field calculated. Kinematic dynamo theory was mainly a matter of trying different flow geometries and testing whether such geometries could sustain a dynamo.^[49]

The first self-consistent dynamo models, ones that determine both the fluid motions and the magnetic field, were developed by two groups in 1995, one in Japan^[50] and one in the United States.^[1][51] The latter received attention because it successfully reproduced some of the characteristics of the Earth's field, including geomagnetic reversals.^[49]

Currents in the ionosphere and magnetosphere

Electric currents induced in the ionosphere generate magnetic fields (ionospheric dynamo region). Such a field is always generated near where the atmosphere is closest to the Sun, causing daily alterations that can deflect surface magnetic fields by as much as one degree. Typical daily variations of field strength are about 25 nanoteslas (nT) (one part in 2000), with variations over a few seconds of typically around 1 nT (one part in 50,000).^[52]

Measurement and analysis

Detection

The Earth's magnetic field strength was measured by Carl Friedrich Gauss in 1835 and has been repeatedly measured since then, showing a relative decay of about 10% over the last 150 years.^[53]
The Magsat satellite and later satellites have used 3-axis vector magnetometers to probe the 3-D structure of the Earth's magnetic field. The later Ørsted satellite allowed a comparison indicating a dynamic geodynamo in action that appears to be giving rise to an alternate pole under the Atlantic Ocean west of S. Africa.^[54]

Governments sometimes operate units that specialize in measurement of the Earth's magnetic field. These are geomagnetic observatories, typically part of a national Geological survey, for example the British Geological Survey's Eskdalemuir Observatory. Such observatories can measure and forecast magnetic conditions such as magnetic storms that sometimes affect communications, electric power, and other human activities.

The International Real-time Magnetic Observatory Network, with over 100 interlinked geomagnetic observatories around the world has been recording the earths magnetic field since 1991.

The military determines local geomagnetic field characteristics, in order to detect anomalies in the natural background that might be caused by a significant metallic object such as a submerged submarine. Typically, these magnetic anomaly detectors are flown in aircraft like the UK's Nimrod or towed as an instrument or an array of instruments from surface ships.

Commercially, geophysical prospecting companies also use magnetic detectors to identify naturally occurring anomalies from ore bodies, such as the Kursk Magnetic Anomaly.

Crustal magnetic anomalies

A model of short-wavelength features of Earth's magnetic field, attributed to lithospheric anomalies.^[55]

Magnetometers detect minute deviations in the Earth's magnetic field caused by iron artifacts, kilns, some types of stone structures, and even ditches and middens in archaeological geophysics. Using magnetic instruments adapted from airborne magnetic anomaly detectors developed during World War II to detect submarines, the magnetic variations across the ocean floor have been mapped. Basalt — the iron-rich, volcanic rock making up the ocean floor — contains a strongly magnetic mineral (magnetite) and can locally distort compass readings. The distortion was recognized by Icelandic mariners as early as the late 18th century. More important, because the presence of magnetite gives the basalt measurable magnetic properties, these magnetic variations have provided another means to study the deep ocean floor. When newly formed rock cools, such magnetic materials record the Earth's magnetic field.

Statistical models

Each measurement of the magnetic field is at a particular place and time. If an accurate estimate of the field at some other place and time is needed, the measurements must be converted to a model and the model used to make predictions.

Spherical harmonics

Schematic representation of spherical harmonics on a sphere and their nodal lines. P_{ℓ m} is equal to 0 along m great circles passing through the poles, and along ℓ-m circles of equal latitude. The function changes sign each ℓtime it crosses one of these lines.

Example of a quadrupole field. This could also be constructed by moving two dipoles together. If this arrangement were placed at the center of the Earth, then a magnetic survey at the surface would find two magnetic north poles (at the geographic poles) and two south poles at the equator.

The most common way of analyzing the global variations in the Earth's magnetic field is to fit the measurements to a set of spherical harmonics. This was first done by Carl Friedrich Gauss.^[56] Spherical harmonics are functions that oscillate over the surface of a sphere. They are the product of two functions, one that depends on latitude and one on longitude. The function of longitude is zero along zero or more great circles passing through the North and South Poles; the number of such nodal lines is the absolute value of the order m. The function of latitude is zero along zero or more latitude circles; this plus the order is equal to the degree ℓ. Each harmonic is equivalent to a particular arrangement of magnetic charges at the center of the Earth. A monopole is an isolated magnetic charge, which has never been observed. A dipole is equivalent to two opposing charges brought close together and a quadrupole to two dipoles brought together. A quadrupole field is shown in the lower figure on the right.^[12]

Spherical harmonics can represent any scalar field (function of position) that satisfies certain properties. A magnetic field is a vector field, but if it is expressed in Cartesian components X, Y, Z, each component is the derivative of the same scalar function called the magnetic potential. Analyses of the Earth's magnetic field use a modified version of the usual spherical harmonics that differ by a multiplicative factor. A least-squares fit to the magnetic field measurements gives the Earth's field as the sum of spherical harmonics, each multiplied by the best-fitting Gauss coefficient g_m^ℓ or h_m^ℓ.^[12]

The lowest-degree Gauss coefficient, g₀⁰, gives the contribution of an isolated magnetic charge, so it is zero. The next three coefficients – g₁⁰, g₁¹, and h₁¹ – determine the direction and magnitude of the dipole contribution. The best fitting dipole is tilted at an angle of about 10° with respect to the rotational axis, as described earlier.^[12]

Radial dependence

Spherical harmonic analysis can be used to distinguish internal from external sources if measurements are available at more than one height (for example, ground observatories and satellites). In that case, each term with coefficient g_m^ℓ or h_m^ℓ can be split into two terms: one that decreases with radius as 1/r^ℓ+1 and one that increases with radius as r^ℓ. The increasing terms fit the external sources (currents in the ionosphere and magnetosphere). However, averaged over a few years the external contributions average to zero.^[12]

The remaining terms predict that the potential of a dipole source (ℓ=1) drops off as 1/r². The magnetic field, being a derivative of the potential, drops off as 1/r³. Quadrupole terms drop off as 1/r⁴, and higher order terms drop off increasingly rapidly with the radius. The radius of the outer core is about half of the radius of the Earth. If the field at the core-mantle boundary is fit to spherical harmonics, the dipole part is smaller by a factor of about 8 at the surface, the quadrupole part by a factor of 16, and so on. Thus, only the components with large wavelengths can be noticeable at the surface. From a variety of arguments, it is usually assumed that only terms up to degree 14 or less have their origin in the core. These have wavelengths of about 2,000 kilometres (1,200 mi) or less. Smaller features are attributed to crustal anomalies.^[12]

Global models

The International Association of Geomagnetism and Aeronomy maintains a standard global field model called the International Geomagnetic Reference Field. It is updated every 5 years. The 11th-generation model, IGRF11, was developed using data from satellites (Ørsted, CHAMP and SAC-C) and a world network of geomagnetic observatories.^[57] The spherical harmonic expansion was truncated at degree 10, with 120 coefficients, until 2000. Subsequent models are truncated at degree 13 (195 coefficients).^[58]

Another global field model, called World Magnetic Model, is produced jointly by the National Geophysical Data Center and the British Geological Survey. This model truncates at degree 12 (168 coefficients). It is the model used by the United States Department of Defense, the Ministry of Defence (United Kingdom), the North Atlantic Treaty Organization, and the International Hydrographic Office as well as in many civilian navigation systems.^[59]

A third model, produced by the Goddard Space Flight Center (NASA and GSFC) and the Danish Space Research Institute, uses a "comprehensive modeling" approach that attempts to reconcile data with greatly varying temporal and spatial resolution from ground and satellite sources.^[60]

Biomagnetism

Animals including birds and turtles can detect the Earth's magnetic field, and use the field to navigate during migration.^[61] Cows and wild deer tend to align their bodies north-south while relaxing, but not when the animals are under high voltage power lines^[clarify], leading researchers to believe magnetism is responsible.^[62][63] In 2011 a group of Czech researchers reported their failed attempt to replicate the finding using different Google Earth images.^[64]