Network science

From Wikipedia, the free encyclopedia

Network science is an interdisciplinary academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks. The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena."^[1]

Background and history

The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this field is the famous Seven Bridges of Königsberg written by Leonhard Euler in 1736. Euler's mathematical description of vertices and edges was the foundation of graph theory, a branch of mathematics that studies the properties of pairwise relations in a network structure. The field of graph theory continued to develop and found applications in chemistry (Sylvester, 1878).

In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. He developed the sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like (Moreno, 1953). The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in The New York Times (April 3, 1933, page 17). The sociogram has found many applications and has grown into the field of social network analysis.

Probabilistic theory in network science developed as an off-shoot of graph theory with Paul Erdős and Alfréd Rényi's eight famous papers on random graphs. For social networks the exponential random graph model or p* is a notational framework used to represent the probability space of a tie occurring in a social network. An alternate approach to network probability structures is the network probability matrix, which models the probability of edges occurring in a network, based on the historic presence or absence of the edge in a sample of networks.

In 1998, David Krackhardt and Kathleen Carley introduced the idea of a meta-network with the PCANS Model. They suggest that "all organizations are structured along these three domains, Individuals, Tasks, and Resources". Their paper introduced the concept that networks occur across multiple domains and that they are interrelated. This field has grown into another sub-discipline of network science called dynamic network analysis.

More recently other network science efforts have focused on mathematically describing different network topologies. Duncan Watts reconciled empirical data on networks with mathematical representation, describing the small-world network. Albert-László Barabási and Reka Albert developed the scale-free network which is a loosely defined network topology that contains hub vertices with many connections, that grow in a way to maintain a constant ratio in the number of the connections versus all other nodes. Although many networks, such as the internet, appear to maintain this aspect, other networks have long tailed distributions of nodes that only approximate scale free ratios.

Department of Defense Initiatives

The U.S. military first became interested in network-centric warfare as an operational concept based on network science in 1996. John A. Parmentola, the U.S. Army Director for Research and Laboratory Management, proposed to the Army’s Board on Science and Technology (BAST) on December 1, 2003 that Network Science become a new Army research area. The BAST, the Division on Engineering and Physical Sciences for the National Research Council (NRC) of the National Academies, serves as a convening authority for the discussion of science and technology issues of importance to the Army and oversees independent Army-related studies conducted by the National Academies. The BAST conducted a study to find out whether identifying and funding a new field of investigation in basic research, Network Science, could help close the gap between what is needed to realize Network-Centric Operations and the current primitive state of fundamental knowledge of networks.

As a result, the BAST issued the NRC study in 2005 titled Network Science (referenced above) that defined a new field of basic research in Network Science for the Army. Based on the findings and recommendations of that study and the subsequent 2007 NRC report titled Strategy for an Army Center for Network Science, Technology, and Experimentation, Army basic research resources were redirected to initiate a new basic research program in Network Science. To build a new theoretical foundation for complex networks, some of the key Network Science research efforts now ongoing in Army laboratories address:

• Mathematical models of network behavior to predict performance with network size, complexity, and environment
• Optimized human performance required for network-enabled warfare
• Networking within ecosystems and at the molecular level in cells.

As initiated in 2004 by Frederick I. Moxley with support he solicited from David S. Alberts, the Department of Defense helped to establish the first Network Science Center in conjunction with the U.S. Army at the United States Military Academy (USMA). Under the tutelage of Dr. Moxley and the faculty of the USMA, the first interdisciplinary undergraduate courses in Network Science were taught to cadets at West Point. In order to better instill the tenets of network science among its cadre of future leaders, the USMA has also instituted a five-course undergraduate minor in Network Science.

In 2006, the U.S. Army and the United Kingdom (UK) formed the Network and Information Science International Technology Alliance, a collaborative partnership among the Army Research Laboratory, UK Ministry of Defense and a consortium of industries and universities in the U.S. and UK. The goal of the alliance is to perform basic research in support of Network- Centric Operations across the needs of both nations.

In 2009, the U.S. Army formed the Network Science CTA, a collaborative research alliance among the Army Research Laboratory, CERDEC, and a consortium of about 30 industrial R&D labs and universities in the U.S. The goal of the alliance is to develop a deep understanding of the underlying commonalities among intertwined social/cognitive, information, and communications networks, and as a result improve our ability to analyze, predict, design, and influence complex systems interweaving many kinds of networks.

Subsequently, as a result of these efforts, the U.S. Department of Defense has sponsored numerous research projects that support Network Science.

Network properties

Often, networks have certain attributes that can be calculated to analyze the properties & characteristics of the network. These network properties often define network models and can be used to analyze how certain models contrast to each other. Many of the definitions for other terms used in network science can be found in Glossary of graph theory.

Density

The density $D$ of a network is defined as a ratio of the number of edges $E$ to the number of possible edges, given by the binomial coefficient ${\tbinom N2}$, giving $D={\frac {2E}{N(N-1)}}.$ Another possible equation is $D={\frac {T}{N(N-1)}}.$, whereas the ties $T$ are unidirectional (Wasserman & Faust 1994).^[2] This gives a better overview over the network density, because unidirectional relationships can be measured.

Size

The size of a network can refer to the number of nodes $N$ or, less commonly, the number of edges $E$ which can range from $N-1$ (a tree) to E (a complete graph).

Average degree 

The degree k of a node is the number of edges connected to it. Closely related to the density of a network is the average degree, <k> =2E. In the ER random graph model, we can compute <k> =p(N−1) where p is the probability of two nodes being connected.

Average path length

Average path length is calculated by finding the shortest path between all pairs of nodes, adding them up, and then dividing by the total number of pairs. This shows us, on average, the number of steps it takes to get from one member of the network to another.

Diameter of a network

As another means of measuring network graphs, we can define the diameter of a network as the longest of all the calculated shortest paths in a network. In other words, once the shortest path length from every node to all other nodes is calculated, the diameter is the longest of all the calculated path lengths. The diameter is representative of the linear size of a network.

Clustering coefficient

The clustering coefficient is a measure of an "all-my-friends-know-each-other" property. This is sometimes described as the friends of my friends are my friends. More precisely, the clustering coefficient of a node is the ratio of existing links connecting a node's neighbors to each other to the maximum possible number of such links. The clustering coefficient for the entire network is the average of the clustering coefficients of all the nodes. A high clustering coefficient for a network is another indication of a small world.
The clustering coefficient of the $i$'th node is

$C_{i}={2e_{i} \over k_{i}{(k_{i}-1)}}\,,$

where $k_{i}$ is the number of neighbours of the $i$'th node, and $e_{i}$ is the number of connections between these neighbours. The maximum possible number of connections between neighbors is, of course,

${{\binom {k}{2}}}={{k(k-1)} \over 2}\,.$

Connectedness

The way in which a network is connected plays a large part into how networks are analyzed and interpreted. Networks are classified in four different categories:

• Clique/Complete Graph: a completely connected network, where all nodes are connected to every other node. These networks are symmetric in that all nodes have in-links and out-links from all others.
• Giant Component: A single connected component which contains most of the nodes in the network.
• Weakly Connected Component: A collection of nodes in which there exists a path from any node to any other, ignoring directionality of the edges.
• Strongly Connected Component: A collection of nodes in which there exists a directed path from any node to any other.

Node centrality

Centrality indices produce rankings which seek to identify the most important nodes in a network model. Different centrality indices encode different contexts for the word "importance." The betweenness centrality, for example, considers a node highly important if it form bridges between many other nodes. The eigenvalue centrality, in contrast, considers a node highly important if many other highly important nodes link to it. Hundreds of such measures have been proposed in the literature.

It is important to remember that centrality indices are only accurate for identifying the most central nodes. The measures are seldom, if ever, meaningful for the remainder of network nodes.^{[3] [4]} Also, their indications are only accurate within their assumed context for importance, and tend to "get it wrong" for other contexts.^[5] For example, imagine two separate communities whose only link is an edge between the most junior member of each community. Since any transfer from one community to the other must go over this link, the two junior members will have high betweenness centrality. But, since they are junior, (presumably) they have few connections to the "important" nodes in their community, meaning their eigenvalue centrality would be quite low.

The concept of centrality in the context of static networks was extended, based on empirical and theoretical research, to dynamic centrality^[6] in the context of time-dependent and temporal networks.^[7][8][9]

Network models

Network models serve as a foundation to understanding interactions within empirical complex networks. Various random graph generation models produce network structures that may be used in comparison to real-world complex networks.

Erdős–Rényi Random Graph model

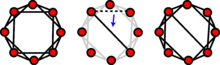
This Erdős–Rényi model is generated with N = 4 nodes. For each edge in the complete graph formed by all N nodes, a random number is generated and compared to a given probability. If the random number is greater than p, an edge is formed on the model.

The Erdős–Rényi model, named for Paul Erdős and Alfréd Rényi, is used for generating random graphs in which edges are set between nodes with equal probabilities. It can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.

To generate an Erdős–Rényi model two parameters must be specified: the number of nodes in the graph generated as N and the probability that a link should be formed between any two nodes as p. A constant 〈k〉 may derived from these two components with the formula 〈k〉 = 2 ⋅ E / N = p ⋅ (N − 1), where E is the expected number of edges.

The Erdős–Rényi model has several interesting characteristics in comparison to other graphs. Because the model is generated without bias to particular nodes, the degree distribution is binomial in nature with regards to the formula:

$P(\operatorname {deg}(v)=k)={n-1 \choose k}p^{k}(1-p)^{{n-1-k}}$.

Also as a result of this characteristic, the clustering coefficient tends to 0. The model tends to form a giant component in situations where 〈k〉 > 1 in a process called percolation. The average path length is relatively short in this model and tends to log N.^[how?]

Watts-Strogatz Small World model

The Watts and Strogatz model uses the concept of rewiring to achieve its structure. The model generator will iterate through each edge in the original lattice structure. An edge may changed its connected vertices according to a given rewiring probability. $<k>=4$ in this example.

The Watts and Strogatz model is a random graph generation model that produces graphs with small-world properties.

An initial lattice structure is used to generate a Watts-Strogatz model. Each node in the network is initially linked to its <$<k>$ closest neighbors. Another parameter is specified as the rewiring probability. Each edge has a probability $p$ that it will be rewired to the graph as a random edge. The expected number of rewired links in the model is $pE=pN<k>/2$.

As the Watts-Strogatz model begins as non-random lattice structure, it has a very high clustering coefficient along with high average path length. Each rewire is likely to create a shortcut between highly connected clusters. As the rewiring probability increases, the clustering coefficient decreases slower than the average path length. In effect, this allows the average path length of the network to decrease significantly with only slightly decreases in clustering coefficient. Higher values of p force more rewired edges, which in effect makes the Watts-Strogatz model a random network.

Barabási–Albert (BA) Preferential Attachment model

The Barabási–Albert model is a random network model used to demonstrate a preferential attachment or a "rich-get-richer" effect. In this model, an edge is most likely to attach to nodes with higher degrees. The network begins with an initial network of m₀ nodes. m₀ ≥ 2 and the degree of each node in the initial network should be at least 1, otherwise it will always remain disconnected from the rest of the network.

In the BA model, new nodes are added to the network one at a time. Each new node is connected to $m$ existing nodes with a probability that is proportional to the number of links that the existing nodes already have. Formally, the probability p_i that the new node is connected to node i is^[10]

$p_{i}={\frac {k_{i}}{\sum _{j}k_{j}}},$

where k_i is the degree of node i. Heavily linked nodes ("hubs") tend to quickly accumulate even more links, while nodes with only a few links are unlikely to be chosen as the destination for a new link. The new nodes have a "preference" to attach themselves to the already heavily linked nodes.

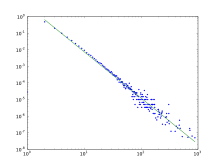
The degree distribution of the BA Model, which follows a power law. In loglog scale the power law function is a straight line.^[11]

The degree distribution resulting from the BA model is scale free, in particular, it is a power law of the form:

$P\left(k\right)\sim k^{{-3}}\,$

Hubs exhibit high betweenness centrality which allows short paths to exist between nodes. As a result the BA model tends to have very short average path lengths. The clustering coefficient of this model also tends to 0. While the diameter, D, of many models including the Erdős Rényi random graph model and several small world networks is proportional to log N, the BA model exhibits D~loglogN (ultr-small word).^[12] Note that the average path length scales with N as the diameter.

Network analysis

Social network analysis

Social network analysis examines the structure of relationships between social entities.^[13] These entities are often persons, but may also be groups, organizations, nation states, web sites, scholarly publications.

Since the 1970s, the empirical study of networks has played a central role in social science, and many of the mathematical and statistical tools used for studying networks have been first developed in sociology.^[14] Amongst many other applications, social network analysis has been used to understand the diffusion of innovations, news and rumors. Similarly, it has been used to examine the spread of both diseases and health-related behaviors. It has also been applied to the study of markets, where it has been used to examine the role of trust in exchange relationships and of social mechanisms in setting prices. Similarly, it has been used to study recruitment into political movements and social organizations. It has also been used to conceptualize scientific disagreements as well as academic prestige. More recently, network analysis (and its close cousin traffic analysis) has gained a significant use in military intelligence, for uncovering insurgent networks of both hierarchical and leaderless nature.^[15][16]

Dynamic network analysis

Dynamic Network Analysis examines the shifting structure of relationships among different classes of entities in complex socio-technical systems effects, and reflects social stability and changes such as the emergence of new groups, topics, and leaders.^[6][7][8][9] Dynamic Network Analysis focuses on meta-networks composed of multiple types of nodes (entities) and multiple types of links. These entities can be highly varied.^[6] Examples include people, organizations, topics, resources, tasks, events, locations, and beliefs.

Dynamic network techniques are particularly useful for assessing trends and changes in networks over time, identification of emergent leaders, and examining the co-evolution of people and ideas.

Biological network analysis

With the recent explosion of publicly available high throughput biological data, the analysis of molecular networks has gained significant interest. The type of analysis in this content are closely related to social network analysis, but often focusing on local patterns in the network. For example network motifs are small subgraphs that are over-represented in the network. Activity motifs are similar over-represented patterns in the attributes of nodes and edges in the network that are over represented given the network structure. The analysis of biological networks has led to the development of network medicine, which looks at the effect of diseases in the interactome.^[17]

Link analysis

Link analysis is a subset of network analysis, exploring associations between objects. An example may be examining the addresses of suspects and victims, the telephone numbers they have dialed and financial transactions that they have partaken in during a given timeframe, and the familial relationships between these subjects as a part of police investigation. Link analysis here provides the crucial relationships and associations between very many objects of different types that are not apparent from isolated pieces of information. Computer-assisted or fully automatic computer-based link analysis is increasingly employed by banks and insurance agencies in fraud detection, by telecommunication operators in telecommunication network analysis, by medical sector in epidemiology and pharmacology, in law enforcement investigations, by search engines for relevance rating (and conversely by the spammers for spamdexing and by business owners for search engine optimization), and everywhere else where relationships between many objects have to be analyzed.

Network robustness

The structural robustness of networks^[18] is studied using percolation theory. When a critical fraction of nodes is removed the network becomes fragmented into small clusters. This phenomenon is called percolation^[19] and it represents an order-disorder type of phase transition with critical exponents.

Pandemic Analysis

The SIR Model is one of the most well known algorithms on predicting the spread of global pandemics within an infectious population.

Susceptible to Infected

$S=\beta (1/N)$

The formula above describes the "force" of infection for each susceptible unit in an infectious population, where β is equivalent to the transmission rate of said disease.

To track the change of those susceptible in an infectious population:
$\Delta S=\beta \times S{1 \over N}\Delta t$

Infected to Recovered

$\Delta I=\mu I\Delta t$

Over time, the number of those infected fluctuates by: the specified rate of recovery, represented by $\mu$ but deducted to one over the average infectious period ${1 \over \tau }$, the numbered of infecious individuals, $I$, and the change in time, $\Delta t$.

Infectious Period

Whether a population will be overcome by a pandemic, with regards to the SIR model, is dependent on the value of $R_{0}$ or the "average people infected by an infected individual."
$R_{0}=\beta \tau ={\beta \over \mu }$

Web Link Analysis

Several Web search ranking algorithms use link-based centrality metrics, including (in order of appearance) Marchiori's Hyper Search, Google's PageRank, Kleinberg's HITS algorithm, the CheiRank and TrustRank algorithms. Link analysis is also conducted in information science and communication science in order to understand and extract information from the structure of collections of web pages. For example the analysis might be of the interlinking between politicians' web sites or blogs.

PageRank

PageRank works by randomly picking "nodes" or websites and then with a certain probability, "randomly jumping" to other nodes. By randomly jumping to these other nodes, it helps PageRank completely traverse the network as some webpages exist on the periphery and would not as readily be assessed.

Each node, $x_{i}$, has a PageRank as defined by the sum of pages $j$ that link to $i$ times one over the outlinks or "out-degree" of $j$ times the "importance" or PageRank of $j$.
$x_{i}=\sum _{{j\rightarrow i}}{1 \over N_{j}}x_{j}^{{(k)}}$

Random Jumping

As explained above, PageRank enlists random jumps in attempts to assign PageRank to every website on the internet. These random jumps find websites that might not be found during the normal search methodologies such as Breadth-First Search and Depth-First Search.

In an improvement over the aforementioned formula for determining PageRank includes adding these random jump components. Without the random jumps, some pages would receive a PageRank of 0 which would not be good.
The first is $\alpha$, or the probability that a random jump will occur. Contrasting is the "damping factor", or $1-\alpha$.
$R{(p)}={\alpha \over N}+(1-\alpha )\sum _{{j\rightarrow i}}{1 \over N_{j}}x_{j}^{{(k)}}$
Another way of looking at it:
$R(A)=\sum {R_{B} \over B_{{(outlinks)}}}+...+{R_{n} \over n_{{(outlinks)}}}$

Centrality measures

Information about the relative importance of nodes and edges in a graph can be obtained through centrality measures, widely used in disciplines like sociology. Centrality measures are essential when a network analysis has to answer questions such as: "Which nodes in the network should be targeted to ensure that a message or information spreads to all or most nodes in the network?" or conversely, "Which nodes should be targeted to curtail the spread of a disease?". Formally established measures of centrality are degree centrality, closeness centrality, betweenness centrality, eigenvector centrality, and katz centrality. The objective of network analysis generally determines the type of centrality measure(s) to be used.^[13]

• Degree centrality of a node in a network is the number of links (vertices) incident on the node.
• Closeness centrality determines how "close" a node is to other nodes in a network by measuring the sum of the shortest distances (geodesic paths) between that node and all other nodes in the network.
• Betweenness centrality determines the relative importance of a node by measuring the amount of traffic flowing through that node to other nodes in the network. This is done by measuring the fraction of paths connecting all pairs of nodes and containing the node of interest. Group Betweenness centrality measures the amount of traffic flowing through a group of nodes.^[20]
• Eigenvector centrality is a more sophisticated version of degree centrality where the centrality of a node not only depends on the number of links incident on the node but also the quality of those links. This quality factor is determined by the eigenvectors of the adjacency matrix of the network.
• Katz centrality of a node is measured by summing the geodesic paths between that node and all (reachable) nodes in the network. These paths are weighted, paths connecting the node with its immediate neighbors carry higher weights than those which connect with nodes farther away from the immediate neighbors.

Spread of content in networks

Content in a complex network can spread via two major methods: conserved spread and non-conserved spread.^[21] In conserved spread, the total amount of content that enters a complex network remains constant as it passes through. The model of conserved spread can best be represented by a pitcher containing a fixed amount of water being poured into a series of funnels connected by tubes . Here, the pitcher represents the original source and the water is the content being spread. The funnels and connecting tubing represent the nodes and the connections between nodes, respectively. As the water passes from one funnel into another, the water disappears instantly from the funnel that was previously exposed to the water. In non-conserved spread, the amount of content changes as it enters and passes through a complex network. The model of non-conserved spread can best be represented by a continuously running faucet running through a series of funnels connected by tubes . Here, the amount of water from the original source is infinite Also, any funnels that have been exposed to the water continue to experience the water even as it passes into successive funnels. The non-conserved model is the most suitable for explaining the transmission of most infectious diseases.

The SIR Model

In 1927, W. O. Kermack and A. G. McKendrick created a model in which they considered a fixed population with only three compartments, susceptible: $S(t)$, infected, $I(t)$, and recovered, $R(t)$.
The compartments used for this model consist of three classes:

• $S(t)$ is used to represent the number of individuals not yet infected with the disease at time t, or those susceptible to the disease
• $I(t)$ denotes the number of individuals who have been infected with the disease and are capable of spreading the disease to those in the susceptible category
• $R(t)$ is the compartment used for those individuals who have been infected and then recovered from the disease. Those in this category are not able to be infected again or to transmit the infection to others.

The flow of this model may be considered as follows:

${\color {blue}{{\mathcal {S}}\rightarrow {\mathcal {I}}\rightarrow {\mathcal {R}}}}$

Using a fixed population, $N=S(t)+I(t)+R(t)$, Kermack and McKendrick derived the following equations:

${\frac {dS}{dt}}=-\beta SI$

${\frac {dI}{dt}}=\beta SI-\gamma I$

${\frac {dR}{dt}}=\gamma I$

Several assumptions were made in the formulation of these equations: First, an individual in the population must be considered as having an equal probability as every other individual of contracting the disease with a rate of $\beta$, which is considered the contact or infection rate of the disease. Therefore, an infected individual makes contact and is able to transmit the disease with $\beta N$ others per unit time and the fraction of contacts by an infected with a susceptible is $S/N$. The number of new infections in unit time per infective then is $\beta N(S/N)$, giving the rate of new infections (or those leaving the susceptible category) as $\beta N(S/N)I=\beta SI$ (Brauer & Castillo-Chavez, 2001). For the second and third equations, consider the population leaving the susceptible class as equal to the number entering the infected class. However, a number equal to the fraction ($\gamma$ which represents the mean recovery rate, or $1/\gamma$ the mean infective period) of infectives are leaving this class per unit time to enter the removed class. These processes which occur simultaneously are referred to as the Law of Mass Action, a widely accepted idea that the rate of contact between two groups in a population is proportional to the size of each of the groups concerned (Daley & Gani, 2005). Finally, it is assumed that the rate of infection and recovery is much faster than the time scale of births and deaths and therefore, these factors are ignored in this model.

More can be read on this model on the Epidemic model page.

Interdependent networks

An interdependent network is a system of coupled networks where nodes of one or more networks depend on nodes in other networks. Such dependencies are enhanced by the developments in modern technology. Dependencies may lead to cascading failures between the networks and a relatively small failure can lead to a catastrophic breakdown of the system. Blackouts are a fascinating demonstration of the important role played by the dependencies between networks. A recent study developed a framework to study the cascading failures in an interdependent networks system.^[22][23]

Network optimization

Network problems that involve finding an optimal way of doing something are studied under the name of combinatorial optimization. Examples include network flow, shortest path problem, transport problem, transshipment problem, location problem, matching problem, assignment problem, packing problem, routing problem, Critical Path Analysis and PERT (Program Evaluation & Review Technique).

Network science research centers

• Duke Network Analysis Center^[24]
• IBM's Network Science Research Center (NSRC)^[25]
• Network Science Collaborative Technology Alliance (US Army Research Laboratory)^[26]
• Network Science and Technology (NEST) Center (Rensselaer Polytechnic Institute)^[27]
• CEU Center for Network Science (Central European University , founded in 2009)
• Center for Networks and Relational Analysis (University of California-Irvine)^[28]
• Interdisciplinary Center for Network Science and Applications (iCeNSA) (University of Notre Dame^[29]
• Technology Center for Networks & Pathways (Johns Hopkins University^[30]
• Yale Institute of Network Science (YINS)^[31]
• Social Cognitive Networks Academic Research Center at RPI (SNARC)^[32]
• Warren Center for Network and Data Sciences at Penn (YINS)^[33]

Network analysis and visualization tools

• Graph-tool and NetworkX, free and efficient Python modules for manipulation and statistical analysis of networks. [2] [3]
• igraph, an open source C library for the analysis of large-scale complex networks, with interfaces to R, Python and Ruby.
• Orange, a free data mining software suite, module orngNetwork
• Pajek, program for (large) network analysis and visualization.
• Tulip, a free data mining and visualization software dedicated to the analysis and visualization of relational data. [4]
• SEMOSS, an RDF-based open source context-aware analytics tool written in Java leveraging the SPARQL query language.
• ORA, a tool for Dynamic Network Analysis and network visualization.^[34]

Climatology

From Wikipedia, the free encyclopedia

Climatology (from Greek κλίμα, klima, "place, zone"; and -λογία, -logia) is the study of climate, scientifically defined as weather conditions averaged over a period of time.^[1] This modern field of study is regarded as a branch of the atmospheric sciences and a subfield of physical geography, which is one of the Earth sciences. Climatology now includes aspects of oceanography and biogeochemistry. Basic knowledge of climate can be used within shorter term weather forecasting using analog techniques such as the El Niño – Southern Oscillation (ENSO), the Madden-Julian Oscillation (MJO), the North Atlantic Oscillation (NAO), the Northern Annualar Mode (NAM) which is also known as the Arctic oscillation (AO), the Northern Pacific (NP) Index, the Pacific Decadal Oscillation (PDO), and the Interdecadal Pacific Oscillation (IPO). Climate models are used for a variety of purposes from study of the dynamics of the weather and climate system to projections of future climate.

History

Chinese scientist Shen Kuo (1031–1095) inferred that climates naturally shifted over an enormous span of time, after observing petrified bamboos found underground near Yanzhou (modern day Yan'an, Shaanxi province), a dry-climate area unsuitable for the growth of bamboo.^[2]

Early climate researchers include Edmund Halley, who published a map of the trade winds in 1686 after a voyage to the southern hemisphere. Benjamin Franklin (1706-1790) first mapped the course of the Gulf Stream for use in sending mail from the United States to Europe. Francis Galton (1822-1911) invented the term anticyclone.^[3] Helmut Landsberg (1906-1985) fostered the use of statistical analysis in climatology, which led to its evolution into a physical science.

Different approaches

Map of the average temperature over 30 years. Data sets formed from the long-term average of historical weather parameters are sometimes called a "climatology".

Climatology is approached in a variety of ways. Paleoclimatology seeks to reconstruct past climates by examining records such as ice cores and tree rings (dendroclimatology). Paleotempestology uses these same records to help determine hurricane frequency over millennia. The study of contemporary climates incorporates meteorological data accumulated over many years, such as records of rainfall, temperature and atmospheric composition. Knowledge of the atmosphere and its dynamics is also embodied in models, either statistical or mathematical, which help by integrating different observations and testing how they fit together. Modeling is used for understanding past, present and potential future climates. Historical climatology is the study of climate as related to human history and thus focuses only on the last few thousand years.

Climate research is made difficult by the large scale, long time periods, and complex processes which govern climate. Climate is governed by physical laws which can be expressed as differential equations. These equations are coupled and nonlinear, so that approximate solutions are obtained by using numerical methods to create global climate models. Climate is sometimes modeled as a stochastic process but this is generally accepted as an approximation to processes that are otherwise too complicated to analyze.

Indices

Scientists use climate indices based on several climate patterns (known as modes of variability) in their attempt to characterize and understand the various climate mechanisms that culminate in our daily weather. Much in the way the Dow Jones Industrial Average, which is based on the stock prices of 30 companies, is used to represent the fluctuations in the stock market as a whole, climate indices are used to represent the essential elements of climate. Climate indices are generally devised with the twin objectives of simplicity and completeness, and each index typically represents the status and timing of the climate factor it represents. By their very nature, indices are simple, and combine many details into a generalized, overall description of the atmosphere or ocean which can be used to characterize the factors which impact the global climate system.

El Niño – Southern Oscillation

El Niño impacts

La Niña impacts

El Niño-Southern Oscillation (ENSO) is a global coupled ocean-atmosphere phenomenon. The Pacific ocean signatures, El Niño and La Niña are important temperature fluctuations in surface waters of the tropical Eastern Pacific Ocean. The name El Niño, from the Spanish for "the little boy", refers to the Christ child, because the phenomenon is usually noticed around Christmas time in the Pacific Ocean off the west coast of South America.^[4] La Niña means "the little girl".^[5] Their effect on climate in the subtropics and the tropics are profound. The atmospheric signature, the Southern Oscillation (SO) reflects the monthly or seasonal fluctuations in the air pressure difference between Tahiti and Darwin. The most recent occurrence of El Niño started in September 2006^[6] and lasted until early 2007.^[7]

ENSO is a set of interacting parts of a single global system of coupled ocean-atmosphere climate fluctuations that come about as a consequence of oceanic and atmospheric circulation. ENSO is the most prominent known source of inter-annual variability in weather and climate around the world. The cycle occurs every two to seven years, with El Niño lasting nine months to two years within the longer term cycle,^[8] though not all areas globally are affected. ENSO has signatures in the Pacific, Atlantic and Indian Oceans.

In the Pacific, during major warm events, El Niño warming extends over much of the tropical Pacific and becomes clearly linked to the SO intensity. While ENSO events are basically in phase between the Pacific and Indian Oceans, ENSO events in the Atlantic Ocean lag behind those in the Pacific by 12–18 months. Many of the countries most affected by ENSO events are developing countries within tropical sections of continents with economies that are largely dependent upon their agricultural and fishery sectors as a major source of food supply, employment, and foreign exchange.^[9] New capabilities to predict the onset of ENSO events in the three oceans can have global socio-economic impacts. While ENSO is a global and natural part of the Earth's climate, whether its intensity or frequency may change as a result of global warming is an important concern. Low-frequency variability has been evidenced: the quasi-decadal oscillation (QDO). Inter-decadal (ID) modulation of ENSO (from PDO or IPO) might exist. This could explain the so-called protracted ENSO of the early 1990s.

Madden–Julian Oscillation

Note how the MJO moves eastward with time.

The Madden–Julian Oscillation (MJO) is an equatorial traveling pattern of anomalous rainfall that is planetary in scale. It is characterized by an eastward progression of large regions of both enhanced and suppressed tropical rainfall, observed mainly over the Indian and Pacific Oceans. The anomalous rainfall is usually first evident over the western Indian Ocean, and remains evident as it propagates over the very warm ocean waters of the western and central tropical Pacific. This pattern of tropical rainfall then generally becomes very nondescript as it moves over the cooler ocean waters of the eastern Pacific but reappears over the tropical Atlantic and Indian Oceans. The wet phase of enhanced convection and precipitation is followed by a dry phase where convection is suppressed. Each cycle lasts approximately 30–60 days. The MJO is also known as the 30–60 day oscillation, 30–60 day wave, or the intraseasonal oscillation.

North Atlantic Oscillation (NAO)

Indices of the NAO are based on the difference of normalized sea level pressure (SLP) between Ponta Delgada, Azores and Stykkisholmur/Reykjavik, Iceland. The SLP anomalies at each station were normalized by division of each seasonal mean pressure by the long-term mean (1865–1984) standard deviation. Normalization is done to avoid the series of being dominated by the greater variability of the northern of the two stations. Positive values of the index indicate stronger-than-average westerlies over the middle latitudes.^[10]

Northern Annular Mode (NAM) or Arctic Oscillation (AO)

The NAM, or AO, is defined as the first EOF of northern hemisphere winter SLP data from the tropics and subtropics. It explains 23% of the average winter (December–March) variance, and it is dominated by the NAO structure in the Atlantic. Although there are some subtle differences from the regional pattern over the Atlantic and Arctic, the main difference is larger amplitude anomalies over the North Pacific of the same sign as those over the Atlantic. This feature gives the NAM a more annular (or zonally symmetric) structure.^[10]

Northern Pacific (NP) Index

The NP Index is the area-weighted sea level pressure over the region 30N–65N, 160E–140W.^[10]

Pacific Decadal Oscillation (PDO)

The PDO is a pattern of Pacific climate variability that shifts phases on at least inter-decadal time scale, usually about 20 to 30 years. The PDO is detected as warm or cool surface waters in the Pacific Ocean, north of 20° N. During a "warm", or "positive", phase, the west Pacific becomes cool and part of the eastern ocean warms; during a "cool" or "negative" phase, the opposite pattern occurs. The mechanism by which the pattern lasts over several years has not been identified; one suggestion is that a thin layer of warm water during summer may shield deeper cold waters. A PDO signal has been reconstructed to 1661 through tree-ring chronologies in the Baja California area.

Interdecadal Pacific Oscillation (IPO)

The Interdecadal Pacific Oscillation (IPO or ID) display similar sea surface temperature (SST) and sea level pressure patterns to the PDO, with a cycle of 15–30 years, but affects both the north and south Pacific. In the tropical Pacific, maximum SST anomalies are found away from the equator. This is quite different from the quasi-decadal oscillation (QDO) with a period of 8–12 years and maximum SST anomalies straddling the equator, thus resembling ENSO.

Models

Climate models use quantitative methods to simulate the interactions of the atmosphere, oceans, land surface, and ice. They are used for a variety of purposes from study of the dynamics of the weather and climate system to projections of future climate. All climate models balance, or very nearly balance, incoming energy as short wave (including visible) electromagnetic radiation to the earth with outgoing energy as long wave (infrared) electromagnetic radiation from the earth. Any unbalance results in a change in the average temperature of the earth.
The most talked-about models of recent years have been those relating temperature to emissions of carbon dioxide (see greenhouse gas). These models predict an upward trend in the surface temperature record, as well as a more rapid increase in temperature at higher latitudes.

Models can range from relatively simple to quite complex:

• A simple radiant heat transfer model that treats the earth as a single point and averages outgoing energy
• this can be expanded vertically (radiative-convective models), or horizontally
• finally, (coupled) atmosphere–ocean–sea ice global climate models discretise and solve the full equations for mass and energy transfer and radiant exchange.

Differences with meteorology

In contrast to meteorology, which focuses on short term weather systems lasting up to a few weeks, climatology studies the frequency and trends of those systems. It studies the periodicity of weather events over years to millennia, as well as changes in long-term average weather patterns, in relation to atmospheric conditions. Climatologists study both the nature of climates – local, regional or global – and the natural or human-induced factors that cause climates to change. Climatology considers the past and can help predict future climate change.

Phenomena of climatological interest include the atmospheric boundary layer, circulation patterns, heat transfer (radiative, convective and latent), interactions between the atmosphere and the oceans and land surface (particularly vegetation, land use and topography), and the chemical and physical composition of the atmosphere.

Use in weather forecasting

A more complicated way of making a forecast, the analog technique requires remembering a previous weather event which is expected to be mimicked by an upcoming event. What makes it a difficult technique to use is that there is rarely a perfect analog for an event in the future.^[11] Some call this type of forecasting pattern recognition, which remains a useful method of observing rainfall over data voids such as oceans with knowledge of how satellite imagery relates to precipitation rates over land,^[12] as well as the forecasting of precipitation amounts and distribution in the future. A variation on this theme is used in Medium Range forecasting, which is known as teleconnections, when you use systems in other locations to help pin down the location of another system within the surrounding regime.^[13] One method of using teleconnections are by using climate indices such as ENSO-related phenomena.^[14]

Small volcanic eruptions could be slowing global warming

Original link:  http://news.agu.org/press-release/small-volcanic-eruptions-could-be-slowing-global-warming/


WASHINGTON, DC— Small volcanic eruptions might eject more of an atmosphere-cooling emissions into Earth’s upper atmosphere than previously thought. New ground-, air- and satellite measurements show that small volcanic eruptions that occurred between 2000 and 2013 have deflected almost double the amount of solar radiation previously estimated, according to a new study accepted to Geophysical Research Letters. By knocking incoming solar energy back out into space, sulfuric acid particles from these recent eruptions could be responsible for decreasing global temperatures by 0.05 to 0.12 degrees Celsius (0.09 to 0.22 degrees Fahrenheit) since 2000. An astronaut on the International Space Station took this striking view of Sarychev Volcano (Kuril Islands, northeast of Japan) in an early stage of eruption on June 12, 2009.

The Sarychev Peak Volcano, on Matua Island, erupted on June 12, 2009. New research shows that eruptions of this size may contribute more to the recent lull in global temperature increases than previously thought.
Credit: NASA

Scientists have long known that volcanoes can cool the atmosphere, mainly by means of sulfur dioxide gas that eruptions expel. Droplets of sulfuric acid that form when the gas combines with oxygen in the upper atmosphere can remain for many months, reflecting sunlight away from Earth and lowering temperatures. However, previous research had suggested that relatively minor eruptions—those in the lower half of a scale used to rate volcano “explosivity”—do not contribute much to this cooling phenomenon.

Now, new ground-, air- and satellite measurements show that small volcanic eruptions that occurred between 2000 and 2013 have deflected almost double the amount of solar radiation previously estimated. By knocking incoming solar energy back out into space, sulfuric acid particles from these recent eruptions could be responsible for decreasing global temperatures by 0.05 to 0.12 degrees Celsius (0.09 to 0.22 degrees Fahrenheit) since 2000, according to the new study accepted to Geophysical Research Letters, a journal of the American Geophysical Union.

These new data could help to explain why increases in global temperatures have slowed over the past 15 years, a period dubbed the ‘global warming hiatus,’ according to the study’s authors.

The warmest year on record is 1998. After that, the steep climb in global temperatures observed over the 20^th century appeared to level off. Scientists previously suggested that weak solar activity or heat uptake by the oceans could be responsible for this lull in temperature increases, but only recently have they thought minor volcanic eruptions might be a factor.

Climate projections typically don’t include the effect of volcanic eruptions, as these events are nearly impossible to predict, according to Alan Robock, a climatologist at Rutgers University in New Brunswick, N.J., who was not involved in the study. Only large eruptions on the scale of the cataclysmic 1991 Mount Pinatubo eruption in the Philippines, which ejected an estimated 20 million metric tons (44 billion pounds) of sulfur, were thought to impact global climate. But according to David Ridley, an atmospheric scientist at the Massachusetts Institute of Technology in Cambridge and lead author of the new study, classic climate models weren’t adding up.

“The prediction of global temperature from the [latest] models indicated continuing strong warming post-2000, when in reality the rate of warming has slowed,” said Ridley. That meant to him that a piece of the puzzle was missing, and he found it at the intersection of two atmospheric layers, the stratosphere and the troposphere– the lowest layer of the atmosphere, where all weather takes place. Those layers meet between 10 and 15 kilometers (six to nine miles) above the Earth.

Traditionally, scientists have used satellites to measure sulfuric acid droplets and other fine, suspended particles, or aerosols, that erupting volcanoes spew into the stratosphere. But ordinary water-vapor clouds in the troposphere can foil data collection below 15 km, Ridley said. “The satellite data does a great job of monitoring the particles above 15 km, which is fine in the tropics. However, towards the poles we are missing more and more of the particles residing in the lower stratosphere that can reach down to 10 km.”

To get around this, the new study combined observations from ground-, air- and space-based instruments to better observe aerosols in the lower portion of the stratosphere.

Four lidar systems measured laser light bouncing off aerosols to estimate the particles’ stratospheric concentrations, while a balloon-borne particle counter and satellite datasets provided cross-checks on the lidar measurements. A global network of ground-based sun-photometers, called AERONET, also detected aerosols by measuring the intensity of sunlight reaching the instruments. Together, these observing systems provided a more complete picture of the total amount of aerosols in the stratosphere, according to the study authors.

Including these new observations in a simple climate model, the researchers found that volcanic eruptions reduced the incoming solar power by -0.19 ± 0.09 watts of sunlight per square meter of the Earth’s surface during the ‘global warming hiatus’, enough to lower global surface temperatures by 0.05 to 0.12 degrees Celsius (0.09 to 0.22 degrees Fahrenheit).  By contrast, other studies have shown that the 1991 Mount Pinatubo eruption warded off about three to five watts per square meter at its peak, but tapered off to background levels in the years following the eruption. The shading from Pinatubo corresponded to a global temperature drop of 0.5 degrees Celsius (0.9 degrees Fahrenheit).

Robock said the new research provides evidence that there may be more aerosols in the atmosphere than previously thought. “This is part of the story about what has been driving climate change for the past 15 years,” he said. “It’s the best analysis we’ve had of the effects of a lot of small volcanic eruptions on climate.”

Ridley said he hopes the new data will make their way into climate models and help explain some of the inconsistencies that climate scientists have noted between the models and what is being observed.

Robock cautioned, however, that the ground-based AERONET instruments that the researchers used were developed to measure aerosols in the troposphere, not the stratosphere.  To build the best climate models, he said, a more robust monitoring system for stratospheric aerosols will need to be developed.

Dr. Willie Soon stands up to climate witch hunt

Statement by Dr. Willie Soon

In recent weeks I have been the target of attacks in the press by various radical environmental and politically motivated groups. This effort should be seen for what it is: a shameless attempt to silence my scientific research and writings, and to make an example out of me as a warning to any other researcher who may dare question in the slightest their fervently held orthodoxy of anthropogenic global warming.

I am saddened and appalled by this effort, not only because of the personal hurt it causes me and my family and friends, but also because of the damage it does to the integrity of the scientific process. I am willing to debate the substance of my research and competing views of climate change with anyone, anytime, anywhere. It is a shame that those who disagree with me resolutely decline all public debate and stoop instead to underhanded and unscientific ad hominem tactics.

Let me be clear. I have never been motivated by financial gain to write any scientific paper, nor have I ever hidden grants or any other alleged conflict of interest. I have been a solar and stellar physicist at the Harvard-Smithsonian Center for Astrophysics for a quarter of a century, during which time I have published numerous peer-reviewed, scholarly articles. The fact that my research has been supported in part by donations to the Smithsonian Institution from many sources, including some energy producers, has long been a matter of public record. In submitting my academic writings I have always complied with what I understood to be disclosure practices in my field generally, consistent with the level of disclosure made by many of my Smithsonian colleagues.

If the standards for disclosure are to change, then let them change evenly. If a journal that has peer-reviewed and published my work concludes that additional disclosures are appropriate, I am happy to comply. I would ask only that other authors—on all sides of the debate—are also required to make similar disclosures. And I call on the media outlets that have so quickly repeated my attackers’ accusations to similarly look into the motivations of and disclosures that may or may not have been made by their preferred, IPCC-linked scientists.

I regret deeply that the attacks on me now appear to have spilled over onto other scientists who have dared to question the degree to which human activities might be causing dangerous global warming, a topic that ought rightly be the subject of rigorous open debate, not personal attack. I similarly regret the terrible message this pillorying sends young researchers about the costs of questioning widely accepted “truths.”

Finally, I thank all my many colleagues and friends who have bravely objected to this smear campaign on my behalf and I challenge all parties involved to focus on real scientific issues for the betterment of humanity.