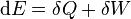From Wikipedia, the free encyclopedia

In a typical lightning strike, 500 megajoules of electric potential energy is converted into the same amount of energy in other forms, mostly light energy, sound energy and thermal energy.
In physics, energy is a property of objects which can be transferred to other objects or converted into different forms, but cannot be created or destroyed.[note 1] It is difficult to give a comprehensive definition of energy because of its many forms, but one common definition is that it is the ability of a system to perform work.[1] In SI units, energy is measured in joules, the energy transferred to an object by the mechanical work of moving it 1 metre against a force of 1 newton.[note 2]
All of the many forms of energy are convertible to other kinds of energy, and obey the conservation of energy. Common energy forms include the kinetic energy of a moving object, the radiant energy carried by light, the potential energy stored by an object's position in a force field,(gravitational, electric or magnetic) elastic energy stored by stretching solid objects, chemical energy released when a fuel burns, and the thermal energy due to an object's temperature.
According to mass–energy equivalence, any object that has mass when stationary,(called rest mass) also has an equivalent amount of energy whose form is called rest energy. Conversely, any additional energy above the rest energy will increase an object's mass. For example, if you had a sensitive enough scale, you could measure an increase in mass after heating an object. Our Sun transforms nuclear potential energy to other forms of energy; its total mass does not decrease due to that in itself (since it still contains the same total energy even if in different forms), but its mass does decrease when the energy escapes out to its surroundings, largely as radiant energy.
For closed systems, the first law of thermodynamics states that a system's energy is constant unless energy is transferred in or out by Work or heat, and that no energy is lost in transfer. This means that it is impossible to create or destroy energy. The second law of thermodynamics states that all systems doing work always lose some energy as waste heat. This creates a limit to the amount of energy that can do work by a heating process, a limit called the available energy. Mechanical and other forms of energy can be transformed in the other direction into thermal energy without such limitations. The total energy of a system can be calculated by adding up all forms of energy in the system. Examples of energy transfer and transformation include generating or making use of electric energy, performing chemical reactions, or lifting an object. Lifting against gravity performs work on the object and stores gravitational potential energy; if it falls, gravity does work on the object which transforms the potential energy to the kinetic energy associated with its speed.
Living organisms require available energy to stay alive, such as the energy humans get from food. Civilisation gets the energy it needs from energy resources such as fossil fuels. The processes of Earth's climate and ecosystem are driven by the radiant energy Earth receives from the sun and the geothermal energy contained within the earth. While total energy is never lost, energy conservation refers to using less available energy, which may be considered lost when it changes to a less useful form, such as waste heat.[2]
Forms

Thermal energy is energy of microscopic constituents of matter, which may include both kinetic and potential energy.
The total energy of a system can be subdivided and classified in various ways. For example, classical mechanics distinguishes between kinetic energy, which is determined by an object's movement through space, and potential energy, which is a function of the position of an object within a field. It may also be convenient to distinguish gravitational energy, thermal energy, several types of nuclear energy (which utilize potentials from the nuclear force and the weak force), electric energy (from the electric field), and magnetic energy (from the magnetic field), among others. Many of these classifications overlap; for instance, thermal energy usually consists partly of kinetic and partly of potential energy. Some types of energy are a varying mix of both potential and kinetic energy. An example is mechanical energy which is the sum of (usually macroscopic) kinetic and potential energy in a system. Elastic energy in materials is also dependent upon electrical potential energy (among atoms and molecules), as is chemical energy, which is stored and released from a reservoir of electrical potential energy between electrons, and the molecules or atomic nuclei that attract them.[need quotation to verify].The list is also not necessarily complete. Whenever physical scientists discover that a certain phenomenon appears to violate the law of energy conservation, new forms are typically added that account for the discrepancy.
Heat and work are special cases in that they are not properties of systems, but are instead properties of processes that transfer energy. In general we cannot measure how much heat or work are present in an object, but rather only how much energy is transferred among objects in certain ways during the occurrence of a given process. Heat and work are measured as positive or negative depending on which side of the transfer we view them from.
Potential energies are often measured as positive or negative depending on whether they are greater or less than the energy of a specified base state or configuration such as two interacting bodies being infinitely far apart. Wave energies (such as radiant or sound energy), kinetic energy, and rest energy are each greater than or equal to zero because they are measured in comparison to a base state of zero energy: "no wave", "no motion", and "no inertia", respectively.
The distinctions between different kinds of energy is not always clear-cut. As Richard Feynman points out:
These notions of potential and kinetic energy depend on a notion of length scale. For example, one can speak of macroscopic potential and kinetic energy, which do not include thermal potential and kinetic energy. Also what is called chemical potential energy is a macroscopic notion, and closer examination shows that it is really the sum of the potential and kinetic energy on the atomic and subatomic scale. Similar remarks apply to nuclear "potential" energy and most other forms of energy. This dependence on length scale is non-problematic if the various length scales are decoupled, as is often the case ... but confusion can arise when different length scales are coupled, for instance when friction converts macroscopic work into microscopic thermal energy.Some examples of different kinds of energy:
| Type of energy | Description |
|---|---|
| Kinetic | (≥0), that of the motion of a body |
| Potential | A category comprising many forms in this list |
| Mechanical | The sum of (usually macroscopic) kinetic and potential energies |
| Mechanical wave | (≥0), a form of mechanical energy propagated by a material's oscillations |
| Chemical | that contained in molecules |
| Electric | that from electric fields |
| Magnetic | that from magnetic fields |
| Radiant | (≥0), that of electromagnetic radiation including light |
| Nuclear | that of binding nucleons to form the atomic nucleus |
| Ionization | that of binding an electron to its atom or molecule |
| Elastic | that of deformation of a material (or its container) exhibiting a restorative force |
| Gravitational | that from gravitational fields |
| Rest | (≥0) that equivalent to an object's rest mass |
| Thermal | A microscopic, disordered equivalent of mechanical energy |
| Heat | an amount of thermal energy being transferred (in a given process) in the direction of decreasing temperature |
| Mechanical work | an amount of energy being transferred in a given process due to displacement in the direction of an applied force |
History

Thomas Young – the first to use the term "energy" in the modern sense.
The word energy derives from the Ancient Greek: ἐνέργεια energeia "activity, operation",[3] which possibly appears for the first time in the work of Aristotle in the 4th century BC. In contrast to the modern definition, energeia was a qualitative philosophical concept, broad enough to include ideas such as happiness and pleasure.
In the late 17th century, Gottfried Leibniz proposed the idea of the Latin: vis viva, or living force, which defined as the product of the mass of an object and its velocity squared; he believed that total vis viva was conserved. To account for slowing due to friction, Leibniz theorized that thermal energy consisted of the random motion of the constituent parts of matter, a view shared by Isaac Newton, although it would be more than a century until this was generally accepted. The modern analog of this property, kinetic energy, differs from vis viva only by a factor of two.
In 1807, Thomas Young was possibly the first to use the term "energy" instead of vis viva, in its modern sense.[4] Gustave-Gaspard Coriolis described "kinetic energy" in 1829 in its modern sense, and in 1853, William Rankine coined the term "potential energy". The law of conservation of energy, was also first postulated in the early 19th century, and applies to any isolated system. It was argued for some years whether heat was a physical substance, dubbed the caloric, or merely a physical quantity, such as momentum. In 1845 James Prescott Joule discovered the link between mechanical work and the generation of heat.
These developments led to the theory of conservation of energy, formalized largely by William Thomson (Lord Kelvin) as the field of thermodynamics. Thermodynamics aided the rapid development of explanations of chemical processes by Rudolf Clausius, Josiah Willard Gibbs, and Walther Nernst. It also led to a mathematical formulation of the concept of entropy by Clausius and to the introduction of laws of radiant energy by Jožef Stefan. According to Noether's theorem, the conservation of energy is a consequence of the fact that the laws of physics do not change over time.[5] Thus, since 1918, theorists have understood that the law of conservation of energy is the direct mathematical consequence of the translational symmetry of the quantity conjugate to energy, namely time.
Measurement and units

A schematic diagram of a Calorimeter - An instrument used by physicists to measure energy. In this example it is X-Rays.
The SI unit of power (energy per unit time) is the watt, which is simply a joule per second. Thus, a joule is a watt-second, so 3600 joules equal a watt-hour. The CGS energy unit is the erg, and the imperial and US customary unit is the foot pound. Other energy units such as the electron volt, food calorie or thermodynamic kcal (based on the temperature change of water in a heating process), and BTU are used in specific areas of science and commerce and have unit conversion factors relating them to the joule.
Because energy is defined as the ability to do work on objects, there is no absolute measure of energy. Only the transition of a system from one state into another can be defined and thus energy is measured in relative terms. The choice of a baseline or zero point is often arbitrary and can be made in whatever way is most convenient for a problem. For example in the case of measuring the energy deposited by X-rays as shown in the accompanying diagram, conventionally the technique most often employed is calorimetry. This is a thermodynamic technique that relies on the measurement of temperature using a thermometer or of intensity of radiation using a bolometer.
Energy density is a term used for the amount of useful energy stored in a given system or region of space per unit volume. For fuels, the energy per unit volume is sometimes a useful parameter. In a few applications, comparing, for example, the effectiveness of hydrogen fuel to gasoline it turns out that hydrogen has a higher specific energy than does gasoline, but, even in liquid form, a much lower energy density.
Scientific use
Classical mechanics
In classical mechanics, energy is a conceptually and mathematically useful property, as it is a conserved quantity.
Several formulations of mechanics have been developed using energy as a core concept.
Work, a form of energy, is force times distance.
 ) is equal to the line integral of the force F along a path C; for details see the mechanical work article. Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.
) is equal to the line integral of the force F along a path C; for details see the mechanical work article. Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.
The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.[7]
Another energy-related concept is called the Lagrangian, after Joseph-Louis Lagrange. This formalism is as fundamental as the Hamiltonian, and both can be used to derive the equations of motion or be derived from them. It was invented in the context of classical mechanics, but is generally useful in modern physics. The Lagrangian is defined as the kinetic energy minus the potential energy. Usually, the Lagrange formalism is mathematically more convenient than the Hamiltonian for non-conservative systems (such as systems with friction).
Noether's theorem (1918) states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalisation of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian; for example, dissipative systems with continuous symmetries need not have a corresponding conservation law.
In biology, energy is an attribute of all biological systems from the biosphere to the smallest living organism. Within an organism it is responsible for growth and development of a biological cell or an organelle of a biological organism. Energy is thus often said to be stored by cells in the structures of molecules of substances such as carbohydrates (including sugars), lipids, and proteins, which release energy when reacted with oxygen in respiration. In human terms, the human equivalent (H-e) (Human energy conversion) indicates, for a given amount of energy expenditure, the relative quantity of energy needed for human metabolism, assuming an average human energy expenditure of 12,500kJ per day and a basal metabolic rate of 80 watts. For example, if our bodies run (on average) at 80 watts, then a light bulb running at 100 watts is running at 1.25 human equivalents (100 ÷ 80) i.e. 1.25 H-e. For a difficult task of only a few seconds' duration, a person can put out thousands of watts, many times the 746 watts in one official horsepower. For tasks lasting a few minutes, a fit human can generate perhaps 1,000 watts.
For an activity that must be sustained for an hour, output drops to around 300; for an activity kept up all day, 150 watts is about the maximum.[8] The human equivalent assists understanding of energy flows in physical and biological systems by expressing energy units in human terms: it provides a "feel" for the use of a given amount of energy[9]
Sunlight is also captured by plants as chemical potential energy in photosynthesis, when carbon dioxide and water (two low-energy compounds) are converted into the high-energy compounds carbohydrates, lipids, and proteins. Plants also release oxygen during photosynthesis, which is utilized by living organisms as an electron acceptor, to release the energy of carbohydrates, lipids, and proteins. Release of the energy stored during photosynthesis as heat or light may be triggered suddenly by a spark, in a forest fire, or it may be made available more slowly for animal or human metabolism, when these molecules are ingested, and catabolism is triggered by enzyme action.
Any living organism relies on an external source of energy—radiation from the Sun in the case of green plants; chemical energy in some form in the case of animals—to be able to grow and reproduce. The daily 1500–2000 Calories (6–8 MJ) recommended for a human adult are taken as a combination of oxygen and food molecules, the latter mostly carbohydrates and fats, of which glucose (C6H12O6) and stearin (C57H110O6) are convenient examples. The food molecules are oxidised to carbon dioxide and water in the mitochondria
Sunlight may be stored as gravitational potential energy after it strikes the Earth, as (for example) water evaporates from oceans and is deposited upon mountains (where, after being released at a hydroelectric dam, it can be used to drive turbines or generators to produce electricity). Sunlight also drives many weather phenomena, save those generated by volcanic events. An example of a solar-mediated weather event is a hurricane, which occurs when large unstable areas of warm ocean, heated over months, give up some of their thermal energy suddenly to power a few days of violent air movement.
In a slower process, radioactive decay of atoms in the core of the Earth releases heat. This thermal energy drives plate tectonics and may lift mountains, via orogenesis. This slow lifting represents a kind of gravitational potential energy storage of the thermal energy, which may be later released to active kinetic energy in landslides, after a triggering event. Earthquakes also release stored elastic potential energy in rocks, a store that has been produced ultimately from the same radioactive heat sources. Thus, according to present understanding, familiar events such as landslides and earthquakes release energy that has been stored as potential energy in the Earth's gravitational field or elastic strain (mechanical potential energy) in rocks. Prior to this, they represent release of energy that has been stored in heavy atoms since the collapse of long-destroyed supernova stars created these atoms.
Work, a form of energy, is force times distance.
 ) is equal to the line integral of the force F along a path C; for details see the mechanical work article. Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.
) is equal to the line integral of the force F along a path C; for details see the mechanical work article. Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.[7]
Another energy-related concept is called the Lagrangian, after Joseph-Louis Lagrange. This formalism is as fundamental as the Hamiltonian, and both can be used to derive the equations of motion or be derived from them. It was invented in the context of classical mechanics, but is generally useful in modern physics. The Lagrangian is defined as the kinetic energy minus the potential energy. Usually, the Lagrange formalism is mathematically more convenient than the Hamiltonian for non-conservative systems (such as systems with friction).
Noether's theorem (1918) states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalisation of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian; for example, dissipative systems with continuous symmetries need not have a corresponding conservation law.
Chemistry
In the context of chemistry, energy is an attribute of a substance as a consequence of its atomic, molecular or aggregate structure. Since a chemical transformation is accompanied by a change in one or more of these kinds of structure, it is invariably accompanied by an increase or decrease of energy of the substances involved. Some energy is transferred between the surroundings and the reactants of the reaction in the form of heat or light; thus the products of a reaction may have more or less energy than the reactants. A reaction is said to be exergonic if the final state is lower on the energy scale than the initial state; in the case of endergonic reactions the situation is the reverse. Chemical reactions are invariably not possible unless the reactants surmount an energy barrier known as the activation energy. The speed of a chemical reaction (at given temperature T) is related to the activation energy E, by the Boltzmann's population factor e−E/kT – that is the probability of molecule to have energy greater than or equal to E at the given temperature T. This exponential dependence of a reaction rate on temperature is known as the Arrhenius equation.The activation energy necessary for a chemical reaction can be in the form of thermal energy.Biology

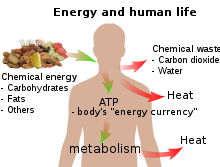
Basic overview of energy and human life.
In biology, energy is an attribute of all biological systems from the biosphere to the smallest living organism. Within an organism it is responsible for growth and development of a biological cell or an organelle of a biological organism. Energy is thus often said to be stored by cells in the structures of molecules of substances such as carbohydrates (including sugars), lipids, and proteins, which release energy when reacted with oxygen in respiration. In human terms, the human equivalent (H-e) (Human energy conversion) indicates, for a given amount of energy expenditure, the relative quantity of energy needed for human metabolism, assuming an average human energy expenditure of 12,500kJ per day and a basal metabolic rate of 80 watts. For example, if our bodies run (on average) at 80 watts, then a light bulb running at 100 watts is running at 1.25 human equivalents (100 ÷ 80) i.e. 1.25 H-e. For a difficult task of only a few seconds' duration, a person can put out thousands of watts, many times the 746 watts in one official horsepower. For tasks lasting a few minutes, a fit human can generate perhaps 1,000 watts.
For an activity that must be sustained for an hour, output drops to around 300; for an activity kept up all day, 150 watts is about the maximum.[8] The human equivalent assists understanding of energy flows in physical and biological systems by expressing energy units in human terms: it provides a "feel" for the use of a given amount of energy[9]
Sunlight is also captured by plants as chemical potential energy in photosynthesis, when carbon dioxide and water (two low-energy compounds) are converted into the high-energy compounds carbohydrates, lipids, and proteins. Plants also release oxygen during photosynthesis, which is utilized by living organisms as an electron acceptor, to release the energy of carbohydrates, lipids, and proteins. Release of the energy stored during photosynthesis as heat or light may be triggered suddenly by a spark, in a forest fire, or it may be made available more slowly for animal or human metabolism, when these molecules are ingested, and catabolism is triggered by enzyme action.
Any living organism relies on an external source of energy—radiation from the Sun in the case of green plants; chemical energy in some form in the case of animals—to be able to grow and reproduce. The daily 1500–2000 Calories (6–8 MJ) recommended for a human adult are taken as a combination of oxygen and food molecules, the latter mostly carbohydrates and fats, of which glucose (C6H12O6) and stearin (C57H110O6) are convenient examples. The food molecules are oxidised to carbon dioxide and water in the mitochondria
-
- C6H12O6 + 6O2 → 6CO2 + 6H2O
- C57H110O6 + 81.5O2 → 57CO2 + 55H2O
-
- ADP + HPO42− → ATP + H2O
- gain in kinetic energy of a sprinter during a 100 m race: 4 kJ
- gain in gravitational potential energy of a 150 kg weight lifted through 2 metres: 3kJ
- Daily food intake of a normal adult: 6–8 MJ
Earth sciences
In geology, continental drift, mountain ranges, volcanoes, and earthquakes are phenomena that can be explained in terms of energy transformations in the Earth's interior.,[11] while meteorological phenomena like wind, rain, hail, snow, lightning, tornadoes and hurricanes, are all a result of energy transformations brought about by solar energy on the atmosphere of the planet Earth.Sunlight may be stored as gravitational potential energy after it strikes the Earth, as (for example) water evaporates from oceans and is deposited upon mountains (where, after being released at a hydroelectric dam, it can be used to drive turbines or generators to produce electricity). Sunlight also drives many weather phenomena, save those generated by volcanic events. An example of a solar-mediated weather event is a hurricane, which occurs when large unstable areas of warm ocean, heated over months, give up some of their thermal energy suddenly to power a few days of violent air movement.
In a slower process, radioactive decay of atoms in the core of the Earth releases heat. This thermal energy drives plate tectonics and may lift mountains, via orogenesis. This slow lifting represents a kind of gravitational potential energy storage of the thermal energy, which may be later released to active kinetic energy in landslides, after a triggering event. Earthquakes also release stored elastic potential energy in rocks, a store that has been produced ultimately from the same radioactive heat sources. Thus, according to present understanding, familiar events such as landslides and earthquakes release energy that has been stored as potential energy in the Earth's gravitational field or elastic strain (mechanical potential energy) in rocks. Prior to this, they represent release of energy that has been stored in heavy atoms since the collapse of long-destroyed supernova stars created these atoms.
Cosmology
In cosmology and astronomy the phenomena of stars, nova, supernova, quasars and gamma ray bursts are the universe's highest-output energy transformations of matter. All stellar phenomena (including solar activity) are driven by various kinds of energy transformations. Energy in such transformations is either from gravitational collapse of matter (usually molecular hydrogen) into various classes of astronomical objects (stars, black holes, etc.), or from nuclear fusion (of lighter elements, primarily hydrogen). The nuclear fusion of hydrogen in the Sun also releases another store of potential energy which was created at the time of the Big Bang. At that time, according to theory, space expanded and the universe cooled too rapidly for hydrogen to completely fuse into heavier elements. This meant that hydrogen represents a store of potential energy that can be released by fusion. Such a fusion process is triggered by heat and pressure generated from gravitational collapse of hydrogen clouds when they produce stars, and some of the fusion energy is then transformed into sunlight.Quantum mechanics
In quantum mechanics, energy is defined in terms of the energy operator as a time derivative of the wave function.
The Schrödinger equation equates the energy operator to the full energy of a particle or a system. In results can be considered as a definition of measurement of energy in quantum mechanics. The Schrödinger equation describes the space- and time-dependence of slow changing (non-relativistic) wave function of quantum systems. The solution of this equation for bound system is discrete (a set of permitted states, each characterized by an energy level) which results in the concept of quanta. In the solution of the Schrödinger equation for any oscillator (vibrator) and for electromagnetic waves in a vacuum, the resulting energy states are related to the frequency by Planck's relation: 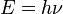 (where
(where 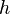 is the Planck's constant and
is the Planck's constant and  the frequency). In the case of electromagnetic wave these energy states are called quanta of light or photons.
the frequency). In the case of electromagnetic wave these energy states are called quanta of light or photons.
In general relativity, the stress–energy tensor serves as the source term for the gravitational field, in rough analogy to the way mass serves as the source term in the non-relativistic Newtonian approximation.[12]
It is not uncommon to hear that energy is "equivalent" to mass. It would be more accurate to state that every energy has an inertia and gravity equivalent, and because mass is a form of energy, then mass too has inertia and gravity associated with it.
In classical physics, energy is a scalar quantity, the canonical conjugate to time. In special relativity energy is also a scalar (although not a Lorentz scalar but a time component of the energy–momentum 4-vector).[12] In other words, energy is invariant with respect to rotations of space, but not invariant with respect to rotations of space-time (= boosts).
There are strict limits to how efficiently energy can be converted into other forms of energy via work, and heat as described by Carnot's theorem and the second law of thermodynamics. These limits are especially evident when an engine is used to perform work. However, some energy transformations can be quite efficient. The direction of transformations in energy (what kind of energy is transformed to what other kind) is often determined by entropy (equal energy spread among all available degrees of freedom) considerations. In practice all energy transformations are permitted on a small scale, but certain larger transformations are not permitted because it is statistically unlikely that energy or matter will randomly move into more concentrated forms or smaller spaces.
Energy transformations in the universe over time are characterized by various kinds of potential energy that has been available since the Big Bang, later being "released" (transformed to more active types of energy such as kinetic or radiant energy), when a triggering mechanism is available. Familiar examples of such processes include nuclear decay, in which energy is released that was originally "stored" in heavy isotopes (such as uranium and thorium), by nucleosynthesis, a process ultimately using the gravitational potential energy released from the gravitational collapse of supernovae, to store energy in the creation of these heavy elements before they were incorporated into the solar system and the Earth. This energy is triggered and released in nuclear fission bombs or in civil nuclear power generation. Similarly, in the case of a chemical explosion, chemical potential energy is transformed to kinetic energy and thermal energy in a very short time. Yet another example is that of a pendulum. At its highest points the kinetic energy is zero and the gravitational potential energy is at maximum. At its lowest point the kinetic energy is at maximum and is equal to the decrease of potential energy. If one (unrealistically) assumes that there is no friction or other losses, the conversion of energy between these processes would be perfect, and the pendulum would continue swinging forever.
Energy is also transferred from potential energy ( ) to kinetic energy (
) to kinetic energy ( ) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:
) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:
 (mass times acceleration due to gravity times the height) and
(mass times acceleration due to gravity times the height) and 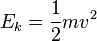 (half mass times velocity squared). Then the total amount of energy can be found by adding
(half mass times velocity squared). Then the total amount of energy can be found by adding  .
.
Matter may be converted to energy (and vice versa), but mass cannot ever be destroyed; rather, mass/energy equivalence remains a constant for both the matter and the energy, during any process when they are converted into each other. However, since is extremely large relative to ordinary human scales, the conversion of ordinary amount of matter (for example, 1 kg) to other forms of energy (such as heat, light, and other radiation) can liberate tremendous amounts of energy (~
is extremely large relative to ordinary human scales, the conversion of ordinary amount of matter (for example, 1 kg) to other forms of energy (such as heat, light, and other radiation) can liberate tremendous amounts of energy (~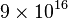 joules = 21 megatons of TNT), as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of a unit of energy is minuscule, which is why a loss of energy (loss of mass) from most systems is difficult to measure by weight, unless the energy loss is very large. Examples of energy transformation into matter (i.e., kinetic energy into particles with rest mass) are found in high-energy nuclear physics.
joules = 21 megatons of TNT), as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of a unit of energy is minuscule, which is why a loss of energy (loss of mass) from most systems is difficult to measure by weight, unless the energy loss is very large. Examples of energy transformation into matter (i.e., kinetic energy into particles with rest mass) are found in high-energy nuclear physics.
As the universe evolves in time, more and more of its energy becomes trapped in irreversible states (i.e., as heat or other kinds of increases in disorder). This has been referred to as the inevitable thermodynamic heat death of the universe. In this heat death the energy of the universe does not change, but the fraction of energy which is available to do work through a heat engine, or be transformed to other usable forms of energy (through the use of generators attached to heat engines), grows less and less.
Richard Feynman said during a 1961 lecture:[14]
This law is a fundamental principle of physics. As shown rigorously by Noether's theorem, the conservation of energy is a mathematical consequence of translational symmetry of time,[16] a property of most phenomena below the cosmic scale that makes them independent of their locations on the time coordinate. Put differently, yesterday, today, and tomorrow are physically indistinguishable. This is because energy is the quantity which is canonical conjugate to time. This mathematical entanglement of energy and time also results in the uncertainty principle - it is impossible to define the exact amount of energy during any definite time interval. The uncertainty principle should not be confused with energy conservation - rather it provides mathematical limits to which energy can in principle be defined and measured.
Each of the basic forces of nature is associated with a different type of potential energy, and all types of potential energy (like all other types of energy) appears as system mass, whenever present. For example, a compressed spring will be slightly more massive than before it was compressed. Likewise, whenever energy is transferred between systems by any mechanism, an associated mass is transferred with it.
In quantum mechanics energy is expressed using the Hamiltonian operator. On any time scales, the uncertainty in the energy is by
In particle physics, this inequality permits a qualitative understanding of virtual particles which carry momentum, exchange by which and with real particles, is responsible for the creation of all known fundamental forces (more accurately known as fundamental interactions). Virtual photons (which are simply lowest quantum mechanical energy state of photons) are also responsible for electrostatic interaction between electric charges (which results in Coulomb law), for spontaneous radiative decay of exited atomic and nuclear states, for the Casimir force, for van der Waals bond forces and some other observable phenomena.
Energy is strictly conserved and is also locally conserved wherever it can be defined. Mathematically, the process of energy transfer is described by the first law of thermodynamics:[note 7]
 is the amount of energy transferred,
is the amount of energy transferred,  represents the work done on the system, and
represents the work done on the system, and 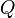 represents the heat flow into the system. As a simplification, the heat term,
represents the heat flow into the system. As a simplification, the heat term, 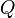 , is sometimes ignored, especially when the thermal efficiency of the transfer is high.
, is sometimes ignored, especially when the thermal efficiency of the transfer is high.
 " which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).
" which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).
 in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.
in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.
This equation is highly specific, ignoring all chemical, electrical, nuclear, and gravitational forces, effects such as advection of any form of energy other than heat and pV-work. The general formulation of the first law (i.e., conservation of energy) is valid even in situations in which the system is not homogeneous. For these cases the change in internal energy of a closed system is expressed in a general form by
 is the heat supplied to the system and
is the heat supplied to the system and 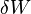 is the work applied to the system.
is the work applied to the system.
This principle is vitally important to understanding the behaviour of a quantity closely related to energy, called entropy. Entropy is a measure of evenness of a distribution of energy between parts of a system. When an isolated system is given more degrees of freedom (i.e., given new available energy states that are the same as existing states), then total energy spreads over all available degrees equally without distinction between "new" and "old" degrees. This mathematical result is called the second law of thermodynamics.
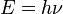 (where
(where 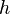 is the Planck's constant and
is the Planck's constant and  the frequency). In the case of electromagnetic wave these energy states are called quanta of light or photons.
the frequency). In the case of electromagnetic wave these energy states are called quanta of light or photons.Relativity
When calculating kinetic energy (work to accelerate a mass from zero speed to some finite speed) relativistically - using Lorentz transformations instead of Newtonian mechanics, Einstein discovered an unexpected by-product of these calculations to be an energy term which does not vanish at zero speed. He called it rest mass energy - energy which every mass must possess even when being at rest. The amount of energy is directly proportional to the mass of body: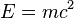 ,
,
- m is the mass,
- c is the speed of light in vacuum,
- E is the rest mass energy.
In general relativity, the stress–energy tensor serves as the source term for the gravitational field, in rough analogy to the way mass serves as the source term in the non-relativistic Newtonian approximation.[12]
It is not uncommon to hear that energy is "equivalent" to mass. It would be more accurate to state that every energy has an inertia and gravity equivalent, and because mass is a form of energy, then mass too has inertia and gravity associated with it.
In classical physics, energy is a scalar quantity, the canonical conjugate to time. In special relativity energy is also a scalar (although not a Lorentz scalar but a time component of the energy–momentum 4-vector).[12] In other words, energy is invariant with respect to rotations of space, but not invariant with respect to rotations of space-time (= boosts).
Transformation
Energy may be transformed between different forms at various efficiencies. Items that transform between these forms are called transducers. Examples of transducers include a battery, from chemical energy to electric energy; a dam: gravitational potential energy to kinetic energy of moving water (and the blades of a turbine) and ultimately to electric energy through an electric generator.There are strict limits to how efficiently energy can be converted into other forms of energy via work, and heat as described by Carnot's theorem and the second law of thermodynamics. These limits are especially evident when an engine is used to perform work. However, some energy transformations can be quite efficient. The direction of transformations in energy (what kind of energy is transformed to what other kind) is often determined by entropy (equal energy spread among all available degrees of freedom) considerations. In practice all energy transformations are permitted on a small scale, but certain larger transformations are not permitted because it is statistically unlikely that energy or matter will randomly move into more concentrated forms or smaller spaces.
Energy transformations in the universe over time are characterized by various kinds of potential energy that has been available since the Big Bang, later being "released" (transformed to more active types of energy such as kinetic or radiant energy), when a triggering mechanism is available. Familiar examples of such processes include nuclear decay, in which energy is released that was originally "stored" in heavy isotopes (such as uranium and thorium), by nucleosynthesis, a process ultimately using the gravitational potential energy released from the gravitational collapse of supernovae, to store energy in the creation of these heavy elements before they were incorporated into the solar system and the Earth. This energy is triggered and released in nuclear fission bombs or in civil nuclear power generation. Similarly, in the case of a chemical explosion, chemical potential energy is transformed to kinetic energy and thermal energy in a very short time. Yet another example is that of a pendulum. At its highest points the kinetic energy is zero and the gravitational potential energy is at maximum. At its lowest point the kinetic energy is at maximum and is equal to the decrease of potential energy. If one (unrealistically) assumes that there is no friction or other losses, the conversion of energy between these processes would be perfect, and the pendulum would continue swinging forever.
Energy is also transferred from potential energy (
 ) to kinetic energy (
) to kinetic energy ( ) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:
) and then back to potential energy constantly. This is referred to as conservation of energy. In this closed system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following: (4)
(4)
 (mass times acceleration due to gravity times the height) and
(mass times acceleration due to gravity times the height) and 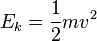 (half mass times velocity squared). Then the total amount of energy can be found by adding
(half mass times velocity squared). Then the total amount of energy can be found by adding  .
.Conservation of energy and mass in transformation
Energy gives rise to weight when it is trapped in a system with zero momentum, where it can be weighed. It is also equivalent to mass, and this mass is always associated with it. Mass is also equivalent to a certain amount of energy, and likewise always appears associated with it, as described in mass-energy equivalence. The formula E = mc², derived by Albert Einstein (1905) quantifies the relationship between rest-mass and rest-energy within the concept of special relativity. In different theoretical frameworks, similar formulas were derived by J. J. Thomson (1881), Henri Poincaré (1900), Friedrich Hasenöhrl (1904) and others (see Mass-energy equivalence#History for further information).Matter may be converted to energy (and vice versa), but mass cannot ever be destroyed; rather, mass/energy equivalence remains a constant for both the matter and the energy, during any process when they are converted into each other. However, since
 is extremely large relative to ordinary human scales, the conversion of ordinary amount of matter (for example, 1 kg) to other forms of energy (such as heat, light, and other radiation) can liberate tremendous amounts of energy (~
is extremely large relative to ordinary human scales, the conversion of ordinary amount of matter (for example, 1 kg) to other forms of energy (such as heat, light, and other radiation) can liberate tremendous amounts of energy (~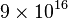 joules = 21 megatons of TNT), as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of a unit of energy is minuscule, which is why a loss of energy (loss of mass) from most systems is difficult to measure by weight, unless the energy loss is very large. Examples of energy transformation into matter (i.e., kinetic energy into particles with rest mass) are found in high-energy nuclear physics.
joules = 21 megatons of TNT), as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of a unit of energy is minuscule, which is why a loss of energy (loss of mass) from most systems is difficult to measure by weight, unless the energy loss is very large. Examples of energy transformation into matter (i.e., kinetic energy into particles with rest mass) are found in high-energy nuclear physics.Reversible and non-reversible transformations
Thermodynamics divides energy transformation into two kinds: reversible processes and irreversible processes. An irreversible process is one in which energy is dissipated (spread) into empty energy states available in a volume, from which it cannot be recovered into more concentrated forms (fewer quantum states), without degradation of even more energy. A reversible process is one in which this sort of dissipation does not happen. For example, conversion of energy from one type of potential field to another, is reversible, as in the pendulum system described above. In processes where heat is generated, quantum states of lower energy, present as possible excitations in fields between atoms, act as a reservoir for part of the energy, from which it cannot be recovered, in order to be converted with 100% efficiency into other forms of energy. In this case, the energy must partly stay as heat, and cannot be completely recovered as usable energy, except at the price of an increase in some other kind of heat-like increase in disorder in quantum states, in the universe (such as an expansion of matter, or a randomisation in a crystal).As the universe evolves in time, more and more of its energy becomes trapped in irreversible states (i.e., as heat or other kinds of increases in disorder). This has been referred to as the inevitable thermodynamic heat death of the universe. In this heat death the energy of the universe does not change, but the fraction of energy which is available to do work through a heat engine, or be transformed to other usable forms of energy (through the use of generators attached to heat engines), grows less and less.
Conservation of energy
According to conservation of energy, energy can neither be created (produced) nor destroyed by itself. It can only be transformed. The total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system. Energy is subject to a strict global conservation law; that is, whenever one measures (or calculates) the total energy of a system of particles whose interactions do not depend explicitly on time, it is found that the total energy of the system always remains constant.[13]Richard Feynman said during a 1961 lecture:[14]
There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law—it is exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.Most kinds of energy (with gravitational energy being a notable exception)[15] are subject to strict local conservation laws as well. In this case, energy can only be exchanged between adjacent regions of space, and all observers agree as to the volumetric density of energy in any given space. There is also a global law of conservation of energy, stating that the total energy of the universe cannot change; this is a corollary of the local law, but not vice versa.[2][14]
This law is a fundamental principle of physics. As shown rigorously by Noether's theorem, the conservation of energy is a mathematical consequence of translational symmetry of time,[16] a property of most phenomena below the cosmic scale that makes them independent of their locations on the time coordinate. Put differently, yesterday, today, and tomorrow are physically indistinguishable. This is because energy is the quantity which is canonical conjugate to time. This mathematical entanglement of energy and time also results in the uncertainty principle - it is impossible to define the exact amount of energy during any definite time interval. The uncertainty principle should not be confused with energy conservation - rather it provides mathematical limits to which energy can in principle be defined and measured.
Each of the basic forces of nature is associated with a different type of potential energy, and all types of potential energy (like all other types of energy) appears as system mass, whenever present. For example, a compressed spring will be slightly more massive than before it was compressed. Likewise, whenever energy is transferred between systems by any mechanism, an associated mass is transferred with it.
In quantum mechanics energy is expressed using the Hamiltonian operator. On any time scales, the uncertainty in the energy is by
In particle physics, this inequality permits a qualitative understanding of virtual particles which carry momentum, exchange by which and with real particles, is responsible for the creation of all known fundamental forces (more accurately known as fundamental interactions). Virtual photons (which are simply lowest quantum mechanical energy state of photons) are also responsible for electrostatic interaction between electric charges (which results in Coulomb law), for spontaneous radiative decay of exited atomic and nuclear states, for the Casimir force, for van der Waals bond forces and some other observable phenomena.
Transfer between systems
Closed systems
Energy transfer usually refers to movements of energy between systems which are closed to transfers of matter. The portion of the energy which is transferred by conservative forces over a distance is measured as the work the source system does on the receiving system. The portion of the energy which does not do work doing during the transfer is called heat.[note 5] Energy can be transferred between systems in a variety of ways. Examples include the transmission of electromagnetic energy via photons, physical collisions which transfer kinetic energy,[note 6] and the conductive transfer of thermal energy.Energy is strictly conserved and is also locally conserved wherever it can be defined. Mathematically, the process of energy transfer is described by the first law of thermodynamics:[note 7]
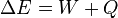 (1)
(1)
 is the amount of energy transferred,
is the amount of energy transferred,  represents the work done on the system, and
represents the work done on the system, and 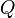 represents the heat flow into the system. As a simplification, the heat term,
represents the heat flow into the system. As a simplification, the heat term, 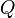 , is sometimes ignored, especially when the thermal efficiency of the transfer is high.
, is sometimes ignored, especially when the thermal efficiency of the transfer is high. (2)
(2)
Open systems
There are other ways in which an open system can gain or lose energy. In chemical systems, energy can be added to a system by means of adding substances with different chemical potentials, which potentials are then extracted (both of these process are illustrated by fueling an auto, a system which gains in energy thereby, without addition of either work or heat). These terms may be added to the above equation, or they can generally be subsumed into a quantity called "energy addition term " which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses).
" which refers to any type of energy carried over the surface of a control volume or system volume. Examples may be seen above, and many others can be imagined (for example, the kinetic energy of a stream of particles entering a system, or energy from a laser beam adds to system energy, without either being either work-done or heat-added, in the classic senses). (3)
(3)
 in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.
in this general equation represents other additional advected energy terms not covered by work done on a system, or heat added to it.Thermodynamics
Internal energy
Internal energy is the sum of all microscopic forms of energy of a system. It is the energy needed to create the system. It is related to the potential energy, e.g., molecular structure, crystal structure, and other geometric aspects, as well as the motion of the particles, in form of kinetic energy. Thermodynamics is chiefly concerned with changes in internal energy and not its absolute value, which is impossible to determine with thermodynamics alone.[17]First law of thermodynamics
The first law of thermodynamics asserts that energy (but not necessarily thermodynamic free energy) is always conserved[18] and that heat flow is a form of energy transfer. For homogeneous systems, with a well-defined temperature and pressure, a commonly used corollary of the first law is that, for a system subject only to pressure forces and heat transfer (e.g., a cylinder-full of gas), the differential change in the internal energy of the system (with a gain in energy signified by a positive quantity) is given as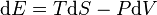 ,
,
This equation is highly specific, ignoring all chemical, electrical, nuclear, and gravitational forces, effects such as advection of any form of energy other than heat and pV-work. The general formulation of the first law (i.e., conservation of energy) is valid even in situations in which the system is not homogeneous. For these cases the change in internal energy of a closed system is expressed in a general form by
 is the heat supplied to the system and
is the heat supplied to the system and 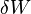 is the work applied to the system.
is the work applied to the system.Equipartition of energy
The energy of a mechanical harmonic oscillator (a mass on a spring) is alternatively kinetic and potential. At two points in the oscillation cycle it is entirely kinetic, and alternatively at two other points it is entirely potential. Over the whole cycle, or over many cycles, net energy is thus equally split between kinetic and potential. This is called equipartition principle; total energy of a system with many degrees of freedom is equally split among all available degrees of freedom.This principle is vitally important to understanding the behaviour of a quantity closely related to energy, called entropy. Entropy is a measure of evenness of a distribution of energy between parts of a system. When an isolated system is given more degrees of freedom (i.e., given new available energy states that are the same as existing states), then total energy spreads over all available degrees equally without distinction between "new" and "old" degrees. This mathematical result is called the second law of thermodynamics.

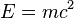 ,
,
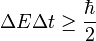
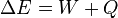


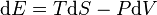 ,
,