From Wikipedia, the free encyclopedia
Valence shell electron pair repulsion (VSEPR) theory is a model used, in chemistry, to predict the geometry of individual molecules from the number of electron pairs surrounding their central atoms.[1] It is also named Gillespie–Nyholm theory after its two main developers. The acronym "VSEPR" is pronounced "vesper" by some chemists.[2]
The premise of VSEPR is that the valence electron pairs surrounding an atom tend to repel each other, and will therefore adopt an arrangement that minimizes this repulsion, thus determining the molecule's geometry. The sum of the number of atoms bonded to a central atom and the number of lone pairs formed by its nonbonding valence electrons is known as the central atom's steric number.
VSEPR theory is usually compared with valence bond theory, which addresses molecular shape through orbitals that are energetically accessible for bonding. Valence bond theory concerns itself with the formation of sigma and pi bonds. Molecular orbital theory is another model for understanding how atoms and electrons are assembled into molecules and polyatomic ions.
VSEPR theory has long been criticized for not being quantitative, and therefore limited to the generation of "crude" (though structurally accurate) molecular geometries of covalently-bonded molecules. However, molecular mechanics force fields based on VSEPR have also been developed.[3]
The number of electron pairs in the valence shell of a central atom is determined after drawing the Lewis structure of the molecule, and expanding it to show all bonding groups and lone pairs of electrons.[8] In VSEPR theory, a double bond or triple bond are treated as a single bonding group.[8]
The electron pairs (or groups if multiple bonds are present) are assumed to lie on the surface of a sphere centered on the central atom and tend to occupy positions that minimizes their mutual repulsions by maximizing the distance between them.[8][9] Gillespie has emphasized that the electron-electron repulsion due to the Pauli exclusion principle is more important in determining molecular geometry than the electrostatic repulsion.[10] The number of electron pairs (or groups), therefore, determine the overall geometry that they will adopt. For example, when there are two electron pairs surrounding the central atom, their mutual repulsion is minimal when they lie at opposite poles of the sphere. Therefore, the central atom is predicted to adopt a linear geometry. If there are 3 electron pairs surrounding the central atom, their repulsion is minimized by placing them at the vertices of an equilateral triangle centered on the atom. Therefore, the predicted geometry is trigonal. Likewise, for 4 electron pairs, the optimal arrangement is tetrahedral.[8]
This overall geometry is further refined by distinguishing between bonding and nonbonding electron pairs. The bonding electron pair shared in a sigma bond with an adjacent atom lies further from the central atom than a nonbonding (lone) pair of that atom, which is held close to its positively-charged nucleus. VSEPR theory therefore views repulsion by the lone pair to be greater than the repulsion by a bonding pair. As such, when a molecule has 2 interactions with different degrees of repulsion, VSEPR theory predicts the structure where lone pairs occupy positions that allow them to experience less repulsion. Lone pair-lone pair (lp-lp) repulsions are considered stronger than lone pair-bonding pair (lp-bp) repulsions, which in turn are considered stronger than bonding pair-bonding pair (bp-bp) repulsions, distinctions that then guide decisions about overall geometry when 2 or more non-equivalent positions are possible.[8] For instance, when 5 ligands or lone pairs surround a central atom, a trigonal bipyramidal molecular geometry is specified. In this geometry, the 2 collinear "axial" positions lie 180° apart from one another, and 90° from each of 3 adjacent "equatorial" positions; these 3 equatorial positions lie 120° apart from each other and experience only two closer proximity 90° neighbors (the axial positions). The axial positions therefore experience more repulsion than the equatorial positions; hence, when there are lone pairs, they tend to occupy equatorial positions.[9]
The difference between lone pairs and bonding pairs may also be used to rationalize deviations from idealized geometries. For example, the H2O molecule has four electron pairs in its valence shell: two lone pairs and two bond pairs. The four electron pairs are spread so as to point roughly towards the apices of a tetrahedron. However, the bond angle between the two O-H bonds is only 104.5°, rather than the 109.5° of a regular tetrahedron, because the two lone pairs (whose density or probability envelopes lie closer to the oxygen nucleus) exert a greater mutual repulsion than the two bond pairs.[8][9]
Based on the steric number and distribution of X's and E's, VSEPR theory makes the predictions in the following tables. Note that the geometries are named according to the atomic positions only and not the electron arrangement. For example the description of AX2E1 as a bent molecule means that the three atoms AX2 are not in one straight line, although the lone pair helps to determine the geometry.
† Electron arrangement including lone pairs, shown in pale yellow
‡ Observed geometry (excluding lone pairs)
When the substituent (X) atoms are not all the same, the geometry is still approximately valid, but the bond angles may be slightly different from the ones where all the outside atoms are the same. For example, the double-bond carbons in alkenes like C2H4 are AX3E0, but the bond angles are not all exactly 120°. Likewise, SOCl2 is AX3E1, but because the X substituents are not identical, the XAX angles are not all equal.
As a tool in predicting the geometry adopted with a given number of electron pairs, an often used physical demonstration of the principle of minimal electron pair repulsion utilizes inflated balloons. Through handling, balloons acquire a slight surface electrostatic charge that results in the adoption of roughly the same geometries when they are tied together at their stems as the corresponding number of electron pairs. For example, five balloons tied together adopt the trigonal bipyramidal geometry, just as do the five bonding pairs of a PCl5 molecule (AX5) or the two bonding and three non-bonding pairs of a XeF2 molecule (AX2E3). The molecular geometry of the former is also trigonal bipyramidal, whereas that of the latter is linear.
The ammonia molecule (NH3) has three pairs of electrons involved in bonding, but there is a lone pair of electrons on the nitrogen atom.[27] It is not bonded with another atom; however, it influences the overall shape through repulsions. As in methane above, there are four regions of electron density. Therefore, the overall orientation of the regions of electron density is tetrahedral. On the other hand, there are only three outer atoms. This is referred to as an AX3E type molecule because the lone pair is represented by an E.[8] By definition, the molecular shape or geometry describes the geometric arrangement of the atomic nuclei only, which is trigonal-pyramidal for NH3.[8]
Steric numbers of 7 or greater are possible, but are less common. The steric number of 7 occurs in iodine heptafluoride (IF7); the base geometry for a steric number of 7 is pentagonal bipyramidal.[9] The most common geometry for a steric number of 8 is a square antiprismatic geometry.[28] Examples of this include the octacyanomolybdate (Mo(CN)4−
8) and octafluorozirconate (ZrF4−
8) anions.[28]
The nonahydridorhenate ion (ReH2−
9) in potassium nonahydridorhenate is a rare example of a compound with a steric number of 9, which has a tricapped trigonal prismatic geometry.[14][29] Another example is the octafluoroxenate ion (XeF2−
8) in nitrosonium octafluoroxenate(VI),[13][30][31] although in this case one of the electron pairs is a lone pair, and therefore the molecule actually has a distorted square antiprismatic geometry.
Possible geometries for steric numbers of 10, 11, 12, or 14 are bicapped square antiprismatic (or bicapped dodecadeltahedral), octadecahedral, icosahedral, and bicapped hexagonal antiprismatic, respectively. No compounds with steric numbers this high involving monodentate ligands exist, and those involving multidentate ligands can often be analysed more simply as complexes with lower steric numbers when some multidentate ligands are treated as a unit.[15]

Many transition metal compounds do not have the geometries predicted by VSEPR, which can be ascribed to there being no lone pairs in the valence shell and the interaction of core d electrons with the ligands.[32] The structure of some of these compounds, including metal hydrides and alkyl complexes such as hexamethyltungsten, can be predicted correctly using the VALBOND theory, which is based on sd hybrid orbitals and the three-center four-electron bonding model.[33][34] Crystal field theory is another theory that can often predict the geometry of coordination complexes.
Some AX6E1 molecules, e.g. xenon hexafluoride (XeF6) and the Te(IV) and Bi(III) anions, TeCl2−
6, TeBr2−
6, BiCl3−
6, BiBr3−
6 and BiI3−
6, are octahedra, rather than pentagonal pyramids, and the lone pair does not affect the geometry to the degree predicted by VSEPR.[40] One rationalization is that steric crowding of the ligands allows little or no room for the non-bonding lone pair;[32] another rationalization is the inert pair effect.[41] Similarly, the octafluoroxenate anion (XeF2−
8) is a square antiprism and not a distorted square antiprism (as predicted by VSEPR theory for an AX8E1 molecule), despite having a lone pair.
2 (180°), NO2 (134°), NO−
2 (115°) indicates that a given set of bonding electron pairs exert a weaker repulsion on a single non-bonding electron than on a pair of non-bonding electrons. In effect, they considered nitrogen dioxide as an AX2E0.5 molecule with a geometry intermediate between NO+
2 and NO−
2. Similarly chlorine dioxide (ClO2) is AX2E1.5 with a geometry intermediate between ClO+
2 and ClO−
2.[citation needed]
Finally the methyl radical (CH3) is predicted to be trigonal pyramidal like the methyl anion (CH−
3), but with a larger bond angle as in the trigonal planar methyl cation (CH+
3). However in this case the VSEPR prediction is not quite true, as CH3 is actually planar, although its distortion to a pyramidal geometry requires very little energy.[43]
The premise of VSEPR is that the valence electron pairs surrounding an atom tend to repel each other, and will therefore adopt an arrangement that minimizes this repulsion, thus determining the molecule's geometry. The sum of the number of atoms bonded to a central atom and the number of lone pairs formed by its nonbonding valence electrons is known as the central atom's steric number.
VSEPR theory is usually compared with valence bond theory, which addresses molecular shape through orbitals that are energetically accessible for bonding. Valence bond theory concerns itself with the formation of sigma and pi bonds. Molecular orbital theory is another model for understanding how atoms and electrons are assembled into molecules and polyatomic ions.
VSEPR theory has long been criticized for not being quantitative, and therefore limited to the generation of "crude" (though structurally accurate) molecular geometries of covalently-bonded molecules. However, molecular mechanics force fields based on VSEPR have also been developed.[3]
History
The idea of a correlation between molecular geometry and number of valence electrons (both shared and unshared) was originally proposed in 1939 by Ryutaro Tsuchida in Japan,[citation needed] and was independently presented in a Bakerian Lecture in 1940 by Nevil Sidgwick and Herbert Powell of the University of Oxford.[4] In 1957, Ronald Gillespie and Ronald Sydney Nyholm of University College London refined this concept into a more detailed theory, capable of choosing between various alternative geometries.[5][6]Description
VSEPR theory, occasionally pronounced "vesper" or "vuh-seh-per",[7] is used to predict the arrangement of electron pairs around non-hydrogen atoms in molecules, especially simple and symmetric molecules, where these key, central atoms participate in bonding to 2 or more other atoms; the geometry of these key atoms and their non-bonding electron pairs in turn determine the geometry of the larger whole.The number of electron pairs in the valence shell of a central atom is determined after drawing the Lewis structure of the molecule, and expanding it to show all bonding groups and lone pairs of electrons.[8] In VSEPR theory, a double bond or triple bond are treated as a single bonding group.[8]
The electron pairs (or groups if multiple bonds are present) are assumed to lie on the surface of a sphere centered on the central atom and tend to occupy positions that minimizes their mutual repulsions by maximizing the distance between them.[8][9] Gillespie has emphasized that the electron-electron repulsion due to the Pauli exclusion principle is more important in determining molecular geometry than the electrostatic repulsion.[10] The number of electron pairs (or groups), therefore, determine the overall geometry that they will adopt. For example, when there are two electron pairs surrounding the central atom, their mutual repulsion is minimal when they lie at opposite poles of the sphere. Therefore, the central atom is predicted to adopt a linear geometry. If there are 3 electron pairs surrounding the central atom, their repulsion is minimized by placing them at the vertices of an equilateral triangle centered on the atom. Therefore, the predicted geometry is trigonal. Likewise, for 4 electron pairs, the optimal arrangement is tetrahedral.[8]
This overall geometry is further refined by distinguishing between bonding and nonbonding electron pairs. The bonding electron pair shared in a sigma bond with an adjacent atom lies further from the central atom than a nonbonding (lone) pair of that atom, which is held close to its positively-charged nucleus. VSEPR theory therefore views repulsion by the lone pair to be greater than the repulsion by a bonding pair. As such, when a molecule has 2 interactions with different degrees of repulsion, VSEPR theory predicts the structure where lone pairs occupy positions that allow them to experience less repulsion. Lone pair-lone pair (lp-lp) repulsions are considered stronger than lone pair-bonding pair (lp-bp) repulsions, which in turn are considered stronger than bonding pair-bonding pair (bp-bp) repulsions, distinctions that then guide decisions about overall geometry when 2 or more non-equivalent positions are possible.[8] For instance, when 5 ligands or lone pairs surround a central atom, a trigonal bipyramidal molecular geometry is specified. In this geometry, the 2 collinear "axial" positions lie 180° apart from one another, and 90° from each of 3 adjacent "equatorial" positions; these 3 equatorial positions lie 120° apart from each other and experience only two closer proximity 90° neighbors (the axial positions). The axial positions therefore experience more repulsion than the equatorial positions; hence, when there are lone pairs, they tend to occupy equatorial positions.[9]
The difference between lone pairs and bonding pairs may also be used to rationalize deviations from idealized geometries. For example, the H2O molecule has four electron pairs in its valence shell: two lone pairs and two bond pairs. The four electron pairs are spread so as to point roughly towards the apices of a tetrahedron. However, the bond angle between the two O-H bonds is only 104.5°, rather than the 109.5° of a regular tetrahedron, because the two lone pairs (whose density or probability envelopes lie closer to the oxygen nucleus) exert a greater mutual repulsion than the two bond pairs.[8][9]
AXE method
The "AXE method" of electron counting is commonly used when applying the VSEPR theory. The A represents the central atom and always has an implied subscript one. The X represents the number of ligands (atoms bonded to A). The E represents the number of lone electron pairs surrounding the central atom.[8] The sum of X and E is known as the steric number.Based on the steric number and distribution of X's and E's, VSEPR theory makes the predictions in the following tables. Note that the geometries are named according to the atomic positions only and not the electron arrangement. For example the description of AX2E1 as a bent molecule means that the three atoms AX2 are not in one straight line, although the lone pair helps to determine the geometry.
| Steric No. |
Molecular geometry[11] 0 lone pair |
Molecular geometry[11] 1 lone pair |
Molecular geometry[11] 2 lone pairs |
Molecular geometry[11] 3 lone pairs |
|---|---|---|---|---|
| 2 | ||||
| 3 |  |
 |
||
| 4 | 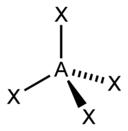 |
 |
 |
|
| 5 |  |
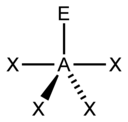 |
 |
 3) |
| 6 | 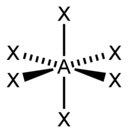 |
 |
 |
|
| 7 |  |
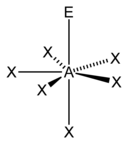 5)[12] |
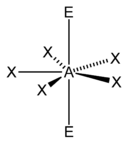 5)[13] |
|
| 8 | (TaF3− 8)[9] |
|||
| 9 | Tricapped trigonal prismatic (ReH2− 9)[14] OR Capped square antiprismatic[citation needed] |
|||
| 10 | Bicapped square antiprismatic OR Bicapped dodecadeltahedral[15] |
|||
| 11 | Octadecahedral[15] | |||
| 12 | Icosahedral[15] | |||
| 13 | ||||
| 14 | Bicapped hexagonal antiprismatic[15] |
| Molecule Type | Shape[11] | Electron arrangement†[11] | Geometry‡[11] | Examples |
|---|---|---|---|---|
| AX2E0 | Linear | BeCl2,[1] HgCl2,[1] CO2[9] | ||
| AX2E1 | Bent |  |
 |
NO− 2,[1] SO2,[11] O3,[1] CCl2 |
| AX2E2 | Bent | 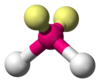 |
 |
H2O,[11] OF2[16] |
| AX2E3 | Linear |  |
XeF2,[11] I− 3,[17] XeCl2 |
|
| AX3E0 | Trigonal planar |  |
 |
BF3,[11] CO2− 3,[18] NO− 3,[1] SO3[9] |
| AX3E1 | Trigonal pyramidal |  |
 |
NH3,[11] PCl3[19] |
| AX3E2 | T-shaped |  |
 |
ClF3,[11] BrF3[20] |
| AX4E0 | Tetrahedral | 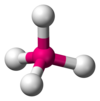 |
 |
CH4,[11] PO3− 4, SO2− 4,[9] ClO− 4,[1] TiCl4,[21] XeO4[22] |
| AX4E1 | Seesaw (also called disphenoidal) |  |
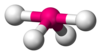 |
SF4[11][23] |
| AX4E2 | Square planar |  |
 |
XeF4[11] |
| AX5E0 | Trigonal bipyramidal |  |
 |
PCl5[11] |
| AX5E1 | Square pyramidal | 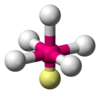 |
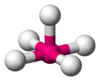 |
ClF5,[20] BrF5,[11] XeOF4[9] |
| AX5E2 | Pentagonal planar |  |
 |
XeF− 5[13] |
| AX6E0 | Octahedral | 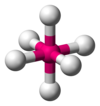 |
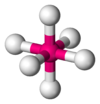 |
SF6,[11] WCl6[24] |
| AX6E1 | Pentagonal pyramidal |  |
 |
XeOF− 5,[12] IOF2− 5[12] |
| AX7E0 | Pentagonal bipyramidal[9] | 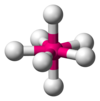 |
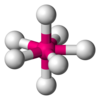 |
IF7[9] |
| AX8E0 | Square antiprismatic[9] |  |
 |
IF− 8, ZrF4− 8, ReF− 8 |
| AX9E0 | Tricapped trigonal prismatic (as drawn) OR capped square antiprismatic |
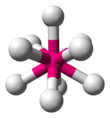 |
 |
ReH2− 9[14] |
When the substituent (X) atoms are not all the same, the geometry is still approximately valid, but the bond angles may be slightly different from the ones where all the outside atoms are the same. For example, the double-bond carbons in alkenes like C2H4 are AX3E0, but the bond angles are not all exactly 120°. Likewise, SOCl2 is AX3E1, but because the X substituents are not identical, the XAX angles are not all equal.
As a tool in predicting the geometry adopted with a given number of electron pairs, an often used physical demonstration of the principle of minimal electron pair repulsion utilizes inflated balloons. Through handling, balloons acquire a slight surface electrostatic charge that results in the adoption of roughly the same geometries when they are tied together at their stems as the corresponding number of electron pairs. For example, five balloons tied together adopt the trigonal bipyramidal geometry, just as do the five bonding pairs of a PCl5 molecule (AX5) or the two bonding and three non-bonding pairs of a XeF2 molecule (AX2E3). The molecular geometry of the former is also trigonal bipyramidal, whereas that of the latter is linear.
Examples
The methane molecule (CH4) is tetrahedral because there are four pairs of electrons. The four hydrogen atoms are positioned at the vertices of a tetrahedron, and the bond angle is cos−1(−1⁄3) ≈ 109°28'.[25][26] This is referred to as an AX4 type of molecule. As mentioned above, A represents the central atom and X represents an outer atom.[8]The ammonia molecule (NH3) has three pairs of electrons involved in bonding, but there is a lone pair of electrons on the nitrogen atom.[27] It is not bonded with another atom; however, it influences the overall shape through repulsions. As in methane above, there are four regions of electron density. Therefore, the overall orientation of the regions of electron density is tetrahedral. On the other hand, there are only three outer atoms. This is referred to as an AX3E type molecule because the lone pair is represented by an E.[8] By definition, the molecular shape or geometry describes the geometric arrangement of the atomic nuclei only, which is trigonal-pyramidal for NH3.[8]
Steric numbers of 7 or greater are possible, but are less common. The steric number of 7 occurs in iodine heptafluoride (IF7); the base geometry for a steric number of 7 is pentagonal bipyramidal.[9] The most common geometry for a steric number of 8 is a square antiprismatic geometry.[28] Examples of this include the octacyanomolybdate (Mo(CN)4−
8) and octafluorozirconate (ZrF4−
8) anions.[28]
The nonahydridorhenate ion (ReH2−
9) in potassium nonahydridorhenate is a rare example of a compound with a steric number of 9, which has a tricapped trigonal prismatic geometry.[14][29] Another example is the octafluoroxenate ion (XeF2−
8) in nitrosonium octafluoroxenate(VI),[13][30][31] although in this case one of the electron pairs is a lone pair, and therefore the molecule actually has a distorted square antiprismatic geometry.
Possible geometries for steric numbers of 10, 11, 12, or 14 are bicapped square antiprismatic (or bicapped dodecadeltahedral), octadecahedral, icosahedral, and bicapped hexagonal antiprismatic, respectively. No compounds with steric numbers this high involving monodentate ligands exist, and those involving multidentate ligands can often be analysed more simply as complexes with lower steric numbers when some multidentate ligands are treated as a unit.[15]
Exceptions
There are groups of compounds where VSEPR fails to predict the correct geometry.Transition metal compounds

Hexamethyltungsten, a transition metal compound whose geometry is different from that predicted by VSEPR.
Many transition metal compounds do not have the geometries predicted by VSEPR, which can be ascribed to there being no lone pairs in the valence shell and the interaction of core d electrons with the ligands.[32] The structure of some of these compounds, including metal hydrides and alkyl complexes such as hexamethyltungsten, can be predicted correctly using the VALBOND theory, which is based on sd hybrid orbitals and the three-center four-electron bonding model.[33][34] Crystal field theory is another theory that can often predict the geometry of coordination complexes.
Some AX2E0 molecules
The gas phase structures of the triatomic halides of the heavier members of group 2, (i.e., calcium, strontium and barium halides, MX2), are not linear as predicted but are bent, (approximate X-M-X angles: CaF2, 145°; SrF2, 120°; BaF2, 108°; SrCl2, 130°; BaCl2, 115°; BaBr2, 115°; BaI2, 105°).[35] It has been proposed by Gillespie that this is caused by interaction of the ligands with the electron core of the metal atom, polarising it so that the inner shell is not spherically symmetric, thus influencing the molecular geometry.[32][36] Ab initio calculations have been cited to propose that contributions from d orbitals in the shell below the valence shell are responsible.[37] Disilynes are also bent, despite having no lone pairs.[38]Some AX2E2 molecules
One example of the AX2E2 geometry is molecular lithium oxide, Li2O, a linear rather than bent structure, which is ascribed to its bonds being essentially ionic and the strong lithium-lithium repulsion that results.[39] Another example is O(SiH3)2 with an Si-O-Si angle of 144.1°, which compares to the angles in Cl2O (110.9°), (CH3)2O (111.7°), and N(CH3)3 (110.9°).[32] Gillespie and Robinson rationalize the Si-O-Si bond angle based on the observed ability of a ligand's lone pair to most greatly repel other electron pairs when the ligand electronegativity is greater than or equal to that of the central atom.[32] In O(SiH3)2, the central atom is more electronegative, and the lone pairs are less localized and more weakly repulsive. The larger Si-O-Si bond angle results from this and strong ligand-ligand repulsion by the relatively large -SiH3 ligand.[32]Some AX6E1 and AX8E1 molecules
Some AX6E1 molecules, e.g. xenon hexafluoride (XeF6) and the Te(IV) and Bi(III) anions, TeCl2−
6, TeBr2−
6, BiCl3−
6, BiBr3−
6 and BiI3−
6, are octahedra, rather than pentagonal pyramids, and the lone pair does not affect the geometry to the degree predicted by VSEPR.[40] One rationalization is that steric crowding of the ligands allows little or no room for the non-bonding lone pair;[32] another rationalization is the inert pair effect.[41] Similarly, the octafluoroxenate anion (XeF2−
8) is a square antiprism and not a distorted square antiprism (as predicted by VSEPR theory for an AX8E1 molecule), despite having a lone pair.
Odd-electron molecules
The VSEPR theory can be extended to molecules with an odd number of electrons by treating the unpaired electron as a "half electron pair" — for example, Gillespie and Nyholm[42] suggested that the decrease in the bond angle in the series NO+2 (180°), NO2 (134°), NO−
2 (115°) indicates that a given set of bonding electron pairs exert a weaker repulsion on a single non-bonding electron than on a pair of non-bonding electrons. In effect, they considered nitrogen dioxide as an AX2E0.5 molecule with a geometry intermediate between NO+
2 and NO−
2. Similarly chlorine dioxide (ClO2) is AX2E1.5 with a geometry intermediate between ClO+
2 and ClO−
2.[citation needed]
Finally the methyl radical (CH3) is predicted to be trigonal pyramidal like the methyl anion (CH−
3), but with a larger bond angle as in the trigonal planar methyl cation (CH+
3). However in this case the VSEPR prediction is not quite true, as CH3 is actually planar, although its distortion to a pyramidal geometry requires very little energy.[43]







But evolution is not obvious at all, and it took thought and experiment and hard tenacious graft to reveal that truth. The real structure of the universe – the atomic, subatomic and quantum – was concealed from our eyes for all but the tiniest fragment of our tenure on Earth. We humans are awful at perceiving objective reality. We come with inbuilt preconceptions and prejudices. We’re dreadful at logic, and see patterns in things that are not there, and skip over trends that are. We attribute cause and agency to chance and coincidence, and blame the innocent as the root of all manner of evil. We use the phrase “common sense” as an admirable quality for scrutinising the world in front of us.
If this all sounds misanthropic, it’s not. Blind, directionless evolution gave us the gumption and the tools to frown at what we see, and ask if it really is how things are. Science is quite the opposite of common sense.
Common sense deceives us all the time: the horizon tells me the Earth is flat; people seem to get better after taking homeopathic pills; spiders are dangerous; a cold snap ridicules global warming. Of course, it is tricky to challenge someone’s opinion successfully if it is based on their learned experience. But that is exactly what science is for. It is to extract human flaws from reality; it is to set aside the bias that we lug around. Our senses and psychology perceive the world in very particular ways that are comically easy to fool. But the great strength of science is that it recognises the human fallibility that cripples our view of the universe. The scientific method attempts to remove these weaknesses.
That is why this should be instilled in us from as early as possible. At school, the facts must be taught, and the histories of those discoveries too. But we must bequeath the next generations the tools to question our limited perception – science as a way of knowing. It is frequently said – often by people like me – that children are born scientists, that their curiosity is inbuilt, and that this is eroded by age. It’s a pleasant sentiment, and certainly children are unsullied by the baggage of a life.
But children are not scientists. As ever, anything of value comes with effort, not by grace. Science is a particular way of thinking, not beset but enabled by doubt, and it comes from teaching. Somewhere in the country there is an eight-year-old girl who will change the world and win a Nobel prize for it. She will make people healthier, or see new stars, or merely reveal wonder. But it will be because her parents and teachers have taught her not to be satisfied with how things appear, and given her the tools to think critically and force the universe to reveal its true nature.
I was prompted to write this after I wrote on the biological non-existence of “race” a few weeks ago, and this prompted ire (and plenty of charmless racial abuse). Much of the commentariat was expressing the view that “obviously race exists because people look different, and these differences broadly cluster into traditional descriptions of race – blacks, whites, Asians”.