Molecular geometry

From Wikipedia, the free encyclopedia

Geometry of the water molecule

Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It determines several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism, and biological activity.^[1][2] The angles between bonds that an atom forms depend only weakly on the rest of molecule, i.e. they can be understood as approximately local and hence transferable properties.

Molecular geometry determination

The molecular geometry can be determined by various spectroscopic methods and diffraction methods. IR, microwave and Raman spectroscopy can give information about the molecule geometry from the details of the vibrational and rotational absorbance detected by these techniques. X-ray crystallography, neutron diffraction and electron diffraction can give molecular structure for crystalline solids based on the distance between nuclei and concentration of electron density. Gas electron diffraction can be used for small molecules in the gas phase. NMR and FRET methods can be used to determine complementary information including relative distances, ^[3][4][5] dihedral angles, ^[6][7] angles, and connectivity. Molecular geometries are best determined at low temperature because at higher temperatures the molecular structure is averaged over more accessible geometries (see next section). Larger molecules often exist in multiple stable geometries (conformational isomerism) that are close in energy on the potential energy surface. Geometries can also be computed by ab initio quantum chemistry methods to high accuracy. The molecular geometry can be different as a solid, in solution, and as a gas.

The position of each atom is determined by the nature of the chemical bonds by which it is connected to its neighboring atoms. The molecular geometry can be described by the positions of these atoms in space, evoking bond lengths of two joined atoms, bond angles of three connected atoms, and torsion angles (dihedral angles) of three consecutive bonds.

The influence of thermal excitation

Since the motions of the atoms in a molecule are determined by quantum mechanics, one must define “motion” in a quantum mechanical way. The overall (external) quantum mechanical motions translation and rotation hardly change the geometry of the molecule. (To some extent rotation influences the geometry via Coriolis forces and centrifugal distortion, but this is negligible for the present discussion.) In addition to translation and rotation, a third type of motion is molecular vibration, which corresponds to internal motions of the atoms such as bond stretching and bond angle variation. The molecular vibrations are harmonic (at least to good approximation), and the atoms oscillate about their equilibrium positions, even at the absolute zero of temperature. At absolute zero all atoms are in their vibrational ground state and show zero point quantum mechanical motion, so that the wavefunction of a single vibrational mode is not a sharp peak, but an exponential of finite width (the wavefunction for n = 0 depicted in the article on the quantum harmonic oscillator). At higher temperatures the vibrational modes may be thermally excited (in a classical interpretation one expresses this by stating that “the molecules will vibrate faster”), but they oscillate still around the recognizable geometry of the molecule.

To get a feeling for the probability that the vibration of molecule may be thermally excited, we inspect the Boltzmann factor , where 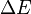is the excitation energy of the vibrational mode, the Boltzmann constant and the absolute temperature. At 298 K (25 °C), typical values for the Boltzmann factor β are: β = 0.089 for ΔE = 500 cm⁻¹ ; β = 0.008 for ΔE = 1000 cm⁻¹ ; β = 7×10⁻⁴ for ΔE = 1500 cm⁻¹. (The reciprocal centimeter is an energy unit that is commonly used in infrared spectroscopy; 1 cm⁻¹ corresponds to 1.23984×10⁻⁴ eV). When an excitation energy is 500 cm⁻¹, then about 8.9 percent of the molecules are thermally excited at room temperature. To put this in perspective: the lowest excitation vibrational energy in water is the bending mode (about 1600 cm⁻¹). Thus, at room temperature less than 0.07 percent of all the molecules of a given amount of water will vibrate faster than at absolute zero.

As stated above, rotation hardly influences the molecular geometry. But, as a quantum mechanical motion, it is thermally excited at relatively (as compared to vibration) low temperatures. From a classical point of view it can be stated that at higher temperatures more molecules will rotate faster, which implies that they have higher angular velocity and angular momentum. In quantum mechanically language: more eigenstates of higher angular momentum become thermally populated with rising temperatures. Typical rotational excitation energies are on the order of a few cm⁻¹. The results of many spectroscopic experiments are broadened because they involve an averaging over rotational states. It is often difficult to extract geometries from spectra at high temperatures, because the number of rotational states probed in the experimental averaging increases with increasing temperature. Thus, many spectroscopic observations can only be expected to yield reliable molecular geometries at temperatures close to absolute zero, because at higher temperatures too many higher rotational states are thermally populated.

Bonding

Molecules, by definition, are most often held together with covalent bonds involving single, double, and/or triple bonds, where a "bond" is a shared pair of electrons (the other method of bonding between atoms is called ionic bonding and involves a positive cation and a negative anion).

Molecular geometries can be specified in terms of bond lengths, bond angles and torsional angles. The bond length is defined to be the average distance between the nuclei of two atoms bonded together in any given molecule. A bond angle is the angle formed between three atoms across at least two bonds. For four atoms bonded together in a chain, the torsional angle is the angle between the plane formed by the first three atoms and the plane formed by the last three atoms.

There exists a mathematical relationship among the bond angles for one central atom and four peripheral atoms (labeled 1 through 4) expressed by the following determinant. This constraint removes one degree of freedom from the choices of (originally) six free bond angles to leave only five choices of bond angles. (Note that the angles , , , and 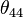are always zero.)

Molecular geometry is determined by the quantum mechanical behavior of the electrons. Using the valence bond approximation this can be understood by the type of bonds between the atoms that make up the molecule. When atoms interact to form a chemical bond, the atomic orbitals of each atom are said to combine in a process called orbital hybridisation. The two most common types of bonds are sigma bonds (usually formed by hybrid orbitals) and pi bonds (formed by unhybridized p orbitals for atoms of main group elements). The geometry can also be understood by molecular orbital theory where the electrons are delocalised.

An understanding of the wavelike behavior of electrons in atoms and molecules is the subject of quantum chemistry.

Isomers

Isomers are types of molecules that share a chemical formula but have different geometries, resulting in very different properties:

• A pure substance is composed of only one type of isomer of a molecule (all have the same geometrical structure).

• Structural isomers have the same chemical formula but different physical arrangements, often forming alternate molecular geometries with very different properties. The atoms are not bonded (connected) together in the same orders.
  • Functional isomers are special kinds of structural isomers, where certain groups of atoms exhibit a special kind of behavior, such as an ether or an alcohol.

• Stereoisomers may have many similar physicochemical properties (melting point, boiling point) and at the same time very different biochemical activities. This is because they exhibit a handedness that is commonly found in living systems. One manifestation of this chirality or handedness is that they have the ability to rotate polarized light in different directions.

• Protein folding concerns the complex geometries and different isomers that proteins can take.

Types of molecular structure

Some common shapes of simple molecules include:

• Linear: In a linear model, atoms are connected in a straight line. The bond angles are set at 180°. A bond angle is very simply the geometric angle between two adjacent bonds. For example, carbon dioxide and nitric oxide have a linear molecular shape.
• Trigonal planar: Just from its name, it can easily be said that molecules with the trigonal planar shape are somewhat triangular and in one plane (flat). Consequently, the bond angles are set at 120°. An example of this is boron trifluoride.
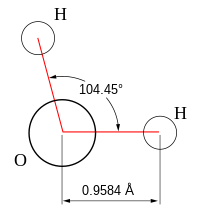
• Bent: Bent or angular molecules have a non-linear shape. A good example is water, or H₂O, which has an angle of about 105°. A water molecule has two pairs of bonded electrons and two unshared lone pairs.
• Tetrahedral: Tetra- signifies four, and -hedral relates to a face of a solid, so "tetrahedral" literally means "having four faces". This shape is found when there are four bonds all on one central atom, with no extra unshared electron pairs. In accordance with the VSEPR (valence-shell electron pair repulsion theory), the bond angles between the electron bonds are arccos(−1/3) = 109.47°. An example of a tetrahedral molecule is methane (CH₄).
• Octahedral: Octa- signifies eight, and -hedral relates to a face of a solid, so "octahedral" literally means "having eight faces". The bond angle is 90 degrees. An example of an octahedral molecule is sulfur hexafluoride (SF₆).
• Trigonal pyramidal: A trigonal pyramidal molecule has a pyramid-like shape with a triangular base. Unlike the linear and trigonal planar shapes but similar to the tetrahedral orientation, pyramidal shapes require three dimensions in order to fully separate the electrons. Here, there are only three pairs of bonded electrons, leaving one unshared lone pair. Lone pair – bond pair repulsions change the bond angle from the tetrahedral angle to a slightly lower value.^[8] An example is NH₃ (ammonia).

VSEPR table

The bond angles in the table below are ideal angles from the simple VSEPR theory, followed by the actual angle for the example given in the following column where this differs. For many cases, such as trigonal pyramidal and bent, the actual angle for the example differs from the ideal angle, but all examples differ by different amounts. For example, the angle in H₂S (92°) differs from the tetrahedral angle by much more than the angle for H₂O (104.48°) does.

Bonding electron pairs	Lone pairs	Electron domains (Steric #)	Shape	Ideal bond angle (example's bond angle)	Example	Image
2	0	2	linear	180°	CO2
3	0	3	trigonal planar	120°	BF3
2	1	3	bent	120° (119°)	SO2
4	0	4	tetrahedral	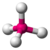109.5°	CH4
3	1	4	trigonal pyramidal	107.3°	NH3
2	2	4	bent	109.5° (104.48°)[9][10]	H2O
5	0	5	trigonal bipyramidal	90°, 120°, 180°	PCl5
4	1	5	seesaw	180°, 120°, 90° (173.1°, 101.6°)	SF4
3	2	5	T-shaped	90°, 180° (87.5°, < 180°)	ClF3
2	3	5	linear	180°	XeF2
6	0	6	octahedral	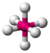90°, 180°	SF6
5	1	6	square pyramidal	90° (84.8°), 180°	BrF5
4	2	6	square planar	90°, 180°	XeF4
7	0	7	pentagonal bipyramidal	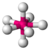90°, 72°, 180°	IF7
6	1	7	pentagonal pyramidal	72°, 90°, 144°	XeOF5−
5	2	7	planar pentagonal	72°, 144°	XeF5−
8	0	8	square antiprismatic		XeF82−
9	0	9	tricapped trigonal prismatic		ReH92−

3D representations

• Line or stick – atomic nuclei are not represented, just the bonds as sticks or lines. As in 2D molecular structures of this type, atoms are implied at each vertex.

• Electron density plot – shows the electron density determined either crystallographically or using quantum mechanics rather than distinct atoms or bonds.

• Ball and stick – atomic nuclei are represented by spheres (balls) and the bonds as sticks.

• Spacefilling models or CPK models (also an atomic coloring scheme in representations) – the molecule is represented by overlapping spheres representing the atoms.

• Cartoon – a representation used for proteins where loops, beta sheets, alpha helices are represented diagrammatically and no atoms or bonds are represented explicitly just the protein backbone as a smooth pipe.

The greater the amount of lone pairs contained in a molecule the smaller the angles between the atoms of that molecule. The VSEPR theory predicts that lone pairs repel each other, thus pushing the different atoms away from them.

Linear combination of atomic orbitals

From Wikipedia, the free encyclopedia

A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry.^[1] In quantum mechanics, electron configurations of atoms are described as wavefunctions. In mathematical sense, these wave functions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond.

It was introduced in 1929 by Sir John Lennard-Jones with the description of bonding in the diatomic molecules of the first main row of the periodic table, but had been used earlier by Linus Pauling for H₂⁺.^[2][3]

A mathematical description follows.

An initial assumption is that the number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion. In a sense, n atomic orbitals combine to form n molecular orbitals, which can be numbered i = 1 to n and which may not all be the same. The expression (linear expansion) for the i th molecular orbital would be:

or

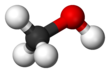
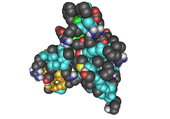
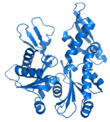
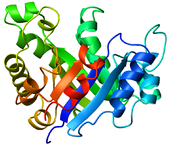
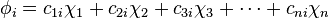
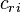where (phi) is a molecular orbital represented as the sum of n atomic orbitals (chi), each multiplied by a corresponding coefficient , and r (numbered 1 to n) represents which atomic orbital is combined in the term. The coefficients are the weights of the contributions of the n atomic orbitals to the molecular orbital. The Hartree–Fock procedure is used to obtain the coefficients of the expansion.

The orbitals are thus expressed as linear combinations of basis functions, and the basis functions are one-electron functions centered on nuclei of the component atoms of the molecule. The atomic orbitals used are typically those of hydrogen-like atoms since these are known analytically i.e. Slater-type orbitals but other choices are possible like Gaussian functions from standard basis sets.

By minimizing the total energy of the system, an appropriate set of coefficients of the linear combinations is determined. This quantitative approach is now known as the Hartree–Fock method. However, since the development of computational chemistry, the LCAO method often refers not to an actual optimization of the wave function but to a qualitative discussion which is very useful for predicting and rationalizing results obtained via more modern methods. In this case, the shape of the molecular orbitals and their respective energies are deduced approximately from comparing the energies of the atomic orbitals of the individual atoms (or molecular fragments) and applying some recipes known as level repulsion and the like. The graphs that are plotted to make this discussion clearer are called correlation diagrams. The required atomic orbital energies can come from calculations or directly from experiment via Koopmans' theorem.

This is done by using the symmetry of the molecules and orbitals involved in bonding. The first step in this process is assigning a point group to the molecule. A common example is water, which is of C_2v symmetry. Then a reducible representation of the bonding is determined demonstrated below for water:

Each operation in the point group is performed upon the molecule. The number of bonds that are unmoved is the character of that operation. This reducible representation is decomposed into the sum of irreducible representations. These irreducible representations correspond to the symmetry of the orbitals involved.

MO diagrams provide simple qualitative LCAO treatment.

Quantitative theories are the Hückel method, the extended Hückel method and the Pariser–Parr–Pople method.