From Wikipedia, the free encyclopedia
In physics, gravitational waves are ripples in the curvature of spacetime that propagate as a wave, travelling outward from the source. Predicted in 1916[1][2] by Albert Einstein to exist on the basis of his theory of general relativity,[3][4] gravitational waves theoretically transport energy as gravitational radiation. Sources of detectable gravitational waves could possibly include binary star systems composed of white dwarfs, neutron stars, or black holes. The existence of gravitational waves is a possible consequence of the Lorentz invariance of general relativity since it brings the concept of a limiting speed of propagation of the physical interactions with it. Gravitational waves cannot exist in the Newtonian theory of gravitation, in which physical interactions propagate at infinite speed.
Although gravitational radiation has not been directly detected, there is indirect evidence for its existence.[5] For example, the 1993 Nobel Prize in Physics was awarded for measurements of the Hulse–Taylor binary system that suggests gravitational waves are more than mathematical anomalies. Various gravitational wave detectors exist and on 17 March 2014, astronomers at the Harvard–Smithsonian Center for Astrophysics claimed that they had detected and produced "the first direct image of gravitational waves across the primordial sky" within the cosmic microwave background, providing strong evidence for inflation and the Big Bang.[6][7][8][9][5] Peer review will be needed before there can be any scientific consensus about these new findings.[10][11] On 19 June 2014, lowered confidence in confirming the cosmic inflation findings was reported;[12][13][14] on 19 September 2014, a further reduction in confidence was reported[15][16] and, on 30 January 2015, even less confidence yet was reported.[17][18]
Introduction

History of the Universe - gravitational waves are hypothesized to arise from cosmic inflation, a faster-than-light expansion just after the Big Bang (17 March 2014).[6][8][9]
In Einstein's theory of general relativity, gravity is treated as a phenomenon resulting from the curvature of spacetime. This curvature is caused by the presence of mass. Generally, the more mass that is contained within a given volume of space, the greater the curvature of spacetime will be at the boundary of this volume.[5] As objects with mass move around in spacetime, the curvature changes to reflect the changed locations of those objects. In certain circumstances, accelerating objects generate changes in this curvature, which propagate outwards at the speed of light in a wave-like manner. These propagating phenomena are known as gravitational waves.
As a gravitational wave passes a distant observer, that observer will find spacetime distorted by the effects of strain. Distances between free objects increase and decrease rhythmically as the wave passes, at a frequency corresponding to that of the wave. This occurs despite such free objects never being subjected to an unbalanced force. The magnitude of this effect decreases inversely with distance from the source. Inspiralling binary neutron stars are predicted to be a powerful source of gravitational waves as they coalesce, due to the very large acceleration of their masses as they orbit close to one another. However, due to the astronomical distances to these sources the effects when measured on Earth are predicted to be very small, having strains of less than 1 part in 1020. Scientists are attempting to demonstrate the existence of these waves with ever more sensitive detectors. The current most sensitive measurement is about one part in 5×1022 (as of 2012) provided by the LIGO and VIRGO observatories.[19] The lack of detection in these observatories provides an upper limit on the frequency of such powerful sources.[20][21] A space based observatory, the Laser Interferometer Space Antenna, is currently under development by ESA.
Gravitational waves should penetrate regions of space that electromagnetic waves cannot. It is hypothesized that they will be able to provide observers on Earth with information about black holes and other exotic objects in the distant Universe. Such systems cannot be observed with more traditional means such as optical telescopes and radio telescopes. In particular, gravitational waves could be of interest to cosmologists as they offer a possible way of observing the very early universe. This is not possible with conventional astronomy, since before recombination the universe was opaque to electromagnetic radiation.[22] Precise measurements of gravitational waves will also allow scientists to test the general theory of relativity more thoroughly.
In principle, gravitational waves could exist at any frequency. However, very low frequency waves would be impossible to detect and there is no credible source for detectable waves of very high frequency. Stephen W. Hawking and Werner Israel list different frequency bands for gravitational waves that could be plausibly detected, ranging from 10−7 Hz up to 1011 Hz.[23]
Effects of a passing gravitational wave
The effects of a passing gravitational wave can be visualized by imagining a perfectly flat region of spacetime with a group of motionless test particles lying in a plane (the surface of your screen). As a gravitational wave passes through the particles along a line perpendicular to the plane of the particles (i.e. following your line of vision into the screen), the particles will follow the distortion in spacetime, oscillating in a "cruciform" manner, as shown in the animations. The area enclosed by the test particles does not change and there is no motion along the direction of propagation.
The oscillations depicted here in the animation are exaggerated for the purpose of discussion—in reality a gravitational wave has a very small amplitude (as formulated in linearized gravity). However they enable us to visualize the kind of oscillations associated with gravitational waves as produced for example by a pair of masses in a circular orbit. In this case the amplitude of the gravitational wave is a constant, but its plane of polarization changes or rotates at twice the orbital rate and so the time-varying gravitational wave size (or 'periodic spacetime strain') exhibits a variation as shown in the animation.[24] If the orbit is elliptical then the gravitational wave's amplitude also varies with time according to Einstein's quadrupole formula.[25]
Like other waves, there are a few useful characteristics describing a gravitational wave:
- Amplitude: Usually denoted
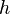 , this is the size of the wave — the fraction of stretching or squeezing in the animation. The amplitude shown here is roughly
, this is the size of the wave — the fraction of stretching or squeezing in the animation. The amplitude shown here is roughly  (or 50%). Gravitational waves passing through the Earth are many billions times weaker than this —
(or 50%). Gravitational waves passing through the Earth are many billions times weaker than this —  . Note that this is not the quantity that would be analogous to what is usually called the amplitude of an electromagnetic wave, which would be
. Note that this is not the quantity that would be analogous to what is usually called the amplitude of an electromagnetic wave, which would be  .
. - Frequency: Usually denoted f, this is the frequency with which the wave oscillates (1 divided by the amount of time between two successive maximum stretches or squeezes)
- Wavelength: Usually denoted
 , this is the distance along the wave between points of maximum stretch or squeeze.
, this is the distance along the wave between points of maximum stretch or squeeze. - Speed: This is the speed at which a point on the wave (for example, a point of maximum stretch or squeeze) travels. For gravitational waves with small amplitudes, this is equal to the speed of light,
 .
.
In the example just discussed, we actually assume something special about the wave. We have assumed that the wave is linearly polarized, with a "plus" polarization, written
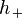 . Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are at 45 degrees, as opposed to 90 degrees. In particular, if we had a "cross"-polarized gravitational wave,
. Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are at 45 degrees, as opposed to 90 degrees. In particular, if we had a "cross"-polarized gravitational wave,  , the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarized waves. Gravitational waves are polarized because of the nature of their sources. The polarization of a wave depends on the angle from the source, as we will see in the next section.
, the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarized waves. Gravitational waves are polarized because of the nature of their sources. The polarization of a wave depends on the angle from the source, as we will see in the next section.Sources of gravitational waves
In general terms, gravitational waves are radiated by objects whose motion involves acceleration, provided that the motion is not perfectly spherically symmetric (like an expanding or contracting sphere) or cylindrically symmetric (like a spinning disk or sphere). A simple example of this principle is provided by the spinning dumbbell. If the dumbbell spins like wheels on an axle, it will not radiate gravitational waves; if it tumbles end over end like two planets orbiting each other, it will radiate gravitational waves. The heavier the dumbbell, and the faster it tumbles, the greater is the gravitational radiation it will give off. If we imagine an extreme case in which the two weights of the dumbbell are massive stars like neutron stars or black holes, orbiting each other quickly, then significant amounts of gravitational radiation would be given off.Some more detailed examples:
- Two objects orbiting each other in a quasi-Keplerian planar orbit (basically, as a planet would orbit the Sun) will radiate.
- A spinning non-axisymmetric planetoid — say with a large bump or dimple on the equator — will radiate.
- A supernova will radiate except in the unlikely event that the explosion is perfectly symmetric.
- An isolated non-spinning solid object moving at a constant velocity will not radiate. This can be regarded as a consequence of the principle of conservation of linear momentum.
- A spinning disk will not radiate. This can be regarded as a consequence of the principle of conservation of angular momentum. However, it will show gravitomagnetic effects.
- A spherically pulsating spherical star (non-zero monopole moment or mass, but zero quadrupole moment) will not radiate, in agreement with Birkhoff's theorem.
Power radiated by orbiting bodies

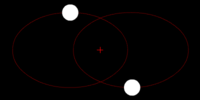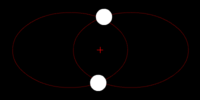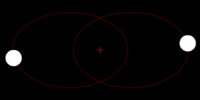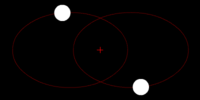
Two stars of dissimilar mass are in circular orbits. Each revolves about their common center of mass (denoted by the small red cross) in a circle with the larger mass having the smaller orbit.
Gravitational waves carry energy away from their sources and, in the case of orbiting bodies, this is associated with an inspiral or decrease in orbit. Imagine for example a simple system of two masses — such as the Earth-Sun system — moving slowly compared to the speed of light in circular orbits. Assume that these two masses orbit each other in a circular orbit in the
 –
– plane. To a good approximation, the masses follow simple Keplerian orbits. However, such an orbit represents a changing quadrupole moment. That is, the system will give off gravitational waves.
plane. To a good approximation, the masses follow simple Keplerian orbits. However, such an orbit represents a changing quadrupole moment. That is, the system will give off gravitational waves.Suppose that the two masses are
 and
and 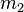 , and they are separated by a distance
, and they are separated by a distance  . The power given off (radiated) by this system is:
. The power given off (radiated) by this system is: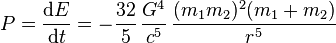 ,[26]
,[26]
 is about 1.5×1011 m and
is about 1.5×1011 m and  and
and 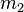 are about 2×1030 and 6×1024 kg respectively. In this case, the power is about 200 watts. This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86×1026 watts).
are about 2×1030 and 6×1024 kg respectively. In this case, the power is about 200 watts. This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86×1026 watts).In theory, the loss of energy through gravitational radiation could eventually drop the Earth into the Sun. However, the total energy of the Earth orbiting the Sun (kinetic energy + gravitational potential energy) is about 1.14×1036 joules of which only 200 joules per second is lost through gravitational radiation, leading to a decay in the orbit by about 1×10−15 meters per day or roughly the diameter of a proton. At this rate, it would take the Earth approximately 1×1013 times more than the current age of the Universe to spiral onto the Sun. This estimate overlooks the decrease in r over time, but the majority of the time the bodies are far apart and only radiating slowly, so the difference is unimportant in this example.
A more dramatic example of radiated gravitational energy is represented by two solar mass (M☉) neutron stars orbiting at a distance from each other of 1.89×108 m (only 0.63 light-seconds apart). [The Sun is 8 light minutes from the Earth.] Plugging their masses into the above equation shows that the gravitational radiation from them would be 1.38×1028 watts, which is about 100 times more than the Sun's electromagnetic radiation.
Orbital decay from gravitational radiation
Gravitational radiation robs the orbiting bodies of energy. It first circularizes their orbits and then gradually shrinks their radius. As the energy of the orbit is reduced, the distance between the bodies decreases, and they rotate more rapidly. The overall angular momentum is reduced however. This reduction corresponds to the angular momentum carried off by gravitational radiation. The rate of decrease of distance between the bodies versus time is given by:[26] ,
,
The orbit decays at a rate proportional to the inverse third power of the radius. When the radius has shrunk to half its initial value, it is shrinking eight times faster than before. By Kepler's Third Law, the new rotation rate at this point will be faster by
 , or nearly three times the previous orbital frequency. As the radius decreases, the power lost to gravitational radiation increases even more. As can be seen from the previous equation, power radiated varies as the inverse fifth power of the radius, or 32 times more in this case.
, or nearly three times the previous orbital frequency. As the radius decreases, the power lost to gravitational radiation increases even more. As can be seen from the previous equation, power radiated varies as the inverse fifth power of the radius, or 32 times more in this case.If we use the previous values for the Sun and the Earth, we find that the Earth's orbit shrinks by 1.1×10−20 meter per second. This is 3.5×10−13 m per year, which is about 1/300 the diameter of a hydrogen atom. The effect of gravitational radiation on the size of the Earth's orbit is negligible over the age of the universe. This is not true for closer orbits.
A more practical example is the orbit of a Sun-like star around a heavy black hole. Our Milky Way has a, potential, 4 million M☉ black hole at its center in Sagittarius A. Such supermassive black holes are being found in the center of almost all galaxies. For this example take a 2 million M☉ black hole with a solar-mass star orbiting it at a radius of 1.89×1010 m (63 light-seconds). The mass of the black hole will be 4×1036 kg and its gravitational radius will be 6×109 m. The orbital period will be 1,000 seconds, or a little under 17 minutes. The solar-mass star will draw closer to the black hole by 7.4 meters per second or 7.4 km per orbit. A collision will not be long in coming.
Assume that a pair of 1 M☉ neutron stars are in circular orbits at a distance of 1.89×108 m (189,000 km). This is a little less than 1/7 the diameter of the Sun or 0.63 light-seconds. Their orbital period would be 1,000 seconds. Substituting the new mass and radius in the above formula gives a rate of orbit decrease of 3.7×10−6 m/s or 3.7 mm per orbit. This is 116 meters per year and is not negligible over cosmic time scales.
Suppose instead that these two neutron stars were orbiting at a distance of 1.89×106 m (1890 km). Their period would be 1 second and their orbital velocity would be about 1/50 of the speed of light. Their orbit would now shrink by 3.7 meters per orbit. A collision is imminent. A runaway loss of energy from the orbit results in an ever more rapid decrease in the distance between the stars. They will eventually merge to form a black hole and cease to radiate gravitational waves. This is referred to as the inspiral.
The above equation can not be applied directly for calculating the lifetime of the orbit, because the rate of change in radius depends on the radius itself, and is thus non-constant with time. The lifetime can be computed by integration of this equation (see next section).
Orbital lifetime limits from gravitational radiation
Orbital lifetime is one of the most important properties of gravitational radiation sources. It determines the average number of binary stars in the universe that are close enough to be detected. Short lifetime binaries are strong sources of gravitational radiation but are few in number. Long lifetime binaries are more plentiful but they are weak sources of gravitational waves. LIGO is most sensitive in the frequency band where two neutron stars are about to merge.This time frame is only a few seconds. It takes luck for the detector to see this blink in time out of a million year orbital lifetime. It is predicted that such a merger will only be seen once per decade or so.
The lifetime of an orbit is given by:[26]
 ,
,
Substituting the values for the mass of the Sun and Earth as well as the orbital radius gives a very large lifetime of 3.44×1030 seconds or 1.09×1023 years (that is approximately 1013 times larger than the age of the universe). The actual figure would be slightly less than that. The Earth will break apart from tidal forces if it orbits closer than a few radii from the Sun. This would form a ring around the Sun and instantly stop the emission of gravitational waves.
If we use a 2 million M☉ black hole with a solar mass star orbiting it at 1.89×1010 meters, we get a lifetime of 6.50×108 seconds or 20.7 years.
Assume that a pair of solar mass neutron stars with a diameter of 10 kilometers are in circular orbits at a distance of 1.89×108 m (189,000 km). Their lifetime is 1.30×1013 seconds or about 414,000 years. Their orbital period will be 1,000 seconds and it could be observed by LISA if they were not too far away. A far greater number of white dwarf binaries exist with orbital periods in this range. White dwarf binaries have masses on the order of our Sun and diameters on the order of our Earth. They cannot get much closer together than 10,000 km before they will merge and cease to radiate gravitational waves. This results in the creation of either a neutron star or a black hole. Until then, their gravitational radiation will be comparable to that of a neutron star binary. LISA is the only gravitational wave experiment that is likely to succeed in detecting such types of binaries.
If the orbit of a neutron star binary has decayed to 1.89×106m (1890 km), its remaining lifetime is 130,000 seconds or about 36 hours. The orbital frequency will vary from 1 revolution per second at the start and 918 revolutions per second when the orbit has shrunk to 20 km at merger. The gravitational radiation emitted will be at twice the orbital frequency. Just before merger, the inspiral can be observed by LIGO if the binary is close enough. LIGO has only a few minutes to observe this merger out of a total orbital lifetime that may have been billions of years. The chance of success with LIGO as initially constructed is quite low despite the large number of such mergers occurring in the universe, because the sensitivity of the instrument does not 'reach' out to enough systems to see events frequently.
No mergers have been seen in the few years that initial LIGO has been in operation, and it is thought that a merger should be seen about once per several tens of years of observing time with initial LIGO.[27] The upgraded Advanced LIGO detector, with a ten times greater sensitivity, 'reaches' out 10 times further—encompassing a volume 1000 times greater, and seeing 1000 times as many candidate sources. Thus, the expectation is that detections will be made at the rate of tens per year.
Wave amplitudes from the Earth–Sun system
We can also think in terms of the amplitude of the wave from a system in circular orbits. Let be the angle between the perpendicular to the plane of the orbit and the line of sight of the observer. Suppose that an observer is outside the system at a distance
be the angle between the perpendicular to the plane of the orbit and the line of sight of the observer. Suppose that an observer is outside the system at a distance  from its center of mass. If R is much greater than a wavelength, the two polarizations of the wave will be
from its center of mass. If R is much greater than a wavelength, the two polarizations of the wave will be -
- plane then
plane then  , and
, and  , so the
, so the  polarization is always zero. We also see that the frequency of the wave given off is twice the rotation frequency. If we put in numbers for the Earth-Sun system, we find:
polarization is always zero. We also see that the frequency of the wave given off is twice the rotation frequency. If we put in numbers for the Earth-Sun system, we find:Radiation from other sources
Although the waves from the Earth-Sun system are minuscule, astronomers can point to other sources for which the radiation should be substantial. One important example is the Hulse-Taylor binary — a pair of stars, one of which is a pulsar.[28] The characteristics of their orbit can be deduced from the Doppler shifting of radio signals given off by the pulsar. Each of the stars are about 1.4 M☉ and the size of their orbit is about 1/75 of the Earth-Sun orbit. This means the distance between the two stars is just a few times larger than the diameter of our own Sun. The combination of greater masses and smaller separation means that the energy given off by the Hulse-Taylor binary will be far greater than the energy given off by the Earth-Sun system — roughly 1022 times as much.The information about the orbit can be used to predict just how much energy (and angular momentum) should be given off in the form of gravitational waves. As the energy is carried off, the stars should draw closer to each other. This effect is called an inspiral, and it can be observed in the pulsar's signals. The measurements on the Hulse-Taylor system have been carried out over more than 30 years. It has been shown that the gravitational radiation predicted by general relativity allows these observations to be matched within 0.2 percent. In 1993, Russell Hulse and Joe Taylor were awarded the Nobel Prize in Physics for this work, which was the first indirect evidence for gravitational waves. The orbital lifetime of this binary system before merger is a few hundred million years.[29]
Inspirals are very important sources of gravitational waves. Any time two compact objects (white dwarfs, neutron stars, or black holes) are in close orbits, they send out intense gravitational waves. As they spiral closer to each other, these waves become more intense. At some point they should become so intense that direct detection by their effect on objects on Earth or in space is possible. This direct detection is the goal of several large scale experiments.[30]
The only difficulty is that most systems like the Hulse-Taylor binary are so far away. The amplitude of waves given off by the Hulse-Taylor binary as seen on Earth would be roughly h ≈ 10−26. There are some sources, however, that astrophysicists expect to find with much larger amplitudes of h ≈ 10−20. At least eight other binary pulsars have been discovered.[31]
Astrophysics and gravitational waves

Two-dimensional representation of gravitational waves generated by two neutron stars orbiting each other.
During the past century, astronomy has been revolutionized by the use of new methods for observing the universe.
Astronomical observations were originally made using visible light. Galileo Galilei pioneered the use of telescopes to enhance these observations. However, visible light is only a small portion of the electromagnetic spectrum, and not all objects in the distant universe shine strongly in this particular band. More useful information may be found, for example, in radio wavelengths. Using radio telescopes, astronomers have found pulsars, quasars, and other extreme objects that push the limits of our understanding of physics. Observations in the microwave band have opened our eyes to the faint imprints of the Big Bang, a discovery Stephen Hawking called the "greatest discovery of the century, if not all time". Similar advances in observations using gamma rays, x-rays, ultraviolet light, and infrared light have also brought new insights to astronomy. As each of these regions of the spectrum has opened, new discoveries have been made that could not have been made otherwise. Astronomers hope that the same holds true of gravitational waves.
Gravitational waves have two important and unique properties. First, there is no need for any type of matter to be present nearby in order for the waves to be generated by a binary system of uncharged black holes, which would emit no electromagnetic radiation. Second, gravitational waves can pass through any intervening matter without being scattered significantly. Whereas light from distant stars may be blocked out by interstellar dust, for example, gravitational waves will pass through essentially unimpeded. These two features allow gravitational waves to carry information about astronomical phenomena never before observed by humans.
The sources of gravitational waves described above are in the low-frequency end of the gravitational-wave spectrum (10−7 to 105 Hz). An astrophysical source at the high-frequency end of the gravitational-wave spectrum (above 105 Hz and probably 1010 Hz) generates[clarification needed] relic gravitational waves that are theorized to be faint imprints of the Big Bang like the cosmic microwave background (see gravitational wave background).[32] At these high frequencies it is potentially possible that the sources may be "man made"[23] that is, gravitational waves generated and detected in the laboratory.[33][34]
Energy, momentum, and angular momentum carried by gravitational waves
Waves familiar from other areas of physics such as water waves, sound waves, and electromagnetic waves are able to carry energy, momentum, and angular momentum. By carrying these away from a source, waves are able to rob that source of its energy as well as its linear and angular momentum. Gravitational waves perform the same function. Thus, for example, a binary system loses angular momentum as the two orbiting objects spiral towards each other—the angular momentum is radiated away by gravitational waves.The waves can also carry off linear momentum, a possibility that has some interesting implications for astrophysics.[35] After two supermassive black holes coalesce, emission of linear momentum can produce a "kick" with amplitude as large as 4000 km/s. This is fast enough to eject the coalesced black hole completely from its host galaxy. Even if the kick is too small to eject the black hole completely, it can remove it temporarily from the nucleus of the galaxy, after which it will oscillate about the center, eventually coming to rest.[36] A kicked black hole can also carry a star cluster with it, forming a hyper-compact stellar system.[37] Or it may carry gas, allowing the recoiling black hole to appear temporarily as a "naked quasar". The quasar SDSS J092712.65+294344.0 is believed to contain a recoiling supermassive black hole.[38]
Detecting gravitational waves
Difficulties in detection

Evidence of gravitational waves in the infant universe may have been uncovered by the BICEP2 radio telescope. The microscopic examination of the focal plane of the BICEP2 detector is shown here.[6][7][8][9][11]
Gravitational waves are not easily detectable. This knowledge gap is primarily due to the massive presence of noise in the low frequencies where antennas currently operate. Gravitational waves are expected to have frequencies
 .[39]
.[39]Ground-based interferometers
Though the Hulse-Taylor observations were very important, they give only indirect evidence for gravitational waves. A more conclusive observation would be a direct measurement of the effect of a passing gravitational wave, which could also provide more information about the system that generated it. Any such direct detection is complicated by the extraordinarily small effect the waves would produce on a detector. The amplitude of a spherical wave will fall off as the inverse of the distance from the source (the term in the formulas for
term in the formulas for 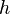 above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitude by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10−20, but generally no bigger.[40]
above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitude by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10−20, but generally no bigger.[40]A simple device theorised to detect the expected wave motion is called a Weber bar — a large, solid bar of metal isolated from outside vibrations. This type of instrument was the first type of gravitational wave detector. Strains in space due to an incident gravitational wave excite the bar's resonant frequency and could thus be amplified to detectable levels. Conceivably, a nearby supernova might be strong enough to be seen without resonant amplification. With this instrument, Joseph Weber claimed to have detected daily signals of gravitational waves. His results, however, were contested in 1974 by physicists Richard Garwin and David Douglass. Modern forms of the Weber bar are still operated, cryogenically cooled, with superconducting quantum interference devices to detect vibration. Weber bars are not sensitive enough to detect anything but extremely powerful gravitational waves.[41]
MiniGRAIL is a spherical gravitational wave antenna using this principle. It is based at Leiden University, consisting of an exactingly machined 1150 kg sphere cryogenically cooled to 20 mK.[42] The spherical configuration allows for equal sensitivity in all directions, and is somewhat experimentally simpler than larger linear devices requiring high vacuum. Events are detected by measuring deformation of the detector sphere. MiniGRAIL is highly sensitive in the 2–4 kHz range, suitable for detecting gravitational waves from rotating neutron star instabilities or small black hole mergers.[43]
A more sensitive class of detector uses laser interferometry to measure gravitational-wave induced motion between separated 'free' masses.[44] This allows the masses to be separated by large distances (increasing the signal size); a further advantage is that it is sensitive to a wide range of frequencies (not just those near a resonance as is the case for Weber bars). Ground-based interferometers are now operational. Currently, the most sensitive is LIGO — the Laser Interferometer Gravitational Wave Observatory. LIGO has three detectors: one in Livingston, Louisiana; the other two (in the same vacuum tubes) at the Hanford site in Richland, Washington. Each consists of two light storage arms that are 2 to 4 kilometers in length. These are at 90 degree angles to each other, with the light passing through 1m diameter vacuum tubes running the entire 4 kilometers. A passing gravitational wave will slightly stretch one arm as it shortens the other. This is precisely the motion to which an interferometer is most sensitive.
Even with such long arms, the strongest gravitational waves will only change the distance between the ends of the arms by at most roughly 10−18 meters. LIGO should be able to detect gravitational waves as small as
 . Upgrades to LIGO and other detectors such as Virgo, GEO 600, and TAMA 300 should increase the sensitivity still further; the next generation of instruments (Advanced LIGO and Advanced Virgo) will be more than ten times more sensitive. Another highly sensitive interferometer (LCGT) is currently in the design phase. A key point is that a tenfold increase in sensitivity (radius of 'reach') increases the volume of space accessible to the instrument by one thousand times. This increases the rate at which detectable signals should be seen from one per tens of years of observation, to tens per year.[27]
. Upgrades to LIGO and other detectors such as Virgo, GEO 600, and TAMA 300 should increase the sensitivity still further; the next generation of instruments (Advanced LIGO and Advanced Virgo) will be more than ten times more sensitive. Another highly sensitive interferometer (LCGT) is currently in the design phase. A key point is that a tenfold increase in sensitivity (radius of 'reach') increases the volume of space accessible to the instrument by one thousand times. This increases the rate at which detectable signals should be seen from one per tens of years of observation, to tens per year.[27]Interferometric detectors are limited at high frequencies by shot noise, which occurs because the lasers produce photons randomly; one analogy is to rainfall—the rate of rainfall, like the laser intensity, is measurable, but the raindrops, like photons, fall at random times, causing fluctuations around the average value. This leads to noise at the output of the detector, much like radio static. In addition, for sufficiently high laser power, the random momentum transferred to the test masses by the laser photons shakes the mirrors, masking signals at low frequencies. Thermal noise (e.g., Brownian motion) is another limit to sensitivity. In addition to these 'stationary' (constant) noise sources, all ground-based detectors are also limited at low frequencies by seismic noise and other forms of environmental vibration, and other 'non-stationary' noise sources; creaks in mechanical structures, lightning or other large electrical disturbances, etc. may also create noise masking an event or may even imitate an event. All these must be taken into account and excluded by analysis before a detection may be considered a true gravitational wave event.
Space-based interferometers, such as LISA and DECIGO, are also being developed. LISA's design calls for three test masses forming an equilateral triangle, with lasers from each spacecraft to each other spacecraft forming two independent interferometers. LISA is planned to occupy a solar orbit trailing the Earth, with each arm of the triangle being five million kilometers. This puts the detector in an excellent vacuum far from Earth-based sources of noise, though it will still be susceptible to shot noise, as well as artifacts caused by cosmic rays and solar wind.
There are currently two detectors focusing on detection at the higher end of the gravitational wave spectrum (10−7 to 105 Hz): one at University of Birmingham, England, and the other at INFN Genoa, Italy. A third is under development at Chongqing University, China. The Birmingham detector measures changes in the polarization state of a microwave beam circulating in a closed loop about one meter across. Two have been fabricated and they are currently expected to be sensitive to periodic spacetime strains of
 , given as an amplitude spectral density. The INFN Genoa detector is a resonant antenna consisting of two coupled spherical superconducting harmonic oscillators a few centimeters in diameter. The oscillators are designed to have (when uncoupled) almost equal resonant frequencies. The system is currently expected to have a sensitivity to periodic spacetime strains of
, given as an amplitude spectral density. The INFN Genoa detector is a resonant antenna consisting of two coupled spherical superconducting harmonic oscillators a few centimeters in diameter. The oscillators are designed to have (when uncoupled) almost equal resonant frequencies. The system is currently expected to have a sensitivity to periodic spacetime strains of 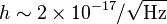 , with an expectation to reach a sensitivity of
, with an expectation to reach a sensitivity of  . The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ?g ~1010 Hz (10 GHz) and h ~10−30-10−31.
. The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ?g ~1010 Hz (10 GHz) and h ~10−30-10−31.Using pulsar timing arrays
Pulsars are rapidly rotating stars. A pulsar emits beams of radio waves that, like lighthouse beams, sweep through the sky as the pulsar rotates. The signal from a pulsar can be detected by radio telescopes as a series of regularly spaced pulses, essentially like the ticks of a clock. Gravitational waves affect the time it takes the pulses to travel from the pulsar to a telescope on Earth. A pulsar timing array uses millisecond pulsars to seek out perturbations due to gravitational waves in measurements of pulse arrival times at a telescope, in other words, to look for deviations in the clock ticks. In particular, pulsar timing arrays can search for a distinct pattern of correlation and anti-correlation between the signals over an array of different pulsars (resulting in the name "pulsar timing array"). Although pulsar pulses travel through space for hundreds or thousands of years to reach us, pulsar timing arrays are sensitive to perturbations in their travel time of much less than a millionth of a second.Globally there are three active pulsar timing array projects. The North American Nanohertz Gravitational Wave Observatory uses data collected by the Arecibo Radio Telescope and Green Bank Telescope. The Parkes Pulsar Timing Array at the Parkes radio-telescope has been collecting data since March 2005. The European Pulsar Timing Array uses data from the four largest telescopes in Europe: the Lovell Telescope, the Westerbork Synthesis Radio Telescope, the Effelsberg Telescope and the Nancay Radio Telescope. (Upon completion the Sardinia Radio Telescope will be added to the EPTA also.) These three projects have begun collaborating under the title of the International Pulsar Timing Array project.
Einstein@Home
In some sense, the easiest signals to detect should be constant sources. Supernovae and neutron star or black hole mergers should have larger amplitudes and be more interesting, but the waves generated will be more complicated.
The waves given off by a spinning, aspherical neutron star would be "monochromatic"—like a pure tone in acoustics. It would not change very much in amplitude or frequency.
The Einstein@Home project is a distributed computing project similar to SETI@home intended to detect this type of simple gravitational wave. By taking data from LIGO and GEO, and sending it out in little pieces to thousands of volunteers for parallel analysis on their home computers, Einstein@Home can sift through the data far more quickly than would be possible otherwise.[45]
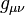 . The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.
. The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.
Spacetime curvature is also expressed with respect to a covariant derivative, , in the form of the Einstein tensor,
, in the form of the Einstein tensor,  . This curvature is related to the stress–energy tensor,
. This curvature is related to the stress–energy tensor, 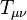 , by the key equation
, by the key equation
 is Newton's gravitational constant, and
is Newton's gravitational constant, and  is the speed of light. We assume geometrized units, so
is the speed of light. We assume geometrized units, so  .
.
With some simple assumptions, Einstein's equations can be rewritten to show explicitly that they are wave equations. To begin with, we adopt some coordinate system, like . We define the "flat-space metric"
. We define the "flat-space metric" 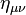 to be the quantity that — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have
to be the quantity that — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have
Tensor indices are raised and lowered using this "flat-space metric".
Now, we can also think of the physical metric as a matrix, and find its determinant,
as a matrix, and find its determinant, 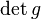 . Finally, we define a quantity
. Finally, we define a quantity
 represents the flat-space derivative operator. These equations say that the divergence of the field is zero. The linear Einstein equations can now be written[46] as
represents the flat-space derivative operator. These equations say that the divergence of the field is zero. The linear Einstein equations can now be written[46] as
 represents the flat-space d'Alembertian operator, and
represents the flat-space d'Alembertian operator, and  represents the stress–energy tensor plus quadratic terms involving
represents the stress–energy tensor plus quadratic terms involving 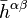 . This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.
. This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.
 tensor. In this case, we can neglect terms quadratic in
tensor. In this case, we can neglect terms quadratic in 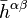 , which means that the
, which means that the  field reduces to the usual stress–energy tensor
field reduces to the usual stress–energy tensor 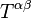 . That is, Einstein's equations become
. That is, Einstein's equations become
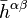 . Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as
. Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as 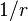 far from the source) can always be written in the form
far from the source) can always be written in the form  , where
, where 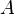 is just some function.
is just some function.
It can be shown[47] that — to a linear approximation — it is always possible to make the field traceless. Now, if we further assume that the source is positioned at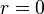 , the general solution to the wave equation in spherical coordinates is
, the general solution to the wave equation in spherical coordinates is
 .
.
Now, because we will eventually only be interested in the spatial components of this equation (time components can be set to zero with a coordinate transformation), and we are integrating this quantity — presumably over a region of which there is no boundary — we can put this in a different form. Ignoring divergences with the help of Stokes' theorem and an empty boundary, we can see that
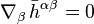 , we know that
, we know that  .
.
With a few simple manipulations, we can use this to prove that
 , the density of mass-energy.
, the density of mass-energy.
To a very good approximation, the density of a simple binary can be described by a pair of delta-functions, which eliminates the integral. Explicitly, if the masses of the two objects are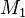 and
and  , and the positions are
, and the positions are 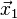 and
and  , then
, then
 . Plugging in the known values of
. Plugging in the known values of 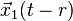 , we obtain the expressions given above for the radiation from a simple binary.
, we obtain the expressions given above for the radiation from a simple binary.
The Einstein@Home project is a distributed computing project similar to SETI@home intended to detect this type of simple gravitational wave. By taking data from LIGO and GEO, and sending it out in little pieces to thousands of volunteers for parallel analysis on their home computers, Einstein@Home can sift through the data far more quickly than would be possible otherwise.[45]
Primordial gravitational waves
Primordial gravitational waves are gravitational waves observed in the cosmic microwave background. They were allegedly detected by the BICEP2 instrument, an announcement being made on 17 March 2014.Mathematics
Einstein's equations form the fundamental law of general relativity. The curvature of spacetime can be expressed mathematically using the metric tensor — denoted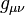 . The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.
. The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.Spacetime curvature is also expressed with respect to a covariant derivative,
 , in the form of the Einstein tensor,
, in the form of the Einstein tensor,  . This curvature is related to the stress–energy tensor,
. This curvature is related to the stress–energy tensor, 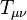 , by the key equation
, by the key equation is Newton's gravitational constant, and
is Newton's gravitational constant, and  is the speed of light. We assume geometrized units, so
is the speed of light. We assume geometrized units, so  .
.With some simple assumptions, Einstein's equations can be rewritten to show explicitly that they are wave equations. To begin with, we adopt some coordinate system, like
 . We define the "flat-space metric"
. We define the "flat-space metric" 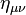 to be the quantity that — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have
to be the quantity that — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we haveTensor indices are raised and lowered using this "flat-space metric".
Now, we can also think of the physical metric
 as a matrix, and find its determinant,
as a matrix, and find its determinant, 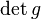 . Finally, we define a quantity
. Finally, we define a quantity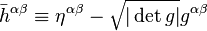 .
.
 represents the flat-space derivative operator. These equations say that the divergence of the field is zero. The linear Einstein equations can now be written[46] as
represents the flat-space derivative operator. These equations say that the divergence of the field is zero. The linear Einstein equations can now be written[46] as ,
,
 represents the flat-space d'Alembertian operator, and
represents the flat-space d'Alembertian operator, and  represents the stress–energy tensor plus quadratic terms involving
represents the stress–energy tensor plus quadratic terms involving 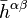 . This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.
. This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.Linear approximation
The equations above are valid everywhere — near a black hole, for instance. However, because of the complicated source term, the solution is generally too difficult to find analytically. We can often assume that space is nearly flat, so the metric is nearly equal to the tensor. In this case, we can neglect terms quadratic in
tensor. In this case, we can neglect terms quadratic in 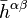 , which means that the
, which means that the  field reduces to the usual stress–energy tensor
field reduces to the usual stress–energy tensor 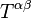 . That is, Einstein's equations become
. That is, Einstein's equations become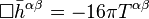 .
.
 .
.
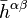 . Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as
. Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as 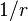 far from the source) can always be written in the form
far from the source) can always be written in the form  , where
, where 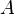 is just some function.
is just some function.It can be shown[47] that — to a linear approximation — it is always possible to make the field traceless. Now, if we further assume that the source is positioned at
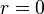 , the general solution to the wave equation in spherical coordinates is
, the general solution to the wave equation in spherical coordinates isRelation to the source
If we know the details of a source — for instance, the parameters of the orbit of a binary — we can relate the source's motion to the gravitational radiation observed far away. With the relation ,
,
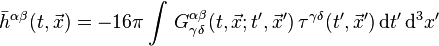 .
.
 ,
,
 .
.
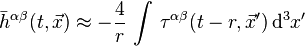 ,
,
 .
.Now, because we will eventually only be interested in the spatial components of this equation (time components can be set to zero with a coordinate transformation), and we are integrating this quantity — presumably over a region of which there is no boundary — we can put this in a different form. Ignoring divergences with the help of Stokes' theorem and an empty boundary, we can see that
 ,
,
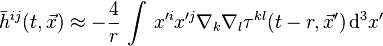 ,
,
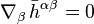 , we know that
, we know that  .
.With a few simple manipulations, we can use this to prove that
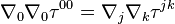 .
.
 .
.
 , the density of mass-energy.
, the density of mass-energy.To a very good approximation, the density of a simple binary can be described by a pair of delta-functions, which eliminates the integral. Explicitly, if the masses of the two objects are
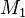 and
and  , and the positions are
, and the positions are 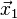 and
and  , then
, then .
.
 .
.
 ,
,
 . Plugging in the known values of
. Plugging in the known values of 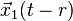 , we obtain the expressions given above for the radiation from a simple binary.
, we obtain the expressions given above for the radiation from a simple binary.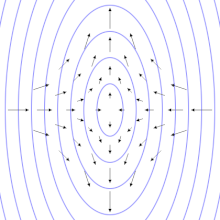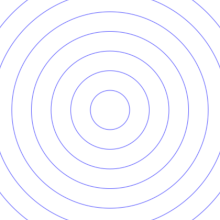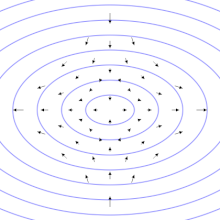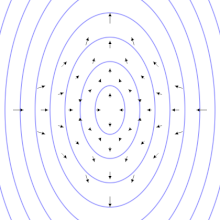


 (or 50%). Gravitational waves passing through the Earth are many billions times weaker than this —
(or 50%). Gravitational waves passing through the Earth are many billions times weaker than this —  . Note that this is not the quantity that would be analogous to what is usually called the amplitude of an electromagnetic wave, which would be
. Note that this is not the quantity that would be analogous to what is usually called the amplitude of an electromagnetic wave, which would be 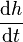 .
. , this is the distance along the wave between points of maximum stretch or squeeze.
, this is the distance along the wave between points of maximum stretch or squeeze.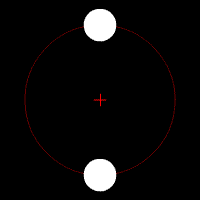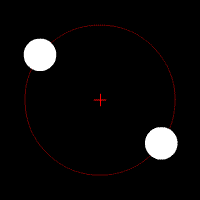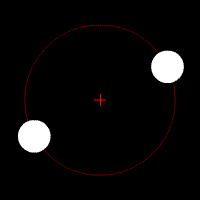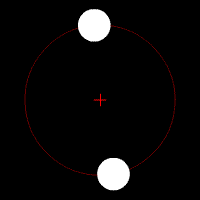
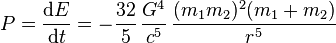 ,
, ,
, ,
,![h_{+} = -\frac{1}{R}\, \frac{G^2}{c^4}\, \frac{2 m_1 m_2}{r} (1+\cos^2\theta) \cos\left[2\omega(t - R)\right],](http://upload.wikimedia.org/math/3/d/9/3d9be0663baddbc7b8fd531d6b20be65.png)
![h_{\times} = -\frac{1}{R}\, \frac{G^2}{c^4}\, \frac{4 m_1 m_2}{r}\, (\cos{\theta})\sin \left[2\omega(t-R)\right].](http://upload.wikimedia.org/math/4/2/a/42a7f53129a3cf3836564daa1b1160cd.png)





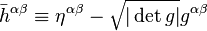 .
.
 ,
,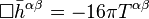 .
. .
.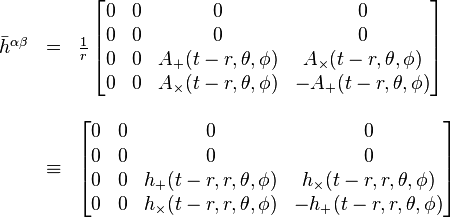
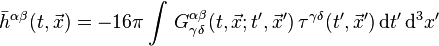 .
. ,
, .
.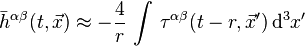 ,
, ,
,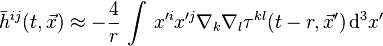 ,
,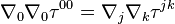 .
. .
. ,
,