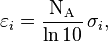Circumstellar habitable zone

From Wikipedia, the free encyclopedia

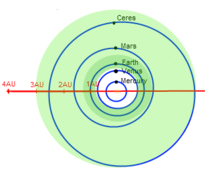
An example of a system based on stellar luminosity for predicting the location of the habitable zone around various types of stars. Planet sizes, star sizes, orbit lengths, and habitable zone sizes are not to scale.

In astronomy and astrobiology, the circumstellar habitable zone (CHZ), or simply the habitable zone, is the region around a star within which planetary-mass objects with sufficient atmospheric pressure can support liquid water at their surfaces.^[1][2] The bounds of the CHZ are calculated using the known requirements of Earth's biosphere, its position in the Solar System and the amount of radiant energy it receives from the Sun. Due to the importance of liquid water to life as it exists on Earth, the nature of the CHZ and the objects within is believed to be instrumental in determining the scope and distribution of Earth-like extraterrestrial life and intelligence.

The habitable zone is also called the Goldilocks zone, a metaphor of the children's fairy tale of Goldilocks and the Three Bears, in which a little girl chooses from sets of three items, ignoring the ones that are too extreme (large or small, hot or cold, etc.), and settling on the one in the middle, which is "just right".

Since the concept was first presented in 1953,^[3] stars have been confirmed to possess a CHZ planet, including some systems that consist of multiple CHZ planets.^[4] Most such planets, being super-Earths or gas giants, are more massive than Earth, because such planets are easier to detect. On November 4, 2013, astronomers reported, based on Kepler data, that there could be as many as 40 billion Earth-sized planets orbiting in the habitable zones of Sun-like stars and red dwarfs in the Milky Way.^[5][6] 11 billion of these may be orbiting Sun-like stars.^[7] The nearest such planet may be 12 light-years away, according to the scientists.^[5][6] The CHZ is also of particular interest to the emerging field of habitability of natural satellites, because planetary-mass moons in the CHZ might outnumber planets.^[8]

In subsequent decades, the CHZ concept began to be challenged as a primary criterion for life. Since the discovery of evidence for extraterrestrial liquid water, substantial quantities of it are now believed to occur outside the circumstellar habitable zone. Sustained by other energy sources, such as tidal heating^[9][10] or radioactive decay^[11] or pressurized by other non-atmospheric means, the basic conditions for water-dependent life may be found even in interstellar space, on rogue planets, or their moons.^[12] Liquid water can also exist at a wider range of temperatures and pressures as a solution, for example with sodium chlorides in seawater on Earth, chlorides and sulphates on Equatorial Mars,^[13] or ammoniates,^[14] due to its different colligative properties. In addition, other circumstellar zones, where non-water solvents favorable to hypothetical life based on alternative biochemistries could exist in liquid form at the surface, have been proposed.^[15]

History

The concept of a Circumstellar Habitable Zone was first introduced in 1953 by Hubertus Strughold, who in his treatise The Green and the Red Planet: A Physiological Study of the Possibility of Life on Mars coined the term "ecosphere" and referred to various "zones" in which life could emerge.^[3][16] In the same year, Harlow Shapley wrote "Liquid Water Belt", which described the same theory in further scientific detail. Both works stressed the importance of liquid water to life.^[17] Su-Shu Huang, an American astrophysicist, first introduced the term "habitable zone" in 1959 to refer to the area around a star where liquid water could exist on a sufficiently large body, and was the first to introduce it in the context of planetary habitability and extraterrestrial life.^[18][19] A major early contributor to habitable zone theory, Huang argued in 1960 that circumstellar habitable zones, and by extension extraterrestrial life, would be uncommon in multiple star systems, given the gravitational instabilities of those systems.^[20]

The theory of habitable zones was further developed in 1964 by Stephen H. Dole in his book Habitable Planets for Man, in which he covered the circumstellar habitable zone itself as well as various other determinants of planetary habitability, eventually estimating the number of habitable planets in the Milky Way to be about 600 million.^[21] At the same time, science-fiction author Isaac Asimov introduced the concept of a circumstellar habitable zone to the general public through his various explorations of space colonization.^[22] The term "Goldilocks zone" emerged in the 1970s, referencing specifically a region around a star whose temperature is "just right" for water to be present in the liquid phase.^[23] In 1993, astronomer James Kasting introduced the term "circumstellar habitable zone" to refer more precisely to the region then (and still) known as the habitable zone.^[18]

An update to habitable-zone theory came in 2000, when astronomers Peter Ward and Donald Brownlee introduced the idea of the "galactic habitable zone", which they later developed with Guillermo Gonzalez.^[24][25] The galactic habitable zone, defined as the region where life is most likely to emerge in a galaxy, encompasses those regions close enough to a galactic center that stars there are enriched with heavier elements, but not so close that star systems, planetary orbits, and the emergence of life would be frequently disrupted by the intense radiation and enormous gravitational forces commonly found at galactic centers.^[24]

Subsequently, several planetary scientists have criticized the circumstellar habitable zone theory for its "carbon chauvinism", proposing that the concept be extended to other solvents, such as ammonia or methane, which could be the basis of life based on an alternative biochemistry.^[15] In 2013, further developments in habitable zone theory were made with the proposal of a circumplanetary habitable zone, also known as the "habitable edge", to encompass the region around a planet where the orbits of natural satellites would not be disrupted, and at the same time tidal heating from the planet would not cause liquid water to boil away.^[26]

Determination of the circumstellar habitable zone

The range of published estimates for the extent of the Sun's CHZ. The conservative CHZ^[21] is indicated by a dark-green band crossing the inner edge of the aphelion of Venus, whereas an extended CHZ,^[27] extending to the orbit of the dwarf planet Ceres, is indicated by a light-green band.

Whether a body is in the circumstellar habitable zone of its host star is dependent on the radius of the planet's orbit (for natural satellites, the host planet's orbit), the mass of the body itself, and the radiative flux of the host star. Given the large spread in the masses of planets within a circumstellar habitable zone, coupled with the discovery of super-Earth planets which can sustain thicker atmospheres and stronger magnetic fields than Earth, circumstellar habitable zones are now split into two separate regions—a "conservative habitable zone" in which lower-mass planets like Earth or Venus can remain habitable, complemented by a larger "extended habitable zone" in which super-Earth planets, with stronger greenhouse effects, can have the right temperature for liquid water to exist at the surface.^[28]

Solar System estimates

Estimates for the habitable zone within the Solar System range from 0.5 to 3.0 astronomical units,^[29] though arriving at these estimates has been challenging for a variety of reasons. Numerous planetary mass objects orbit within, or close to, this range and as such receive sufficient sunlight to raise temperatures above the freezing point of water. However their atmospheric conditions vary substantially. The aphelion of Venus, for example, touches the inner edge of the zone and while atmospheric pressure at the surface is sufficient for liquid water, a strong greenhouse effect raises surface temperatures to 462 °C (864 °F) at which water can only exist as vapour.^[30] The entire orbits of the Moon,^[31] Mars,^[32] and numerous asteroids also lie within various estimates of the habitable zone. Only at Mars' lowest elevations (less than 30% of the planet's surface) is atmospheric pressure and temperature sufficient for water to, if present, exist in liquid form for short periods.^[33] At Hellas Basin, for example, atmospheric pressures can reach 1,115 Pa and temperatures above zero (around the triple point for water) for 70 days in the Martian year.^[33] Despite indirect evidence in the form of seasonal flows on warm Martian slopes,^{[34][35][36][37]} no confirmation has been made of the presence of liquid water there. While other objects orbit partly within this zone, including comets, Ceres^[38] is the only one of planetary mass. A combination of low mass and an inability to mitigate evaporation and atmosphere loss against the solar wind make it impossible for these bodies to sustain liquid water on their surface. Most estimates, therefore, are inferred from the effect that a repositioned orbit would have on the habitability of Earth or Venus.

According to extended habitable zone theory, planetary mass objects with atmospheres capable of inducing sufficient radiative forcing could possess liquid water farther out from the Sun. Such objects could include those whose atmospheres contain a high component of greenhouse gas and terrestrial planets much more massive than Earth (Super-Earth class planets), that have retained atmospheres with surface pressures of up to 100 kbar. There are no examples of such objects in the Solar System to study and not enough is known about the nature of atmospheres of these kinds of extrasolar objects and the net temperature effect of such atmospheres including induced albedo, anti-greenhouse or other possible heat sources cannot be determined by their position in the habitable zone.

Estimates of the circumstellar-habitable-zone boundaries of the Solar System

Inner edge (AU)	Outer edge (AU)	Year	Notes
0.725	1.24	Dole 1964[21]	Used optically thin atmospheres and fixed albedos. Places the aphelion of Venus just inside the zone.
	1.385–1.398	Budyko 1969[39]	Based on studies of ice albedo feedback models to determine the point at which Earth would experience global glaciation. This estimate was supported in studies by Sellers 1969[40] and North 1975.[41]
0.88–0.912		Rasool and De Bergh 1970[42]	Based on studies of Venus's atmosphere, Rasool and De Bergh concluded that this is the minimum distance at which Earth would have formed stable oceans.
0.95	1.01	Hart et al. 1979[43]	Based on computer modelling and simulations of the evolution of Earth's atmospheric composition and surface temperature. This estimate has often been cited by subsequent publications.
	3.0	Fogg 1992[27]	Used the carbon cycle to estimate the outer edge of the circumstellar habitable zone.
	1.37	Kasting et al. 1993[18]	Noted the cooling effect of cloud albedo.
	2.0	Spiegel et al. 2010[44]	Proposed that seasonal liquid water is possible to this limit when combining high obliquity and orbital eccentricity.
0.75		Abe et al. 2011[45]	Found that land-dominated "desert planets" with water at the poles could exist closer to the Sun than watery planets like Earth.
0.77—0.87	1.02—1.18	Vladilo et al. 2013[46]	Inner edge of circumstellar habitable zone is closer and outer edge is farther for higher atmospheric pressures; determined minimum atmospheric pressure required to be 15 millibar.
0.99	1.688	Kopparapu et al. 2013[1]	Revised estimates using updated runaway greenhouse and water loss algorithms. According to this measure Earth is at the inner edge of the HZ and close to, but just outside, the runaway greenhouse limit. This applies to a planet with Earth-like atmospheric composition and pressure.
0.5		Zsom et al. 2013 [47]	Estimate based on various possible combinations of atmospheric composition, pressure and relative humidity of the planet's atmosphere.

Extrasolar extrapolation

Astronomers use stellar flux and the inverse-square law to extrapolate cirumstellar-habitable-zone models created for the Solar System to other stars. For example, although the Solar System has a circumstellar habitable zone centered at 1.34 AU from the Sun,^[1] a star with 0.25 times the luminosity of the Sun would have a habitable zone centered at , or 0.5, the distance from the star, corresponding to a distance of 0.67 AU. Various complicating factors, though, including the individual characteristics of stars themselves, mean that extrasolar extrapolation of the CHZ concept is more complex.

Spectral types and star-system characteristics

Play media

A video explaining the significance of the 2011 discovery of a planet in the circumbinary habitable zone of Kepler-47.

Some scientists argue that the concept of a circumstellar habitable zone is actually limited to stars in certain types of systems or of certain spectral types. Binary systems, for example, have circumstellar habitable zones that differ from those of single-star planetary systems, in addition to the orbital-stability concerns inherent with a three-body configuration.^[48] If the Solar System were such a binary system, the outer limits of the resulting circumstellar habitable zone could extend as far as 2.4 AU.^[49][50]

With regard to spectral types, Zoltán Balog proposes that O-type stars cannot form planets due to the photoevaporation caused by their strong ultraviolet emissions.^[51] Studying ultraviolet emissions, Andrea Buccino found that only 40 percent of stars studied (including the Sun) had overlapping liquid water and ultraviolet habitable zones.^[52] Stars smaller than the Sun, on the other hand, have distinct impediments to habitability. Michael Hart, for example, proposed that only main-sequence stars of spectral class K0 or brighter could possess habitable zones, an idea which has evolved in modern times into the concept of a tidal locking radius for red dwarfs. Within this radius, which is coincidental with the red-dwarf habitable zone, it has been suggested that the volcanism caused by tidal heating could cause a "tidal Venus" planet with high temperatures and no ability to support life.^[53]

Others maintain that circumstellar habitable zones are more common and that it is indeed possible for water to exist on planets orbiting cooler stars. Climate modelling from 2013 supports the idea that red dwarf stars can support planets with relatively constant temperatures over their surfaces in spite of tidal locking.^[54] Astronomy professor Eric Agol argues that even white dwarfs may support a relatively brief habitable zone through planetary migration.^[55] At the same time, others have written in similar support of semi-stable, temporary habitable zones around brown dwarfs.^[53]

Stellar evolution

Natural defenses against space weather, such as the magnetosphere depicted in this artistic rendition, may be required for planets to sustain surface water for prolonged periods.

Circumstellar habitable zones change over time with stellar evolution. For example, hot O-type stars, which may remain on the main sequence for fewer than 10 million years,^[56] would have rapidly changing habitable zones not conducive to the development of life. Red dwarf stars, on the other hand, which can live for hundreds of billions of years on the main sequence, would have planets with ample time for life to develop and evolve.^[57][58] Even while stars are on the main sequence, though, their energy output steadily increases, pushing their habitable zones farther and farther out; our Sun, for example, was only 75 percent as bright in the Archaean as it is now,^[59] and in the future continued increases in energy output will put Earth outside the Sun's habitable zone, even before it reaches the red giant phase.^[60] In order to deal with this increase in luminosity, the concept of a continuously habitable zone has been introduced. As the name suggests, the continuously habitable zone is a region around a star in which planetary-mass bodies can sustain liquid water for a given period of time. Like the general circumstellar habitable zone, the continuously habitable zone of a star is divided into a conservative and extended region.^[60]

In red dwarf systems, gigantic stellar flares which could double a star's brightness in minutes^[61] and huge starspots which can cover 20 percent of the star's surface area,^[62] have the potential to strip an otherwise habitable planet of its atmosphere and water.^[63] As with more massive stars, though, stellar evolution changes their nature,^[64] so by about 1.2 billion years of age, red dwarfs generally become sufficiently constant to allow for the development of life.^[63][65]

Once a star has evolved sufficiently to become a red giant, its circumstellar habitable zone will change dramatically from its main-sequence size. For example, the Sun is expected to engulf the previously-habitable Earth as a red giant.^[66] However, once a red giant star reaches the horizontal branch, it achieves a new equilibrium and can sustain a circumstellar habitable zone, which in the case of the Sun would range from 7 to 22 AU.^[67] At such stage, Saturn's moon Titan would likely be habitable in Earth's sense.^[68] Given that this new equilibrium lasts for about 1 Gyr, and because life on Earth emerged by 0.7 Gyr from the formation of the Solar System at latest, life could conceivably develop on planetary mass objects in the habitable zone of red giants.^[67] However, around such a helium-burning star, important life processes like photosynthesis could only happen around planets where the atmosphere has been artificially seeded with carbon dioxide, as by the time a solar-mass star becomes a red giant, planetary-mass bodies would have already absorbed much of their free carbon dioxide.^[69]

Desert planets

A planet's atmospheric conditions influence its ability to retain heat, so that the location of the habitable zone is also specific to each type of planet: desert planets (also known as dry planets), with very little water, will have less water vapor in the atmosphere than Earth and so have a reduced greenhouse effect, meaning that a desert planet could maintain oases of water closer to its star than Earth is to the Sun. The lack of water also means there is less ice to reflect heat into space, so the outer edge of desert-planet habitable zones is further out.^[70][71]

Other considerations

Earth's hydrosphere. Water covers 71% of Earth's surface, with the global ocean accounting for 97.3% of the water distribution on Earth.

A planet cannot have a hydrosphere—a key ingredient for the formation of carbon-based life—unless there is a source for water within its stellar system. The origin of water on Earth is still not completely understood; possible sources include the result of impacts with icy bodies, outgassing, mineralization, leakage from hydrous minerals from the lithosphere, and photolysis.^[72][73] For an extrasolar system, an icy body from beyond the frost line could migrate into the habitable zone of its star, creating an ocean planet with seas hundreds of kilometers deep^[74] such as GJ 1214 b^[75][76] or Kepler-22b may be.^[77]

Maintenance of liquid surface water also requires a sufficiently thick atmosphere. Possible origins of terrestrial atmospheres are currently theorised to outgassing, impact degassing and ingassing.^[78] Atmospheres are thought to be maintained through similar processes along with biogeochemical cycles and the mitigation of atmospheric escape.^[79] In a 2013 study led by Italian astronomer Giovanni Vladilo, it was shown that the size of the circumstellar habitable zone increased with greater atmospheric pressure.^[46] Below an atmospheric pressure of about 15 millibars, it was found that habitability could not be maintained^[46] because even a small shift in pressure or temperature could render water unable to form a liquid.^[80]

In the case of planets orbiting in the CHZs of red dwarf stars, the extremely close distances to the stars cause tidal locking, an important factor in habitability. For a tidally locked planet, the sidereal day is as long as the orbital period, causing one side to permanently face the host star and the other side to face away. In the past, such tidal locking was believed to cause extreme heat on the star-facing side and bitter cold on the opposite side, making many red dwarf planets uninhabitable; however, a 2013 paper written by geophysicist Jun Yang of the University of Chicago and collaborators, using three-dimensional climate models, showed that the side of a red dwarf planet facing the host star would have extensive cloud cover, increasing its Bond albedo and reducing significantly temperature differences between the two sides.^[54]

Planetary-mass natural satellites have the potential to be habitable as well. However, these bodies need to fulfill additional parameters, in particular being located within the circumplanetary habitable zones of their host planets.^[26] More specifically, planets need to be far enough from their host giant planets that they are not transformed by tidal heating into volcanic worlds like Io,^[26] but must still remain within the Hill radius of the planet so that they are not pulled out of orbit of their host planet.^[81] Red dwarfs that have masses less than 20 percent of that of the Sun cannot have habitable moons around giant planets, as the small size of the circumstellar habitable zone would put a habitable moon so close to a star that it would be stripped from its host planet. In such a system, a moon close enough to its host planet to maintain its orbit would have tidal heating so intense as to eliminate any prospects of habitability.^[26]

Artists concept of a planet on an eccentric orbit that passes through the CHZ for only part of its year

A planetary object that orbits a star with high orbital eccentricity may spend only some of its year in the CHZ and experience a large variation in temperature and atmospheric pressure. This would result in dramatic seasonal phase shifts where liquid water may exist only intermittently. It is possible that subsurface habitats could be insulated from such changes and that extremophiles on or near the surface might survive through adaptions such as hibernation (cryptobiosis) and/or hyperthermostability. Tardigrades, for example, can survive in a dehydrated state temperatures between 0.150 K (−273 °C)^[82] and 424 K (151 °C).^[83] Life on a planetary object orbiting outside CHZ might hibernate on the cold side as the planet approaches the apastron where the planet is coolest and become active on approach to the periastron when the planet is sufficiently warm.^[84]

Extrasolar discoveries

Among exoplanets, a review in 2015 came to the conclusion that Kepler-62f, Kepler-186f and Kepler-442b were likely the best candidates for being potentially habitable.^[85] These are at a distance of 1200, 490 and 1,120 light-years away, respectively. Of these, Kepler-186f is in similar size to Earth with its 1.2-Earth-radius measure, and it is located towards the outer edge of the habitable zone around its red dwarf sun. Among nearest terrestrial exoplanet candidates, Tau Ceti e is merely 11.9 light-years away. It's in the inner edge of its solar system's habitable zone, giving it an estimated average surface temperature of 68 °C (154 °F).^[86]
Studies that have attempted to estimate the number of terrestrial planets within the circumstellar habitable zone tend to reflect the availability of scientific data. A 2013 study by Ravi Kumar Kopparapu put η_e, the fraction of stars with planets in the CHZ, at 0.48,^[1] meaning that there may be roughly 95–180 billion habitable planets in the Milky Way.^[87] However, this is merely a statistical prediction; only a small fraction of these possible planets have yet been discovered.^[88]

Previous studies have been more conservative. In 2011, Seth Borenstein concluded that there are roughly 500 million habitable planets in the Milky Way.^[89] NASA's Jet Propulsion Laboratory 2011 study, based on observations from the Kepler mission, raised the number somewhat, concluding that about "1.4 to 2.7 percent" of all stars of spectral class F, G, and K are expected to have planets in their CHZs.^[90][91]

Early findings

The first discoveries of extrasolar planets in the CHZ occurred just a few years after the first extrasolar planets were discovered. One of the first discoveries was 70 Virginis b, a gas giant initially nicknamed "Goldilocks" due to it being neither "too hot" nor "too cold." Later study revealed temperatures analogous to Venus ruling out any potential for liquid water.^[92] 16 Cygni Bb, also discovered in 1996, has an extremely eccentric orbit that causes extreme seasonal effects on the planet's surface. In spite of this, simulations have suggested that it is possible for a terrestrial natural satellite to support water at its surface year-round.^[93]
Gliese 876 b, discovered in 1998, and Gliese 876 c, discovered in 2001, are both gas giants discovered in the habitable zone around Gliese 876. Although they are not thought to themselves possess significant water at their surfaces, both may have habitable moons.^[94] Upsilon Andromedae d, discovered in 1999, is a gas giant in its star's circumstellar habitable zone considered to be large enough to favor the formation of large, Earth-like moons.^[95]

Announced on April 4, 2001, HD 28185 b is a gas giant found to orbit entirely within its star's circumstellar habitable zone^[96] and has a low orbital eccentricity, comparable to that of Mars in the Solar System.^[97] Tidal interactions suggest that HD 28185 b could harbor habitable Earth-mass satellites in orbit around it for many billions of years,^[98] though it is unclear whether such satellites could form in the first place.^[99]

HD 69830 d, a gas giant with 17 times the mass of Earth, was in 2006 found orbiting within the circumstellar habitable zone of HD 69830, 41 light years away from Earth.^[100] The following year, 55 Cancri f was discovered within the CHZ of its host star 55 Cancri A.^[101][102] Although conditions on this massive and dense planet are not conducive to the formation of water or life as we know it, a hypothetical moon of this planet with the proper mass and composition could be able to support liquid water at its surface.^[103]

Habitable super-Earths

The habitable zone of Gliese 581 compared with our Solar System's habitable zone.

The 2007 discovery of Gliese 581 c, the first super-Earth in the circumstellar habitable zone, created significant interest in the system by the scientific community, although the planet was later found to have surface conditions that likely resemble Venus more than Earth.^[104] Gliese 581 d, another planet in the same system and thought to be a better candidate for habitability, was also announced in 2007. Its existence was later disconfirmed in 2014. Gliese 581 g, yet another planet thought to have been discovered in the circumstellar habitable zone of the system, was considered to be more habitable than both Gliese 581 c and d. However, its existence was also disconfirmed in 2014.^[105]

A diagram comparing size (artist's impression) and orbital position of planet Kepler-22b within Sun-like star Kepler 22's habitable zone and that of Earth in the Solar System

Discovered in August 2011, HD 85512 b was initially believed to be habitable,^[106] but the new circumstellar-habitable-zone criteria devised by Kopparapu et al. in 2013 place the planet outside the circumstellar habitable zone.^[88] With an increase in the intensity of exoplanet discovery, the Earth Similarity Index was devised in October 2011 as a way of comparing planetary properties, such as surface temperature and density, to those of Earth in order to better gauge the habitability of extrasolar bodies.^[107]

Kepler-22 b, discovered in December 2011 by the Kepler space probe,^[108] is the first transiting exoplanet discovered around a sunlike star. With a radius 2.4 times that of Earth, Kepler-22b has been predicted by some to be an ocean planet.^[109] Gliese 667 Cc, discovered in 2011 but announced in 2012,^[110] is a super-Earth orbiting in the circumstellar habitable zone of Gliese 667 C. Subsequently in June 2013, two other habitable super-Earths orbiting the same star, Gliese 667 Cf and Gliese 667 Ce, were discovered in the CHZ.^[111]

Gliese 163 c, discovered in September 2012 in orbit around the red dwarf Gliese 163^[112] is located 49 light years from Earth. The planet has 6.9 Earth masses and 1.8–2.4 Earth radii, and with its close orbit receives 40 percent more stellar radiation than Earth, leading to surface temperatures of about 60° C.^{[113][114][115]} HD 40307 g, a candidate planet tentatively discovered in November 2012, is in the circumstellar habitable zone of HD 40307.^[116] In December 2012, Tau Ceti e and Tau Ceti f were found in the circumstellar habitable zone of Tau Ceti, a sunlike star just 12 light years away.^[117] Although more massive than Earth, they are among the least massive planets found to date orbiting in the zone;^[118] however, Tau Ceti f, like HD 85512 b, did not fit the new circumstellar-habitable-zone criteria established by the 2013 Kopparapu study.^[119]

Earth-sized planets and Solar analogs

Comparison of the CHZ position of Earth-radius planet Kepler-186f and the Solar System (17 April 2014)

While larger than Kepler 186f, Kepler-452b's orbit and star are more similar to Earth's.

Recent discoveries have uncovered planets that are believed to be similar in many ways to the Earth (that is Earth analogs, or terrestrial planets relatively high Earth Similarity Indexes). While there is no universal definition of "Earth-sized", ranges are typically defined by mass. The lower range used in many definitions of the Super-Earth class is 1.9 Earth masses, likewise, Sub-Earths range up to the size of Venus (~0.815 Earth masses). An upper limit of 1.5 Earth radii is also considered, given that above 1.5 R_⊕ the average planet density rapidly decreases with increasing radius, indicating that these planets have a large fraction of volatiles by volume overlying a rocky core.^[120]

On 7 January 2013, astronomers from the Kepler team announced the discovery of Kepler-69c (formerly KOI-172.02), an Earth-like exoplanet candidate (1.7 times the radius of Earth) orbiting Kepler-69, a star similar to our Sun, in the CHZ and a "prime candidate to host alien life".^{[121][122][123][124]} The discovery of two planets orbiting in the habitable zone of Kepler-62, by the Kepler team was announced on April 19, 2013. The planets, named Kepler-62e and Kepler-62f, are likely solid planets with sizes 1.6 and 1.4 times the radius of Earth, respectively.^{[123][125][126]}

With a radius measured at 1.1 Earth, Kepler-186f, discovery announced in April 2014, is the closest yet size to Earth of an exoplanet confirmed by the transit method^{[127][128][129]} though its mass remains unknown and its parent star is not a Solar analog.

On 6 January 2015, NASA announced the 1000th confirmed exoplanet discovered by the Kepler Space Telescope. Three of the newly confirmed exoplanets were found to orbit within habitable zones of their related stars: two of the three, Kepler-438b and Kepler-442b, are near-Earth-size and likely rocky; the third, Kepler-440b, is a super-Earth.^[130]{ Announced 16 January, EPIC 201367065 d is a planet of 1.5 Earth radii found to orbit within a habitable zone (as calculated by Selsis, Kasting et al.) of EPIC 201367065, receiving 1.4 times the intensity of visible light as Earth.^[131]

Kepler-452b, publicly announced on 23 July 2015 is 50% bigger than Earth, likely rocky and takes approximately 385 Earth days orbit in the habitable zone of its G-class (solar analog) star Kepler-452.^[132][133]

Notable exoplanets – Kepler Space Telescope
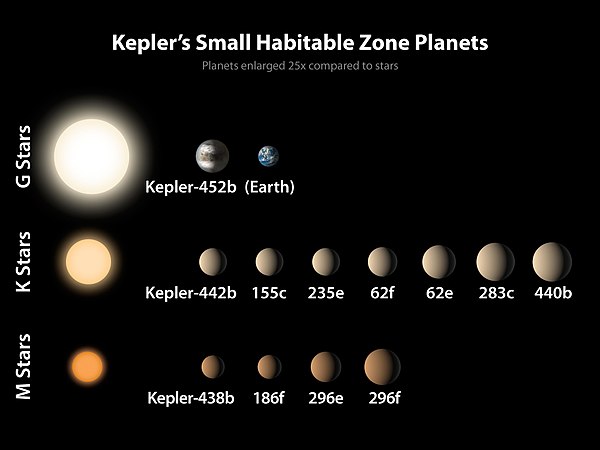
Confirmed small exoplanets in habitable zones. (Kepler-62e, Kepler-62f, Kepler-186f, Kepler-296e, Kepler-296f, Kepler-438b, Kepler-440b, Kepler-442b) (Kepler Space Telescope; January 6, 2015).[130]

Habitability outside the CHZ

The discovery of hydrocarbon lakes on Saturn's moon Titan has begun to call into question the carbon chauvinism that underpins CHZ theory.

Liquid-water environments have been found to exist in the absence of atmospheric pressure, and at temperatures outside the CHZ temperature range. For example, Saturn's moon Titan and Jupiter's Europa, both outside the habitable zone, may hold large volumes of liquid water in subsurface oceans.^[134]

Outside the CHZ, tidal heating and radioactive decay are two possible heat sources that could contribute to the existence of liquid water.^[9][10] Abbot and Switzer (2011) put forward the possibility that subsurface water could exist on rogue planets as a result of radioactive decay-based heating and insulation by a thick surface layer of ice.^[12]

With some theorising that life on Earth may have actually originated in stable, subsurface habitats,^[135][136] it has been suggested that it may be common for wet subsurface extraterrestrial habitats such as these to 'teem with life'.^[137] Indeed, on Earth itself living organisms may be found more than 6 kilometres below the surface.^[138]

Another possibility is that outside the CHZ organisms may use alternative biochemistries that do not require water at all. Astrobiologists, including NASA's Christopher McKay, have suggested that methane may be a solvent conducive to the development of "cryolife", with the Sun's "methane habitable zone" being centered on 1,610,000,000 km (1.0×10⁹ mi; 11 AU) from the star.^[15] This distance is coincidental with the location of Titan, whose lakes and rain of methane make it an ideal location to find McKay's proposed cryolife.^[15] In addition, testing of a number of organisms has found some are capable of surviving in extra-CHZ conditions.^[139]

Significance for complex and intelligent life

The Rare Earth hypothesis argues that complex and intelligent life is uncommon and that the CHZ is one of many critical factors. According to Ward & Brownlee (2004) and others, not only is a CHZ orbit and surface water a primary requirement to sustain life but a requirement to support the secondary conditions required for multicellular life to emerge and evolve. The secondary habitability factors are both geological (the role of surface water in sustaining necessary plate tectonics)^[24] and biochemical (the role of radiant energy in support photosynthesis for necessary atmospheric oxygenation).^[140] But others, such as Ian Stewart and Jack Cohen in their 2002 book Evolving the Alien argue that complex intelligent life may arise outside the CHZ.^[141] Intelligent life outside the CHZ may have evolved in subsurface environments, from alternative biochemistries^[141] or even from nuclear reactions.^[142]

On Earth, complex multicellular life has been found with the potential to survive the conditions that might exist outside the CHZ. An animal example of such a life form is the tardigrade, which can withstand both temperatures well above the boiling point of water and the vacuum of outer space.^[143] In addition, the plant Rhizocarpon geographicum has been found to survive in an environment where the atmospheric pressure is far too low for surface liquid water and where the radiant energy is also much lower than that which most plants require to photosynthesize.^[144][145] If the human race, however, is to colonize other planets, true Earth analogs in the CHZ are most likely to provide the closest natural habitats for human beings; this concept was the basis of Stephen H. Dole's 1964 study. With suitable temperature, gravity, atmospheric pressure and the presence of water, the necessity of spacesuits may be eliminated and complex Earth-life can be allowed to flourish.^[21]

Planets in the CHZ remain of paramount interest to researchers looking for intelligent life elsewhere in the universe.^[146] The 1961 Drake equation, still used as means of calculating the number of intelligent civilizations in our galaxy, contains a parameter η_e, which is generally considered to imply the fraction of stars that have planetary mass objects orbiting within the CHZ. A low value lends support to the Rare Earth hypothesis, which posits that intelligent life is a rarity in the Universe, whereas a high value provides evidence for the Copernican mediocrity principle, the view that habitability—and therefore life—is common throughout the Universe.^[24] A 1971 NASA report by Drake and Bernard Oliver proposed the "waterhole", based on the spectral absorption lines of the hydrogen and hydroxyl components of water, as a good, obvious band for communication with extraterrestrial intelligence^[147][148] that has since been widely adopted by astronomers involved in the search for extraterrestrial intelligence. According to Jill Tarter, Margaret Turnbull and many others, CHZ candidates are the priority targets to narrow waterhole searches^[149][150] and the Allen Telescope Array now extends Project Phoenix to such candidates.^[151]

Because the CHZ is considered the most likely habitat for intelligent life, METI efforts have also been focused on systems likely to have planets there. The 2001 Teen Age Message and the 2003 Cosmic Call 2, for example, were sent to the 47 Ursae Majoris system, known to contain three Jupiter-mass planets and possibly with a terrestrial planet in the CHZ.^{[152][153][154][155]} The Teen Age Message, and the later Wow! reply, were also directed to the 55 Cancri system, which has a gas giant in its CHZ.^[101] A Message to Earth in 2008, and Hello From Earth in 2009, were directed to the Gliese 581 system, containing three planets in the CHZ—Gliese 581 c, d, and the unconfirmed g.^[156]

Beer–Lambert law

From Wikipedia, the free encyclopedia

An example of Beer–Lambert law: green laser light in a solution of Rhodamine 6B. The beam radiant power becomes weaker as it passes through solution

The Beer–Lambert law, also known as Beer's law, the Lambert–Beer law, or the Beer–Lambert–Bouguer law relates the attenuation of light to the properties of the material through which the light is traveling. The law is commonly applied to chemical analysis measurements and used in understanding attenuation in physical optics, for photons, neutrons or rarefied gases. In mathematical physics, this law arises as a solution of the BGK equation.

History

The law was discovered by Pierre Bouguer before 1729.^[1] It is often attributed to Johann Heinrich Lambert, who cited Bouguer's Essai d'optique sur la gradation de la lumière (Claude Jombert, Paris, 1729)—and even quoted from it—in his Photometria in 1760.^[2] Lambert's law stated that absorbance of a material sample is directly proportional to its thickness (path length). Much later, August Beer discovered another attenuation relation in 1852. Beer's law stated that absorbance is proportional to the concentrations of the attenuating species in the material sample in 1852.^[3] The modern derivation of the Beer–Lambert law combines the two laws and correlates the absorbance to both the concentrations of the attenuating species as well as the thickness of the material sample.^[4]

Beer–Lambert law

By definition, the transmittance of material sample is related to its optical depth τ and to its absorbance A as

where

• Φ_e^t is the radiant flux transmitted by that material sample;
• Φ_eⁱ is the radiant flux received by that material sample.

The Beer–Lambert law states that, for N attenuating species in the material sample,

or equivalently that

where

• σ_i is the attenuation cross section of the attenuating species i in the material sample;
• n_i is the number density of the attenuating species i in the material sample;
• ε_i is the molar attenuation coefficient of the attenuating species i in the material sample;
• c_i is the amount concentration of the attenuating species i in the material sample;
• ℓ is the path length of the beam of light through the material sample.

Attenuation cross section and molar attenuation coefficient are related by

and number density and amount concentration by

where N_A is the Avogadro constant.
In case of uniform attenuation, these relations become^[5]

or equivalently

Cases of non-uniform attenuation occur in atmospheric science applications and radiation shielding theory for instance.

The law tends to break down at very high concentrations, especially if the material is highly scattering. If the radiation is especially intense, nonlinear optical processes can also cause variances. The main reason, however, is the following. At high concentrations, the molecules are closer to each other and begin to interact with each other. This interaction will change several properties of the molecule, and thus will change the attenuation.

Expression with attenuation coefficient

The Beer–Lambert law can be expressed in terms of attenuation coefficient, but in this case is better called Lambert's law since amount concentration, from Beer's law, is hidden inside the attenuation coefficient. The (Napierian) attenuation coefficient μ and the decadic attenuation coefficient μ₁₀ = μ/ln 10 of a material sample are related to its number densities and amount concentrations as

respectively, by definition of attenuation cross section and molar attenuation coefficient. Then the Beer–Lambert law becomes

and

In case of uniform attenuation, these relations become

or equivalently

Derivation

In concept, the derivation of the Beer–Lambert law is straightforward. Assume that a beam of light enters a material sample. Define z as an axis parallel to the direction of the beam. Divide the material sample into thin slices, perpendicular to the beam of light, with thickness dz sufficiently small that one particle in a slice cannot obscure another particle in the same slice when viewed along the z direction. The radiant flux of the light that emerges from a slice is reduced, compared to that of the light that entered, by dΦ_e(z) = −μ(z)Φ_e(z) dz, where μ is the (Napierian) attenuation coefficient, which yields the following first-order linear ODE:

The attenuation is caused by the photons that did not make it to the other side of the slice because of scattering or absorption. The solution to this differential equation is obtained by multiplying the integrating factor

throughout to obtain

which simplifies due to the product rule (applied backwards) to

Integrating both sides and solving for Φ_e for a material of real thickness ℓ, with the incident radiant flux upon the slice Φ_eⁱ = Φ_e(0) and the transmitted radiant flux Φ_e^t = Φ_e(ℓ ) gives

and finally

Since the decadic attenuation coefficient μ₁₀ is related to the (Napierian) attenuation coefficient by μ₁₀ = μ/ln 10, one also have

To describe the attenuation coefficient in a way independent of the number densities n_i of the N attenuating species of the material sample, one introduces the attenuation cross section σ_i = μ_i(z)/n_i(z). σ_i has the dimension of an area; it expresses the likelihood of interaction between the particles of the beam and the particles of the specie i in the material sample:

One can also use the molar attenuation coefficients ε_i = (N_A/ln 10)σ_i, where N_A is the Avogadro constant, to describe the attenuation coefficient in a way independent of the amount concentrations c_i(z) = n_i(z)/N_A of the attenuating species of the material sample:

Validity

Under certain conditions Beer–Lambert law fails to maintain a linear relationship between attenuation and concentration of analyte.^[6] These deviations are classified into three categories:

1. Real—fundamental deviations due to the limitations of the law itself.
2. Chemical—deviations observed due to specific chemical species of the sample which is being analyzed.
3. Instrument—deviations which occur due to how the attenuation measurements are made.

There are at least six conditions that need to be fulfilled in order for Beer–Lambert law to be valid. These are:

1. The attenuators must act independently of each other.
2. The attenuating medium must be homogeneous in the interaction volume.
3. The attenuating medium must not scatter the radiation—no turbidity—unless this is accounted for as in DOAS.
4. The incident radiation must consist of parallel rays, each traversing the same length in the absorbing medium.
5. The incident radiation should preferably be monochromatic, or have at least a width that is narrower than that of the attenuating transition. Otherwise a spectrometer as detector for the power is needed instead of a photodiode which has not a selective wavelength dependence.
6. The incident flux must not influence the atoms or molecules; it should only act as a non-invasive probe of the species under study. In particular, this implies that the light should not cause optical saturation or optical pumping, since such effects will deplete the lower level and possibly give rise to stimulated emission.

If any of these conditions are not fulfilled, there will be deviations from Beer–Lambert law.

Chemical analysis by spectrophotometry

Beer–Lambert law can be applied to the analysis of a mixture by spectrophotometry, without the need for extensive pre-processing of the sample. An example is the determination of bilirubin in blood plasma samples. The spectrum of pure bilirubin is known, so the molar attenuation coefficient ε is known. Measurements of decadic attenuation coefficient μ₁₀ are made at one wavelength λ that is nearly unique for bilirubin and at a second wavelength in order to correct for possible interferences. The amount concentration c is then given by

For a more complicated example, consider a mixture in solution containing two species at amount concentrations c₁ and c₂. The decadic attenuation coefficient at any wavelength λ is, given by

Therefore, measurements at two wavelengths yields two equations in two unknowns and will suffice to determine the amount concentrations c₁ and c₂ as long as the molar attenuation coefficient of the two components, ε₁ and ε₂ are known at both wavelengths. This two system equation can be solved using Cramer's rule. In practice it is better to use linear least squares to determine the two amount concentrations from measurements made at more than two wavelengths. Mixtures containing more than two components can be analyzed in the same way, using a minimum of N wavelengths for a mixture containing N components.

The law is used widely in infra-red spectroscopy and near-infrared spectroscopy for analysis of polymer degradation and oxidation (also in biological tissue). The carbonyl group attenuation at about 6 micrometres can be detected quite easily, and degree of oxidation of the polymer calculated.

Beer–Lambert law in the atmosphere

This law is also applied to describe the attenuation of solar or stellar radiation as it travels through the atmosphere. In this case, there is scattering of radiation as well as absorption. The optical depth for a slant path is τ′ = mτ, where τ refers to a vertical path, m is called the relative airmass, and for a plane-parallel atmosphere it is determined as m = sec θ where θ is the zenith angle corresponding to the given path. The Beer–Lambert law for the atmosphere is usually written

where each τ_x is the optical depth whose subscript identifies the source of the absorption or scattering it describes:

• a refers to aerosols (that absorb and scatter);
• g are uniformly mixed gases (mainly carbon dioxide (CO₂) and molecular oxygen (O₂) which only absorb);
• NO₂ is nitrogen dioxide, mainly due to urban pollution (absorption only);
• RS are effects due to Raman scattering in the atmosphere;
• w is water vapour absorption;
• O₃ is ozone (absorption only);
• r is Rayleigh scattering from molecular oxygen (O₂) and nitrogen (N₂) (responsible for the blue color of the sky);
• the selection of the attenuators which have to be considered depends on the wavelength range and can include various other compounds. This can include tetraoxygen, HONO, formaldehyde, glyoxal, a series of halogen radicals and others.

m is the optical mass or airmass factor, a term approximately equal (for small and moderate values of θ) to 1/cos θ, where θ is the observed object's zenith angle (the angle measured from the direction perpendicular to the Earth's surface at the observation site). This equation can be used to retrieve τ_a, the aerosol optical thickness, which is necessary for the correction of satellite images and also important in accounting for the role of aerosols in climate.