Chaos theory

From Wikipedia, the free encyclopedia

A plot of the Lorenz attractor for values r = 28, σ = 10, b = 8/3

A double-rod pendulum animation showing chaotic behavior. Starting the pendulum from a slightly different initial condition would result in a completely different trajectory. The double-rod pendulum is one of the simplest dynamical systems with chaotic solutions.

Chaos theory is a branch of mathematics focusing on the behavior of dynamical systems that are highly sensitive to initial conditions. 'Chaos' is an interdisciplinary theory stating that within the apparent randomness of chaotic complex systems, there are underlying patterns, constant feedback loops, repetition, self-similarity, fractals, self-organization, and reliance on programming at the initial point known as sensitive dependence on initial conditions. The butterfly effect describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state, e.g. a butterfly flapping its wings in China can cause a hurricane in Texas.^[1]

Small differences in initial conditions such as those due to rounding errors in numerical computation yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general.^[2][3] This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved.^[4] In other words, the deterministic nature of these systems does not make them predictable.^[5][6] This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:^[7]

Chaos: When the present determines the future, but the approximate present does not approximately determine the future.

Chaotic behavior exists in many natural systems, such as weather and climate.^[8][9] It also occurs spontaneously in some systems with artificial components, such as road traffic.^[10] This behavior can be studied through analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps. Chaos theory has applications in several disciplines, including meteorology, anthropology,^[11][12] sociology, physics,^[13] environmental science, computer science, engineering, economics, biology, ecology, and philosophy. The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory, and self-assembly processes.

Introduction

Chaos theory concerns deterministic systems whose behavior can in principle be predicted. Chaotic systems are predictable for a while and then 'appear' to become random.^[3] The amount of time that the behavior of a chaotic system can be effectively predicted depends on three things: How much uncertainty can be tolerated in the forecast, how accurately its current state can be measured, and a time scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, about 1 millisecond; weather systems, a few days (unproven); the solar system, 50 million years. In chaotic systems, the uncertainty in a forecast increases exponentially with elapsed time. Hence, mathematically, doubling the forecast time more than squares the proportional uncertainty in the forecast. This means, in practice, a meaningful prediction cannot be made over an interval of more than two or three times the Lyapunov time. When meaningful predictions cannot be made, the system appears random.^[14]

Chaotic dynamics

The map defined by x → 4 x (1 – x) and y → (x + y) mod 1 displays sensitivity to initial x positions. Here, two series of x and y values diverge markedly over time from a tiny initial difference. Note, however, that the y coordinate is defined modulo one at each step, so the square region is actually depicting a cylinder, and the two points are closer than they look.

In common usage, "chaos" means "a state of disorder".^[15] However, in chaos theory, the term is defined more precisely. Although no universally accepted mathematical definition of chaos exists, a commonly used definition originally formulated by Robert L. Devaney says that, to classify a dynamical system as chaotic, it must have these properties:^[16]

1. it must be sensitive to initial conditions
2. it must be topologically mixing
3. it must have dense periodic orbits

In some cases, the last two properties in the above have been shown to actually imply sensitivity to initial conditions.^[17][18] In these cases, while it is often the most practically significant property, "sensitivity to initial conditions" need not be stated in the definition.

If attention is restricted to intervals, the second property implies the other two.^[19] An alternative, and in general weaker, definition of chaos uses only the first two properties in the above list.^[20]

Chaos as a spontaneous breakdown of topological supersymmetry

In continuous time dynamical systems, chaos is the phenomenon of the spontaneous breakdown of topological supersymmetry which is an intrinsic property of evolution operators of all stochastic and deterministic (partial) differential equations.^[21][22] This picture of dynamical chaos works not only for deterministic models but also for models with external noise, which is an important generalization from the physical point of view because in reality all dynamical systems experience influence from their stochastic environments. Within this picture, the long-range dynamical behavior associated with chaotic dynamics, e.g., the butterfly effect, is a consequence of the Goldstone's theorem in the application to the spontaneous topological supersymmetry breaking.

Sensitivity to initial conditions

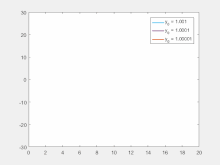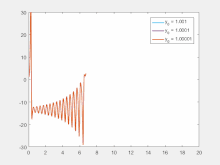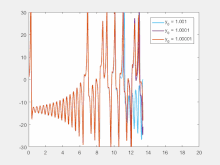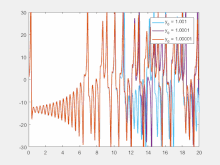
Lorenz equations used to generate plots for the y variable. The initial conditions for x and z were kept the same but those for y were changed between 1.001, 1.0001 and 1.00001. The values for ${\displaystyle \rho }$, ${\displaystyle \sigma }$ and ${\displaystyle \beta }$ were 45.92,16 and 4 respectively. As can be seen, even the slightest difference in initial values causes significant changes after about 12 seconds of evolution in the three cases. This is an example of sensitive dependence on initial conditions.

Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points with significantly different future paths, or trajectories. Thus, an arbitrarily small change, or perturbation, of the current trajectory may lead to significantly different future behavior.

Sensitivity to initial conditions is popularly known as the "butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science in Washington, D.C., entitled Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events leading to large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the system might have been vastly different.

A consequence of sensitivity to initial conditions is that if we start with a limited amount of information about the system (as is usually the case in practice), then beyond a certain time the system is no longer predictable. This is most prevalent in the case of weather, which is generally predictable only about a week ahead.^[23] Of course, this does not mean that we cannot say anything about events far in the future; some restrictions on the system are present. With weather, we know that the temperature will not naturally reach 100 °C or fall to −130 °C on earth (during the current geologic era), but we can't say exactly what day will have the hottest temperature of the year.

In more mathematical terms, the Lyapunov exponent measures the sensitivity to initial conditions. Given two starting trajectories in the phase space that are infinitesimally close, with initial separation ${\displaystyle \delta \mathbf {Z} _{0}}$, the two trajectories end up diverging at a rate given by

${\displaystyle |\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|,}$

where t is the time and λ is the Lyapunov exponent. The rate of separation depends on the orientation of the initial separation vector, so a whole spectrum of Lyapunov exponents exist. The number of Lyapunov exponents is equal to the number of dimensions of the phase space, though it is common to just refer to the largest one. For example, the maximal Lyapunov exponent (MLE) is most often used because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.

Also, other properties relate to sensitivity of initial conditions, such as measure-theoretical mixing (as discussed in ergodic theory) and properties of a K-system.^[6]

Topological mixing

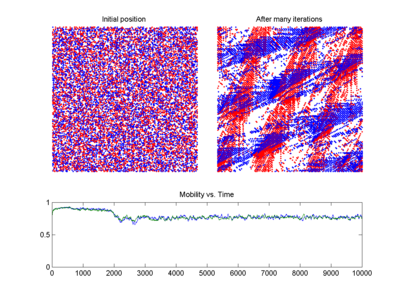
Six iterations of a set of states ${\displaystyle [x,y]}$ passed through the logistic map. (a) the blue plot (legend 1) shows the first iterate (initial condition), which essentially forms a circle. Animation shows the first to the sixth iteration of the circular initial conditions. It can be seen that mixing occurs as we progress in iterations. The sixth iteration shows that the points are almost completely scattered in the phase space. Had we progressed further in iterations, the mixing would have been homogeneous and irreversible. The logistic map has equation ${\displaystyle x_{k+1}=4x_{k}(1-x_{k})}$. To expand the state-space of the logistic map into two dimensions, a second state, ${\displaystyle y}$, was created as ${\displaystyle y_{k+1}=x_{k}+y_{k}}$, if ${\displaystyle x_{k}+y_{k}<1 annotation="">$ and ${\displaystyle y_{k+1}=x_{k}+y_{k}-1}$ otherwise.

The map defined by x → 4 x (1 – x) and y → (x + y) mod 1 also displays topological mixing. Here, the blue region is transformed by the dynamics first to the purple region, then to the pink and red regions, and eventually to a cloud of vertical lines scattered across the space.

Topological mixing (or topological transitivity) means that the system evolves over time so that any given region or open set of its phase space eventually overlaps with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.

Topological mixing is often omitted from popular accounts of chaos, which equate chaos with only sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points eventually becomes widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behavior: all points except 0 tend to positive or negative infinity.

Density of periodic orbits

For a chaotic system to have dense periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits.^[24] The one-dimensional logistic map defined by x → 4 x (1 – x) is one of the simplest systems with density of periodic orbits. For example, ${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$ → ${\displaystyle {\tfrac {5+{\sqrt {5}}}{8}}}$ → ${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$ (or approximately 0.3454915 → 0.9045085 → 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).^[25]

Sharkovskii's theorem is the basis of the Li and Yorke^[26] (1975) proof that any continuous one-dimensional system that exhibits a regular cycle of period three will also display regular cycles of every other length, as well as completely chaotic orbits.

Strange attractors

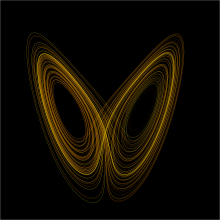
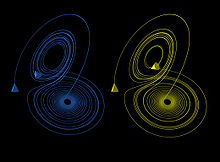
The Lorenz attractor displays chaotic behavior. These two plots demonstrate sensitive dependence on initial conditions within the region of phase space occupied by the attractor.

Some dynamical systems, like the one-dimensional logistic map defined by x → 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor, since then a large set of initial conditions leads to orbits that converge to this chaotic region.^[27]

An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it was not only one of the first, but it is also one of the most complex and as such gives rise to a very interesting pattern, that with a little imagination, looks like the wings of a butterfly.

Unlike fixed-point attractors and limit cycles, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set, which forms at the boundary between basins of attraction of fixed points. Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and the fractal dimension can be calculated for them.

Minimum complexity of a chaotic system

Bifurcation diagram of the logistic map x → r x (1 – x). Each vertical slice shows the attractor for a specific value of r. The diagram displays period-doubling as r increases, eventually producing chaos.

Discrete chaotic systems, such as the logistic map, can exhibit strange attractors whatever their dimensionality. In contrast, for continuous dynamical systems, the Poincaré–Bendixson theorem shows that a strange attractor can only arise in three or more dimensions. Finite-dimensional linear systems are never chaotic; for a dynamical system to display chaotic behavior, it must be either nonlinear or infinite-dimensional.

The Poincaré–Bendixson theorem states that a two-dimensional differential equation has very regular behavior. The Lorenz attractor discussed below is generated by a system of three differential equations such as:

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma y-\sigma x,\\{\frac {\mathrm {d} y}{\mathrm {d} t}}&=\rho x-xz-y,\\{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}}$

where ${\displaystyle x}$, ${\displaystyle y}$, and ${\displaystyle z}$ make up the system state, ${\displaystyle t}$ is time, and ${\displaystyle \sigma }$, ${\displaystyle \rho }$, ${\displaystyle \beta }$ are the system parameters. Five of the terms on the right hand side are linear, while two are quadratic; a total of seven terms. Another well-known chaotic attractor is generated by the Rössler equations, which have only one nonlinear term out of seven. Sprott^[28] found a three-dimensional system with just five terms, that had only one nonlinear term, which exhibits chaos for certain parameter values. Zhang and Heidel^[29][30] showed that, at least for dissipative and conservative quadratic systems, three-dimensional quadratic systems with only three or four terms on the right-hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic to a two-dimensional surface and therefore solutions are well behaved.

While the Poincaré–Bendixson theorem shows that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can exhibit chaotic behavior.^[31] Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite dimensional.^[32] A theory of linear chaos is being developed in a branch of mathematical analysis known as functional analysis.

Jerk systems

In physics, jerk is the third derivative of position, with respect to time. As such, differential equations of the form

${\displaystyle J\left({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\right)=0}$

are sometimes called Jerk equations. It has been shown that a jerk equation, which is equivalent to a system of three first order, ordinary, non-linear differential equations, is in a certain sense the minimal setting for solutions showing chaotic behaviour. This motivates mathematical interest in jerk systems. Systems involving a fourth or higher derivative are called accordingly hyperjerk systems.^[33]

A jerk system's behavior is described by a jerk equation, and for certain jerk equations, simple electronic circuits can model solutions. These circuits are known as jerk circuits.

One of the most interesting properties of jerk circuits is the possibility of chaotic behavior. In fact, certain well-known chaotic systems, such as the Lorenz attractor and the Rössler map, are conventionally described as a system of three first-order differential equations that can combine into a single (although rather complicated) jerk equation. Nonlinear jerk systems are in a sense minimally complex systems to show chaotic behaviour; there is no chaotic system involving only two first-order, ordinary differential equations (the system resulting in an equation of second order only).

An example of a jerk equation with nonlinearity in the magnitude of ${\displaystyle x}$ is:

${\displaystyle {\frac {\mathrm {d} ^{3}x}{\mathrm {d} t^{3}}}+A{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+{\frac {\mathrm {d} x}{\mathrm {d} t}}-|x|+1=0.}$

Here, A is an adjustable parameter. This equation has a chaotic solution for A=3/5 and can be implemented with the following jerk circuit; the required nonlinearity is brought about by the two diodes:

In the above circuit, all resistors are of equal value, except ${\displaystyle R_{A}=R/A=5R/3}$, and all capacitors are of equal size. The dominant frequency is ${\displaystyle 1/2\pi RC}$. The output of op amp 0 will correspond to the x variable, the output of 1 corresponds to the first derivative of x and the output of 2 corresponds to the second derivative.

Spontaneous order

Under the right conditions, chaos spontaneously evolves into a lockstep pattern. In the Kuramoto model, four conditions suffice to produce synchronization in a chaotic system. Examples include the coupled oscillation of Christiaan Huygens' pendulums, fireflies, neurons, the London Millennium Bridge resonance, and large arrays of Josephson junctions.^[34]

History

Barnsley fern created using the chaos game. Natural forms (ferns, clouds, mountains, etc.) may be recreated through an iterated function system (IFS).

An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits that are nonperiodic, and yet not forever increasing nor approaching a fixed point.^[35][36][37] In 1898 Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature, called "Hadamard's billiards".^[38] Hadamard was able to show that all trajectories are unstable, in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent.

Chaos theory began in the field of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by George David Birkhoff,^[39] Andrey Nikolaevich Kolmogorov,^[40][41][42] Mary Lucy Cartwright and John Edensor Littlewood,^[43] and Stephen Smale.^[44] Except for Smale, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood.^{[citation needed]} Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.

Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident to some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behavior of certain experiments like that of the logistic map. What had been attributed to measure imprecision and simple "noise" was considered by chaos theorists as a full component of the studied systems.

The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems. As a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers and noticed, on November 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.^[45][46]

Turbulence in the tip vortex from an airplane wing. Studies of the critical point beyond which a system creates turbulence were important for chaos theory, analyzed for example by the Soviet physicist Lev Landau, who developed the Landau-Hopf theory of turbulence. David Ruelle and Floris Takens later predicted, against Landau, that fluid turbulence could develop through a strange attractor, a main concept of chaos theory.

Edward Lorenz was an early pioneer of the theory. His interest in chaos came about accidentally through his work on weather prediction in 1961.^[8] Lorenz was using a simple digital computer, a Royal McBee LGP-30, to run his weather simulation. He wanted to see a sequence of data again, and to save time he started the simulation in the middle of its course. He did this by entering a printout of the data that corresponded to conditions in the middle of the original simulation. To his surprise, the weather the machine began to predict was completely different from the previous calculation. Lorenz tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 printed as 0.506. This difference is tiny, and the consensus at the time would have been that it should have no practical effect. However, Lorenz discovered that small changes in initial conditions produced large changes in long-term outcome.^[47] Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modelling cannot, in general, make precise long-term weather predictions.

In 1963, Benoit Mandelbrot found recurring patterns at every scale in data on cotton prices.^[48] Beforehand he had studied information theory and concluded noise was patterned like a Cantor set: on any scale the proportion of noise-containing periods to error-free periods was a constant – thus errors were inevitable and must be planned for by incorporating redundancy.^[49] Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards).^[50][51] This challenged the idea that changes in price were normally distributed. In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device.^[52] Arguing that a ball of twine appears as a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (examples include the Menger sponge, the Sierpiński gasket, and the Koch curve or snowflake, which is infinitely long yet encloses a finite space and has a fractal dimension of circa 1.2619). In 1982 Mandelbrot published The Fractal Geometry of Nature, which became a classic of chaos theory.^[53] Biological systems such as the branching of the circulatory and bronchial systems proved to fit a fractal model.^[54]

In December 1977, the New York Academy of Sciences organized the first symposium on chaos, attended by David Ruelle, Robert May, James A. Yorke (coiner of the term "chaos" as used in mathematics), Robert Shaw, and the meteorologist Edward Lorenz. The following year, independently Pierre Coullet and Charles Tresser with the article "Iterations d'endomorphismes et groupe de renormalisation" and Mitchell Feigenbaum with the article "Quantitative Universality for a Class of Nonlinear Transformations" described logistic maps.^[55][56] They notably discovered the universality in chaos, permitting the application of chaos theory to many different phenomena.

In 1979, Albert J. Libchaber, during a symposium organized in Aspen by Pierre Hohenberg, presented his experimental observation of the bifurcation cascade that leads to chaos and turbulence in Rayleigh–Bénard convection systems. He was awarded the Wolf Prize in Physics in 1986 along with Mitchell J. Feigenbaum for their inspiring achievements.^[57]

In 1986, the New York Academy of Sciences co-organized with the National Institute of Mental Health and the Office of Naval Research the first important conference on chaos in biology and medicine. There, Bernardo Huberman presented a mathematical model of the eye tracking disorder among schizophrenics.^[58] This led to a renewal of physiology in the 1980s through the application of chaos theory, for example, in the study of pathological cardiac cycles.

In 1987, Per Bak, Chao Tang and Kurt Wiesenfeld published a paper in Physical Review Letters^[59] describing for the first time self-organized criticality (SOC), considered one of the mechanisms by which complexity arises in nature.

Alongside largely lab-based approaches such as the Bak–Tang–Wiesenfeld sandpile, many other investigations have focused on large-scale natural or social systems that are known (or suspected) to display scale-invariant behavior. Although these approaches were not always welcomed (at least initially) by specialists in the subjects examined, SOC has nevertheless become established as a strong candidate for explaining a number of natural phenomena, including earthquakes, (which, long before SOC was discovered, were known as a source of scale-invariant behavior such as the Gutenberg–Richter law describing the statistical distribution of earthquake sizes, and the Omori law^[60] describing the frequency of aftershocks), solar flares, fluctuations in economic systems such as financial markets (references to SOC are common in econophysics), landscape formation, forest fires, landslides, epidemics, and biological evolution (where SOC has been invoked, for example, as the dynamical mechanism behind the theory of "punctuated equilibria" put forward by Niles Eldredge and Stephen Jay Gould). Given the implications of a scale-free distribution of event sizes, some researchers have suggested that another phenomenon that should be considered an example of SOC is the occurrence of wars. These investigations of SOC have included both attempts at modelling (either developing new models or adapting existing ones to the specifics of a given natural system), and extensive data analysis to determine the existence and/or characteristics of natural scaling laws.

In the same year, James Gleick published Chaos: Making a New Science, which became a best-seller and introduced the general principles of chaos theory as well as its history to the broad public, though his history under-emphasized important Soviet contributions.^{[citation needed][61]} Initially the domain of a few, isolated individuals, chaos theory progressively emerged as a transdisciplinary and institutional discipline, mainly under the name of nonlinear systems analysis. Alluding to Thomas Kuhn's concept of a paradigm shift exposed in The Structure of Scientific Revolutions (1962), many "chaologists" (as some described themselves) claimed that this new theory was an example of such a shift, a thesis upheld by Gleick.

The availability of cheaper, more powerful computers broadens the applicability of chaos theory. Currently, chaos theory remains an active area of research,^[62] involving many different disciplines (mathematics, topology, physics,^[63] social systems, population modeling, biology, meteorology, astrophysics, information theory, computational neuroscience, etc.).

Applications

A conus textile shell, similar in appearance to Rule 30, a cellular automaton with chaotic behaviour.^[64]

Chaos theory was born from observing weather patterns, but it has become applicable to a variety of other situations. Some areas benefiting from chaos theory today are geology, mathematics, microbiology, biology, computer science, economics,^[65][66][67] engineering,^[68] finance,^[69][70] algorithmic trading,^[71][72][73] meteorology, philosophy, anthropology,^[11][12] physics,^[74][75][76] politics, population dynamics,^[77] psychology,^[10] and robotics. A few categories are listed below with examples, but this is by no means a comprehensive list as new applications are appearing.

Cryptography

Chaos theory has been used for many years in cryptography. In the past few decades, chaos and nonlinear dynamics have been used in the design of hundreds of cryptographic primitives. These algorithms include image encryption algorithms, hash functions, secure pseudo-random number generators, stream ciphers, watermarking and steganography.^[78] The majority of these algorithms are based on uni-modal chaotic maps and a big portion of these algorithms use the control parameters and the initial condition of the chaotic maps as their keys.^[79] From a wider perspective, without loss of generality, the similarities between the chaotic maps and the cryptographic systems is the main motivation for the design of chaos based cryptographic algorithms.^[78] One type of encryption, secret key or symmetric key, relies on diffusion and confusion, which is modeled well by chaos theory.^[80] Another type of computing, DNA computing, when paired with chaos theory, offers a way to encrypt images and other information.^[81] Many of the DNA-Chaos cryptographic algorithms are proven to be either not secure, or the technique applied is suggested to be not efficient.^[82][83][84]

Robotics

Robotics is another area that has recently benefited from chaos theory. Instead of robots acting in a trial-and-error type of refinement to interact with their environment, chaos theory has been used to build a predictive model.^[85] Chaotic dynamics have been exhibited by passive walking biped robots.^[86]

Biology

For over a hundred years, biologists have been keeping track of populations of different species with population models. Most models are continuous, but recently scientists have been able to implement chaotic models in certain populations.^[87] For example, a study on models of Canadian lynx showed there was chaotic behavior in the population growth.^[88] Chaos can also be found in ecological systems, such as hydrology. While a chaotic model for hydrology has its shortcomings, there is still much to learn from looking at the data through the lens of chaos theory.^[89] Another biological application is found in cardiotocography. Fetal surveillance is a delicate balance of obtaining accurate information while being as noninvasive as possible. Better models of warning signs of fetal hypoxia can be obtained through chaotic modeling.^[90]

Other areas

In chemistry, predicting gas solubility is essential to manufacturing polymers, but models using particle swarm optimization (PSO) tend to converge to the wrong points. An improved version of PSO has been created by introducing chaos, which keeps the simulations from getting stuck.^[91] In celestial mechanics, especially when observing asteroids, applying chaos theory leads to better predictions about when these objects will approach Earth and other planets.^[92] Four of the five moons of Pluto rotate chaotically. In quantum physics and electrical engineering, the study of large arrays of Josephson junctions benefitted greatly from chaos theory.^[93] Closer to home, coal mines have always been dangerous places where frequent natural gas leaks cause many deaths. Until recently, there was no reliable way to predict when they would occur. But these gas leaks have chaotic tendencies that, when properly modeled, can be predicted fairly accurately.^[94]

Chaos theory can be applied outside of the natural sciences. By adapting a model of career counseling to include a chaotic interpretation of the relationship between employees and the job market, better suggestions can be made to people struggling with career decisions.^[95] Modern organizations are increasingly seen as open complex adaptive systems with fundamental natural nonlinear structures, subject to internal and external forces that may contribute chaos. For instance, team building and group development is increasingly being researched as an inherently unpredictable system, as the uncertainty of different individuals meeting for the first time makes the trajectory of the team unknowable.^[96] The chaos metaphor—used in verbal theories—grounded on mathematical models and psychological aspects of human behavior provides helpful insights to describing the complexity of small work groups, that go beyond the metaphor itself.^[97]

It is possible that economic models can also be improved through an application of chaos theory, but predicting the health of an economic system and what factors influence it most is an extremely complex task.^[98] Economic and financial systems are fundamentally different from those in the classical natural sciences since the former are inherently stochastic in nature, as they result from the interactions of people, and thus pure deterministic models are unlikely to provide accurate representations of the data. The empirical literature that tests for chaos in economics and finance presents very mixed results, in part due to confusion between specific tests for chaos and more general tests for non-linear relationships.^[99]

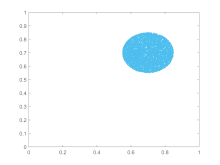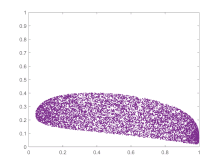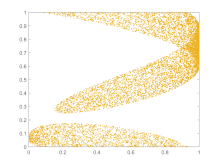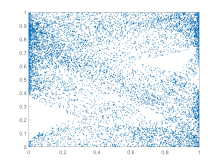
Traffic forecasting also benefits from applications of chaos theory. Better predictions of when traffic will occur lets measures be taken to disperse it before it would have occurred. Combining chaos theory principles with a few other methods has led to a more accurate short-term prediction model (see the plot of the BML traffic model at right).^[100]

Chaos theory can be applied in psychology. For example, in modeling group behavior in which heterogeneous members may behave as if sharing to different degrees what in Wilfred Bion's theory is a basic assumption, the group dynamics is the result of the individual dynamics of the members: each individual reproduces the group dynamics in a different scale, and the chaotic behavior of the group is reflected in each member.^[101]

Chaos theory has been applied to environmental water cycle data (aka hydrological data), such as rainfall and streamflow.^[102] These studies have yielded controversial results, because the methods for detecting a chaotic signature are often relatively subjective. Early studies tended to "succeed" in finding chaos, whereas subsequent studies and meta-analyses called those studies into question and provided explanations for why these datasets are not likely to have low-dimension chaotic dynamics.^[103]

Human skin color

From Wikipedia, the free encyclopedia

Extended Coloured family from South Africa showing some spectrum of human skin coloration

Human skin color ranges in variety from the darkest brown to the lightest hues. An individual's skin pigmentation is the result of genetics, being the product of both of the individual's biological parents' genetic makeup. In evolution, skin pigmentation in human beings evolved by a process of natural selection primarily to regulate the amount of ultraviolet radiation penetrating the skin, controlling its biochemical effects.^[1]

The actual skin color of different humans is affected by many substances, although the single most important substance is the pigment melanin. Melanin is produced within the skin in cells called melanocytes and it is the main determinant of the skin color of darker-skinned humans. The skin color of people with light skin is determined mainly by the bluish-white connective tissue under the dermis and by the hemoglobin circulating in the veins of the dermis. The red color underlying the skin becomes more visible, especially in the face, when, as consequence of physical exercise or the stimulation of the nervous system (anger, fear), arterioles dilate.^[2] Color is not entirely uniform across an individual's skin; for example, the skin of the palm and the sole is lighter than most other skin, and this is especially noticeable in darker-skinned people.^[3]

There is a direct correlation between the geographic distribution of ultraviolet radiation (UVR) and the distribution of indigenous skin pigmentation around the world. Areas that receive higher amounts of UVR, generally located closer to the equator, tend to have darker-skinned populations. Areas that are far from the tropics and closer to the poles have lower intensity of UVR, which is reflected in lighter-skinned populations.^[4] Researchers suggest that human populations over the past 50,000 years have changed from dark-skinned to light-skinned and vice versa as they migrated to different UV zones,^[5] and that such major changes in pigmentation may have happened in as little as 100 generations (≈2,500 years) through selective sweeps.^[5][6][7] Natural skin color can also darken as a result of tanning due to exposure to sunlight. The leading theory is that skin color adapts to intense sunlight irradiation to provide partial protection against the ultraviolet fraction that produces damage and thus mutations in the DNA of the skin cells.^[8][9] In addition, it has been observed that adult human females on average are significantly lighter in skin pigmentation than males. Females need more calcium during pregnancy and lactation. The body synthesizes vitamin D from sunlight, which helps it absorb calcium. Females evolved to have lighter skin so their bodies absorb more calcium.^[10]

The social significance of differences in skin color has varied across cultures and over time, as demonstrated with regard to social status and discrimination.

Melanin and genes

Melanin is produced by cells called melanocytes in a process called melanogenesis. Melanin is made within small membrane–bound packages called melanosomes. As they become full of melanin, they move into the slender arms of melanocytes, from where they are transferred to the keratinocytes. Under normal conditions, melanosomes cover the upper part of the keratinocytes and protect them from genetic damage. One melanocyte supplies melanin to thirty-six keratinocytes according to signals from the keratinocytes. They also regulate melanin production and replication of melanocytes.^[7] People have different skin colors mainly because their melanocytes produce different amount and kinds of melanin.
The genetic mechanism behind human skin color is mainly regulated by the enzyme tyrosinase, which creates the color of the skin, eyes, and hair shades.^[11][12] Differences in skin color are also attributed to differences in size and distribution of melanosomes in the skin.^[7] Melanocytes produce two types of melanin. The most common form of biological melanin is eumelanin, a brown-black polymer of dihydroxyindole carboxylic acids, and their reduced forms. Most are derived from the amino acid tyrosine. Eumelanin is found in hair, areola, and skin, and the hair colors gray, black, blond, and brown. In humans, it is more abundant in people with dark skin. Pheomelanin, a pink to red hue is found in particularly large quantities in red hair,^[13] the lips, nipples, glans of the penis, and vagina.^[14]

Both the amount and type of melanin produced is controlled by a number of genes that operate under incomplete dominance.^[15] One copy of each of the various genes is inherited from each parent. Each gene can come in several alleles, resulting in the great variety of human skin tones. Melanin controls the amount of ultraviolet (UV) radiation from the sun that penetrates the skin by absorption. While UV radiation can assist in the production of vitamin D, excessive exposure to UV can damage health.

Evolution of skin color

Loss of body hair in Hominini species is assumed to be related to the emergence of bipedalism some 5 to 7 million years ago.^[16] Bipedal hominin body hair may have disappeared gradually to allow better heat dissipation through sweating.^[10][17]

Reconstruction of a female Homo erectus based on fossils dated c. 1.5 million years ago, the estimated time for the emergence of skin pigmentation in early humans (John Gurche, Smithsonian Museum of Natural History, 2010).

The emergence of skin pigmentation dates to after this, perhaps some 1.5 million years ago (about the time of the emergence of Homo heidelbergensis), when the earth endured a megadrought that drove early humans into arid, open landscapes. Such conditions likely caused excess UV-B radiation. This favored the emergence of skin pigmentation in order to protect from folate depletion due to the increased exposure to sunlight.^[8][9] A theory that the pigmentation helped counter xeric stress by increasing the epidermal permeability barrier^[18] has been disproved.^[8]

With the evolution of hairless skin, abundant sweat glands, and skin rich in melanin, early humans could walk, run, and forage for food for long periods of time under the hot sun without brain damage due to overheating, giving them an evolutionary advantage over other species.^[7] By 1.2 million years ago, around the time of Homo ergaster, archaic humans (including the ancestors of Homo sapiens) had exactly the same receptor protein as modern sub-Saharan Africans.^[17]

This was the genotype inherited by anatomically modern humans, but retained only by part of the extant populations, thus forming an aspect of human genetic variation. About 100,000–70,000 years ago, some anatomically modern humans (Homo sapiens) began to migrate away from the tropics to the north where they were exposed to less intense sunlight. This was possibly in part due to the need for greater use of clothing to protect against the colder climate. Under these conditions there was less photodestruction of folate and so the evolutionary pressure working against the survival of lighter-skinned gene variants was reduced. In addition, lighter skin is able to generate more vitamin D (cholecalciferol) than darker skin, so it would have represented a health benefit in reduced sunlight if there were limited sources of vitamin D.^[10] Hence the leading hypothesis for the evolution of human skin color proposes that:

1. From about 1.2 million years ago to less than 100,000 years ago, archaic humans, including archaic Homo sapiens, were dark-skinned.
2. As Homo sapiens populations began to migrate, the evolutionary constraint keeping skin dark decreased proportionally to the distance north a population migrated, resulting in a range of skin tones within northern populations.
3. At some point, some northern populations experienced positive selection for lighter skin due to the increased production of vitamin D from sunlight and the genes for darker skin disappeared from these populations.
4. Subsequent migrations into different UV environments and admixture between populations have resulted in the varied range of skin pigmentations we see today.

The genetic mutations leading to light skin, though partially different among East Asians and Western Europeans,^[19] suggest the two groups experienced a similar selective pressure after settlement in northern latitudes.^[20] At what point these developments took place for sub-populations of Homo sapiens (and whether light skin also occurred independently in Homo neanderthalensis) is under debate. There is a long-standing hypothesis that the selection for lighter skin due to higher vitamin D absorption occurred soon after the Out of Africa migration some time before 40,000 years ago. A number of researchers disagree with this and suggest that the northern latitudes permitted enough synthesis of vitamin D combined with food sources from hunting to keep populations healthy, and only when agriculture was adopted was there a need for lighter skin to maximize the synthesis of vitamin D.^{[citation needed]}

The theory suggests that the reduction of game meat, fish, and some plants from the diet resulted in skin turning light many thousands of years after settlement in Eurasia.^[21] This theory is partially supported by a study into the SLC24A5 gene which found that the allele associated with light skin in Europe "determined […] that 18,000 years had passed since the light-skin allele was fixed in Europeans" but may have originated as recently as 12,000–6,000 years ago "given the imprecision of method" ,^[22] which is in line with the earliest evidence of farming.^[23]

Research by Nina Jablonski suggests that an estimated time of about 10,000 to 20,000 years is enough for human populations to achieve optimal skin pigmentation in a particular geographic area but that development of ideal skin coloration may happen faster if the evolutionary pressure is stronger, even in as little as 100 generations.^[5] The length of time is also affected by cultural practices such as food intake, clothing, body coverings, and shelter usage which can alter the ways in which the environment affects populations.^[7]

Reconstruction of the head of the Shanidar 1 fossil, a Neanderthal male who lived c. 70,000 years ago (John Gurche 2010). Examination of the genome of late Neanderthals suggests that at least some populations may have developed light skin by 40,000 years ago.^[24]

One of the most recently proposed drivers of the evolution of skin pigmentation in humans is based on research that shows a superior barrier function in darkly pigmented skin. Most protective functions of the skin, including the permeability barrier and the antimicrobial barrier, reside in the stratum corneum (SC) and the researchers surmise that the SC has undergone the most genetic change since the loss of human body hair. Natural selection would have favored mutations that protect this essential barrier; one such protective adaptation is the pigmentation of interfollicular epidermis, because it improves barrier function as compared to non-pigmented skin. In lush rainforests, however, where UV-B radiation and xeric stress were not in excess, light pigmentation would not have been nearly as detrimental. This explains the side-by-side residence of lightly pigmented and darkly pigmented peoples.^[18]

Population and admixture studies suggest a three-way model for the evolution of human skin color, with dark skin evolving in early hominids in Africa and light skin evolving partly separately at least two times after modern humans had expanded out of Africa.^{[19][25][26][27][28][29]}

For the most part, the evolution of light skin has followed different genetic paths in Western and Eastern Eurasian populations. Two genes however, KITLG and ASIP, have mutations associated with lighter skin that have high frequencies in Eurasian populations and have estimated origin dates after humans spread out of Africa but before the divergence of the two lineages.^[27]

Genetics

The evolutionary genetic architecture of skin pigmentation in Northern Europeans, West Africans and East Asians.

The understanding of the genetic mechanisms underlying human skin color variation is still incomplete, however genetic studies have discovered a number of genes that affect human skin color in specific populations, and have shown that this happens independently of other physical features such as eye and hair color. Different populations have different allele frequencies of these genes, and it is the combination of these allele variations that bring about the complex, continuous variation in skin coloration we can observe today in modern humans. Population and admixture studies suggest a 3-way model for the evolution of human skin color, with dark skin evolving in early hominids in sub-Saharan Africa and light skin evolving independently in Europe and East Asia after modern humans had expanded out of Africa.^{[19][25][26][27][28][29]}

Dark skin

All modern humans share a common ancestor who lived around 200,000 years ago in Africa.^[30] Comparisons between known skin pigmentation genes in chimpanzees and modern Africans show that dark skin evolved along with the loss of body hair about 1.2 million years ago and that this common ancestor had dark skin.^[31] Investigations into dark skinned populations in South Asia and Melanesia indicate that skin pigmentation in these populations is due to the preservation of this ancestral state and not due to new variations on a previously lightened population.^[10][32]

• MC1R

The melanocortin 1 receptor (MC1R) gene is primarily responsible for determining whether pheomelanin and eumelanin is produced in the human body. Research shows at least 10 differences in MC1R between African and chimpanzee samples and that the gene has probably undergone a strong positive selection (a selective sweep) in early Hominins around 1.2 million years ago.^[33] This is consistent with positive selection for the high-eumelanin phenotype seen in Africa and other environments with high UV exposure.^[31][32]

Light skin

For the most part, the evolution of light skin has followed different genetic paths in European and East Asian populations. Two genes however, KITLG and ASIP, have mutations associated with lighter skin that have high frequencies in both European and East Asian populations. They are thought to have originated after humans spread out of Africa but before the divergence of the European and Asian lineages around 30,000 years ago.^[27] Two subsequent genome-wide association studies found no significant correlation between these genes and skin color, and suggest that the earlier findings may have been the result of incorrect correction methods and small panel sizes, or that the genes have an effect too small to be detected by the larger studies.^[34][35]

• KITLG

The KIT ligand (KITLG) gene is involved in the permanent survival, proliferation and migration of melanocytes.^[36] A mutation in this gene, A326G (rs642742^[37]), has been positively associated with variations of skin color in African-Americans of mixed West African and European descent and is estimated to account for 15–20% of the melanin difference between African and European populations.^[38] This allele shows signs of strong positive selection outside Africa^[29][39] and occurs in over 80% of European and Asian samples, compared with less than 10% in African samples.^[38]

• ASIP

Agouti signalling peptide (ASIP) acts as an inverse agonist, binding in place of alpha-MSH and thus inhibiting eumelanin production. Studies have found two alleles in the vicinity of ASIP are associated with skin color variation in humans. One, rs2424984^[40] has been identified as an indicator of skin reflectance in a forensics analysis of human phenotypes across Caucasian, African-American, South Asian, East Asian, Hispanic and Native American populations^[41] and is about 3 times more common in non-African populations than in Africa.^[42] The other allele, 8188G (rs6058017^[43]) is significantly associated with skin color variation in African-Americans and the ancestral version occurs in only 12% of European and 28% of East Asian samples compared with 80% of West African samples.^[44][45]

Europe

A number of genes have been positively associated with the skin pigmentation difference between European and non-European populations. Mutations in SLC24A5 and SLC45A2 are believed to account for the bulk of this variation and show very strong signs of selection. A variation in TYR has also been identified as a contributor.

Research indicates the selection for the light-skin alleles of these genes in Europeans is comparatively recent, having occurred later than 20,000 years ago and perhaps as recently as 12,000 to 6,000 years ago.^[27] In the 1970s, Luca Cavalli-Sforza suggested that the selective sweep that rendered light skin ubiquitous in Europe might be correlated with the advent of farming and thus have taken place only around 6,000 years ago;^[22] This scenario found support in a 2014 analysis of mesolithic (7,000 years old) hunter-gatherer DNA from La Braña, Spain, which showed the version of these genes corresponding to dark skin color.^[46] In 2015 researchers analysed for light skin genes in the DNA of 94 ancient skeletons ranging from 8,000 to 3,000 years old from Europe and Russia. They found c. 8,000-year-old hunter-gatherers in Spain, Luxembourg, and Hungary were dark skinned while similarly aged hunter gatherers in Sweden were light skinned (having predominately derived alleles of SLC24A5, SLC45A2 and also HERC2/OCA2). Neolithic farmers entering Europe at around the same time were intermediate, being nearly fixed for the derived SLC24A5 variant but only having the derived SLC45A2 allele in low frequencies. The SLC24A5 variant spread very rapidly throughout central and southern Europe from about 8,000 years ago, whereas the light skin variant of SLC45A2 spread throughout Europe after 5,800 years ago.^[47][48]

• SLC24A5

Global frequency distribution of the SLC24A5 gene's ancestral Ala111 allele (yellow) and its derived Ala111Thr allele (blue).

Solute carrier family 24 member 5 (SLC24A5) regulates calcium in melanocytes and is important in the process of melanogenesis.^[49] The SLC24A5 gene's derived Ala111Thr allele (rs1426654^[50]) has been shown to be a major factor in light skin pigmentation and is common in Western Eurasia.^[41] Recent studies have found that the variant represents as much as 25–40% of the average skin tone difference between Europeans and West Africans.^[19][51] This derived allele is a reliable predictor of phenotype across a range of populations.^[52] It has been the subject of recent selection in Western Eurasia, and is fixed in European populations.^[27][53][54]

• SLC45A2

Solute carrier family 45 member 2 (SLC45A2 or MATP) aids in the transport and processing of tyrosine, a precursor to melanin. It has also been shown to be one of the significant components of the skin color of modern Europeans through its Phe374Leu (rs16891982^[55]) allele that has been directly correlated with skin color variation in mixed-race populations.^[41][52] This variation is ubiquitous in European populations but extremely rare elsewhere and shows strong signs of selection.^[53][54][56]

• TYR

The TYR gene encodes the enzyme tyrosinase, which is involved in the production of melanin from tyrosine. It has an allele, Ser192Tyr (rs1042602^[57]), found solely in 40–50% of Europeans^[19][27] and linked to light-colored skin in studies of both mixed-race South Asian^[52] and African-American^[58] populations.

East Asia

A number of genes known to affect skin color have alleles that show signs of positive selection in East Asian populations. Of these only OCA2 has been directly related to skin color measurements, while DCT, MC1R and ATTRN are marked as candidate genes for future study.

• OCA2

Global frequency distribution of the OCA2 gene's ancestral allele (blue) and derived His615Arg allele (yellow).

Oculocutaneous albinism II (OCA2) assists in the regulation of pH in melanocytes. The OCA2 gene's derived His615Arg (rs1800414^[59]) allele has been shown to account for about 8% of the skin tone difference between African and East Asian populations in studies of an East Asian population living in Toronto and a Chinese Han population. This variant is essentially restricted to East Asia, with highest frequencies in Eastern East Asia (49–63%), midrange frequencies in Southeast Asia, and the lowest frequencies in Western China and some Eastern European populations.^[28][60]

• Candidate Genes

A number of studies have found genes linked to human skin pigmentation that have alleles with statistically significant frequencies in Chinese and East Asian populations. While not linked to measurements of skin tone variation directly, dopachrome tautomerase (DCT or TYRP2 rs2031526^[61]),^[62] melanocortin 1 receptor (MC1R) Arg163Gln (rs885479^[63])^[64] and attractin (ATRN)^[19] have been indicated as potential contributors to the evolution of light skin in East Asian populations.

Tanning response

Tanning response in humans is controlled by a variety of genes. MC1R variants Arg151Sys (rs1805007^[65]), Arg160Trp (rs1805008^[66]), Asp294Sys (rs1805009^[67]), Val60Leu (rs1805005^[68]) and Val92Met (rs2228479^[69]) have been associated with reduced tanning response in European and/or East Asian populations. These alleles show no signs of positive selection and only occur in relatively small numbers, reaching a peak in Europe with around 28% of the population having at least one allele of one of the variations.^[32][70] A study of self-reported tanning ability and skin type in American non-Hispanic Caucasians found that SLC24A5 Phe374Leu is significantly associated with reduced tanning ability and also associated TYR Arg402Gln (rs1126809^[71]), OCA2 Arg305Trp (rs1800401^[72]) and a 2-SNP haplotype in ASIP (rs4911414^[73] and rs1015362^[74]) to skin type variation within a "fair/medium/olive" context.^[75]

Albinism

Oculocutaneous albinism (OCA) is a lack of pigment in the eyes, skin and sometimes hair that occurs in a very small fraction of the population. The four known types of OCA are caused by mutations in the TYR, OCA2, TYRP1, and SLC45A2 genes.^[76]

Age

In hominids the parts of the body not covered with hair, like the face and the back of the hands, start out pale in infants and turn darker as animals are exposed to more sun. All human babies are born pale, regardless of what their adult color will be. In humans, melanin production does not peak until after puberty.^[7]

The skin of children becomes darker as they go through puberty and experience the effects of sex hormones.^{[citation needed]} This darkening is especially noticeable in the skin of the nipples, the areola of the nipples, the labia majora in females, and the scrotum in males. In some people, the armpits become slightly darker during puberty. The interaction of genetic, hormonal, and environmental factors on skin coloration with age is still not adequately understood, but it is known that men are at their darkest baseline skin color around the age of 30, without considering the effects of tanning. Around the same age, women experience darkening of some areas of their skin.^[7]

Human skin color fades with age. Humans over the age of thirty experience a decrease in melanin-producing cells by about 10 to 20 percent per decade as melanocyte stem cells gradually die. The skin of face and hands has about twice the amount of pigment cells as unexposed areas of the body, as chronic exposure to the sun continues to stimulate melanocytes. The blotchy appearance of skin color in the face and hands of older people is due to the uneven distribution of pigment cells and to changes in the interaction between melanocytes and keratinocytes.^[7]

Sexual dimorphism

It has been observed that adult human females are consistently lighter in skin pigmentation than males in the same population.^[10] This form of sexual dimorphism is due to the requirement in human females for high amounts of calcium during pregnancy and lactation. Breastfeeding newborns, whose skeletons are growing, require high amounts of calcium intake from the mother's milk (about 4 times more than during prenatal development),^[77] part of which comes from reserves in the mother's skeleton. Adequate vitamin D resources are needed to absorb calcium from the diet, and it has been shown that deficiencies of vitamin D and calcium increase the likelihood of various birth defects such as spina bifida and rickets. Natural selection has led to females with lighter skin than males in all indigenous populations because women must get enough vitamin D and calcium to support the development of fetus and nursing infant and to maintain their own health.^[7]

The sexes also differ in how they change their skin color with age. Men and women are not born with different skin color, they begin to diverge during puberty with the influence of sex hormones. Women can also change pigmentation in certain parts of their body, such as the areola, during the menstrual cycle and pregnancy and between 50 and 70% of pregnant women will develop the "mask of pregnancy" (melasma or chloasma) in the cheeks, upper lips, forehead, and chin.^[7] This is caused by increases in the female hormones estrogen and progesterone and it can develop in women who take birth control pills or participate in hormone replacement therapy.^[78]

Disorders of pigmentation

Uneven pigmentation of some sort affects most people, regardless of bioethnic background or skin color. Skin may either appear lighter, or darker than normal, or lack pigmentation at all; there may be blotchy, uneven areas, patches of brown to gray discoloration or freckling. Apart from blood-related conditions such as jaundice, carotenosis, or argyria, skin pigmentation disorders generally occur because the body produces either too much or too little melanin.

Depigmentation

Various types of albinism are a result of genetic mutations affecting different parts of the melanin production pathway. In a person with albinism, melanocytes can be entirely absent, or fail to produce melanin, or melanosomes can fail to mature and be transferred to keranocytes. The ability to produce melanin in patches around the body is a condition known as vitiligo.

Albinism

Some types of albinism affect only the skin and hair, while other types affect the skin, hair and eyes, and in rare cases only the eyes. All of them are caused by different genetic mutations. Albinism is a recessively inherited trait in humans where both pigmented parents may be carriers of the gene and pass it down to their children. Each child has a 25% chance of being albino and a 75% chance of having normally pigmented skin.^[79] One common type of albinism is oculocutaneous albinism or OCA, which has many subtypes caused by different genetic mutations. Albinism is a serious problem in areas of high sunlight intensity, leading to extreme sun sensitivity, skin cancer, and eye damage.^[7]

Albinism is more common in some parts of the world than in others, but it is estimated that 1 in 70 humans carry the gene for OCA. The most severe type of albinism is OCA1A, which is characterized by complete, lifelong loss of melanin production, other forms of OCA1B, OCA2, OCA3, OCA4, show some form of melanin accumulation and are less severe.^[7] The four known types of OCA are caused by mutations in the TYR, OCA2, TYRP1, and SLC45A2 genes.^[76]

Albinos often face social and cultural challenges (even threats), as the condition is often a source of ridicule, racism, fear, and violence. Many cultures around the world have developed beliefs regarding people with albinism. Albinos are persecuted in Tanzania by witchdoctors, who use the body parts of albinos as ingredients in rituals and potions, as they are thought to possess magical power.^[80]

Vitiligo

Vitiligo is a condition that causes depigmentation of sections of skin. It occurs when melanocytes die or are unable to function. The cause of vitiligo is unknown, but research suggests that it may arise from autoimmune, genetic, oxidative stress, neural, or viral causes.^[81] The incidence worldwide is less than 1%.^[82] Individuals affected by vitiligo sometimes suffer psychological discomfort because of their appearance.^[7]

Hyperpigmentation

Increased melanin production, also known as hyperpigmentation, can be a few different phenomena:

• Melasma describes the darkening of the skin.
• Chloasma describes skin discolorations caused by hormones. These hormonal changes are usually the result of pregnancy, birth control pills or estrogen replacement therapy.
• Solar lentigo, also known as "liver spots" or "senile freckles", refers to darkened spots on the skin caused by aging and the sun. These spots are quite common in adults with a long history of unprotected sun exposure.

Aside from sun exposure and hormones, hyperpigmentation can be caused by skin damage, such as remnants of blemishes, wounds or rashes.^[83] This is especially true for those with darker skin tones.

The most typical cause of darkened areas of skin, brown spots or areas of discoloration is unprotected sun exposure. Once incorrectly referred to as liver spots, these pigment problems are not connected with the liver.

On lighter to medium skin tones, solar lentigenes emerge as small- to medium-sized brown patches of freckling that can grow and accumulate over time on areas of the body that receive the most unprotected sun exposure, such as the back of the hands, forearms, chest, and face. For those with darker skin colors, these discolorations can appear as patches or areas of ashen-gray skin.

Exposure to sun

A suntanned arm showing darker skin where it has been exposed. This pattern of tanning is often called a farmer's tan.

Melanin in the skin protects the body by absorbing solar radiation. In general, the more melanin there is in the skin the more solar radiation can be absorbed. Excessive solar radiation causes direct and indirect DNA damage to the skin and the body naturally combats and seeks to repair the damage and protect the skin by creating and releasing further melanin into the skin's cells. With the production of the melanin, the skin color darkens, but can also cause sunburn. The tanning process can also be created by artificial UV radiation.

There are two different mechanisms involved. Firstly, the UVA-radiation creates oxidative stress, which in turn oxidizes existing melanin and leads to rapid darkening of the melanin, also known as IPD (immediate pigment darkening). Secondly, there is an increase in production of melanin known as melanogenesis.^[84] Melanogenesis leads to delayed tanning and first becomes visible about 72 hours after exposure. The tan that is created by an increased melanogenesis lasts much longer than the one that is caused by oxidation of existing melanin. Tanning involves not just the increased melanin production in response to UV radiation but the thickening of the top layer of the epidermis, the stratum corneum.^[7]

A person's natural skin color affects their reaction to exposure to the sun. Generally, those who start out with darker skin color and more melanin have better abilities to tan. Individuals with very light skin and albinos have no ability to tan.^[85] The biggest differences resulting from sun exposure are visible in individuals who start out with moderately pigmented brown skin: the change is dramatically visible as tan lines, where parts of the skin which tanned are delineated from unexposed skin.^[7]

Modern lifestyles and mobility have created mismatch between skin color and environment for many individuals. Vitamin D deficiencies and UVR overexposure are concerns for many. It is important for these people individually to adjust their diet and lifestyle according to their skin color, the environment they live in, and the time of year.^[7] For practical purposes, such as exposure time for sun tanning, six skin types are distinguished following Fitzpatrick (1975), listed in order of decreasing lightness:

Fitzpatrick scale

The following list shows the six categories of the Fitzpatrick scale in relation to the 36 categories of the older von Luschan scale:^[86][87]

Type	Also called	Sunburning	Tanning behavior	Von Luschan's chromatic scale
I	Light, pale white	Always	Never	0–6
II	White, fair	Usually	Minimally	7–13
III	Medium, white to light brown	Sometimes	Uniformly	14–20
IV	Olive, moderate brown	Rarely	Easily	21–27
V	Brown, dark brown	Very rarely	Very easily	28–34
VI	Very dark brown to black	Never	Never	35–36

Dark skin with large concentrations of melanin protects against ultraviolet light and skin cancers; light-skinned people have about a tenfold greater risk of dying from skin cancer, compared with dark-skinned persons, under equal sunlight exposure. Furthermore, UV-A rays from sunlight are believed to interact with folic acid in ways that may damage health.^[88] In a number of traditional societies the sun was avoided as much as possible, especially around noon when the ultraviolet radiation in sunlight is at its most intense. Midday was a time when people stayed in the shade and had the main meal followed by a nap,^[89] a practice similar to the modern siesta.

Geographic variation

1959 map of human skin color distribution by R. Biassutti in the Von Luschan's chromatic scale for classifying skin color.

Approximately 10% of the variance in skin color occurs within regions, and approximately 90% occurs between regions.^[90] Because skin color has been under strong selective pressure, similar skin colors can result from convergent adaptation rather than from genetic relatedness; populations with similar pigmentation may be genetically no more similar than other widely separated groups. Furthermore, in some parts of the world where people from different regions have mixed extensively, the connection between skin color and ancestry has substantially weakened.^[91] In Brazil, for example, skin color is not closely associated with the percentage of recent African ancestors a person has, as estimated from an analysis of genetic variants differing in frequency among continent groups.^[92]

In general, people living close to the equator are highly darkly pigmented, and those living near the poles are generally very lightly pigmented. The rest of humanity shows a high degree of skin color variation between these two extremes, generally correlating with UV exposure. The main exception to this rule is in the New World, where people have only lived for about 10,000 to 15,000 years and show a less pronounced degree of skin pigmentation.^[7]

In recent times, humans have become increasingly mobile as a consequence of improved technology, domestication, environmental change, strong curiosity, and risk-taking. Migrations over the last 4000 years, and especially the last 400 years, have been the fastest in human history and have led to many people settling in places far away from their ancestral homelands. This means that skin colors today are not as confined to geographical location as they were previously.^[7]

Social status, colorism and racism

Skin colors according to von Luschan's chromatic scale

According to classical scholar Frank Snowden, skin color did not determine social status in ancient Egypt, Greece or Rome. These ancient civilizations viewed relations between the major power and the subordinate state as more significant in a person's status than their skin colors.^{[93][need quotation to verify]}

Nevertheless, some social groups favor specific skin coloring. The preferred skin tone varies by culture and has varied over time. A number of indigenous African groups, such as the Maasai, associated pale skin with being cursed or caused by evil spirits associated with witchcraft. They would abandon their children born with conditions such as albinism and showed a sexual preference for darker skin.^[94]

Many cultures have historically favored lighter skin for women. Before the Industrial Revolution, inhabitants of the continent of Europe preferred pale skin, which they interpreted as a sign of high social status. The poorer classes worked outdoors and got darker skin from exposure to the sun, while the upper class stayed indoors and had light skin. Hence light skin became associated with wealth and high position.^[95] Women would put lead-based cosmetics on their skin to whiten their skin tone artificially.^[96] However, when not strictly monitored, these cosmetics caused lead poisoning. Other methods also aimed at achieving a light-skinned appearance, including the use of arsenic to whiten skin, and powders. Women would wear full-length clothes when outdoors, and would utilize gloves and parasols.

Colonization and enslavement as carried out by European countries became involved with colorism and racism, associated with the belief that people with dark skin were uncivilized, inferior, and should be subordinate to lighter-skinned invaders. This has been perpetuated^{[by whom?]} in modern times.^[97] Institutionalized slavery in North America led people to perceive lighter-skinned African-Americans as more intelligent, cooperative, and beautiful.^[98] Such lighter-skinned individuals had a greater likelihood of working as house slaves and of receiving preferential treatment from plantation owners and from overseers. For example, they had a chance to get an education,^[99] while darker African-Americans worked in the fields and did not get an education.^[100] The preference for fair skin remained prominent until the end of the Victorian era, but racial stereotypes about worth and beauty persisted in the last half of the 20th century and continue in the present day. African-American journalist Jill Nelson wrote that, "To be both prettiest and black was impossible,"^[101] and elaborated:

We learn as girls that in ways both subtle and obvious, personal and political, our value as females is largely determined by how we look. … For black women, the domination of physical aspects of beauty in women's definition and value render us invisible, partially erased, or obsessed, sometimes for a lifetime, since most of us lack the major talismans of Western beauty. Black women find themselves involved in a lifelong effort to self-define in a culture that provides them no positive reflection.^[101]

A Vietnamese motorcyclist wears long gloves to block the sun, despite the tropical heat.

A preference for fair or lighter skin continues in some countries, including Latin American countries where whites form a minority.^[102] In Brazil, a dark-skinned person is more likely to experience discrimination.^[103] Many actors and actresses in Latin America have European features—blond hair, blue eyes, and pale skin.^[104][105] A light-skinned person is considered^{[by whom?]} more privileged and has a higher social status;^[105] a person with light skin is considered more beautiful^[105] and lighter skin suggests that the person has more wealth.^[105] Skin color is such an obsession in some countries that specific words describe distinct skin tones - from (for example) "jincha", Puerto Rican slang for "glass of milk" to "morena", literally "brown".^[105]

In India, society regards pale skin as more attractive and associates dark skin with lower class status; this results in a massive market for skin-whitening creams.^[106] Fairer skin-tones also correlate to higher caste-status in the Hindu social order – although the system is not based on skin tone.^[107] Actors and actresses in Indian cinema tend to have light skin tones, and Indian cinematographers have used graphics and intense lighting to achieve more "desirable" skin tones.^[108] Fair skin tones are claimed^{[by whom?]} to be an asset in Indian marketing.^[109]

Skin-whitening products have remained popular over time, often due to historical beliefs and perceptions about fair skin. Sales of skin-whitening products across the world grew from $40 billion to $43 billion in 2008.^[110] In South and East Asian countries, people have traditionally seen light skin as more attractive, and a preference for lighter skin remains prevalent. In ancient China and Japan, for example, pale skin can be traced back to ancient drawings depicting women and goddesses with fair skin tones.^{[citation needed]} In ancient China, Japan, and Southeast Asia, pale skin was seen as a sign of wealth. Thus skin-whitening cosmetic products are popular in East Asia.^[111] Four out of ten women surveyed in Hong Kong, Malaysia, the Philippines and South Korea used a skin-whitening cream, and more than 60 companies globally compete for Asia's estimated $18 billion market.^[112] Changes in regulations in the cosmetic industry led to skin-care companies introducing harm-free skin lighteners. In Japan, the geisha have a reputation for their white-painted faces, and the appeal of the bihaku (美白), or "beautiful white", ideal leads many Japanese women to avoid any form of tanning.^[113] There are exceptions to this, with Japanese fashion trends such as ganguro emphasizing tanned skin. Skin whitening is also not uncommon in Africa,^[114][115] and several research projects have suggested a general preference for lighter skin in the African-American community.^[116] In contrast, one study on men of the Bikosso tribe in Cameroon found no preference for attractiveness of females based on lighter skin color, bringing into question the universality of earlier studies that had exclusively focused on skin-color preferences among non-African populations.^[117]

Significant exceptions to a preference for lighter skin started to appear in Western culture in the mid-20th century.^[118] Though sun-tanned skin was once associated with the sun-exposed manual labor of the lower class, the associations became dramatically reversed during this time—a change usually credited to the trendsetting Frenchwoman Coco Chanel (1883-1971) presenting tanned skin as fashionable, healthy, and luxurious.^[119] As of 2017, though an overall preference for lighter skin remains prevalent in the United States, many within the country regard tanned skin as both more attractive and healthier than pale or very dark skin.^{[120][121][122]} Western mass media and popular culture continued^[when?] to reinforce negative stereotypes about dark skin,^[123] but in some circles pale skin has become associated with indoor office-work while tanned skin has become associated with increased leisure time, sportiness and good health that comes with wealth and higher social status.^[95] Studies have also emerged indicating that the degree of tanning is directly related to how attractive a young woman is.^[124][125]