Population inversion

From Wikipedia, the free encyclopedia

In science, specifically statistical mechanics, a population inversion occurs while a system (such as a group of atoms or molecules) exists in a state in which more members of the system are in higher, excited states than in lower, unexcited energy states. It is called an "inversion" because in many familiar and commonly encountered physical systems, this is not possible. The concept is of fundamental importance in laser science because the production of a population inversion is a necessary step in the workings of a standard laser.

Boltzmann distributions and thermal equilibrium

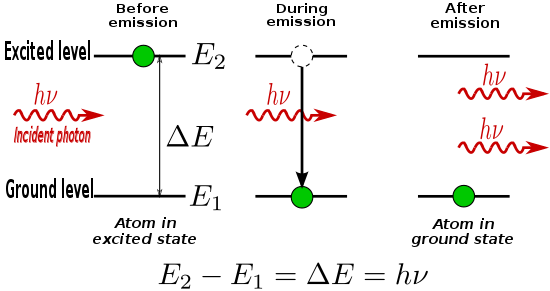
To understand the concept of a population inversion, it is necessary to understand some thermodynamics and the way that light interacts with matter. To do so, it is useful to consider a very simple assembly of atoms forming a laser medium.

Assume there are a group of N atoms, each of which is capable of being in one of two energy states: either

1. The ground state, with energy E₁; or
2. The excited state, with energy E₂, with E₂ > E₁.

The number of these atoms which are in the ground state is given by N₁, and the number in the excited state N₂. Since there are N atoms in total,

${\displaystyle N_{1}+N_{2}=N}$

The energy difference between the two states, given by

${\displaystyle \Delta E_{12}=E_{2}-E_{1},}$

determines the characteristic frequency ${\textstyle \nu _{12}}$ of light which will interact with the atoms; This is given by the relation

${\displaystyle E_{2}-E_{1}=\Delta E_{12}=h\nu _{12},}$

h being Planck's constant.

If the group of atoms is in thermal equilibrium, it can be shown from Maxwell–Boltzmann statistics that the ratio of the number of atoms in each state is given by the ratio of two Boltzmann distributions, the Boltzmann factor:

${\displaystyle {\frac {N_{2}}{N_{1}}}=\exp {\frac {-(E_{2}-E_{1})}{kT}},}$

where T is the thermodynamic temperature of the group of atoms, and k is Boltzmann's constant.

We may calculate the ratio of the populations of the two states at room temperature (T ≈ 300 K) for an energy difference ΔE that corresponds to light of a frequency corresponding to visible light (ν ≈ 5×10¹⁴ Hz). In this case ΔE = E₂ - E₁ ≈ 2.07 eV, and kT ≈ 0.026 eV. Since E₂ - E₁ ≫ kT, it follows that the argument of the exponential in the equation above is a large negative number, and as such N₂/N₁ is vanishingly small; i.e., there are almost no atoms in the excited state. When in thermal equilibrium, then, it is seen that the lower energy state is more populated than the higher energy state, and this is the normal state of the system. As T increases, the number of electrons in the high-energy state (N₂) increases, but N₂ never exceeds N₁ for a system at thermal equilibrium; rather, at infinite temperature, the populations N₂ and N₁ become equal. In other words, a population inversion (N₂/N₁ > 1) can never exist for a system at thermal equilibrium. To achieve population inversion therefore requires pushing the system into a non-equilibrated state.

The interaction of light with matter

There are three types of possible interactions between a system of atoms and light that are of interest:

Absorption

If light (photons) of frequency ν₁₂ passes through the group of atoms, there is a possibility of the light being absorbed by electrons which are in the ground state, which will cause them to be excited to the higher energy state. The rate of absorption is proportional to the radiation intensity of the light, and also to the number of atoms currently in the ground state, N₁.

Spontaneous emission

If atoms are in the excited state, spontaneous decay events to the ground state will occur at a rate proportional to N₂, the number of atoms in the excited state. The energy difference between the two states ΔE₂₁ is emitted from the atom as a photon of frequency ν₂₁ as given by the frequency-energy relation above.
The photons are emitted stochastically, and there is no fixed phase relationship between photons emitted from a group of excited atoms; in other words, spontaneous emission is incoherent. In the absence of other processes, the number of atoms in the excited state at time t, is given by

${\displaystyle N_{2}(t)=N_{2}(0)\exp {\frac {-t}{\tau _{21}}},}$

where N₂(0) is the number of excited atoms at time t = 0, and τ₂₁ is the mean lifetime of the transition between the two states.

Stimulated emission

If an atom is already in the excited state, it may be agitated by the passage of a photon that has a frequency ν₂₁ corresponding to the energy gap ΔE of the excited state to ground state transition. In this case, the excited atom relaxes to the ground state, and it produces a second photon of frequency ν₂₁. The original photon is not absorbed by the atom, and so the result is two photons of the same frequency. This process is known as stimulated emission.

Specifically, an excited atom will act like a small electric dipole which will oscillate with the external field provided. One of the consequences of this oscillation is that it encourages electrons to decay to the lowest energy state. When this happens due to the presence of the electromagnetic field from a photon, a photon is released in the same phase and direction as the "stimulating" photon, and is called stimulated emission.

The rate at which stimulated emission occurs is proportional to the number of atoms N₂ in the excited state, and the radiation density of the light. The base probability of a photon causing stimulated emission in a single excited atom was shown by Albert Einstein to be exactly equal to the probability of a photon being absorbed by an atom in the ground state. Therefore, when the numbers of atoms in the ground and excited states are equal, the rate of stimulated emission is equal to the rate of absorption for a given radiation density.

The critical detail of stimulated emission is that the induced photon has the same frequency and phase as the incident photon. In other words, the two photons are coherent. It is this property that allows optical amplification, and the production of a laser system. During the operation of a laser, all three light-matter interactions described above are taking place. Initially, atoms are energized from the ground state to the excited state by a process called pumping, described below. Some of these atoms decay via spontaneous emission, releasing incoherent light as photons of frequency, ν. These photons are fed back into the laser medium, usually by an optical resonator. Some of these photons are absorbed by the atoms in the ground state, and the photons are lost to the laser process. However, some photons cause stimulated emission in excited-state atoms, releasing another coherent photon. In effect, this results in optical amplification.

If the number of photons being amplified per unit time is greater than the number of photons being absorbed, then the net result is a continuously increasing number of photons being produced; the laser medium is said to have a gain of greater than unity.

Recall from the descriptions of absorption and stimulated emission above that the rates of these two processes are proportional to the number of atoms in the ground and excited states, N₁ and N₂, respectively. If the ground state has a higher population than the excited state (N₁ > N₂), then the absorption process dominates, and there is a net attenuation of photons. If the populations of the two states are the same (N₁ = N₂), the rate of absorption of light exactly balances the rate of emission; the medium is then said to be optically transparent.

If the higher energy state has a greater population than the lower energy state (N₁ < N₂), then the emission process dominates, and light in the system undergoes a net increase in intensity. It is thus clear that to produce a faster rate of stimulated emissions than absorptions, it is required that the ratio of the populations of the two states is such that N₂/N₁ > 1; In other words, a population inversion is required for laser operation.

Selection rules

Many transitions involving electromagnetic radiation are strictly forbidden under quantum mechanics. The allowed transitions are described by so-called selection rules, which describe the conditions under which a radiative transition is allowed. For instance, transitions are only allowed if ΔS = 0, S being the total spin angular momentum of the system. In real materials other effects, such as interactions with the crystal lattice, intervene to circumvent the formal rules by providing alternate mechanisms. In these systems the forbidden transitions can occur, but usually at slower rates than allowed transitions. A classic example is phosphorescence where a material has a ground state with S = 0, an excited state with S = 0, and an intermediate state with S = 1. The transition from the intermediate state to the ground state by emission of light is slow because of the selection rules. Thus emission may continue after the external illumination is removed. In contrast fluorescence in materials is characterized by emission which ceases when the external illumination is removed.
Transitions which do not involve the absorption or emission of radiation are not affected by selection rules. Radiationless transition between levels, such as between the excited S = 0 and S = 1 states, may proceed quickly enough to siphon off a portion of the S = 0 population before it spontaneously returns to the ground state.

The existence of intermediate states in materials is essential to the technique of optical pumping of lasers (see below).

Creating a population inversion

As described above, a population inversion is required for laser operation, but cannot be achieved in our theoretical group of atoms with two energy-levels when they are in thermal equilibrium. In fact, any method by which the atoms are directly and continuously excited from the ground state to the excited state (such as optical absorption) will eventually reach equilibrium with the de-exciting processes of spontaneous and stimulated emission. At best, an equal population of the two states, N₁ = N₂ = N/2, can be achieved, resulting in optical transparency but no net optical gain.

Three-level lasers

A three-level laser energy diagram.

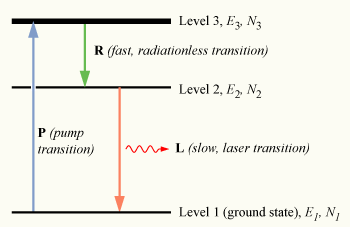
To achieve non-equilibrium conditions, an indirect method of populating the excited state must be used. To understand how this is done, we may use a slightly more realistic model, that of a three-level laser. Again consider a group of N atoms, this time with each atom able to exist in any of three energy states, levels 1, 2 and 3, with energies E₁, E₂, and E₃, and populations N₁, N₂, and N₃, respectively.

We assume that E₁ < E₂ < E₃; that is, the energy of level 2 lies between that of the ground state and level 3.

Initially, the system of atoms is at thermal equilibrium, and the majority of the atoms will be in the ground state, i.e., N₁ ≈ N, N₂ ≈ N₃ ≈ 0. If we now subject the atoms to light of a frequency ${\displaystyle \scriptstyle \nu _{13}\,=\,{\frac {1}{h}}\left(E_{3}-E_{1}\right)}$, the process of optical absorption will excite electrons from the ground state to level 3. This process is called pumping, and does not necessarily always directly involve light absorption; other methods of exciting the laser medium, such as electrical discharge or chemical reactions, may be used. The level 3 is sometimes referred to as the pump level or pump band, and the energy transition E₁ → E₃ as the pump transition, which is shown as the arrow marked P in the diagram on the right.

If we continuously pump electrons, we will excite an appreciable number of them into level 3, such that N₃ > 0. To have a medium suitable for laser operation, it is necessary that these excited atoms quickly decay to level 2. The energy released in this transition may be emitted as a photon (spontaneous emission), however in practice the 3→2 transition (labeled R in the diagram) is usually radiationless, with the energy being transferred to vibrational motion (heat) of the host material surrounding the atoms, without the generation of a photon.

An electron in level 2 may decay by spontaneous emission to the ground state, releasing a photon of frequency ν₁₂ (given by E₂ – E₁ = hν₁₂), which is shown as the transition L, called the laser transition in the diagram. If the lifetime of this transition, τ₂₁ is much longer than the lifetime of the radiationless 3 → 2 transition τ₃₂ (if τ₂₁ ≫ τ₃₂, known as a favourable lifetime ratio), the population of the E₃ will be essentially zero (N₃ ≈ 0) and a population of excited state atoms will accumulate in level 2 (N₂ > 0). If over half the N atoms can be accumulated in this state, this will exceed the population of the ground state N₁. A population inversion (N₂ > N₁ ) has thus been achieved between level 1 and 2, and optical amplification at the frequency ν₂₁ can be obtained.

Because at least half the population of atoms must be excited from the ground state to obtain a population inversion, the laser medium must be very strongly pumped. This makes three-level lasers rather inefficient, despite being the first type of laser to be discovered (based on a ruby laser medium, by Theodore Maiman in 1960). A three-level system could also have a radiative transition between level 3 and 2, and a non-radiative transition between 2 and 1. In this case, the pumping requirements are weaker. In practice, most lasers are four-level lasers, described below.

Four-level lasers

A four-level laser energy diagram.

Here, there are four energy levels, energies E₁, E₂, E₃, E₄, and populations N₁, N₂, N₃, N₄, respectively. The energies of each level are such that E₁ < E₂ < E₃ < E₄.

In this system, the pumping transition P excites the atoms in the ground state (level 1) into the pump band (level 4). From level 4, the atoms again decay by a fast, non-radiative transition Ra into the level 3. Since the lifetime of the laser transition L is long compared to that of Ra (τ₃₂ ≫ τ₄₃), a population accumulates in level 3 (the upper laser level), which may relax by spontaneous or stimulated emission into level 2 (the lower laser level). This level likewise has a fast, non-radiative decay Rb into the ground state.

As before, the presence of a fast, radiationless decay transition results in the population of the pump band being quickly depleted (N₄ ≈ 0). In a four-level system, any atom in the lower laser level E₂ is also quickly de-excited, leading to a negligible population in that state (N₂ ≈ 0). This is important, since any appreciable population accumulating in level 3, the upper laser level, will form a population inversion with respect to level 2. That is, as long as N₃ > 0, then N₃ > N₂, and a population inversion is achieved. Thus optical amplification, and laser operation, can take place at a frequency of ν₃₂ (E₃-E₂ = hν₃₂).

Since only a few atoms must be excited into the upper laser level to form a population inversion, a four-level laser is much more efficient than a three-level one, and most practical lasers are of this type. In reality, many more than four energy levels may be involved in the laser process, with complex excitation and relaxation processes involved between these levels. In particular, the pump band may consist of several distinct energy levels, or a continuum of levels, which allow optical pumping of the medium over a wide range of wavelengths.

Note that in both three- and four-level lasers, the energy of the pumping transition is greater than that of the laser transition. This means that, if the laser is optically pumped, the frequency of the pumping light must be greater than that of the resulting laser light. In other words, the pump wavelength is shorter than the laser wavelength. It is possible in some media to use multiple photon absorptions between multiple lower-energy transitions to reach the pump level; such lasers are called up-conversion lasers.

While in many lasers the laser process involves the transition of atoms between different electronic energy states, as described in the model above, this is not the only mechanism that can result in laser action. For example, there are many common lasers (e.g., dye lasers, carbon dioxide lasers) where the laser medium consists of complete molecules, and energy states correspond to vibrational and rotational modes of oscillation of the molecules. This is the case with water masers, that occur in nature.

In some media it is possible, by imposing an additional optical or microwave field, to use quantum coherence effects to reduce the likelihood of an excited-state to ground-state transition. This technique, known as lasing without inversion, allows optical amplification to take place without producing a population inversion between the two states.

Other methods of creating a population inversion

Stimulated emission was first observed in the microwave region of the electromagnetic spectrum, giving rise to the acronym MASER for Microwave Amplification by Stimulated Emission of Radiation. In the microwave region, the Boltzmann distribution of molecules among energy states is such that, at room temperature all states are populated almost equally.

To create a population inversion under these conditions, it is necessary to selectively remove some atoms or molecules from the system based on differences in properties. For instance, in a hydrogen maser, the well-known 21cm wave transition in atomic hydrogen, where the lone electron flips its spin state from parallel to the nuclear spin to antiparallel, can be used to create a population inversion because the parallel state has a magnetic moment and the antiparallel state does not. A strong inhomogeneous magnetic field will separate out atoms in the higher energy state from a beam of mixed state atoms. The separated population represents a population inversion which can exhibit stimulated emissions.

Stimulated emission

From Wikipedia, the free encyclopedia

 

Laser light is a type of stimulated emission of radiation.

Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron (or other excited molecular state), causing it to drop to a lower energy level. The liberated energy transfers to the electromagnetic field, creating a new photon with a phase, frequency, polarization, and direction of travel that are all identical to the photons of the incident wave. This is in contrast to spontaneous emission, which occurs at random intervals without regard to the ambient electromagnetic field.

The process is identical in form to atomic absorption in which the energy of an absorbed photon causes an identical but opposite atomic transition: from the lower level to a higher energy level. In normal media at thermal equilibrium, absorption exceeds stimulated emission because there are more electrons in the lower energy states than in the higher energy states. However, when a population inversion is present, the rate of stimulated emission exceeds that of absorption, and a net optical amplification can be achieved. Such a gain medium, along with an optical resonator, is at the heart of a laser or maser. Lacking a feedback mechanism, laser amplifiers and superluminescent sources also function on the basis of stimulated emission.

Overview

Electrons and their interactions with electromagnetic fields are important in our understanding of chemistry and physics. In the classical view, the energy of an electron orbiting an atomic nucleus is larger for orbits further from the nucleus of an atom. However, quantum mechanical effects force electrons to take on discrete positions in orbitals. Thus, electrons are found in specific energy levels of an atom, two of which are shown below:

When an electron absorbs energy either from light (photons) or heat (phonons), it receives that incident quantum of energy. But transitions are only allowed between discrete energy levels such as the two shown above. This leads to emission lines and absorption lines.

When an electron is excited from a lower to a higher energy level, it unlikely for it to stay that way forever. An electron in an excited state may decay to a lower energy state which is not occupied, according to a particular time constant characterizing that transition. When such an electron decays without external influence, emitting a photon, that is called "spontaneous emission". The phase and direction associated with the photon that is emitted is random. A material with many atoms in such an excited state may thus result in radiation which has a narrow spectrum (centered around one wavelength of light), but the individual photons would have no common phase relationship and would also emanate in random directions. This is the mechanism of fluorescence and thermal emission.

An external electromagnetic field at a frequency associated with a transition can affect the quantum mechanical state of the atom without being absorbed. As the electron in the atom makes a transition between two stationary states (neither of which shows a dipole field), it enters a transition state which does have a dipole field, and which acts like a small electric dipole, and this dipole oscillates at a characteristic frequency. In response to the external electric field at this frequency, the probability of the electron's entering this transition state is greatly increased. Thus, the rate of transitions between two stationary states is increased beyond that of spontaneous emission. A transition from the higher to a lower energy state produces an additional photon with the same phase and direction as the incident photon; this is the process of stimulated emission.

History

Stimulated emission was a theoretical discovery by Einstein^[1][2] within the framework of the old quantum theory, wherein the emission is described in terms of photons that are the quanta of the EM field. Stimulated emission can also occur in classical models, without reference to photons or quantum-mechanics.^[3]

Mathematical model

Stimulated emission can be modelled mathematically by considering an atom that may be in one of two electronic energy states, a lower level state (possibly the ground state) (1) and an excited state (2), with energies E₁ and E₂ respectively.

If the atom is in the excited state, it may decay into the lower state by the process of spontaneous emission, releasing the difference in energies between the two states as a photon. The photon will have frequency ν₀ and energy hν₀, given by:

${\displaystyle E_{2}-E_{1}=h\,\nu _{0}}$

where h is Planck's constant.

Alternatively, if the excited-state atom is perturbed by an electric field of frequency ν₀, it may emit an additional photon of the same frequency and in phase, thus augmenting the external field, leaving the atom in the lower energy state. This process is known as stimulated emission.

In a group of such atoms, if the number of atoms in the excited state is given by N₂, the rate at which stimulated emission occurs is given by

${\displaystyle {\frac {\partial N_{2}}{\partial t}}=-{\frac {\partial N_{1}}{\partial t}}=-B_{21}\,\rho (\nu )\,N_{2}}$

where the proportionality constant B₂₁ is known as the Einstein B coefficient for that particular transition, and ρ(ν) is the radiation density of the incident field at frequency ν. The rate of emission is thus proportional to the number of atoms in the excited state N₂, and to the density of incident photons.

At the same time, there will be a process of atomic absorption which removes energy from the field while raising electrons from the lower state to the upper state. Its rate is given by an essentially identical equation,

${\displaystyle {\frac {\partial N_{2}}{\partial t}}=-{\frac {\partial N_{1}}{\partial t}}=B_{12}\,\rho (\nu )\,N_{1}}$.

The rate of absorption is thus proportional to the number of atoms in the lower state, N₁. Einstein showed that the coefficient for this transition must be identical to that for stimulated emission:

${\displaystyle B_{12}=B_{21}}$.

Thus absorption and stimulated emission are reverse processes proceeding at somewhat different rates. Another way of viewing this is to look at the net stimulated emission or absorption viewing it as a single process. The net rate of transitions from E₂ to E₁ due to this combined process can be found by adding their respective rates, given above:

${\displaystyle {\frac {\partial N_{1}^{\text{net}}}{\partial t}}=-{\frac {\partial N_{2}^{\text{net}}}{\partial t}}=B_{21}\,\rho (\nu )\,(N_{2}-N_{1})=B_{21}\,\rho (\nu )\,\Delta N}$.

Thus a net power is released into the electric field equal to the photon energy hν times this net transition rate. In order for this to be a positive number, indicating net stimulated emission, there must be more atoms in the excited state than in the lower level: ${\displaystyle \Delta N>0}$. Otherwise there is net absorption and the power of the wave is reduced during passage through the medium. The special condition ${\displaystyle N_{2}>N_{1}}$ is known as a population inversion, a rather unusual condition that must be effected in the gain medium of a laser.

The notable characteristic of stimulated emission compared to everyday light sources (which depend on spontaneous emission) is that the emitted photons have the same frequency, phase, polarization, and direction of propagation as the incident photons. The photons involved are thus mutually coherent. When a population inversion (${\displaystyle \Delta N>0}$) is present, therefore, optical amplification of incident radiation will take place.

Although energy generated by stimulated emission is always at the exact frequency of the field which has stimulated it, the above rate equation refers only to excitation at the particular optical frequency ${\displaystyle \nu _{0}}$ corresponding to the energy of the transition. At frequencies offset from ${\displaystyle \nu _{0}}$ the strength of stimulated (or spontaneous) emission will be decreased according to the so-called line shape. Considering only homogeneous broadening affecting an atomic or molecular resonance, the spectral line shape function is described as a Lorentzian distribution

${\displaystyle g'(\nu )={1 \over \pi }{(\Gamma /2) \over (\nu -\nu _{0})^{2}+(\Gamma /2)^{2}}}$

where ${\displaystyle \Gamma \,}$ is the full width at half maximum or FWHM bandwidth.

The peak value of the Lorentzian line shape occurs at the line center, ${\displaystyle \nu =\nu _{0}}$. A line shape function can be normalized so that its value at ${\displaystyle \nu _{0}}$ is unity; in the case of a Lorentzian we obtain

${\displaystyle g(\nu )={g'(\nu ) \over g'(\nu _{0})}={(\Gamma /2)^{2} \over (\nu -\nu _{0})^{2}+(\Gamma /2)^{2}}}$.

Thus stimulated emission at frequencies away from ${\displaystyle \nu _{0}}$ is reduced by this factor. In practice there may also be broadening of the line shape due to inhomogeneous broadening, most notably due to the Doppler effect resulting from the distribution of velocities in a gas at a certain temperature. This has a Gaussian shape and reduces the peak strength of the line shape function. In a practical problem the full line shape function can be computed through a convolution of the individual line shape functions involved. Therefore, optical amplification will add power to an incident optical field at frequency ${\displaystyle \nu }$ at a rate given by

${\displaystyle P=h\nu \,g(\nu )\,B_{21}\,\rho (\nu )\,\Delta N}$.

Stimulated emission cross section

The stimulated emission cross section is

${\displaystyle \sigma _{21}(\nu )=A_{21}{\frac {\lambda ^{2}}{8\pi n^{2}}}g(\nu )}$

where

A₂₁ is the Einstein A coefficient,

λ is the wavelength in vacuum,

n is the refractive index of the medium (dimensionless), and

g(ν) is the spectral line shape function.

Optical amplification

Stimulated emission can provide a physical mechanism for optical amplification. If an external source of energy stimulates more than 50% of the atoms in the ground state to transition into the excited state, then what is called a population inversion is created. When light of the appropriate frequency passes through the inverted medium, the photons are either absorbed by the atoms that remain in the ground state or the photons stimulate the excited atoms to emit additional photons of the same frequency, phase, and direction. Since more atoms are in the excited state than in the ground state then an amplification of the input intensity results.

The population inversion, in units of atoms per cubic meter, is

${\displaystyle \Delta N_{21}=N_{2}-{g_{2} \over g_{1}}N_{1}}$

where g₁ and g₂ are the degeneracies of energy levels 1 and 2, respectively.

Small signal gain equation

The intensity (in watts per square meter) of the stimulated emission is governed by the following differential equation:

${\displaystyle {dI \over dz}=\sigma _{21}(\nu )\cdot \Delta N_{21}\cdot I(z)}$

as long as the intensity I(z) is small enough so that it does not have a significant effect on the magnitude of the population inversion. Grouping the first two factors together, this equation simplifies as

${\displaystyle {dI \over dz}=\gamma _{0}(\nu )\cdot I(z)}$

where

${\displaystyle \gamma _{0}(\nu )=\sigma _{21}(\nu )\cdot \Delta N_{21}}$

is the small-signal gain coefficient (in units of radians per meter). We can solve the differential equation using separation of variables:

${\displaystyle {dI \over I(z)}=\gamma _{0}(\nu )\cdot dz}$

Integrating, we find:

${\displaystyle \ln \left({I(z) \over I_{in}}\right)=\gamma _{0}(\nu )\cdot z}$

or

${\displaystyle I(z)=I_{in}e^{\gamma _{0}(\nu )z}}$

where

${\displaystyle I_{in}=I(z=0)\,}$ is the optical intensity of the input signal (in watts per square meter).

Saturation intensity

The saturation intensity I_S is defined as the input intensity at which the gain of the optical amplifier drops to exactly half of the small-signal gain. We can compute the saturation intensity as

${\displaystyle I_{S}={h\nu \over \sigma (\nu )\cdot \tau _{S}}}$

where

h is Planck's constant, and

τ_S is the saturation time constant, which depends^{[citation needed]} on the spontaneous emission lifetimes of the various transitions between the energy levels related to the amplification.

${\displaystyle \nu }$ is the frequency in Hz

General gain equation

The general form of the gain equation, which applies regardless of the input intensity, derives from the general differential equation for the intensity I as a function of position z in the gain medium:

${\displaystyle {dI \over dz}={\gamma _{0}(\nu ) \over 1+{\bar {g}}(\nu ){I(z) \over I_{S}}}\cdot I(z)}$

where ${\displaystyle I_{S}}$ is saturation intensity. To solve, we first rearrange the equation in order to separate the variables, intensity I and position z:

${\displaystyle {dI \over I(z)}\left[1+{\bar {g}}(\nu ){I(z) \over I_{S}}\right]=\gamma _{0}(\nu )\cdot dz}$

Integrating both sides, we obtain

${\displaystyle \ln \left({I(z) \over I_{in}}\right)+{\bar {g}}(\nu ){I(z)-I_{in} \over I_{S}}=\gamma _{0}(\nu )\cdot z}$

or

${\displaystyle \ln \left({I(z) \over I_{in}}\right)+{\bar {g}}(\nu ){I_{in} \over I_{S}}\left({I(z) \over I_{in}}-1\right)=\gamma _{0}(\nu )\cdot z}$

The gain G of the amplifier is defined as the optical intensity I at position z divided by the input intensity:

${\displaystyle G=G(z)={I(z) \over I_{in}}}$

Substituting this definition into the prior equation, we find the general gain equation:

${\displaystyle \ln \left(G\right)+{\bar {g}}(\nu ){I_{in} \over I_{S}}\left(G-1\right)=\gamma _{0}(\nu )\cdot z}$

Small signal approximation

In the special case where the input signal is small compared to the saturation intensity, in other words,

${\displaystyle I_{in}\ll I_{S}\,}$

then the general gain equation gives the small signal gain as

${\displaystyle \ln(G)=\ln(G_{0})=\gamma _{0}(\nu )\cdot z}$

or

${\displaystyle G=G_{0}=e^{\gamma _{0}(\nu )z}}$

which is identical to the small signal gain equation (see above).

Large signal asymptotic behavior

For large input signals, where

${\displaystyle I_{in}\gg I_{S}\,}$

the gain approaches unity

${\displaystyle G\rightarrow 1}$

and the general gain equation approaches a linear asymptote:

${\displaystyle I(z)=I_{in}+{\gamma _{0}(\nu )\cdot z \over {\bar {g}}(\nu )}I_{S}}$