Regression analysis

From Wikipedia, the free encyclopedia

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships among variables. It includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables (or 'predictors'). More specifically, regression analysis helps one understand how the typical value of the dependent variable (or 'criterion variable') changes when any one of the independent variables is varied, while the other independent variables are held fixed.

Most commonly, regression analysis estimates the conditional expectation of the dependent variable given the independent variables – that is, the average value of the dependent variable when the independent variables are fixed. Less commonly, the focus is on a quantile, or other location parameter of the conditional distribution of the dependent variable given the independent variables. In all cases, a function of the independent variables called the regression function is to be estimated. In regression analysis, it is also of interest to characterize the variation of the dependent variable around the prediction of the regression function using a probability distribution. A related but distinct approach is Necessary Condition Analysis^[1] (NCA), which estimates the maximum (rather than average) value of the dependent variable for a given value of the independent variable (ceiling line rather than central line) in order to identify what value of the independent variable is necessary but not sufficient for a given value of the dependent variable.

Regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of machine learning. Regression analysis is also used to understand which among the independent variables are related to the dependent variable, and to explore the forms of these relationships. In restricted circumstances, regression analysis can be used to infer causal relationships between the independent and dependent variables. However this can lead to illusions or false relationships, so caution is advisable;^[2] for example, correlation does not prove causation.

Many techniques for carrying out regression analysis have been developed. Familiar methods such as linear regression and ordinary least squares regression are parametric, in that the regression function is defined in terms of a finite number of unknown parameters that are estimated from the data.  Nonparametric regression refers to techniques that allow the regression function to lie in a specified set of functions, which may be infinite-dimensional.

The performance of regression analysis methods in practice depends on the form of the data generating process, and how it relates to the regression approach being used. Since the true form of the data-generating process is generally not known, regression analysis often depends to some extent on making assumptions about this process. These assumptions are sometimes testable if a sufficient quantity of data is available. Regression models for prediction are often useful even when the assumptions are moderately violated, although they may not perform optimally. However, in many applications, especially with small effects or questions of causality based on observational data, regression methods can give misleading results.^[3][4]

In a narrower sense, regression may refer specifically to the estimation of continuous response (dependent) variables, as opposed to the discrete response variables used in classification.^[5] The case of a continuous dependent variable may be more specifically referred to as metric regression to distinguish it from related problems.^[6]

History

The earliest form of regression was the method of least squares, which was published by Legendre in 1805,^[7] and by Gauss in 1809.^[8] Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the Sun (mostly comets, but also later the then newly discovered minor planets). Gauss published a further development of the theory of least squares in 1821,^[9] including a version of the Gauss–Markov theorem.

The term "regression" was coined by Francis Galton in the nineteenth century to describe a biological phenomenon. The phenomenon was that the heights of descendants of tall ancestors tend to regress down towards a normal average (a phenomenon also known as regression toward the mean).^[10][11] For Galton, regression had only this biological meaning,^[12][13] but his work was later extended by Udny Yule and Karl Pearson to a more general statistical context.^[14][15] In the work of Yule and Pearson, the joint distribution of the response and explanatory variables is assumed to be Gaussian. This assumption was weakened by R.A. Fisher in his works of 1922 and 1925.^[16][17][18] Fisher assumed that the conditional distribution of the response variable is Gaussian, but the joint distribution need not be. In this respect, Fisher's assumption is closer to Gauss's formulation of 1821.

In the 1950s and 1960s, economists used electromechanical desk "calculators" to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the result from one regression.^[19]

Regression methods continue to be an area of active research. In recent decades, new methods have been developed for robust regression, regression involving correlated responses such as time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other complex data objects, regression methods accommodating various types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with error, regression with more predictor variables than observations, and causal inference with regression.

Regression models

Regression models involve the following parameters and variables:

• The unknown parameters, denoted as ${\displaystyle \beta }$, which may represent a scalar or a vector.
• The independent variables, ${\displaystyle X}$.
• The dependent variable, ${\displaystyle Y}$.

In various fields of application, different terminologies are used in place of dependent and independent variables.

A regression model relates ${\displaystyle Y}$ to a function of ${\displaystyle X}$ and ${\displaystyle \beta }$.

${\displaystyle Y\approx f(X,\beta ).}$

The approximation is usually formalized as ${\displaystyle \operatorname {E} (Y|X)=f(X,\beta )}$. To carry out regression analysis, the form of the function ${\displaystyle f}$ must be specified. Sometimes the form of this function is based on knowledge about the relationship between ${\displaystyle Y}$ and ${\displaystyle X}$ that does not rely on the data. If no such knowledge is available, a flexible or convenient form for ${\displaystyle f}$ is chosen.

Assume now that the vector of unknown parameters ${\displaystyle \beta }$ is of length ${\displaystyle k}$. In order to perform a regression analysis the user must provide information about the dependent variable ${\displaystyle Y}$:

• If ${\displaystyle N}$ data points of the form ${\displaystyle (Y,X)}$ are observed, where ${\displaystyle N$, most classical approaches to regression analysis cannot be performed: since the system of equations defining the regression model is underdetermined, there are not enough data to recover ${\displaystyle \beta }$.
• If exactly ${\displaystyle N=k}$ data points are observed, and the function ${\displaystyle f}$ is linear, the equations ${\displaystyle Y=f(X,\beta )}$ can be solved exactly rather than approximately. This reduces to solving a set of ${\displaystyle N}$ equations with ${\displaystyle N}$ unknowns (the elements of ${\displaystyle \beta )}$, which has a unique solution as long as the ${\displaystyle X}$ are linearly independent. If ${\displaystyle f}$ is nonlinear, a solution may not exist, or many solutions may exist.
• The most common situation is where ${\displaystyle N>k}$ data points are observed. In this case, there is enough information in the data to estimate a unique value for ${\displaystyle \beta }$ that best fits the data in some sense, and the regression model when applied to the data can be viewed as an overdetermined system in ${\displaystyle \beta }$.

In the last case, the regression analysis provides the tools for:

1. Finding a solution for unknown parameters ${\displaystyle \beta }$ that will, for example, minimize the distance between the measured and predicted values of the dependent variable ${\displaystyle Y}$ (also known as method of least squares).
2. Under certain statistical assumptions, the regression analysis uses the surplus of information to provide statistical information about the unknown parameters ${\displaystyle \beta }$ and predicted values of the dependent variable ${\displaystyle Y}$.

Necessary number of independent measurements

Consider a regression model which has three unknown parameters, ${\displaystyle \beta _{0}}$, ${\displaystyle \beta _{1}}$, and ${\displaystyle \beta _{2}}$. Suppose an experimenter performs 10 measurements all at exactly the same value of independent variable vector ${\displaystyle X}$ (which contains the independent variables ${\displaystyle X_{1}}$, ${\displaystyle X_{2}}$, and ${\displaystyle X_{3}}$). In this case, regression analysis fails to give a unique set of estimated values for the three unknown parameters; the experimenter did not provide enough information. The best one can do is to estimate the average value and the standard deviation of the dependent variable ${\displaystyle Y}$. Similarly, measuring at two different values of ${\displaystyle X}$ would give enough data for a regression with two unknowns, but not for three or more unknowns.

If the experimenter had performed measurements at three different values of the independent variable vector ${\displaystyle X}$, then regression analysis would provide a unique set of estimates for the three unknown parameters in ${\displaystyle \beta }$.

In the case of general linear regression, the above statement is equivalent to the requirement that the matrix ${\displaystyle X^{\top }X}$ is invertible.

When the number of measurements, ${\displaystyle N}$, is larger than the number of unknown parameters, ${\displaystyle k}$, and the measurement errors ${\displaystyle \epsilon _{i}}$ are normally distributed then the excess of information contained in ${\displaystyle (N-k)}$ measurements is used to make statistical predictions about the unknown parameters. This excess of information is referred to as the degrees of freedom of the regression.

Underlying assumptions

Classical assumptions for regression analysis include:

• The sample is representative of the population for the inference prediction.
• The error is a random variable with a mean of zero conditional on the explanatory variables.
• The independent variables are measured with no error. (Note: If this is not so, modeling may be done instead using errors-in-variables model techniques).
• The independent variables (predictors) are linearly independent, i.e. it is not possible to express any predictor as a linear combination of the others.
• The errors are uncorrelated, that is, the variance–covariance matrix of the errors is diagonal and each non-zero element is the variance of the error.
• The variance of the error is constant across observations (homoscedasticity). If not, weighted least squares or other methods might instead be used.

These are sufficient conditions for the least-squares estimator to possess desirable properties; in particular, these assumptions imply that the parameter estimates will be unbiased, consistent, and efficient in the class of linear unbiased estimators. It is important to note that actual data rarely satisfies the assumptions. That is, the method is used even though the assumptions are not true. Variation from the assumptions can sometimes be used as a measure of how far the model is from being useful. Many of these assumptions may be relaxed in more advanced treatments. Reports of statistical analyses usually include analyses of tests on the sample data and methodology for the fit and usefulness of the model.

Independent and dependent variables often refer to values measured at point locations. There may be spatial trends and spatial autocorrelation in the variables that violate statistical assumptions of regression. Geographic weighted regression is one technique to deal with such data.^[20] Also, variables may include values aggregated by areas. With aggregated data the modifiable areal unit problem can cause extreme variation in regression parameters.^[21] When analyzing data aggregated by political boundaries, postal codes or census areas results may be very distinct with a different choice of units.

Linear regression

In linear regression, the model specification is that the dependent variable, ${\displaystyle y_{i}}$ is a linear combination of the parameters (but need not be linear in the independent variables). For example, in simple linear regression for modeling ${\displaystyle n}$ data points there is one independent variable: ${\displaystyle x_{i}}$, and two parameters, ${\displaystyle \beta _{0}}$ and ${\displaystyle \beta _{1}}$:

straight line: ${\displaystyle y_{i}=\beta _{0}+\beta _{1}x_{i}+\varepsilon _{i},\quad i=1,\dots ,n.\!}$

In multiple linear regression, there are several independent variables or functions of independent variables.

Adding a term in ${\displaystyle x_{i}^{2}}$ to the preceding regression gives:

parabola: ${\displaystyle y_{i}=\beta _{0}+\beta _{1}x_{i}+\beta _{2}x_{i}^{2}+\varepsilon _{i},\ i=1,\dots ,n.\!}$

This is still linear regression; although the expression on the right hand side is quadratic in the independent variable ${\displaystyle x_{i}}$, it is linear in the parameters ${\displaystyle \beta _{0}}$, ${\displaystyle \beta _{1}}$ and ${\displaystyle \beta _{2}.}$

In both cases, ${\displaystyle \varepsilon _{i}}$ is an error term and the subscript ${\displaystyle i}$ indexes a particular observation.

Returning our attention to the straight line case: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:

${\displaystyle {\widehat {y}}_{i}={\widehat {\beta }}_{0}+{\widehat {\beta }}_{1}x_{i}.}$

The residual, ${\displaystyle e_{i}=y_{i}-{\widehat {y}}_{i}}$, is the difference between the value of the dependent variable predicted by the model, ${\displaystyle {\widehat {y}}_{i}}$, and the true value of the dependent variable, ${\displaystyle y_{i}}$. One method of estimation is ordinary least squares. This method obtains parameter estimates that minimize the sum of squared residuals, SSR:

${\displaystyle SSR=\sum _{i=1}^{n}e_{i}^{2}.\,}$

Minimization of this function results in a set of normal equations, a set of simultaneous linear equations in the parameters, which are solved to yield the parameter estimators, ${\displaystyle {\widehat {\beta }}_{0},{\widehat {\beta }}_{1}}$.

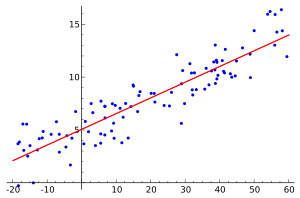
Illustration of linear regression on a data set.

In the case of simple regression, the formulas for the least squares estimates are

${\displaystyle {\widehat {\beta }}_{1}={\frac {\sum (x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sum (x_{i}-{\bar {x}})^{2}}}{\text{ and }}{\widehat {\beta }}_{0}={\bar {y}}-{\widehat {\beta }}_{1}{\bar {x}}}$

where ${\displaystyle {\bar {x}}}$ is the mean (average) of the ${\displaystyle x}$ values and ${\displaystyle {\bar {y}}}$ is the mean of the ${\displaystyle y}$ values.

Under the assumption that the population error term has a constant variance, the estimate of that variance is given by:

${\displaystyle {\hat {\sigma }}_{\varepsilon }^{2}={\frac {SSR}{n-2}}.\,}$

This is called the mean square error (MSE) of the regression. The denominator is the sample size reduced by the number of model parameters estimated from the same data, ${\displaystyle (n-p)}$ for ${\displaystyle p}$ regressors or ${\displaystyle (n-p-1)}$ if an intercept is used.^[22] In this case, ${\displaystyle p=1}$ so the denominator is ${\displaystyle n-2}$.

The standard errors of the parameter estimates are given by

${\displaystyle {\hat {\sigma }}_{\beta _{1}}={\hat {\sigma }}_{\varepsilon }{\sqrt {\frac {1}{\sum (x_{i}-{\bar {x}})^{2}}}}}$

${\displaystyle {\hat {\sigma }}_{\beta _{0}}={\hat {\sigma }}_{\varepsilon }{\sqrt {{\frac {1}{n}}+{\frac {{\bar {x}}^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}}}={\hat {\sigma }}_{\beta _{1}}{\sqrt {\frac {\sum x_{i}^{2}}{n}}}}$.

Under the further assumption that the population error term is normally distributed, the researcher can use these estimated standard errors to create confidence intervals and conduct hypothesis tests about the population parameters.

General linear model

In the more general multiple regression model, there are ${\displaystyle p}$ independent variables:

${\displaystyle y_{i}=\beta _{1}x_{i1}+\beta _{2}x_{i2}+\cdots +\beta _{p}x_{ip}+\varepsilon _{i},\,}$

where ${\displaystyle x_{ij}}$ is the ${\displaystyle i}$-th observation on the ${\displaystyle j}$-th independent variable. If the first independent variable takes the value 1 for all ${\displaystyle i}$, ${\displaystyle x_{i1}=1}$, then ${\displaystyle \beta _{1}}$ is called the regression intercept.

The least squares parameter estimates are obtained from ${\displaystyle p}$ normal equations. The residual can be written as

${\displaystyle \varepsilon _{i}=y_{i}-{\hat {\beta }}_{1}x_{i1}-\cdots -{\hat {\beta }}_{p}x_{ip}.}$

The normal equations are

${\displaystyle \sum _{i=1}^{n}\sum _{k=1}^{p}x_{ij}x_{ik}{\hat {\beta }}_{k}=\sum _{i=1}^{n}x_{ij}y_{i},\ j=1,\dots ,p.\,}$

In matrix notation, the normal equations are written as

${\displaystyle \mathbf {(X^{\top }X){\hat {\boldsymbol {\beta }}}={}X^{\top }Y} ,\,}$

where the ${\displaystyle ij}$ element of ${\displaystyle \mathbf {X} }$ is ${\displaystyle x_{ij}}$, the ${\displaystyle i}$ element of the column vector ${\displaystyle Y}$ is ${\displaystyle y_{i}}$, and the ${\displaystyle j}$ element of ${\displaystyle {\hat {\boldsymbol {\beta }}}}$ is ${\displaystyle {\hat {\beta }}_{j}}$. Thus ${\displaystyle \mathbf {X} }$ is ${\displaystyle n\times p}$, ${\displaystyle Y}$ is ${\displaystyle n\times 1}$, and ${\displaystyle {\hat {\boldsymbol {\beta }}}}$ is ${\displaystyle p\times 1}$. The solution is

${\displaystyle \mathbf {{\hat {\boldsymbol {\beta }}}={}(X^{\top }X)^{-1}X^{\top }Y} .\,}$

Diagnostics

Once a regression model has been constructed, it may be important to confirm the goodness of fit of the model and the statistical significance of the estimated parameters. Commonly used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-test of the overall fit, followed by t-tests of individual parameters.

Interpretations of these diagnostic tests rest heavily on the model assumptions. Although examination of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model's assumptions are violated. For example, if the error term does not have a normal distribution, in small samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can be invoked such that hypothesis testing may proceed using asymptotic approximations.

Limited dependent variables

Limited dependent variables, which are response variables that are categorical variables or are variables constrained to fall only in a certain range, often arise in econometrics.

The response variable may be non-continuous ("limited" to lie on some subset of the real line). For binary (zero or one) variables, if analysis proceeds with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than two values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest. An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an event, then count models like the Poisson regression or the negative binomial model may be used

Interpolation and extrapolation

In the middle, the interpolated straight line represents the best balance between the points above and below this line. The dotted lines represent the two extreme lines. The first curves represent the estimated values. The outer curves represent a prediction for a new measurement^[23].

Regression models predict a value of the Y variable given known values of the X variables. Prediction within the range of values in the dataset used for model-fitting is known informally as interpolation. Prediction outside this range of the data is known as extrapolation. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.

It is generally advised^{[citation needed]} that when performing extrapolation, one should accompany the estimated value of the dependent variable with a prediction interval that represents the uncertainty. Such intervals tend to expand rapidly as the values of the independent variable(s) moved outside the range covered by the observed data.

For such reasons and others, some tend to say that it might be unwise to undertake extrapolation.^[24]

However, this does not cover the full set of modeling errors that may be made: in particular, the assumption of a particular form for the relation between Y and X. A properly conducted regression analysis will include an assessment of how well the assumed form is matched by the observed data, but it can only do so within the range of values of the independent variables actually available. This means that any extrapolation is particularly reliant on the assumptions being made about the structural form of the regression relationship. Best-practice advice here^{[citation needed]} is that a linear-in-variables and linear-in-parameters relationship should not be chosen simply for computational convenience, but that all available knowledge should be deployed in constructing a regression model. If this knowledge includes the fact that the dependent variable cannot go outside a certain range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly near such bounds. The implications of this step of choosing an appropriate functional form for the regression can be great when extrapolation is considered. At a minimum, it can ensure that any extrapolation arising from a fitted model is "realistic" (or in accord with what is known).

Nonlinear regression

When the model function is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences between linear and non-linear least squares.

Power and sample size calculations

There are no generally agreed methods for relating the number of observations versus the number of independent variables in the model. One rule of thumb suggested by Good and Hardin is ${\displaystyle N=m^{n}}$, where ${\displaystyle N}$ is the sample size, ${\displaystyle n}$ is the number of independent variables and ${\displaystyle m}$ is the number of observations needed to reach the desired precision if the model had only one independent variable.^[25] For example, a researcher is building a linear regression model using a dataset that contains 1000 patients (${\displaystyle N}$). If the researcher decides that five observations are needed to precisely define a straight line (${\displaystyle m}$), then the maximum number of independent variables the model can support is 4, because

${\displaystyle {\frac {\log {1000}}{\log {5}}}=4.29}$.

Other methods

Although the parameters of a regression model are usually estimated using the method of least squares, other methods which have been used include:

• Bayesian methods, e.g. Bayesian linear regression
• Percentage regression, for situations where reducing percentage errors is deemed more appropriate.^[26]
• Least absolute deviations, which is more robust in the presence of outliers, leading to quantile regression
• Nonparametric regression, requires a large number of observations and is computationally intensive
• Distance metric learning, which is learned by the search of a meaningful distance metric in a given input space.^[27]

Software

All major statistical software packages perform least squares regression analysis and inference.  Simple linear regression and multiple regression using least squares can be done in some spreadsheet applications and on some calculators. While many statistical software packages can perform various types of nonparametric and robust regression, these methods are less standardized; different software packages implement different methods, and a method with a given name may be implemented differently in different packages. Specialized regression software has been developed for use in fields such as survey analysis and neuroimaging.

Statistical inference

From Wikipedia, the free encyclopedia

Statistical inference is the process of using data analysis to deduce properties of an underlying probability distribution.^[1] Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population.

Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population.

Introduction

Statistical inference makes propositions about a population, using data drawn from the population with some form of sampling. Given a hypothesis about a population, for which we wish to draw inferences, statistical inference consists of (first) selecting a statistical model of the process that generates the data and (second) deducing propositions from the model.^{[citation needed]}

Konishi & Kitagawa state, "The majority of the problems in statistical inference can be considered to be problems related to statistical modeling".^[2] Relatedly, Sir David Cox has said, "How [the] translation from subject-matter problem to statistical model is done is often the most critical part of an analysis".^[3]

The conclusion of a statistical inference is a statistical proposition.^{[citation needed]} Some common forms of statistical proposition are the following:

• a point estimate, i.e. a particular value that best approximates some parameter of interest;
• an interval estimate, e.g. a confidence interval (or set estimate), i.e. an interval constructed using a dataset drawn from a population so that, under repeated sampling of such datasets, such intervals would contain the true parameter value with the probability at the stated confidence level;
• a credible interval, i.e. a set of values containing, for example, 95% of posterior belief;
• rejection of a hypothesis;^[a]
• clustering or classification of data points into groups.

Models and assumptions

Any statistical inference requires some assumptions. A statistical model is a set of assumptions concerning the generation of the observed data and similar data. Descriptions of statistical models usually emphasize the role of population quantities of interest, about which we wish to draw inference.^[4] Descriptive statistics are typically used as a preliminary step before more formal inferences are drawn.^[5]

Degree of models/assumptions

Statisticians distinguish between three levels of modeling assumptions;

• Fully parametric: The probability distributions describing the data-generation process are assumed to be fully described by a family of probability distributions involving only a finite number of unknown parameters.^[4] For example, one may assume that the distribution of population values is truly Normal, with unknown mean and variance, and that datasets are generated by 'simple' random sampling. The family of generalized linear models is a widely used and flexible class of parametric models.
• Non-parametric: The assumptions made about the process generating the data are much less than in parametric statistics and may be minimal.^[6] For example, every continuous probability distribution has a median, which may be estimated using the sample median or the Hodges–Lehmann–Sen estimator, which has good properties when the data arise from simple random sampling.
• Semi-parametric: This term typically implies assumptions 'in between' fully and non-parametric approaches. For example, one may assume that a population distribution has a finite mean. Furthermore, one may assume that the mean response level in the population depends in a truly linear manner on some covariate (a parametric assumption) but not make any parametric assumption describing the variance around that mean (i.e. about the presence or possible form of any heteroscedasticity). More generally, semi-parametric models can often be separated into 'structural' and 'random variation' components. One component is treated parametrically and the other non-parametrically. The well-known Cox model is a set of semi-parametric assumptions.

Importance of valid models/assumptions

Whatever level of assumption is made, correctly calibrated inference in general requires these assumptions to be correct; i.e. that the data-generating mechanisms really have been correctly specified.

Incorrect assumptions of 'simple' random sampling can invalidate statistical inference.^[7] More complex semi- and fully parametric assumptions are also cause for concern. For example, incorrectly assuming the Cox model can in some cases lead to faulty conclusions.^[8] Incorrect assumptions of Normality in the population also invalidates some forms of regression-based inference.^[9] The use of any parametric model is viewed skeptically by most experts in sampling human populations: "most sampling statisticians, when they deal with confidence intervals at all, limit themselves to statements about [estimators] based on very large samples, where the central limit theorem ensures that these [estimators] will have distributions that are nearly normal."^[10] In particular, a normal distribution "would be a totally unrealistic and catastrophically unwise assumption to make if we were dealing with any kind of economic population."^[10] Here, the central limit theorem states that the distribution of the sample mean "for very large samples" is approximately normally distributed, if the distribution is not heavy tailed.

Approximate distributions

Given the difficulty in specifying exact distributions of sample statistics, many methods have been developed for approximating these.

With finite samples, approximation results measure how close a limiting distribution approaches the statistic's sample distribution: For example, with 10,000 independent samples the normal distribution approximates (to two digits of accuracy) the distribution of the sample mean for many population distributions, by the Berry–Esseen theorem.^[11] Yet for many practical purposes, the normal approximation provides a good approximation to the sample-mean's distribution when there are 10 (or more) independent samples, according to simulation studies and statisticians' experience.^[11] Following Kolmogorov's work in the 1950s, advanced statistics uses approximation theory and functional analysis to quantify the error of approximation. In this approach, the metric geometry of probability distributions is studied; this approach quantifies approximation error with, for example, the Kullback–Leibler divergence, Bregman divergence, and the Hellinger distance.^[12][13][14]

With indefinitely large samples, limiting results like the central limit theorem describe the sample statistic's limiting distribution, if one exists. Limiting results are not statements about finite samples, and indeed are irrelevant to finite samples.^[15][16][17] However, the asymptotic theory of limiting distributions is often invoked for work with finite samples. For example, limiting results are often invoked to justify the generalized method of moments and the use of generalized estimating equations, which are popular in econometrics and biostatistics. The magnitude of the difference between the limiting distribution and the true distribution (formally, the 'error' of the approximation) can be assessed using simulation.^[18] The heuristic application of limiting results to finite samples is common practice in many applications, especially with low-dimensional models with log-concave likelihoods (such as with one-parameter exponential families).

Randomization-based models

For a given dataset that was produced by a randomization design, the randomization distribution of a statistic (under the null-hypothesis) is defined by evaluating the test statistic for all of the plans that could have been generated by the randomization design. In frequentist inference, randomization allows inferences to be based on the randomization distribution rather than a subjective model, and this is important especially in survey sampling and design of experiments.^[19][20] Statistical inference from randomized studies is also more straightforward than many other situations.^[21][22][23] In Bayesian inference, randomization is also of importance: in survey sampling, use of sampling without replacement ensures the exchangeability of the sample with the population; in randomized experiments, randomization warrants a missing at random assumption for covariate information.^[24]

Objective randomization allows properly inductive procedures.^{[25][26][27][28]} Many statisticians prefer randomization-based analysis of data that was generated by well-defined randomization procedures.^[29] (However, it is true that in fields of science with developed theoretical knowledge and experimental control, randomized experiments may increase the costs of experimentation without improving the quality of inferences.^[30][31]) Similarly, results from randomized experiments are recommended by leading statistical authorities as allowing inferences with greater reliability than do observational studies of the same phenomena.^[32] However, a good observational study may be better than a bad randomized experiment.

The statistical analysis of a randomized experiment may be based on the randomization scheme stated in the experimental protocol and does not need a subjective model.^[33][34]

However, at any time, some hypotheses cannot be tested using objective statistical models, which accurately describe randomized experiments or random samples. In some cases, such randomized studies are uneconomical or unethical.

Model-based analysis of randomized experiments

It is standard practice to refer to a statistical model, often a linear model, when analyzing data from randomized experiments. However, the randomization scheme guides the choice of a statistical model. It is not possible to choose an appropriate model without knowing the randomization scheme.^[20] Seriously misleading results can be obtained analyzing data from randomized experiments while ignoring the experimental protocol; common mistakes include forgetting the blocking used in an experiment and confusing repeated measurements on the same experimental unit with independent replicates of the treatment applied to different experimental units.^[35]

Paradigms for inference

Different schools of statistical inference have become established. These schools—or "paradigms"—are not mutually exclusive, and methods that work well under one paradigm often have attractive interpretations under other paradigms.

Bandyopadhyay & Forster^[36] describe four paradigms: "(i) classical statistics or error statistics, (ii) Bayesian statistics, (iii) likelihood-based statistics, and (iv) the Akaikean-Information Criterion-based statistics". The classical (or frequentist) paradigm, the Bayesian paradigm, and the AIC-based paradigm are summarized below. The likelihood-based paradigm is essentially a sub-paradigm of the AIC-based paradigm.

Frequentist inference

This paradigm calibrates the plausibility of propositions by considering (notional) repeated sampling of a population distribution to produce datasets similar to the one at hand. By considering the dataset's characteristics under repeated sampling, the frequentist properties of a statistical proposition can be quantified—although in practice this quantification may be challenging.

Examples of frequentist inference

• p-value
• Confidence interval

Frequentist inference, objectivity, and decision theory

One interpretation of frequentist inference (or classical inference) is that it is applicable only in terms of frequency probability; that is, in terms of repeated sampling from a population. However, the approach of Neyman^[37] develops these procedures in terms of pre-experiment probabilities. That is, before undertaking an experiment, one decides on a rule for coming to a conclusion such that the probability of being correct is controlled in a suitable way: such a probability need not have a frequentist or repeated sampling interpretation. In contrast, Bayesian inference works in terms of conditional probabilities (i.e. probabilities conditional on the observed data), compared to the marginal (but conditioned on unknown parameters) probabilities used in the frequentist approach.

The frequentist procedures of significance testing and confidence intervals can be constructed without regard to utility functions. However, some elements of frequentist statistics, such as statistical decision theory, do incorporate utility functions.^{[citation needed]} In particular, frequentist developments of optimal inference (such as minimum-variance unbiased estimators, or uniformly most powerful testing) make use of loss functions, which play the role of (negative) utility functions. Loss functions need not be explicitly stated for statistical theorists to prove that a statistical procedure has an optimality property.^[38] However, loss-functions are often useful for stating optimality properties: for example, median-unbiased estimators are optimal under absolute value loss functions, in that they minimize expected loss, and least squares estimators are optimal under squared error loss functions, in that they minimize expected loss.

While statisticians using frequentist inference must choose for themselves the parameters of interest, and the estimators/test statistic to be used, the absence of obviously explicit utilities and prior distributions has helped frequentist procedures to become widely viewed as 'objective'.^{[citation needed]}

Bayesian inference

The Bayesian calculus describes degrees of belief using the 'language' of probability; beliefs are positive, integrate to one, and obey probability axioms. Bayesian inference uses the available posterior beliefs as the basis for making statistical propositions. There are several different justifications for using the Bayesian approach.

Examples of Bayesian inference

• Credible interval for interval estimation
• Bayes factors for model comparison

Bayesian inference, subjectivity and decision theory

Many informal Bayesian inferences are based on "intuitively reasonable" summaries of the posterior. For example, the posterior mean, median and mode, highest posterior density intervals, and Bayes Factors can all be motivated in this way. While a user's utility function need not be stated for this sort of inference, these summaries do all depend (to some extent) on stated prior beliefs, and are generally viewed as subjective conclusions. (Methods of prior construction which do not require external input have been proposed but not yet fully developed.)

Formally, Bayesian inference is calibrated with reference to an explicitly stated utility, or loss function; the 'Bayes rule' is the one which maximizes expected utility, averaged over the posterior uncertainty. Formal Bayesian inference therefore automatically provides optimal decisions in a decision theoretic sense. Given assumptions, data and utility, Bayesian inference can be made for essentially any problem, although not every statistical inference need have a Bayesian interpretation. Analyses which are not formally Bayesian can be (logically) incoherent; a feature of Bayesian procedures which use proper priors (i.e. those integrable to one) is that they are guaranteed to be coherent. Some advocates of Bayesian inference assert that inference must take place in this decision-theoretic framework, and that Bayesian inference should not conclude with the evaluation and summarization of posterior beliefs.

AIC-based inference

The Akaike information criterion (AIC) is an estimator of the relative quality of statistical models for a given set of data. Given a collection of models for the data, AIC estimates the quality of each model, relative to each of the other models. Thus, AIC provides a means for model selection.

AIC is founded on information theory: it offers an estimate of the relative information lost when a given model is used to represent the process that generated the data. (In doing so, it deals with the trade-off between the goodness of fit of the model and the simplicity of the model.)

Other paradigms for inference

Minimum description length

The minimum description length (MDL) principle has been developed from ideas in information theory^[39] and the theory of Kolmogorov complexity.^[40] The (MDL) principle selects statistical models that maximally compress the data; inference proceeds without assuming counterfactual or non-falsifiable "data-generating mechanisms" or probability models for the data, as might be done in frequentist or Bayesian approaches.

However, if a "data generating mechanism" does exist in reality, then according to Shannon's source coding theorem it provides the MDL description of the data, on average and asymptotically.^[41] In minimizing description length (or descriptive complexity), MDL estimation is similar to maximum likelihood estimation and maximum a posteriori estimation (using maximum-entropy Bayesian priors). However, MDL avoids assuming that the underlying probability model is known; the MDL principle can also be applied without assumptions that e.g. the data arose from independent sampling.^[41][42]

The MDL principle has been applied in communication-coding theory in information theory, in linear regression,^[42] and in data mining.^[40]

The evaluation of MDL-based inferential procedures often uses techniques or criteria from computational complexity theory.^[43]

Fiducial inference

Fiducial inference was an approach to statistical inference based on fiducial probability, also known as a "fiducial distribution". In subsequent work, this approach has been called ill-defined, extremely limited in applicability, and even fallacious.^[44][45] However this argument is the same as that which shows^[46] that a so-called confidence distribution is not a valid probability distribution and, since this has not invalidated the application of confidence intervals, it does not necessarily invalidate conclusions drawn from fiducial arguments. An attempt was made to reinterpret the early work of Fisher's fiducial argument as a special case of an inference theory using Upper and lower probabilities.^[47]

Structural inference

Developing ideas of Fisher and of Pitman from 1938 to 1939,^[48] George A. Barnard developed "structural inference" or "pivotal inference",^[49] an approach using invariant probabilities on group families. Barnard reformulated the arguments behind fiducial inference on a restricted class of models on which "fiducial" procedures would be well-defined and useful.

Statistical model

From Wikipedia, the free encyclopedia

A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of some sample data and similar data from a larger population. A statistical model represents, often in considerably idealized form, the data-generating process.

The assumptions embodied by a statistical model describe a set of probability distributions, some of which are assumed to adequately approximate the distribution from which a particular data set is sampled. The probability distributions inherent in statistical models are what distinguishes statistical models from other, non-statistical, mathematical models.

A statistical model is usually specified by mathematical equations that relate one or more random variables and possibly other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman Adèr quoting Kenneth Bollen).^[1]

All statistical hypothesis tests and all statistical estimators are derived from statistical models. More generally, statistical models are part of the foundation of statistical inference.

Formal definition

In mathematical terms, a statistical model is usually thought of as a pair (${\displaystyle S,{\mathcal {P}}}$), where ${\displaystyle S}$ is the set of possible observations, i.e. the sample space, and ${\displaystyle {\mathcal {P}}}$ is a set of probability distributions on ${\displaystyle S}$.^[2]

The intuition behind this definition is as follows. It is assumed that there is a "true" probability distribution induced by the process that generates the observed data. We choose ${\displaystyle {\mathcal {P}}}$ to represent a set (of distributions) which contains a distribution that adequately approximates the true distribution. Note that we do not require that ${\displaystyle {\mathcal {P}}}$ contains the true distribution, and in practice that is rarely the case. Indeed, as Burnham & Anderson state, "A model is a simplification or approximation of reality and hence will not reflect all of reality"^[3]—whence the saying "all models are wrong".

The set ${\displaystyle {\mathcal {P}}}$ is almost always parameterized: ${\displaystyle {\mathcal {P}}=\{P_{\theta }:\theta \in \Theta \}}$. The set ${\displaystyle \Theta }$ defines the parameters of the model. A parameterization is generally required to have distinct parameter values give rise to distinct distributions, i.e. ${\displaystyle P_{\theta _{1}}=P_{\theta _{2}}\Rightarrow \theta _{1}=\theta _{2}}$ must hold (in other words, it must be injective). A parameterization that meets the requirement is said to be identifiable.^[2]

An example

Suppose that we have a population of school children, with the ages of the children distributed uniformly, in the population. The height of a child will be stochastically related to the age: e.g. when we know that a child is of age 7, this influences the chance of the child being 5 feet tall. We could formalize that relationship in a linear regression model, like this: height_i = b₀ + b₁age_i + ε_i, where b₀ is the intercept, b₁ is a parameter that age is multiplied by in obtaining a prediction of height, ε_i is the error term, and i identifies the child. This implies that height is predicted by age, with some error.

An admissible model must be consistent with all the data points. Thus, a straight line (height_i = b₀ + b₁age_i) cannot be the equation for a model of the data. The line cannot be the equation for a model, unless it exactly fits all the data points—i.e. all the data points lie perfectly on the line. The error term, ε_i, must be included in the equation, so that the model is consistent with all the data points.

To do statistical inference, we would first need to assume some probability distributions for the ε_i. For instance, we might assume that the ε_i distributions are i.i.d. Gaussian, with zero mean. In this instance, the model would have 3 parameters: b₀, b₁, and the variance of the Gaussian distribution.

We can formally specify the model in the form (${\displaystyle S,{\mathcal {P}}}$) as follows. The sample space, ${\displaystyle S}$, of our model comprises the set of all possible pairs (age, height). Each possible value of ${\displaystyle \theta }$ = (b₀, b₁, σ²) determines a distribution on ${\displaystyle S}$; denote that distribution by ${\displaystyle P_{\theta }}$. If ${\displaystyle \Theta }$ is the set of all possible values of ${\displaystyle \theta }$, then ${\displaystyle {\mathcal {P}}=\{P_{\theta }:\theta \in \Theta \}}$. (The parameterization is identifiable, and this is easy to check.)

In this example, the model is determined by (1) specifying ${\displaystyle S}$ and (2) making some assumptions relevant to ${\displaystyle {\mathcal {P}}}$. There are two assumptions: that height can be approximated by a linear function of age; that errors in the approximation are distributed as i.i.d. Gaussian. The assumptions are sufficient to specify ${\displaystyle {\mathcal {P}}}$—as they are required to do.

General remarks

A statistical model is a special class of mathematical model. What distinguishes a statistical model from other mathematical models is that a statistical model is non-deterministic. Thus, in a statistical model specified via mathematical equations, some of the variables do not have specific values, but instead have probability distributions; i.e. some of the variables are stochastic. In the example above, ε is a stochastic variable; without that variable, the model would be deterministic.

Statistical models are often used even when the physical process being modeled is deterministic. For instance, coin tossing is, in principle, a deterministic process; yet it is commonly modeled as stochastic (via a Bernoulli process).

There are three purposes for a statistical model, according to Konishi & Kitagawa.^[4]

• Predictions
• Extraction of information
• Description of stochastic structures

Dimension of a model

Suppose that we have a statistical model (${\displaystyle S,{\mathcal {P}}}$) with ${\displaystyle {\mathcal {P}}=\{P_{\theta }:\theta \in \Theta \}}$. The model is said to be parametric if ${\displaystyle \Theta }$ has a finite dimension. In notation, we write that ${\displaystyle \Theta \subseteq \mathbb {R} ^{k}}$ where k is a positive integer (${\displaystyle \mathbb {R} }$ denotes the real numbers; other sets can be used, in principle). Here, k is called the dimension of the model.

As an example, if we assume that data arise from a univariate Gaussian distribution, then we are assuming that

${\displaystyle {\mathcal {P}}=\left\{P_{\mu ,\sigma }(x)\equiv {\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right):\mu \in \mathbb {R} ,\sigma >0\right\}}$.

In this example, the dimension, k, equals 2.

As another example, suppose that the data consists of points (x, y) that we assume are distributed according to a straight line with i.i.d. Gaussian residuals (with zero mean). Then the dimension of the statistical model is 3: the intercept of the line, the slope of the line, and the variance of the distribution of the residuals. (Note that in geometry, a straight line has dimension 1.)

Although formally ${\displaystyle \theta \in \Theta }$ is a single parameter that has dimension k, it is sometimes regarded as comprising k separate parameters. For example, with the univariate Gaussian distribution, ${\displaystyle \theta }$ is a single parameter with dimension 2, but it is sometimes regarded as comprising 2 separate parameters—the mean and the standard deviation.

A statistical model is nonparametric if the parameter set ${\displaystyle \Theta }$ is infinite dimensional. A statistical model is semiparametric if it has both finite-dimensional and infinite-dimensional parameters. Formally, if k is the dimension of ${\displaystyle \Theta }$ and n is the number of samples, both semiparametric and nonparametric models have ${\displaystyle k\rightarrow \infty }$ as ${\displaystyle n\rightarrow \infty }$. If ${\displaystyle k/n\rightarrow 0}$ as ${\displaystyle n\rightarrow \infty }$, then the model is semiparametric; otherwise, the model is nonparametric.

Parametric models are by far the most commonly used statistical models. Regarding semiparametric and nonparametric models, Sir David Cox has said, "These typically involve fewer assumptions of structure and distributional form but usually contain strong assumptions about independencies".^[5]

Nested models

Two statistical models are nested if the first model can be transformed into the second model by imposing constraints on the parameters of the first model. As an example, the set of all Gaussian distributions has, nested within it, the set of zero-mean Gaussian distributions: we constrain the mean in the set of all Gaussian distributions to get the zero-mean distributions. As a second example, the quadratic model

y = b₀ + b₁x + b₂x² + ε,    ε ~ 𝒩(0, σ²)

has, nested within it, the linear model

y = b₀ + b₁x + ε,    ε ~ 𝒩(0, σ²)

—we constrain the parameter b₂ to equal 0.

In both those examples, the first model has a higher dimension than the second model (for the first example, the zero-mean model has dimension 1). Such is often, but not always, the case. As a different example, the set of positive-mean Gaussian distributions, which has dimension 2, is nested within the set of all Gaussian distributions.

Comparing models

It is assumed that there is a "true" probability distribution underlying the observed data, induced by the process that generated the data. The main goal of model selection is to make statements about which elements of ${\displaystyle {\mathcal {P}}}$ are most likely to adequately approximate the true distribution.

Models can be compared to each other by exploratory data analysis or confirmatory data analysis. In exploratory analysis, a variety of models are formulated and an assessment is performed of how well each one describes the data. In confirmatory analysis, a previously formulated model or models are compared to the data. Common criteria for comparing models include R², Bayes factor, and the likelihood-ratio test together with its generalization relative likelihood.

Konishi & Kitagawa state: "The majority of the problems in statistical inference can be considered to be problems related to statistical modeling. They are typically formulated as comparisons of several statistical models."^[6] Relatedly, Sir David Cox has said, "How [the] translation from subject-matter problem to statistical model is done is often the most critical part of an analysis".^[7]