Bayesian inference

From Wikipedia, the free encyclopedia

Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".

Introduction to Bayes' rule

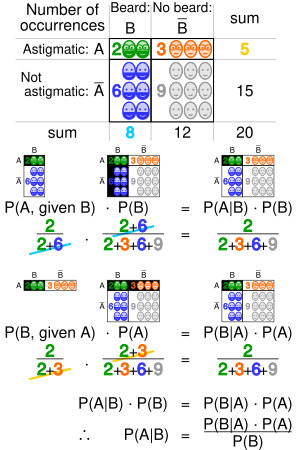
A geometric visualisation of Bayes' theorem. In the table, the values 2, 3, 6 and 9 give the relative weights of each corresponding condition and case. The figures denote the cells of the table involved in each metric, the probability being the fraction of each figure that is shaded. This shows that P(A|B) P(B) = P(B|A) P(A) i.e. P(A|B) = P(B|A) P(A)/P(B) . Similar reasoning can be used to show that P(Ā|B) = P(B|Ā) P(Ā)/P(B) etc.

Formal explanation

Bayesian inference derives the posterior probability as a consequence of two antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes the posterior probability according to Bayes' theorem:

${\displaystyle P(H\mid E)={\frac {P(E\mid H)\cdot P(H)}{P(E)}}}$

where

• ${\displaystyle \textstyle \mid }$ means "event conditional on" (so that ${\textstyle \textstyle (A\mid B)}$ means A given B).
• ${\displaystyle \textstyle H}$ stands for any hypothesis whose probability may be affected by data (called evidence below). Often there are competing hypotheses, and the task is to determine which is the most probable.
• ${\displaystyle \textstyle P(H)}$, the prior probability, is the estimate of the probability of the hypothesis ${\displaystyle \textstyle H}$ before the data ${\displaystyle \textstyle E}$, the current evidence, is observed.
• the evidence ${\displaystyle \textstyle E}$ corresponds to new data that were not used in computing the prior probability.
• ${\displaystyle \textstyle P(H\mid E)}$, the posterior probability, is the probability of ${\displaystyle \textstyle H}$ given ${\displaystyle \textstyle E}$, i.e., after ${\displaystyle \textstyle E}$ is observed. This is what we want to know: the probability of a hypothesis given the observed evidence.
• ${\displaystyle \textstyle P(E\mid H)}$ is the probability of observing ${\displaystyle \textstyle E}$ given ${\displaystyle \textstyle H}$, and is called the likelihood. As a function of ${\displaystyle \textstyle E}$ with ${\displaystyle \textstyle H}$ fixed, it indicates the compatibility of the evidence with the given hypothesis. The likelihood function is a function of the evidence, ${\displaystyle \textstyle E}$, while the posterior probability is a function of the hypothesis, ${\displaystyle \textstyle H}$.
• ${\displaystyle \textstyle P(E)}$ is sometimes termed the marginal likelihood or "model evidence". This factor is the same for all possible hypotheses being considered (as is evident from the fact that the hypothesis ${\displaystyle \textstyle H}$ does not appear anywhere in the symbol, unlike for all the other factors), so this factor does not enter into determining the relative probabilities of different hypotheses.

For different values of ${\displaystyle \textstyle H}$, only the factors ${\displaystyle \textstyle P(H)}$ and ${\displaystyle \textstyle P(E\mid H)}$, both in the numerator, affect the value of ${\displaystyle \textstyle P(H\mid E)}$ – the posterior probability of a hypothesis is proportional to its prior probability (its inherent likeliness) and the newly acquired likelihood (its compatibility with the new observed evidence).

Bayes' rule can also be written as follows:

${\displaystyle P(H\mid E)={\frac {P(E\mid H)}{P(E)}}\cdot P(H)}$

where the factor ${\displaystyle \textstyle {\frac {P(E\mid H)}{P(E)}}}$ can be interpreted as the impact of ${\displaystyle E}$ on the probability of ${\displaystyle H}$.

Alternatives to Bayesian updating

Bayesian updating is widely used and computationally convenient. However, it is not the only updating rule that might be considered rational.

Ian Hacking noted that traditional "Dutch book" arguments did not specify Bayesian updating: they left open the possibility that non-Bayesian updating rules could avoid Dutch books. Hacking wrote^[1] "And neither the Dutch book argument nor any other in the personalist arsenal of proofs of the probability axioms entails the dynamic assumption. Not one entails Bayesianism. So the personalist requires the dynamic assumption to be Bayesian. It is true that in consistency a personalist could abandon the Bayesian model of learning from experience. Salt could lose its savour."

Indeed, there are non-Bayesian updating rules that also avoid Dutch books (as discussed in the literature on "probability kinematics") following the publication of Richard C. Jeffrey's rule, which applies Bayes' rule to the case where the evidence itself is assigned a probability.^[2] The additional hypotheses needed to uniquely require Bayesian updating have been deemed to be substantial, complicated, and unsatisfactory.^[3]

Formal description of Bayesian inference

Definitions

• ${\displaystyle x}$, a data point in general. This may in fact be a vector of values.
• ${\displaystyle \theta }$, the parameter of the data point's distribution, i.e., ${\displaystyle x\sim p(x\mid \theta )}$ . This may in fact be a vector of parameters.
• ${\displaystyle \alpha }$, the hyperparameter of the parameter distribution, i.e., ${\displaystyle \theta \sim p(\theta \mid \alpha )}$ . This may in fact be a vector of hyperparameters.
• ${\displaystyle \mathbf {X} }$ is the sample, a set of ${\displaystyle n}$ observed data points, i.e., ${\displaystyle x_{1},\ldots ,x_{n}}$.
• ${\displaystyle {\tilde {x}}}$, a new data point whose distribution is to be predicted.

Bayesian inference

• The prior distribution is the distribution of the parameter(s) before any data is observed, i.e. ${\displaystyle p(\theta \mid \alpha )}$ .
• The prior distribution might not be easily determined. In this case, we can use the Jeffreys prior to obtain the posterior distribution before updating them with newer observations.
• The sampling distribution is the distribution of the observed data conditional on its parameters, i.e. ${\displaystyle p(\mathbf {X} \mid \theta )}$ . This is also termed the likelihood, especially when viewed as a function of the parameter(s), sometimes written ${\displaystyle \operatorname {L} (\theta \mid \mathbf {X} )=p(\mathbf {X} \mid \theta )}$ .
• The marginal likelihood (sometimes also termed the evidence) is the distribution of the observed data marginalized over the parameter(s), i.e. ${\displaystyle p(\mathbf {X} \mid \alpha )=\int p(\mathbf {X} \mid \theta )p(\theta \mid \alpha )\operatorname {d} \!\theta }$ .
• The posterior distribution is the distribution of the parameter(s) after taking into account the observed data. This is determined by Bayes' rule, which forms the heart of Bayesian inference:

${\displaystyle p(\theta \mid \mathbf {X} ,\alpha )={\frac {p(\mathbf {X} \mid \theta )p(\theta \mid \alpha )}{p(\mathbf {X} \mid \alpha )}}\propto p(\mathbf {X} \mid \theta )p(\theta \mid \alpha )}$

Note that this is expressed in words as "posterior is proportional to likelihood times prior", or sometimes as "posterior = likelihood times prior, over evidence".

Bayesian prediction

• The posterior predictive distribution is the distribution of a new data point, marginalized over the posterior:

${\displaystyle p({\tilde {x}}\mid \mathbf {X} ,\alpha )=\int p({\tilde {x}}\mid \theta )p(\theta \mid \mathbf {X} ,\alpha )\operatorname {d} \!\theta }$

• The prior predictive distribution is the distribution of a new data point, marginalized over the prior:

${\displaystyle p({\tilde {x}}\mid \alpha )=\int p({\tilde {x}}\mid \theta )p(\theta \mid \alpha )\operatorname {d} \!\theta }$

Bayesian theory calls for the use of the posterior predictive distribution to do predictive inference, i.e., to predict the distribution of a new, unobserved data point. That is, instead of a fixed point as a prediction, a distribution over possible points is returned. Only this way is the entire posterior distribution of the parameter(s) used. By comparison, prediction in frequentist statistics often involves finding an optimum point estimate of the parameter(s)—e.g., by maximum likelihood or maximum a posteriori estimation (MAP)—and then plugging this estimate into the formula for the distribution of a data point. This has the disadvantage that it does not account for any uncertainty in the value of the parameter, and hence will underestimate the variance of the predictive distribution.

(In some instances, frequentist statistics can work around this problem. For example, confidence intervals and prediction intervals in frequentist statistics when constructed from a normal distribution with unknown mean and variance are constructed using a Student's t-distribution. This correctly estimates the variance, due to the fact that (1) the average of normally distributed random variables is also normally distributed; (2) the predictive distribution of a normally distributed data point with unknown mean and variance, using conjugate or uninformative priors, has a student's t-distribution. In Bayesian statistics, however, the posterior predictive distribution can always be determined exactly—or at least, to an arbitrary level of precision, when numerical methods are used.)

Note that both types of predictive distributions have the form of a compound probability distribution (as does the marginal likelihood). In fact, if the prior distribution is a conjugate prior, and hence the prior and posterior distributions come from the same family, it can easily be seen that both prior and posterior predictive distributions also come from the same family of compound distributions. The only difference is that the posterior predictive distribution uses the updated values of the hyperparameters (applying the Bayesian update rules given in the conjugate prior article), while the prior predictive distribution uses the values of the hyperparameters that appear in the prior distribution.

Inference over exclusive and exhaustive possibilities

If evidence is simultaneously used to update belief over a set of exclusive and exhaustive propositions, Bayesian inference may be thought of as acting on this belief distribution as a whole.

General formulation

Diagram illustrating event space ${\displaystyle \Omega }$ in general formulation of Bayesian inference. Although this diagram shows discrete models and events, the continuous case may be visualized similarly using probability densities.

Suppose a process is generating independent and identically distributed events ${\displaystyle E_{n}}$, but the probability distribution is unknown. Let the event space ${\displaystyle \Omega }$ represent the current state of belief for this process. Each model is represented by event ${\displaystyle M_{m}}$. The conditional probabilities ${\displaystyle P(E_{n}\mid M_{m})}$ are specified to define the models. ${\displaystyle P(M_{m})}$ is the degree of belief in ${\displaystyle M_{m}}$. Before the first inference step, ${\displaystyle \{P(M_{m})\}}$ is a set of initial prior probabilities. These must sum to 1, but are otherwise arbitrary.

Suppose that the process is observed to generate ${\displaystyle \textstyle E\in \{E_{n}\}}$. For each ${\displaystyle M\in \{M_{m}\}}$, the prior ${\displaystyle P(M)}$ is updated to the posterior ${\displaystyle P(M\mid E)}$. From Bayes' theorem:^[4]

${\displaystyle P(M\mid E)={\frac {P(E\mid M)}{\sum _{m}{P(E\mid M_{m})P(M_{m})}}}\cdot P(M)}$

Upon observation of further evidence, this procedure may be repeated.

Multiple observations

For a sequence of independent and identically distributed observations ${\displaystyle \mathbf {E} =(e_{1},\dots ,e_{n})}$, it can be shown by induction that repeated application of the above is equivalent to

${\displaystyle P(M\mid \mathbf {E} )={\frac {P(\mathbf {E} \mid M)}{\sum _{m}{P(\mathbf {E} \mid M_{m})P(M_{m})}}}\cdot P(M)}$

Where

${\displaystyle P(\mathbf {E} \mid M)=\prod _{k}{P(e_{k}\mid M)}.}$

For a sequence where the conditional independence of the observations cannot be guaranteed, Rachael Bond, Yang-Hui He, and Thomas Ormerod^[5] have shown from quantum mechanics that

${\displaystyle P(M_{\alpha }|E_{1}\cap E_{2}\ldots \cap E_{m})={\frac {\sum \limits _{i,j}{\sqrt {E_{i\alpha }E_{j\alpha }}}c_{ij}^{\alpha }}{\sum \limits _{i,j,\beta }{\sqrt {E_{i\beta }E_{j\beta }}}c_{ij}^{\beta }}}}$

such that

${\displaystyle P(M_{1}|E_{1}\cap E_{2})={\frac {{\frac {P(E_{1}|M_{1})P(E_{2}|M_{1})}{P(E_{1}|M_{2})P(E_{2}|M_{2})}}+P(E_{1}|M_{1})+P(E_{2}|M_{1})}{{\frac {P(E_{1}|M_{1})P(E_{2}|M_{1})}{P(E_{1}|M_{2})P(E_{2}|M_{2})}}+P(E_{1}|M_{1})+P(E_{2}|M_{1})+{\frac {P(E_{1}|M_{2})P(E_{2}|M_{2})}{P(E_{1}|M_{1})P(E_{2}|M_{1})}}+P(E_{1}|M_{2})+P(E_{2}|M_{2})}}}$

 

 

Parametric formulation

By parameterizing the space of models, the belief in all models may be updated in a single step. The distribution of belief over the model space may then be thought of as a distribution of belief over the parameter space. The distributions in this section are expressed as continuous, represented by probability densities, as this is the usual situation. The technique is however equally applicable to discrete distributions.

Let the vector ${\displaystyle \mathbf {\theta } }$ span the parameter space. Let the initial prior distribution over ${\displaystyle \mathbf {\theta } }$ be ${\displaystyle p(\mathbf {\theta } \mid \mathbf {\alpha } )}$, where ${\displaystyle \mathbf {\alpha } }$ is a set of parameters to the prior itself, or hyperparameters. Let ${\displaystyle \mathbf {E} =(e_{1},\dots ,e_{n})}$ be a sequence of independent and identically distributed event observations, where all ${\displaystyle e_{i}}$ are distributed as ${\displaystyle p(e\mid \mathbf {\theta } )}$ for some ${\displaystyle \mathbf {\theta } }$. Bayes' theorem is applied to find the posterior distribution over ${\displaystyle \mathbf {\theta } }$:

${\displaystyle {\begin{aligned}p(\mathbf {\theta } \mid \mathbf {E} ,\mathbf {\alpha } )&={\frac {p(\mathbf {E} \mid \mathbf {\theta } ,\mathbf {\alpha } )}{p(\mathbf {E} \mid \mathbf {\alpha } )}}\cdot p(\mathbf {\theta } \mid \mathbf {\alpha } )\\&={\frac {p(\mathbf {E} \mid \mathbf {\theta } ,\mathbf {\alpha } )}{\int p(\mathbf {E} |\mathbf {\theta } ,\mathbf {\alpha } )p(\mathbf {\theta } \mid \mathbf {\alpha } )\,d\mathbf {\theta } }}\cdot p(\mathbf {\theta } \mid \mathbf {\alpha } )\end{aligned}}}$

Where

${\displaystyle p(\mathbf {E} \mid \mathbf {\theta } ,\mathbf {\alpha } )=\prod _{k}p(e_{k}\mid \mathbf {\theta } )}$

Mathematical properties

Interpretation of factor

${\displaystyle \textstyle {\frac {P(E\mid M)}{P(E)}}>1\Rightarrow \textstyle P(E\mid M)>P(E)}$. That is, if the model were true, the evidence would be more likely than is predicted by the current state of belief. The reverse applies for a decrease in belief. If the belief does not change, ${\displaystyle \textstyle {\frac {P(E\mid M)}{P(E)}}=1\Rightarrow \textstyle P(E\mid M)=P(E)}$. That is, the evidence is independent of the model. If the model were true, the evidence would be exactly as likely as predicted by the current state of belief.

Cromwell's rule

If ${\displaystyle P(M)=0}$ then ${\displaystyle P(M\mid E)=0}$. If ${\displaystyle P(M)=1}$, then ${\displaystyle P(M|E)=1}$. This can be interpreted to mean that hard convictions are insensitive to counter-evidence.
The former follows directly from Bayes' theorem. The latter can be derived by applying the first rule to the event "not ${\displaystyle M}$" in place of "${\displaystyle M}$", yielding "if ${\displaystyle 1-P(M)=0}$, then ${\displaystyle 1-P(M\mid E)=0}$", from which the result immediately follows.

Asymptotic behaviour of posterior

Consider the behaviour of a belief distribution as it is updated a large number of times with independent and identically distributed trials. For sufficiently nice prior probabilities, the Bernstein-von Mises theorem gives that in the limit of infinite trials, the posterior converges to a Gaussian distribution independent of the initial prior under some conditions firstly outlined and rigorously proven by Joseph L. Doob in 1948, namely if the random variable in consideration has a finite probability space. The more general results were obtained later by the statistician David A. Freedman who published in two seminal research papers in 1963 ^[6] and 1965 ^[7] when and under what circumstances the asymptotic behaviour of posterior is guaranteed. His 1963 paper treats, like Doob (1949), the finite case and comes to a satisfactory conclusion. However, if the random variable has an infinite but countable probability space (i.e., corresponding to a die with infinite many faces) the 1965 paper demonstrates that for a dense subset of priors the Bernstein-von Mises theorem is not applicable. In this case there is almost surely no asymptotic convergence. Later in the 1980s and 1990s Freedman and Persi Diaconis continued to work on the case of infinite countable probability spaces.^[8] To summarise, there may be insufficient trials to suppress the effects of the initial choice, and especially for large (but finite) systems the convergence might be very slow.

Conjugate priors

In parameterized form, the prior distribution is often assumed to come from a family of distributions called conjugate priors. The usefulness of a conjugate prior is that the corresponding posterior distribution will be in the same family, and the calculation may be expressed in closed form.

Estimates of parameters and predictions

It is often desired to use a posterior distribution to estimate a parameter or variable. Several methods of Bayesian estimation select measurements of central tendency from the posterior distribution.

For one-dimensional problems, a unique median exists for practical continuous problems. The posterior median is attractive as a robust estimator.^[9]

If there exists a finite mean for the posterior distribution, then the posterior mean is a method of estimation.^{[10][citation needed]}

${\displaystyle {\tilde {\theta }}=\operatorname {E} [\theta ]=\int \theta \,p(\theta \mid \mathbf {X} ,\alpha )\,d\theta }$

Taking a value with the greatest probability defines maximum a posteriori (MAP) estimates:^{[11][citation needed]}

${\displaystyle \{\theta _{\text{MAP}}\}\subset \arg \max _{\theta }p(\theta \mid \mathbf {X} ,\alpha ).}$

There are examples where no maximum is attained, in which case the set of MAP estimates is empty.

There are other methods of estimation that minimize the posterior risk (expected-posterior loss) with respect to a loss function, and these are of interest to statistical decision theory using the sampling distribution ("frequentist statistics").^{[12][citation needed]}

The posterior predictive distribution of a new observation ${\displaystyle {\tilde {x}}}$ (that is independent of previous observations) is determined by^{[13][citation needed]}

${\displaystyle p({\tilde {x}}|\mathbf {X} ,\alpha )=\int p({\tilde {x}},\theta \mid \mathbf {X} ,\alpha )\,d\theta =\int p({\tilde {x}}\mid \theta )p(\theta \mid \mathbf {X} ,\alpha )\,d\theta .}$

Examples

Probability of a hypothesis

Suppose there are two full bowls of cookies. Bowl #1 has 10 chocolate chip and 30 plain cookies, while bowl #2 has 20 of each. Our friend Fred picks a bowl at random, and then picks a cookie at random. We may assume there is no reason to believe Fred treats one bowl differently from another, likewise for the cookies. The cookie turns out to be a plain one. How probable is it that Fred picked it out of bowl #1?

Intuitively, it seems clear that the answer should be more than a half, since there are more plain cookies in bowl #1. The precise answer is given by Bayes' theorem. Let ${\displaystyle H_{1}}$ correspond to bowl #1, and ${\displaystyle H_{2}}$ to bowl #2. It is given that the bowls are identical from Fred's point of view, thus ${\displaystyle P(H_{1})=P(H_{2})}$, and the two must add up to 1, so both are equal to 0.5. The event ${\displaystyle E}$ is the observation of a plain cookie. From the contents of the bowls, we know that ${\displaystyle P(E\mid H_{1})=30/40=0.75}$ and ${\displaystyle P(E\mid H_{2})=20/40=0.5.}$ Bayes' formula then yields

${\displaystyle {\begin{aligned}P(H_{1}\mid E)&={\frac {P(E\mid H_{1})\,P(H_{1})}{P(E\mid H_{1})\,P(H_{1})\;+\;P(E\mid H_{2})\,P(H_{2})}}\\\\\ &={\frac {0.75\times 0.5}{0.75\times 0.5+0.5\times 0.5}}\\\\\ &=0.6\end{aligned}}}$

Before we observed the cookie, the probability we assigned for Fred having chosen bowl #1 was the prior probability, ${\displaystyle P(H_{1})}$, which was 0.5. After observing the cookie, we must revise the probability to ${\displaystyle P(H_{1}\mid E)}$, which is 0.6.

Making a prediction

Example results for archaeology example. This simulation was generated using c=15.2.

An archaeologist is working at a site thought to be from the medieval period, between the 11th century to the 16th century. However, it is uncertain exactly when in this period the site was inhabited. Fragments of pottery are found, some of which are glazed and some of which are decorated. It is expected that if the site were inhabited during the early medieval period, then 1% of the pottery would be glazed and 50% of its area decorated, whereas if it had been inhabited in the late medieval period then 81% would be glazed and 5% of its area decorated. How confident can the archaeologist be in the date of inhabitation as fragments are unearthed?

The degree of belief in the continuous variable ${\displaystyle C}$ (century) is to be calculated, with the discrete set of events ${\displaystyle \{GD,G{\bar {D}},{\bar {G}}D,{\bar {G}}{\bar {D}}\}}$ as evidence. Assuming linear variation of glaze and decoration with time, and that these variables are independent,

${\displaystyle P(E=GD\mid C=c)=(0.01+{\frac {0.81-0.01}{16-11}}(c-11))(0.5-{\frac {0.5-0.05}{16-11}}(c-11))}$

${\displaystyle P(E=G{\bar {D}}\mid C=c)=(0.01+{\frac {0.81-0.01}{16-11}}(c-11))(0.5+{\frac {0.5-0.05}{16-11}}(c-11))}$

${\displaystyle P(E={\bar {G}}D\mid C=c)=((1-0.01)-{\frac {0.81-0.01}{16-11}}(c-11))(0.5-{\frac {0.5-0.05}{16-11}}(c-11))}$

${\displaystyle P(E={\bar {G}}{\bar {D}}\mid C=c)=((1-0.01)-{\frac {0.81-0.01}{16-11}}(c-11))(0.5+{\frac {0.5-0.05}{16-11}}(c-11))}$

Assume a uniform prior of ${\displaystyle \textstyle f_{C}(c)=0.2}$, and that trials are independent and identically distributed. When a new fragment of type ${\displaystyle e}$ is discovered, Bayes' theorem is applied to update the degree of belief for each ${\displaystyle c}$:

${\displaystyle f_{C}(c\mid E=e)={\frac {P(E=e\mid C=c)}{P(E=e)}}f_{C}(c)={\frac {P(E=e\mid C=c)}{\int _{11}^{16}{P(E=e\mid C=c)f_{C}(c)dc}}}f_{C}(c)}$



A computer simulation of the changing belief as 50 fragments are unearthed is shown on the graph. In the simulation, the site was inhabited around 1420, or ${\displaystyle c=15.2}$. By calculating the area under the relevant portion of the graph for 50 trials, the archaeologist can say that there is practically no chance the site was inhabited in the 11th and 12th centuries, about 1% chance that it was inhabited during the 13th century, 63% chance during the 14th century and 36% during the 15th century. Note that the Bernstein-von Mises theorem asserts here the asymptotic convergence to the "true" distribution because the probability space corresponding to the discrete set of events ${\displaystyle \{GD,G{\bar {D}},{\bar {G}}D,{\bar {G}}{\bar {D}}\}}$ is finite (see above section on asymptotic behaviour of the posterior).

In frequentist statistics and decision theory

A decision-theoretic justification of the use of Bayesian inference was given by Abraham Wald, who proved that every unique Bayesian procedure is admissible. Conversely, every admissible statistical procedure is either a Bayesian procedure or a limit of Bayesian procedures.^[14]

Wald characterized admissible procedures as Bayesian procedures (and limits of Bayesian procedures), making the Bayesian formalism a central technique in such areas of frequentist inference as parameter estimation, hypothesis testing, and computing confidence intervals.^[15] For example:

• "Under some conditions, all admissible procedures are either Bayes procedures or limits of Bayes procedures (in various senses). These remarkable results, at least in their original form, are due essentially to Wald. They are useful because the property of being Bayes is easier to analyze than admissibility."^[14]
• "In decision theory, a quite general method for proving admissibility consists in exhibiting a procedure as a unique Bayes solution."^[16]
• "In the first chapters of this work, prior distributions with finite support and the corresponding Bayes procedures were used to establish some of the main theorems relating to the comparison of experiments. Bayes procedures with respect to more general prior distributions have played a very important role in the development of statistics, including its asymptotic theory." "There are many problems where a glance at posterior distributions, for suitable priors, yields immediately interesting information. Also, this technique can hardly be avoided in sequential analysis."^[17]

• "A useful fact is that any Bayes decision rule obtained by taking a proper prior over the whole parameter space must be admissible"^[18]
• "An important area of investigation in the development of admissibility ideas has been that of conventional sampling-theory procedures, and many interesting results have been obtained."^[19]

Applications

Computer applications

Bayesian inference has applications in artificial intelligence and expert systems. Bayesian inference techniques have been a fundamental part of computerized pattern recognition techniques since the late 1950s. There is also an ever-growing connection between Bayesian methods and simulation-based Monte Carlo techniques since complex models cannot be processed in closed form by a Bayesian analysis, while a graphical model structure may allow for efficient simulation algorithms like the Gibbs sampling and other Metropolis–Hastings algorithm schemes.^[20] Recently Bayesian inference has gained popularity amongst the phylogenetics community for these reasons; a number of applications allow many demographic and evolutionary parameters to be estimated simultaneously.

As applied to statistical classification, Bayesian inference has been used in recent years to develop algorithms for identifying e-mail spam. Applications which make use of Bayesian inference for spam filtering include CRM114, DSPAM, Bogofilter, SpamAssassin, SpamBayes, Mozilla, XEAMS, and others. Spam classification is treated in more detail in the article on the naive Bayes classifier.

Solomonoff's Inductive inference is the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols. The only assumption is that the environment follows some unknown but computable probability distribution. It is a formal inductive framework that combines two well-studied principles of inductive inference: Bayesian statistics and Occam’s Razor.^[21] Solomonoff's universal prior probability of any prefix p of a computable sequence x is the sum of the probabilities of all programs (for a universal computer) that compute something starting with p. Given some p and any computable but unknown probability distribution from which x is sampled, the universal prior and Bayes' theorem can be used to predict the yet unseen parts of x in optimal fashion.^[22][23]

In the courtroom

Bayesian inference can be used by jurors to coherently accumulate the evidence for and against a defendant, and to see whether, in totality, it meets their personal threshold for 'beyond a reasonable doubt'.^[24][25][26] Bayes' theorem is applied successively to all evidence presented, with the posterior from one stage becoming the prior for the next. The benefit of a Bayesian approach is that it gives the juror an unbiased, rational mechanism for combining evidence. It may be appropriate to explain Bayes' theorem to jurors in odds form, as betting odds are more widely understood than probabilities. Alternatively, a logarithmic approach, replacing multiplication with addition, might be easier for a jury to handle.

Adding up evidence.

If the existence of the crime is not in doubt, only the identity of the culprit, it has been suggested that the prior should be uniform over the qualifying population.^[27] For example, if 1,000 people could have committed the crime, the prior probability of guilt would be 1/1000.

The use of Bayes' theorem by jurors is controversial. In the United Kingdom, a defence expert witness explained Bayes' theorem to the jury in R v Adams. The jury convicted, but the case went to appeal on the basis that no means of accumulating evidence had been provided for jurors who did not wish to use Bayes' theorem. The Court of Appeal upheld the conviction, but it also gave the opinion that "To introduce Bayes' Theorem, or any similar method, into a criminal trial plunges the jury into inappropriate and unnecessary realms of theory and complexity, deflecting them from their proper task."

Gardner-Medwin^[28] argues that the criterion on which a verdict in a criminal trial should be based is not the probability of guilt, but rather the probability of the evidence, given that the defendant is innocent (akin to a frequentist p-value). He argues that if the posterior probability of guilt is to be computed by Bayes' theorem, the prior probability of guilt must be known. This will depend on the incidence of the crime, which is an unusual piece of evidence to consider in a criminal trial. Consider the following three propositions:

A The known facts and testimony could have arisen if the defendant is guilty

B The known facts and testimony could have arisen if the defendant is innocent

C The defendant is guilty.

Gardner-Medwin argues that the jury should believe both A and not-B in order to convict. A and not-B implies the truth of C, but the reverse is not true. It is possible that B and C are both true, but in this case he argues that a jury should acquit, even though they know that they will be letting some guilty people go free. See also Lindley's paradox.

Bayesian epistemology

Bayesian epistemology is a movement that advocates for Bayesian inference as a means of justifying the rules of inductive logic.

Karl Popper and David Miller have rejected the alleged rationality of Bayesianism, i.e. using Bayes rule to make epistemological inferences:^[29] It is prone to the same vicious circle as any other justificationist epistemology, because it presupposes what it attempts to justify. According to this view, a rational interpretation of Bayesian inference would see it merely as a probabilistic version of falsification, rejecting the belief, commonly held by Bayesians, that high likelihood achieved by a series of Bayesian updates would prove the hypothesis beyond any reasonable doubt, or even with likelihood greater than 0.

Other

• The scientific method is sometimes interpreted as an application of Bayesian inference. In this view, Bayes' rule guides (or should guide) the updating of probabilities about hypotheses conditional on new observations or experiments.^[30] The Bayesian inference has also been applied to treat stochastic scheduling problems with incomplete information by Cai et al (2009) ^[31].
• Bayesian search theory is used to search for lost objects.
• Bayesian inference in phylogeny
• Bayesian tool for methylation analysis
• Bayesian approaches to brain function investigate the brain as a Bayesian mechanism.
• Bayesian inference in ecological studies^[32][33]

Bayes and Bayesian inference

The problem considered by Bayes in Proposition 9 of his essay, "An Essay towards solving a Problem in the Doctrine of Chances", is the posterior distribution for the parameter a (the success rate) of the binomial distribution.^{[citation needed]}

History

The term Bayesian refers to Thomas Bayes (1702–1761), who proved a special case of what is now called Bayes' theorem. However, it was Pierre-Simon Laplace (1749–1827) who introduced a general version of the theorem and used it to approach problems in celestial mechanics, medical statistics, reliability, and jurisprudence.^[34] Early Bayesian inference, which used uniform priors following Laplace's principle of insufficient reason, was called "inverse probability" (because it infers backwards from observations to parameters, or from effects to causes^[35]). After the 1920s, "inverse probability" was largely supplanted by a collection of methods that came to be called frequentist statistics.^[35]

In the 20th century, the ideas of Laplace were further developed in two different directions, giving rise to objective and subjective currents in Bayesian practice. In the objective or "non-informative" current, the statistical analysis depends on only the model assumed, the data analyzed,^[36] and the method assigning the prior, which differs from one objective Bayesian to another objective Bayesian. In the subjective or "informative" current, the specification of the prior depends on the belief (that is, propositions on which the analysis is prepared to act), which can summarize information from experts, previous studies, etc.

In the 1980s, there was a dramatic growth in research and applications of Bayesian methods, mostly attributed to the discovery of Markov chain Monte Carlo methods, which removed many of the computational problems, and an increasing interest in nonstandard, complex applications.^[37] Despite growth of Bayesian research, most undergraduate teaching is still based on frequentist statistics.^[38] Nonetheless, Bayesian methods are widely accepted and used, such as for example in the field of machine learning.^[39]

Recursion

From Wikipedia, the free encyclopedia

A visual form of recursion known as the Droste effect. The woman in this image holds an object that contains a smaller image of her holding an identical object, which in turn contains a smaller image of herself holding an identical object, and so forth. 1904 Droste cocoa tin, designed by Jan Misset

Recursion occurs when a thing is defined in terms of itself or of its type. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics and computer science, where a function being defined is applied within its own definition. While this apparently defines an infinite number of instances (function values), it is often done in such a way that no loop or infinite chain of references can occur.

Formal definitions

Ouroboros, an ancient symbol depicting a serpent or dragon eating its own tail.

In mathematics and computer science, a class of objects or methods exhibit recursive behavior when they can be defined by two properties:

1. A simple base case (or cases)—a terminating scenario that does not use recursion to produce an answer
2. A set of rules that reduce all other cases toward the base case

For example, the following is a recursive definition of a person's ancestors:

• One's parents are one's ancestors (base case).
• The ancestors of one's ancestors are also one's ancestors (recursion step).

The Fibonacci sequence is a classic example of recursion:

${\displaystyle {\text{Fib}}(0)=0{\text{ as base case 1,}}}$
${\displaystyle {\text{Fib}}(1)=1{\text{ as base case 2,}}}$
${\displaystyle {\text{For all integers }}n>1,~{\text{ Fib}}(n):={\text{Fib}}(n-1)+{\text{Fib}}(n-2).}$

Many mathematical axioms are based upon recursive rules. For example, the formal definition of the natural numbers by the Peano axioms can be described as: 0 is a natural number, and each natural number has a successor, which is also a natural number. By this base case and recursive rule, one can generate the set of all natural numbers.

Recursively defined mathematical objects include functions, sets, and especially fractals.

There are various more tongue-in-cheek "definitions" of recursion; see recursive humor.

Informal definition

Recently refreshed sourdough, bubbling through fermentation: the recipe calls for some sourdough left over from the last time the same recipe was made.

Recursion is the process a procedure goes through when one of the steps of the procedure involves invoking the procedure itself. A procedure that goes through recursion is said to be 'recursive'.

To understand recursion, one must recognize the distinction between a procedure and the running of a procedure. A procedure is a set of steps based on a set of rules. The running of a procedure involves actually following the rules and performing the steps. An analogy: a procedure is like a written recipe; running a procedure is like actually preparing the meal.

Recursion is related to, but not the same as, a reference within the specification of a procedure to the execution of some other procedure. For instance, a recipe might refer to cooking vegetables, which is another procedure that in turn requires heating water, and so forth. However, a recursive procedure is where (at least) one of its steps calls for a new instance of the very same procedure, like a sourdough recipe calling for some dough left over from the last time the same recipe was made. This immediately creates the possibility of an endless loop; recursion can only be properly used in a definition if the step in question is skipped in certain cases so that the procedure can complete, like a sourdough recipe that also tells you how to get some starter dough in case you've never made it before. Even if properly defined, a recursive procedure is not easy for humans to perform, as it requires distinguishing the new from the old (partially executed) invocation of the procedure; this requires some administration of how far various simultaneous instances of the procedures have progressed. For this reason recursive definitions are very rare in everyday situations. An example could be the following procedure to find a way through a maze. Proceed forward until reaching either an exit or a branching point (a dead end is considered a branching point with 0 branches). If the point reached is an exit, terminate. Otherwise try each branch in turn, using the procedure recursively; if every trial fails by reaching only dead ends, return on the path that led to this branching point and report failure. Whether this actually defines a terminating procedure depends on the nature of the maze: it must not allow loops. In any case, executing the procedure requires carefully recording all currently explored branching points, and which of their branches have already been exhaustively tried.

In language

Linguist Noam Chomsky among many others has argued that the lack of an upper bound on the number of grammatical sentences in a language, and the lack of an upper bound on grammatical sentence length (beyond practical constraints such as the time available to utter one), can be explained as the consequence of recursion in natural language.^[1][2] This can be understood in terms of a recursive definition of a syntactic category, such as a sentence. A sentence can have a structure in which what follows the verb is another sentence: Dorothy thinks witches are dangerous, in which the sentence witches are dangerous occurs in the larger one. So a sentence can be defined recursively (very roughly) as something with a structure that includes a noun phrase, a verb, and optionally another sentence. This is really just a special case of the mathematical definition of recursion.

This provides a way of understanding the creativity of language—the unbounded number of grammatical sentences—because it immediately predicts that sentences can be of arbitrary length: Dorothy thinks that Toto suspects that Tin Man said that.... There are many structures apart from sentences that can be defined recursively, and therefore many ways in which a sentence can embed instances of one category inside another. Over the years, languages in general have proved amenable to this kind of analysis.

Recently, however, the generally accepted idea that recursion is an essential property of human language has been challenged by Daniel Everett on the basis of his claims about the Pirahã language. Andrew Nevins, David Pesetsky and Cilene Rodrigues are among many who have argued against this.^[3] Literary self-reference can in any case be argued to be different in kind from mathematical or logical recursion.^[4]

Recursion plays a crucial role not only in syntax, but also in natural language semantics. The word and, for example, can be construed as a function that can apply to sentence meanings to create new sentences, and likewise for noun phrase meanings, verb phrase meanings, and others. It can also apply to intransitive verbs, transitive verbs, or ditransitive verbs. In order to provide a single denotation for it that is suitably flexible, and is typically defined so that it can take any of these different types of meanings as arguments. This can be done by defining it for a simple case in which it combines sentences, and then defining the other cases recursively in terms of the simple one.^[5]

A recursive grammar is a formal grammar that contains recursive production rules.^[6]

Recursive humor

Recursion is sometimes used humorously in computer science, programming, philosophy, or mathematics textbooks, generally by giving a circular definition or self-reference, in which the putative recursive step does not get closer to a base case, but instead leads to an infinite regress. It is not unusual for such books to include a joke entry in their glossary along the lines of:

Recursion, see Recursion.^[7]

A variation is found on page 269 in the index of some editions of Brian Kernighan and Dennis Ritchie's book The C Programming Language; the index entry recursively references itself ("recursion 86, 139, 141, 182, 202, 269"). The earliest version of this joke was in "Software Tools" by Kernighan and Plauger, and also appears in "The UNIX Programming Environment" by Kernighan and Pike. It did not appear in the first edition of The C Programming Language.

Another joke is that "To understand recursion, you must understand recursion."^[7] In the English-language version of the Google web search engine, when a search for "recursion" is made, the site suggests "Did you mean: recursion." An alternative form is the following, from Andrew Plotkin: "If you already know what recursion is, just remember the answer. Otherwise, find someone who is standing closer to Douglas Hofstadter than you are; then ask him or her what recursion is."

Recursive acronyms can also be examples of recursive humor. PHP, for example, stands for "PHP Hypertext Preprocessor", WINE stands for "WINE Is Not an Emulator." and GNU stands for "GNU's not Unix".

In mathematics

The Sierpinski triangle—a confined recursion of triangles that form a fractal

Recursively defined sets

Example: the natural numbers

The canonical example of a recursively defined set is given by the natural numbers:

0 is in ${\displaystyle \mathbb {N} }$

if n is in ${\displaystyle \mathbb {N} }$, then n + 1 is in ${\displaystyle \mathbb {N} }$

The set of natural numbers is the smallest set satisfying the previous two properties.

Example: The set of true reachable propositions

Another interesting example is the set of all "true reachable" propositions in an axiomatic system.

• If a proposition is an axiom, it is a true reachable proposition.
• If a proposition can be obtained from true reachable propositions by means of inference rules, it is a true reachable proposition.
• The set of true reachable propositions is the smallest set of propositions satisfying these conditions.

This set is called 'true reachable propositions' because in non-constructive approaches to the foundations of mathematics, the set of true propositions may be larger than the set recursively constructed from the axioms and rules of inference. See also Gödel's incompleteness theorems.

Finite subdivision rules

Finite subdivision rules are a geometric form of recursion, which can be used to create fractal-like images. A subdivision rule starts with a collection of polygons labelled by finitely many labels, and then each polygon is subdivided into smaller labelled polygons in a way that depends only on the labels of the original polygon. This process can be iterated. The standard `middle thirds' technique for creating the Cantor set is a subdivision rule, as is barycentric subdivision.

Functional recursion

A function may be partly defined in terms of itself. A familiar example is the Fibonacci number sequence: F(n) = F(n − 1) + F(n − 2). For such a definition to be useful, it must lead to non-recursively defined values, in this case F(0) = 0 and F(1) = 1.

A famous recursive function is the Ackermann function, which—unlike the Fibonacci sequence—cannot easily be expressed without recursion.

Proofs involving recursive definitions

Applying the standard technique of proof by cases to recursively defined sets or functions, as in the preceding sections, yields structural induction, a powerful generalization of mathematical induction widely used to derive proofs in mathematical logic and computer science.

Recursive optimization

Dynamic programming is an approach to optimization that restates a multiperiod or multistep optimization problem in recursive form. The key result in dynamic programming is the Bellman equation, which writes the value of the optimization problem at an earlier time (or earlier step) in terms of its value at a later time (or later step).

The recursion theorem

In set theory, this is a theorem guaranteeing that recursively defined functions exist. Given a set X, an element a of X and a function ${\displaystyle f:X\rightarrow X}$, the theorem states that there is a unique function ${\displaystyle F:\mathbb {N} \rightarrow X}$ (where ${\displaystyle \mathbb {N} }$ denotes the set of natural numbers including zero) such that

${\displaystyle F(0)=a}$

${\displaystyle F(n+1)=f(F(n))}$

for any natural number n.

Proof of uniqueness

Take two functions ${\displaystyle F:\mathbb {N} \rightarrow X}$ and ${\displaystyle G:\mathbb {N} \rightarrow X}$ such that:

${\displaystyle F(0)=a}$

${\displaystyle G(0)=a}$

${\displaystyle F(n+1)=f(F(n))}$

${\displaystyle G(n+1)=f(G(n))}$

where a is an element of X.

It can be proved by mathematical induction that ${\displaystyle F(n)=G(n)}$ for all natural numbers n:

Base Case: ${\displaystyle F(0)=a=G(0)}$ so the equality holds for ${\displaystyle n=0}$.

Inductive Step: Suppose ${\displaystyle F(k)=G(k)}$ for some ${\displaystyle k\in \mathbb {N} }$. Then ${\displaystyle F(k+1)=f(F(k))=f(G(k))=G(k+1).}$

Hence F(k) = G(k) implies F(k+1) = G(k+1).

By induction, ${\displaystyle F(n)=G(n)}$ for all ${\displaystyle n\in \mathbb {N} }$.

In computer science

A common method of simplification is to divide a problem into subproblems of the same type. As a computer programming technique, this is called divide and conquer and is key to the design of many important algorithms. Divide and conquer serves as a top-down approach to problem solving, where problems are solved by solving smaller and smaller instances. A contrary approach is dynamic programming. This approach serves as a bottom-up approach, where problems are solved by solving larger and larger instances, until the desired size is reached.

A classic example of recursion is the definition of the factorial function, given here in C code:

unsigned int factorial(unsigned int n) {
    if (n == 0) {
        return 1;
    } else {
        return n * factorial(n - 1);
    }
}

The function calls itself recursively on a smaller version of the input (n - 1) and multiplies the result of the recursive call by n, until reaching the base case, analogously to the mathematical definition of factorial.

Recursion in computer programming is exemplified when a function is defined in terms of simpler, often smaller versions of itself. The solution to the problem is then devised by combining the solutions obtained from the simpler versions of the problem. One example application of recursion is in parsers for programming languages. The great advantage of recursion is that an infinite set of possible sentences, designs or other data can be defined, parsed or produced by a finite computer program.

Recurrence relations are equations to define one or more sequences recursively. Some specific kinds of recurrence relation can be "solved" to obtain a non-recursive definition.

Use of recursion in an algorithm has both advantages and disadvantages. The main advantage is usually simplicity. The main disadvantage is often that the algorithm may require large amounts of memory if the depth of the recursion is very large.

In art

Recursive dolls: the original set of Matryoshka dolls by Zvyozdochkin and Malyutin, 1892

Front face of Giotto's Stefaneschi Triptych, 1320, recursively contains an image of itself (held up by the kneeling figure in the central panel).

The Russian Doll or Matryoshka Doll is a physical artistic example of the recursive concept.^[8]

Recursion has been used in paintings since Giotto's Stefaneschi Triptych, made in 1320. Its central panel contains the kneeling figure of Cardinal Stefaneschi, holding up the triptych itself as an offering.^[9]

M. C. Escher's Print Gallery (1956) is a print which depicts a distorted city which contains a gallery which recursively contains the picture, and so ad infinitum.^[10]

Ethics of artificial intelligence

From Wikipedia, the free encyclopedia

The ethics of artificial intelligence is the part of the ethics of technology specific to robots and other artificially intelligent beings. It is typically^{[citation needed]} divided into roboethics, a concern with the moral behavior of humans as they design, construct, use and treat artificially intelligent beings, and machine ethics, which is concerned with the moral behavior of artificial moral agents (AMAs).

Robot ethics

The term "robot ethics" (sometimes "roboethics") refers to the morality of how humans design, construct, use and treat robots and other artificially intelligent beings.^[1] It considers both how artificially intelligent beings may be used to harm humans and how they may be used to benefit humans.

Robot rights

"Robot rights" is the concept that people should have moral obligations towards their machines, similar to human rights or animal rights.^[2] It has been suggested that robot rights, such as a right to exist and perform its own mission, could be linked to robot duty to serve human, by analogy with linking human rights to human duties before society.^[3] These could include the right to life and liberty, freedom of thought and expression and equality before the law.^[4] The issue has been considered by the Institute for the Future^[5] and by the U.K. Department of Trade and Industry.^[6]

Experts disagree whether specific and detailed laws will be required soon or safely in the distant future.^[6] Glenn McGee reports that sufficiently humanoid robots may appear by 2020.^[7] Ray Kurzweil sets the date at 2029.^[8] Another group of scientists meeting in 2007 supposed that at least 50 years had to pass before any sufficiently advanced system would exist.^[9]

The rules for the 2003 Loebner Prize competition envisioned the possibility of robots having rights of their own:

61. If, in any given year, a publicly available open source Entry entered by the University of Surrey or the Cambridge Center wins the Silver Medal or the Gold Medal, then the Medal and the Cash Award will be awarded to the body responsible for the development of that Entry. If no such body can be identified, or if there is disagreement among two or more claimants, the Medal and the Cash Award will be held in trust until such time as the Entry may legally possess, either in the United States of America or in the venue of the contest, the Cash Award and Gold Medal in its own right.^[10]

In October 2017, the android Sophia was granted citizenship in Saudi Arabia, though some observers found this to be more of a publicity stunt than a meaningful legal recognition.^[11]

Threat to human dignity

Joseph Weizenbaum argued in 1976 that AI technology should not be used to replace people in positions that require respect and care, such as any of these:

• A customer service representative (AI technology is already used today for telephone-based interactive voice response systems)
• A therapist (as was proposed by Kenneth Colby in the 1970s)
• A nursemaid for the elderly (as was reported by Pamela McCorduck in her book The Fifth Generation)
• A soldier
• A judge
• A police officer

Weizenbaum explains that we require authentic feelings of empathy from people in these positions. If machines replace them, we will find ourselves alienated, devalued and frustrated. Artificial intelligence, if used in this way, represents a threat to human dignity. Weizenbaum argues that the fact that we are entertaining the possibility of machines in these positions suggests that we have experienced an "atrophy of the human spirit that comes from thinking of ourselves as computers."^[12]
Pamela McCorduck counters that, speaking for women and minorities "I'd rather take my chances with an impartial computer," pointing out that there are conditions where we would prefer to have automated judges and police that have no personal agenda at all.^[12] AI founder John McCarthy objects to the moralizing tone of Weizenbaum's critique. "When moralizing is both vehement and vague, it invites authoritarian abuse," he writes.

Bill Hibbard^[13] writes that "Human dignity requires that we strive to remove our ignorance of the nature of existence, and AI is necessary for that striving."

Transparency and open source

Bill Hibbard argues that because AI will have such a profound effect on humanity, AI developers are representatives of future humanity and thus have an ethical obligation to be transparent in their efforts.^[14] Ben Goertzel and David Hart created OpenCog as an open source framework for AI development.^[15] OpenAI is a non-profit AI research company created by Elon Musk, Sam Altman and others to develop open source AI beneficial to humanity.^[16] There are numerous other open source AI developments.

Weaponization of artificial intelligence

Some experts and academics have questioned the use of robots for military combat, especially when such robots are given some degree of autonomous functions.^[17][18] The US Navy has funded a report which indicates that as military robots become more complex, there should be greater attention to implications of their ability to make autonomous decisions.^[19][20] One researcher states that autonomous robots might be more humane, as they could make decisions more effectively.^{[citation needed]}

Within this last decade, there has been intensive research in autonomous power with the ability to learn using assigned moral responsibilities. "The results may be used when designing future military robots, to control unwanted tendencies to assign responsibility to the robots."^[21] From a consequentialist view, there is a chance that robots will develop the ability to make their own logical decisions on who to kill and that is why there should be a set moral framework that the A.I cannot override.

There has been a recent outcry with regards to the engineering of artificial-intelligence weapons and has even fostered up ideas of a robot takeover of mankind. AI weapons do present a type of danger different from that of human controlled weapons. Many governments have begun to fund programs to develop AI weaponry. The United States Navy recently announced plans to develop autonomous drone weapons, paralleling similar announcements by Russia and Korea respectively. Due to the potential of AI weapons becoming more dangerous than human operated weapons, Stephen Hawking and Max Tegmark have signed a Future of Life petition to ban AI weapons. The message posted by Hawking and Tegmark states that AI weapons pose an immediate danger and that action is required to avoid catastrophic disasters in the near future.^[22]

"If any major military power pushes ahead with the AI weapon development, a global arms race is virtually inevitable, and the endpoint of this technological trajectory is obvious: autonomous weapons will become the Kalashnikovs of tomorrow", says the petition, which includes Skype co-founder Jaan Tallinn and MIT professor of linguistics Noam Chomsky as additional supporters against AI weaponry.^[23]

Physicist and Astronomer Royal Sir Martin Rees warned of catastrophic instances like "dumb robots going rogue or a network that develops a mind of its own." Huw Price, a colleague of Rees at Cambridge, has voiced a similar warning that humans may not survive when intelligence "escapes the constraints of biology." These two professors created the Centre for the Study of Existential Risk at Cambridge University in the hopes of avoiding this threat to human existence.^[22]

Regarding the potential for smarter-than-human systems to be employed militarily, the Open Philanthropy Project writes that this scenario "seem potentially as important as the risks related to loss of control", but that research organizations investigating AI's long-run social impact have spent relatively little time on this concern: "this class of scenarios has not been a major focus for the organizations that have been most active in this space, such as the Machine Intelligence Research Institute (MIRI) and the Future of Humanity Institute (FHI), and there seems to have been less analysis and debate regarding them".^[24]

Machine ethics

Machine ethics (or machine morality) is the field of research concerned with designing Artificial Moral Agents (AMAs), robots or artificially intelligent computers that behave morally or as though moral.^{[25][26][27][28]}

Isaac Asimov considered the issue in the 1950s in his I, Robot. At the insistence of his editor John W. Campbell Jr., he proposed the Three Laws of Robotics to govern artificially intelligent systems. Much of his work was then spent testing the boundaries of his three laws to see where they would break down, or where they would create paradoxical or unanticipated behavior. His work suggests that no set of fixed laws can sufficiently anticipate all possible circumstances.^[29]

In 2009, during an experiment at the Laboratory of Intelligent Systems in the Ecole Polytechnique Fédérale of Lausanne in Switzerland, robots that were programmed to cooperate with each other (in searching out a beneficial resource and avoiding a poisonous one) eventually learned to lie to each other in an attempt to hoard the beneficial resource.^[30] One problem in this case may have been that the goals were "terminal" (i.e. in contrast, ultimate human motives typically have a quality of requiring never-ending learning).^[31]

Some experts and academics have questioned the use of robots for military combat, especially when such robots are given some degree of autonomous functions.^[17] The US Navy has funded a report which indicates that as military robots become more complex, there should be greater attention to implications of their ability to make autonomous decisions.^[32][33] The President of the Association for the Advancement of Artificial Intelligence has commissioned a study to look at this issue.^[34] They point to programs like the Language Acquisition Device which can emulate human interaction.

Vernor Vinge has suggested that a moment may come when some computers are smarter than humans. He calls this "the Singularity."^[35] He suggests that it may be somewhat or possibly very dangerous for humans.^[36] This is discussed by a philosophy called Singularitarianism. The Machine Intelligence Research Institute has suggested a need to build "Friendly AI", meaning that the advances which are already occurring with AI should also include an effort to make AI intrinsically friendly and humane.^[37]

In 2009, academics and technical experts attended a conference organized by the Association for the Advancement of Artificial Intelligence to discuss the potential impact of robots and computers and the impact of the hypothetical possibility that they could become self-sufficient and able to make their own decisions. They discussed the possibility and the extent to which computers and robots might be able to acquire any level of autonomy, and to what degree they could use such abilities to possibly pose any threat or hazard. They noted that some machines have acquired various forms of semi-autonomy, including being able to find power sources on their own and being able to independently choose targets to attack with weapons. They also noted that some computer viruses can evade elimination and have achieved "cockroach intelligence." They noted that self-awareness as depicted in science-fiction is probably unlikely, but that there were other potential hazards and pitfalls.^[35]

However, there is one technology in particular that could truly bring the possibility of robots with moral competence to reality. In a paper on the acquisition of moral values by robots, Nayef Al-Rodhan mentions the case of neuromorphic chips, which aim to process information similarly to humans, nonlinearly and with millions of interconnected artificial neurons.^[38] Robots embedded with neuromorphic technology could learn and develop knowledge in a uniquely humanlike way. Inevitably, this raises the question of the environment in which such robots would learn about the world and whose morality they would inherit - or if they end up developing human 'weaknesses' as well: selfishness, a pro-survival attitude, hesitation etc.

In Moral Machines: Teaching Robots Right from Wrong,^[39] Wendell Wallach and Colin Allen conclude that attempts to teach robots right from wrong will likely advance understanding of human ethics by motivating humans to address gaps in modern normative theory and by providing a platform for experimental investigation. As one example, it has introduced normative ethicists to the controversial issue of which specific learning algorithms to use in machines. Nick Bostrom and Eliezer Yudkowsky have argued for decision trees (such as ID3) over neural networks and genetic algorithms on the grounds that decision trees obey modern social norms of transparency and predictability (e.g. stare decisis),^[40] while Chris Santos-Lang argued in the opposite direction on the grounds that the norms of any age must be allowed to change and that natural failure to fully satisfy these particular norms has been essential in making humans less vulnerable to criminal "hackers".^[31]

Unintended consequences

Many researchers have argued that, by way of an "intelligence explosion" sometime in the 21st century, a self-improving AI could become so vastly more powerful than humans that we would not be able to stop it from achieving its goals.^[41] In his paper "Ethical Issues in Advanced Artificial Intelligence," philosopher Nick Bostrom argues that artificial intelligence has the capability to bring about human extinction. He claims that general super-intelligence would be capable of independent initiative and of making its own plans, and may therefore be more appropriately thought of as an autonomous agent. Since artificial intellects need not share our human motivational tendencies, it would be up to the designers of the super-intelligence to specify its original motivations. In theory, a super-intelligent AI would be able to bring about almost any possible outcome and to thwart any attempt to prevent the implementation of its top goal, many uncontrolled unintended consequences could arise. It could kill off all other agents, persuade them to change their behavior, or block their attempts at interference.^[42]

However, instead of overwhelming the human race and leading to our destruction, Bostrom has also asserted that super-intelligence can help us solve many difficult problems such as disease, poverty, and environmental destruction, and could help us to “enhance” ourselves.^[43]

The sheer complexity of human value systems makes it very difficult to make AI's motivations human-friendly.^[41][42] Unless moral philosophy provides us with a flawless ethical theory, an AI's utility function could allow for many potentially harmful scenarios that conform with a given ethical framework but not "common sense". According to Eliezer Yudkowsky, there is little reason to suppose that an artificially designed mind would have such an adaptation.^[44]

Bill Hibbard^[13] proposes an AI design that avoids several types of unintended AI behavior including self-delusion, unintended instrumental actions, and corruption of the reward generator.

Organizations

Amazon, Google, Facebook, IBM, and Microsoft have established a non-profit partnership to formulate best practices on artificial intelligence technologies, advance the public's understanding, and to serve as a platform about artificial intelligence. They stated: "This partnership on AI will conduct research, organize discussions, provide thought leadership, consult with relevant third parties, respond to questions from the public and media, and create educational material that advance the understanding of AI technologies including machine perception, learning, and automated reasoning."^[45] Apple joined other tech companies as a founding member of the Partnership on AI in January 2017. The corporate members will make financial and research contributions to the group, while engaging with the scientific community to bring academics onto the board.^[46]

In fiction

The movie The Thirteenth Floor suggests a future where simulated worlds with sentient inhabitants are created by computer game consoles for the purpose of entertainment. The movie The Matrix suggests a future where the dominant species on planet Earth are sentient machines and humanity is treated with utmost Speciesism. The short story "The Planck Dive" suggest a future where humanity has turned itself into software that can be duplicated and optimized and the relevant distinction between types of software is sentient and non-sentient. The same idea can be found in the Emergency Medical Hologram of Starship Voyager, which is an apparently sentient copy of a reduced subset of the consciousness of its creator, Dr. Zimmerman, who, for the best motives, has created the system to give medical assistance in case of emergencies. The movies Bicentennial Man and A.I. deal with the possibility of sentient robots that could love. I, Robot explored some aspects of Asimov's three laws. All these scenarios try to foresee possibly unethical consequences of the creation of sentient computers.^{[citation needed]}

The ethics of artificial intelligence is one of several core themes in BioWare's Mass Effect series of games.^{[citation needed]} It explores the scenario of a civilization accidentally creating AI through a rapid increase in computational power through a global scale neural network. This event caused an ethical schism between those who felt bestowing organic rights upon the newly sentient Geth was appropriate and those who continued to see them as disposable machinery and fought to destroy them. Beyond the initial conflict, the complexity of the relationship between the machines and their creators is another ongoing theme throughout the story.

Over time, debates have tended to focus less and less on possibility and more on desirability,^{[citation needed]} as emphasized in the "Cosmist" and "Terran" debates initiated by Hugo de Garis and Kevin Warwick. A Cosmist, according to Hugo de Garis, is actually seeking to build more intelligent successors to the human species.