Parity (physics)

From Wikipedia, the free encyclopedia

In quantum mechanics, a parity transformation (also called parity inversion) is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates (a point reflection):

${\displaystyle \mathbf {P} :{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\-y\\-z\end{pmatrix}}.}$

It can also be thought of as a test for chirality of a physical phenomenon, in that a parity inversion transforms a phenomenon into its mirror image. All fundamental interactions of elementary particles, with the exception of the weak interaction, are symmetric under parity. The weak interaction is chiral and thus provides a means for probing chirality in physics. In interactions that are symmetric under parity, such as electromagnetism in atomic and molecular physics, parity serves as a powerful controlling principle underlying quantum transitions.

A matrix representation of P (in any number of dimensions) has determinant equal to −1, and hence is distinct from a rotation, which has a determinant equal to 1. In a two-dimensional plane, a simultaneous flip of all coordinates in sign is not a parity transformation; it is the same as a 180°-rotation.

In quantum mechanics, wave functions which are unchanged by a parity transformation are described as even functions, while those which change sign under a parity transformation are odd functions.

Simple symmetry relations

Under rotations, classical geometrical objects can be classified into scalars, vectors, and tensors of higher rank. In classical physics, physical configurations need to transform under representations of every symmetry group.

Quantum theory predicts that states in a Hilbert space do not need to transform under representations of the group of rotations, but only under projective representations. The word projective refers to the fact that if one projects out the phase of each state, where we recall that the overall phase of a quantum state is not an observable, then a projective representation reduces to an ordinary representation. All representations are also projective representations, but the converse is not true, therefore the projective representation condition on quantum states is weaker than the representation condition on classical states.

The projective representations of any group are isomorphic to the ordinary representations of a central extension of the group. For example, projective representations of the 3-dimensional rotation group, which is the special orthogonal group SO(3), are ordinary representations of the special unitary group SU(2) (see Representation theory of SU(2)). Projective representations of the rotation group that are not representations are called spinors, and so quantum states may transform not only as tensors but also as spinors.

If one adds to this a classification by parity, these can be extended, for example, into notions of

• scalars (P = +1) and pseudoscalars (P = −1) which are rotationally invariant.
• vectors (P = −1) and axial vectors (also called pseudovectors) (P = +1) which both transform as vectors under rotation.

One can define reflections such as

${\displaystyle V_{x}:{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\y\\z\end{pmatrix}},}$

which also have negative determinant and form a valid parity transformation. Then, combining them with rotations (or successively performing x-, y-, and z-reflections) one can recover the particular parity transformation defined earlier. The first parity transformation given does not work in an even number of dimensions, though, because it results in a positive determinant. In odd number of dimensions only the latter example of a parity transformation (or any reflection of an odd number of coordinates) can be used.

Parity forms the abelian group ${\displaystyle \mathbb {Z} _{2}}$ due to the relation ${\displaystyle {\hat {\mathcal {P}}}^{2}={\hat {1}}}$. All Abelian groups have only one-dimensional irreducible representations. For ${\displaystyle \mathbb {Z} _{2}}$, there are two irreducible representations: one is even under parity, ${\displaystyle {\hat {\mathcal {P}}}\phi =+\phi }$, the other is odd, ${\displaystyle {\hat {\mathcal {P}}}\phi =-\phi }$. These are useful in quantum mechanics. However, as is elaborated below, in quantum mechanics states need not transform under actual representations of parity but only under projective representations and so in principle a parity transformation may rotate a state by any phase.

Classical mechanics

Newton's equation of motion ${\displaystyle {\vec {F}}=m\,{\vec {a}}}$ (if the mass is constant) equates two vectors, and hence is invariant under parity. The law of gravity also involves only vectors and is also, therefore, invariant under parity.

However, angular momentum ${\displaystyle {\vec {L}}}$ is an axial vector,

${\displaystyle {\vec {L}}={\vec {r}}\times {\vec {p}}}$,

${\displaystyle {\hat {P}}\left({\vec {L}}\right)=-\,{\vec {r}}\times -\,{\vec {p}}={\vec {L}}}$.

In classical electrodynamics, the charge density ${\displaystyle \rho }$ is a scalar, the electric field, ${\displaystyle {\vec {E}}}$, and current ${\displaystyle {\vec {j}}}$ are vectors, but the magnetic field, ${\displaystyle {\vec {H}}}$ is an axial vector. However, Maxwell's equations are invariant under parity because the curl of an axial vector is a vector.

Effect of spatial inversion on some variables of classical physics

Even

Classical variables, predominantly scalar quantities, which do not change upon spatial inversion include:

${\displaystyle \ t}$, the time when an event occurs

${\displaystyle \ m}$, the mass of a particle

${\displaystyle \ E}$, the energy of the particle

${\displaystyle \ P}$, power (rate of work done)

${\displaystyle \ \rho }$, the electric charge density

${\displaystyle \ V}$, the electric potential (voltage)

${\displaystyle \ \rho }$, energy density of the electromagnetic field

${\displaystyle \mathbf {L} }$, the angular momentum of a particle (both orbital and spin) (axial vector)

${\displaystyle \mathbf {B} }$, the magnetic field (axial vector)

${\displaystyle \mathbf {H} }$, the auxiliary magnetic field

${\displaystyle \mathbf {M} }$, the magnetization

${\displaystyle \ T_{ij}}$ Maxwell stress tensor.

All masses, charges, coupling constants, and other physical constants, except those associated with the weak force

Odd

Classical variables, predominantly vector quantities, which have their sign flipped by spatial inversion include:

${\displaystyle \ h}$, the helicity

${\displaystyle \ \Phi }$, the magnetic flux

${\displaystyle \mathbf {x} }$, the position of a particle in three-space

${\displaystyle \mathbf {v} }$, the velocity of a particle

${\displaystyle \mathbf {a} }$, the acceleration of the particle

${\displaystyle \mathbf {p} }$, the linear momentum of a particle

${\displaystyle \mathbf {F} }$, the force exerted on a particle

${\displaystyle \mathbf {J} }$, the electric current density

${\displaystyle \mathbf {E} }$, the electric field

${\displaystyle \mathbf {D} }$, the electric displacement field

${\displaystyle \mathbf {P} }$, the electric polarization

${\displaystyle \mathbf {A} }$, the electromagnetic vector potential

${\displaystyle \mathbf {S} }$, Poynting vector.

Quantum mechanics

Possible eigenvalues

Two dimensional representations of parity are given by a pair of quantum states which go into each other under parity. However, this representation can always be reduced to linear combinations of states, each of which is either even or odd under parity. One says that all irreducible representations of parity are one-dimensional.

In quantum mechanics, spacetime transformations act on quantum states. The parity transformation, ${\displaystyle {\hat {\mathcal {P}}}}$, is a unitary operator, in general acting on a state ${\displaystyle \psi }$ as follows: ${\displaystyle {\hat {\mathcal {P}}}\,\psi _{\left(r\right)}=e^{\frac {i\phi }{2}}\psi _{\left(-r\right)}}$.

One must then have ${\displaystyle {\hat {\mathcal {P}}}^{2}\,\psi _{\left(r\right)}=e^{i\phi }\psi _{\left(r\right)}}$, since an overall phase is unobservable. The operator ${\displaystyle {\hat {\mathcal {P}}}^{2}}$, which reverses the parity of a state twice, leaves the spacetime invariant, and so is an internal symmetry which rotates its eigenstates by phases ${\displaystyle e^{i\phi }}$. If ${\displaystyle {\hat {\mathcal {P}}}^{2}}$ is an element ${\displaystyle e^{iQ}}$ of a continuous U(1) symmetry group of phase rotations, then ${\displaystyle e^{-iQ}}$is part of this U(1) and so is also a symmetry. In particular, we can define ${\displaystyle {\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{\frac {iQ}{2}}}}$, which is also a symmetry, and so we can choose to call ${\displaystyle {\hat {\mathcal {P}}}'}$ our parity operator, instead of ${\displaystyle {\hat {\mathcal {P}}}^{2}}$. Note that ${\displaystyle {{\hat {\mathcal {P}}}'}^{2}=1}$ and so ${\displaystyle {\hat {\mathcal {P}}}'}$ has eigenvalues ${\displaystyle \pm 1}$. Wave functions with eigenvalue +1 under a parity transformation are even functions, while eigenvalue -1 corresponds to odd functions.^[1] However, when no such symmetry group exists, it may be that all parity transformations have some eigenvalues which are phases other than ${\displaystyle \pm 1}$.

For electronic wavefunctions, even states are usually indicated by a subscript g for gerade (German: even) and odd states by a subscript u for ungerade (German: odd). For example, the lowest energy level of the hydrogen molecule ion (H₂⁺) is labelled ${\displaystyle 1\sigma _{g}}$ and the next-closest (higher) energy level is labelled ${\displaystyle 1\sigma _{u}}$.^[2]

The wave functions of a particle moving into an external potential, which is centrosymmetric (potential energy invariant with respect to a space inversion, symmetric to the origin), either remain invariable or change signs: these two possible states are called the even state or odd state of the wave functions.^[3]

The law of conservation of parity of particle (not true for the beta decay of nuclei^[4]) states that, if an isolated ensemble of particles has a definite parity, then the parity remains invariable in the process of ensemble evolution.

The parity of the states of a particle moving in a spherically symmetric external field is determined by the angular momentum, and the particle state is defined by three quantum numbers: total energy, angular momentum and the projection of angular momentum.^[3]

Consequences of parity symmetry

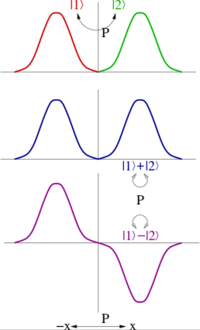
When parity generates the Abelian group ℤ₂, one can always take linear combinations of quantum states such that they are either even or odd under parity (see the figure). Thus the parity of such states is ±1. The parity of a multiparticle state is the product of the parities of each state; in other words parity is a multiplicative quantum number.

In quantum mechanics, Hamiltonians are invariant (symmetric) under a parity transformation if ${\displaystyle {\hat {\mathcal {P}}}}$ commutes with the Hamiltonian. In non-relativistic quantum mechanics, this happens for any potential which is scalar, i.e., ${\displaystyle V=V{\left(r\right)}}$, hence the potential is spherically symmetric. The following facts can be easily proven:

• If ${\displaystyle \left|\varphi \right\rangle }$ and ${\displaystyle \left|\psi \right\rangle }$ have the same parity, then ${\displaystyle \left\langle \varphi \right|{\hat {X}}\left|\psi \right\rangle =0}$ where ${\displaystyle {\hat {X}}}$ is the position operator.
• For a state ${\displaystyle \left|{\vec {L}},L_{z}\right\rangle }$ of orbital angular momentum ${\displaystyle {\vec {L}}}$ with z-axis projection ${\displaystyle L_{z}}$, then ${\displaystyle {\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle }$.
• If ${\displaystyle \left[{\hat {H}},{\hat {P}}\right]=0}$, then atomic dipole transitions only occur between states of opposite parity.^[5]
• If ${\displaystyle \left[{\hat {H}},{\hat {P}}\right]=0}$, then a non-degenerate eigenstate of ${\displaystyle {\hat {H}}}$ is also an eigenstate of the parity operator; i.e., a non-degenerate eigenfunction of ${\displaystyle {\hat {H}}}$ is either invariant to ${\displaystyle {\hat {\mathcal {P}}}}$ or is changed in sign by ${\displaystyle {\hat {\mathcal {P}}}}$.

Some of the non-degenerate eigenfunctions of ${\displaystyle {\hat {H}}}$ are unaffected (invariant) by parity ${\displaystyle {\hat {\mathcal {P}}}}$ and the others will be merely reversed in sign when the Hamiltonian operator and the parity operator commute:

${\displaystyle {\hat {\mathcal {P}}}\left|\psi \right\rangle =c\left|\psi \right\rangle }$,

where ${\displaystyle c}$ is a constant, the eigenvalue of ${\displaystyle {\hat {\mathcal {P}}}}$,

${\displaystyle {\hat {\mathcal {P}}}^{2}\left|\psi \right\rangle =c\,{\hat {\mathcal {P}}}\left|\psi \right\rangle }$.

Many-particle systems: atoms, molecules, nuclei

The overall parity of a many-particle system is the product of the parities of the one-particle states. It is -1 if an odd number of particles are in odd-parity states, and +1 otherwise. Different notations are in use to denote the parity of nuclei, atoms, and molecules.

Atoms

Atomic orbitals have parity (-1)^ℓ, where the exponent ℓ is the azimuthal quantum number. The parity is odd for orbitals p, f, ... with ℓ = 1, 3, ..., and an atomic state has odd parity if an odd number of electrons occupy these orbitals. For example, the ground state of the nitrogen atom has the electron configuration 1s²2s²2p³, and is identified by the term symbol ⁴S^o, where the superscript o denotes odd parity. However the third excited term at about 83,300 cm⁻¹ above the ground state has electron configuration 1s²2s²2p²3s has even parity since there are only two 2p electrons, and its term symbol is ⁴P (without an o superscript).^[6]

Molecules

Only some molecules have a centre of symmetry, including all homonuclear diatomic molecules as well as certain symmetric molecules including ethylene, benzene, xenon tetrafluoride and sulphur hexafluoride. For such centrosymmetric molecules, the parity each molecular orbital is either g (gerade or even) or u (ungerade or odd). An electronic state is u if and only if it contains an odd number of electrons in u orbitals.

For molecules with no centre of symmetry, including all heteronuclear diatomics as well as the majority of polyatomics, inversion is not a symmetry operation and the orbitals and states cannot be described as even or odd.

Nuclei

In atomic nuclei, the state of each nucleon (proton or nucleon) has even or odd parity, and nucleon configurations can be predicted using the nuclear shell model. As for electrons in atoms, the nucleon state has odd overall parity if and only if the number of nucleons in odd-parity states is odd. The parity is usually written as a + (even) or – (odd) following the nuclear spin value. For example the isotopes of oxygen include ¹⁷O(5/2+), meaning that the spin is 5/2 and the parity is even. The shell model explains this because the first 16 nucleons are paired so that each pair has spin zero and even parity, and the last nucleon is in the 1d_5/2 shell which has even parity since ℓ = 2 for a d orbital.^[7]

Quantum field theory

The intrinsic parity assignments in this section are true for relativistic quantum mechanics as well as quantum field theory.

If we can show that the vacuum state is invariant under parity, ${\displaystyle {\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle }$, the Hamiltonian is parity invariant ${\displaystyle \left[{\hat {H}},{\hat {\mathcal {P}}}\right]}$ and the quantization conditions remain unchanged under parity, then it follows that every state has good parity, and this parity is conserved in any reaction.

To show that quantum electrodynamics is invariant under parity, we have to prove that the action is invariant and the quantization is also invariant. For simplicity we will assume that canonical quantization is used; the vacuum state is then invariant under parity by construction. The invariance of the action follows from the classical invariance of Maxwell's equations. The invariance of the canonical quantization procedure can be worked out, and turns out to depend on the transformation of the annihilation operator^{[citation needed]}:

Pa(p, ±)P⁺ = −a(−p, ±)

where p denotes the momentum of a photon and ± refers to its polarization state. This is equivalent to the statement that the photon has odd intrinsic parity. Similarly all vector bosons can be shown to have odd intrinsic parity, and all axial-vectors to have even intrinsic parity.

There is a straightforward extension of these arguments to scalar field theories which shows that scalars have even parity, since

Pa(p)P⁺ = a(−p).

This is true even for a complex scalar field. (Details of spinors are dealt with in the article on the Dirac equation, where it is shown that fermions and antifermions have opposite intrinsic parity.)

With fermions, there is a slight complication because there is more than one spin group.

Parity in the standard model

Fixing the global symmetries

In the Standard Model of fundamental interactions there are precisely three global internal U(1) symmetry groups available, with charges equal to the baryon number B, the lepton number L and the electric charge Q. The product of the parity operator with any combination of these rotations is another parity operator. It is conventional to choose one specific combination of these rotations to define a standard parity operator, and other parity operators are related to the standard one by internal rotations. One way to fix a standard parity operator is to assign the parities of three particles with linearly independent charges B, L and Q. In general one assigns the parity of the most common massive particles, the proton, the neutron and the electron, to be +1.

Steven Weinberg has shown that if P² = (−1)^F, where F is the fermion number operator, then, since the fermion number is the sum of the lepton number plus the baryon number, F = B + L, for all particles in the Standard Model and since lepton number and baryon number are charges Q of continuous symmetries e^iQ, it is possible to redefine the parity operator so that P² = 1. However, if there exist Majorana neutrinos, which experimentalists today believe is possible, their fermion number is equal to one because they are neutrinos while their baryon and lepton numbers are zero because they are Majorana, and so (−1)^F would not be embedded in a continuous symmetry group. Thus Majorana neutrinos would have parity ±i.

Parity of the pion

In 1954, a paper by William Chinowsky and Jack Steinberger demonstrated that the pion has negative parity.^[8] They studied the decay of an "atom" made from a deuteron (²
₁H⁺) and a negatively charged pion (
π⁻) in a state with zero orbital angular momentum ${\displaystyle L=0}$ into two neutrons (${\displaystyle n}$).

Neutrons are fermions and so obey Fermi–Dirac statistics, which implies that the final state is antisymmetric. Using the fact that the deuteron has spin one and the pion spin zero together with the antisymmetry of the final state they concluded that the two neutrons must have orbital angular momentum ${\displaystyle L=1}$. The total parity is the product of the intrinsic parities of the particles and the extrinsic parity of the spherical harmonic function ${\displaystyle \left(-1\right)^{L}}$. Since the orbital momentum changes from zero to one in this process, if the process is to conserve the total parity then the products of the intrinsic parities of the initial and final particles must have opposite sign. A deuteron nucleus is made from a proton and a neutron, and so using the aforementioned convention that protons and neutrons have intrinsic parities equal to ${\displaystyle +1}$ they argued that the parity of the pion is equal to minus the product of the parities of the two neutrons divided by that of the proton and neutron in the deuteron, explicitly ${\displaystyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1}$. Thus they concluded that the pion is a pseudoscalar particle.

Parity violation

Top: P-symmetry: A clock built like its mirrored image will behave like the mirrored image of the original clock.
Bottom: P-asymmetry: A clock built like its mirrored image will not behave like the mirrored image of the original clock.

Although parity is conserved in electromagnetism, strong interactions and gravity, it turns out to be violated in weak interactions. The Standard Model incorporates parity violation by expressing the weak interaction as a chiral gauge interaction. Only the left-handed components of particles and right-handed components of antiparticles participate in weak interactions in the Standard Model. This implies that parity is not a symmetry of our universe, unless a hidden mirror sector exists in which parity is violated in the opposite way.

By the mid-20th century, it had been suggested by several scientists that parity might not be conserved (in different contexts), but without solid evidence these suggestions were not considered important. Then, in 1956, a careful review and analysis by theoretical physicists Tsung Dao Lee and Chen Ning Yang^[9] went further, showing that while parity conservation had been verified in decays by the strong or electromagnetic interactions, it was untested in the weak interaction. They proposed several possible direct experimental tests. They were mostly ignored,^{[citation needed]} but Lee was able to convince his Columbia colleague Chien-Shiung Wu to try it.^{[citation needed]} She needed special cryogenic facilities and expertise, so the experiment was done at the National Bureau of Standards.

In 1957 Wu, E. Ambler, R. W. Hayward, D. D. Hoppes, and R. P. Hudson found a clear violation of parity conservation in the beta decay of cobalt-60.^[10] As the experiment was winding down, with double-checking in progress, Wu informed Lee and Yang of their positive results, and saying the results need further examination, she asked them not to publicize the results first. However, Lee revealed the results to his Columbia colleagues on 4 January 1957 at a "Friday Lunch" gathering of the Physics Department of Columbia. Three of them, R. L. Garwin, Leon Lederman, and R. Weinrich modified an existing cyclotron experiment, and they immediately verified the parity violation.^[11] They delayed publication of their results until after Wu's group was ready, and the two papers appeared back to back in the same physics journal.

After the fact, it was noted that an obscure 1928 experiment had in effect reported parity violation in weak decays, but since the appropriate concepts had not yet been developed, those results had no impact.^[12] The discovery of parity violation immediately explained the outstanding τ–θ puzzle in the physics of kaons.

In 2010, it was reported that physicists working with the Relativistic Heavy Ion Collider (RHIC) had created a short-lived parity symmetry-breaking bubble in quark-gluon plasmas. An experiment conducted by several physicists including Yale's Jack Sandweiss as part of the STAR collaboration, suggested that parity may also be violated in the strong interaction.^[13]

Intrinsic parity of hadrons

To every particle one can assign an intrinsic parity as long as nature preserves parity. Although weak interactions do not, one can still assign a parity to any hadron by examining the strong interaction reaction that produces it, or through decays not involving the weak interaction, such as rho meson decay to pions.

Flatness problem

From Wikipedia, the free encyclopedia

The local geometry of the universe is determined by whether the relative density Ω is less than, equal to or greater than 1. From top to bottom: a spherical universe with greater than critical density (Ω>1, k>0); a hyperbolic, underdense universe (Ω<1 a="" and="" critical="" density="" diagrams="" div="" exactly="" flat="" four-dimensional.="" is="" k="0)." spahe="" the="" universe="" unlike="" with="">

The flatness problem is a cosmological fine-tuning problem within the Big Bang model of the universe. Such problems arise from the observation that some of the initial conditions of the universe appear to be fine-tuned to very 'special' values, and that small deviations from these values would have extreme effects on the appearance of the universe at the current time.

In the case of the flatness problem, the parameter which appears fine-tuned is the density of matter and energy in the universe. This value affects the curvature of space-time, with a very specific critical value being required for a flat universe. The current density of the universe is observed to be very close to this critical value. Since the total density departs rapidly from the critical value over cosmic time,^[1] the early universe must have had a density even closer to the critical density, departing from it by one part in 10⁶² or less. This leads cosmologists to question how the initial density came to be so closely fine-tuned to this 'special' value.

The problem was first mentioned by Robert Dicke in 1969.^{[2]:62,[3]:61} The most commonly accepted solution among cosmologists is cosmic inflation, the idea that the universe went through a brief period of extremely rapid expansion in the first fraction of a second after the Big Bang; along with the monopole problem and the horizon problem, the flatness problem is one of the three primary motivations for inflationary theory.^[4]

Energy density and the Friedmann equation

According to Einstein's field equations of general relativity, the structure of spacetime is affected by the presence of matter and energy. On small scales space appears flat – as does the surface of the Earth if one looks at a small area. On large scales however, space is bent by the gravitational effect of matter. Since relativity indicates that matter and energy are equivalent, this effect is also produced by the presence of energy (such as light and other electromagnetic radiation) in addition to matter. The amount of bending (or curvature) of the universe depends on the density of matter/energy present.

This relationship can be expressed by the first Friedmann equation. In a universe without a cosmological constant, this is:

${\displaystyle H^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}}$

Here ${\displaystyle H}$ is the Hubble parameter, a measure of the rate at which the universe is expanding. ${\displaystyle \rho }$ is the total density of mass and energy in the universe, ${\displaystyle a}$ is the scale factor (essentially the 'size' of the universe), and ${\displaystyle k}$ is the curvature parameter — that is, a measure of how curved spacetime is. A positive, zero or negative value of ${\displaystyle k}$ corresponds to a respectively closed, flat or open universe. The constants ${\displaystyle G}$ and ${\displaystyle c}$ are Newton's gravitational constant and the speed of light, respectively.

Cosmologists often simplify this equation by defining a critical density, ${\displaystyle \rho _{c}}$. For a given value of ${\displaystyle H}$, this is defined as the density required for a flat universe, i.e. ${\displaystyle k=0}$. Thus the above equation implies

${\displaystyle \rho _{c}={\frac {3H^{2}}{8\pi G}}}$.

Since the constant ${\displaystyle G}$ is known and the expansion rate ${\displaystyle H}$ can be measured by observing the speed at which distant galaxies are receding from us, ${\displaystyle \rho _{c}}$ can be determined. Its value is currently around 10⁻²⁶ kg m⁻³. The ratio of the actual density to this critical value is called Ω, and its difference from 1 determines the geometry of the universe: Ω > 1 corresponds to a greater than critical density, ${\displaystyle \rho >\rho _{c}}$, and hence a closed universe. Ω < 1 gives a low density open universe, and Ω equal to exactly 1 gives a flat universe.

The Friedmann equation,

${\displaystyle {\frac {3a^{2}}{8\pi G}}H^{2}=\rho a^{2}-{\frac {3kc^{2}}{8\pi G}},}$

can be re-arranged into

${\displaystyle \rho _{c}a^{2}-\rho a^{2}=-{\frac {3kc^{2}}{8\pi G}},}$

which after factoring ${\displaystyle \rho a^{2}}$, and using ${\displaystyle \Omega =\rho /\rho _{c}}$, leads to

${\displaystyle (\Omega ^{-1}-1)\rho a^{2}={\frac {-3kc^{2}}{8\pi G}}.}$^[5]

The right hand side of the last expression above contains constants only and therefore the left hand side must remain constant throughout the evolution of the universe.

As the universe expands the scale factor ${\displaystyle a}$ increases, but the density ${\displaystyle \rho }$ decreases as matter (or energy) becomes spread out. For the standard model of the universe which contains mainly matter and radiation for most of its history, ${\displaystyle \rho }$ decreases more quickly than ${\displaystyle a^{2}}$ increases, and so the factor ${\displaystyle \rho a^{2}}$ will decrease. Since the time of the Planck era, shortly after the Big Bang, this term has decreased by a factor of around ${\displaystyle 10^{60},}$^[5] and so ${\displaystyle (\Omega ^{-1}-1)}$ must have increased by a similar amount to retain the constant value of their product.

Current value of Ω

The relative density Ω against cosmic time t (neither axis to scale). Each curve represents a possible universe: note that Ω diverges rapidly from 1. The blue curve is a universe similar to our own, which at the present time (right of the graph) has a small |Ω − 1| and therefore must have begun with Ω very close to 1 indeed. The red curve is a hypothetical different universe in which the initial value of Ω differed slightly too much from 1: by the present day it has diverged extremely and would not be able to support galaxies, stars or planets.

Measurement

The value of Ω at the present time is denoted Ω₀. This value can be deduced by measuring the curvature of spacetime (since Ω = 1, or ${\displaystyle \rho =\rho _{c}}$, is defined as the density for which the curvature k = 0). The curvature can be inferred from a number of observations.

One such observation is that of anisotropies (that is, variations with direction - see below) in the Cosmic Microwave Background (CMB) radiation. The CMB is electromagnetic radiation which fills the universe, left over from an early stage in its history when it was filled with photons and a hot, dense plasma. This plasma cooled as the universe expanded, and when it cooled enough to form stable atoms it no longer absorbed the photons. The photons present at that stage have been propagating ever since, growing fainter and less energetic as they spread through the ever-expanding universe.

The temperature of this radiation is almost the same at all points on the sky, but there is a slight variation (around one part in 100,000) between the temperature received from different directions. The angular scale of these fluctuations - the typical angle between a hot patch and a cold patch on the sky^{[nb 1]} - depends on the curvature of the universe which in turn depends on its density as described above. Thus, measurements of this angular scale allow an estimation of Ω₀.^{[6][nb 2]}

Another probe of Ω₀ is the frequency of Type-Ia supernovae at different distances from Earth.^[7][8] These supernovae, the explosions of degenerate white dwarf stars, are a type of standard candle; this means that the processes governing their intrinsic brightness are well understood so that a measure of apparent brightness when seen from Earth can be used to derive accurate distance measures for them (the apparent brightness decreasing in proportion to the square of the distance - see luminosity distance). Comparing this distance to the redshift of the supernovae gives a measure of the rate at which the universe has been expanding at different points in history. Since the expansion rate evolves differently over time in cosmologies with different total densities, Ω₀ can be inferred from the supernovae data.

Data from the Wilkinson Microwave Anisotropy Probe (measuring CMB anisotropies) combined with that from the Sloan Digital Sky Survey and observations of type-Ia supernovae constrain Ω₀ to be 1 within 1%.^[9] In other words, the term |Ω − 1| is currently less than 0.01, and therefore must have been less than 10⁻⁶² at the Planck era.

Implication

This tiny value is the crux of the flatness problem. If the initial density of the universe could take any value, it would seem extremely surprising to find it so 'finely tuned' to the critical value ${\displaystyle \rho _{c}}$. Indeed, a very small departure of Ω from 1 in the early universe would have been magnified during billions of years of expansion to create a current density very far from critical. In the case of an overdensity (${\displaystyle \rho >\rho _{c}}$) this would lead to a universe so dense it would cease expanding and collapse into a Big Crunch (an opposite to the Big Bang in which all matter and energy falls back into an extremely dense state) in a few years or less; in the case of an underdensity (${\displaystyle \rho <\rho _{c}}$) it would expand so quickly and become so sparse it would soon seem essentially empty, and gravity would not be strong enough by comparison to cause matter to collapse and form galaxies. In either case the universe would contain no complex structures such as galaxies, stars, planets and any form of life.^[10]

This problem with the Big Bang model was first pointed out by Robert Dicke in 1969,^[11] and it motivated a search for some reason the density should take such a specific value.

Solutions to the problem

Some cosmologists agreed with Dicke that the flatness problem was a serious one, in need of a fundamental reason for the closeness of the density to criticality. But there was also a school of thought which denied that there was a problem to solve, arguing instead that since the universe must have some density it may as well have one close to ${\displaystyle \rho _{crit}}$ as far from it, and that speculating on a reason for any particular value was "beyond the domain of science".^[11] Enough cosmologists saw the problem as a real one, however, for various solutions to be proposed.

Anthropic principle

One solution to the problem is to invoke the anthropic principle, which states that humans should take into account the conditions necessary for them to exist when speculating about causes of the universe's properties. If two types of universe seem equally likely but only one is suitable for the evolution of intelligent life, the anthropic principle suggests that finding ourselves in that universe is no surprise: if the other universe had existed instead, there would be no observers to notice the fact.

The principle can be applied to solve the flatness problem in two somewhat different ways. The first (an application of the 'strong anthropic principle') was suggested by C. B. Collins and Stephen Hawking,^[12] who in 1973 considered the existence of an infinite number of universes such that every possible combination of initial properties was held by some universe. In such a situation, they argued, only those universes with exactly the correct density for forming galaxies and stars would give rise to intelligent observers such as humans: therefore, the fact that we observe Ω to be so close to 1 would be "simply a reflection of our own existence."^[12]

An alternative approach, which makes use of the 'weak anthropic principle', is to suppose that the universe is infinite in size, but with the density varying in different places (i.e. an inhomogeneous universe). Thus some regions will be over-dense (Ω > 1) and some under-dense (Ω < 1). These regions may be extremely far apart - perhaps so far that light has not had time to travel from one to another during the age of the universe (that is, they lie outside one another's cosmological horizons). Therefore, each region would behave essentially as a separate universe: if we happened to live in a large patch of almost-critical density we would have no way of knowing of the existence of far-off under- or over-dense patches since no light or other signal has reached us from them. An appeal to the anthropic principle can then be made, arguing that intelligent life would only arise in those patches with Ω very close to 1, and that therefore our living in such a patch is unsurprising.^[13]

This latter argument makes use of a version of the anthropic principle which is 'weaker' in the sense that it requires no speculation on multiple universes, or on the probabilities of various different universes existing instead of the current one. It requires only a single universe which is infinite - or merely large enough that many disconnected patches can form - and that the density varies in different regions (which is certainly the case on smaller scales, giving rise to galactic clusters and voids).

However, the anthropic principle has been criticised by many scientists.^[14] For example, in 1979 Bernard Carr and Martin Rees argued that the principle “is entirely post hoc: it has not yet been used to predict any feature of the Universe.”^[14][15] Others have taken objection to its philosophical basis, with Ernan McMullin writing in 1994 that "the weak Anthropic principle is trivial ... and the strong Anthropic principle is indefensible." Since many physicists and philosophers of science do not consider the principle to be compatible with the scientific method,^[14] another explanation for the flatness problem was needed.

Inflation

The standard solution to the flatness problem invokes cosmic inflation, a process whereby the universe expands exponentially quickly (i.e. ${\displaystyle a}$ grows as ${\displaystyle e^{\lambda t}}$ with time ${\displaystyle t}$, for some constant ${\displaystyle \lambda }$) during a short period in its early history. The theory of inflation was first proposed in 1979, and published in 1981, by Alan Guth.^[16][17] His two main motivations for doing so were the flatness problem and the horizon problem, another fine-tuning problem of physical cosmology.
The proposed cause of inflation is a field which permeates space and drives the expansion. The field contains a certain energy density, but unlike the density of the matter or radiation present in the late universe, which decrease over time, the density of the inflationary field remains roughly constant as space expands. Therefore, the term ${\displaystyle \rho a^{2}}$ increases extremely rapidly as the scale factor ${\displaystyle a}$ grows exponentially. Recalling the Friedmann Equation

${\displaystyle (\Omega ^{-1}-1)\rho a^{2}={\frac {-3kc^{2}}{8\pi G}}}$,

and the fact that the right-hand side of this expression is constant, the term ${\displaystyle |\Omega ^{-1}-1|}$ must therefore decrease with time.

Thus if ${\displaystyle |\Omega ^{-1}-1|}$ initially takes any arbitrary value, a period of inflation can force it down towards 0 and leave it extremely small - around ${\displaystyle 10^{-62}}$ as required above, for example. Subsequent evolution of the universe will cause the value to grow, bringing it to the currently observed value of around 0.01. Thus the sensitive dependence on the initial value of Ω has been removed: a large and therefore 'unsurprising' starting value need not become amplified and lead to a very curved universe with no opportunity to form galaxies and other structures.

This success in solving the flatness problem is considered one of the major motivations for inflationary theory.^[4][18]

Post inflation

Although inflationary theory is regarded as having had much success, and the evidence for it is compelling, it is not universally accepted: cosmologists recognize that there are still gaps in the theory and are open to the possibility that future observations will disprove it.^[19][20] In particular, in the absence of any firm evidence for what the field driving inflation should be, many different versions of the theory have been proposed.^[21] Many of these contain parameters or initial conditions which themselves require fine-tuning^[21] in much the way that the early density does without inflation.

For these reasons work is still being done on alternative solutions to the flatness problem. These have included non-standard interpretations of the effect of dark energy^[22] and gravity,^[23] particle production in an oscillating universe,^[24] and use of a Bayesian statistical approach to argue that the problem is non-existent. The latter argument, suggested for example by Evrard and Coles, maintains that the idea that Ω being close to 1 is 'unlikely' is based on assumptions about the likely distribution of the parameter which are not necessarily justified.^[25] Despite this ongoing work, inflation remains by far the dominant explanation for the flatness problem.^[1][4]

Einstein–Cartan theory

The flatness problem is naturally solved by the Einstein–Cartan–Sciama–Kibble theory of gravity, without an exotic form of matter required in inflationary theory.^[26][27] This theory extends general relativity by removing a constraint of the symmetry of the affine connection and regarding its antisymmetric part, the torsion tensor, as a dynamical variable. It has no free parameters. Including torsion gives the correct conservation law for the total (orbital plus intrinsic) angular momentum of matter in the presence of gravity. The minimal coupling between torsion and Dirac spinors obeying the nonlinear Dirac equation generates a spin-spin interaction which is significant in fermionic matter at extremely high densities. Such an interaction averts the unphysical big bang singularity, replacing it with a bounce at a finite minimum scale factor, before which the Universe was contracting. The rapid expansion immediately after the big bounce explains why the present Universe at largest scales appears spatially flat, homogeneous and isotropic. As the density of the Universe decreases, the effects of torsion weaken and the Universe smoothly enters the radiation-dominated era.