String field theory

From Wikipedia, the free encyclopedia

Jump to navigation Jump to search

String field theory (SFT) is a formalism in string theory in which the dynamics of relativistic strings is reformulated in the language of quantum field theory. This is accomplished at the level of perturbation theory by finding a collection of vertices for joining and splitting strings, as well as string propagators, that give a Feynman diagram-like expansion for string scattering amplitudes. In most string field theories, this expansion is encoded by a classical action found by second-quantizing the free string and adding interaction terms. As is usually the case in second quantization, a classical field configuration of the second-quantized theory is given by a wave function in the original theory. In the case of string field theory, this implies that a classical configuration, usually called the string field, is given by an element of the free string Fock space.

The principal advantages of the formalism are that it allows the computation of off-shell amplitudes and, when a classical action is available, gives non-perturbative information that cannot be seen directly from the standard genus expansion of string scattering. In particular, following the work of Ashoke Sen,^[1] it has been useful in the study of tachyon condensation on unstable D-branes. It has also had applications to topological string theory,^[2] non-commutative geometry,^[3] and strings in low dimensions.^[4]

String field theories come in a number of varieties depending on which type of string is second quantized: Open string field theories describe the scattering of open strings, closed string field theories describe closed strings, while open-closed string field theories include both open and closed strings.

In addition, depending on the method used to fix the worldsheet diffeomorphisms and conformal transformations in the original free string theory, the resulting string field theories can be very different. Using light cone gauge, yields light-cone string field theories whereas using BRST quantization, one finds covariant string field theories. There are also hybrid string field theories, known as covariantized light-cone string field theories which use elements of both light-cone and BRST gauge-fixed string field theories.^[5]

A final form of string field theory, known as background independent open string field theory, takes a very different form; instead of second quantizing the worldsheet string theory, it second quantizes the space of two-dimensional quantum field theories.^[6]

Light-cone string field theory

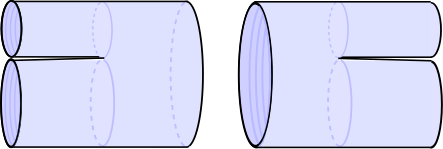
Light-cone string field theories were introduced by Stanley Mandelstam^[7] and developed by Mandelstam, Michael Green, John Schwarz and Lars Brink.^[8] An explicit description of the second-quantization of the light-cone string was given by Michio Kaku and Keiji Kikkawa.^[9]

Light-cone string field theories were the first string field theories to be constructed and are based on the simplicity of string scattering in light-cone gauge. For example, in the bosonic closed string case, the worldsheet scattering diagrams naturally take a Feynman diagram-like form, being built from two ingredients, a propagator,

and two vertices for splitting and joining strings, which can be used to glue three propagators together,

These vertices and propagators produce a single cover of the moduli space of ${\displaystyle n}$-point closed string scattering amplitudes so no higher order vertices are required.^[10] Similar vertices exist for the open string.

When one considers light-cone quantized superstrings, the discussion is more subtle as divergences can arise when the light-cone vertices collide.^[11] To produce a consistent theory, it is necessary to introduce higher order vertices, called contact terms, to cancel the divergences.

Light-cone string field theories have the disadvantage that they break manifest Lorentz invariance. However, in backgrounds with light-like killing vectors, they can considerably simplify the quantization of the string action. Moreover, until the advent of the Berkovits string^[12] it was the only known method for quantizing strings in the presence of Ramond–Ramond fields. In recent research, light-cone string field theory played an important role in understanding strings in pp-wave backgrounds.^[13]

Free covariant string field theory

An important step in the construction of covariant string field theories (preserving manifest Lorentz invariance) was the construction of a covariant kinetic term. This kinetic term can be considered a string field theory in its own right: the string field theory of free strings. Since the work of Warren Siegel,^[14] it has been standard to first BRST-quantize the free string theory and then second quantize so that the classical fields of the string field theory include ghosts as well as matter fields. For example, in the case of the bosonic open string theory in 26-dimensional flat spacetime, a general element of the Fock-space of the BRST quantized string takes the form (in radial quantization in the upper half plane),

${\displaystyle |\Psi \rangle =\int d^{26}p\left(T(p)c_{1}e^{ip\cdot X}|0\rangle +A_{\mu }(p)\partial X^{\mu }c_{1}e^{ip\cdot X}|0\rangle +\chi (p)c_{0}e^{ip\cdot X}|0\rangle +\ldots \right),}$

where ${\displaystyle |0\rangle }$ is the free string vacuum and the dots represent more massive fields. In the language of worldsheet string theory, ${\displaystyle T(p)}$, ${\displaystyle A_{\mu }(p)}$, and ${\displaystyle \chi (p)}$ represent the amplitudes for the string to be found in the various basis states. After second quantization, they are interpreted instead as classical fields representing the tachyon ${\displaystyle T}$, gauge field ${\displaystyle A_{\mu }}$ and a ghost field ${\displaystyle \chi }$.

In the worldsheet string theory, the unphysical elements of the Fock space are removed by imposing the condition ${\displaystyle Q_{B}|\Psi \rangle =0}$ as well as the equivalence relation ${\displaystyle |\Psi \rangle \sim |\Psi \rangle +Q_{B}|\Lambda \rangle }$. After second quantization, the equivalence relation is interpreted as a gauge invariance, whereas the condition that ${\displaystyle |\Psi \rangle }$ is physical is interpreted as an equation of motion. Because the physical fields live at ghostnumber one, it is also assumed that the string field ${\displaystyle |\Psi \rangle }$ is a ghostnumber one element of the Fock space.

In the case of the open bosonic string a gauge-unfixed action with the appropriate symmetries and equations of motion was originally obtained by André Neveu, Hermann Nicolai and Peter C. West.^[15] It is given by

${\displaystyle S_{\text{free open}}(\Psi )={\tfrac {1}{2}}\langle \Psi |Q_{B}|\Psi \rangle \ ,}$

where ${\displaystyle \langle \Psi |}$ is the BPZ-dual of ${\displaystyle |\Psi \rangle }$.^[16]

For the bosonic closed string, construction of a BRST-invariant kinetic term requires additionally that one impose ${\displaystyle (L_{0}-{\tilde {L}}_{0})|\Psi \rangle =0}$ and ${\displaystyle (b_{0}-{\tilde {b}}_{0})|\Psi \rangle =0}$. The kinetic term is then

${\displaystyle S_{\text{free closed}}={\tfrac {1}{2}}\langle \Psi |(c_{0}-{\tilde {c}}_{0})Q_{B}|\Psi \rangle \ .}$

Additional considerations are required for the superstrings to deal with the superghost zero-modes.

Witten's cubic open string field theory

The best studied and simplest of covariant interacting string field theories was constructed by Edward Witten.^[17] It describes the dynamics of bosonic open strings and is given by adding to the free open string action a cubic vertex:

${\displaystyle S(\Psi )={\tfrac {1}{2}}\langle \Psi |Q_{B}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi ,\Psi ,\Psi \rangle }$,

where, as in the free case, ${\displaystyle \Psi }$ is a ghostnumber one element of the BRST-quantized free bosonic open-string Fock-space.

The cubic vertex,

${\displaystyle \langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle }$

is a triliniar map which takes three string fields of total ghostnumber three and yields a number. Following Witten, who was motivated by ideas from noncommutative geometry, it is conventional to introduce the ${\displaystyle *}$-product defined implicitly through

${\displaystyle \langle \Sigma |\Psi _{1}*\Psi _{2}\rangle =\langle \Sigma ,\Psi _{1},\Psi _{2}\rangle \ .}$

The ${\displaystyle *}$-product and cubic vertex satisfy a number of important properties (allowing the ${\displaystyle \Psi _{i}}$ to be general ghost number fields):

1. Cyclicity :

   ${\displaystyle \langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle =(-1)^{gn(\Psi _{3})*(gn(\Psi _{2})+gn(\Psi _{1}))}\langle \Psi _{3},\Psi _{1},\Psi _{2}\rangle }$

2. BRST invariance :

   ${\displaystyle Q_{B}\langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle =\langle Q_{B}\Psi _{1},\Psi _{2},\Psi _{3}\rangle +(-1)^{gn(\Psi _{1})}\langle \Psi _{1},Q_{B}\Psi _{2},\Psi _{3}\rangle +(-1)^{gn(\Psi _{1})+gn(\Psi _{2})}\langle \Psi _{1},\Psi _{2},Q_{B}\Psi _{3}\rangle }$

   For the ${\displaystyle *}$-product, this implies that ${\displaystyle Q_{B}}$ acts as a graded derivation
   

   ${\displaystyle Q_{B}(\Psi _{1}*\Psi _{2})=(Q_{B}\Psi _{1})*\Psi _{2}+(-1)^{gn(\Psi _{1})}\Psi _{1}*(Q_{B}\Psi _{2})}$

3. Associativity

   ${\displaystyle \left(\Psi _{1}*\Psi _{2}\right)*\Psi _{3}=\Psi _{1}*(\Psi _{2}*\Psi _{3})}$

   In terms of the cubic vertex,
   

   ${\displaystyle \langle \Psi _{1},\Psi _{2}*\Psi _{3},\Psi _{4}\rangle =\langle \Psi _{1},\Psi _{2},\Psi _{3}*\Psi _{4}\rangle }$

In these equations, ${\displaystyle gn(\Psi )}$ denotes the ghost number of ${\displaystyle \Psi }$.

Gauge invariance

These properties of the cubic vertex are sufficient to show that ${\displaystyle S(\Psi )}$ is invariant under the Yang–Mills-like gauge transformation,

${\displaystyle \Psi \to \Psi +Q_{B}\Lambda +\Psi *\Lambda -\Lambda *\Psi \ ,}$

where ${\displaystyle \Lambda }$ is an infinitesimal gauge parameter. Finite gauge transformations take the form

${\displaystyle \Psi \to e^{-\Lambda }(\Psi +Q_{B})e^{\Lambda }}$

where the exponential is defined by,

${\displaystyle e^{\Lambda }=1+\Lambda +{\tfrac {1}{2}}\Lambda *\Lambda +{\tfrac {1}{3!}}\Lambda *\Lambda *\Lambda +\ldots }$

Equations of motion

The equations of motion are given by the following equation:

${\displaystyle Q_{B}\Psi +\Psi *\Psi =0\left.\right.\ .}$

Because the string field ${\displaystyle \Psi }$ is an infinite collection of ordinary classical fields, these equations represent an infinite collection of non-linear coupled differential equations. There have been two approaches to finding solutions: First, numerically, one can truncate the string field to include only fields with mass less than a fixed bound, a procedure known as "level truncation".^[18] This reduces the equations of motion to a finite number of coupled differential equations and has led to the discovery of many solutions.^[19] Second, following the work of Martin Schnabl ^[20] one can seek analytic solutions by carefully picking an ansatz which has simple behavior under star multiplication and action by the BRST operator. This has led to solutions representing marginal deformations, the tachyon vacuum solution^[21] and time-independent D-brane systems^[22].

Quantization

To consistently quantize ${\displaystyle S(\Psi )}$ one has to fix a gauge. The traditional choice has been Feynman–Siegel gauge,

${\displaystyle b_{0}\Psi =0\left.\right.\ .}$

Because the gauge transformations are themselves redundant (there are gauge transformations of the gauge transformations), the gauge fixing procedure requires introducing an infinite number of ghosts via the BV formalism.^[23] The complete gauge fixed action is given by

${\displaystyle S_{\text{gauge-fixed}}={\tfrac {1}{2}}\langle \Psi |c_{0}L_{0}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi ,\Psi ,\Psi \rangle \ ,}$

where the field ${\displaystyle \Psi }$ is now allowed to be of arbitrary ghostnumber. In this gauge, the Feynman diagrams are constructed from a single propagator and vertex. The propagator takes the form of a strip of worldsheet of width ${\displaystyle \pi }$ and length ${\displaystyle T}$

There is also an insertion of an integral of the ${\displaystyle b}$-ghost along the red line. The modulus, ${\displaystyle T}$ is integrated from 0 to ${\displaystyle \infty }$.

The three vertex can be described as a way of gluing three propagators together, as shown in the following picture:

In order to represent the vertex embedded in three dimensions, the propagators have been folded in half along their midpoints. The resulting geometry is completely flat except for a single curvature singularity where the midpoints of the three propagators meet.

These Feynman diagrams generate a complete cover of the moduli space of open string scattering diagrams. It follows that, for on-shell amplitudes, the n-point open string amplitudes computed using Witten's open string field theory are identical to those computed using standard worldsheet methods.^[24]

Supersymmetric covariant open string field theories

There are two main constructions of supersymmetric extensions of Witten's cubic open string field theory. The first is very similar in form to its bosonic cousin and is known as modified cubic superstring field theory. The second, due to Nathan Berkovits is very different and is based on a WZW-type action.

Modified cubic superstring field theory

The first consistent extension of Witten's bosonic open string field theory to the RNS string was constructed by Christian Preitschopf, Charles Thorn and Scott Yost and independently by Irina Aref'eva, P. B. Medvedev and A. P. Zubarev.^[25] The NS string field is taken to be a ghostnumber one picture zero string field in the small Hilbert space (i.e. ${\displaystyle \eta _{0}|\Psi \rangle =0}$). The action takes a very similar form to bosonic action,

${\displaystyle S(\Psi )={\tfrac {1}{2}}\langle \Psi |Y(i)Y(-i)Q_{B}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi |Y(i)Y(-i)|\Psi *\Psi \rangle \ ,}$

where,

${\displaystyle Y(z)=-\partial \xi e^{-2\phi }c(z)}$

is the inverse picture changing operator. The suggested ${\displaystyle -{\tfrac {1}{2}}}$ picture number extension of this theory to the Ramond sector might be problematic.

This action has been shown to reproduce tree-level amplitudes and has a tachyon vacuum solution with the correct energy.^[26] The one subtlety in the action is the insertion of picture changing operators at the midpoint, which imply that the linearized equations of motion take the form

${\displaystyle Y(i)Y(-i)Q_{B}\Psi =0\left.\right.\ .}$

Because ${\displaystyle Y(i)Y(-i)}$ has a non-trivial kernel, there are potentially extra solutions that are not in the cohomology of ${\displaystyle Q_{B}}$.^[27] However, such solutions would have operator insertions near the midpoint and would be potentially singular, and importance of this problem remains unclear.

Berkovits superstring field theory

A very different supersymmetric action for the open string was constructed by Nathan Berkovits. It takes the form^[28]

${\displaystyle S={\tfrac {1}{2}}\langle e^{-\Phi }Q_{B}e^{\Phi }|e^{-\Phi }\eta _{0}e^{\Phi }\rangle -{\tfrac {1}{2}}\int _{0}^{1}dt\langle e^{-{\hat {\Phi }}}\partial _{t}e^{\hat {\Phi }}|\{e^{-{\hat {\Phi }}}Q_{B}e^{\hat {\Phi }},e^{-{\hat {\Phi }}}\eta _{0}e^{\hat {\Phi }}\}\rangle }$

where all of the products are performed using the ${\displaystyle *}$-product including the anticommutator ${\displaystyle \{,\}}$, and ${\displaystyle {\hat {\Phi }}(t)}$ is any string field such that ${\displaystyle {\hat {\Phi }}(0)=0}$ and ${\displaystyle {\hat {\Phi }}(1)=\Phi }$. The string field ${\displaystyle \Phi }$ is taken to be in the NS sector of the large Hilbert space, i.e. including the zero mode of ${\displaystyle \xi }$. It is not known how to incorporate the R sector, although some preliminary ideas exist.^[29]

The equations of motion take the form

${\displaystyle \eta _{0}\left(e^{-\Phi }Q_{B}e^{\Phi }\right)=0.}$

The action is invariant under the gauge transformation

${\displaystyle e^{\Phi }\to e^{Q_{B}\Lambda }e^{\Phi }e^{\eta _{0}\Lambda '}.}$

The principal advantage of this action is that it free from any insertions of picture-changing operators. It has been shown to reproduce correctly tree level amplitudes^[30] and has been found, numerically, to have a tachyon vacuum with appropriate energy.^[31] The known analytic solutions to the classical equations of motion include the tachyon vacuum^[32] and marginal deformations.

Other formulations of covariant open superstring field theory

A formulation of superstring field theory using the non-minimal pure-spinor variables was introduced by Berkovits.^[33] The action is cubic and includes a midpoint insertion whose kernel is trivial. As always within the pure-spinor formulation, the Ramond sector can be easily treated. However, it is not known how to incorporate the GSO- sectors into the formalism.

In an attempt to resolve the allegedly problematic midpoint insertion of the modified cubic theory, Berkovits and Siegel proposed a superstring field theory based on a non-minimal extension of the RNS string,^[34] which uses a midpoint insertion with no kernel. It is not clear if such insertions are in any way better than midpoint insertions with non-trivial kernels.

Covariant closed string field theory

Covariant closed string field theories are considerably more complicated than their open string cousins. Even if one wants to construct a string field theory which only reproduces tree-level interactions between closed strings, the classical action must contain an infinite number of vertices ^[35] consisting of string polyhedra.^[36]

If one demands that on-shell scattering diagrams be reproduced to all orders in the string coupling, one must also include additional vertices arising from higher genus (and hence higher order in ${\displaystyle \hbar }$) as well. In general, a manifestly BV invariant, quantizable action takes the form^[37]

${\displaystyle S(\Psi )=\hbar \sum _{g\geq 0}(\hbar g_{c})^{g-1}\sum _{n\geq 0}{\frac {1}{n!}}\{\Psi ^{n}\}_{g}}$

where ${\displaystyle \{\Psi ^{n}\}_{g}}$ denotes an ${\displaystyle n}$th order vertex arising from a genus ${\displaystyle g}$ surface and ${\displaystyle g_{c}}$ is the closed string coupling. The structure of the vertices is in principle determined by a minimal area prescription,^[38] although, even for the polyhedral vertices, explicit computations have only been performed to quintic order.^[39]

Covariant heterotic string field theory

A formulation of the NS sector of the heterotic string was given by Berkovits, Okawa and Zwiebach.^[40] The formulation amalgams bosonic closed string field theory with Berkovits' superstring field theory.

Michio Kaku

From Wikipedia, the free encyclopedia

 

Michio Kaku
Kaku at Campus Party Brasil in 2012
Born	January 24, 1947 (age 71)[1] San Jose, California, United States
Residence	New York City, United States
Nationality	American
Alma mater	Harvard University (B.Sc., 1968) University of California, Berkeley (Ph.D., 1972)
Known for	String field theory Physics of the Impossible Physics of the Future The Future of the Mind
Spouse(s)	Shizue Kaku
Children	2
Awards	Klopsteg Memorial Award (2008)
Scientific career
Fields	Theoretical physics
Institutions	City University of New York New York University Institute for Advanced Study
Doctoral advisor	Stanley Mandelstam
Website	MKaku.org

Michio Kaku (/ˈmiːtʃioʊ ˈkɑːkuː/; born 24 January 1947) is an American theoretical physicist, futurist, and popularizer of science. He is a professor of theoretical physics in the City College of New York and CUNY Graduate Center. Kaku has written several books about physics and related topics, has made frequent appearances on radio, television, and film, and writes online blogs and articles. He has written three New York Times best sellers: Physics of the Impossible (2008), Physics of the Future (2011), and The Future of the Mind (2014). Kaku has hosted several TV specials for the BBC, the Discovery Channel, the History Channel, and the Science Channel.

Early life

Kaku was born in San Jose, California, to American Japanese parents.^[2] His father, born in California and educated in both Japan and the United States, was fluent in Japanese and English. Both his parents were interned in the Tule Lake War Relocation Center during World War II, where they met and where his older brother was born.

While attending Cubberley High School in Palo Alto, Kaku assembled a particle accelerator in his parents' garage for a science fair project.^{[citation needed]} His admitted goal was to generate "a beam of gamma rays powerful enough to create antimatter." At the National Science Fair in Albuquerque, New Mexico, he attracted the attention of physicist Edward Teller, who took Kaku as a protégé, awarding him the Hertz Engineering Scholarship. Kaku graduated summa cum laude from Harvard University in 1968 and was first in his physics class.^{[citation needed]} He attended the Berkeley Radiation Laboratory at the University of California, Berkeley, and received a Ph.D. in 1972, and that same year held a lectureship at Princeton University.

Kaku was drafted into the United States Army during the Vietnam War. He completed his basic training at Fort Benning, Georgia, and advanced infantry training at Fort Lewis, Washington.^[3] However, the Vietnam War ended before he was deployed as an infantryman.

Academic career

As part of the research program in 1975 and 1977 at the department of physics at The City College of The City University of New York, Kaku worked on research on quantum mechanics.^[4][5] He was a Visitor and Member (1973 and 1990) at the Institute for Advanced Study in Princeton and New York University. He currently holds the Henry Semat Chair and Professorship in theoretical physics at the City College of New York.^[6]

Kaku had a role in breaking the SSFL (Santa Susana Field Laboratory) story in 1979.^{[citation needed]} The Santa Susana facility run by RocketDyne was responsible for an experimental sodium reactor which had an accident in Simi Valley in the 1950s. Kaku was a student involved in breaking the story of the leak of radiation.^{[citation needed]}

Kaku has had more than 70 articles published in physics journals such as Physical Review, covering topics such as superstring theory, supergravity, supersymmetry, and hadronic physics.^[7] In 1974, Kaku and Prof. Keiji Kikkawa of Osaka University co-authored the first papers describing string theory in a field form.^[8]

Kaku is the author of several textbooks on string theory and quantum field theory.

Popular science

Kaku is most widely known as a popularizer of science^[9] and physics outreach specialist. He has written books and appeared on many television programs as well as film. He also hosts a weekly radio program.

Books

Kaku is the author of various popular science books:

• Beyond Einstein: The Cosmic Quest for the Theory of the Universe (with Jennifer Thompson) (1987)
• Hyperspace: A Scientific Odyssey through Parallel Universes, Time Warps, and the Tenth Dimension (1994)
• Visions: How Science Will Revolutionize the 21st Century (1998)
• Einstein's Cosmos: How Albert Einstein's Vision Transformed Our Understanding of Space and Time (2004)
• Parallel Worlds: A Journey through Creation, Higher Dimensions, and the Future of the Cosmos (2004)
• Physics of the Impossible: A Scientific Exploration into the World of Phasers, Force Fields, Teleportation, and Time Travel (2008)
• Physics of the Future: How Science Will Shape Human Destiny and Our Daily Lives by the Year 2100 (2011)
• The Future of the Mind: The Scientific Quest to Understand, Enhance, and Empower the Mind (2014)
• The Future of Humanity: Terraforming Mars, Interstellar Travel, Immortality, and Our Destiny Beyond Earth (2018)

Hyperspace was a bestseller and voted one of the best science books of the year by The New York Times^[9] and The Washington Post. Parallel Worlds was a finalist for the Samuel Johnson Prize for nonfiction in the UK.^[10]

Radio

Kaku is the host of the weekly one-hour radio program Exploration, produced by the Pacifica Foundation's WBAI in New York. Exploration is syndicated to community and independent radio stations and makes previous broadcasts available on the program's website. Kaku defines the show as dealing with the general topics of science, war, peace and the environment.

In April 2006, Kaku began broadcasting Science Fantastic on 90 commercial radio stations in the United States. It is syndicated by Talk Radio Network and now^[when?] reaches 130 radio stations and America's Talk on XM and remains the only nationally syndicated science radio program. Featured guests include Nobel laureates and top researchers in the fields of string theory, time travel, black holes, gene therapy, aging, space travel, artificial intelligence and SETI. When Kaku is busy filming for television, Science Fantastic goes on hiatus, sometimes for several months. Kaku is also a frequent guest on many programs, where he is outspoken in all areas and issues he considers of importance, such as the program Coast to Coast AM where, on 30 November 2007, he reaffirmed his belief that the existence of extraterrestrial life is a certainty.^[11] During the debut of Art Bell's new radio show Dark Matter on September 16, 2013, Bell referred to Kaku as "the next Carl Sagan", referring to Kaku's similar ability to explain complex science so anyone can understand it.

Kaku has appeared on many mainstream talk shows, discussing popular fiction such as Back to the Future, Lost, and the theories behind the time travel these and other fictional entertainment focus on.

Television and film

Kaku has appeared in many forms of media and on many programs and networks, including Good Morning America, The Screen Savers, Larry King Live, 60 Minutes, Imus In The Morning, Nightline, 20/20, Naked Science, CNN, ABC News, CBS News, NBC News, Al Jazeera English, Fox News Channel, The History Channel, Conan, The Science Channel, The Discovery Channel, TLC, Countdown with Keith Olbermann, The Colbert Report, The Art Bell Show and its successor, Coast to Coast AM, BBC World News America, The Covino & Rich Show, Head Rush, Late Show with David Letterman, and Real Time with Bill Maher. He was interviewed for two PBS documentaries, The Path to Nuclear Fission: The Story of Lise Meitner and Otto Hahn and Out from the Shadows: The Story of Irène Joliot-Curie and Frédéric Joliot-Curie, which were produced and directed by his former WBAI radio colleague Rosemarie Reed.^[12]

In 1999, Kaku was one of the scientists profiled in the feature-length film Me & Isaac Newton, directed by Michael Apted. It played theatrically in the United States, was later broadcast on national TV, and won several film awards.^{[citation needed]}

In 2005, Kaku appeared in the short documentary film Obsessed & Scientific about the possibility of time travel and the people who dream about it. It screened at the Montreal World Film Festival; a feature film expansion is in development talks. Kaku also appeared in the ABC documentary UFOs: Seeing Is Believing, in which he suggested that while he believes it is extremely unlikely that extraterrestrials have ever actually visited Earth, we must keep our minds open to the possible existence of civilizations a million years ahead of us in technology, where entirely new avenues of physics open up. He also discussed the future of interstellar exploration and alien life in the Discovery Channel special Alien Planet as one of the multiple speakers who co-hosted the show, and Einstein's Theory of Relativity on The History Channel.^{[citation needed]}

In February 2006, Kaku appeared as presenter in the BBC-TV four-part documentary Time which seeks to explore the mysterious nature of time. Part one of the series concerns personal time, and how we perceive and measure the passing of time. The second in the series deals with cheating time, exploring possibilities of extending the lifespan of organisms. The geological time covered in part three explores the ages of the Earth and the Sun. Part four covers the topics of cosmological time, the beginning of time and the events that occurred at the instant of the big bang.

On January 28, 2007, Kaku hosted the Discovery Channel series 2057. This three-hour program discussed how medicine, the city, and energy could change over the next 50 years.

In 2008, Kaku hosted the three-hour BBC-TV documentary Visions of the Future, on the future of computers, medicine, and quantum physics, and he appeared in several episodes of the History Channel's Universe series.

On December 1, 2009, he began hosting a 12-episode weekly TV series for the Science Channel at 10 pm, called Sci Fi Science: Physics of the Impossible, based on his best-selling book. Each 30-minute episode discusses the scientific basis behind imaginative schemes, such as time travel, parallel universes, warp drive, star ships, light sabers, force fields, teleportation, invisibility, death stars, and even superpowers and flying saucers. Each episode includes interviews with the world's top scientists working on prototypes of these technologies, interviews with science fiction fans, clips from science fiction movies, and special effects and computer graphics. Although these inventions are impossible today, the series discusses when these technologies might become feasible in the future.

In 2010, he began to appear in a series on the website Gametrailers.com called Science of Games, discussing the scientific aspects of various popular video games such as Mass Effect 2 and Star Wars: The Force Unleashed.

Kaku is popular in mainstream media because of his knowledge and his accessible approach to presenting complex subjects in science. While his technical writings are confined to theoretical physics, his public speaking and media appearances cover a broad range of topics, from the Kardashev scale to more esoteric subjects such as wormholes and time travel. In January 2007, Kaku visited Oman. While there, he talked at length to select members of that country's decision makers. In an interview with local media, Kaku elaborated on his vision of mankind's future. Kaku considers climate change and terrorism as serious threats in man's evolution from a Type 0 civilization to Type 1 on the Kardashev scale.^[13]

He is featured in Symphony of Science's songs, "The Quantum World", "Our Place in the Cosmos", "The Secret of the Stars", and "Monsters of the Cosmos"

On October 11, 2010, Michio Kaku appeared in the BBC program "What Happened Before the Big Bang" (along with Laura Mersini-Houghton, Andrei Linde, Roger Penrose, Lee Smolin, Neil Turok, and other notable cosmologists and physicists), where he propounded his theory of the universe created out of nothing.^[14]

Over 22–25 January 2011, Kaku was invited to the fifth annual Global Competitiveness Forum (GCF), held in Riyadh, Saudi Arabia, next to renowned specialists including the British journalist Nick Pope, the Canadian ufologist Stanton Friedman, and the French astrophysicist Jacques Vallée.^[15]

Kaku appears on the DVD and Blu-ray extras of the 2012 version of Total Recall, discussing the technological aspects of the future explored in the film.

Web Series

In 2018, Kaku hosts the web series Next World with Michio Kaku on CuriosityStream.

Policy advocacy and activism

Kaku has publicly stated his concerns over matters including people denying the anthropogenic cause of global warming, nuclear armament, nuclear power and what he believes to be the general misuse of science.^[16] He was critical of the Cassini–Huygens space probe because of the 72 pounds (33 kg) of plutonium contained in the craft for use by its radioisotope thermoelectric generator. Conscious of the possibility of casualties if the probe's fuel were dispersed into the environment during a malfunction and crash as the probe was making a 'sling-shot' maneuver around Earth, Kaku publicly criticized NASA's risk assessment.^[17] He has yet to comment on the successful mission.

His remark from an interview in support of SETI, "We could be in the middle of an intergalactic conversation... and we wouldn't even know", is used in the third Symphony of Science installment "Our Place in the Cosmos". Michio Kaku is also a member of the CuriosityStream Advisory Board.^[18]

Personal life

Kaku is married to Shizue Kaku and has two daughters, Alyson and Michelle.^[19][20]

In popular culture

In 2016, Kaku appeared in a TV commercial for TurboTax.^[21]

Works

• Kaku, Michio; Trainer, Jennifer, eds. (1982). Nuclear Power: Both Sides. New York: Norton. ISBN 0-393-01631-5.
• Kaku, Michio; Jennifer Trainer Thompson (1987). Beyond Einstein: Superstrings and the Quest for the Final Theory. Oxford: Oxford University Press. ISBN 0-19-286196-4.
• Kaku, Michio; Daniel Axelrod (1987). To Win a Nuclear War: The Pentagon's Secret War Plans. Boston: South End Press. ISBN 0-89608-321-7.
• Kaku, Michio (1993). Quantum Field Theory: A Modern Introduction. New York: Oxford University Press. ISBN 0-19-507652-4.
• Kaku, Michio (1994). Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the Tenth Dimension. Oxford: Oxford University Press. ISBN 0-19-286189-1.
• Kaku, Michio (1998). Visions: How Science Will Revolutionize the 21st Century. New York: Oxford University Press. ISBN 0-19-288018-7.
• Kaku, Michio (1999). Introduction to Superstrings and M-Theory. New York: Springer. ISBN 0-387-98589-1.
• Kaku, Michio (1999). Strings, Conformal Fields, and M-Theory. New York: Springer. ISBN 0-387-98892-0.
• Kaku, Michio (2004). Einstein's Cosmos: How Albert Einstein's Vision Transformed Our Understanding of Space and Time. London: Weidenfeld & Nicolson. ISBN 0-297-84755-4.
• Kaku, Michio (2004). Parallel Worlds: The Science of Alternative Universes and Our Future in the Cosmos. London: Allen Lane. ISBN 0-7139-9728-1.
• Kaku, Michio (2008). "M-Theory: The Mother of All Superstrings" in Riffing on Strings: Creative Writing Inspired by String Theory. New York: Scriblerus. ISBN 978-0-9802114-0-5.
• Kaku, Michio (2008). Physics of the Impossible. New York: Doubleday. ISBN 978-0-385-52069-0.
• Kaku, Michio (2011). Physics of the Future: How Science will Shape Human Destiny and our Daily Lives by the Year 2100. New York: Doubleday. LCCN 2010026569.
• Kaku, Michio (2014). The Future of the Mind: The Scientific Quest to Understand, Enhance, and Empower the Mind. New York: Doubleday. ISBN 978-0385530828.
• Kaku, Michio (2018). The Future of Humanity: Terraforming Mars, Interstellar Travel, Immortality, and Our Destiny Beyond Earth. New York: Doubleday. ISBN 978-0385542760.

Filmography

• We Are the Guinea Pigs (1980)
• Borders (1989)
• Synthetic Pleasures (1995)
• Einstein Revealed (1996)
• Future Fantastic (1996)
• Stephen Hawking's Universe (1997)
• Bioperfection: Building a New Human Race (1998)
• Me & Isaac Newton (1999)
• Space: The Final Junkyard (1999)
• Ghosts: Caught on Tape (2000)
• Big Questions (2001)
• Parallel Universes (2001)
• Horizon: "Time travel" (2003)
• Robo Sapiens (2003)
• Brilliant Minds: Secret Of The Cosmos (2003)
• Nova: "The Elegant Universe" (2003)
• Hawking (2004)
• The Screen Savers (2004)
• Unscrewed with Martin Sargent (2004)
• Alien Planet (2005)
• ABC News "UFOs: Seeing Is Believing" (2005)
• HARDtalk Extra (2005)
• Last Days on Earth (2005)
• Obsessed & Scientific (2005)
• Horizon: "Einstein's Unfinished Symphony" (2005)
• Exodus Earth (2006)
• Time (2006)
• 2057 (2007)
• The Universe (2007)
• Futurecar (2007)
• Attack of the Show! (2007)
• Visions of the Future (2008)
• Horizon: "The President's Guide to Science" (2008)
• Stephen Hawking: Master of the Universe (2008)
• Horizon: "Who's Afraid of a Big Black Hole" (2009–2010)
• Sci Fi Science: Physics of the Impossible (2009–2010)
• Horizon: "What Happened Before the Big Bang?" (2010)
• GameTrailers TV With Geoff Keighley: "The Science of Games" (2010)
• How the Universe Works (2010)
• Seeing Black Holes (2010)
• Prophets of Science Fiction (2011)
• Through the Wormhole (2011)
• Horizon: "What Happened Before the Big Bang?" (2011)
• The Science of Doctor Who (2012)
• Horizon: "The Hunt for Higgs" (2012)
• The Principle: "The Principle" (2014)