Protein folding

From Wikipedia, the free encyclopedia

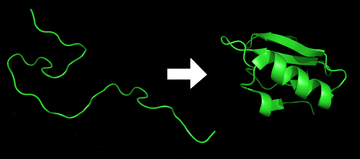
Protein before and after folding.

Results of protein folding.

Protein folding is the physical process by which a protein chain acquires its native 3-dimensional structure, a conformation that is usually biologically functional, in an expeditious and reproducible manner. It is the physical process by which a polypeptide folds into its characteristic and functional three-dimensional structure from random coil.^[1] Each protein exists as an unfolded polypeptide or random coil when translated from a sequence of mRNA to a linear chain of amino acids. This polypeptide lacks any stable (long-lasting) three-dimensional structure (the left hand side of the first figure). As the polypeptide chain is being synthesized by a ribosome, the linear chain begins to fold into its three dimensional structure. Folding begins to occur even during translation of the polypeptide chain. Amino acids interact with each other to produce a well-defined three-dimensional structure, the folded protein (the right hand side of the figure), known as the native state. The resulting three-dimensional structure is determined by the amino acid sequence or primary structure (Anfinsen's dogma).^[2] The energy landscape describes the folding pathways in which the unfolded protein is able to assume its native state.

The correct three-dimensional structure is essential to function, although some parts of functional proteins may remain unfolded,^[3] so that protein dynamics is important. Failure to fold into native structure generally produces inactive proteins, but in some instances misfolded proteins have modified or toxic functionality. Several neurodegenerative and other diseases are believed to result from the accumulation of amyloid fibrils formed by misfolded proteins.^[4] Many allergies are caused by incorrect folding of some proteins, because the immune system does not produce antibodies for certain protein structures.^[5]

Denaturation of proteins is a process of transition from the folded to the unfolded state.

Process of protein folding

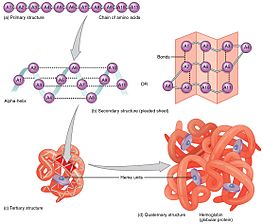
Primary structure

The primary structure of a protein, its linear amino-acid sequence, determines its native conformation.^[6] The specific amino acid residues and their position in the polypeptide chain are the determining factors for which portions of the protein fold closely together and form its three dimensional conformation. The amino acid composition is not as important as the sequence.^[7] The essential fact of folding, however, remains that the amino acid sequence of each protein contains the information that specifies both the native structure and the pathway to attain that state. This is not to say that nearly identical amino acid sequences always fold similarly.^[8] Conformations differ based on environmental factors as well; similar proteins fold differently based on where they are found.

Secondary structure

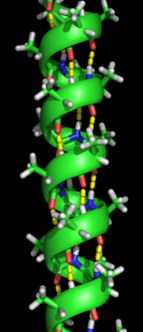
The alpha helix spiral formation.

An anti-parallel beta pleated sheet displaying hydrogen bonding within the backbone.

Formation of a secondary structure is the first step in the folding process that a protein takes to assume its native structure. Characteristic of secondary structure are the structures known as alpha helices and beta sheets that fold rapidly because they are stabilized by intramolecular hydrogen bonds, as was first characterized by Linus Pauling. Formation of intramolecular hydrogen bonds provides another important contribution to protein stability.^[9] α-helices are formed by hydrogen bonding of the backbone to form a spiral shape (refer to figure on the right).^[7] The β pleated sheet is a structure that forms with the backbone bending over itself to form the hydrogen bonds (as displayed in the figure to the left). The hydrogen bonds are between the amide hydrogen and carbonyl oxygen of the peptide bond. There exists anti-parallel β pleated sheets and parallel β pleated sheets where the stability of the hydrogen bonds is stronger in the anti-parallel β sheet as it hydrogen bonds with the ideal 180 degree angle compared to the slanted hydrogen bonds formed by parallel sheets.^[7]

Tertiary structure

The alpha helices and beta pleated sheets can be amphipathic in nature, or contain a hydrophilic portion and a hydrophobic portion. This property of secondary structures aids in the tertiary structure of a protein in which the folding occurs so that the hydrophilic sides are facing the aqueous environment surrounding the protein and the hydrophobic sides are facing the hydrophobic core of the protein.^[10] Secondary structure hierarchically gives way to tertiary structure formation. Once the protein's tertiary structure is formed and stabilized by the hydrophobic interactions, there may also be covalent bonding in the form of disulfide bridges formed between two cysteine residues. Tertiary structure of a protein involves a single polypeptide chain; however, additional interactions of folded polypeptide chains give rise to quaternary structure formation.^[11]

Quaternary structure

Tertiary structure may give way to the formation of quaternary structure in some proteins, which usually involves the "assembly" or "coassembly" of subunits that have already folded; in other words, multiple polypeptide chains could interact to form a fully functional quaternary protein.^[7]

Driving forces of protein folding

All forms of protein structure summarized.

Folding is a spontaneous process that is mainly guided by hydrophobic interactions, formation of intramolecular hydrogen bonds, van der Waals forces, and it is opposed by conformational entropy.^[12] The process of folding often begins co-translationally, so that the N-terminus of the protein begins to fold while the C-terminal portion of the protein is still being synthesized by the ribosome; however, a protein molecule may fold spontaneously during or after biosynthesis. While these macromolecules may be regarded as "folding themselves", the process also depends on the solvent (water or lipid bilayer),^[13] the concentration of salts, the pH, the temperature, the possible presence of cofactors and of molecular chaperones. Proteins will have limitations on their folding abilities by the restricted bending angles or conformations that are possible. These allowable angles of protein folding are described with a two-dimensional plot known as the Ramachandran plot, depicted with psi and phi angles of allowable rotation.^[14]

Hydrophobic effect

Hydrophobic collapse. In the compact fold (to the right), the hydrophobic amino acids (shown as black spheres) collapse toward the center to become shielded from aqueous environment.

Protein folding must be thermodynamically favorable within a cell in order for it to be a spontaneous reaction. Since it is known that protein folding is a spontaneous reaction, then it must assume a negative Gibbs free energy value. Gibbs free energy in protein folding is directly related to enthalpy and entropy.^[7] For a negative delta G to arise and for protein folding to become thermodynamically favorable, then either enthalpy, entropy, or both terms must be favorable.

Play media

Entropy is decreased as the water molecules become more orderly near the hydrophobic solute.

Minimizing the number of hydrophobic side-chains exposed to water is an important driving force behind the folding process.^[15] The hydrophobic effect is the phenomenon in which the hydrophobic chains of a protein collapse into the core of the protein (away from the hydrophilic environment).^[7] In an aqueous environment, the water molecules tend to aggregate around the hydrophobic regions or side chains of the protein, creating water shells of ordered water molecules.^[16] An ordering of water molecules around a hydrophobic region increases order in a system and therefore contributes a negative change in entropy (less entropy in the system). The water molecules are fixed in these water cages which drives the hydrophobic collapse, or the inward folding of the hydrophobic groups. The hydrophobic collapse introduces entropy back to the system via the breaking of the water cages which frees the ordered water molecules.^[7] The multitude of hydrophobic groups interacting within the core of the globular folded protein contributes a significant amount to protein stability after folding, because of the vastly accumulated van der Waals forces (specifically London Dispersion forces).^[7] The hydrophobic effect exists as a driving force in thermodynamics only if there is the presence of an aqueous medium with an amphiphilic molecule containing a large hydrophobic region.^[17] The strength of hydrogen bonds depends on their environment; thus, H-bonds enveloped in a hydrophobic core contribute more than H-bonds exposed to the aqueous environment to the stability of the native state.^[18]

Chaperones

Example of a small eukaryotic heat shock protein.

Molecular chaperones are a class of proteins that aid in the correct folding of other proteins in vivo. Chaperones exist in all cellular compartments and interact with the polypeptide chain in order to allow the native three-dimensional conformation of the protein to form; however, chaperones themselves are not included in the final structure of the protein they are assisting in.^[19] Chaperones may assist in folding even when the nascent polypeptide is being synthesized by the ribosome.^[20] Molecular chaperones operate by binding to stabilize an otherwise unstable structure of a protein in its folding pathway, but chaperones do not contain the necessary information to know the correct native structure of the protein they are aiding; rather, chaperones work by preventing incorrect folding conformations.^[20] In this way, chaperones do not actually increase the rate of individual steps involved in the folding pathway toward the native structure; instead, they work by reducing possible unwanted aggregations of the polypeptide chain that might otherwise slow down the search for the proper intermediate and they provide a more efficient pathway for the polypeptide chain to assume the correct conformations.^[19] Chaperones are not to be confused with folding catalysts, which actually do catalyze the otherwise slow steps in the folding pathway. Examples of folding catalysts are protein disulfide isomerases and peptidyl-prolyl isomerases that may be involved in formation of disulfide bonds or interconversion between cis and trans stereoisomers, respectively.^[20] Chaperones are shown to be critical in the process of protein folding in vivo because they provide the protein with the aid needed to assume its proper alignments and conformations efficiently enough to become "biologically relevant".^[21] This means that the polypeptide chain could theoretically fold into its native structure without the aid of chaperones, as demonstrated by protein folding experiments conducted in vitro;^[21] however, this process proves to be too inefficient or too slow to exist in biological systems; therefore, chaperones are necessary for protein folding in vivo. Along with its role in aiding native structure formation, chaperones are shown to be involved in various roles such as protein transport, degradation, and even allow denatured proteins exposed to certain external denaturant factors an opportunity to refold into their correct native structures.^[22]

A fully denatured protein lacks both tertiary and secondary structure, and exists as a so-called random coil. Under certain conditions some proteins can refold; however, in many cases, denaturation is irreversible.^[23] Cells sometimes protect their proteins against the denaturing influence of heat with enzymes known as heat shock proteins (a type of chaperone), which assist other proteins both in folding and in remaining folded. Some proteins never fold in cells at all except with the assistance of chaperones which either isolate individual proteins so that their folding is not interrupted by interactions with other proteins or help to unfold misfolded proteins, allowing them to refold into the correct native structure.^[24] This function is crucial to prevent the risk of precipitation into insoluble amorphous aggregates. The external factors involved in protein denaturation or disruption of the native state include temperature, external fields (electric, magnetic),^[25] molecular crowding,^[26] and even the limitation of space, which can have a big influence on the folding of proteins.^[27] High concentrations of solutes, extremes of pH, mechanical forces, and the presence of chemical denaturants can contribute to protein denaturation, as well. These individual factors are categorized together as stresses. Chaperones are shown to exist in increasing concentrations during times of cellular stress and help the proper folding of emerging proteins as well as denatured or misfolded ones.^[19]

Under some conditions proteins will not fold into their biochemically functional forms. Temperatures above or below the range that cells tend to live in will cause thermally unstable proteins to unfold or denature (this is why boiling makes an egg white turn opaque). Protein thermal stability is far from constant, however; for example, hyperthermophilic bacteria have been found that grow at temperatures as high as 122 °C,^[28] which of course requires that their full complement of vital proteins and protein assemblies be stable at that temperature or above.

Computational methods for studying protein folding

The study of protein folding includes three main aspects related to the prediction of protein stability, kinetics, and structure. A recent review summarizes the available computational methods for protein folding. ^[29]

Energy landscape of protein folding

The energy funnel by which an unfolded polypeptide chain assumes its native structure.

The protein folding phenomenon was largely an experimental endeavor until the formulation of an energy landscape theory of proteins by Joseph Bryngelson and Peter Wolynes in the late 1980s and early 1990s. This approach introduced the principle of minimal frustration.^[30] This principle says that nature has chosen amino acid sequences so that the folded state of the protein is very stable. In addition, the undesired interactions between amino acids along the folding pathway are reduced, making the acquisition of the folded state a very fast process. Even though nature has reduced the level of frustration in proteins, some degree of it remains up to now as can be observed in the presence of local minima in the energy landscape of proteins. A consequence of these evolutionarily selected sequences is that proteins are generally thought to have globally "funneled energy landscapes" (coined by José Onuchic)^[31] that are largely directed toward the native state. This "folding funnel" landscape allows the protein to fold to the native state through any of a large number of pathways and intermediates, rather than being restricted to a single mechanism. The theory is supported by both computational simulations of model proteins and experimental studies,^[30] and it has been used to improve methods for protein structure prediction and design.^[30] The description of protein folding by the leveling free-energy landscape is also consistent with the 2nd law of thermodynamics.^[32] Physically, thinking of landscapes in terms of visualizable potential or total energy surfaces simply with maxima, saddle points, minima, and funnels, rather like geographic landscapes, is perhaps a little misleading. The relevant description is really a high-dimensional phase space in which manifolds might take a variety of more complicated topological forms.^[33]

The unfolded polypeptide chain begins at the top of the funnel where it may assume the largest number of unfolded variations and is in its highest energy state. Energy landscapes such as these indicate that there are a large number of initial possibilities, but only a single native state is possible; however, it does not reveal the numerous folding pathways that are possible. A different molecule of the same exact protein may be able to follow marginally different folding pathways, seeking different lower energy intermediates, as long as the same native structure is reached.^[34] Different pathways may have different frequencies of utilization depending on the thermodynamic favorability of each pathway. This means that if one pathway is found to be more thermodynamically favorable than another, it is likely to be used more frequently in the pursuit of the native structure.^[34] As the protein begins to fold and assume its various conformations, it always seeks a more thermodynamically favorable structure than before and thus continues through the energy funnel. Formation of secondary structures is a strong indication of increased stability within the protein, and only one combination of secondary structures assumed by the polypeptide backbone will have the lowest energy and therefore be present in the native state of the protein.^[34] Among the first structures to form once the polypeptide begins to fold are alpha helices and beta turns, where alpha helices can form in as little as 100 nanoseconds and beta turns in 1 microsecond.^[19]

There exists a saddle point in the energy funnel landscape where the transition state for a particular protein is found.^[19] The transition state in the energy funnel diagram is the conformation that must be assumed by every molecule of that protein if the protein wishes to finally assume the native structure. No protein may assume the native structure without first passing through the transition state.^[19] The transition state can be referred to as a variant or premature form of the native state rather than just another intermediary step.^[35] The folding of the transition state is shown to be rate-determining, and even though it exists in a higher energy state than the native fold, it greatly resembles the native structure. Within the transition state, there exists a nucleus around which the protein is able to fold, formed by a process referred to as "nucleation condensation" where the structure begins to collapse onto the nucleus.^[35]

Two models of protein folding are currently being confirmed:

• The diffusion collision model, in which first a nucleus forms, then the secondary structure, and finally these secondary structures collide and pack tightly together.
• The nucleation-condensation model, in which the secondary and tertiary structures of the protein are made at the same time.

Recent studies have shown that some proteins show characteristics of both of these folding models.

For the most part, scientists have been able to study many identical molecules folding together en masse. At the coarsest level, it appears that in transitioning to the native state, a given amino acid sequence takes roughly the same route and proceeds through roughly the same intermediates and transition states. Often folding involves first the establishment of regular secondary and supersecondary structures, in particular alpha helices and beta sheets, and afterward tertiary structure.

Modeling of protein folding

Folding@home uses Markov state models, like the one diagrammed here, to model the possible shapes and folding pathways a protein can take as it condenses from its initial randomly coiled state (left) into its native 3D structure (right).

De novo or ab initio techniques for computational protein structure prediction are related to, but strictly distinct from, experimental studies of protein folding. Molecular Dynamics (MD) is an important tool for studying protein folding and dynamics in silico.^[36] First equilibrium folding simulations were done using implicit solvent model and umbrella sampling.^[37] Because of computational cost, ab initio MD folding simulations with explicit water are limited to peptides and very small proteins.^[38][39] MD simulations of larger proteins remain restricted to dynamics of the experimental structure or its high-temperature unfolding. Long-time folding processes (beyond about 1 millisecond), like folding of small-size proteins (about 50 residues) or larger, can be accessed using coarse-grained models.^[40][41][42]

The 100-petaFLOP distributed computing project Folding@home created by Vijay Pande's group at Stanford University simulates protein folding using the idle processing time of CPUs and GPUs of personal computers from volunteers. The project aims to understand protein misfolding and accelerate drug design for disease research.

Long continuous-trajectory simulations have been performed on Anton, a massively parallel supercomputer designed and built around custom ASICs and interconnects by D. E. Shaw Research. The longest published result of a simulation performed using Anton is a 2.936 millisecond simulation of NTL9 at 355 K.^[43]

Experimental techniques for studying protein folding

While inferences about protein folding can be made through mutation studies, typically, experimental techniques for studying protein folding rely on the gradual unfolding or folding of proteins and observing conformational changes using standard non-crystallographic techniques.

X-ray crystallography

Steps of x-ray crystallography.

X-ray crystallography is one of the more efficient and important methods for attempting to decipher the three dimensional configuration of a folded protein.^[44] To be able to conduct X-ray crystallography, the protein under investigation must be located inside a crystal lattice. To place a protein inside a crystal lattice, one must have a suitable solvent for crystallization, obtain a pure protein at supersaturated levels in solution, and precipitate the crystals in solution.^[45] Once a protein is crystallized, x-ray beams can be concentrated through the crystal lattice which would diffract the beams or shoot them outwards in various directions. These exiting beams are correlated to the specific three-dimensional configuration of the protein enclosed within. The x-rays specifically interact with the electron clouds surrounding the individual atoms within the protein crystal lattice and produce a discernible diffraction pattern.^[10] Only by relating the electron density clouds with the amplitude of the x-rays can this pattern be read and lead to assumptions of the phases or phase angles involved that complicate this method.^[46] Without the relation established through a mathematical basis known as Fourier transform, the "phase problem" would render predicting the diffraction patterns very difficult.^[10] Emerging methods like multiple isomorphous replacement use the presence of a heavy metal ion to diffract the x-rays into a more predictable manner, reducing the number of variables involved and resolving the phase problem.^[44]

Fluorescence spectroscopy

Fluorescence spectroscopy is a highly sensitive method for studying the folding state of proteins. Three amino acids, phenylalanine (Phe), tyrosine (Tyr) and tryptophan (Trp), have intrinsic fluorescence properties, but only Tyr and Trp are used experimentally because their quantum yields are high enough to give good fluorescence signals. Both Trp and Tyr are excited by a wavelength of 280 nm, whereas only Trp is excited by a wavelength of 295 nm. Because of their aromatic character, Trp and Tyr residues are often found fully or partially buried in the hydrophobic core of proteins, at the interface between two protein domains, or at the interface between subunits of oligomeric proteins. In this apolar environment, they have high quantum yields and therefore high fluorescence intensities. Upon disruption of the protein’s tertiary or quaternary structure, these side chains become more exposed to the hydrophilic environment of the solvent, and their quantum yields decrease, leading to low fluorescence intensities. For Trp residues, the wavelength of their maximal fluorescence emission also depend on their environment.

Fluorescence spectroscopy can be used to characterize the equilibrium unfolding of proteins by measuring the variation in the intensity of fluorescence emission or in the wavelength of maximal emission as functions of a denaturant value.^[47][48] The denaturant can be a chemical molecule (urea, guanidinium hydrochloride), temperature, pH, pressure, etc. The equilibrium between the different but discrete protein states, i.e. native state, intermediate states, unfolded state, depends on the denaturant value; therefore, the global fluorescence signal of their equilibrium mixture also depends on this value. One thus obtains a profile relating the global protein signal to the denaturant value. The profile of equilibrium unfolding may enable one to detect and identify intermediates of unfolding.^[49][50] General equations have been developed by Hugues Bedouelle to obtain the thermodynamic parameters that characterize the unfolding equilibria for homomeric or heteromeric proteins, up to trimers and potentially tetramers, from such profiles.^[47] Fluorescence spectroscopy can be combined with fast-mixing devices such as stopped flow, to measure protein folding kinetics,^[51] generate a chevron plot and derive a Phi value analysis.

Circular dichroism

Circular dichroism is one of the most general and basic tools to study protein folding. Circular dichroism spectroscopy measures the absorption of circularly polarized light. In proteins, structures such as alpha helices and beta sheets are chiral, and thus absorb such light. The absorption of this light acts as a marker of the degree of foldedness of the protein ensemble. This technique has been used to measure equilibrium unfolding of the protein by measuring the change in this absorption as a function of denaturant concentration or temperature. A denaturant melt measures the free energy of unfolding as well as the protein's m value, or denaturant dependence. A temperature melt measures the melting temperature (T_m) of the protein.^[47] As for fluorescence spectroscopy, circular-dichroism spectroscopy can be combined with fast-mixing devices such as stopped flow to measure protein folding kinetics and to generate chevron plots.

Vibrational circular dichroism of proteins

The more recent developments of vibrational circular dichroism (VCD) techniques for proteins, currently involving Fourier transform (FFT) instruments, provide powerful means for determining protein conformations in solution even for very large protein molecules. Such VCD studies of proteins are often combined with X-ray diffraction of protein crystals, FT-IR data for protein solutions in heavy water (D₂O), or ab initio quantum computations to provide unambiguous structural assignments that are unobtainable from CD.^{[citation needed]}

Protein nuclear magnetic resonance spectroscopy

Protein folding is routinely studied using NMR spectroscopy, for example by monitoring hydrogen-deuterium exchange of backbone amide protons of proteins in their native state, which provides both the residue-specific stability and overall stability of proteins.^[52]

Dual polarisation interferometry

Dual polarisation interferometry is a surface-based technique for measuring the optical properties of molecular layers. When used to characterize protein folding, it measures the conformation by determining the overall size of a monolayer of the protein and its density in real time at sub-Angstrom resolution,^[53] although real-time measurement of the kinetics of protein folding are limited to processes that occur slower than ~10 Hz. Similar to circular dichroism, the stimulus for folding can be a denaturant or temperature.

Studies of folding with high time resolution

The study of protein folding has been greatly advanced in recent years by the development of fast, time-resolved techniques. Experimenters rapidly trigger the folding of a sample of unfolded protein and observe the resulting dynamics. Fast techniques in use include neutron scattering,^[54] ultrafast mixing of solutions, photochemical methods, and laser temperature jump spectroscopy. Among the many scientists who have contributed to the development of these techniques are Jeremy Cook, Heinrich Roder, Harry Gray, Martin Gruebele, Brian Dyer, William Eaton, Sheena Radford, Chris Dobson, Alan Fersht, Bengt Nölting and Lars Konermann.

Proteolysis

Proteolysis is routinely used to probe the fraction unfolded under a wide range of solution conditions (e.g. Fast parallel proteolysis (FASTpp).^[55][56]

Optical tweezers

Single molecule techniques such as optical tweezers and AFM have been used to understand protein folding mechanisms of isolated proteins as well as proteins with chaperones.^[57] Optical tweezers have been used to stretch single protein molecules from their C- and N-termini and unfold them to allow study of the subsequent refolding.^[58] The technique allows one to measure folding rates at single-molecule level; for example, optical tweezers have been recently applied to study folding and unfolding of proteins involved in blood coagulation. von Willebrand factor (vWF) is a protein with an essential role in blood clot formation process. It discovered – using single molecule optical tweezers measurement – that calcium-bound vWF acts as a shear force sensor in the blood. Shear force leads to unfolding of the A2 domain of vWF, whose refolding rate is dramatically enhanced in the presence of calcium.^[59] Recently, it was also shown that the simple src SH3 domain accesses multiple unfolding pathways under force.^[60]

Other information

Incorrect protein folding and neurodegenerative disease

A protein is considered to be misfolded if it cannot achieve its normal native state. This can be due to mutations in the amino acid sequence or a disruption of the normal folding process by external factors.^[61] The misfolded protein typically contains β-sheets that are organized in a supramolecular arrangement known as a cross-β structure. These β-sheet-rich assemblies are very stable, very insoluble, and generally resistant to proteolysis.^[62] The structural stability of these fibrillar assemblies is caused by extensive interactions between the protein monomers, formed by backbone hydrogen bonds between their β-strands.^[62] The misfolding of proteins can trigger the further misfolding and accumulation of other proteins into aggregates or oligomers. The increased levels of aggregated proteins in the cell leads to formation of amyloid-like structures which can cause degenerative disorders and cell death.^[61] The amyloids are fibrillary structure that contain intermolecular hydrogen bonds, which are highly insoluble, and made from converted protein aggregates.^[61] Therefore, the proteasome pathway may not be efficient enough to degrade the misfolded proteins prior to aggregation. Misfolded proteins can interact with one another and form structured aggregates and gain toxicity through intermolecular interactions.^[61]

Aggregated proteins are associated with prion-related illnesses such as Creutzfeldt–Jakob disease, bovine spongiform encephalopathy (mad cow disease), amyloid-related illnesses such as Alzheimer's disease and familial amyloid cardiomyopathy or polyneuropathy,^[63] as well as intracellular aggregation diseases such as Huntington's and Parkinson's disease.^[4][64] These age onset degenerative diseases are associated with the aggregation of misfolded proteins into insoluble, extracellular aggregates and/or intracellular inclusions including cross-β amyloid fibrils. It is not completely clear whether the aggregates are the cause or merely a reflection of the loss of protein homeostasis, the balance between synthesis, folding, aggregation and protein turnover. Recently the European Medicines Agency approved the use of Tafamidis or Vyndaqel (a kinetic stabilizer of tetrameric transthyretin) for the treatment of transthyretin amyloid diseases. This suggests that the process of amyloid fibril formation (and not the fibrils themselves) causes the degeneration of post-mitotic tissue in human amyloid diseases.^[65] Misfolding and excessive degradation instead of folding and function leads to a number of proteopathy diseases such as antitrypsin-associated emphysema, cystic fibrosis and the lysosomal storage diseases, where loss of function is the origin of the disorder. While protein replacement therapy has historically been used to correct the latter disorders, an emerging approach is to use pharmaceutical chaperones to fold mutated proteins to render them functional.

Levinthal's paradox and kinetics

In 1969, Cyrus Levinthal noted that, because of the very large number of degrees of freedom in an unfolded polypeptide chain, the molecule has an astronomical number of possible conformations. An estimate of 3³⁰⁰ or 10¹⁴³ was made in one of his papers.^[66] Levinthal's paradox^[67] is a thought experiment based on the observation that if a protein were folded by sequentially sampling of all possible conformations, it would take an astronomical amount of time to do so, even if the conformations were sampled at a rapid rate (on the nanosecond or picosecond scale). Based upon the observation that proteins fold much faster than this, Levinthal then proposed that a random conformational search does not occur, and the protein must, therefore, fold through a series of meta-stable intermediate states.

The duration of the folding process varies dramatically depending on the protein of interest. When studied outside the cell, the slowest folding proteins require many minutes or hours to fold primarily due to proline isomerization, and must pass through a number of intermediate states, like checkpoints, before the process is complete.^[68] On the other hand, very small single-domain proteins with lengths of up to a hundred amino acids typically fold in a single step.^[69] Time scales of milliseconds are the norm and the very fastest known protein folding reactions are complete within a few microseconds.^[70]

Introduction to entropy

From Wikipedia, the free encyclopedia

Entropy is an important concept in the branch of physics known as thermodynamics. The idea of "irreversibility" is central to the understanding of entropy. Everyone has an intuitive understanding of irreversibility. If one watches a movie of everyday life running forward and in reverse, it is easy to distinguish between the two. The movie running in reverse shows impossible things happening – water jumping out of a glass into a pitcher above it, smoke going down a chimney, water in a glass freezing to form ice cubes, crashed cars reassembling themselves, and so on. The intuitive meaning of expressions such as "you can't unscramble an egg", or "you can't take the cream out of the coffee" is that these are irreversible processes. No matter how long you wait, the cream won't jump out of the coffee into the creamer.

In thermodynamics, one says that the "forward" processes – pouring water from a pitcher, smoke going up a chimney, etc. – are "irreversible": they cannot happen in reverse. All real physical processes involving systems in everyday life, with many atoms or molecules, are irreversible. For an irreversible process in an isolated system (a system not subject to outside influence), the thermodynamic state variable known as entropy is never decreasing. In everyday life, there may be processes in which the increase of entropy is practically unobservable, almost zero. In these cases, a movie of the process run in reverse will not seem unlikely. For example, in a 1-second video of the collision of two billiard balls, it will be hard to distinguish the forward and the backward case, because the increase of entropy during that time is relatively small. In thermodynamics, one says that this process is practically "reversible", with an entropy increase that is practically zero. The statement of the fact that the entropy of an isolated system never decreases is known as the second law of thermodynamics.

Classical thermodynamics is a physical theory which describes a "system" in terms of the thermodynamic variables of the system or its parts. Some thermodynamic variables are familiar: temperature, pressure, volume. Entropy is a thermodynamic variable which is less familiar and not as easily understood. A "system" is any region of space containing matter and energy: A cup of coffee, a glass of icewater, an automobile, an egg. Thermodynamic variables do not give a "complete" picture of the system. Thermodynamics makes no assumptions about the microscopic nature of a system and does not describe nor does it take into account the positions and velocities of the individual atoms and molecules which make up the system. Thermodynamics deals with matter in a macroscopic sense; it would be valid even if the atomic theory of matter were wrong. This is an important quality, because it means that reasoning based on thermodynamics is unlikely to require alteration as new facts about atomic structure and atomic interactions are found. The essence of thermodynamics is embodied in the four laws of thermodynamics.

Unfortunately, thermodynamics provides little insight into what is happening at a microscopic level.  Statistical mechanics is a physical theory which explains thermodynamics in microscopic terms. It explains thermodynamics in terms of the possible detailed microscopic situations the system may be in when the thermodynamic variables of the system are known. These are known as "microstates" whereas the description of the system in thermodynamic terms specifies the "macrostate" of the system. Many different microstates can yield the same macrostate. It is important to understand that statistical mechanics does not define temperature, pressure, entropy, etc. They are already defined by thermodynamics. Statistical mechanics serves to explain thermodynamics in terms of microscopic behavior of the atoms and molecules in the system.^{[1]:p.329,333}

In statistical mechanics, the entropy of a system is described as a measure of how many different microstates there are that could give rise to the macrostate that the system is in. The entropy of the system is given by Ludwig Boltzmann's famous equation:

${\displaystyle S=k\log(W)}$

where S is the entropy of the macrostate, k is Boltzmann's constant, and W is the total number of possible microstates that might yield the macrostate. The concept of irreversibility stems from the idea that if you have a system in an "unlikely" macrostate (log(W ) is relatively small) it will soon move to the "most likely" macrostate (with larger log(W )) and the entropy S will increase. A glass of warm water with an ice cube in it is unlikely to just happen, it must have been recently created, and the system will move to a more likely macrostate in which the ice cube is partially or entirely melted and the water is cooled. Statistical mechanics shows that the number of microstates which give ice and warm water is much smaller than the number of microstates that give the reduced ice mass and cooler water.

Explanation

The concept of thermodynamic entropy arises from the second law of thermodynamics. This law of entropy increase quantifies the reduction in the capacity of a system for change or determines whether a thermodynamic process may occur. For example, heat always flows from a region of higher temperature to one with lower temperature until temperature becomes uniform.

Entropy is calculated in two ways, the first is the entropy change (ΔS) to a system containing a sub-system which undergoes heat transfer to its surroundings (inside the system of interest). It is based on the macroscopic relationship between heat flow into the sub-system and the temperature at which it occurs summed over the boundary of that sub-system. The second calculates the absolute entropy (S) of a system based on the microscopic behaviour of its individual particles. This is based on the natural logarithm of the number of microstates possible in a particular macrostate (W or Ω) called the thermodynamic probability. Roughly, it gives the probability of the system's being in that state. In this sense it effectively defines entropy independently from its effects due to changes which may involve heat, mechanical, electrical, chemical energies etc. but also includes logical states such as information.

Following the formalism of Clausius, the first calculation can be mathematically stated as:^[2]

${\displaystyle {\rm {\delta }}S={\frac {{\rm {\delta }}q}{T}}.}$

Where δS is the increase or decrease in entropy, δq is the heat added to the system or subtracted from it, and T is temperature. The equal sign indicates that the change is reversible, because Clausius shows a proportional relationship between entropy and the energy flow, in a system, the heat energy can be transformed into work, and work can be transformed into heat through a cyclical process.^[3] If the temperature is allowed to vary, the equation must be integrated over the temperature path. This calculation of entropy change does not allow the determination of absolute value, only differences. In this context, the Second Law of Thermodynamics may be stated that for heat transferred over any valid process for any system, whether isolated or not,

${\displaystyle {{\rm {\delta }}S}\geq {\frac {{\rm {\delta }}q}{T}}.}$

According to the first law of thermodynamics, which deals with the conservation of energy, the loss δq of heat will result in a decrease in the internal energy of the thermodynamic system. Thermodynamic entropy provides a comparative measure of the amount of decrease in internal energy and the corresponding increase in internal energy of the surroundings at a given temperature. A simple and more concrete visualization of the second law is that energy of all types changes from being localized to becoming dispersed or spread out, if it is not hindered from doing so. Entropy change is the quantitative measure of that kind of a spontaneous process: how much energy has flowed or how widely it has become spread out at a specific temperature.

The second calculation defines entropy in absolute terms and comes from statistical mechanics. The entropy of a particular macrostate is defined to be Boltzmann's constant times the natural logarithm of the number of microstates corresponding to that macrostate, or mathematically

${\displaystyle S=k_{B}\ln \Omega ,\!}$

Where S is the entropy, k_B is Boltzmann's constant, and Ω is the number of microstates.

The macrostate of a system is what we know about the system, for example the temperature, pressure, and volume of a gas in a box. For each set of values of temperature, pressure, and volume there are many arrangements of molecules which result in those values. The number of arrangements of molecules which could result in the same values for temperature, pressure and volume is the number of microstates.

The concept of entropy has been developed to describe any of several phenomena, depending on the field and the context in which it is being used. Information entropy takes the mathematical concepts of statistical thermodynamics into areas of probability theory unconnected with heat and energy.

Ice melting provides an example of entropy increasing

Example of increasing entropy

Ice melting provides an example in which entropy increases in a small system, a thermodynamic system consisting of the surroundings (the warm room) and the entity of glass container, ice and water which has been allowed to reach thermodynamic equilibrium at the melting temperature of ice. In this system, some heat (δQ) from the warmer surroundings at 298 K (25 °C; 77 °F) transfers to the cooler system of ice and water at its constant temperature (T) of 273 K (0 °C; 32 °F), the melting temperature of ice. The entropy of the system, which is δQ/T, increases by δQ/273 K. The heat δQ for this process is the energy required to change water from the solid state to the liquid state, and is called the enthalpy of fusion, i.e. ΔH for ice fusion.

It is important to realize that the entropy of the surrounding room decreases less than the entropy of the ice and water increases: the room temperature of 298 K is larger than 273 K and therefore the ratio, (entropy change), of δQ/298 K for the surroundings is smaller than the ratio (entropy change), of δQ/273 K for the ice and water system. This is always true in spontaneous events in a thermodynamic system and it shows the predictive importance of entropy: the final net entropy after such an event is always greater than was the initial entropy.

As the temperature of the cool water rises to that of the room and the room further cools imperceptibly, the sum of the δQ/T over the continuous range, “at many increments”, in the initially cool to finally warm water can be found by calculus. The entire miniature ‘universe’, i.e. this thermodynamic system, has increased in entropy. Energy has spontaneously become more dispersed and spread out in that ‘universe’ than when the glass of ice and water was introduced and became a 'system' within it.

Origins and uses

Originally, entropy was named to describe the "waste heat," or more accurately, energy loss, from heat engines and other mechanical devices which could never run with 100% efficiency in converting energy into work. Later, the term came to acquire several additional descriptions, as more was understood about the behavior of molecules on the microscopic level. In the late 19th century, the word "disorder" was used by Ludwig Boltzmann in developing statistical views of entropy using probability theory to describe the increased molecular movement on the microscopic level. That was before quantum behavior came to be better understood by Werner Heisenberg and those who followed. Descriptions of thermodynamic (heat) entropy on the microscopic level are found in statistical thermodynamics and statistical mechanics.

For most of the 20th century, textbooks tended to describe entropy as "disorder", following Boltzmann's early conceptualisation of the "motional" (i.e. kinetic) energy of molecules. More recently, there has been a trend in chemistry and physics textbooks to describe entropy as energy dispersal.^[4] Entropy can also involve the dispersal of particles, which are themselves energetic. Thus there are instances where both particles and energy disperse at different rates when substances are mixed together.

The mathematics developed in statistical thermodynamics were found to be applicable in other disciplines. In particular, information sciences developed the concept of information entropy which lacks the Boltzmann constant inherent in thermodynamic entropy.

Heat and entropy

At a microscopic level, kinetic energy of molecules is responsible for the temperature of a substance or a system. “Heat” is the kinetic energy of molecules being transferred: when motional energy is transferred from hotter surroundings to a cooler system, faster-moving molecules in the surroundings collide with the walls of the system which transfers some of their energy to the molecules of the system and makes them move faster.

• Molecules in a gas like nitrogen at room temperature at any instant are moving at an average speed of nearly 500 miles per hour (210 m/s), repeatedly colliding and therefore exchanging energy so that their individual speeds are always changing. Assuming an ideal-gas model, average kinetic energy increases linearly with absolute temperature, so the average speed increases as the square root of temperature.
  
  
  • Thus motional molecular energy (‘heat energy’) from hotter surroundings, like faster-moving molecules in a flame or violently vibrating iron atoms in a hot plate, will melt or boil a substance (the system) at the temperature of its melting or boiling point. That amount of motional energy from the surroundings that is required for melting or boiling is called the phase-change energy, specifically the enthalpy of fusion or of vaporization, respectively. This phase-change energy breaks bonds between the molecules in the system (not chemical bonds inside the molecules that hold the atoms together) rather than contributing to the motional energy and making the molecules move any faster – so it does not raise the temperature, but instead enables the molecules to break free to move as a liquid or as a vapor.
  • In terms of energy, when a solid becomes a liquid or a vapor, motional energy coming from the surroundings is changed to ‘potential energy‘ in the substance (phase change energy, which is released back to the surroundings when the surroundings become cooler than the substance's boiling or melting temperature, respectively). Phase-change energy increases the entropy of a substance or system because it is energy that must be spread out in the system from the surroundings so that the substance can exist as a liquid or vapor at a temperature above its melting or boiling point. When this process occurs in a 'universe' that consists of the surroundings plus the system, the total energy of the 'universe' becomes more dispersed or spread out as part of the greater energy that was only in the hotter surroundings transfers so that some is in the cooler system. This energy dispersal increases the entropy of the 'universe'.

The important overall principle is that ”Energy of all types changes from being localized to becoming dispersed or spread out, if not hindered from doing so. Entropy (or better, entropy change) is the quantitative measure of that kind of a spontaneous process: how much energy has been transferred/T or how widely it has become spread out at a specific temperature."^{[citation needed]}

Classical calculation of entropy

When entropy was first defined and used in 1865 the very existence of atoms was still controversial and there was no concept that temperature was due to the motional energy of molecules or that “heat” was actually the transferring of that motional molecular energy from one place to another. Entropy change, ${\displaystyle \Delta S}$, was described in macroscopic terms that could be directly measured, such as volume, temperature, or pressure. However, today the classical equation of entropy, ${\displaystyle \Delta S={\frac {q_{rev}}{T}}}$ can be explained, part by part, in modern terms describing how molecules are responsible for what is happening:

• ${\displaystyle \Delta S}$ is the change in entropy of a system (some physical substance of interest) after some motional energy (“heat”) has been transferred to it by fast-moving molecules. So, ${\displaystyle \Delta S=S_{final}-S_{initial}}$.
• Then, ${\displaystyle \Delta S=S_{final}-S_{initial}={\frac {q_{rev}}{T}}}$, the quotient of the motional energy (“heat”) q that is transferred "reversibly" (rev) to the system from the surroundings (or from another system in contact with the first system) divided by T, the absolute temperature at which the transfer occurs.
  
  
  • “Reversible” or “reversibly” (rev) simply means that T, the temperature of the system, has to stay (almost) exactly the same while any energy is being transferred to or from it. That’s easy in the case of phase changes, where the system absolutely must stay in the solid or liquid form until enough energy is given to it to break bonds between the molecules before it can change to a liquid or a gas. For example, in the melting of ice at 273.15 K, no matter what temperature the surroundings are – from 273.20 K to 500 K or even higher, the temperature of the ice will stay at 273.15 K until the last molecules in the ice are changed to liquid water, i.e., until all the hydrogen bonds between the water molecules in ice are broken and new, less-exactly fixed hydrogen bonds between liquid water molecules are formed. This amount of energy necessary for ice melting per mole has been found to be 6008 joules at 273 K. Therefore, the entropy change per mole is
    
    ${\displaystyle {\frac {q_{rev}}{T}}={\frac {6008J}{273K}}}$, or 22 J/K.
    
  • When the temperature isn't at the melting or boiling point of a substance no intermolecular bond-breaking is possible, and so any motional molecular energy (“heat”) from the surroundings transferred to a system raises its temperature, making its molecules move faster and faster. As the temperature is constantly rising, there is no longer a particular value of “T” at which energy is transferred. However, a "reversible" energy transfer can be measured at a very small temperature increase, and a cumulative total can be found by adding each of many small temperature intervals or increments. For example, to find the entropy change ${\displaystyle {\frac {q_{rev}}{T}}}$ from 300 K to 310 K, measure the amount of energy transferred at dozens or hundreds of temperature increments, say from 300.00 K to 300.01 K and then 300.01 to 300.02 and so on, dividing the q by each T, and finally adding them all.
  • Calculus can be used to make this calculation easier if the effect of energy input to the system is linearly dependent on the temperature change, as in simple heating of a system at moderate to relatively high temperatures. Thus, the energy being transferred “per incremental change in temperature” (the heat capacity, ${\displaystyle C_{p}}$), multiplied by the integral of
    
    ${\displaystyle {\frac {dT}{T}}}$ from ${\displaystyle T_{initial}}$ to ${\displaystyle T_{final}}$, is directly given by ${\displaystyle \Delta S=C_{p}\ln {\frac {T_{final}}{T_{initial}}}}$.

Introductory descriptions of entropy

• As a measure of disorder: Traditionally, 20th century textbooks have introduced entropy as order and disorder so that it provides "a measurement of the disorder or randomness of a system". It has been argued that ambiguities in the terms used (such as "disorder" and "chaos") contribute to widespread confusion and can hinder comprehension of entropy for most students. On the other hand, "disorder" may be very clearly defined as the Shannon entropy of the probability distribution of microstates given a particular macrostate,^[1]:p.379 in which case the connection of "disorder" to thermodynamic entropy is straightforward, but not immediately obvious to anyone unfamiliar with information theory.
• Energy dispersal: A more recent formulation associated with Frank L. Lambert describes entropy as energy dispersal.^[4] As with "disorder", the meaning of the term "dispersal" must be taken in a very specific way, which is quite different than the lay meaning of "dispersal". While an increase in entropy is often associated with a spatial reduction in the concentration of the energy density, and never with an increase, counterexamples exist which illustrate that the concept of "dispersal" is not immediately obvious. Most counterexamples may be included in the concept of "dispersal" when the "space" in which the dispersal occurs includes the space of quantum energy levels versus population numbers, but this reduces the effectiveness of the spreading concept as an introduction to the concept of entropy.
• As a measure of energy unavailable for work: This is an often-repeated phrase which requires considerable clarification in order to be understood. It is not true except for cyclic reversible processes and is in this sense misleading. Given a container of gas, ALL of its internal energy may be converted to work. (More accurately, the amount of work that may be converted can be made arbitrarily close to the total internal energy.) More precisely, for an isolated system comprising two closed systems at different temperatures, in a process of equilibration the amount of entropy lost by the hot system is a measure of the amount of energy lost by the hot system that is unavailable for work. As a description of the fundamental nature of entropy, it can be misleading in this sense.

Entropic force

From Wikipedia, the free encyclopedia

In physics, an entropic force acting in a system is a force resulting from the entire system's thermodynamical tendency to increase its entropy, rather than from a particular underlying microscopic force.^[1]

For instance, the internal energy of an ideal gas depends only on its temperature, and not on the volume of its containing box, so it is not an energy effect that tends to increase the volume of the box as gas pressure does. This implies that the pressure of an ideal gas has an entropic origin.^[2]

What is the origin of such an entropic force? The most general answer is that the effect of thermal fluctuations tends to bring a thermodynamic system toward a macroscopic state that corresponds to a maximum in the number of microscopic states (or micro-states) that are compatible with this macroscopic state. In other words, thermal fluctuations tend to bring a system toward its macroscopic state of maximum entropy.^[2]

Mathematical formulation

In the canonical ensemble, the entropic force ${\displaystyle \mathbf {F} }$ associated to a macrostate partition ${\displaystyle \{\mathbf {X} \}}$ is given by:^[3][4]

${\displaystyle \mathbf {F} (\mathbf {X_{0}} )=T\nabla _{\mathbf {X} }S(\mathbf {X} )|_{\mathbf {X} _{0}}}$



where ${\displaystyle T}$ is the temperature, ${\displaystyle S(\mathbf {X} )}$ is the entropy associated to the macrostate ${\displaystyle \mathbf {X} }$ and ${\displaystyle \mathbf {X_{0}} }$ is the present macrostate.

Examples

Brownian motion

The entropic approach to Brownian movement was initially proposed by R. M. Neumann.^[3][5] Neumann derived the entropic force for a particle undergoing three-dimensional Brownian motion using the Boltzmann equation, denoting this force as a diffusional driving force or radial force. In the paper, three example systems are shown to exhibit such a force:

• electrostatic system of molten salt
• surface tension and
• Elasticity of rubber.

Polymers

A standard example of an entropic force is the elasticity of a freely-jointed polymer molecule.^[5] For an ideal chain, maximizing its entropy means reducing the distance between its two free ends. Consequently, a force that tends to collapse the chain is exerted by the ideal chain between its two free ends. This entropic force is proportional to the distance between the two ends.^[2][6] The entropic force by a freely-jointed chain has a clear mechanical origin, and can be computed using constrained Lagrangian dynamics.^[7]

Hydrophobic force

Water drops on the surface of grass.

Another example of an entropic force is the hydrophobic force. At room temperature, it partly originates from the loss of entropy by the 3D network of water molecules when they interact with molecules of dissolved substance. Each water molecule is capable of

• donating two hydrogen bonds through the two protons
• accepting two more hydrogen bonds through the two sp³-hybridized lone pairs

Therefore, water molecules can form an extended three-dimensional network. Introduction of a non-hydrogen-bonding surface disrupts this network. The water molecules rearrange themselves around the surface, so as to minimize the number of disrupted hydrogen bonds. This is in contrast to hydrogen fluoride (which can accept 3 but donate only 1) or ammonia (which can donate 3 but accept only 1), which mainly form linear chains.

If the introduced surface had an ionic or polar nature, there would be water molecules standing upright on 1 (along the axis of an orbital for ionic bond) or 2 (along a resultant polarity axis) of the four sp³ orbitals.^[8] These orientations allow easy movement, i.e. degrees of freedom, and thus lowers entropy minimally. But a non-hydrogen-bonding surface with a moderate curvature forces the water molecule to sit tight on the surface, spreading 3 hydrogen bonds tangential to the surface, which then become locked in a clathrate-like basket shape. Water molecules involved in this clathrate-like basket around the non-hydrogen-bonding surface are constrained in their orientation. Thus, any event that would minimize such a surface is entropically favored. For example, when two such hydrophobic particles come very close, the clathrate-like baskets surrounding them merge. This releases some of the water molecules into the bulk of the water, leading to an increase in entropy.

Another related and counter-intuitive example of entropic force is protein folding, which is a spontaneous process and where hydrophobic effect also plays a role.^[9] Structures of water-soluble proteins typically have a core in which hydrophobic side chains are buried from water, which stabilizes the folded state.^[10] Charged and polar side chains are situated on the solvent-exposed surface where they interact with surrounding water molecules. Minimizing the number of hydrophobic side chains exposed to water is the principal driving force behind the folding process,^{[10][11] [12]} although formation of hydrogen bonds within the protein also stabilizes protein structure.^[13][14]

Colloids

Entropic forces are important and widespread in the physics of colloids,^[15] where they are responsible for the depletion force, and the ordering of hard particles, such as the crystallization of hard spheres, the isotropic-nematic transition in liquid crystal phases of hard rods, and the ordering of hard polyhedra.^[15][16] Entropic forces arise in colloidal systems due to the osmotic pressure that comes from particle crowding. This was first discovered in, and is most intuitive for, colloid-polymer mixtures described by the Asakura-Oosawa model. In this model, polymers are approximated as finite-sized spheres that can penetrate one another, but cannot penetrate the colloidal particles. The inability of the polymers to penetrate the colloids leads to a region around the colloids in which the polymer density is reduced. If the regions of reduced polymer density around two colloids overlap with one another, by means of the colloids approaching one another, the polymers in the system gain an additional free volume that is equal to the volume of the intersection of the reduced density regions. The additional free volume causes an increase in the entropy of the polymers, and drives them to form locally dense-packed aggregates. A similar effect occurs in sufficiently dense colloidal systems without polymers, where osmotic pressure also drives the local dense packing^[15] of colloids into a diverse array of structures ^[16] that can be rationally designed by modifying the shape of the particles.^[17]

Controversial examples

Some forces that are generally regarded as conventional forces have been argued to be actually entropic in nature. These theories remain controversial and are the subject of ongoing work. Matt Visser, professor of mathematics at Victoria University of Wellington, NZ in "Conservative Entropic Forces" ^[18] criticizes selected approaches but generally concludes:

There is no reasonable doubt concerning the physical reality of entropic forces, and no reasonable doubt that classical (and semi-classical) general relativity is closely related to thermodynamics. Based on the work of Jacobson, Thanu Padmanabhan, and others, there are also good reasons to suspect a thermodynamic interpretation of the fully relativistic Einstein equations might be possible.

Gravity

In 2009, Erik Verlinde argued that gravity can be explained as an entropic force.^[19] It claimed (similar to Jacobson's result) that gravity is a consequence of the "information associated with the positions of material bodies". This model combines the thermodynamic approach to gravity with Gerard 't Hooft's holographic principle. It implies that gravity is not a fundamental interaction, but an emergent phenomenon.^[19]

Other forces

In the wake of the discussion started by Erik Verlinde, entropic explanations for other fundamental forces have been suggested,^[18] including Coulomb's law,^[20][21][22] the electroweak and strong forces.^[23] The same approach was argued to explain dark matter, dark energy and Pioneer effect.^[24]

Links to adaptive behavior

It was argued that causal entropic forces lead to spontaneous emergence of tool use and social cooperation.^[25][26][27] Causal entropic forces by definition maximize entropy production between the present and future time horizon, rather than just greedily maximizing instantaneous entropy production like typical entropic forces.

A formal simultaneous connection between the mathematical structure of the discovered laws of nature, intelligence and the entropy-like measures of complexity was previously noted in 2000 by Andrei Soklakov^[28][29] in the context of Occam's razor principle.