From Wikipedia, the free encyclopedia
Visualization of heat transfer in a pump casing, created by solving the
heat equation.
Heat is being generated internally in the casing and being cooled at the boundary, providing a
steady state temperature distribution.
A
differential equation is a
mathematical equation that relates some
function with its
derivatives.
In applications, the functions usually represent physical quantities,
the derivatives represent their rates of change, and the equation
defines a relationship between the two. Because such relations are
extremely common, differential equations play a prominent role in many
disciplines including
engineering,
physics,
economics, and
biology.
In
pure mathematics,
differential equations are studied from several different perspectives,
mostly concerned with their solutions—the set of functions that satisfy
the equation. Only the simplest differential equations are solvable by
explicit formulas; however, some properties of solutions of a given
differential equation may be determined without finding their exact
form.
If a self-contained formula for the solution is not available, the
solution may be numerically approximated using computers. The theory of
dynamical systems puts emphasis on
qualitative analysis of systems described by differential equations, while many
numerical methods have been developed to determine solutions with a given degree of accuracy.
History
Differential equations first came into existence with the invention of
calculus by
Newton and
Leibniz. In Chapter 2 of his 1671 work
"Methodus fluxionum et Serierum Infinitarum",
[1] Isaac Newton listed three kinds of differential equations:
![{\displaystyle {\begin{aligned}&{\frac {dy}{dx}}=f(x)\\[5pt]&{\frac {dy}{dx}}=f(x,y)\\[5pt]&x_{1}{\frac {\partial y}{\partial x_{1}}}+x_{2}{\frac {\partial y}{\partial x_{2}}}=y\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a1cd29ae411a2d09205b3b39aec038af563d5e2)
He solves these examples and others using infinite series and discusses the non-uniqueness of solutions.
Jacob Bernoulli proposed the
Bernoulli differential equation in 1695.
[2] This is an
ordinary differential equation of the form

for which the following year Leibniz obtained solutions by simplifying it.
[3]
Historically, the problem of a vibrating string such as that of a
musical instrument was studied by
Jean le Rond d'Alembert,
Leonhard Euler,
Daniel Bernoulli, and
Joseph-Louis Lagrange.
[4][5][6][7]
In 1746, d’Alembert discovered the one-dimensional wave equation, and
within ten years Euler discovered the three-dimensional wave equation.
[8]
The
Euler–Lagrange equation was developed in the 1750s by Euler and Lagrange in connection with their studies of the
tautochrone
problem. This is the problem of determining a curve on which a weighted
particle will fall to a fixed point in a fixed amount of time,
independent of the starting point.
Lagrange solved this problem in 1755 and sent the solution to Euler. Both further developed Lagrange's method and applied it to
mechanics, which led to the formulation of
Lagrangian mechanics.
In 1822,
Fourier published his work on
heat flow in
Théorie analytique de la chaleur (The Analytic Theory of Heat),
[9] in which he based his reasoning on
Newton's law of cooling,
namely, that the flow of heat between two adjacent molecules is
proportional to the extremely small difference of their temperatures.
Contained in this book was Fourier's proposal of his
heat equation for conductive diffusion of heat. This partial differential equation is now taught to every student of mathematical physics.
Example
For example, in
classical mechanics, the motion of a body is described by its position and velocity as the time value varies.
Newton's laws
allow these variables to be expressed dynamically (given the position,
velocity, acceleration and various forces acting on the body) as a
differential equation for the unknown position of the body as a function
of time.
In some cases, this differential equation (called an
equation of motion) may be solved explicitly.
An example of modelling a real world problem using differential
equations is the determination of the velocity of a ball falling through
the air, considering only gravity and air resistance. The ball's
acceleration towards the ground is the acceleration due to gravity minus
the acceleration due to air resistance. Gravity is considered constant,
and air resistance may be modeled as proportional to the ball's
velocity. This means that the ball's acceleration, which is a derivative
of its velocity, depends on the velocity (and the velocity depends on
time). Finding the velocity as a function of time involves solving a
differential equation and verifying its validity.
Types
Differential
equations can be divided into several types. Apart from describing the
properties of the equation itself, these classes of differential
equations can help inform the choice of approach to a solution. Commonly
used distinctions include whether the equation is: Ordinary/Partial,
Linear/Non-linear, and Homogeneous/Inhomogeneous. This list is far from
exhaustive; there are many other properties and subclasses of
differential equations which can be very useful in specific contexts.
Ordinary differential equations
An
ordinary differential equation (
ODE) is an equation containing an unknown
function of one real or complex variable x, its derivatives, and some given functions of
x. The unknown function is generally represented by a
variable (often denoted
y), which, therefore,
depends on
x. Thus
x is often called the
independent variable of the equation. The term "
ordinary" is used in contrast with the term
partial differential equation, which may be with respect to
more than one independent variable.
Linear differential equations are the differential equations that are
linear
in the unknown function and its derivatives. Their theory is well
developed, and, in many cases, one may express their solutions in terms
of
integrals.
Most ODEs that are encountered in
physics are linear, and, therefore, most
special functions may be defined as solutions of linear differential equations.
As, in general, the solutions of a differential equation cannot be expressed by a
closed-form expression,
numerical methods are commonly used for solving differential equations on a computer.
Partial differential equations
A
partial differential equation (
PDE) is a differential equation that contains unknown
multivariable functions and their
partial derivatives. (This is in contrast to
ordinary differential equations,
which deal with functions of a single variable and their derivatives.)
PDEs are used to formulate problems involving functions of several
variables, and are either solved in closed form, or used to create a
relevant
computer model.
PDEs can be used to describe a wide variety of phenomena in nature such as
sound,
heat,
electrostatics,
electrodynamics,
fluid flow,
elasticity, or
quantum mechanics.
These seemingly distinct physical phenomena can be formalised similarly
in terms of PDEs. Just as ordinary differential equations often model
one-dimensional
dynamical systems, partial differential equations often model
multidimensional systems. PDEs find their generalisation in
stochastic partial differential equations.
Non-linear differential equations
Non-linear differential equations are formed by the
products of the unknown function and its derivatives are allowed and its degree is
>
1. There are very few methods of solving nonlinear differential
equations exactly; those that are known typically depend on the equation
having particular
symmetries. Nonlinear differential equations can exhibit very complicated behavior over extended time intervals, characteristic of
chaos.
Even the fundamental questions of existence, uniqueness, and
extendability of solutions for nonlinear differential equations, and
well-posedness of initial and boundary value problems for nonlinear PDEs
are hard problems and their resolution in special cases is considered
to be a significant advance in the mathematical theory (cf.
Navier–Stokes existence and smoothness).
However, if the differential equation is a correctly formulated
representation of a meaningful physical process, then one expects it to
have a solution.
[10]
Linear differential equations frequently appear as
approximations
to nonlinear equations. These approximations are only valid under
restricted conditions. For example, the harmonic oscillator equation is
an approximation to the nonlinear pendulum equation that is valid for
small amplitude oscillations.
Equation order
Differential equations are described by their order, determined by the term with the
highest derivatives. An equation containing only first derivatives is a
first-order differential equation, an equation containing the
second derivative is a
second-order differential equation, and so on.
[11][12] Differential equations that describe natural phenomena almost always
have only first and second order derivatives in them, but there are some
exceptions, such as the
thin film equation, which is a fourth order partial differential equation.
Examples
In the first group of examples, let
u be an unknown function of
x, and let
c &
ω be known constants. Note both ordinary and partial differential equations are broadly classified as
linear and
nonlinear.
- Inhomogeneous first-order linear constant coefficient ordinary differential equation:
-

- Homogeneous second-order linear ordinary differential equation:
-

- Homogeneous second-order linear constant coefficient ordinary differential equation describing the harmonic oscillator:
-

- Inhomogeneous first-order nonlinear ordinary differential equation:
-

- Second-order nonlinear (due to sine function) ordinary differential equation describing the motion of a pendulum of length L:
-

In the next group of examples, the unknown function
u depends on two variables
x and
t or
x and
y.
- Homogeneous first-order linear partial differential equation:
-

- Homogeneous second-order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:
-

-

Existence of solutions
Solving differential equations is not like solving
algebraic equations.
Not only are their solutions often unclear, but whether solutions are
unique or exist at all are also notable subjects of interest.
For first order initial value problems, the
Peano existence theorem gives one set of circumstances in which a solution exists. Given any point

in the xy-plane, define some rectangular region

, such that
![Z=[l,m]\times [n,p]](https://wikimedia.org/api/rest_v1/media/math/render/svg/515b71ad3b5fc01ff532df8cb71018baca811973)
and

is in the interior of

. If we are given a differential equation

and the condition that

when

, then there is locally a solution to this problem if

and

are both continuous on

. This solution exists on some interval with its center at

. The solution may not be unique. (See
Ordinary differential equation for other results.)
However, this only helps us with first order initial value problems.
Suppose we had a linear initial value problem of the nth order:

such that

For any nonzero

, if

and

are continuous on some interval containing

,

is unique and exists.
[13]
Related concepts
Connection to difference equations
The theory of differential equations is closely related to the theory of
difference equations,
in which the coordinates assume only discrete values, and the
relationship involves values of the unknown function or functions and
values at nearby coordinates. Many methods to compute numerical
solutions of differential equations or study the properties of
differential equations involve the approximation of the solution of a
differential equation by the solution of a corresponding difference
equation.
Applications
The study of differential equations is a wide field in
pure and
applied mathematics,
physics, and
engineering.
All of these disciplines are concerned with the properties of
differential equations of various types. Pure mathematics focuses on the
existence and uniqueness of solutions, while applied mathematics
emphasizes the rigorous justification of the methods for approximating
solutions. Differential equations play an important role in modelling
virtually every physical, technical, or biological process, from
celestial motion, to bridge design, to interactions between neurons. Differential equations such as those used to solve real-life problems
may not necessarily be directly solvable, i.e. do not have
closed form solutions. Instead, solutions can be approximated using
numerical methods.
Many fundamental laws of
physics and
chemistry can be formulated as differential equations. In
biology and
economics, differential equations are used to
model
the behavior of complex systems. The mathematical theory of
differential equations first developed together with the sciences where
the equations had originated and where the results found application.
However, diverse problems, sometimes originating in quite distinct
scientific fields, may give rise to identical differential equations.
Whenever this happens, mathematical theory behind the equations can be
viewed as a unifying principle behind diverse phenomena. As an example,
consider the propagation of light and sound in the atmosphere, and of
waves on the surface of a pond. All of them may be described by the same
second-order
partial differential equation, the
wave equation,
which allows us to think of light and sound as forms of waves, much
like familiar waves in the water. Conduction of heat, the theory of
which was developed by
Joseph Fourier, is governed by another second-order partial differential equation, the
heat equation. It turns out that many
diffusion processes, while seemingly different, are described by the same equation; the
Black–Scholes equation in finance is, for instance, related to the heat equation.
Physics
Classical mechanics
So long as the force acting on a particle is known,
Newton's second law
is sufficient to describe the motion of a particle. Once independent
relations for each force acting on a particle are available, they can be
substituted into Newton's second law to obtain an
ordinary differential equation, which is called the
equation of motion.
Electrodynamics
Maxwell's equations are a set of
partial differential equations that, together with the
Lorentz force law, form the foundation of
classical electrodynamics, classical
optics, and
electric circuits. These fields in turn underlie modern electrical and communications technologies. Maxwell's equations describe how
electric and
magnetic fields are generated and altered by each other and by
charges and
currents. They are named after the Scottish physicist and mathematician
James Clerk Maxwell, who published an early form of those equations between 1861 and 1862.
General relativity
The
Einstein field equations (EFE; also known as "Einstein's equations") are a set of ten
partial differential equations in
Albert Einstein's
general theory of relativity which describe the
fundamental interaction of
gravitation as a result of
spacetime being
curved by
matter and
energy.
[14] First published by Einstein in 1915
[15] as a
tensor equation, the EFE equate local spacetime
curvature (expressed by the
Einstein tensor) with the local energy and
momentum within that spacetime (expressed by the
stress–energy tensor).
[16]
Quantum mechanics
In quantum mechanics, the analogue of Newton's law is
Schrödinger's equation
(a partial differential equation) for a quantum system (usually atoms,
molecules, and subatomic particles whether free, bound, or localized).
It is not a simple algebraic equation, but in general a
linear partial differential equation, describing the time-evolution of the system's
wave function (also called a "state function").
[17]
Biology
Predator-prey equations
The
Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order,
non-linear, differential equations frequently used to describe the
population dynamics of two species that interact, one as a predator and the other as prey.
Chemistry
The
rate law or
rate equation for a
chemical reaction is a differential equation that links the
reaction rate with concentrations or pressures of reactants and constant parameters (normally rate coefficients and partial
reaction orders).
[18] To determine the rate equation for a particular system one combines the reaction rate with a
mass balance for the system.
[19] In addition, a range of differential equations are present in the study of
thermodynamics and
quantum mechanics.
Economics
 are the variables or unknowns, and
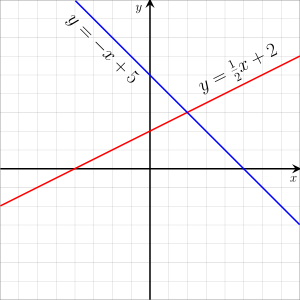
are the variables or unknowns, and  are coefficients, which are often real numbers, but may be parameters, or even any expression that does not contain the unknowns. In other words, a linear equation is obtained by equating to zero a linear polynomial.
are coefficients, which are often real numbers, but may be parameters, or even any expression that does not contain the unknowns. In other words, a linear equation is obtained by equating to zero a linear polynomial. are real numbers. The graph of such a linear function is thus the set of the solutions of this linear equation, which is a line in the Euclidean plane of slope m and y-intercept
are real numbers. The graph of such a linear function is thus the set of the solutions of this linear equation, which is a line in the Euclidean plane of slope m and y-intercept  .
. , so
, so  . Expressing y as a function of x gives the form:
. Expressing y as a function of x gives the form: , so
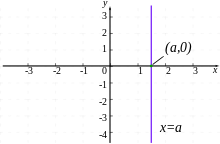
, so  , expressing the x intercept in terms of the y intercept and slope, or conversely.
, expressing the x intercept in terms of the y intercept and slope, or conversely. and
and  are unique points on the line, then
are unique points on the line, then  will also be a point on the line if the following is true:
will also be a point on the line if the following is true: ,
,  and
and  . Thus
. Thus  and
and  , then the above equation becomes:
, then the above equation becomes: would result in the “Two-point form” shown above, but leaving it here allows the equation to still be valid when
would result in the “Two-point form” shown above, but leaving it here allows the equation to still be valid when  .
.





































![{\displaystyle {\begin{aligned}&{\frac {dy}{dx}}=f(x)\\[5pt]&{\frac {dy}{dx}}=f(x,y)\\[5pt]&x_{1}{\frac {\partial y}{\partial x_{1}}}+x_{2}{\frac {\partial y}{\partial x_{2}}}=y\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a1cd29ae411a2d09205b3b39aec038af563d5e2)











![Z=[l,m]\times [n,p]](https://wikimedia.org/api/rest_v1/media/math/render/svg/515b71ad3b5fc01ff532df8cb71018baca811973)













![{\frac {\partial k(t)}{\partial t}}=s[k(t)]^{\alpha }-\delta k(t)](https://wikimedia.org/api/rest_v1/media/math/render/svg/5784be3732078094538b9f4b94468d3f242dc23b)
