From Wikipedia, the free encyclopedia
Parmenides was among the first to propose an ontological characterization of the fundamental nature of reality.
Ontology is the
philosophical study of the nature of
being,
becoming,
existence, or
reality, as well as the basic
categories of being and their relations.
[1] Traditionally listed as a part of the major branch of philosophy known as
metaphysics, ontology often deals with questions concerning what
entities exist or may be said to exist and how such entities may be grouped, related within a
hierarchy, and subdivided according to similarities and differences. A very simple
definition of ontology is that it is the examination of what is meant by 'being'.
Etymology
The
compound word
ontology combines
onto-, from the
Greek ὄν,
on (
gen. ὄντος,
ontos), i.e. "being; that which is", which is the
present participle of the
verb εἰμί,
eimí, i.e. "to be, I am", and
-λογία,
-logia, i.e. "logical discourse", see
classical compounds for this type of word formation.
[2][3]
While the
etymology is Greek, the oldest extant record of the word itself, the
New Latin form
ontologia, appeared in 1606 in the work
Ogdoas Scholastica by
Jacob Lorhard (
Lorhardus) and in 1613 in the
Lexicon philosophicum by
Rudolf Göckel (
Goclenius).
The first occurrence in English of
ontology as recorded by the
OED (
Oxford English Dictionary, online edition, 2008) came in a work by Gideon Harvey (1636/7–1702):
Archelogia
philosophica nova; or, New principles of Philosophy. Containing
Philosophy in general, Metaphysicks or Ontology, Dynamilogy or a
Discourse of Power, Religio Philosophi or Natural Theology, Physicks or
Natural philosophy, London, Thomson, 1663. The word was first used
in its Latin form by philosophers based on the Latin roots, which
themselves are based on the Greek.
Leibniz is the only one of the great philosophers of the 17th century to have used the term
ontology.
[4]
Overview
Some philosophers, notably in the traditions of the
Platonic school, contend that all nouns (including
abstract nouns) refer to existent entities.
[citation needed]
Other philosophers contend that nouns do not always name entities, but
that some provide a kind of shorthand for reference to a collection
either of
objects or of
events. In this latter view,
mind, instead of referring to an entity, refers to a collection of
mental events experienced by a
person;
society refers to a collection of
persons with some shared characteristics, and
geometry refers to a collection of specific kinds of intellectual activities.
Between these poles of
realism and
nominalism stand a variety of
other positions.
Some fundamental questions
Principal questions of ontology include:
- "What can be said to exist?"
- "What is a thing?"[6]
- "Into what categories, if any, can we sort existing things?"
- "What are the meanings of being?"
- "What are the various modes of being of entities?"
Various
philosophers
have provided different answers to these questions. One common approach
involves dividing the extant subjects and predicates into groups called
categories.
Such lists of categories differ widely from one another, and it is
through the co-ordination of different categorical schemes that ontology
relates to such fields as
library science and
artificial intelligence. Such an understanding of ontological categories, however, is merely
taxonomic, classificatory. Aristotle's categories are the ways in which a being may be addressed simply as a being, such as:
[7]
- what it is (its 'whatness', quiddity, haecceity or essence)
- how it is (its 'howness' or qualitativeness)
- how much it is (quantitativeness)
- where it is, its relatedness to other beings
Further examples of ontological questions include:
[citation needed]
- What is existence, i.e. what does it mean for a being to be?
- Is existence a property?
- Is existence a genus or general class that is simply divided up by specific differences?
- Which entities, if any, are fundamental?
- Are all entities objects?
- How do the properties of an object relate to the object itself?
- Do physical properties actually exist?
- What features are the essential, as opposed to merely accidental attributes of a given object?
- How many levels of existence or ontological levels are there? And what constitutes a "level"?
- What is a physical object?
- Can one give an account of what it means to say that a physical object exists?
- Can one give an account of what it means to say that a non-physical entity exists?
- What constitutes the identity of an object?
- When does an object go out of existence, as opposed to merely changing?
- Do beings exist other than in the modes of objectivity and
subjectivity, i.e. is the subject/object split of modern philosophy
inevitable?
Concepts
Essential ontological
dichotomies include:
Types
Philosophers can classify ontologies in various ways, using criteria such as the degree of abstraction and field of application:
[8]
- Upper ontology: concepts supporting development of an ontology, meta-ontology
- Domain ontology: concepts relevant to a particular topic or
area of interest, for example, to information technology or to computer
languages, or to particular branches of science
- Interface ontology: concepts relevant to the juncture of two disciplines
- Process ontology: inputs, outputs, constraints, sequencing information, involved in business or engineering processes
History
Origins
Ontology was referred to as
Tattva Mimamsa by ancient Indian
philosophers going back as early as Vedas.
[citation needed] Ontology is an aspect of the
Samkhya school of philosophy from the first millennium BCE.
[9] The concept of
Guna which describes the three properties (
sattva,
rajas and
tamas) present in differing proportions in all existing things, is a notable concept of this school.
Parmenides and monism
Parmenides
was among the first in the Greek tradition to propose an ontological
characterization of the fundamental nature of existence. In his prologue
or
proem he describes two views of
existence; initially that nothing comes from nothing, and therefore
existence is
eternal. Consequently, our opinions about truth must often be false and deceitful. Most of
western philosophy — including the fundamental concepts of
falsifiability
— have emerged from this view. This posits that existence is what may
be conceived of by thought, created, or possessed. Hence, there may be
neither void nor vacuum; and true reality neither may come into being
nor vanish from existence. Rather, the entirety of creation is eternal,
uniform, and immutable, though not infinite (he characterized its shape
as that of a perfect sphere). Parmenides thus posits that change, as
perceived in everyday experience, is illusory. Everything that may be
apprehended is but one part of a single entity. This idea somewhat
anticipates the modern concept of an ultimate
grand unification theory that finally describes all of existence in terms of one inter-related
sub-atomic reality which applies to everything.
Ontological pluralism
The opposite of
eleatic monism is the pluralistic conception of
Being. In the 5th century BC,
Anaxagoras and
Leucippus replaced
[10] the reality of Being (unique and unchanging) with that of
Becoming and therefore by a more fundamental and elementary
ontic
plurality. This thesis originated in the Hellenic world, stated in two
different ways by Anaxagoras and by Leucippus. The first theory dealt
with "seeds" (which Aristotle referred to as "homeomeries") of the
various substances. The second was the atomistic theory,
[11] which dealt with reality as based on the
vacuum, the atoms and their intrinsic movement in it.
The materialist
atomism proposed by Leucippus was
indeterminist, but then developed by
Democritus in a
deterministic way. It was later (4th century BC) that the original atomism was taken again as indeterministic by
Epicurus. He confirmed the reality as composed of an infinity of indivisible, unchangeable corpuscles or
atoms (
atomon,
lit. 'uncuttable'), but he gives weight to characterize atoms while for
Leucippus they are characterized by a "figure", an "order" and a
"position" in the cosmos.
[12] They are, besides, creating the whole with the intrinsic movement in the
vacuum, producing the diverse flux of being. Their movement is influenced by the
parenklisis (
Lucretius names it
clinamen) and that is determined by the
chance. These ideas foreshadowed our understanding of
traditional physics until the nature of atoms was discovered in the 20th century.
[13]
Plato
Plato developed this distinction between true reality and illusion, in arguing that what is real are eternal and unchanging
Forms or Ideas (a precursor to
universals),
of which things experienced in sensation are at best merely copies, and
real only in so far as they copy ('partake of') such Forms. In general,
Plato presumes that all nouns (e.g., 'Beauty') refer to real entities,
whether sensible bodies or insensible Forms. Hence, in
The Sophist
Plato argues that Being is a Form in which all existent things
participate and which they have in common (though it is unclear whether
'Being' is intended in the sense of
existence,
copula, or
identity); and argues, against Parmenides, that Forms must exist not only of Being, but also of
Negation and of non-Being (or Difference).
In his
Categories,
Aristotle identifies ten possible kinds of things that may be the
subject or the predicate of a proposition. For Aristotle there are four
different ontological dimensions:
- according to the various categories or ways of addressing a being as such
- according to its truth or falsity (e.g. fake gold, counterfeit money)
- whether it exists in and of itself or simply 'comes along' by accident
- according to its potency, movement (energy) or finished presence (Metaphysics Book Theta).
According to
Avicenna, and in an interpretation of Greek Aristotelian and Platonist ontological doctrines in medieval
metaphysics, being is either necessary, contingent
qua possible, or impossible. Necessary being is that which cannot but be, since its non-being entails a contradiction. Contingent
qua
possible being is neither necessary nor impossible for it to be or not
to be. It is ontologically neutral, and is brought from potential
existing into actual existence by way of a cause that is external to its
essence. Its being is borrowed unlike the necessary existent, which is
self-subsisting and is impossible for it not to be. As for the
impossible, it necessarily does not exist, and the affirmation of its
being is a contradiction.
[14]
Other ontological topics
Ontological formations
The
concept of 'ontological formations' refers to formations of social
relations understood as dominant ways of living. Temporal, spatial,
corporeal, epistemological and performative relations are taken to be
central to understanding a dominant formation. That is, a particular
ontological formation is based on how ontological categories of time,
space, embodiment, knowing and performing are lived—objectively and
subjectively. Different ontological formations include the customary
(including the tribal), the traditional, the modern and the postmodern.
The concept was first introduced by
Paul James' Globalism, Nationalism, Tribalism[15] together with a series of writers including Damian Grenfell and
Manfred Steger.
In the
engaged theory
approach, ontological formations are seen as layered and intersecting
rather than singular formations. They are 'formations of being'. This
approach avoids the usual problems of a Great Divide being posited
between the modern and the pre-modern. From a philosophical distinction
concerning different formations of being, the concept then provides a
way of translating into practical understandings concerning how humans
might design cities and communities that live creatively across
different ontological formations, for example cities that are not
completely dominated by modern valences of spatial configuration. Here
the work of Tony Fry is important.
[16]
Ontological and epistemological certainty
René Descartes, with
je pense donc je suis or
cogito ergo sum or "I think, therefore I am", argued that "the self" is something that we can know exists with
epistemological certainty. Descartes argued further that this knowledge could lead to a proof of the certainty of the
existence of God, using the
ontological argument that had been formulated first by
Anselm of Canterbury.
Certainty about the existence of "the self" and "the other",
however, came under increasing criticism in the 20th century.
Sociological theorists, most notably
George Herbert Mead and
Erving Goffman, saw the
Cartesian Other
as a "Generalized Other", the imaginary audience that individuals use
when thinking about the self. According to Mead, "we do not assume there
is a self to begin with. Self is not presupposed as a stuff out of
which the world arises. Rather, the self arises in the world".
[17][18] The Cartesian Other was also used by
Sigmund Freud, who saw the
superego as an abstract regulatory force, and
Émile Durkheim who viewed this as a psychologically manifested entity which represented God in society at large.
Body and environment, questioning the meaning of being
Schools of
subjectivism,
objectivism and
relativism existed at various times in the 20th century, and the
postmodernists and
body philosophers tried to reframe all these questions in terms of bodies taking some specific
action
in an environment. This relied to a great degree on insights derived
from scientific research into animals taking instinctive action in
natural and artificial settings—as studied by
biology,
ecology,
[19] and
cognitive science.
The processes by which bodies related to environments became of great concern, and the idea of
being
itself became difficult to really define. What did people mean when
they said "A is B", "A must be B", "A was B"...? Some linguists
advocated dropping the verb "to be" from the English language, leaving "
E Prime", supposedly less prone to bad abstractions. Others, mostly philosophers, tried to dig into the word and its usage.
Martin Heidegger distinguished
human being as
existence
from the being of things in the world. Heidegger proposes that our way
of being human and the way the world is for us are cast historically
through a fundamental ontological questioning. These fundamental
ontological categories provide the basis for communication in an age: a
horizon of unspoken and seemingly unquestionable background meanings,
such as human beings understood unquestioningly as subjects and other
entities understood unquestioningly as objects. Because these basic
ontological meanings both generate and are regenerated in everyday
interactions, the locus of our way of being in a historical epoch is the
communicative event of language in use.
[17] For Heidegger, however, communication in the
first place is not among human beings, but language itself shapes up in response to questioning (the inexhaustible meaning of) being.
[20] Even the focus of traditional ontology on the 'whatness' or
quidditas of beings in their substantial, standing presence can be shifted to pose the question of the 'whoness' of human being itself.
[21]
Ontology and language
Some philosophers suggest that the question of "What is?" is (at least in part) an issue of
usage rather than a question about facts.
[22] This perspective is conveyed by an analogy made by
Donald Davidson:
Suppose a person refers to a 'cup' as a 'chair' and makes some comments
pertinent to a cup, but uses the word 'chair' consistently throughout
instead of 'cup'. One might readily catch on that this person simply
calls a 'cup' a 'chair' and the oddity is explained.
[23]
Analogously, if we find people asserting 'there are' such-and-such, and
we do not ourselves think that 'such-and-such' exist, we might conclude
that these people are not nuts (Davidson calls this assumption
'charity'), they simply use 'there are' differently than we do. The
question of
What is? is at least partially a topic in the philosophy of language, and is not entirely about ontology itself.
[24] This viewpoint has been expressed by
Eli Hirsch.
[25][26]
Hirsch interprets
Hilary Putnam as asserting that different concepts of "the existence of something" can be correct.
[26]
This position does not contradict the view that some things do exist,
but points out that different 'languages' will have different rules
about assigning this property.
[26][27] How to determine the 'fitness' of a 'language' to the world then becomes a subject for investigation.
Common to all
Indo-European copula
languages is the double use of the verb "to be" in both stating that
entity X exists ("X is.") as well as stating that X has a property ("X
is P"). It is sometimes argued that a third use is also distinct,
stating that X is a member of a class ("X is a C"). In other language
families these roles may have completely different verbs and are less
likely to be confused with one another. For example they might say
something like "the car has redness" rather than "the car is red".
Hence any discussion of "being" in Indo-European language philosophy may
need to make distinctions between these senses.
[citation needed]
Ontology and human geography
In
human geography there are two types of ontology: small "o" which
accounts for the practical orientation, describing functions of being a
part of the group, thought to oversimplify and ignore key activities.
The other "o", or big "O", systematically, logically, and rationally
describes the essential characteristics and universal traits. This
concept relates closely to Plato's view that the human mind can only
perceive a bigger world if they continue to live within the confines of
their "caves". However, in spite of the differences, ontology relies on
the symbolic agreements among members. That said, ontology is crucial
for the axiomatic language frameworks.
[28]
Reality and actuality
According to
A.N. Whitehead,
for ontology, it is useful to distinguish the terms 'reality' and
'actuality'. In this view, an 'actual entity' has a philosophical status
of fundamental ontological priority, while a 'real entity' is one which
may be actual, or may derive its reality from its logical relation to
some actual entity or entities. For example, an occasion in the life of
Socrates is an actual entity. But Socrates' being a man does not make
'man' an actual entity, because it refers indeterminately to many actual
entities, such as several occasions in the life of Socrates, and also
to several occasions in the lives of Alcibiades, and of others. But the
notion of man is real; it derives its reality from its reference to
those many actual occasions, each of which is an actual entity. An
actual occasion is a concrete entity, while terms such as 'man' are
abstractions from many concrete relevant entities.
According to Whitehead, an actual entity must earn its
philosophical status of fundamental ontological priority by satisfying
several philosophical criteria, as follows.
- There is no going behind an actual entity, to find something
more fundamental in fact or in efficacy. This criterion is to be
regarded as expressing an axiom, or postulated distinguished doctrine.
- An actual entity must be completely determinate in the sense that
there may be no confusion about its identity that would allow it to be
confounded with another actual entity. In this sense an actual entity is
completely concrete, with no potential to be something other than
itself. It is what it is. It is a source of potentiality for the
creation of other actual entities, of which it may be said to be a part
cause. Likewise it is the concretion or realization of potentialities of
other actual entities which are its partial causes.
- Causation between actual entities is essential to their actuality.
Consequently, for Whitehead, each actual entity has its distinct and
definite extension in physical Minkowski space,
and so is uniquely identifiable. A description in Minkowski space
supports descriptions in time and space for particular observers.
- It is part of the aim of the philosophy of such an ontology as Whitehead's that the actual entities should be all alike, qua actual entities; they should all satisfy a single definite set of well stated ontological criteria of actuality.
Whitehead proposed that his notion of an occasion of experience
satisfies the criteria for its status as the philosophically preferred
definition of an actual entity. From a purely logical point of view,
each occasion of experience has in full measure the characters of both
objective and subjective reality. Subjectivity and objectivity refer to
different aspects of an occasion of experience, and in no way do they
exclude each other.
[29]
Examples of other philosophical proposals or candidates as actual
entities, in this view, are Aristotle's 'substances', Leibniz' monads,
and Descartes
′res verae' , and the more modern 'states of
affairs'. Aristotle's substances, such as Socrates, have behind them as
more fundamental the 'primary substances', and in this sense do not
satisfy Whitehead's criteria. Whitehead is not happy with Leibniz'
monads as actual entities because they are "windowless" and do not cause
each other. 'States of affairs' are often not closely defined, often
without specific mention of extension in physical Minkowski space; they
are therefore not necessarily processes of becoming, but may be as their
name suggests, simply static states in some sense. States of affairs
are contingent on particulars, and therefore have something behind them.
[30]
One summary of the Whiteheadian actual entity is that it is a process
of becoming. Another summary, referring to its causal linkage to other
actual entities, is that it is "all window", in contrast with Leibniz'
windowless monads.
This view allows philosophical entities other than actual
entities to really exist, but not as fundamentally and primarily factual
or causally efficacious; they have existence as abstractions, with
reality only derived from their reference to actual entities. A
Whiteheadian actual entity has a unique and completely definite place
and time. Whiteheadian abstractions are not so tightly defined in time
and place, and in the extreme, some are timeless and placeless, or
'eternal' entities. All abstractions have logical or conceptual rather
than efficacious existence; their lack of definite time does not make
them unreal if they refer to actual entities. Whitehead calls this 'the
ontological principle'.
Microcosmic ontology
There
is an established and long philosophical history of the concept of
atoms as microscopic physical objects.They are far too small to be
visible to the naked eye. It was as recent as the nineteenth century
that precise estimates of the sizes of putative physical
atoms began to become plausible. Almost direct empirical observation of atomic effects was due to the theoretical investigation of
Brownian motion by
Albert Einstein
in the very early twentieth century. But even then, the real existence
of atoms was debated by some. Such debate might be labeled 'microcosmic
ontology'. Here the word 'microcosm' is used to indicate a physical
world of small entities, such as for example atoms.
Subatomic particles are usually considered to be much smaller
than atoms. Their real or actual existence may be very difficult to
demonstrate empirically.
[31] A distinction is sometimes drawn between actual and
virtual
subatomic particles. Reasonably, one may ask, in what sense, if any, do
virtual particles exist as physical entities? For atomic and subatomic
particles, difficult questions arise, such as do they possess a precise
position, or a precise momentum? A question that continues to be
controversial is 'to what kind of physical thing, if any, does the
quantum mechanical wave function refer?'.
[6]
Ontological argument
The first ontological argument in the
Western Christian tradition
[32] was proposed by
Anselm of Canterbury in his 1078 work
Proslogion.
Anselm defined God as "that than which nothing greater can be thought",
and argued that this being must exist in the mind, even in the mind of
the person who denies the existence of God. He suggested that, if the
greatest possible being exists in the mind, it must also exist in
reality. If it only exists in the mind, then an even greater being must
be possible—one which exists both in the mind and in reality. Therefore,
this greatest possible being must exist in reality. Seventeenth century
French philosopher
René Descartes
deployed a similar argument. Descartes published several variations of
his argument, each of which centred on the idea that God's existence is
immediately inferable from a "clear and distinct" idea of a supremely
perfect being. In the early eighteenth century,
Gottfried Leibniz
augmented Descartes' ideas in an attempt to prove that a "supremely
perfect" being is a coherent concept. A more recent ontological argument
came from
Kurt Gödel, who proposed a
formal argument
for God's existence. Norman Malcolm revived the ontological argument in
1960 when he located a second, stronger ontological argument in
Anselm's work;
Alvin Plantinga challenged this argument and proposed an alternative, based on
modal logic. Attempts have also been made to validate Anselm's proof using an
automated theorem prover. Other arguments have been categorised as ontological, including those made by Islamic philosophers
Mulla Sadra and
Allama Tabatabai.



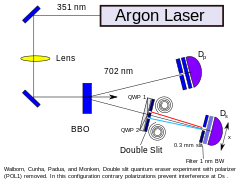
 and for the set of photons where Alice measured anti-clockwise
polarization, Bob's subset of photons is distributed according to
and for the set of photons where Alice measured anti-clockwise
polarization, Bob's subset of photons is distributed according to 
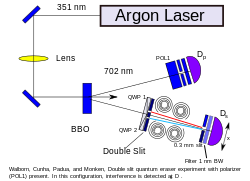
![{\displaystyle h(x)={\frac {1}{\sqrt {2}}}\left[f_{1}(x)+f_{2}(x)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7eab93156d532bf369c53f87674afd60d4b296a)
 is the phase difference between the two wave function at position x
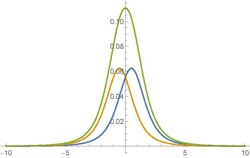
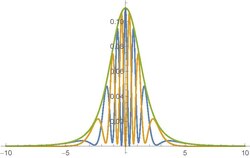
on the screen. The pattern is now indeed an interference pattern!
Likewise, if Alice detects a vertically polarized photon then the wave
amplitude of Bob's photon is
is the phase difference between the two wave function at position x
on the screen. The pattern is now indeed an interference pattern!
Likewise, if Alice detects a vertically polarized photon then the wave
amplitude of Bob's photon is![{\displaystyle v(x)={\frac {i}{\sqrt {2}}}\left[f_{1}(x)-f_{2}(x)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15f312a86519a1963cb59e53d95330256b27087f)