Radiometric dating

From Wikipedia, the free encyclopedia

 

Radiometric dating or radioactive dating is a technique used to date materials such as rocks or carbon, in which trace radioactive impurities were selectively incorporated when they were formed. The method compares the abundance of a naturally occurring radioactive isotope within the material to the abundance of its decay products, which form at a known constant rate of decay. The use of radiometric dating was first published in 1907 by Bertram Boltwood and is now the principal source of information about the absolute age of rocks and other geological features, including the age of fossilized life forms or the age of the Earth itself, and can also be used to date a wide range of natural and man-made materials.

Together with stratigraphic principles, radiometric dating methods are used in geochronology to establish the geologic time scale.^[3] Among the best-known techniques are radiocarbon dating, potassium–argon dating and uranium–lead dating. By allowing the establishment of geological timescales, it provides a significant source of information about the ages of fossils and the deduced rates of evolutionary change. Radiometric dating is also used to date archaeological materials, including ancient artifacts.

Different methods of radiometric dating vary in the timescale over which they are accurate and the materials to which they can be applied.

Fundamentals of radiometric dating

Radioactive decay

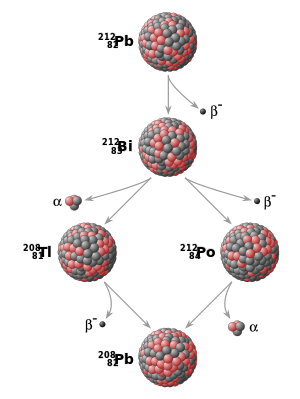
Example of a radioactive decay chain from lead-212 (²¹²Pb) to lead-208 (²⁰⁸Pb) . Each parent nuclide spontaneously decays into a daughter nuclide (the decay product) via an α decay or a β⁻ decay. The final decay product, lead-208 (²⁰⁸Pb), is stable and can no longer undergo spontaneous radioactive decay.

All ordinary matter is made up of combinations of chemical elements, each with its own atomic number, indicating the number of protons in the atomic nucleus. Additionally, elements may exist in different isotopes, with each isotope of an element differing in the number of neutrons in the nucleus. A particular isotope of a particular element is called a nuclide. Some nuclides are inherently unstable. That is, at some point in time, an atom of such a nuclide will undergo radioactive decay and spontaneously transform into a different nuclide. This transformation may be accomplished in a number of different ways, including alpha decay (emission of alpha particles) and beta decay (electron emission, positron emission, or electron capture). Another possibility is spontaneous fission into two or more nuclides.

While the moment in time at which a particular nucleus decays is unpredictable, a collection of atoms of a radioactive nuclide decays exponentially at a rate described by a parameter known as the half-life, usually given in units of years when discussing dating techniques. After one half-life has elapsed, one half of the atoms of the nuclide in question will have decayed into a "daughter" nuclide or decay product. In many cases, the daughter nuclide itself is radioactive, resulting in a decay chain, eventually ending with the formation of a stable (nonradioactive) daughter nuclide; each step in such a chain is characterized by a distinct half-life. In these cases, usually the half-life of interest in radiometric dating is the longest one in the chain, which is the rate-limiting factor in the ultimate transformation of the radioactive nuclide into its stable daughter. Isotopic systems that have been exploited for radiometric dating have half-lives ranging from only about 10 years (e.g., tritium) to over 100 billion years (e.g., samarium-147).^[4]

For most radioactive nuclides, the half-life depends solely on nuclear properties and is essentially a constant. It is not affected by external factors such as temperature, pressure, chemical environment, or presence of a magnetic or electric field.^[5][6][7] The only exceptions are nuclides that decay by the process of electron capture, such as beryllium-7, strontium-85, and zirconium-89, whose decay rate may be affected by local electron density. For all other nuclides, the proportion of the original nuclide to its decay products changes in a predictable way as the original nuclide decays over time. This predictability allows the relative abundances of related nuclides to be used as a clock to measure the time from the incorporation of the original nuclides into a material to the present.

Accuracy of radiometric dating

Thermal ionization mass spectrometer used in radiometric dating.

The basic equation of radiometric dating requires that neither the parent nuclide nor the daughter product can enter or leave the material after its formation. The possible confounding effects of contamination of parent and daughter isotopes have to be considered, as do the effects of any loss or gain of such isotopes since the sample was created. It is therefore essential to have as much information as possible about the material being dated and to check for possible signs of alteration.^[8] Precision is enhanced if measurements are taken on multiple samples from different locations of the rock body. Alternatively, if several different minerals can be dated from the same sample and are assumed to be formed by the same event and were in equilibrium with the reservoir when they formed, they should form an isochron. This can reduce the problem of contamination. In uranium–lead dating, the concordia diagram is used which also decreases the problem of nuclide loss. Finally, correlation between different isotopic dating methods may be required to confirm the age of a sample. For example, the age of the Amitsoq gneisses from western Greenland was determined to be 3.6 ± 0.05 million years ago (MA) using uranium–lead dating and 3.56 ± 0.10 Ma using lead–lead dating, results that are consistent with each other.^{[9]:142–143}

Accurate radiometric dating generally requires that the parent has a long enough half-life that it will be present in significant amounts at the time of measurement (except as described below under "Dating with short-lived extinct radionuclides"), the half-life of the parent is accurately known, and enough of the daughter product is produced to be accurately measured and distinguished from the initial amount of the daughter present in the material. The procedures used to isolate and analyze the parent and daughter nuclides must be precise and accurate. This normally involves isotope-ratio mass spectrometry.^[10]

The precision of a dating method depends in part on the half-life of the radioactive isotope involved. For instance, carbon-14 has a half-life of 5,730 years. After an organism has been dead for 60,000 years, so little carbon-14 is left that accurate dating cannot be established. On the other hand, the concentration of carbon-14 falls off so steeply that the age of relatively young remains can be determined precisely to within a few decades.^[11]

Closure temperature

If a material that selectively rejects the daughter nuclide is heated, any daughter nuclides that have been accumulated over time will be lost through diffusion, setting the isotopic "clock" to zero. The temperature at which this happens is known as the closure temperature or blocking temperature and is specific to a particular material and isotopic system. These temperatures are experimentally determined in the lab by artificially resetting sample minerals using a high-temperature furnace. As the mineral cools, the crystal structure begins to form and diffusion of isotopes is less easy. At a certain temperature, the crystal structure has formed sufficiently to prevent diffusion of isotopes. This temperature is what is known as closure temperature and represents the temperature below which the mineral is a closed system to isotopes. Thus an igneous or metamorphic rock or melt, which is slowly cooling, does not begin to exhibit measurable radioactive decay until it cools below the closure temperature. The age that can be calculated by radiometric dating is thus the time at which the rock or mineral cooled to closure temperature.^[12][13] Dating of different minerals and/or isotope systems (with differing closure temperatures) within the same rock can therefore enable the tracking of the thermal history of the rock in question with time, and thus the history of metamorphic events may become known in detail. This field is known as thermochronology or thermochronometry.

The age equation

Sm/Nd isochron plotted of samples ^[14] from the Great Dyke, Zimbabwe. The age is calculated from the slope of the isochron (line) and the original composition from the intercept of the isochron with the y-axis.

The mathematical expression that relates radioactive decay to geologic time is^[12][15]

D = D₀ + N(t) (e^λt − 1)

where

t is age of the sample,

D is number of atoms of the daughter isotope in the sample,

D₀ is number of atoms of the daughter isotope in the original composition,

N is number of atoms of the parent isotope in the sample at time t (the present), given by N(t) = N_oe^-λt, and

λ is the decay constant of the parent isotope, equal to the inverse of the radioactive half-life of the parent isotope^[16] times the natural logarithm of 2.

The equation is most conveniently expressed in terms of the measured quantity N(t) rather than the constant initial value N_o.

The above equation makes use of information on the composition of parent and daughter isotopes at the time the material being tested cooled below its closure temperature. This is well-established for most isotopic systems.^[13][17] However, construction of an isochron does not require information on the original compositions, using merely the present ratios of the parent and daughter isotopes to a standard isotope. Plotting an isochron is used to solve the age equation graphically and calculate the age of the sample and the original composition.

Modern dating methods

Radiometric dating has been carried out since 1905 when it was invented by Ernest Rutherford as a method by which one might determine the age of the Earth. In the century since then the techniques have been greatly improved and expanded.^[16] Dating can now be performed on samples as small as a nanogram using a mass spectrometer. The mass spectrometer was invented in the 1940s and began to be used in radiometric dating in the 1950s. It operates by generating a beam of ionized atoms from the sample under test. The ions then travel through a magnetic field, which diverts them into different sampling sensors, known as "Faraday cups", depending on their mass and level of ionization. On impact in the cups, the ions set up a very weak current that can be measured to determine the rate of impacts and the relative concentrations of different atoms in the beams.

Uranium–lead dating method

A concordia diagram as used in uranium–lead dating, with data from the Pfunze Belt, Zimbabwe.^[18] All the samples show loss of lead isotopes, but the intercept of the errorchron (straight line through the sample points) and the concordia (curve) shows the correct age of the rock.^[13]

Uranium–lead radiometric dating involves using uranium-235 or uranium-238 to date a substance's absolute age. This scheme has been refined to the point that the error margin in dates of rocks can be as low as less than two million years in two-and-a-half billion years.^[14][19] An error margin of 2–5% has been achieved on younger Mesozoic rocks.^[20]

Uranium–lead dating is often performed on the mineral zircon (ZrSiO₄), though it can be used on other materials, such as baddeleyite, as well as monazite (see: monazite geochronology).^[21] Zircon and baddeleyite incorporate uranium atoms into their crystalline structure as substitutes for zirconium, but strongly reject lead. Zircon has a very high closure temperature, is resistant to mechanical weathering and is very chemically inert. Zircon also forms multiple crystal layers during metamorphic events, which each may record an isotopic age of the event. In situ micro-beam analysis can be achieved via laser ICP-MS or SIMS techniques.^[22]

One of its great advantages is that any sample provides two clocks, one based on uranium-235's decay to lead-207 with a half-life of about 700 million years, and one based on uranium-238's decay to lead-206 with a half-life of about 4.5 billion years, providing a built-in crosscheck that allows accurate determination of the age of the sample even if some of the lead has been lost. This can be seen in the concordia diagram, where the samples plot along an errorchron (straight line) which intersects the concordia curve at the age of the sample.

Samarium–neodymium dating method

This involves the alpha decay of ¹⁴⁷Sm to ¹⁴³Nd with a half-life of 1.06 x 10¹¹ years. Accuracy levels of within twenty million years in ages of two-and-a-half billion years are achievable.^[23]

Potassium–argon dating method

This involves electron capture or positron decay of potassium-40 to argon-40. Potassium-40 has a half-life of 1.3 billion years, and so this method is applicable to the oldest rocks. Radioactive potassium-40 is common in micas, feldspars, and hornblendes, though the closure temperature is fairly low in these materials, about 350 °C (mica) to 500 °C (hornblende).

Rubidium–strontium dating method

This is based on the beta decay of rubidium-87 to strontium-87, with a half-life of 50 billion years. This scheme is used to date old igneous and metamorphic rocks, and has also been used to date lunar samples. Closure temperatures are so high that they are not a concern. Rubidium-strontium dating is not as precise as the uranium-lead method, with errors of 30 to 50 million years for a 3-billion-year-old sample.

Uranium–thorium dating method

A relatively short-range dating technique is based on the decay of uranium-234 into thorium-230, a substance with a half-life of about 80,000 years. It is accompanied by a sister process, in which uranium-235 decays into protactinium-231, which has a half-life of 32,760 years.
While uranium is water-soluble, thorium and protactinium are not, and so they are selectively precipitated into ocean-floor sediments, from which their ratios are measured. The scheme has a range of several hundred thousand years. A related method is ionium–thorium dating, which measures the ratio of ionium (thorium-230) to thorium-232 in ocean sediment.

Radiocarbon dating method

Ale's Stones at Kåseberga, around ten kilometres south east of Ystad, Sweden were dated at 56 CE using the carbon-14 method on organic material found at the site.^[24]

Radiocarbon dating is also simply called Carbon-14 dating. Carbon-14 is a radioactive isotope of carbon, with a half-life of 5,730 years,^[25][26] (which is very short compared with the above isotopes) and decays into nitrogen.^[27] In other radiometric dating methods, the heavy parent isotopes were produced by nucleosynthesis in supernovas, meaning that any parent isotope with a short half-life should be extinct by now. Carbon-14, though, is continuously created through collisions of neutrons generated by cosmic rays with nitrogen in the upper atmosphere and thus remains at a near-constant level on Earth. The carbon-14 ends up as a trace component in atmospheric carbon dioxide (CO₂).

A carbon-based life form acquires carbon during its lifetime. Plants acquire it through photosynthesis, and animals acquire it from consumption of plants and other animals. When an organism dies, it ceases to take in new carbon-14, and the existing isotope decays with a characteristic half-life (5730 years). The proportion of carbon-14 left when the remains of the organism are examined provides an indication of the time elapsed since its death. This makes carbon-14 an ideal dating method to date the age of bones or the remains of an organism. The carbon-14 dating limit lies around 58,000 to 62,000 years.^[28]

The rate of creation of carbon-14 appears to be roughly constant, as cross-checks of carbon-14 dating with other dating methods show it gives consistent results. However, local eruptions of volcanoes or other events that give off large amounts of carbon dioxide can reduce local concentrations of carbon-14 and give inaccurate dates. The releases of carbon dioxide into the biosphere as a consequence of industrialization have also depressed the proportion of carbon-14 by a few percent; conversely, the amount of carbon-14 was increased by above-ground nuclear bomb tests that were conducted into the early 1960s. Also, an increase in the solar wind or the Earth's magnetic field above the current value would depress the amount of carbon-14 created in the atmosphere.

Fission track dating method

Apatite crystals are widely used in fission track dating.

This involves inspection of a polished slice of a material to determine the density of "track" markings left in it by the spontaneous fission of uranium-238 impurities. The uranium content of the sample has to be known, but that can be determined by placing a plastic film over the polished slice of the material, and bombarding it with slow neutrons. This causes induced fission of ²³⁵U, as opposed to the spontaneous fission of ²³⁸U. The fission tracks produced by this process are recorded in the plastic film. The uranium content of the material can then be calculated from the number of tracks and the neutron flux.

This scheme has application over a wide range of geologic dates. For dates up to a few million years micas, tektites (glass fragments from volcanic eruptions), and meteorites are best used. Older materials can be dated using zircon, apatite, titanite, epidote and garnet which have a variable amount of uranium content.^[29] Because the fission tracks are healed by temperatures over about 200 °C the technique has limitations as well as benefits. The technique has potential applications for detailing the thermal history of a deposit.

Chlorine-36 dating method

Large amounts of otherwise rare ³⁶Cl (half-life ~300ky) were produced by irradiation of seawater during atmospheric detonations of nuclear weapons between 1952 and 1958. The residence time of ³⁶Cl in the atmosphere is about 1 week. Thus, as an event marker of 1950s water in soil and ground water, ³⁶Cl is also useful for dating waters less than 50 years before the present. ³⁶Cl has seen use in other areas of the geological sciences, including dating ice and sediments.

Luminescence dating methods

Luminescence dating methods are not radiometric dating methods in that they do not rely on abundances of isotopes to calculate age. Instead, they are a consequence of background radiation on certain minerals. Over time, ionizing radiation is absorbed by mineral grains in sediments and archaeological materials such as quartz and potassium feldspar. The radiation causes charge to remain within the grains in structurally unstable "electron traps". Exposure to sunlight or heat releases these charges, effectively "bleaching" the sample and resetting the clock to zero. The trapped charge accumulates over time at a rate determined by the amount of background radiation at the location where the sample was buried. Stimulating these mineral grains using either light (optically stimulated luminescence or infrared stimulated luminescence dating) or heat (thermoluminescence dating) causes a luminescence signal to be emitted as the stored unstable electron energy is released, the intensity of which varies depending on the amount of radiation absorbed during burial and specific properties of the mineral.
These methods can be used to date the age of a sediment layer, as layers deposited on top would prevent the grains from being "bleached" and reset by sunlight. Pottery shards can be dated to the last time they experienced significant heat, generally when they were fired in a kiln.

Other methods

Other methods include:

• argon–argon (Ar–Ar)
• iodine–xenon (I–Xe)
• lanthanum–barium (La–Ba)
• lead–lead (Pb–Pb)
• lutetium–hafnium (Lu–Hf)
• potassium–calcium (K–Ca)
• rhenium–osmium (Re–Os)
• uranium–lead–helium (U–Pb–He)
• uranium–uranium (U–U)
• krypton–krypton (Kr–Kr)
• beryllium (¹⁰Be–⁹Be)^[30]

Dating with decay products of short-lived extinct radionuclides

Absolute radiometric dating requires a measurable fraction of parent nucleus to remain in the sample rock. For rocks dating back to the beginning of the solar system, this requires extremely long-lived parent isotopes, making measurement of such rocks' exact ages imprecise. To be able to distinguish the relative ages of rocks from such old material, and to get a better time resolution than that available from long-lived isotopes, short-lived isotopes that are no longer present in the rock can be used.^[31]

At the beginning of the solar system, there were several relatively short-lived radionuclides like ²⁶Al, ⁶⁰Fe, ⁵³Mn, and ¹²⁹I present within the solar nebula. These radionuclides—possibly produced by the explosion of a supernova—are extinct today, but their decay products can be detected in very old material, such as that which constitutes meteorites. By measuring the decay products of extinct radionuclides with a mass spectrometer and using isochronplots, it is possible to determine relative ages of different events in the early history of the solar system. Dating methods based on extinct radionuclides can also be calibrated with the U-Pb method to give absolute ages. Thus both the approximate age and a high time resolution can be obtained. Generally a shorter half-life leads to a higher time resolution at the expense of timescale.

The ¹²⁹I – ¹²⁹Xe chronometer

¹²⁹I beta-decays to ¹²⁹Xe with a half-life of 16 million years. The iodine-xenon chronometer^[32] is an isochron technique. Samples are exposed to neutrons in a nuclear reactor. This converts the only stable isotope of iodine (¹²⁷I) into ¹²⁸Xe via neutron capture followed by beta decay (of ¹²⁸I). After irradiation, samples are heated in a series of steps and the xenon isotopic signature of the gas evolved in each step is analysed. When a consistent ¹²⁹Xe/¹²⁸Xe ratio is observed across several consecutive temperature steps, it can be interpreted as corresponding to a time at which the sample stopped losing xenon.
Samples of a meteorite called Shallowater are usually included in the irradiation to monitor the conversion efficiency from ¹²⁷I to ¹²⁸Xe. The difference between the measured ¹²⁹Xe/¹²⁸Xe ratios of the sample and Shallowater then corresponds to the different ratios of ¹²⁹I/¹²⁷I when they each stopped losing xenon. This in turn corresponds to a difference in age of closure in the early solar system.

The ²⁶Al – ²⁶Mg chronometer

Another example of short-lived extinct radionuclide dating is the ²⁶Al – ²⁶Mg chronometer, which can be used to estimate the relative ages of chondrules. ²⁶Al decays to ²⁶Mg with a half-life of 720,000 years. The dating is simply a question of finding the deviation from the natural abundance of ²⁶Mg (the product of ²⁶Al decay) in comparison with the ratio of the stable isotopes ²⁷Al/²⁴Mg.

The excess of ²⁶Mg (often designated ²⁶Mg* ) is found by comparing the ²⁶Mg/²⁷Mg ratio to that of other Solar System materials.^[33]

The ²⁶Al – ²⁶Mg chronometer gives an estimate of the time period for formation of primitive meteorites of only a few million years (1.4 million years for Chondrule formation).

Isotope geochemistry

From Wikipedia, the free encyclopedia

Isotope geochemistry is an aspect of geology based upon the study of natural variations in the relative abundances of isotopes of various elements. Variations in isotopic abundance are measured by isotope ratio mass spectrometry, and can reveal information about the ages and origins of rock, air or water bodies, or processes of mixing between them.

Stable isotope geochemistry is largely concerned with isotopic variations arising from mass-dependent isotope fractionation, whereas radiogenic isotope geochemistry is concerned with the products of natural radioactivity.

Stable isotope geochemistry

For most stable isotopes, the magnitude of fractionation from kinetic and equilibrium fractionation is very small; for this reason, enrichments are typically reported in "per mil" (‰, parts per thousand).^[1] These enrichments (δ) represent the ratio of heavy isotope to light isotope in the sample over the ratio of a standard. That is,

${\displaystyle \delta {\ce {^{13}C}}=\left({\frac {\left({\frac {{\ce {^{13}C}}}{{\ce {^{12}C}}}}\right)_{sample}}{\left({\frac {{\ce {^{13}C}}}{{\ce {^{12}C}}}}\right)_{standard}}}-1\right)\times 1000}$ ‰

Carbon

Carbon has two stable isotopes, ¹²C and ¹³C, and one radioactive isotope, ¹⁴C.

The stable carbon isotope ratio, δ¹³C, is measured against Vienna Pee Dee Belemnite (VPDB).^[2] The stable carbon isotopes are fractionated primarily by photosynthesis (Faure, 2004). The ¹³C/¹²C ratio is also an indicator of paleoclimate: a change in the ratio in the remains of plants indicates a change in the amount of photosynthetic activity, and thus in how favorable the environment was for the plants. During photosynthesis, organisms using the C₃ pathway show different enrichments compared to those using the C₄ pathway, allowing scientists not only to distinguish organic matter from abiotic carbon, but also what type of photosynthetic pathway the organic matter was using.^[1] Occasional spikes in the global ¹³C/¹²C ratio have also been useful as stratigraphic markers for chemostratigraphy, especially during the Paleozoic.^[3]

The ¹⁴C ratio has been used to track ocean circulation, among other things.

Nitrogen

Nitrogen has two stable isotopes, ¹⁴N, and ¹⁵N. The ratio between these is measured relative to nitrogen in ambient air.^[2] Nitrogen ratios are frequently linked to agricultural activities. Nitrogen isotope data has also been used to measure the amount of exchange of air between the stratosphere and troposphere using data from the greenhouse gas N₂O.^[4]

Oxygen

Oxygen has three stable isotopes, ¹⁶O, ¹⁷O, and ¹⁸O. Oxygen ratios are measured relative to Vienna Standard Mean Ocean Water (VSMOW) or Vienna Pee Dee Belemnite (VPDB).^[2] Variations in oxygen isotope ratios are used to track both water movement, paleoclimate,^[1] and atmospheric gases such as ozone and carbon dioxide.^[5] Typically, the VPDB oxygen reference is used for paleoclimate, while VSMOW is used for most other applications.^[1] Oxygen isotopes appear in anomalous ratios in atmospheric ozone, resulting from mass-independent fractionation.^[6] Isotope ratios in fossilized foraminifera have been used to deduce the temperature of ancient seas.^[7]

Sulfur

Sulfur has four stable isotopes, with the following abundances: ³²S (0.9502), ³³S (0.0075), ³⁴S (0.0421) and ³⁶S (0.0002). These abundances are compared to those found in Cañon Diablo troilite.^[5] Variations in sulfur isotope ratios are used to study the origin of sulfur in an orebody and the temperature of formation of sulfur–bearing minerals.^[8]

Radiogenic isotope geochemistry

Radiogenic isotopes provide powerful tracers for studying the ages and origins of Earth systems.^[9] They are particularly useful to understand mixing processes between different components, because (heavy) radiogenic isotope ratios are not usually fractionated by chemical processes.

Radiogenic isotope tracers are most powerful when used together with other tracers: The more tracers used, the more control on mixing processes. An example of this application is to the evolution of the Earth's crust and Earth's mantle through geological time.

Lead–lead isotope geochemistry

Lead has four stable isotopes - ²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb, ²⁰⁸Pb and one common radioactive isotope ²⁰²Pb with a half-life of ~53,000 years.

Lead is created in the Earth via decay of transuranic elements, primarily uranium and thorium.

Lead isotope geochemistry is useful for providing isotopic dates on a variety of materials. Because the lead isotopes are created by decay of different transuranic elements, the ratios of the four lead isotopes to one another can be very useful in tracking the source of melts in igneous rocks, the source of sediments and even the origin of people via isotopic fingerprinting of their teeth, skin and bones.

It has been used to date ice cores from the Arctic shelf, and provides information on the source of atmospheric lead pollution.

Lead–lead isotopes has been successfully used in forensic science to fingerprint bullets, because each batch of ammunition has its own peculiar ²⁰⁴Pb/²⁰⁶Pb vs ²⁰⁷Pb/²⁰⁸Pb ratio.

Samarium–neodymium

Samarium–neodymium is an isotope system which can be utilised to provide a date as well as isotopic fingerprints of geological materials, and various other materials including archaeological finds (pots, ceramics).

¹⁴⁷Sm decays to produce ¹⁴³Nd with a half life of 1.06x10¹¹ years.

Dating is achieved usually by trying to produce an isochron of several minerals within a rock specimen. The initial ¹⁴³Nd/¹⁴⁴Nd ratio is determined.

This initial ratio is modelled relative to CHUR - the Chondritic Uniform Reservoir - which is an approximation of the chondritic material which formed the solar system. CHUR was determined by analysing chondrite and achondrite meteorites.

The difference in the ratio of the sample relative to CHUR can give information on a model age of extraction from the mantle (for which an assumed evolution has been calculated relative to CHUR) and to whether this was extracted from a granitic source (depleted in radiogenic Nd), the mantle, or an enriched source.

Rhenium–osmium

Rhenium and osmium are siderophile elements which are present at very low abundances in the crust. Rhenium undergoes radioactive decay to produce osmium. The ratio of non-radiogenic osmium to radiogenic osmium throughout time varies.

Rhenium prefers to enter sulfides more readily than osmium. Hence, during melting of the mantle, rhenium is stripped out, and prevents the osmium–osmium ratio from changing appreciably. This locks in an initial osmium ratio of the sample at the time of the melting event. Osmium–osmium initial ratios are used to determine the source characteristic and age of mantle melting events.

Noble gas isotopes

Natural isotopic variations amongst the noble gases result from both radiogenic and nucleogenic production processes. Because of their unique properties, it is useful to distinguish them from the conventional radiogenic isotope systems described above.

Helium-3

Helium-3 was trapped in the planet when it formed. Some ³He is being added by meteoric dust, primarily collecting on the bottom of oceans (although due to subduction, all oceanic tectonic plates are younger than continental plates). However, ³He will be degassed from oceanic sediment during subduction, so cosmogenic ³He is not affecting the concentration or noble gas ratios of the mantle.
Helium-3 is created by cosmic ray bombardment, and by lithium spallation reactions which generally occur in the crust. Lithium spallation is the process by which a high-energy neutron bombards a lithium atom, creating a ³He and a ⁴He ion. This requires significant lithium to adversely affect the ³He/⁴He ratio.

All degassed helium is lost to space eventually, due to the average speed of helium exceeding the escape velocity for the Earth. Thus, it is assumed the helium content and ratios of Earth's atmosphere have remained essentially stable.

It has been observed that ³He is present in volcano emissions and oceanic ridge samples. How ³He is stored in the planet is under investigation, but it is associated with the mantle and is used as a marker of material of deep origin.

Due to similarities in helium and carbon in magma chemistry, outgassing of helium requires the loss of volatile components (water, carbon dioxide) from the mantle, which happens at depths of less than 60 km. However, ³He is transported to the surface primarily trapped in the crystal lattice of minerals within fluid inclusions.

Helium-4 is created by radiogenic production (by decay of uranium/thorium-series elements). The continental crust has become enriched with those elements relative to the mantle and thus more He⁴ is produced in the crust than in the mantle.

The ratio (R) of ³He to ⁴He is often used to represent ³He content. R usually is given as a multiple of the present atmospheric ratio (Ra).

Common values for R/Ra:

• Old continental crust: less than 1
• mid-ocean ridge basalt (MORB): 7 to 9
• Spreading ridge rocks: 9.1 plus or minus 3.6
• Hotspot rocks: 5 to 42
• Ocean and terrestrial water: 1
• Sedimentary formation water: less than 1
• Thermal spring water: 3 to 11

³He/⁴He isotope chemistry is being used to date groundwaters, estimate groundwater flow rates, track water pollution, and provide insights into hydrothermal processes, igneous geology and ore genesis.

• (U-Th)/He dating of apatite as a thermal history tool
• USGS: Helium Discharge at Mammoth Mountain Fumarole (MMF)

Uranium-series isotopes

U-series isotopes are unique amongst radiogenic isotopes because, being in the U-series decay chains, they are both radiogenic and radioactive. Because their abundances are normally quoted as activity ratios rather than atomic ratios, they are best considered separately from the other radiogenic isotope systems.

Protactinium/Thorium - ²³¹Pa / ²³⁰Th

Uranium is well mixed in the ocean, and its decay produces ²³¹Pa and ²³⁰Th at a constant activity ratio (0.093). The decay products are rapidly removed by adsorption on settling particles, but not at equal rates. ²³¹Pa has a residence equivalent to the residence time of deep water in the Atlantic basin (around 1000 yrs) but ²³⁰Th is removed more rapidly (centuries). Thermohaline circulation effectively exports ²³¹Pa from the Atlantic into the Southern Ocean, while most of the ²³⁰Th remains in Atlantic sediments. As a result, there is a relationship between ²³¹Pa/²³⁰Th in Atlantic sediments and the rate of overturning: faster overturning produces lower sediment ²³¹Pa/²³⁰Th ratio, while slower overturning increases this ratio. The combination of δ¹³C and ²³¹Pa/²³⁰Th can therefore provide a more complete insight into past circulation changes.

Anthropogenic isotopes

Tritium/helium-3

Tritium was released to the atmosphere during atmospheric testing of nuclear bombs. Radioactive decay of tritium produces the noble gas helium-3. Comparing the ratio of tritium to helium-3 (³H/³He) allows estimation of the age of recent ground waters.

• USGS Tritium/Helium-3 Dating
• Hydrologic Isotope Tracers - Helium

Primordial nuclide

From Wikipedia, the free encyclopedia

Relative abundance of the chemical elements in the Earth's upper continental crust, on a per-atom basis

In geochemistry, geophysics and geonuclear physics, primordial nuclides, also known as primordial isotopes, are nuclides found on Earth that have existed in their current form since before Earth was formed. Primordial nuclides were present in the interstellar medium from which the solar system was formed, and were formed in the Big Bang, by nucleosynthesis in stars and supernovae followed by mass ejection, by cosmic ray spallation, and potentially from other processes. They are the stable nuclides plus the long-lived fraction of radionuclides surviving in the primordial solar nebula through planet accretion until the present. Only 286 such nuclides are known.

All of the known 253 stable nuclides occur as primordial nuclides, plus another 33 nuclides that have half-lives long enough to have survived from the formation of the Earth. These 33 primordial radionuclides represent isotopes of 28 separate elements. Cadmium, tellurium, neodymium, samarium and uranium each have two primordial radioisotopes (¹¹³Cd
, ¹¹⁶Cd
; ¹²⁸Te
, ¹³⁰Te
; ¹⁴⁴Nd
, ¹⁵⁰Nd
; ¹⁴⁷Sm
, ¹⁴⁸Sm
; and ²³⁵U
, ²³⁸U
).

Because the age of the Earth is 4.58×10⁹ years (4.6 billion years), this means that the half-life of the given nuclides must be greater than about 1×10⁸ years (100 million years) for practical considerations. For example, for a nuclide with half-life 6×10⁷ years (60 million years), this means 77 half-lives have elapsed, meaning that for each mole (6.02×10²³ atoms) of that nuclide being present at the formation of Earth, only 4 atoms remain today.

The shortest-lived primordial nuclides (i.e. nuclides with shortest half-lives) are:

..., ²³²Th
, ²³⁸U
, ⁴⁰K
, and ²³⁵U
.

These are the 4 nuclides with half-lives comparable to, or less than, the estimated age of the universe. (In the case of ²³²Th, it has a half life of more than 14 billion years, slightly longer than the age of the universe.) For a complete list of the 33 known primordial radionuclides, including the next 29 with half-lives much longer than the age of the universe, see the complete list in the section below. For practical purposes, nuclides with half-lives much longer than the age of the universe may be treated as if they really were stable. ²³²Th and ²³⁸U have half-lives long enough that their decay is limited over geological time scales; ⁴⁰K and ²³⁵U have shorter half-lives and are hence severely depleted, but are still long-lived enough to persist significantly in nature.

The next longest-living nuclide after the end of the list given in the table is ²⁴⁴Pu
, with a half-life of 8.08×10⁷ years. It has been reported to exist in nature as a primordial nuclide, although later studies could not detect it.^[1] Likewise, the second-longest-lived non-primordial ¹⁴⁶Sm
has a half-life of 6.8×10⁷ years, about double that of the third-longest-lived non-primordial ⁹²Nb
(3.5×10⁷ years).^[2] Taking into account that all these nuclides must exist since at least 4.6×10⁹ years, ²⁴⁴Pu must survive 57 half-lives (and hence be reduced by a factor of 2⁵⁷ ≈ 1.4 × 10¹⁷), ¹⁴⁶Sm must survive 67 (and be reduced by 2⁶⁷ ≈ 1.5 × 10²⁰), and ⁹²Nb must survive 130 (and be reduced by 2¹³⁰ ≈ 1.4 × 10³⁹). Considering the likely initial abundances of these nuclides, possibly measurable quantities of ²⁴⁴Pu and ¹⁴⁶Sm should persist today, while they should not for ⁹²Nb and all shorter-lived nuclides. Nuclides such as ⁹²Nb that were present in the primordial solar nebula but have long since decayed away completely are termed extinct radionuclides if they have no other means of being regenerated.^[3]

Although it is estimated that about 33 primordial nuclides are radioactive (list below), it becomes very difficult to determine the exact total number of radioactive primordials, because the total number of stable nuclides is uncertain. There exist many extremely long-lived nuclides whose half-lives are still unknown. For example, it is predicted theoretically that all isotopes of tungsten, including those indicated by even the most modern empirical methods to be stable, must be radioactive and can decay by alpha emission, but as of 2013 this could only be measured experimentally for ¹⁸⁰W
.^[4] Similarly, all four primordial isotopes of lead are expected to decay to mercury, but the predicted half-lives are so long (some exceeding 10¹⁰⁰ years) that this can hardly be observed in the near future. Nevertheless, the number of nuclides with half-lives so long that they cannot be measured with present instruments—and are considered from this viewpoint to be stable nuclides—is limited. Even when a "stable" nuclide is found to be radioactive, the fact merely moves it from the stable to the unstable list of primordial nuclides, and the total number of primordial nuclides remains unchanged.

Because primordial chemical elements often consist of more than one primordial isotope, there are only 83 distinct primordial chemical elements. Of these, 80 have at least one observationally stable isotope and three additional primordial elements have only radioactive isotopes (bismuth, thorium, and uranium).

Naturally occurring nuclides that are not primordial

Some unstable isotopes which occur naturally (such as ¹⁴C
, ³H
, and ²³⁹Pu
) are not primordial, as they must be constantly regenerated. This occurs by cosmic radiation (in the case of cosmogenic nuclides such as ¹⁴C
and ³H
), or (rarely) by such processes as geonuclear transmutation (neutron capture of uranium in the case of ²³⁷Np
and ²³⁹Pu
). Other examples of common naturally occurring but non-primordial nuclides are isotopes of radon, polonium, and radium, which are all radiogenic nuclide daughters of uranium decay and are found in uranium ores. A similar radiogenic series is derived from the long-lived radioactive primordial nuclide ²³²Th. All of such nuclides have shorter half-lives than their parent radioactive primordial nuclides. Some other geogenic nuclides do not occur in the decay chains of ²³²Th, ²³⁵U, or ²³⁸U but can still fleetingly occur naturally as products of the spontaneous fission of one of these three long-lived nuclides, such as ¹²⁶Sn, which makes up about 10⁻¹⁴ of all natural tin.^[5]

Primordial elements

There are 253 stable primordial nuclides and 33 radioactive primordial nuclides, but only 80 primordial stable elements (1 through 82, i.e. hydrogen through lead, exclusive of 43 and 61, technetium and promethium respectively) and three radioactive primordial elements (bismuth, thorium, and uranium). Bismuth's half-life is so long that it is often classed with the 80 primordial stable elements instead, since its radioactivity is not a cause for serious concern. The numbers of elements are smaller, because many primordial elements are represented by more than one primordial nuclide. See chemical element for more information.

Naturally occurring stable nuclides

As noted, these number about 253. For a complete list noting which of the "stable" 253 nuclides may be in some respect unstable, see list of nuclides and stable nuclide. These questions do not impact the question of whether a nuclide is primordial, since all "nearly stable" nuclides, with half-lives longer than the age of the universe, are primordial also.

List of 33 radioactive primordial nuclides and measured half-lives

These 33 primordial nuclides represent radioisotopes of 28 distinct chemical elements (cadmium, neodymium, samarium, tellurium, and uranium each have two primordial radioisotopes). The radionuclides are listed in order of stability, with the longest half-life beginning the list. These radionuclides in many cases are so nearly stable that they compete for abundance with stable isotopes of their respective elements. For three chemical elements, a very long lived radioactive primordial nuclide is found to be the most abundant nuclide for an element that also has a stable nuclide. These unusual elements are tellurium, indium, and rhenium.

The longest has a half-life of 2.2×10²⁴ years, which is 160 trillion times the age of the Universe. Only four of these 33 nuclides have half-lives shorter than, or equal to, the age of the universe. Most of the remaining 29 have half-lives much longer. The shortest-lived primordial isotope, ²³⁵U, has a half-life of 704 million years, about one sixth of the age of the Earth and Solar System.

no	nuclide	energy	half- life (years)	decay mode	decay energy (MeV)	approx. ratio half-life to age of universe
254	128Te	8.743261	2.2×1024	2 β−	2.530	160 trillion
255	78Kr	9.022349	9.2×1021	KK	2.846	670 billion
256	136Xe	8.706805	2.165×1021	2 β−	2.462	150 billion
257	76Ge	9.034656	1.8×1021	2 β−	2.039	130 billion
258	130Ba	8.742574	1.2×1021	KK	2.620	90 billion
259	82Se	9.017596	1.1×1020	2 β−	2.995	8 billion
260	116Cd	8.836146	3.102×1019	2 β−	2.809	2 billion
261	48Ca	8.992452	2.301×1019	2 β−	4.274, .0058	2 billion
262	96Zr	8.961359	2.0×1019	2 β−	3.4	1 billion
263	209Bi	8.158689	1.9×1019	α	3.137	1 billion
264	130Te	8.766578	8.806×1018	2 β−	.868	600 million
265	150Nd	8.562594	7.905×1018	2 β−	3.367	600 million
266	100Mo	8.933167	7.804×1018	2 β−	3.035	600 million
267	151Eu	8.565759	5.004×1018	α	1.9644	300 million
268	180W	8.347127	1.801×1018	α	2.509	100 million
269	50V	9.055759	1.4×1017	β+ or β−	2.205, 1.038	10 million
270	113Cd	8.859372	7.7×1015	β−	.321	600,000
271	148Sm	8.607423	7.005×1015	α	1.986	500,000
272	144Nd	8.652947	2.292×1015	α	1.905	200,000
273	186Os	8.302508	2.002×1015	α	2.823	100,000
274	174Hf	8.392287	2.002×1015	α	2.497	100,000
275	115In	8.849910	4.4×1014	β−	.499	30,000
276	152Gd	8.562868	1.1×1014	α	2.203	8000
277	190Pt	8.267764	6.5×1011	α	3.252	60
278	147Sm	8.610593	1.061×1011	α	2.310	8
279	138La	8.698320	1.021×1011	K or β−	1.737, 1.044	7
280	87Rb	9.043718	4.972×1010	β−	.283	4
281	187Re	8.291732	4.122×1010	β−	.0026	3
282	176Lu	8.374665	3.764×1010	β−	1.193	3
283	232Th	7.918533	1.406×1010	α or SF	4.083	1
284	238U	7.872551	4.471×109	α or SF or 2 β−	4.270	0.3
285	40K	8.909707	1.25×109	β− or K or β+	1.311, 1.505, 1.505	0.09
286	235U	7.897198	7.04×108	α or SF	4.679	0.05

List legends

no (number)

A running positive integer for reference. These numbers may change slightly in the future since there are 163 nuclides now classified as stable, but which are theoretically predicted to be unstable (see Stable nuclide#Still-unobserved decay), so that future experiments may show that some are in fact unstable. The number starts at 254, to follow the 253 nuclides (or stable isotopes) not yet found to be radioactive.

nuclide column

Nuclide identifiers are given by their mass number A and the symbol for the corresponding chemical element (implies a unique proton number).

energy column

The column labeled "energy" denotes the mass of the average nucleon of this nuclide relative to the mass of a neutron (so all nuclides get a positive value) in MeV/c², formally: m_n − m_nuclide / A.

half-life column

All times are given in years.

decay mode column

α	α decay
β−	β− decay
K	electron capture
KK	double electron capture
β+	β+ decay
SF	spontaneous fission
2 β−	double β− decay
2 β+	double β+ decay
I	isomeric transition
p	proton emission
n	neutron emission

decay energy column

Multiple values for (maximal) decay energy in MeV are mapped to decay modes in their order.