Neutron

From Wikipedia, the free encyclopedia

Neutron

The quark content of the neutron. The color assignment of individual quarks is arbitrary, but all three colors must be present. Forces between quarks are mediated by gluons.
Classification	Baryon
Composition	1 up quark, 2 down quarks
Statistics	Fermionic
Interactions	Gravity, weak, strong, electromagnetic
Symbol	n , n0, N0
Antiparticle	Antineutron
Theorized	Ernest Rutherford[1] (1920)
Discovered	James Chadwick[2] (1932)
Mass	1.674927471(21)×10−27 kg[3] 939.5654133(58) MeV/c2[3] 1.00866491588(49) u[3]
Mean lifetime	881.5(15) s (free)
Electric charge	0 e (−2±8)×10−22 e (experimental limits)[4]
Electric dipole moment	< 2.9×10−26 e⋅cm (experimental upper limit)
Electric polarizability	1.16(15)×10−3 fm3
Magnetic moment	−0.96623650(23)×10−26 J·T−1[3] −1.04187563(25)×10−3 μB[3] −1.91304273(45) μN[3]
Magnetic polarizability	3.7(20)×10−4 fm3
Spin	1/2
Isospin	−1/2
Parity	+1
Condensed	I(JP) = 1/2(1/2+)

The neutron is a subatomic particle, symbol
n
or
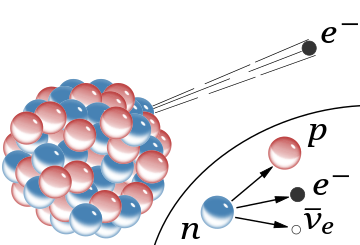
n⁰, with no net electric charge and a mass slightly larger than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons behave similarly within the nucleus, and each has a mass of approximately one atomic mass unit, they are both referred to as nucleons. Their properties and interactions are described by nuclear physics.

The chemical and nuclear properties of the nucleus are determined by the number of protons, called the atomic number, and the number of neutrons, called the neutron number. The atomic mass number is the total number of nucleons. For example, carbon has atomic number 6, and its abundant carbon-12 isotope has 6 neutrons, whereas its rare carbon-13 isotope has 7 neutrons. Some elements occur in nature with only one stable isotope, such as fluorine. Other elements occur with many stable isotopes, such as tin with ten stable isotopes.

Within the nucleus, protons and neutrons are bound together through the nuclear force. Neutrons are required for the stability of nuclei, with the exception of the single-proton hydrogen atom. Neutrons are produced copiously in nuclear fission and fusion. They are a primary contributor to the nucleosynthesis of chemical elements within stars through fission, fusion, and neutron capture processes.

The neutron is essential to the production of nuclear power. In the decade after the neutron was discovered by James Chadwick in 1932,^[6] neutrons were used to induce many different types of nuclear transmutations. With the discovery of nuclear fission in 1938,^[7] it was quickly realized that, if a fission event produced neutrons, each of these neutrons might cause further fission events, etc., in a cascade known as a nuclear chain reaction.^[8] These events and findings led to the first self-sustaining nuclear reactor (Chicago Pile-1, 1942) and the first nuclear weapon (Trinity, 1945).

Free neutrons, while not directly ionizing atoms, cause ionizing radiation. As such they can be a biological hazard, depending upon dose.^[8] A small natural "neutron background" flux of free neutrons exists on Earth, caused by cosmic ray showers, and by the natural radioactivity of spontaneously fissionable elements in the Earth's crust.^[9] Dedicated neutron sources like neutron generators, research reactors and spallation sources produce free neutrons for use in irradiation and in neutron scattering experiments.

Description

Atomic nuclei are formed by a number of protons, Z the atomic number, and a number of neutrons, N the neutron number, bound together by the nuclear force. The atomic number defines the chemical properties of the atom, and the neutron number determines the isotope or nuclide.^[8] The terms isotope and nuclide are often used synonymously, but they refer to chemical and nuclear properties, respectively. Strictly speaking, isotopes are two or more nuclides with the same number of protons; nuclides with the same number of neutrons are called isotones. The atomic mass number, symbol A, equals Z+N. Nuclides with the same atomic mass number are called isobars. The nucleus of the most common isotope of the hydrogen atom (with the chemical symbol ¹H) is a lone proton. The nuclei of the heavy hydrogen isotopes deuterium (D or ²H) and tritium (T or ³H) contain one proton bound to one and two neutrons, respectively. All other types of atomic nuclei are composed of two or more protons and various numbers of neutrons. The most common nuclide of the common chemical element lead, ²⁰⁸Pb, has 82 protons and 126 neutrons, for example. The table of nuclides comprises all the known nuclides. Even though it is not a chemical element, the neutron is included in this table.^[10]

The free neutron has a mass of 939,565,413.3 eV/c², or 1.674927471×10⁻²⁷ kg, or 1.00866491588 u.^[3] The neutron has a mean square radius of about 0.8×10⁻¹⁵ m, or 0.8 fm,^[11] and it is a spin-½ fermion.^[12] The neutron has no measurable electric charge. With its positive electric charge, the proton is directly influenced by electric fields, whereas the neutron is unaffected by electric fields. The neutron has a magnetic moment, however, so the neutron is influenced by magnetic fields. The neutron's magnetic moment has a negative value, because its orientation is opposite to the neutron's spin.^[13]

A free neutron is unstable, decaying to a proton, electron and antineutrino with a mean lifetime of just under 15 minutes (881.5±1.5 s).^[14] This radioactive decay, known as beta decay, is possible because the mass of the neutron is slightly greater than the proton. The free proton is stable. Neutrons or protons bound in a nucleus can be stable or unstable, however, depending on the nuclide. Beta decay, in which neutrons decay to protons, or vice versa, is governed by the weak force, and it requires the emission or absorption of electrons and neutrinos, or their antiparticles.

Nuclear fission caused by absorption of a neutron by uranium-235. The heavy nuclide fragments into lighter components and additional neutrons.

Protons and neutrons behave almost identically under the influence of the nuclear force within the nucleus. The concept of isospin, in which the proton and neutron are viewed as two quantum states of the same particle, is used to model the interactions of nucleons by the nuclear or weak forces. Because of the strength of the nuclear force at short distances, the binding energy of nucleons is more than seven orders of magnitude larger than the electromagnetic energy binding electrons in atoms.  Nuclear reactions (such as nuclear fission) therefore have an energy density that is more than ten million times that of chemical reactions. Because of the mass–energy equivalence, nuclear binding energies add or subtract from the mass of nuclei. Ultimately, the ability of the nuclear force to store energy arising from the electromagnetic repulsion of nuclear components is the basis for most of the energy that makes nuclear reactors or bombs possible. In nuclear fission, the absorption of a neutron by a heavy nuclide (e.g., uranium-235) causes the nuclide to become unstable and break into light nuclides and additional neutrons. The positively charged light nuclides then repel, releasing electromagnetic potential energy.

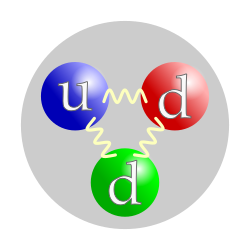
The neutron is classified as a hadron, because it is a composite particle made of quarks. The neutron is also classified as a baryon, because it is composed of three valence quarks.^[15] The finite size of the neutron and its magnetic moment indicates that the neutron is a composite particle, as opposed to being an elementary particle. A neutron contains two down quarks with charge −​¹⁄₃ e and one up quark with charge +​²⁄₃ e.

Like protons, the quarks of the neutron are held together by the strong force, mediated by gluons.^[16] The nuclear force results from secondary effects of the more fundamental strong force.

Discovery

The story of the discovery of the neutron and its properties is central to the extraordinary developments in atomic physics that occurred in the first half of the 20th century, leading ultimately to the atomic bomb in 1945. In the 1911 Rutherford model, the atom consisted of a small positively charged massive nucleus surrounded by a much larger cloud of negatively charged electrons. In 1920, Rutherford suggested that the nucleus consisted of positive protons and neutrally-charged particles, suggested to be a proton and an electron bound in some way.^[17] Electrons were assumed to reside within the nucleus because it was known that beta radiation consisted of electrons emitted from the nucleus.^[17] Rutherford called these uncharged particles neutrons, by the Latin root for neutralis (neuter) and the Greek suffix -on (a suffix used in the names of subatomic particles, i.e. electron and proton).^[18][19] References to the word neutron in connection with the atom can be found in the literature as early as 1899, however.^[20]

Throughout the 1920s, physicists assumed that the atomic nucleus was composed of protons and "nuclear electrons"^[21][22] but there were obvious problems. It was difficult to reconcile the proton–electron model for nuclei with the Heisenberg uncertainty relation of quantum mechanics.^[23][24] The Klein paradox,^[25] discovered by Oskar Klein in 1928, presented further quantum mechanical objections to the notion of an electron confined within a nucleus.^[23] Observed properties of atoms and molecules were inconsistent with the nuclear spin expected from the proton–electron hypothesis. Since both protons and electrons carry an intrinsic spin of ½ ħ, there is no way to arrange an odd number of spins ±½ ħ to give a spin integer multiple of ħ. Nuclei with integer spin are common, e.g., ¹⁴N.

In 1931, Walther Bothe and Herbert Becker found that if alpha particle radiation from polonium fell on beryllium, boron, or lithium, an unusually penetrating radiation was produced. The radiation was not influenced by an electric field, so Bothe and Becker assumed it was gamma radiation.^[26][27] The following year Irène Joliot-Curie and Frédéric Joliot-Curie in Paris showed that if this "gamma" radiation fell on paraffin, or any other hydrogen-containing compound, it ejected protons of very high energy.^[28] Neither Rutherford nor James Chadwick at the Cavendish Laboratory in Cambridge were convinced by the gamma ray interpretation.^[29] Chadwick quickly performed a series of experiments that showed that the new radiation consisted of uncharged particles with about the same mass as the proton.^[6][30][31] These particles were neutrons. Chadwick won the Nobel Prize in Physics for this discovery in 1935.^[2]
 

Models depicting the nucleus and electron energy levels in hydrogen, helium, lithium, and neon atoms. In reality, the diameter of the nucleus is about 100,000 times smaller than the diameter of the atom.

Models for atomic nucleus consisting of protons and neutrons were quickly developed by Werner Heisenberg^[32][33][34] and others.^[35][36] The proton–neutron model explained the puzzle of nuclear spins. The origins of beta radiation were explained by Enrico Fermi in 1934 by the process of beta decay, in which the neutron decays to a proton by creating an electron and a (as yet undiscovered) neutrino.^[37] In 1935 Chadwick and his doctoral student Maurice Goldhaber, reported the first accurate measurement of the mass of the neutron.^[38][39]

By 1934, Fermi had bombarded heavier elements with neutrons to induce radioactivity in elements of high atomic number. In 1938, Fermi received the Nobel Prize in Physics "for his demonstrations of the existence of new radioactive elements produced by neutron irradiation, and for his related discovery of nuclear reactions brought about by slow neutrons".^[40] In 1938 Otto Hahn, Lise Meitner, and Fritz Strassmann discovered nuclear fission, or the fractionation of uranium nuclei into light elements, induced by neutron bombardment.^[41][42][43] In 1945 Hahn received the 1944 Nobel Prize in Chemistry "for his discovery of the fission of heavy atomic nuclei."^[44][45][46] The discovery of nuclear fission would lead to the development of nuclear power and the atomic bomb by the end of World War II.

Beta decay and the stability of the nucleus

The Feynman diagram for beta decay of a neutron into a proton, electron, and electron antineutrino via an intermediate heavy W boson

Under the Standard Model of particle physics, the only possible decay mode for the neutron that conserves baryon number is for one of the neutron's quarks to change flavour via the weak interaction. The decay of one of the neutron's down quarks into a lighter up quark can be achieved by the emission of a W boson. By this process, the Standard Model description of beta decay, the neutron decays into a proton (which contains one down and two up quarks), an electron, and an electron antineutrino.

Since interacting protons have a mutual electromagnetic repulsion that is stronger than their attractive nuclear interaction, neutrons are a necessary constituent of any atomic nucleus that contains more than one proton (see diproton and neutron–proton ratio).^[47] Neutrons bind with protons and one another in the nucleus via the nuclear force, effectively moderating the repulsive forces between the protons and stabilizing the nucleus.

Free neutron decay

Outside the nucleus, free neutrons are unstable and have a mean lifetime of 881.5±1.5 s (about 14 minutes, 42 seconds); therefore the half-life for this process (which differs from the mean lifetime by a factor of ln(2) = 0.693) is 611.0±1.0 s (about 10 minutes, 11 seconds).^[14] Beta decay of the neutron, described above, can be denoted by the radioactive decay:^[48]

n⁰ →
p⁺ +
e⁻ +
ν
_e

where
p⁺,
e⁻, and
ν
_e denote the proton, electron and electron antineutrino, respectively. For the free neutron the decay energy for this process (based on the masses of the neutron, proton, and electron) is 0.782343 MeV. The maximal energy of the beta decay electron (in the process wherein the neutrino receives a vanishingly small amount of kinetic energy) has been measured at 0.782 ± 0.013 MeV.^[49] The latter number is not well-enough measured to determine the comparatively tiny rest mass of the neutrino (which must in theory be subtracted from the maximal electron kinetic energy) as well as neutrino mass is constrained by many other methods.

A small fraction (about one in 1000) of free neutrons decay with the same products, but add an extra particle in the form of an emitted gamma ray:

n⁰ →
p⁺ +
e⁻ +
ν
_e +
γ

This gamma ray may be thought of as a sort of "internal bremsstrahlung" that arises as the emitted beta particle interacts with the charge of the proton in an electromagnetic way. Internal bremsstrahlung gamma ray production is also a minor feature of beta decays of bound neutrons (as discussed below).

A schematic of the nucleus of an atom indicating
β⁻ radiation, the emission of a fast electron from the nucleus (the accompanying antineutrino is omitted). In the Rutherford model for the nucleus, red spheres were protons with positive charge and blue spheres were protons tightly bound to an electron with no net charge.
The inset shows beta decay of a free neutron as it is understood today; an electron and antineutrino are created in this process.

A very small minority of neutron decays (about four per million) are so-called "two-body (neutron) decays", in which a proton, electron and antineutrino are produced as usual, but the electron fails to gain the 13.6 eV necessary energy to escape the proton (the ionization energy of hydrogen), and therefore simply remains bound to it, as a neutral hydrogen atom (one of the "two bodies"). In this type of free neutron decay, almost all of the neutron decay energy is carried off by the antineutrino (the other "body"). (The hydrogen atom recoils with a speed of only about (decay energy)/(hydrogen rest energy) times the speed of light, or 250 km/s.)

The transformation of a free proton to a neutron (plus a positron and a neutrino) is energetically impossible, since a free neutron has a greater mass than a free proton. But a high-energy collision of a proton and an electron or neutrino can result in a neutron.

Bound neutron decay

While a free neutron has a half life of about 10.2 min, most neutrons within nuclei are stable. According to the nuclear shell model, the protons and neutrons of a nuclide are a quantum mechanical system organized into discrete energy levels with unique quantum numbers. For a neutron to decay, the resulting proton requires an available state at lower energy than the initial neutron state. In stable nuclei the possible lower energy states are all filled, meaning they are each occupied by two protons with spin up and spin down. The Pauli exclusion principle therefore disallows the decay of a neutron to a proton within stable nuclei. The situation is similar to electrons of an atom, where electrons have distinct atomic orbitals and are prevented from decaying to lower energy states, with the emission of a photon, by the exclusion principle.

Neutrons in unstable nuclei can decay by beta decay as described above. In this case, an energetically allowed quantum state is available for the proton resulting from the decay. One example of this decay is carbon-14 (6 protons, 8 neutrons) that decays to nitrogen-14 (7 protons, 7 neutrons) with a half-life of about 5,730 years.

Inside a nucleus, a proton can transform into a neutron via inverse beta decay, if an energetically allowed quantum state is available for the neutron. This transformation occurs by emission of a positron and an electron neutrino:

p⁺ →
n⁰ +
e⁺ +
ν
_e

The transformation of a proton to a neutron inside of a nucleus is also possible through electron capture:

p⁺ +
e⁻ →
n⁰ +
ν
_e

Positron capture by neutrons in nuclei that contain an excess of neutrons is also possible, but is hindered because positrons are repelled by the positive nucleus, and quickly annihilate when they encounter electrons.

Competition of beta decay types

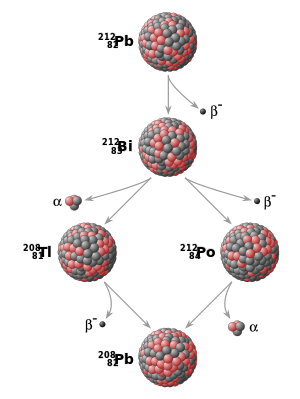
Three types of beta decay in competition are illustrated by the single isotope copper-64 (29 protons, 35 neutrons), which has a half-life of about 12.7 hours. This isotope has one unpaired proton and one unpaired neutron, so either the proton or the neutron can decay. This particular nuclide is almost equally likely to undergo proton decay (by positron emission, 18% or by electron capture, 43%) or neutron decay (by electron emission, 39%).

Intrinsic properties

Mass

The mass of a neutron cannot be directly determined by mass spectrometry due to lack of electric charge. However, since the masses of a proton and of a deuteron can be measured with a mass spectrometer, the mass of a neutron can be deduced by subtracting proton mass from deuteron mass, with the difference being the mass of the neutron plus the binding energy of deuterium (expressed as a positive emitted energy). The latter can be directly measured by measuring the energy (${\displaystyle B_{d}}$) of the single 0.7822 MeV gamma photon emitted when neutrons are captured by protons (this is exothermic and happens with zero-energy neutrons), plus the small recoil kinetic energy (${\displaystyle E_{rd}}$) of the deuteron (about 0.06% of the total energy).

${\displaystyle m_{n}=m_{d}-m_{p}+B_{d}-E_{rd}}$

The energy of the gamma ray can be measured to high precision by X-ray diffraction techniques, as was first done by Bell and Elliot in 1948. The best modern (1986) values for neutron mass by this technique are provided by Greene, et al.^[50] These give a neutron mass of:

m_neutron= 1.008644904(14) u

The value for the neutron mass in MeV is less accurately known, due to less accuracy in the known conversion of u to MeV:^[51]

m_neutron= 939.56563(28) MeV/c².

Another method to determine the mass of a neutron starts from the beta decay of the neutron, when the momenta of the resulting proton and electron are measured.

Electric charge

The total electric charge of the neutron is 0 e. This zero value has been tested experimentally, and the present experimental limit for the charge of the neutron is −2(8)×10⁻²² e,^[4]   or −3(13)×10⁻⁴¹ C. This value is consistent with zero, given the experimental uncertainties (indicated in parentheses). By comparison, the charge of the proton is +1 e.

Magnetic moment

Even though the neutron is a neutral particle, the magnetic moment of a neutron is not zero. The neutron is not affected by electric fields, but it is affected by magnetic fields. The magnetic moment of the neutron is an indication of its quark substructure and internal charge distribution.^[52] The value for the neutron's magnetic moment was first directly measured by Luis Alvarez and Felix Bloch at Berkeley, California, in 1940,^[53] using an extension of the magnetic resonance methods developed by Rabi. Alvarez and Bloch determined the magnetic moment of the neutron to be μ_n= −1.93(2) μ_N, where μ_N is the nuclear magneton.

In the quark model for hadrons, the neutron is composed of one up quark (charge +2/3 e) and two down quarks (charge −1/3 e).^[52] The magnetic moment of the neutron can be modeled as a sum of the magnetic moments of the constituent quarks.^[54] The calculation assumes that the quarks behave like pointlike Dirac particles, each having their own magnetic moment. Simplistically, the magnetic moment of the neutron can be viewed as resulting from the vector sum of the three quark magnetic moments, plus the orbital magnetic moments caused by the movement of the three charged quarks within the neutron.

In one of the early successes of the Standard Model (SU(6) theory, now understood in terms of quark behavior), in 1964 Mirza A. B. Beg, Benjamin W. Lee, and Abraham Pais theoretically calculated the ratio of proton to neutron magnetic moments to be −3/2, which agrees with the experimental value to within 3%.^[55][56][57] The measured value for this ratio is −1.45989805(34).^[3] A contradiction of the quantum mechanical basis of this calculation with the Pauli exclusion principle, led to the discovery of the color charge for quarks by Oscar W. Greenberg in 1964.^[55]

The above treatment compares neutrons with protons, allowing the complex behavior of quarks to be subtracted out between models, and merely exploring what the effects would be of differing quark charges (or quark type). Such calculations are enough to show that the interior of neutrons is very much like that of protons, save for the difference in quark composition with a down quark in the neutron replacing an up quark in the proton.

Attempts have been made to quantitatively recover the neutron magnetic moment from first principles. From the nonrelativistic, quantum mechanical wavefunction for baryons composed of three quarks, a straightforward calculation gives fairly accurate estimates for the magnetic moments of neutrons, protons, and other baryons.^[54] For a neutron, the end result of this calculation is that the magnetic moment of the neutron is given by μ_n= 4/3 μ_d − 1/3 μ_u, where μ_d and μ_u are the magnetic moments for the down and up quarks, respectively. This result combines the intrinsic magnetic moments of the quarks with their orbital magnetic moments, and assumes the three quarks are in a particular, dominant quantum state.

Baryon	Magnetic moment of quark model	Computed (${\displaystyle \mu _{\mathrm {N} }}$)	Observed (${\displaystyle \mu _{\mathrm {N} }}$)
p	4/3 μu − 1/3 μd	2.79	2.793
n	4/3 μd − 1/3 μu	−1.86	−1.913

The results of this calculation are encouraging, but the masses of the up or down quarks were assumed to be 1/3 the mass of a nucleon.^[54] The masses of the quarks are actually only about 1% that of a nucleon.^[58] The discrepancy stems from the complexity of the Standard Model for nucleons, where most of their mass originates in the gluon fields, virtual particles, and their associated energy that are essential aspects of the strong force.^[58][59] Furthermore, the complex system of quarks and gluons that constitute a neutron requires a relativistic treatment.^[60] The nucleon magnetic moment has been successfully computed numerically from first principles, however, including all the effects mentioned and using more realistic values for the quark masses. The calculation gave results that were in fair agreement with measurement, but it required significant computing resources.^[61][62]

Spin

The neutron is a spin 1/2 particle, that is, it is a fermion with intrinsic angular momentum equal to 1/2 ħ, where ħ is the reduced Planck constant. For many years after the discovery of the neutron, its exact spin was ambiguous. Although it was assumed to be a spin 1/2 Dirac particle, the possibility that the neutron was a spin 3/2 particle lingered. The interactions of the neutron's magnetic moment with an external magnetic field were exploited to finally determine the spin of the neutron.^[63] In 1949, Hughes and Burgy measured neutrons reflected from a ferromagnetic mirror and found that the angular distribution of the reflections was consistent with spin 1/2.^[64] In 1954, Sherwood, Stephenson, and Bernstein employed neutrons in a Stern–Gerlach experiment that used a magnetic field to separate the neutron spin states. They recorded two such spin states, consistent with a spin 1/2 particle.^[63][65]

As a fermion, the neutron is subject to the Pauli exclusion principle; two neutrons cannot have the same quantum numbers. This is the source of the degeneracy pressure which makes neutron stars possible.

Structure and geometry of charge distribution

An article published in 2007 featuring a model-independent analysis concluded that the neutron has a negatively charged exterior, a positively charged middle, and a negative core.^[66] In a simplified classical view, the negative "skin" of the neutron assists it to be attracted to the protons with which it interacts in the nucleus. (However, the main attraction between neutrons and protons is via the nuclear force, which does not involve charge.)

The simplified classical view of the neutron's charge distribution also "explains" the fact that the neutron magnetic dipole points in the opposite direction from its spin angular momentum vector (as compared to the proton). This gives the neutron, in effect, a magnetic moment which resembles a negatively charged particle. This can be reconciled classically with a neutral neutron composed of a charge distribution in which the negative sub-parts of the neutron have a larger average radius of distribution, and therefore contribute more to the particle's magnetic dipole moment, than do the positive parts that are, on average, nearer the core.

Electric dipole moment

The Standard Model of particle physics predicts a tiny separation of positive and negative charge within the neutron leading to a permanent electric dipole moment.^[67] The predicted value is, however, well below the current sensitivity of experiments. From several unsolved puzzles in particle physics, it is clear that the Standard Model is not the final and full description of all particles and their interactions. New theories going beyond the Standard Model generally lead to much larger predictions for the electric dipole moment of the neutron. Currently, there are at least four experiments trying to measure for the first time a finite neutron electric dipole moment, including:

• Cryogenic neutron EDM experiment being set up at the Institut Laue–Langevin^[68]
• nEDM experiment under construction at the new UCN source at the Paul Scherrer Institute^[69]
• nEDM experiment being envisaged at the Spallation Neutron Source^[70][71]
• nEDM experiment being built at the Institut Laue–Langevin^[72]

Anti-neutron

The antineutron is the antiparticle of the neutron. It was discovered by Bruce Cork in the year 1956, a year after the antiproton was discovered. CPT-symmetry puts strong constraints on the relative properties of particles and antiparticles, so studying antineutrons yields provide stringent tests on CPT-symmetry. The fractional difference in the masses of the neutron and antineutron is (9±6)×10⁻⁵. Since the difference is only about two standard deviations away from zero, this does not give any convincing evidence of CPT-violation.^[14]

Neutron compounds

Dineutrons and tetraneutrons

The existence of stable clusters of 4 neutrons, or tetraneutrons, has been hypothesised by a team led by Francisco-Miguel Marqués at the CNRS Laboratory for Nuclear Physics based on observations of the disintegration of beryllium-14 nuclei. This is particularly interesting because current theory suggests that these clusters should not be stable.

In February 2016, Japanese physicist Susumu Shimoura of the University of Tokyo and co-workers reported they had observed the purported tetraneutrons for the first time experimentally.^[73] Nuclear physicists around the world say this discovery, if confirmed, would be a milestone in the field of nuclear physics and certainly would deepen our understanding of the nuclear forces.^[74][75]

The dineutron is another hypothetical particle. In 2012, Artemis Spyrou from Michigan State University and coworkers reported that they observed, for the first time, the dineutron emission in the decay of ¹⁶Be. The dineutron character is evidenced by a small emission angle between the two neutrons. The authors measured the two-neutron separation energy to be 1.35(10) MeV, in good agreement with shell model calculations, using standard interactions for this mass region.^[76]

Neutronium and neutron stars

At extremely high pressures and temperatures, nucleons and electrons are believed to collapse into bulk neutronic matter, called neutronium. This is presumed to happen in neutron stars.
The extreme pressure inside a neutron star may deform the neutrons into a cubic symmetry, allowing tighter packing of neutrons.^[77]

Detection

The common means of detecting a charged particle by looking for a track of ionization (such as in a cloud chamber) does not work for neutrons directly. Neutrons that elastically scatter off atoms can create an ionization track that is detectable, but the experiments are not as simple to carry out; other means for detecting neutrons, consisting of allowing them to interact with atomic nuclei, are more commonly used. The commonly used methods to detect neutrons can therefore be categorized according to the nuclear processes relied upon, mainly neutron capture or elastic scattering.^[78]

Neutron detection by neutron capture

A common method for detecting neutrons involves converting the energy released from neutron capture reactions into electrical signals. Certain nuclides have a high neutron capture cross section, which is the probability of absorbing a neutron. Upon neutron capture, the compound nucleus emits more easily detectable radiation, for example an alpha particle, which is then detected. The nuclides ³He
, ⁶Li
, ¹⁰B
, ²³³U
, ²³⁵U
, ²³⁷Np
, and ²³⁹Pu
are useful for this purpose.

Neutron detection by elastic scattering

Neutrons can elastically scatter off nuclei, causing the struck nucleus to recoil. Kinematically, a neutron can transfer more energy to a light nucleus such as hydrogen or helium than to a heavier nucleus. Detectors relying on elastic scattering are called fast neutron detectors. Recoiling nuclei can ionize and excite further atoms through collisions. Charge and/or scintillation light produced in this way can be collected to produce a detected signal. A major challenge in fast neutron detection is discerning such signals from erroneous signals produced by gamma radiation in the same detector.

Fast neutron detectors have the advantage of not requiring a moderator, and are therefore capable of measuring the neutron's energy, time of arrival, and in certain cases direction of incidence.

Sources and production

Free neutrons are unstable, although they have the longest half-life of any unstable subatomic particle by several orders of magnitude. Their half-life is still only about 10 minutes, however, so they can be obtained only from sources that produce them continuously.

Natural neutron background. A small natural background flux of free neutrons exists everywhere on Earth. In the atmosphere and deep into the ocean, the "neutron background" is caused by muons produced by cosmic ray interaction with the atmosphere. These high-energy muons are capable of penetration to considerable depths in water and soil. There, in striking atomic nuclei, among other reactions they induce spallation reactions in which a neutron is liberated from the nucleus. Within the Earth's crust a second source is neutrons produced primarily by spontaneous fission of uranium and thorium present in crustal minerals. The neutron background is not strong enough to be a biological hazard, but it is of importance to very high resolution particle detectors that are looking for very rare events, such as (hypothesized) interactions that might be caused by particles of dark matter.^[9] Recent research has shown that even thunderstorms can produce neutrons with energies of up to several tens of MeV.^[79] Recent research has shown that the fluence of these neutrons lies between 10⁻⁹ and 10⁻¹³ per ms and per m² depending on the detection altitude. The energy of most of these neutrons, even with initial energies of 20 MeV, decreases down to the keV range within 1 ms.^[80]

Even stronger neutron background radiation is produced at the surface of Mars, where the atmosphere is thick enough to generate neutrons from cosmic ray muon production and neutron-spallation, but not thick enough to provide significant protection from the neutrons produced. These neutrons not only produce a Martian surface neutron radiation hazard from direct downward-going neutron radiation but may also produce a significant hazard from reflection of neutrons from the Martian surface, which will produce reflected neutron radiation penetrating upward into a Martian craft or habitat from the floor.^[81]

Sources of neutrons for research. These include certain types of radioactive decay (spontaneous fission and neutron emission), and from certain nuclear reactions. Convenient nuclear reactions include tabletop reactions such as natural alpha and gamma bombardment of certain nuclides, often beryllium or deuterium, and induced nuclear fission, such as occurs in nuclear reactors. In addition, high-energy nuclear reactions (such as occur in cosmic radiation showers or accelerator collisions) also produce neutrons from disintegration of target nuclei. Small (tabletop) particle accelerators optimized to produce free neutrons in this way, are called neutron generators.

In practice, the most commonly used small laboratory sources of neutrons use radioactive decay to power neutron production. One noted neutron-producing radioisotope, californium-252 decays (half-life 2.65 years) by spontaneous fission 3% of the time with production of 3.7 neutrons per fission, and is used alone as a neutron source from this process. Nuclear reaction sources (that involve two materials) powered by radioisotopes use an alpha decay source plus a beryllium target, or else a source of high-energy gamma radiation from a source that undergoes beta decay followed by gamma decay, which produces photoneutrons on interaction of the high-energy gamma ray with ordinary stable beryllium, or else with the deuterium in heavy water. A popular source of the latter type is radioactive antimony-124 plus beryllium, a system with a half-life of 60.9 days, which can be constructed from natural antimony (which is 42.8% stable antimony-123) by activating it with neutrons in a nuclear reactor, then transported to where the neutron source is needed.^[82]
 

Institut Laue–Langevin (ILL) in Grenoble, France – a major neutron research facility.

Nuclear fission reactors naturally produce free neutrons; their role is to sustain the energy-producing chain reaction. The intense neutron radiation can also be used to produce various radioisotopes through the process of neutron activation, which is a type of neutron capture.

Experimental nuclear fusion reactors produce free neutrons as a waste product. However, it is these neutrons that possess most of the energy, and converting that energy to a useful form has proved a difficult engineering challenge. Fusion reactors that generate neutrons are likely to create radioactive waste, but the waste is composed of neutron-activated lighter isotopes, which have relatively short (50–100 years) decay periods as compared to typical half-lives of 10,000 years^{[citation needed]} for fission waste, which is long due primarily to the long half-life of alpha-emitting transuranic actinides.^[83]

Neutron beams and modification of beams after production

Free neutron beams are obtained from neutron sources by neutron transport. For access to intense neutron sources, researchers must go to a specialized neutron facility that operates a research reactor or a spallation source.

The neutron's lack of total electric charge makes it difficult to steer or accelerate them. Charged particles can be accelerated, decelerated, or deflected by electric or magnetic fields. These methods have little effect on neutrons. However, some effects may be attained by use of inhomogeneous magnetic fields because of the neutron's magnetic moment. Neutrons can be controlled by methods that include moderation, reflection, and velocity selection. Thermal neutrons can be polarized by transmission through magnetic materials in a method analogous to the Faraday effect for photons. Cold neutrons of wavelengths of 6–7 angstroms can be produced in beams of a high degree of polarization, by use of magnetic mirrors and magnetized interference filters.^[84]

Applications

The neutron plays an important role in many nuclear reactions. For example, neutron capture often results in neutron activation, inducing radioactivity. In particular, knowledge of neutrons and their behavior has been important in the development of nuclear reactors and nuclear weapons. The fissioning of elements like uranium-235 and plutonium-239 is caused by their absorption of neutrons.

Cold, thermal, and hot neutron radiation is commonly employed in neutron scattering facilities, where the radiation is used in a similar way one uses X-rays for the analysis of condensed matter. Neutrons are complementary to the latter in terms of atomic contrasts by different scattering cross sections; sensitivity to magnetism; energy range for inelastic neutron spectroscopy; and deep penetration into matter.

The development of "neutron lenses" based on total internal reflection within hollow glass capillary tubes or by reflection from dimpled aluminum plates has driven ongoing research into neutron microscopy and neutron/gamma ray tomography.^[85][86][87]

A major use of neutrons is to excite delayed and prompt gamma rays from elements in materials. This forms the basis of neutron activation analysis (NAA) and prompt gamma neutron activation analysis (PGNAA). NAA is most often used to analyze small samples of materials in a nuclear reactor whilst PGNAA is most often used to analyze subterranean rocks around bore holes and industrial bulk materials on conveyor belts.

Another use of neutron emitters is the detection of light nuclei, in particular the hydrogen found in water molecules. When a fast neutron collides with a light nucleus, it loses a large fraction of its energy. By measuring the rate at which slow neutrons return to the probe after reflecting off of hydrogen nuclei, a neutron probe may determine the water content in soil.

Medical therapies

Because neutron radiation is both penetrating and ionizing, it can be exploited for medical treatments. Neutron radiation can have the unfortunate side-effect of leaving the affected area radioactive, however. Neutron tomography is therefore not a viable medical application.

Fast neutron therapy utilizes high-energy neutrons typically greater than 20 MeV to treat cancer. Radiation therapy of cancers is based upon the biological response of cells to ionizing radiation. If radiation is delivered in small sessions to damage cancerous areas, normal tissue will have time to repair itself, while tumor cells often cannot.^[88] Neutron radiation can deliver energy to a cancerous region at a rate an order of magnitude larger than gamma radiation^[89]

Beams of low-energy neutrons are used in boron capture therapy to treat cancer. In boron capture therapy, the patient is given a drug that contains boron and that preferentially accumulates in the tumor to be targeted. The tumor is then bombarded with very low-energy neutrons (although often higher than thermal energy) which are captured by the boron-10 isotope in the boron, which produces an excited state of boron-11 that then decays to produce lithium-7 and an alpha particle that have sufficient energy to kill the malignant cell, but insufficient range to damage nearby cells. For such a therapy to be applied to the treatment of cancer, a neutron source having an intensity of the order of a thousand million (10⁹) neutrons per second per cm² is preferred. Such fluxes require a research nuclear reactor.

Protection

Exposure to free neutrons can be hazardous, since the interaction of neutrons with molecules in the body can cause disruption to molecules and atoms, and can also cause reactions that give rise to other forms of radiation (such as protons). The normal precautions of radiation protection apply: Avoid exposure, stay as far from the source as possible, and keep exposure time to a minimum. Some particular thought must be given to how to protect from neutron exposure, however. For other types of radiation, e.g., alpha particles, beta particles, or gamma rays, material of a high atomic number and with high density make for good shielding; frequently, lead is used. However, this approach will not work with neutrons, since the absorption of neutrons does not increase straightforwardly with atomic number, as it does with alpha, beta, and gamma radiation. Instead one needs to look at the particular interactions neutrons have with matter (see the section on detection above). For example, hydrogen-rich materials are often used to shield against neutrons, since ordinary hydrogen both scatters and slows neutrons. This often means that simple concrete blocks or even paraffin-loaded plastic blocks afford better protection from neutrons than do far more dense materials. After slowing, neutrons may then be absorbed with an isotope that has high affinity for slow neutrons without causing secondary capture radiation, such as lithium-6.

Hydrogen-rich ordinary water affects neutron absorption in nuclear fission reactors: Usually, neutrons are so strongly absorbed by normal water that fuel enrichment with fissionable isotope is required. The deuterium in heavy water has a very much lower absorption affinity for neutrons than does protium (normal light hydrogen). Deuterium is, therefore, used in CANDU-type reactors, in order to slow (moderate) neutron velocity, to increase the probability of nuclear fission compared to neutron capture.

Neutron temperature

Thermal neutrons

A thermal neutron is a free neutron that is Boltzmann distributed with kT= 0.0253 eV (4.0×10⁻²¹ J) at room temperature. This gives characteristic (not average, or median) speed of 2.2 km/s. The name 'thermal' comes from their energy being that of the room temperature gas or material they are permeating. (see kinetic theory for energies and speeds of molecules). After a number of collisions (often in the range of 10–20) with nuclei, neutrons arrive at this energy level, provided that they are not absorbed.

In many substances, thermal neutron reactions show a much larger effective cross-section than reactions involving faster neutrons, and thermal neutrons can therefore be absorbed more readily (i.e., with higher probability) by any atomic nuclei that they collide with, creating a heavier — and often unstable — isotope of the chemical element as a result.

Most fission reactors use a neutron moderator to slow down, or thermalize the neutrons that are emitted by nuclear fission so that they are more easily captured, causing further fission. Others, called fast breeder reactors, use fission energy neutrons directly.

Cold neutrons

Cold neutrons are thermal neutrons that have been equilibrated in a very cold substance such as liquid deuterium. Such a cold source is placed in the moderator of a research reactor or spallation source. Cold neutrons are particularly valuable for neutron scattering experiments.^{[citation needed]}

Cold neutron source providing neutrons at about the temperature of liquid hydrogen

Ultracold neutrons

Ultracold neutrons are produced by elastically scattering cold neutrons in substances with a temperature of a few kelvins, such as solid deuterium or superfluid helium. An alternative production method is the mechanical deceleration of cold neutrons.

Fission energy neutrons

A fast neutron is a free neutron with a kinetic energy level close to 1 MeV (1.6×10⁻¹³ J), hence a speed of ~14000 km/s (~ 5% of the speed of light). They are named fission energy or fast neutrons to distinguish them from lower-energy thermal neutrons, and high-energy neutrons produced in cosmic showers or accelerators. Fast neutrons are produced by nuclear processes such as nuclear fission. Neutrons produced in fission, as noted above, have a Maxwell–Boltzmann distribution of kinetic energies from 0 to ~14 MeV, a mean energy of 2 MeV (for U-235 fission neutrons), and a mode of only 0.75 MeV, which means that more than half of them do not qualify as fast (and thus have almost no chance of initiating fission in fertile materials, such as U-238 and Th-232).

Fast neutrons can be made into thermal neutrons via a process called moderation. This is done with a neutron moderator. In reactors, typically heavy water, light water, or graphite are used to moderate neutrons.

Fusion neutrons

The fusion reaction rate increases rapidly with temperature until it maximizes and then gradually drops off. The DT rate peaks at a lower temperature (about 70 keV, or 800 million kelvins) and at a higher value than other reactions commonly considered for fusion energy.

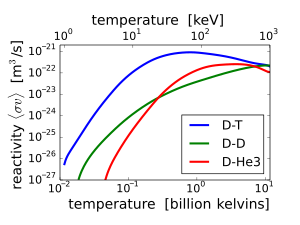
D–T (deuterium–tritium) fusion is the fusion reaction that produces the most energetic neutrons, with 14.1 MeV of kinetic energy and traveling at 17% of the speed of light. D–T fusion is also the easiest fusion reaction to ignite, reaching near-peak rates even when the deuterium and tritium nuclei have only a thousandth as much kinetic energy as the 14.1 MeV that will be produced.

14.1 MeV neutrons have about 10 times as much energy as fission neutrons, and are very effective at fissioning even non-fissile heavy nuclei, and these high-energy fissions produce more neutrons on average than fissions by lower-energy neutrons. This makes D–T fusion neutron sources such as proposed tokamak power reactors useful for transmutation of transuranic waste. 14.1 MeV neutrons can also produce neutrons by knocking them loose from nuclei.

On the other hand, these very high-energy neutrons are less likely to simply be captured without causing fission or spallation. For these reasons, nuclear weapon design extensively utilizes D–T fusion 14.1 MeV neutrons to cause more fission. Fusion neutrons are able to cause fission in ordinarily non-fissile materials, such as depleted uranium (uranium-238), and these materials have been used in the jackets of thermonuclear weapons. Fusion neutrons also can cause fission in substances that are unsuitable or difficult to make into primary fission bombs, such as reactor grade plutonium. This physical fact thus causes ordinary non-weapons grade materials to become of concern in certain nuclear proliferation discussions and treaties.

Other fusion reactions produce much less energetic neutrons. D–D fusion produces a 2.45 MeV neutron and helium-3 half of the time, and produces tritium and a proton but no neutron the rest of the time. D–³He fusion produces no neutron.

Intermediate-energy neutrons

Transmutation flow in light water reactor, which is a thermal-spectrum reactor

A fission energy neutron that has slowed down but not yet reached thermal energies is called an epithermal neutron.

Cross sections for both capture and fission reactions often have multiple resonance peaks at specific energies in the epithermal energy range. These are of less significance in a fast neutron reactor, where most neutrons are absorbed before slowing down to this range, or in a well-moderated thermal reactor, where epithermal neutrons interact mostly with moderator nuclei, not with either fissile or fertile actinide nuclides. However, in a partially moderated reactor with more interactions of epithermal neutrons with heavy metal nuclei, there are greater possibilities for transient changes in reactivity that might make reactor control more difficult.

Ratios of capture reactions to fission reactions are also worse (more captures without fission) in most nuclear fuels such as plutonium-239, making epithermal-spectrum reactors using these fuels less desirable, as captures not only waste the one neutron captured but also usually result in a nuclide that is not fissile with thermal or epithermal neutrons, though still fissionable with fast neutrons. The exception is uranium-233 of the thorium cycle, which has good capture-fission ratios at all neutron energies.

High-energy neutrons

High-energy neutrons have much more energy than fission energy neutrons and are generated as secondary particles by particle accelerators or in the atmosphere from cosmic rays. These high-energy neutrons are extremely efficient at ionization and far more likely to cause cell death than X-rays or protons.

We Earth Neurons

September 18, 2001 by Daniel Dennett
Original link:  http://www.kurzweilai.net/we-earth-neurons

Daniel Dennett on knowledge sharing and the fate of the planet, in which he contrasts individuals and their brains with the trillions of neurons that compose them. The planet has grown its own nervous system: us.

Some years ago a friend of mine in the Peace Corps told me about his efforts on behalf of a tribe of gentle Indians deep in the Brazilian forest. I asked him if he had been required to tell them about the conflict between the USA and the USSR. Not at all, he replied. There would be no point in it. They had not only never heard of either America or the Soviet Union, they had never even heard of Brazil! Who would have guessed that it is still possible to be a human being living in, and subject to the laws of, a nation without the slightest knowledge of that fact? If we find this astonishing, it is because we human beings, unlike all other species on the planet, are knowers. We are the ones–the only ones–who have figured out what we are, and where we are, in this great universe. And we are even beginning to figure out how we got here.

These quite recent discoveries are unnerving, to say the least. What you are–what each of us is–is an assemblage of roughly a trillion cells, of thousands of different sorts. Most of these cells are “daughters” of the egg and sperm cell whose union started you (there are also millions of hitchhikers from thousands of different lineages stowed away in your body), but each cell is a mindless mechanism, a largely autonomous micro-robot, no more conscious than a bacterium, and not a single one of the cells that compose you knows who you are, or cares.

Each trillion-robot team is gathered together in a breathtakingly efficient regime that has no dictator but manages to keep itself organized to repel outsiders, banish the weak, enforce iron rules of discipline–and serve as the headquarters of one conscious self, one mind. These communities of cells are fascistic in the extreme, but your interests and values have almost nothing to do with the limited goals of the cells that compose you–fortunately. Some people are gentle and generous, others are ruthless; some are pornographers and others devote their lives to the service of God, and it has been tempting over the ages to imagine that these striking differences must be due to the special features of some extra thing (a soul) installed somehow in the bodily headquarters, but what we now have figured out is that there is no such extra ingredient; we are each made of mindless robots and nothing else, no non-physical, non-robotic ingredients at all. The differences between people are all due to the way their particular robotic teams are put together, over a lifetime of growth and experience. The difference between speaking French and speaking Chinese is a difference in the organization of the working parts, and so are all the other differences of personality–and knowledge.

Four and a half billion years ago, the earth was formed, and it was utterly without life. And so it stayed for perhaps as long as a billion years. For another billion years, the planet’s oceans teemed with life, but it was all blind and deaf. Simple cells multiplied, engulfing each other, exploiting each other in a thousand ways, but oblivious to the world beyond their membranes. Then much larger, more complex cells evolved–eukaryotes–still clueless and robotic, but with enough internal machinery to begin to specialize. So it continued for more than two billion more years, the time it took for the algorithms of evolution to hit upon good ways of banding these workers together into multi-cellular organisms composed of millions, billions and, (eventually) trillions of cells, each doing its particular mechanical routine, but now yoked into specialized service, as part of an eye or an ear or a lung or a kidney. These organisms (not the individual team members composing them) had become long-distance knowers, able to spy supper trying to appear inconspicuous in the middle distance, able to hear danger threatening from afar. But still, even these whole organisms knew not what they were. Their instincts guaranteed that they tried to mate with the right sorts, and flock with the right sorts, but just as those Brazilians didn’t know they were Brazilians, no buffalo has ever known it’s a buffalo.

In just one species, our species, a new trick evolved: language. It has provided us a broad highway of knowledge-sharing, on every topic. Conversation unites us, in spite of our different languages. We can all know quite a lot about what it is like to be a Vietnamese fisherman or a Bulgarian taxi driver, an eighty-year-old nun or a five-year-old boy blind from birth, a chess master or a prostitute. No matter how different from one another we people are, scattered around the globe, we can explore our differences and communicate about them. No matter how similar to one another buffalos are, standing shoulder to shoulder in a herd, they cannot know much of anything about their similarities, let alone their differences, because they can’t compare notes. They can have similar experiences, side by side, but they really can’t share experiences the way we do.

Even in our species, it has taken thousands of years of communication for us to begin to find the keys to our own identities. It has been only a few hundred years that we’ve known that we are mammals, and only a few decades that we’ve understood in considerable detail how we have evolved, along with all other living things, from those simple beginnings. We are outnumbered on this planet by our distant cousins, the ants, and outweighed by yet more distant relatives we share with the ants, the bacteria, but though we are in the minority, our capacity for long-distance knowledge gives us powers that dwarf the powers of all the rest of the life on the planet. Now, for the first time in its billions of years of history, our planet is protected by far-seeing sentinels, able to anticipate danger from the distant future–a comet on a collision course, or global warming–and devise schemes for doing something about it. The planet has finally grown its own nervous system: us.

We may not be up to the job. We may destroy the planet instead of saving it, largely because we are such free-thinking, creative, unruly explorers and adventurers, so unlike the trillions of slavish workers that compose us. Brains are for anticipating the future, so that timely steps can be taken in better directions, but even the smartest of beasts have very limited time horizons, and little if any ability to imagine alternative worlds. We human beings, in contrast, have discovered the mixed blessing of being able to think even about our own deaths and beyond, and a huge portion of our energy expenditure over the last ten thousand years or so has been devoted to assuaging the concerns provoked by this unsettling new vista. If you burn more calories than you take in, you soon die. If you find some tricks that provide you a surplus of calories, what might you spend them on? You might devote person-centuries of labor to building temples and tombs and sacrificial pyres on which you destroy some of your most precious possessions–and even some of your very own children. Why would you want to do that? These strange and awful expenditures give us clues about some of the hidden costs of our heightened powers of imagination. We did not come by our knowledge painlessly.

Radiometric dating

From Wikipedia, the free encyclopedia

 

Radiometric dating or radioactive dating is a technique used to date materials such as rocks or carbon, in which trace radioactive impurities were selectively incorporated when they were formed. The method compares the abundance of a naturally occurring radioactive isotope within the material to the abundance of its decay products, which form at a known constant rate of decay. The use of radiometric dating was first published in 1907 by Bertram Boltwood and is now the principal source of information about the absolute age of rocks and other geological features, including the age of fossilized life forms or the age of the Earth itself, and can also be used to date a wide range of natural and man-made materials.

Together with stratigraphic principles, radiometric dating methods are used in geochronology to establish the geologic time scale.^[3] Among the best-known techniques are radiocarbon dating, potassium–argon dating and uranium–lead dating. By allowing the establishment of geological timescales, it provides a significant source of information about the ages of fossils and the deduced rates of evolutionary change. Radiometric dating is also used to date archaeological materials, including ancient artifacts.

Different methods of radiometric dating vary in the timescale over which they are accurate and the materials to which they can be applied.

Fundamentals of radiometric dating

Radioactive decay

Example of a radioactive decay chain from lead-212 (²¹²Pb) to lead-208 (²⁰⁸Pb) . Each parent nuclide spontaneously decays into a daughter nuclide (the decay product) via an α decay or a β⁻ decay. The final decay product, lead-208 (²⁰⁸Pb), is stable and can no longer undergo spontaneous radioactive decay.

All ordinary matter is made up of combinations of chemical elements, each with its own atomic number, indicating the number of protons in the atomic nucleus. Additionally, elements may exist in different isotopes, with each isotope of an element differing in the number of neutrons in the nucleus. A particular isotope of a particular element is called a nuclide. Some nuclides are inherently unstable. That is, at some point in time, an atom of such a nuclide will undergo radioactive decay and spontaneously transform into a different nuclide. This transformation may be accomplished in a number of different ways, including alpha decay (emission of alpha particles) and beta decay (electron emission, positron emission, or electron capture). Another possibility is spontaneous fission into two or more nuclides.

While the moment in time at which a particular nucleus decays is unpredictable, a collection of atoms of a radioactive nuclide decays exponentially at a rate described by a parameter known as the half-life, usually given in units of years when discussing dating techniques. After one half-life has elapsed, one half of the atoms of the nuclide in question will have decayed into a "daughter" nuclide or decay product. In many cases, the daughter nuclide itself is radioactive, resulting in a decay chain, eventually ending with the formation of a stable (nonradioactive) daughter nuclide; each step in such a chain is characterized by a distinct half-life. In these cases, usually the half-life of interest in radiometric dating is the longest one in the chain, which is the rate-limiting factor in the ultimate transformation of the radioactive nuclide into its stable daughter. Isotopic systems that have been exploited for radiometric dating have half-lives ranging from only about 10 years (e.g., tritium) to over 100 billion years (e.g., samarium-147).^[4]

For most radioactive nuclides, the half-life depends solely on nuclear properties and is essentially a constant. It is not affected by external factors such as temperature, pressure, chemical environment, or presence of a magnetic or electric field.^[5][6][7] The only exceptions are nuclides that decay by the process of electron capture, such as beryllium-7, strontium-85, and zirconium-89, whose decay rate may be affected by local electron density. For all other nuclides, the proportion of the original nuclide to its decay products changes in a predictable way as the original nuclide decays over time. This predictability allows the relative abundances of related nuclides to be used as a clock to measure the time from the incorporation of the original nuclides into a material to the present.

Accuracy of radiometric dating

Thermal ionization mass spectrometer used in radiometric dating.

The basic equation of radiometric dating requires that neither the parent nuclide nor the daughter product can enter or leave the material after its formation. The possible confounding effects of contamination of parent and daughter isotopes have to be considered, as do the effects of any loss or gain of such isotopes since the sample was created. It is therefore essential to have as much information as possible about the material being dated and to check for possible signs of alteration.^[8] Precision is enhanced if measurements are taken on multiple samples from different locations of the rock body. Alternatively, if several different minerals can be dated from the same sample and are assumed to be formed by the same event and were in equilibrium with the reservoir when they formed, they should form an isochron. This can reduce the problem of contamination. In uranium–lead dating, the concordia diagram is used which also decreases the problem of nuclide loss. Finally, correlation between different isotopic dating methods may be required to confirm the age of a sample. For example, the age of the Amitsoq gneisses from western Greenland was determined to be 3.6 ± 0.05 million years ago (MA) using uranium–lead dating and 3.56 ± 0.10 Ma using lead–lead dating, results that are consistent with each other.^{[9]:142–143}

Accurate radiometric dating generally requires that the parent has a long enough half-life that it will be present in significant amounts at the time of measurement (except as described below under "Dating with short-lived extinct radionuclides"), the half-life of the parent is accurately known, and enough of the daughter product is produced to be accurately measured and distinguished from the initial amount of the daughter present in the material. The procedures used to isolate and analyze the parent and daughter nuclides must be precise and accurate. This normally involves isotope-ratio mass spectrometry.^[10]

The precision of a dating method depends in part on the half-life of the radioactive isotope involved. For instance, carbon-14 has a half-life of 5,730 years. After an organism has been dead for 60,000 years, so little carbon-14 is left that accurate dating cannot be established. On the other hand, the concentration of carbon-14 falls off so steeply that the age of relatively young remains can be determined precisely to within a few decades.^[11]

Closure temperature

If a material that selectively rejects the daughter nuclide is heated, any daughter nuclides that have been accumulated over time will be lost through diffusion, setting the isotopic "clock" to zero. The temperature at which this happens is known as the closure temperature or blocking temperature and is specific to a particular material and isotopic system. These temperatures are experimentally determined in the lab by artificially resetting sample minerals using a high-temperature furnace. As the mineral cools, the crystal structure begins to form and diffusion of isotopes is less easy. At a certain temperature, the crystal structure has formed sufficiently to prevent diffusion of isotopes. This temperature is what is known as closure temperature and represents the temperature below which the mineral is a closed system to isotopes. Thus an igneous or metamorphic rock or melt, which is slowly cooling, does not begin to exhibit measurable radioactive decay until it cools below the closure temperature. The age that can be calculated by radiometric dating is thus the time at which the rock or mineral cooled to closure temperature.^[12][13] Dating of different minerals and/or isotope systems (with differing closure temperatures) within the same rock can therefore enable the tracking of the thermal history of the rock in question with time, and thus the history of metamorphic events may become known in detail. This field is known as thermochronology or thermochronometry.

The age equation

Sm/Nd isochron plotted of samples ^[14] from the Great Dyke, Zimbabwe. The age is calculated from the slope of the isochron (line) and the original composition from the intercept of the isochron with the y-axis.

The mathematical expression that relates radioactive decay to geologic time is^[12][15]

D = D₀ + N(t) (e^λt − 1)

where

t is age of the sample,

D is number of atoms of the daughter isotope in the sample,

D₀ is number of atoms of the daughter isotope in the original composition,

N is number of atoms of the parent isotope in the sample at time t (the present), given by N(t) = N_oe^-λt, and

λ is the decay constant of the parent isotope, equal to the inverse of the radioactive half-life of the parent isotope^[16] times the natural logarithm of 2.

The equation is most conveniently expressed in terms of the measured quantity N(t) rather than the constant initial value N_o.

The above equation makes use of information on the composition of parent and daughter isotopes at the time the material being tested cooled below its closure temperature. This is well-established for most isotopic systems.^[13][17] However, construction of an isochron does not require information on the original compositions, using merely the present ratios of the parent and daughter isotopes to a standard isotope. Plotting an isochron is used to solve the age equation graphically and calculate the age of the sample and the original composition.

Modern dating methods

Radiometric dating has been carried out since 1905 when it was invented by Ernest Rutherford as a method by which one might determine the age of the Earth. In the century since then the techniques have been greatly improved and expanded.^[16] Dating can now be performed on samples as small as a nanogram using a mass spectrometer. The mass spectrometer was invented in the 1940s and began to be used in radiometric dating in the 1950s. It operates by generating a beam of ionized atoms from the sample under test. The ions then travel through a magnetic field, which diverts them into different sampling sensors, known as "Faraday cups", depending on their mass and level of ionization. On impact in the cups, the ions set up a very weak current that can be measured to determine the rate of impacts and the relative concentrations of different atoms in the beams.

Uranium–lead dating method

A concordia diagram as used in uranium–lead dating, with data from the Pfunze Belt, Zimbabwe.^[18] All the samples show loss of lead isotopes, but the intercept of the errorchron (straight line through the sample points) and the concordia (curve) shows the correct age of the rock.^[13]

Uranium–lead radiometric dating involves using uranium-235 or uranium-238 to date a substance's absolute age. This scheme has been refined to the point that the error margin in dates of rocks can be as low as less than two million years in two-and-a-half billion years.^[14][19] An error margin of 2–5% has been achieved on younger Mesozoic rocks.^[20]

Uranium–lead dating is often performed on the mineral zircon (ZrSiO₄), though it can be used on other materials, such as baddeleyite, as well as monazite (see: monazite geochronology).^[21] Zircon and baddeleyite incorporate uranium atoms into their crystalline structure as substitutes for zirconium, but strongly reject lead. Zircon has a very high closure temperature, is resistant to mechanical weathering and is very chemically inert. Zircon also forms multiple crystal layers during metamorphic events, which each may record an isotopic age of the event. In situ micro-beam analysis can be achieved via laser ICP-MS or SIMS techniques.^[22]

One of its great advantages is that any sample provides two clocks, one based on uranium-235's decay to lead-207 with a half-life of about 700 million years, and one based on uranium-238's decay to lead-206 with a half-life of about 4.5 billion years, providing a built-in crosscheck that allows accurate determination of the age of the sample even if some of the lead has been lost. This can be seen in the concordia diagram, where the samples plot along an errorchron (straight line) which intersects the concordia curve at the age of the sample.

Samarium–neodymium dating method

This involves the alpha decay of ¹⁴⁷Sm to ¹⁴³Nd with a half-life of 1.06 x 10¹¹ years. Accuracy levels of within twenty million years in ages of two-and-a-half billion years are achievable.^[23]

Potassium–argon dating method

This involves electron capture or positron decay of potassium-40 to argon-40. Potassium-40 has a half-life of 1.3 billion years, and so this method is applicable to the oldest rocks. Radioactive potassium-40 is common in micas, feldspars, and hornblendes, though the closure temperature is fairly low in these materials, about 350 °C (mica) to 500 °C (hornblende).

Rubidium–strontium dating method

This is based on the beta decay of rubidium-87 to strontium-87, with a half-life of 50 billion years. This scheme is used to date old igneous and metamorphic rocks, and has also been used to date lunar samples. Closure temperatures are so high that they are not a concern. Rubidium-strontium dating is not as precise as the uranium-lead method, with errors of 30 to 50 million years for a 3-billion-year-old sample.

Uranium–thorium dating method

A relatively short-range dating technique is based on the decay of uranium-234 into thorium-230, a substance with a half-life of about 80,000 years. It is accompanied by a sister process, in which uranium-235 decays into protactinium-231, which has a half-life of 32,760 years.
While uranium is water-soluble, thorium and protactinium are not, and so they are selectively precipitated into ocean-floor sediments, from which their ratios are measured. The scheme has a range of several hundred thousand years. A related method is ionium–thorium dating, which measures the ratio of ionium (thorium-230) to thorium-232 in ocean sediment.

Radiocarbon dating method

Ale's Stones at Kåseberga, around ten kilometres south east of Ystad, Sweden were dated at 56 CE using the carbon-14 method on organic material found at the site.^[24]

Radiocarbon dating is also simply called Carbon-14 dating. Carbon-14 is a radioactive isotope of carbon, with a half-life of 5,730 years,^[25][26] (which is very short compared with the above isotopes) and decays into nitrogen.^[27] In other radiometric dating methods, the heavy parent isotopes were produced by nucleosynthesis in supernovas, meaning that any parent isotope with a short half-life should be extinct by now. Carbon-14, though, is continuously created through collisions of neutrons generated by cosmic rays with nitrogen in the upper atmosphere and thus remains at a near-constant level on Earth. The carbon-14 ends up as a trace component in atmospheric carbon dioxide (CO₂).

A carbon-based life form acquires carbon during its lifetime. Plants acquire it through photosynthesis, and animals acquire it from consumption of plants and other animals. When an organism dies, it ceases to take in new carbon-14, and the existing isotope decays with a characteristic half-life (5730 years). The proportion of carbon-14 left when the remains of the organism are examined provides an indication of the time elapsed since its death. This makes carbon-14 an ideal dating method to date the age of bones or the remains of an organism. The carbon-14 dating limit lies around 58,000 to 62,000 years.^[28]

The rate of creation of carbon-14 appears to be roughly constant, as cross-checks of carbon-14 dating with other dating methods show it gives consistent results. However, local eruptions of volcanoes or other events that give off large amounts of carbon dioxide can reduce local concentrations of carbon-14 and give inaccurate dates. The releases of carbon dioxide into the biosphere as a consequence of industrialization have also depressed the proportion of carbon-14 by a few percent; conversely, the amount of carbon-14 was increased by above-ground nuclear bomb tests that were conducted into the early 1960s. Also, an increase in the solar wind or the Earth's magnetic field above the current value would depress the amount of carbon-14 created in the atmosphere.

Fission track dating method

Apatite crystals are widely used in fission track dating.

This involves inspection of a polished slice of a material to determine the density of "track" markings left in it by the spontaneous fission of uranium-238 impurities. The uranium content of the sample has to be known, but that can be determined by placing a plastic film over the polished slice of the material, and bombarding it with slow neutrons. This causes induced fission of ²³⁵U, as opposed to the spontaneous fission of ²³⁸U. The fission tracks produced by this process are recorded in the plastic film. The uranium content of the material can then be calculated from the number of tracks and the neutron flux.

This scheme has application over a wide range of geologic dates. For dates up to a few million years micas, tektites (glass fragments from volcanic eruptions), and meteorites are best used. Older materials can be dated using zircon, apatite, titanite, epidote and garnet which have a variable amount of uranium content.^[29] Because the fission tracks are healed by temperatures over about 200 °C the technique has limitations as well as benefits. The technique has potential applications for detailing the thermal history of a deposit.

Chlorine-36 dating method

Large amounts of otherwise rare ³⁶Cl (half-life ~300ky) were produced by irradiation of seawater during atmospheric detonations of nuclear weapons between 1952 and 1958. The residence time of ³⁶Cl in the atmosphere is about 1 week. Thus, as an event marker of 1950s water in soil and ground water, ³⁶Cl is also useful for dating waters less than 50 years before the present. ³⁶Cl has seen use in other areas of the geological sciences, including dating ice and sediments.

Luminescence dating methods

Luminescence dating methods are not radiometric dating methods in that they do not rely on abundances of isotopes to calculate age. Instead, they are a consequence of background radiation on certain minerals. Over time, ionizing radiation is absorbed by mineral grains in sediments and archaeological materials such as quartz and potassium feldspar. The radiation causes charge to remain within the grains in structurally unstable "electron traps". Exposure to sunlight or heat releases these charges, effectively "bleaching" the sample and resetting the clock to zero. The trapped charge accumulates over time at a rate determined by the amount of background radiation at the location where the sample was buried. Stimulating these mineral grains using either light (optically stimulated luminescence or infrared stimulated luminescence dating) or heat (thermoluminescence dating) causes a luminescence signal to be emitted as the stored unstable electron energy is released, the intensity of which varies depending on the amount of radiation absorbed during burial and specific properties of the mineral.
These methods can be used to date the age of a sediment layer, as layers deposited on top would prevent the grains from being "bleached" and reset by sunlight. Pottery shards can be dated to the last time they experienced significant heat, generally when they were fired in a kiln.

Other methods

Other methods include:

• argon–argon (Ar–Ar)
• iodine–xenon (I–Xe)
• lanthanum–barium (La–Ba)
• lead–lead (Pb–Pb)
• lutetium–hafnium (Lu–Hf)
• potassium–calcium (K–Ca)
• rhenium–osmium (Re–Os)
• uranium–lead–helium (U–Pb–He)
• uranium–uranium (U–U)
• krypton–krypton (Kr–Kr)
• beryllium (¹⁰Be–⁹Be)^[30]

Dating with decay products of short-lived extinct radionuclides

Absolute radiometric dating requires a measurable fraction of parent nucleus to remain in the sample rock. For rocks dating back to the beginning of the solar system, this requires extremely long-lived parent isotopes, making measurement of such rocks' exact ages imprecise. To be able to distinguish the relative ages of rocks from such old material, and to get a better time resolution than that available from long-lived isotopes, short-lived isotopes that are no longer present in the rock can be used.^[31]

At the beginning of the solar system, there were several relatively short-lived radionuclides like ²⁶Al, ⁶⁰Fe, ⁵³Mn, and ¹²⁹I present within the solar nebula. These radionuclides—possibly produced by the explosion of a supernova—are extinct today, but their decay products can be detected in very old material, such as that which constitutes meteorites. By measuring the decay products of extinct radionuclides with a mass spectrometer and using isochronplots, it is possible to determine relative ages of different events in the early history of the solar system. Dating methods based on extinct radionuclides can also be calibrated with the U-Pb method to give absolute ages. Thus both the approximate age and a high time resolution can be obtained. Generally a shorter half-life leads to a higher time resolution at the expense of timescale.

The ¹²⁹I – ¹²⁹Xe chronometer

¹²⁹I beta-decays to ¹²⁹Xe with a half-life of 16 million years. The iodine-xenon chronometer^[32] is an isochron technique. Samples are exposed to neutrons in a nuclear reactor. This converts the only stable isotope of iodine (¹²⁷I) into ¹²⁸Xe via neutron capture followed by beta decay (of ¹²⁸I). After irradiation, samples are heated in a series of steps and the xenon isotopic signature of the gas evolved in each step is analysed. When a consistent ¹²⁹Xe/¹²⁸Xe ratio is observed across several consecutive temperature steps, it can be interpreted as corresponding to a time at which the sample stopped losing xenon.
Samples of a meteorite called Shallowater are usually included in the irradiation to monitor the conversion efficiency from ¹²⁷I to ¹²⁸Xe. The difference between the measured ¹²⁹Xe/¹²⁸Xe ratios of the sample and Shallowater then corresponds to the different ratios of ¹²⁹I/¹²⁷I when they each stopped losing xenon. This in turn corresponds to a difference in age of closure in the early solar system.

The ²⁶Al – ²⁶Mg chronometer

Another example of short-lived extinct radionuclide dating is the ²⁶Al – ²⁶Mg chronometer, which can be used to estimate the relative ages of chondrules. ²⁶Al decays to ²⁶Mg with a half-life of 720,000 years. The dating is simply a question of finding the deviation from the natural abundance of ²⁶Mg (the product of ²⁶Al decay) in comparison with the ratio of the stable isotopes ²⁷Al/²⁴Mg.

The excess of ²⁶Mg (often designated ²⁶Mg* ) is found by comparing the ²⁶Mg/²⁷Mg ratio to that of other Solar System materials.^[33]

The ²⁶Al – ²⁶Mg chronometer gives an estimate of the time period for formation of primitive meteorites of only a few million years (1.4 million years for Chondrule formation).