Muon

From Wikipedia, the free encyclopedia

 

Muon

The Moon's cosmic ray shadow, as seen in secondary muons generated by cosmic rays in the atmosphere, and detected 700 meters below ground, at the Soudan II detector
Composition	Elementary particle
Statistics	Fermionic
Generation	Second
Interactions	Gravity, Electromagnetic, Weak
Symbol	μ−
Antiparticle	Antimuon ( μ+)
Discovered	Carl D. Anderson, Seth Neddermeyer (1936)
Mass	105.6583745(24) MeV/c2[1]
Mean lifetime	2.1969811(22)×10−6 s[2][3]
Decays into	e−, ν e, ν μ[3] (most common)
Electric charge	−1 e
Color charge	None
Spin	1/2
Weak isospin	LH: −1/2, RH: 0
Weak hypercharge	LH: −1, RH: −2

The muon (/ˈmjuːɒn/; from the Greek letter mu (μ) used to represent it) is an elementary particle similar to the electron, with an electric charge of −1 e and a spin of 1/2, but with a much greater mass. It is classified as a lepton. As is the case with other leptons, the muon is not believed to have any sub-structure—that is, it is not thought to be composed of any simpler particles.

The muon is an unstable subatomic particle with a mean lifetime of 2.2 μs, much longer than many other subatomic particles. As with the decay of the non-elementary neutron (with a lifetime around 15 minutes), muon decay is slow (by subatomic standards) because the decay is mediated by the weak interaction exclusively (rather than the more powerful strong interaction or electromagnetic interaction), and because the mass difference between the muon and the set of its decay products is small, providing few kinetic degrees of freedom for decay. Muon decay almost always produces at least three particles, which must include an electron of the same charge as the muon and two neutrinos of different types.

Like all elementary particles, the muon has a corresponding antiparticle of opposite charge (+1 e) but equal mass and spin: the antimuon (also called a positive muon). Muons are denoted by
μ⁻ and antimuons by
μ⁺. Muons were previously called mu mesons, but are not classified as mesons by modern particle physicists (see § History), and that name is no longer used by the physics community.

Muons have a mass of 105.7 MeV/c², which is about 207 times that of the electron. Due to their greater mass, muons are not as sharply accelerated when they encounter electromagnetic fields, and do not emit as much bremsstrahlung (deceleration radiation). This allows muons of a given energy to penetrate far more deeply into matter than electrons since the deceleration of electrons and muons is primarily due to energy loss by the bremsstrahlung mechanism. As an example, so-called "secondary muons", generated by cosmic rays hitting the atmosphere, can penetrate to the Earth's surface, and even into deep mines.

Because muons have a very large mass and energy compared with the decay energy of radioactivity, they are never produced by radioactive decay. They are, however, produced in copious amounts in high-energy interactions in normal matter, in certain particle accelerator experiments with hadrons, or naturally in cosmic ray interactions with matter. These interactions usually produce pi mesons initially, which most often decay to muons.

As with the case of the other charged leptons, the muon has an associated muon neutrino, denoted by
ν
_μ, which is not the same particle as the electron neutrino, and does not participate in the same nuclear reactions.

History

Muons were discovered by Carl D. Anderson and Seth Neddermeyer at Caltech in 1936, while studying cosmic radiation. Anderson noticed particles that curved differently from electrons and other known particles when passed through a magnetic field. They were negatively charged but curved less sharply than electrons, but more sharply than protons, for particles of the same velocity. It was assumed that the magnitude of their negative electric charge was equal to that of the electron, and so to account for the difference in curvature, it was supposed that their mass was greater than an electron but smaller than a proton. Thus Anderson initially called the new particle a mesotron, adopting the prefix meso- from the Greek word for "mid-". The existence of the muon was confirmed in 1937 by J. C. Street and E. C. Stevenson's cloud chamber experiment.^[4]

A particle with a mass in the meson range had been predicted before the discovery of any mesons, by theorist Hideki Yukawa:^[5]

It seems natural to modify the theory of Heisenberg and Fermi in the following way. The transition of a heavy particle from neutron state to proton state is not always accompanied by the emission of light particles. The transition is sometimes taken up by another heavy particle.

Because of its mass, the mu meson was initially thought to be Yukawa's particle, but it later proved to have the wrong properties. Yukawa's predicted particle, the pi meson, was finally identified in 1947 (again from cosmic ray interactions), and shown to differ from the earlier-discovered mu meson by having the correct properties to be a particle which mediated the nuclear force.

With two particles now known with the intermediate mass, the more general term meson was adopted to refer to any such particle within the correct mass range between electrons and nucleons. Further, in order to differentiate between the two different types of mesons after the second meson was discovered, the initial mesotron particle was renamed the mu meson (the Greek letter μ (mu) corresponds to m), and the new 1947 meson (Yukawa's particle) was named the pi meson.

As more types of mesons were discovered in accelerator experiments later, it was eventually found that the mu meson significantly differed not only from the pi meson (of about the same mass), but also from all other types of mesons. The difference, in part, was that mu mesons did not interact with the nuclear force, as pi mesons did (and were required to do, in Yukawa's theory). Newer mesons also showed evidence of behaving like the pi meson in nuclear interactions, but not like the mu meson. Also, the mu meson's decay products included both a neutrino and an antineutrino, rather than just one or the other, as was observed in the decay of other charged mesons.

In the eventual Standard Model of particle physics codified in the 1970s, all mesons other than the mu meson were understood to be hadrons—that is, particles made of quarks—and thus subject to the nuclear force. In the quark model, a meson was no longer defined by mass (for some had been discovered that were very massive—more than nucleons), but instead were particles composed of exactly two quarks (a quark and antiquark), unlike the baryons, which are defined as particles composed of three quarks (protons and neutrons were the lightest baryons). Mu mesons, however, had shown themselves to be fundamental particles (leptons) like electrons, with no quark structure. Thus, mu mesons were not mesons at all, in the new sense and use of the term meson used with the quark model of particle structure.

With this change in definition, the term mu meson was abandoned, and replaced whenever possible with the modern term muon, making the term mu meson only historical. In the new quark model, other types of mesons sometimes continued to be referred to in shorter terminology (e.g., pion for pi meson), but in the case of the muon, it retained the shorter name and was never again properly referred to by older "mu meson" terminology.

The eventual recognition of the "mu meson" muon as a simple "heavy electron" with no role at all in the nuclear interaction, seemed so incongruous and surprising at the time, that Nobel laureate I. I. Rabi famously quipped, "Who ordered that?"^[6]

In the Rossi–Hall experiment (1941), muons were used to observe the time dilation (or alternatively, length contraction) predicted by special relativity, for the first time.

Muon sources

Muons arriving on the Earth's surface are created indirectly as decay products of collisions of cosmic rays with particles of the Earth's atmosphere.^[7]

About 10,000 muons reach every square meter of the earth's surface a minute; these charged particles form as by-products of cosmic rays colliding with molecules in the upper atmosphere. Traveling at relativistic speeds, muons can penetrate tens of meters into rocks and other matter before attenuating as a result of absorption or deflection by other atoms.^[8]

When a cosmic ray proton impacts atomic nuclei in the upper atmosphere, pions are created. These decay within a relatively short distance (meters) into muons (their preferred decay product), and muon neutrinos. The muons from these high energy cosmic rays generally continue in about the same direction as the original proton, at a velocity near the speed of light. Although their lifetime without relativistic effects would allow a half-survival distance of only about 456 m (2.197 µs×ln(2) × 0.9997×c) at most (as seen from Earth) the time dilation effect of special relativity (from the viewpoint of the Earth) allows cosmic ray secondary muons to survive the flight to the Earth's surface, since in the Earth frame, the muons have a longer half life due to their velocity. From the viewpoint (inertial frame) of the muon, on the other hand, it is the length contraction effect of special relativity which allows this penetration, since in the muon frame, its lifetime is unaffected, but the length contraction causes distances through the atmosphere and Earth to be far shorter than these distances in the Earth rest-frame. Both effects are equally valid ways of explaining the fast muon's unusual survival over distances.

Since muons are unusually penetrative of ordinary matter, like neutrinos, they are also detectable deep underground (700 meters at the Soudan 2 detector) and underwater, where they form a major part of the natural background ionizing radiation. Like cosmic rays, as noted, this secondary muon radiation is also directional.

The same nuclear reaction described above (i.e. hadron-hadron impacts to produce pion beams, which then quickly decay to muon beams over short distances) is used by particle physicists to produce muon beams, such as the beam used for the muon g − 2 experiment.^[9]

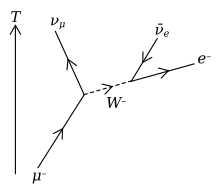
Muon decay

The most common decay of the muon

Muons are unstable elementary particles and are heavier than electrons and neutrinos but lighter than all other matter particles. They decay via the weak interaction. Because leptonic family numbers are conserved in the absence of an extremely unlikely immediate neutrino oscillation, one of the product neutrinos of muon decay must be a muon-type neutrino and the other an electron-type antineutrino (antimuon decay produces the corresponding antiparticles, as detailed below). Because charge must be conserved, one of the products of muon decay is always an electron of the same charge as the muon (a positron if it is a positive muon). Thus all muons decay to at least an electron, and two neutrinos. Sometimes, besides these necessary products, additional other particles that have no net charge and spin of zero (e.g., a pair of photons, or an electron-positron pair), are produced.

The dominant muon decay mode (sometimes called the Michel decay after Louis Michel) is the simplest possible: the muon decays to an electron, an electron antineutrino, and a muon neutrino. Antimuons, in mirror fashion, most often decay to the corresponding antiparticles: a positron, an electron neutrino, and a muon antineutrino. In formulaic terms, these two decays are:

μ⁻ →
e⁻ +
ν
_e +
ν
_μ

μ⁺ →
e⁺ +
ν
_e +
ν
_μ

The mean lifetime, τ = ħ/Γ, of the (positive) muon is (2.1969811±0.0000022 ) µs.^[2] The equality of the muon and antimuon lifetimes has been established to better than one part in 10⁴.

Prohibited decays

Certain neutrino-less decay modes are kinematically allowed but are, for all practical purposes, forbidden in the Standard Model, even given that neutrinos have mass and oscillate. Examples forbidden by lepton flavour conservation are:

μ⁻ →
e⁻ +
γ

and

μ⁻ →
e⁻ +
e⁺ +
e⁻ .

To be precise: in the Standard Model with neutrino mass, a decay like
μ⁻ →
e⁻ +
γ
is technically possible, for example by neutrino oscillation of a virtual muon neutrino into an electron neutrino, but such a decay is astronomically unlikely and therefore should be experimentally unobservable: less than one in 10⁵⁰ muon decays should produce such a decay.

Observation of such decay modes would constitute clear evidence for theories beyond the Standard Model. Upper limits for the branching fractions of such decay modes were measured in many experiments starting more than 50 years ago. The current upper limit for the
μ⁺ →
e⁺ +
γ
branching fraction was measured 2009–2013 in the MEG experiment and is 4.2 × 10⁻¹³. ^[10]

Theoretical decay rate

The muon decay width which follows from Fermi's golden rule follows Sargent's law of fifth-power dependence on m_μ ,

${\displaystyle \Gamma ={\frac {G_{F}^{2}m_{\mu }^{5}}{192\pi ^{3}}}I\left({\frac {m_{e}^{2}}{m_{\mu }^{2}}}\right),}$

where ${\displaystyle I(x)=1-8x-12x^{2}\ln x+8x^{3}-x^{4}}$, ${\displaystyle G_{F}}$ is the Fermi coupling constant and ${\displaystyle x=2E_{e}/{m_{\mu }}c^{2}}$ is the fraction of the maximum energy transmitted to the electron.

The decay distributions of the electron in muon decays have been parameterised using the so-called Michel parameters. The values of these four parameters are predicted unambiguously in the Standard Model of particle physics, thus muon decays represent a good test of the space-time structure of the weak interaction. No deviation from the Standard Model predictions has yet been found.

For the decay of the muon, the expected decay distribution for the Standard Model values of Michel parameters is

${\displaystyle {\frac {d^{2}\Gamma }{dx\,d\cos \theta }}\sim x^{2}[(3-2x)+P_{\mu }\cos \theta (1-2x)]}$

where ${\displaystyle \theta }$ is the angle between the muon's polarization vector ${\displaystyle \mathbf {P} _{\mu }}$ and the decay-electron momentum vector, and ${\displaystyle P_{\mu }=|\mathbf {P} _{\mu }|}$ is the fraction of muons that are forward-polarized. Integrating this expression over electron energy gives the angular distribution of the daughter electrons:

${\displaystyle {\frac {d\Gamma }{d\cos \theta }}\sim 1-{\frac {1}{3}}P_{\mu }\cos \theta .}$

The electron energy distribution integrated over the polar angle (valid for ${\displaystyle x<1 annotation="">$) is

${\displaystyle {\frac {d\Gamma }{dx}}\sim (3x^{2}-2x^{3}).}$

Due to the muons decaying by the weak interaction, parity conservation is violated. Replacing the ${\displaystyle \cos \theta }$ term in the expected decay values of the Michel Parameters with a ${\displaystyle \cos \omega t}$ term, where ω is the Larmor frequency from Larmor precession of the muon in a uniform magnetic field, given by:

${\displaystyle \omega ={\frac {egB}{2m}}}$

where m is mass of the muon, e is charge, g is the muon g-factor and B is applied field.

A change in the electron distribution computed using the standard, unprecessional, Michel Parameters can be seen displaying a periodicity of π radians. This can be shown to physically correspond to a phase change of π, introduced in the electron distribution as the angular momentum is changed by the action of the charge conjugation operator, which is conserved by the weak interaction.

The observation of parity violation in muon decay can be compared to the concept of violation of parity in weak interactions in general as an extension of The Wu Experiment, as well as the change of angular momentum introduced by a phase change of π corresponding to the charge-parity operator being invariant in this interaction. This fact is true for all lepton interactions in The Standard Model.

Muonic atoms

The muon was the first elementary particle discovered that does not appear in ordinary atoms.

Negative muon atoms

Negative muons can, however, form muonic atoms (previously called mu-mesic atoms), by replacing an electron in ordinary atoms. Muonic hydrogen atoms are much smaller than typical hydrogen atoms because the much larger mass of the muon gives it a much more localized ground-state wavefunction than is observed for the electron. In multi-electron atoms, when only one of the electrons is replaced by a muon, the size of the atom continues to be determined by the other electrons, and the atomic size is nearly unchanged. However, in such cases the orbital of the muon continues to be smaller and far closer to the nucleus than the atomic orbitals of the electrons.

Muonic helium is created by substituting a muon for one of the electrons in helium-4. The muon orbits much closer to the nucleus, so muonic helium can therefore be regarded like an isotope of helium whose nucleus consists of two neutrons, two protons and a muon, with a single electron outside. Colloquially, it could be called "helium 4.1", since the mass of the muon is slightly greater than 0.1 amu. Chemically, muonic helium, possessing an unpaired valence electron, can bond with other atoms, and behaves more like a hydrogen atom than an inert helium atom.^[11][12][13]

Muonic heavy hydrogen atoms with a negative muon may undergo nuclear fusion in the process of muon-catalyzed fusion, after the muon may leave the new atom to induce fusion in another hydrogen molecule. This process continues until the negative muon is trapped by a helium atom, and cannot leave until it decays.

Finally, a possible fate of negative muons bound to conventional atoms is that they are captured by the weak-force by protons in nuclei in a sort of electron-capture-like process. When this happens, the proton becomes a neutron and a muon neutrino is emitted.

Positive muon atoms

A positive muon, when stopped in ordinary matter, cannot be captured by a proton since it would need to be an antiproton. The positive muon is also not attracted to the nucleus of atoms. Instead, it binds a random electron and with this electron forms an exotic atom known as muonium (Mu) atom. In this atom, the muon acts as the nucleus. The positive muon, in this context, can be considered a pseudo-isotope of hydrogen with one ninth of the mass of the proton. Because the reduced mass of muonium, and hence its Bohr radius, is very close to that of hydrogen, this short-lived "atom" (or a muon and electron) behaves chemically—to a first approximation—like the isotopes of hydrogen (protium, deuterium and tritium).

Use in measurement of the proton charge radius

The experimental technique that is expected to provide the most precise determination of the root-mean-square charge radius of the proton is the measurement of the frequency of photons (precise "color" of light ) emitted or absorbed by atomic transitions in muonic hydrogen. This form of hydrogen atom is composed of a negatively charged muon bound to a proton. The muon is particularly well suited for this purpose because its much larger mass results in a much more compact bound state and hence a larger probability for it to be found inside the proton in muonic hydrogen compared to the electron in atomic hydrogen.^[14] The Lamb shift in muonic hydrogen was measured by driving the muon from a 2s state up to an excited 2p state using a laser. The frequency of the photons required to induce two such (slightly different) transitions were reported in 2014 to be 50 and 55 THz which, according to present theories of quantum electrodynamics, yield an appropriately averaged value of 0.84087±0.00039 fm for the charge radius of the proton.^[15]
The internationally accepted value of the proton's charge radius is based on a suitable average of results from older measurements of effects caused by the nonzero size of the proton on scattering of electrons by nuclei and the light spectrum (photon energies) from excited atomic hydrogen. The official value updated in 2014 is 0.8751±0.0061 fm (see orders of magnitude for comparison to other sizes).^[16] The expected precision of this result is inferior to that from muonic hydrogen by about a factor of fifteen, yet they disagree by about 5.6 times the nominal uncertainty in the difference (a discrepancy called 5.6σ in scientific notation). A conference of the world experts on this topic led to the decision to exclude the muon result from influencing the official 2014 value, in order to avoid hiding the mysterious discrepancy.^[17] This "proton radius puzzle" remained unresolved as of late 2015, and has attracted much attention, in part because of the possibility that both measurements are valid, which would imply the influence of some "new physics".^[18]

Anomalous magnetic dipole moment

The anomalous magnetic dipole moment is the difference between the experimentally observed value of the magnetic dipole moment and the theoretical value predicted by the Dirac equation. The measurement and prediction of this value is very important in the precision tests of QED (quantum electrodynamics). The E821 experiment^[19] at Brookhaven National Laboratory (BNL) studied the precession of muon and anti-muon in a constant external magnetic field as they circulated in a confining storage ring. E821 reported the following average value^[20] in 2006:

${\displaystyle a={\frac {g-2}{2}}=0.00116592080(54)(33)}$

where the first errors are statistical and the second systematic.

The prediction for the value of the muon anomalous magnetic moment includes three parts:

α_μ^SM = α_μ^QED + α_μ^EW + α_μ^had.

The difference between the g-factors of the muon and the electron is due to their difference in mass. Because of the muon's larger mass, contributions to the theoretical calculation of its anomalous magnetic dipole moment from Standard Model weak interactions and from contributions involving hadrons are important at the current level of precision, whereas these effects are not important for the electron. The muon's anomalous magnetic dipole moment is also sensitive to contributions from new physics beyond the Standard Model, such as supersymmetry. For this reason, the muon's anomalous magnetic moment is normally used as a probe for new physics beyond the Standard Model rather than as a test of QED.^[21] Muon g−2, a new experiment at Fermilab using the E821 magnet will improve the precision of this measurement.^[22]

Muon radiography and tomography

Since muons are much more deeply penetrating than X-rays or gamma rays, muon imaging can be used with much thicker material or, with cosmic ray sources, larger objects. One example is commercial muon tomography used to image entire cargo containers to detect shielded nuclear material, as well as explosives or other contraband.^[23]
The technique of muon transmission radiography based on cosmic ray sources was first used in the 1950s to measure the depth of the overburden of a tunnel in Australia^[24] and in the 1960s to search for possible hidden chambers in the Pyramid of Chephren in Giza.^[25] In 2017, the discovery of a large void (with a length of 30 m minimum) by observation of cosmic-ray muons was reported. ^[26]

In 2003, the scientists at Los Alamos National Laboratory developed a new imaging technique: muon scattering tomography. With muon scattering tomography, both incoming and outgoing trajectories for each particle are reconstructed, such as with sealed aluminum drift tubes.^[27] Since the development of this technique, several companies have started to use it.

In August 2014, Decision Sciences International Corporation announced it had been awarded a contract by Toshiba for use of its muon tracking detectors in reclaiming the Fukushima nuclear complex.^[28] The Fukushima Daiichi Tracker (FDT) was proposed to make a few months of muon measurements to show the distribution of the reactor cores.

In December 2014, Tepco reported that they would be using two different muon imaging techniques at Fukushima, "Muon Scanning Method" on Unit 1 (the most badly damaged, where the fuel may have left the reactor vessel) and "Muon Scattering Method" on Unit 2.^[29]

The International Research Institute for Nuclear Decommissioning IRID in Japan and the High Energy Accelerator Research Organization KEK call the method they developed for Unit 1 the muon permeation method; 1,200 optical fibers for wavelength conversion light up when muons come into contact with them.^[30] After a month of data collection, it is hoped to reveal the location and amount of fuel debris still inside the reactor. The measurements began in February 2015.

Are We Becoming an Endangered Species? Technology and Ethics in the Twenty First Century

November 20, 2001 by Ray Kurzweil
Original link:  http://www.kurzweilai.net/are-we-becoming-an-endangered-species-technology-and-ethics-in-the-twenty-first-century

Ray Kurzweil addresses questions presented at Are We Becoming an Endangered Species? Technology and Ethics in the 21st Century, a conference on technology and ethics sponsored by Washington National Cathedral. Other panelists are Anne Foerst, Bill Joy and Bill Mckibben.

Bill McKibben, Ray Kurzweil, Judy Woodruff, Bill Joy, and Anne Foerst discuss the dangers of genetic engineering, nanotechnology and robotics.

Ray Kurzweil: Questions and Answers

Ray Kurzweil, how do you respond to Mr. Joy’s concerns? Do scientific and technological advances pose a real threat to humanity, or do they promise to enhance life?

The answer is both, and we don’t have to look further than today to see what I call the deeply intertwined promise and peril of technology.

Imagine going back in time, let’s say a couple hundred years, and describing the dangers that lay ahead, perils such as weapons capable of destroying all mammalian life on Earth. People in the eighteenth century listening to this litany of dangers, assuming they believed you, would probably think it mad to take such risks.

And then you could go on and describe the actual suffering that lay ahead, for example 100 million people killed in two great twentieth-century world wars, made possible by technology, and so on. Suppose further that we provide these people circa eighteenth century a choice to relinquish these then future technologies, they just might choose to do so, particularly if we were to emphasize the painful side of the equation.

Our eighteenth century forbears, if provided with the visions of a reliable futurist of that day, and if given a choice, might very well have embraced the view of my fellow panelist Bill McKibben who says today that we “must now grapple squarely with the idea of a world that has enough wealth and enough technological capability, and should not pursue more.”

Judy Woodruff interviews Ray Kurzweil at Washington National Cathedral.


Now I believe that implementing such a choice would require a Brave New World type of totalitarian government in which the government uses technology to ban the further development of technology, but let’s put that perspective aside for a moment, and pursue this scenario further. What if our forefathers, and foremothers, had made such a decision? Would that have been so bad?

Well, for starters, most of us here today would not be here today, because life expectancy would have remained what it was back then, which was about 35 years of age. Furthermore, you would have been busy with the extraordinary toil and labor of everyday life with many hours required just to prepare the evening meal. The vast majority of humanity pursued lives that were labor-intensive, poverty-stricken, disease-ridden, and disaster-prone.

This basic equation has not changed. Technology has to a great extent liberated at least many of us from the enormous difficulty and fragility that characterized human life up until recent times. But there is still a great deal of affliction and distress that needs to be conquered, and that indeed can be overcome by technological advances that are close at hand. We are on the verge of multiple revolutions in biotechnology — genomics, proteomics, rational drug design, therapeutic cloning of cells, tissues, and organs, and others — that will save tens of millions of lives and alleviate enormous suffering. Ultimately, nanotechnology will provide the ability to create any physical product. Combined with other emerging technologies, we have the potential to largely eliminate poverty which also causes enormous misery.

And yes, as Bill Joy, and others, including myself, have pointed out, these same technologies can be applied in destructive ways, and invariably they will be. However, we have to be mindful of the fact that our defensive technologies and protective measures will evolve along with the offensive potentials. If we take the future dangers such as Bill and others have described, and imagine them foisted on today’s unprepared world, then it does sound like we’re doomed. But that’s not the delicate balance that we’re facing. The defense will evolve along with the offense. And I don’t agree with Bill that defense is necessarily weaker than offense. The reality is more complex.

We do have one contemporary example from which we can take a measure of comfort. Bill Joy talks about the dangers of self-replication, and we do have today a new form of fully nonbiological self-replicating entity that didn’t exist just a few decades ago: the computer virus. When this form of destructive intruder first appeared, strong concerns were voiced that as they became more sophisticated, software pathogens had the potential to overwhelm, even destroy, the computer network medium they live in. Yet the immune system that has evolved in response to this challenge has been largely effective. The injury is but a small fraction of the benefit we receive from computer technology. That would not be the case if one imagines today’s sophisticated software viruses foisted on the unprepared world of six or seven years ago.

One might counter that computer viruses do not have the lethal potential of biological viruses or self-replicating nanotechnology. Although true, this only strengthens my observation. The fact that computer viruses are usually not deadly to humans means that our response to the danger is that much less intense. Conversely, when it comes to self-replicating entities that are potentially lethal, our response on all levels will be vastly more serious.

Having said all this, I do have a specific proposal that I would like to share, which I will introduce a little later in our discussion.

Mr. Kurzweil, given humanity’s track record with chemical and biological weapons, are we not guaranteed that terrorists and/or malevolent governments will abuse GNR (Genetic, Nanotechnology, Robotics) technologies? If so, how do we address this problem without an outright ban on the technologies?

Yes, these technologies will be abused. However, an outright ban, in my view, would be destructive, morally indefensible, and in any event would not address the dangers.

Nanotechnology, for example, is not a specific well-defined field. It is simply the inevitable end-result of the trend toward miniaturization which permeates virtually all technology. We’ve all seen pervasive miniaturization in our lifetimes. Technology in all forms — electronic, mechanical, biological, and others — is shrinking, currently at a rate of 5.6 per linear dimension per decade. The inescapable result will be nanotechnology.

With regard to more intelligent computers and software, it’s an inescapable economic imperative affecting every company from large firms like Sun and Microsoft to small emerging companies.

With regard to biotechnology, are we going to tell the many millions of cancer sufferers around the world that although we are on the verge of new treatments that may save their lives, we’re nonetheless canceling all of this research.

Banning these new technologies would condemn not just millions, but billions of people to the anguish of disease and poverty that we would otherwise be able to alleviate. And attempting to ban these technologies won’t even eliminate the danger because it will only push these technologies underground where development would continue unimpeded by ethics and regulation.

We often go through three stages in examining the impact of future technology: awe and wonderment at its potential to overcome age-old problems, then a sense of dread at a new set of grave dangers that accompany these new technologies, followed by the realization that the only viable and responsible path is to set a careful course that can realize the promise while managing the peril.

The only viable approach is a combination of strong ethical standards, technology-enhanced law enforcement, and, most importantly, the development of both technical safeguards and technological immune systems to combat specific dangers.

And along those lines, I have a specific proposal. I do believe that we need to increase the priority of developing defensive technologies, not just for the vulnerabilities that society has identified since September 11, which are manifold, but the new ones attendant to the emerging technologies we’re discussing this evening. We spend hundreds of billions of dollars a year on defense, and the danger from abuse of GNR technologies should be a primary target of these expenditures. Specifically, I am proposing that we set up a major program to be administered by the National Science Foundation and the National Institutes of Health. This new program would have a budget equaling the current budget for NSF and NIH. It would be devoted to developing defensive strategies, technologies, and ethical standards addressed at specific identified dangers associated with the new technologies funded by the conventional NSF and NIH budgets. There are other things we need to do as well, but this would be a practical way of significantly increasing the priority of addressing the dangers of emerging technologies.

If humans are going to play God, perhaps we should look at who is in the game. Mr. Kurzweil, isn’t it true that both the technological and scientific fields lack broad participation by women, lower socioeconomic classes and sexual and ethnic minorities? If so, shouldn’t we be concerned about the missing voices? What impact does the narrowly defined demographic have on technology and science?

I think it would be great to have more women in science, and it would lead to better decision making at all levels. To take an extreme example of the impact of not having sufficient participation by women, the Taliban have had no women in decision-making roles, and look at the quality of their decision-making.

To return to our own society, there are more women today in computer science, life sciences, and other scientific fields compared to 20 years ago, but clearly more progress is needed. With regard to ethnic groups such as Afro-Americans, the progress has been even less satisfactory, and I agree that addressing this is an urgent problem.

However, the real issue goes beyond direct participation in science and engineering. It has been said that war is too important to leave to the generals. It is also the case that science and engineering is too important to leave to the scientists and engineers. The advancement of technology from both the public and private sectors has a profound impact on every facet of our lives, from the nature of sexuality to the meaning of life and death.

To the extent that technology is shaped by market forces, then we all play a role as consumers. To the extent that science policy is shaped by government, then the political process is influential. But in order for everyone to play a role in playing God, there does need to be a meaningful dialog. And this in turn requires building bridges from the often incomprehensible world of scientific terminology to the everyday world that the educated lay public can understand.

Your work, Anne (Foerst), is unique and important in this regard, in that you’ve been building a bridge from the world of theology to the world of artificial intelligence, two seemingly disparate but surprisingly related fields. And Judy (Woodruff), journalism is certainly critical in that most people get their understanding of science and technology from the news.

We have many grave vulnerabilities in our society already. We can make a long list of exposures, and the press has been quite active in reporting on these since September 11. This does, incidentally, represent somewhat of a dilemma. On the one hand, reporting on these dangers is the way in which a democratic society generates the political will to address problems. On the other hand, if I were a terrorist, I would be reading the New York Times, and watching CNN, to get ideas and suggestions on the myriad ways in which society is susceptible to attack.

However, with regard to the GNR dangers, I believe this dilemma is somewhat alleviated because the dangers are further in the future. Now is the ideal time to be debating these emerging risks. It is also the right time to begin laying the scientific groundwork to develop the actual safeguards and defenses. We urgently need to increase the priority of this effort. That’s why I’ve proposed a specific action item that for every dollar we spend on new technologies that can improve our lives, we spend another dollar to protect ourselves from the downsides of those same technologies.

How do you view the intrinsic worth of a “post-biological” world?

We’ve heard some discussion this evening on the dangers of ethnic and gender chauvinism. Along these lines, I would argue against human chauvinism and even biological chauvinism. On the other hand, I also feel that we need to revere and protect our biological heritage. And I do believe that these two positions are not incompatible.

We are in the early stages of a deep merger between the biological and nonbiological world. We already have replacement parts and augmentations for most of the organs and systems in our bodies. There is a broad variety of neural implants already in use. I have a deaf friend who I can now speak to on the telephone because of his cochlear implant. And he plans to have it upgraded to a new version that will provide a resolution of over a thousand frequencies that may restore his ability to appreciate music. There are Parkinson’s patients who have had their ability to move restored through an implant that replaces the biological cells destroyed by that disease.

By 2030, this merger of biological and nonbiological intelligence will be in high gear, and there will be many ways in which the two forms of intelligence work intimately together. So it won’t be possible to come into a room and say, humans on the left, and machines on the right. There just won’t be a clear distinction.

Since we’re in a beautiful house of worship, let me relate this impending biological — nonbiological merger to a view of spiritual values.

I regard the freeing of the human mind from its severe physical limitations of scope and duration as the necessary next step in evolution. Evolution, in my view, represents the purpose of life. That is, the purpose of life — and of our lives — is to evolve.

What does it mean to evolve? Evolution moves toward greater complexity, greater elegance, greater knowledge, greater intelligence, greater beauty, greater creativity, and more of other abstract and subtle attributes such as love. And God has been called all these things, only without any limitation: all knowing, unbounded intelligence, infinite beauty, unlimited creativity, infinite love, and so on. Of course, even the accelerating growth of evolution never quite achieves an infinite level, but as it explodes exponentially, it certainly moves rapidly in that direction. So evolution moves inexorably closer to our conception of God, albeit never quite reaching this ideal. Thus the freeing of our thinking from the severe limitations of its biological form may be regarded as an essential spiritual quest.

Quarkonium

From Wikipedia, the free encyclopedia

 

In particle physics, quarkonium (from quark and -onium, pl. quarkonia) designates a flavorless meson whose constituents are a heavy quark and its own antiquark, making it a neutral particle.

Background

Light quarks

Light quarks (up, down, and strange) are much less massive than the heavier quarks, and so the physical states actually seen in experiments (η, η′, and π⁰ mesons) are quantum mechanical mixtures of the light quark states. The much larger mass differences between the charm and bottom quarks and the lighter quarks results in states that are well defined in terms of a quark–antiquark pair of a given flavor.

Heavy quarks

Examples of quarkonia are the J/ψ meson (the ground state of charmonium,
c

c
) and the
ϒ
meson (bottomonium,
b

b
). Because of the high mass of the top quark, toponium does not exist, since the top quark decays through the electroweak interaction before a bound state can form (a rare example of a weak process proceeding more quickly than a strong process). Usually, the word "quarkonium" refers only to charmonium and bottomonium, and not to any of the lighter quark–antiquark states.

Charmonium

Charmonium

In the following table, the same particle can be named with the spectroscopic notation or with its mass. In some cases excitation series are used: Ψ' is the first excitation of Ψ (for historical reasons, this one is called J/ψ particle); Ψ" is a second excitation, and so on. That is, names in the same cell are synonymous.

Some of the states are predicted, but have not been identified; others are unconfirmed. The quantum numbers of the X(3872) particle have been measured recently by the LHCb experiment at CERN^[1] . This measurement shed some light on its identity, excluding the third option among the three envised, which are :

• a charmonium hybrid state;
• a ${\displaystyle D^{0}{\bar {D}}^{*0}}$ molecule.
• a candidate for the 1¹D₂ state;

In 2005, the BaBar experiment announced the discovery of a new state: Y(4260).^[2][3] CLEO and  Belle have since corroborated these observations. At first, Y(4260) was thought to be a charmonium state, but the evidence suggests more exotic explanations, such as a D "molecule", a 4-quark construct, or a hybrid meson.

Term symbol

n2S + 1LJ	IG(JPC)	Particle	mass (MeV/c2) [1]
11S0	0+(0−+)	ηc(1S)	2983.4±0.5
13S1	0−(1−−)	J/ψ(1S)	3096.900±0.006
11P1	0−(1+−)	hc(1P)	3525.38±0.11
13P0	0+(0++)	χc0(1P)	3414.75±0.31
13P1	0+(1++)	χc1(1P)	3510.66±0.07
13P2	0+(2++)	χc2(1P)	3556.20±0.09
21S0	0+(0−+)	ηc(2S), or η′ c	3639.2±1.2
23S1	0−(1−−)	ψ(3686)	3686.097±0.025
11D2	0+(2−+)	ηc2(1D)†	3639.2±1.2
13D1	0−(1−−)	ψ(3770)	3773.13±0.35
13D2	0−(2−−)	ψ2(1D)
13D3	0−(3−−)	ψ3(1D)†
21P1	0−(1+−)	hc(2P)†
23P0	0+(0++)	χc0(2P)†
23P1	0+(1++)	χc1(2P)†
23P2	0+(2++)	χc2(2P)†
????	0+(1++)†	X(3872)	3871.69±0.17
????	??(1−−)	Y(4260)	4263+8 −9

Notes:

^* Needs confirmation.

^† Predicted, but not yet identified.

^† Interpretation as a 1⁻⁻ charmonium state not favored.

Bottomonium

In the following table, the same particle can be named with the spectroscopic notation or with its mass.
Some of the states are predicted, but have not been identified; others are unconfirmed.

Term symbol n2S+1LJ	IG(JPC)	Particle	mass (MeV/c2)[2]
11S0	0+(0−+)	ηb(1S)	9390.9±2.8
13S1	0−(1−−)	Υ(1S)	9460.30±0.26
11P1	0−(1+−)	hb(1P)
13P0	0+(0++)	χb0(1P)	9859.44±0.52
13P1	0+(1++)	χb1(1P)	9892.76±0.40
13P2	0+(2++)	χb2(1P)	9912.21±0.40
21S0	0+(0−+)	ηb(2S)
23S1	0−(1−−)	Υ(2S)	10023.26±0.31
11D2	0+(2−+)	ηb2(1D)
13D1	0−(1−−)	Υ(1D)
13D2	0−(2−−)	Υ2(1D)	10161.1±1.7
13D3	0−(3−−)	Υ3(1D)
21P1	0−(1+−)	hb(2P)
23P0	0+(0++)	χb0(2P)	10232.5±0.6
23P1	0+(1++)	χb1(2P)	10255.46±0.55
23P2	0+(2++)	χb2(2P)	10268.65±0.55
33S1	0−(1−−)	Υ(3S)	10355.2±0.5
33PJ	0+(J++)	χb(3P)	10530±5 (stat.) ± 9 (syst.)[4]
43S1	0−(1−−)	Υ(4S) or Υ(10580)	10579.4±1.2
53S1	0−(1−−)	Υ(5S) or Υ(10860)	10865±8
63S1	0−(1−−)	Υ(11020)	11019±8

Notes:

^* Preliminary results. Confirmation needed.

The Υ(1S) state was discovered by the E288 experiment team, headed by Leon Lederman, at Fermilab in 1977, and was the first particle containing a bottom quark to be discovered. The χ_b (3P) state was the first particle discovered in the Large Hadron Collider. The article about this discovery was first submitted to arXiv on 21 December 2011.^[4][5] On April 2012, Tevatron's DØ experiment confirms the result in a paper published in Phys. Rev. D.^[6][7]

Toponium

The theta meson is not expected to be physically observable, as top quarks decay too fast to form mesons.

QCD and quarkonia

The computation of the properties of mesons in Quantum chromodynamics (QCD) is a fully non-perturbative one. As a result, the only general method available is a direct computation using lattice QCD (LQCD) techniques. However, other techniques are effective for heavy quarkonia as well.
The light quarks in a meson move at relativistic speeds, since the mass of the bound state is much larger than the mass of the quark. However, the speed of the charm and the bottom quarks in their respective quarkonia is sufficiently smaller, so that relativistic effects affect these states much less. It is estimated that the speed, v, is roughly 0.3 times the speed of light for charmonia and roughly 0.1 times the speed of light for bottomonia. The computation can then be approximated by an expansion in powers of v/c and v²/c². This technique is called non-relativistic QCD (NRQCD).

NRQCD has also been quantized as a lattice gauge theory, which provides another technique for LQCD calculations to use. Good agreement with the bottomonium masses has been found, and this provides one of the best non-perturbative tests of LQCD. For charmonium masses the agreement is not as good, but the LQCD community is actively working on improving their techniques. Work is also being done on calculations of such properties as widths of quarkonia states and transition rates between the states.

An early, but still effective, technique uses models of the effective potential to calculate masses of quarkonia states. In this technique, one uses the fact that the motion of the quarks that comprise the quarkonium state is non-relativistic to assume that they move in a static potential, much like non-relativistic models of the hydrogen atom. One of the most popular potential models is the so-called Cornell potential

${\displaystyle V(r)=-{\frac {a}{r}}+br}$^[8]

where ${\displaystyle r}$ is the effective radius of the quarkonium state, ${\displaystyle a}$ and ${\displaystyle b}$ are parameters. This potential has two parts. The first part, ${\displaystyle a/r}$ corresponds to the potential induced by one-gluon exchange between the quark and its anti-quark, and is known as the Coulombic part of the potential, since its ${\displaystyle 1/r}$ form is identical to the well-known Coulombic potential induced by the electromagnetic force. The second part, ${\displaystyle br}$, is known as the confinement part of the potential, and parameterizes the poorly understood non-perturbative effects of QCD. Generally, when using this approach, a convenient form for the wave function of the quarks is taken, and then ${\displaystyle a}$ and ${\displaystyle b}$ are determined by fitting the results of the calculations to the masses of well-measured quarkonium states. Relativistic and other effects can be incorporated into this approach by adding extra terms to the potential, much in the same way that they are for the hydrogen atom in non-relativistic quantum mechanics. This form has been derived from QCD up to ${\displaystyle {\mathcal {O}}(\Lambda _{\text{QCD}}^{3}r^{2})}$ by Y. Sumino in 2003.^[9] It is popular because it allows for accurate predictions of quarkonia parameters without a lengthy lattice computation, and provides a separation between the short-distance Coulombic effects and the long-distance confinement effects that can be useful in understanding the quark/anti-quark force generated by QCD.

Quarkonia have been suggested as a diagnostic tool of the formation of the quark–gluon plasma: both disappearance and enhancement of their formation depending on the yield of heavy quarks in plasma can occur.