Newton's law of universal gravitation

From Wikipedia, the free encyclopedia

Newton's law of universal gravitation states that every particle attracts every other particle in the universe with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This is a general physical law derived from empirical observations by what Isaac Newton called inductive reasoning. It is a part of classical mechanics and was formulated in Newton's work Philosophiæ Naturalis Principia Mathematica ("the Principia"), first published on 5 July 1686. When Newton's book was presented in 1686 to the Royal Society, Robert Hooke made a claim that Newton had obtained the inverse square law from him.

In today's language, the law states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses, and inversely proportional to the square of the distance between them.

The equation for universal gravitation thus takes the form:

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$

where F is the gravitational force acting between two objects, m₁ and m₂ are the masses of the objects, r is the distance between the centers of their masses, and G is the gravitational constant.

The first test of Newton's theory of gravitation between masses in the laboratory was the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798. It took place 111 years after the publication of Newton's Principia and approximately 71 years after his death.

Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of the electrical force arising between two charged bodies. Both are inverse-square laws, where force is inversely proportional to the square of the distance between the bodies. Coulomb's law has the product of two charges in place of the product of the masses, and the electrostatic constant in place of the gravitational constant.

Newton's law has since been superseded by Albert Einstein's theory of general relativity, but it continues to be used as an excellent approximation of the effects of gravity in most applications. Relativity is required only when there is a need for extreme precision, or when dealing with very strong gravitational fields, such as those found near extremely massive and dense objects, or at very close distances (such as Mercury's orbit around the Sun).

History

Early history

The relation of the distance of objects in free fall to the square of the time taken had recently been confirmed by Grimaldi and Riccioli between 1640 and 1650. They had also made a calculation of the gravitational constant by recording the oscillations of a pendulum.

A modern assessment about the early history of the inverse square law is that "by the late 1670s", the assumption of an "inverse proportion between gravity and the square of distance was rather common and had been advanced by a number of different people for different reasons".^[5] The same author credits Robert Hooke with a significant and seminal contribution, but treats Hooke's claim of priority on the inverse square point as irrelevant, as several individuals besides Newton and Hooke had suggested it. He points instead to the idea of "compounding the celestial motions" and the conversion of Newton's thinking away from "centrifugal" and towards "centripetal" force as Hooke's significant contributions.

Newton gave credit in his Principia to two people: Bullialdus (who wrote without proof that there was a force on the Earth towards the Sun), and Borelli (who wrote that all planets were attracted towards the Sun). The main influence may have been Borelli, whose book Newton had a copy of.

Hooke's work and claims

Robert Hooke published his ideas about the "System of the World" in the 1660s, when he read to the Royal Society on March 21, 1666, a paper "concerning the inflection of a direct motion into a curve by a supervening attractive principle", and he published them again in somewhat developed form in 1674, as an addition to "An Attempt to Prove the Motion of the Earth from Observations". Hooke announced in 1674 that he planned to "explain a System of the World differing in many particulars from any yet known", based on three "Suppositions": that "all Celestial Bodies whatsoever, have an attraction or gravitating power towards their own Centers" and "they do also attract all the other Celestial Bodies that are within the sphere of their activity"; that "all bodies whatsoever that are put into a direct and simple motion, will so continue to move forward in a straight line, till they are by some other effectual powers deflected and bent..."; and that "these attractive powers are so much the more powerful in operating, by how much the nearer the body wrought upon is to their own Centers". Thus Hooke clearly postulated mutual attractions between the Sun and planets, in a way that increased with nearness to the attracting body, together with a principle of linear inertia.

Hooke's statements up to 1674 made no mention, however, that an inverse square law applies or might apply to these attractions. Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. He also did not provide accompanying evidence or mathematical demonstration. On the latter two aspects, Hooke himself stated in 1674: "Now what these several degrees [of attraction] are I have not yet experimentally verified"; and as to his whole proposal: "This I only hint at present", "having my self many other things in hand which I would first compleat, and therefore cannot so well attend it" (i.e. "prosecuting this Inquiry"). It was later on, in writing on 6 January 1679|80^[12] to Newton, that Hooke communicated his "supposition ... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance." (The inference about the velocity was incorrect.)

Hooke's correspondence with Newton during 1679–1680 not only mentioned this inverse square supposition for the decline of attraction with increasing distance, but also, in Hooke's opening letter to Newton, of 24 November 1679, an approach of "compounding the celestial motions of the planets of a direct motion by the tangent & an attractive motion towards the central body".

Newton's work and claims

Newton, faced in May 1686 with Hooke's claim on the inverse square law, denied that Hooke was to be credited as author of the idea. Among the reasons, Newton recalled that the idea had been discussed with Sir Christopher Wren previous to Hooke's 1679 letter. Newton also pointed out and acknowledged prior work of others, including Bullialdus, (who suggested, but without demonstration, that there was an attractive force from the Sun in the inverse square proportion to the distance), and Borelli (who suggested, also without demonstration, that there was a centrifugal tendency in counterbalance with a gravitational attraction towards the Sun so as to make the planets move in ellipses). D T Whiteside has described the contribution to Newton's thinking that came from Borelli's book, a copy of which was in Newton's library at his death.

Newton further defended his work by saying that had he first heard of the inverse square proportion from Hooke, he would still have some rights to it in view of his demonstrations of its accuracy. Hooke, without evidence in favor of the supposition, could only guess that the inverse square law was approximately valid at great distances from the center. According to Newton, while the 'Principia' was still at pre-publication stage, there were so many a-priori reasons to doubt the accuracy of the inverse-square law (especially close to an attracting sphere) that "without my (Newton's) Demonstrations, to which Mr Hooke is yet a stranger, it cannot believed by a judicious Philosopher to be any where accurate."

This remark refers among other things to Newton's finding, supported by mathematical demonstration, that if the inverse square law applies to tiny particles, then even a large spherically symmetrical mass also attracts masses external to its surface, even close up, exactly as if all its own mass were concentrated at its center. Thus Newton gave a justification, otherwise lacking, for applying the inverse square law to large spherical planetary masses as if they were tiny particles. In addition, Newton had formulated, in Propositions 43-45 of Book 1 and associated sections of Book 3, a sensitive test of the accuracy of the inverse square law, in which he showed that only where the law of force is calculated as the inverse square of the distance will the directions of orientation of the planets' orbital ellipses stay constant as they are observed to do apart from small effects attributable to inter-planetary perturbations.

In regard to evidence that still survives of the earlier history, manuscripts written by Newton in the 1660s show that Newton himself had, by 1669, arrived at proofs that in a circular case of planetary motion, "endeavour to recede" (what was later called centrifugal force) had an inverse-square relation with distance from the center. After his 1679-1680 correspondence with Hooke, Newton adopted the language of inward or centripetal force. According to Newton scholar J. Bruce Brackenridge, although much has been made of the change in language and difference of point of view, as between centrifugal or centripetal forces, the actual computations and proofs remained the same either way. They also involved the combination of tangential and radial displacements, which Newton was making in the 1660s. The lesson offered by Hooke to Newton here, although significant, was one of perspective and did not change the analysis. This background shows there was basis for Newton to deny deriving the inverse square law from Hooke.

Newton's acknowledgment

On the other hand, Newton did accept and acknowledge, in all editions of the Principia, that Hooke (but not exclusively Hooke) had separately appreciated the inverse square law in the solar system. Newton acknowledged Wren, Hooke and Halley in this connection in the Scholium to Proposition 4 in Book 1. Newton also acknowledged to Halley that his correspondence with Hooke in 1679-80 had reawakened his dormant interest in astronomical matters, but that did not mean, according to Newton, that Hooke had told Newton anything new or original: "yet am I not beholden to him for any light into that business but only for the diversion he gave me from my other studies to think on these things & for his dogmaticalness in writing as if he had found the motion in the Ellipsis, which inclined me to try it ..."

Modern priority controversy

Since the time of Newton and Hooke, scholarly discussion has also touched on the question of whether Hooke's 1679 mention of 'compounding the motions' provided Newton with something new and valuable, even though that was not a claim actually voiced by Hooke at the time. As described above, Newton's manuscripts of the 1660s do show him actually combining tangential motion with the effects of radially directed force or endeavour, for example in his derivation of the inverse square relation for the circular case. They also show Newton clearly expressing the concept of linear inertia—for which he was indebted to Descartes' work, published in 1644 (as Hooke probably was). These matters do not appear to have been learned by Newton from Hooke.

Nevertheless, a number of authors have had more to say about what Newton gained from Hooke and some aspects remain controversial. The fact that most of Hooke's private papers had been destroyed or have disappeared does not help to establish the truth.

Newton's role in relation to the inverse square law was not as it has sometimes been represented. He did not claim to think it up as a bare idea. What Newton did was to show how the inverse-square law of attraction had many necessary mathematical connections with observable features of the motions of bodies in the solar system; and that they were related in such a way that the observational evidence and the mathematical demonstrations, taken together, gave reason to believe that the inverse square law was not just approximately true but exactly true (to the accuracy achievable in Newton's time and for about two centuries afterwards – and with some loose ends of points that could not yet be certainly examined, where the implications of the theory had not yet been adequately identified or calculated).

Plagiarism dispute

In 1686, when the first book of Newton's Principia was presented to the Royal Society, Robert Hooke accused Newton of plagiarism by claiming that he had taken from him the "notion" of "the rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center". At the same time (according to Edmond Halley's contemporary report) Hooke agreed that "the Demonstration of the Curves generated thereby" was wholly Newton's.

In this way, the question arose as to what, if anything, Newton owed to Hooke. This is a subject extensively discussed since that time and on which some points, outlined below, continue to excite controversy.

About thirty years after Newton's death in 1727, Alexis Clairaut, a mathematical astronomer eminent in his own right in the field of gravitational studies, wrote after reviewing what Hooke published, that "One must not think that this idea ... of Hooke diminishes Newton's glory"; and that "the example of Hooke" serves "to show what a distance there is between a truth that is glimpsed and a truth that is demonstrated".

Modern form

In modern language, the law states the following:

Every point mass attracts every single other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:
${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$ where: F is the force between the masses; G is the gravitational constant (6.674×10−11 N · (m/kg)2); m1 is the first mass; m2 is the second mass; r is the distance between the centers of the masses.

Error plot showing experimental values for big G.

Assuming SI units, F is measured in newtons (N), m₁ and m₂ in kilograms (kg), r in meters (m), and the constant G is approximately equal to 6.674×10⁻¹¹ N m² kg⁻². The value of the constant G was first accurately determined from the results of the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798, although Cavendish did not himself calculate a numerical value for G. This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.

Bodies with spatial extent

Gravitational field strength within the Earth

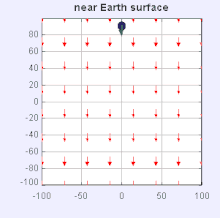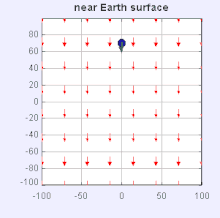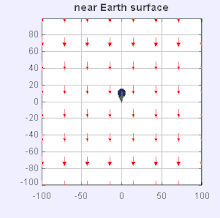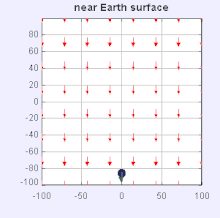
Gravity field near the surface of the Earth – an object is shown accelerating toward the surface

If the bodies in question have spatial extent (as opposed to being point masses), then the gravitational force between them is calculated by summing the contributions of the notional point masses which constitute the bodies. In the limit, as the component point masses become "infinitely small", this entails integrating the force (in vector form, see below) over the extents of the two bodies.

In this way, it can be shown that an object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object's mass were concentrated at a point at its centre. (This is not generally true for non-spherically-symmetrical bodies.)

For points inside a spherically-symmetric distribution of matter, Newton's Shell theorem can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r₀ from the center of the mass distribution:

• The portion of the mass that is located at radii r < r₀ causes the same force at r₀ as if all of the mass enclosed within a sphere of radius r₀ was concentrated at the center of the mass distribution (as noted above).
• The portion of the mass that is located at radii r > r₀ exerts no net gravitational force at the distance r₀ from the center. That is, the individual gravitational forces exerted by the elements of the sphere out there, on the point at r₀, cancel each other out.

As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere.

Furthermore, inside a uniform sphere the gravity increases linearly with the distance from the center; the increase due to the additional mass is 1.5 times the decrease due to the larger distance from the center. Thus, if a spherically symmetric body has a uniform core and a uniform mantle with a density that is less than 2/3 of that of the core, then the gravity initially decreases outwardly beyond the boundary, and if the sphere is large enough, further outward the gravity increases again, and eventually it exceeds the gravity at the core/mantle boundary. The gravity of the Earth may be highest at the core/mantle boundary.

Vector form

Gravity field surrounding Earth from a macroscopic perspective.

Newton's law of universal gravitation can be written as a vector equation to account for the direction of the gravitational force as well as its magnitude. In this formula, quantities in bold represent vectors.

${\displaystyle \mathbf {F} _{21}=-G{m_{1}m_{2} \over {\vert \mathbf {r} _{12}\vert }^{2}}\,\mathbf {\hat {r}} _{12}}$

where

F₂₁ is the force applied on object 2 exerted by object 1,

G is the gravitational constant,

m₁ and m₂ are respectively the masses of objects 1 and 2,

|r₁₂| = |r₂ − r₁| is the distance between objects 1 and 2, and

${\displaystyle \mathbf {\hat {r}} _{12}\ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathbf {r} _{2}-\mathbf {r} _{1}}{\vert \mathbf {r} _{2}-\mathbf {r} _{1}\vert }}}$ is the unit vector from object 1 to 2.

It can be seen that the vector form of the equation is the same as the scalar form given earlier, except that F is now a vector quantity, and the right hand side is multiplied by the appropriate unit vector. Also, it can be seen that F₁₂ = −F₂₁.

Gravitational field

The gravitational field is a vector field that describes the gravitational force which would be applied on an object in any given point in space, per unit mass. It is actually equal to the gravitational acceleration at that point.

It is a generalisation of the vector form, which becomes particularly useful if more than 2 objects are involved (such as a rocket between the Earth and the Moon). For 2 objects (e.g. object 2 is a rocket, object 1 the Earth), we simply write r instead of r₁₂ and m instead of m₂ and define the gravitational field g(r) as:

${\displaystyle \mathbf {g} (\mathbf {r} )=-G{m_{1} \over {{\vert \mathbf {r} \vert }^{2}}}\,\mathbf {\hat {r}} }$

so that we can write:

${\displaystyle \mathbf {F} (\mathbf {r} )=m\mathbf {g} (\mathbf {r} ).}$

This formulation is dependent on the objects causing the field. The field has units of acceleration; in SI, this is m/s².

Gravitational fields are also conservative; that is, the work done by gravity from one position to another is path-independent. This has the consequence that there exists a gravitational potential field V(r) such that

${\displaystyle \mathbf {g} (\mathbf {r} )=-\nabla V(\mathbf {r} ).}$

If m₁ is a point mass or the mass of a sphere with homogeneous mass distribution, the force field g(r) outside the sphere is isotropic, i.e., depends only on the distance r from the center of the sphere. In that case

${\displaystyle V(r)=-G{\frac {m_{1}}{r}}.}$

the gravitational field is on, inside and outside of symmetric masses.

As per Gauss Law, field in a symmetric body can be found by the mathematical equation:

${\displaystyle \partial V}$ ${\displaystyle \mathbf {g(r)} \cdot d\mathbf {A} =-4\pi GM_{\text{enc}},}$

where ${\displaystyle \partial V}$ is a closed surface and ${\displaystyle M_{\text{enc}}}$ is the mass enclosed by the surface.

Hence, for a hollow sphere of radius ${\displaystyle R}$ and total mass ${\displaystyle M}$,

${\displaystyle |\mathbf {g(r)} |={\begin{cases}0,&{\mbox{if }}r$

For a uniform solid sphere of radius ${\displaystyle R}$ and total mass ${\displaystyle M}$,

${\displaystyle |\mathbf {g(r)} |={\begin{cases}{\dfrac {GMr}{R^{3}}},&{\mbox{if }}r$

Problematic aspects

Newton's description of gravity is sufficiently accurate for many practical purposes and is therefore widely used. Deviations from it are small when the dimensionless quantities φ/c² and (v/c)² are both much less than one, where φ is the gravitational potential, v is the velocity of the objects being studied, and c is the speed of light. For example, Newtonian gravity provides an accurate description of the Earth/Sun system, since

${\displaystyle {\frac {\Phi }{c^{2}}}={\frac {GM_{\mathrm {sun} }}{r_{\mathrm {orbit} }c^{2}}}\sim 10^{-8},\quad \left({\frac {v_{\mathrm {Earth} }}{c}}\right)^{2}=\left({\frac {2\pi r_{\mathrm {orbit} }}{(1\ \mathrm {yr} )c}}\right)^{2}\sim 10^{-8}}$

where r_orbit is the radius of the Earth's orbit around the Sun.

In situations where either dimensionless parameter is large, then general relativity must be used to describe the system. General relativity reduces to Newtonian gravity in the limit of small potential and low velocities, so Newton's law of gravitation is often said to be the low-gravity limit of general relativity.

Theoretical concerns with Newton's expression

• There is no immediate prospect of identifying the mediator of gravity. Attempts by physicists to identify the relationship between the gravitational force and other known fundamental forces are not yet resolved, although considerable headway has been made over the last 50 years (See: Theory of everything and Standard Model). Newton himself felt that the concept of an inexplicable action at a distance was unsatisfactory (see "Newton's reservations" below), but that there was nothing more that he could do at the time.
• Newton's theory of gravitation requires that the gravitational force be transmitted instantaneously. Given the classical assumptions of the nature of space and time before the development of General Relativity, a significant propagation delay in gravity leads to unstable planetary and stellar orbits.

Observations conflicting with Newton's formula

• Newton's Theory does not fully explain the precession of the perihelion of the orbits of the planets, especially of planet Mercury, which was detected long after the life of Newton. There is a 43 arcsecond per century discrepancy between the Newtonian calculation, which arises only from the gravitational attractions from the other planets, and the observed precession, made with advanced telescopes during the 19th century.
• The predicted angular deflection of light rays by gravity that is calculated by using Newton's Theory is only one-half of the deflection that is actually observed by astronomers. Calculations using General Relativity are in much closer agreement with the astronomical observations.
• In spiral galaxies, the orbiting of stars around their centers seems to strongly disobey Newton's law of universal gravitation. Astrophysicists, however, explain this spectacular phenomenon in the framework of Newton's laws, with the presence of large amounts of dark matter.

Newton's reservations

While Newton was able to formulate his law of gravity in his monumental work, he was deeply uncomfortable with the notion of "action at a distance" that his equations implied. In 1692, in his third letter to Bentley, he wrote: "That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it."
 
He never, in his words, "assigned the cause of this power". In all other cases, he used the phenomenon of motion to explain the origin of various forces acting on bodies, but in the case of gravity, he was unable to experimentally identify the motion that produces the force of gravity (although he invented two mechanical hypotheses in 1675 and 1717). Moreover, he refused to even offer a hypothesis as to the cause of this force on grounds that to do so was contrary to sound science. He lamented that "philosophers have hitherto attempted the search of nature in vain" for the source of the gravitational force, as he was convinced "by many reasons" that there were "causes hitherto unknown" that were fundamental to all the "phenomena of nature". These fundamental phenomena are still under investigation and, though hypotheses abound, the definitive answer has yet to be found. And in Newton's 1713 General Scholium in the second edition of Principia: "I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypotheses.... It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies."

Einstein's solution

These objections were explained by Einstein's theory of general relativity, in which gravitation is an attribute of curved spacetime instead of being due to a force propagated between bodies. In Einstein's theory, energy and momentum distort spacetime in their vicinity, and other particles move in trajectories determined by the geometry of spacetime. This allowed a description of the motions of light and mass that was consistent with all available observations. In general relativity, the gravitational force is a fictitious force due to the curvature of spacetime, because the gravitational acceleration of a body in free fall is due to its world line being a geodesic of spacetime.

Extensions

Newton was the first to consider in his Principia an extended expression of his law of gravity including an inverse-cube term of the form

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}+B{\frac {m_{1}m_{2}}{r^{3}}}\ }$, ${\displaystyle B}$ a constant

attempting to explain the Moon's apsidal motion. Other extensions were proposed by Laplace (around 1790) and Decombes (1913):

${\displaystyle F(r)=k{\frac {m_{1}m_{2}}{r^{2}}}\exp(-\alpha r)}$ (Laplace)

${\displaystyle F(r)=k{\frac {m_{1}m_{2}}{r^{2}}}\left(1+{\alpha \over {r^{3}}}\right)}$ (Decombes)

In recent years, quests for non-inverse square terms in the law of gravity have been carried out by neutron interferometry.

Solutions of Newton's law of universal gravitation

The n-body problem is an ancient, classical problem of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem — from the time of the Greeks and on — has been motivated by the desire to understand the motions of the Sun, planets and the visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem too. The n-body problem in general relativity is considerably more difficult to solve.

The classical physical problem can be informally stated as: given the quasi-steady orbital properties (instantaneous position, velocity and time) of a group of celestial bodies, predict their interactive forces; and consequently, predict their true orbital motions for all future times.

The two-body problem has been completely solved, as has the restricted three-body problem.

Newton's Opticks

From Wikipedia, the free encyclopedia

The first, 1704, edition of Opticks: or, a treatise of the reflexions, refractions, inflexions and colours of light.

Opticks: or, A Treatise of the Reflexions, Refractions, Inflexions and Colours of Light is a book by English natural philosopher Isaac Newton that was published in English in 1704. (A scholarly Latin translation appeared in 1706.) The book analyzes the fundamental nature of light by means of the refraction of light with prisms and lenses, the diffraction of light by closely spaced sheets of glass, and the behaviour of color mixtures with spectral lights or pigment powders. It is considered one of the great works of science in history. Opticks was Newton's second major book on physical science. Newton's name did not appear on the title page of the first edition of Opticks.

Overview

The publication of Opticks represented a major contribution to science, different from but in some ways rivalling the Principia. Opticks is largely a record of experiments and the deductions made from them, covering a wide range of topics in what was later to be known as physical optics. That is, this work is not a geometric discussion of catoptrics or dioptrics, the traditional subjects of reflection of light by mirrors of different shapes and the exploration of how light is "bent" as it passes from one medium, such as air, into another, such as water or glass. Rather, the Opticks is a study of the nature of light and colour and the various phenomena of diffraction, which Newton called the "inflexion" of light.

In this book Newton sets forth in full his experiments, first reported to the Royal Society of London in 1672, on dispersion, or the separation of light into a spectrum of its component colours. He demonstrates how the appearance of color arises from selective absorption, reflection, or transmission of the various component parts of the incident light.

The major significance of Newton's work is that it overturned the dogma, attributed to Aristotle or Theophrastus and accepted by scholars in Newton's time, that "pure" light (such as the light attributed to the Sun) is fundamentally white or colourless, and is altered into color by mixture with darkness caused by interactions with matter. Newton showed just the opposite was true: light is composed of different spectral hues (he describes seven — red, orange, yellow, green, blue, indigo and violet), and all colours, including white, are formed by various mixtures of these hues. He demonstrates that color arises from a physical property of light — each hue is refracted at a characteristic angle by a prism or lens — but he clearly states that color is a sensation within the mind and not an inherent property of material objects or of light itself. For example, he demonstrates that a red violet (magenta) color can be mixed by overlapping the red and violet ends of two spectra, although this color does not appear in the spectrum and therefore is not a "color of light". By connecting the red and violet ends of the spectrum, he organised all colours as a color circle that both quantitatively predicts color mixtures and qualitatively describes the perceived similarity among hues.

Opticks and the Principia

Opticks differs in many respects from the Principia. It was first published in English rather than in the Latin used by European philosophers, contributing to the development of a vernacular science literature. This marks a significant transition in the history of the English Language. With Britain's growing confidence and world influence, due at least in part to people like Newton, the English language was rapidly becoming the language of science and business. The book is a model of popular science exposition: although Newton's English is somewhat dated—he shows a fondness for lengthy sentences with much embedded qualifications—the book can still be easily understood by a modern reader. In contrast, few readers of Newton's time found the Principia accessible or even comprehensible. His formal but flexible style shows colloquialisms and metaphorical word choice.

Unlike the Principia, Opticks is not developed using the geometric convention of propositions proved by deduction from either previous propositions, lemmas or first principles (or axioms). Instead, axioms define the meaning of technical terms or fundamental properties of matter and light, and the stated propositions are demonstrated by means of specific, carefully described experiments. The first sentence of the book declares My Design in this Book is not to explain the Properties of Light by Hypotheses, but to propose and prove them by Reason and Experiments. In an Experimentum crucis or "critical experiment" (Book I, Part II, Theorem ii), Newton showed that the color of light corresponded to its "degree of refrangibility" (angle of refraction), and that this angle cannot be changed by additional reflection or refraction or by passing the light through a coloured filter.

The work is a vade mecum of the experimenter's art, displaying in many examples how to use observation to propose factual generalisations about the physical world and then exclude competing explanations by specific experimental tests. However, unlike the Principia, which vowed Non fingo hypotheses or "I make no hypotheses" outside the deductive method, the Opticks develops conjectures about light that go beyond the experimental evidence: for example, that the physical behaviour of light was due its "corpuscular" nature as small particles, or that perceived colours were harmonically proportioned like the tones of a diatonic musical scale.

The Queries

Opticks concludes with a set of "Queries." In the first edition, these were sixteen such Queries; that number was increased in the Latin edition, published in 1706, and then in the revised English edition, published in 1717/18. The first set of Queries were brief, but the later ones became short essays, filling many pages. In the fourth edition of 1730, there were 31 Queries, and it was the famous "31st Query" that, over the next two hundred years, stimulated a great deal of speculation and development on theories of chemical affinity.

These Queries, especially the later ones, deal with a wide range of physical phenomena, far transcending any narrow interpretation of the subject matter of "optics." They concern the nature and transmission of heat; the possible cause of gravity; electrical phenomena; the nature of chemical action; the way in which God created matter in "the Beginning;" the proper way to do science; and even the ethical conduct of human beings. These Queries are not really questions in the ordinary sense. They are almost all posed in the negative, as rhetorical questions. That is, Newton does not ask whether light "is" or "may be" a "body." Rather, he declares: "Is not Light a Body?" Not only does this form indicate that Newton had an answer, but that it may go on for many pages. Clearly, as Stephen Hales (a firm Newtonian of the early eighteenth century) declared, this was Newton's mode of explaining "by Query."

Multiverse

Newton suggests the idea of a multiverse in this passage:

And since Space is divisible in infinitum, and Matter is not necessarily in all places, it may be also allow'd that God is able to create Particles of Matter of several Sizes and Figures, and in several Proportions to Space, and perhaps of different Densities and Forces, and thereby to vary the Laws of Nature, and make Worlds of several sorts in several Parts of the Universe. At least, I see nothing of Contradiction in all this.

Reception

The Opticks was widely read and debated in England and on the Continent. The early presentation of the work to the Royal Society stimulated a bitter dispute between Newton and Robert Hooke over the "corpuscular" or particle theory of light, which prompted Newton to postpone publication of the work until after Hooke's death in 1703. On the Continent, and in France in particular, both the Principia and the Opticks were initially rejected by many natural philosophers, who continued to defend Cartesian natural philosophy and the Aristotelian version of color, and claimed to find Newton's prism experiments difficult to replicate. Indeed, the Aristotelian theory of the fundamental nature of white light was defended into the 19th century, for example by the German writer Johann Wolfgang von Goethe in his Farbenlehre.

Newtonian science became a central issue in the assault waged by the philosophes in the Age of Enlightenment against a natural philosophy based on the authority of ancient Greek or Roman naturalists or on deductive reasoning from first principles (the method advocated by French philosopher René Descartes), rather than on the application of mathematical reasoning to experience or experiment. Voltaire popularised Newtonian science, including the content of both the Principia and the Opticks, in his Elements de la philosophie de Newton (1738), and after about 1750 the combination of the experimental methods exemplified by the Opticks and the mathematical methods exemplified by the Principia were established as a unified and comprehensive model of Newtonian science. Some of the primary adepts in this new philosophy were such prominent figures as Benjamin Franklin, Antoine-Laurent Lavoisier, and James Black.

Subsequent to Newton, much has been amended. Young and Fresnel combined Newton's particle theory with Huygens' wave theory to show that colour is the visible manifestation of light's wavelength. Science also slowly came to realise the difference between perception of colour and mathematisable optics. The German poet Goethe, with his epic diatribe Theory of Colours, could not shake the Newtonian foundation - but "one hole Goethe did find in Newton's armour.. Newton had committed himself to the doctrine that refraction without colour was impossible. He therefore thought that the object-glasses of telescopes must for ever remain imperfect, achromatism and refraction being incompatible. This inference was proved by Dollond to be wrong." (John Tyndall, 1880)

Bertrand paradox (probability)

From Wikipedia, the free encyclopedia

The Bertrand paradox is a problem within the classical interpretation of probability theory. Joseph Bertrand introduced it in his work Calcul des probabilités (1889) as an example to show that probabilities may not be well defined if the mechanism or method that produces the random variable is not clearly defined.

Bertrand's formulation of the problem

The Bertrand paradox goes as follows: Consider an equilateral triangle inscribed in a circle. Suppose a chord of the circle is chosen at random. What is the probability that the chord is longer than a side of the triangle?

Bertrand gave three arguments, all apparently valid, yet yielding different results.

1. 

Random chords, selection method 1; red = longer than triangle side, blue = shorter

The "random endpoints" method: Choose two random points on the circumference of the circle and draw the chord joining them. To calculate the probability in question imagine the triangle rotated so its vertex coincides with one of the chord endpoints. Observe that if the other chord endpoint lies on the arc between the endpoints of the triangle side opposite the first point, the chord is longer than a side of the triangle. The length of the arc is one third of the circumference of the circle, therefore the probability that a random chord is longer than a side of the inscribed triangle is 1/3.

Random chords, selection method 2

The "random radius" method: Choose a radius of the circle, choose a point on the radius and construct the chord through this point and perpendicular to the radius. To calculate the probability in question imagine the triangle rotated so a side is perpendicular to the radius. The chord is longer than a side of the triangle if the chosen point is nearer the center of the circle than the point where the side of the triangle intersects the radius. The side of the triangle bisects the radius, therefore the probability a random chord is longer than a side of the inscribed triangle is 1/2.

3. Random chords, selection method 3
   
   The "random midpoint" method: Choose a point anywhere within the circle and construct a chord with the chosen point as its midpoint. The chord is longer than a side of the inscribed triangle if the chosen point falls within a concentric circle of radius 1/2 the radius of the larger circle. The area of the smaller circle is one fourth the area of the larger circle, therefore the probability a random chord is longer than a side of the inscribed triangle is 1/4.

As presented above, the selection methods differ in the weight they give to chords which are diameters. In method 1, each chord can be chosen in exactly one way, regardless of whether or not it is a diameter. In method 2, each diameter can be chosen in two ways, whereas each other chord can be chosen in only one way. In method 3, each choice of midpoint corresponds to a single chord, except the center of the circle, which is the midpoint of all the diameters. These issues can be avoided by "regularizing" the problem so as to exclude diameters, without affecting the resulting probabilities.

The selection methods can also be visualized as follows. A chord which is not a diameter is uniquely identified by its midpoint. Each of the three selection methods presented above yields a different distribution of midpoints. Methods 1 and 2 yield two different nonuniform distributions, while method 3 yields a uniform distribution. On the other hand, if one looks at the images of the chords below, the chords of method 2 give the circle a homogeneously shaded look, while method 1 and 3 do not.

Midpoints of the chords chosen at random using method 1

Midpoints of the chords chosen at random using method 2

Midpoints of the chords chosen at random using method 3

Chords chosen at random, method 1

Chords chosen at random, method 2

Chords chosen at random, method 3

Other distributions can easily be imagined, many of which will yield a different proportion of chords which are longer than a side of the inscribed triangle.

Classical solution

The problem's classical solution hinges on the method by which a chord is chosen "at random". It turns out that if, and only if, the method of random selection is specified, does the problem have a well-defined solution. This is because each different method has a different underlying distribution of chords. The three solutions presented by Bertrand correspond to different selection methods, and in the absence of further information there is no reason to prefer one over another; accordingly the problem as stated has no unique solution.

An example of how to make the solution unique is to specify that the endpoints of the chord are uniformly distributed between 0 and c, where c is the circumference of the circle. This distribution is the same as that in Bertrand's first argument, and the resulting unique probability is 1/3.
This and other paradoxes of the classical interpretation of probability justified more stringent formulations, including frequentist probability and subjectivist Bayesian probability.

Jaynes's solution using the "maximum ignorance" principle

In his 1973 paper "The Well-Posed Problem", Edwin Jaynes proposed a solution to Bertrand's paradox, based on the principle of "maximum ignorance"—that we should not use any information that is not given in the statement of the problem. Jaynes pointed out that Bertrand's problem does not specify the position or size of the circle, and argued that therefore any definite and objective solution must be "indifferent" to size and position. In other words: the solution must be both scale and translation invariant.

To illustrate: assume that chords are laid at random onto a circle with a diameter of 2, for example by throwing straws onto it from far away. Now another circle with a smaller diameter (e.g., 1.1) is laid into the larger circle. Then the distribution of the chords on that smaller circle needs to be the same as on the larger circle. If the smaller circle is moved around within the larger circle, the probability must not change either. It can be seen very easily that there would be a change for method 3: the chord distribution on the small red circle looks qualitatively different from the distribution on the large circle:

The same occurs for method 1, though it is harder to see in a graphical representation. Method 2 is the only one that is both scale invariant and translation invariant; method 3 is just scale invariant, method 1 is neither.

However, Jaynes did not just use invariances to accept or reject given methods: this would leave the possibility that there is another not yet described method that would meet his common-sense criteria. Jaynes used the integral equations describing the invariances to directly determine the probability distribution. In this problem, the integral equations indeed have a unique solution, and it is precisely what was called "method 2" above, the random radius method.

In a 2015 article, Alon Drory claims that Jaynes' principle can also yield Bertrand's other two solutions. Drory argues that the mathematical implementation of the above invariance properties is not unique, but depends on the underlying procedure of random selection that one uses. He shows that each of Bertrand's three solutions can be derived using rotational, scaling, and translational invariance, concluding that Jaynes' principle is just as subject to interpretation as the principle of indifference itself.

Physical experiments

"Method 2" is the only solution that fulfills the transformation invariants that are present in certain physical systems—such as in statistical mechanics and gas physics—as well as in Jaynes's proposed experiment of throwing straws from a distance onto a small circle. Nevertheless, one can design other practical experiments that give answers according to the other methods. For example, in order to arrive at the solution of "method 1", the random endpoints method, one can affix a spinner to the center of the circle, and let the results of two independent spins mark the endpoints of the chord. In order to arrive at the solution of "method 3", one could cover the circle with molasses and mark the first point that a fly lands on as the midpoint of the chord. Several observers have designed experiments in order to obtain the different solutions and verified the results empirically.

Recent developments

In his 2007 paper, "Bertrand’s Paradox and the Principle of Indifference", Nicholas Shackel affirms that after more than a century the paradox remains unresolved, and continues to stand in refutation of the principle of indifference. Also, in his 2013 paper, "Bertrand’s paradox revisited: Why Bertrand’s ‘solutions’ are all inapplicable", Darrell P. Rowbottom shows that Bertrand’s proposed solutions are all inapplicable to his own question, so that the paradox would be much harder to solve than previously anticipated.

Shackel emphasizes that two different approaches have been generally adopted so far in trying to solve Bertrand's paradox: those where a distinction between non-equivalent problems was considered, and those where the problem was assumed to be a well-posed one. Shackel cites Louis Marinoff as a typical representative of the distinction strategy, and Edwin Jaynes as a typical representative of the well-posing strategy.

However, in a recent work, "Solving the hard problem of Bertrand's paradox", Diederik Aerts and Massimiliano Sassoli de Bianchi consider that a mixed strategy is necessary to tackle Bertrand's paradox. According to these authors, the problem needs first to be disambiguated by specifying in a very clear way the nature of the entity which is subjected to the randomization, and only once this is done the problem can be considered to be a well-posed one, in the Jaynes sense, so that the principle of maximum ignorance can be used to solve it. To this end, and since the problem doesn't specify how the chord has to be selected, the principle needs to be applied not at the level of the different possible choices of a chord, but at the much deeper level of the different possible ways of choosing a chord. This requires the calculation of a meta average over all the possible ways of selecting a chord, which the authors call a universal average. To handle it, they use a discretization method inspired by what is done in the definition of the probability law in the Wiener processes. The result they obtain is in agreement with the numerical result of Jaynes, although their well-posed problem is different from that of Jaynes.