Photon

From Wikipedia, the free encyclopedia

Photon

Composition	Elementary particle
Statistics	Bosonic
Interactions	Electromagnetic, Weak, Gravity
Symbol	γ
Theorized	Albert Einstein
Mass	0 < 1×10−18 eV/c2
Mean lifetime	Stable[1]
Electric charge	0 < 1×10−35 e
Spin	1
Parity	−1[1]
C parity	−1[1]
Condensed	I(JPC)=0,1(1−−)

The photon is a type of elementary particle, the quantum of the electromagnetic field including electromagnetic radiation such as light, and the force carrier for the electromagnetic force (even when static via virtual particles). The photon has zero rest mass and always moves at the speed of light within a vacuum.

Like all elementary particles, photons are currently best explained by quantum mechanics and exhibit wave–particle duality, exhibiting properties of both waves and particles. For example, a single photon may be refracted by a lens and exhibit wave interference with itself, and it can behave as a particle with definite and finite measurable position or momentum, though not both at the same time. The photon's wave and quantum qualities are two observable aspects of a single phenomenon – they cannot be described by any mechanical model; a representation of this dual property of light that assumes certain points on the wavefront to be the seat of the energy is not possible. The quanta in a light wave are not spatially localized.

The modern concept of the photon was developed gradually by Albert Einstein in the early 20th century to explain experimental observations that did not fit the classical wave model of light. The benefit of the photon model was that it accounted for the frequency dependence of light's energy, and explained the ability of matter and electromagnetic radiation to be in thermal equilibrium. The photon model accounted for anomalous observations, including the properties of black-body radiation, that others (notably Max Planck) had tried to explain using semiclassical models. In that model, light was described by Maxwell's equations, but material objects emitted and absorbed light in quantized amounts (i.e., they change energy only by certain particular discrete amounts). Although these semiclassical models contributed to the development of quantum mechanics, many further experiments beginning with the phenomenon of Compton scattering of single photons by electrons, validated Einstein's hypothesis that light itself is quantized. In 1926 the optical physicist Frithiof Wolfers and the chemist Gilbert N. Lewis coined the name "photon" for these particles. After Arthur H. Compton won the Nobel Prize in 1927 for his scattering studies, most scientists accepted that light quanta have an independent existence, and the term "photon" was accepted.

In the Standard Model of particle physics, photons and other elementary particles are described as a necessary consequence of physical laws having a certain symmetry at every point in spacetime. The intrinsic properties of particles, such as charge, mass, and spin, are determined by this gauge symmetry. The photon concept has led to momentous advances in experimental and theoretical physics, including lasers, Bose–Einstein condensation, quantum field theory, and the probabilistic interpretation of quantum mechanics. It has been applied to photochemistry, high-resolution microscopy, and measurements of molecular distances. Recently, photons have been studied as elements of quantum computers, and for applications in optical imaging and optical communication such as quantum cryptography.

Nomenclature

The word quanta (singular quantum, Latin for how much) was used before 1900 to mean particles or amounts of different quantities, including electricity. In 1900, the German physicist Max Planck was studying black-body radiation: he suggested that the experimental observations would be explained if the energy carried by electromagnetic waves could only be released in "packets" of energy. In his 1901 article  in Annalen der Physik he called these packets "energy elements". In 1905, Albert Einstein published a paper in which he proposed that many light-related phenomena—including black-body radiation and the photoelectric effect—would be better explained by modelling electromagnetic waves as consisting of spatially localized, discrete wave-packets. He called such a wave-packet the light quantum (German: das Lichtquant). The name photon derives from the Greek word for light, φῶς (transliterated phôs). Arthur Compton used photon in 1928, referring to Gilbert N. Lewis. The same name was used earlier, by the American physicist and psychologist Leonard T. Troland, who coined the word in 1916, in 1921 by the Irish physicist John Joly, in 1924 by the French physiologist René Wurmser (1890–1993) and in 1926 by the French physicist Frithiof Wolfers (1891–1971). The name was suggested initially as a unit related to the illumination of the eye and the resulting sensation of light and was used later in a physiological context. Although Wolfers's and Lewis's theories were contradicted by many experiments and never accepted, the new name was adopted very soon by most physicists after Compton used it.

In physics, a photon is usually denoted by the symbol γ (the Greek letter gamma). This symbol for the photon probably derives from gamma rays, which were discovered in 1900 by Paul Villard, named by Ernest Rutherford in 1903, and shown to be a form of electromagnetic radiation in 1914 by Rutherford and Edward Andrade. In chemistry and optical engineering, photons are usually symbolized by hν, which is the photon energy, where h is Planck constant and the Greek letter ν (nu) is the photon's frequency. Much less commonly, the photon can be symbolized by hf, where its frequency is denoted by f.

Physical properties

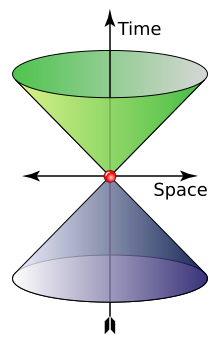
The cone shows possible values of wave 4-vector of a photon. The "time" axis gives the angular frequency (rad⋅s⁻¹) and the "space" axis represents the angular wavenumber (rad⋅m⁻¹). Green and indigo represent left and right polarization

A photon is massless, has no electric charge, and is a stable particle. A photon has two possible polarization states. In the momentum representation of the photon, which is preferred in quantum field theory, a photon is described by its wave vector, which determines its wavelength λ and its direction of propagation. A photon's wave vector may not be zero and can be represented either as a spatial 3-vector or as a (relativistic) four-vector; in the latter case it belongs to the light cone (pictured). Different signs of the four-vector denote different circular polarizations, but in the 3-vector representation one should account for the polarization state separately; it actually is a spin quantum number. In both cases the space of possible wave vectors is three-dimensional.

The photon is the gauge boson for electromagnetism, and therefore all other quantum numbers of the photon (such as lepton number, baryon number, and flavour quantum numbers) are zero. Also, the photon does not obey the Pauli exclusion principle.


Photons are emitted in many natural processes. For example, when a charge is accelerated it emits synchrotron radiation. During a molecular, atomic or nuclear transition to a lower energy level, photons of various energy will be emitted, ranging from radio waves to gamma rays. Photons can also be emitted when a particle and its corresponding antiparticle are annihilated (for example, electron–positron annihilation).

In empty space, the photon moves at c (the speed of light) and its energy and momentum are related by E = pc, where p is the magnitude of the momentum vector p. This derives from the following relativistic relation, with m = 0:

${\displaystyle E^{2}=p^{2}c^{2}+m^{2}c^{4}.}$

The energy and momentum of a photon depend only on its frequency (ν) or inversely, its wavelength (λ):

${\displaystyle E=\hbar \omega =h\nu ={\frac {hc}{\lambda }}}$

${\displaystyle {\boldsymbol {p}}=\hbar {\boldsymbol {k}},}$

where k is the wave vector (where the wave number k = |k| = 2π/λ), ω = 2πν is the angular frequency, and ħ = h/2π is the reduced Planck constant.

Since p points in the direction of the photon's propagation, the magnitude of the momentum is

${\displaystyle p=\hbar k={\frac {h\nu }{c}}={\frac {h}{\lambda }}.}$

The photon also carries a quantity called spin angular momentum that does not depend on its frequency. The magnitude of its spin is √2ħ and the component measured along its direction of motion, its helicity, must be ±ħ. These two possible helicities, called right-handed and left-handed, correspond to the two possible circular polarization states of the photon.

To illustrate the significance of these formulae, the annihilation of a particle with its antiparticle in free space must result in the creation of at least two photons for the following reason. In the center of momentum frame, the colliding antiparticles have no net momentum, whereas a single photon always has momentum (since, as we have seen, it is determined by the photon's frequency or wavelength, which cannot be zero). Hence, conservation of momentum (or equivalently, translational invariance) requires that at least two photons are created, with zero net momentum. (However, it is possible if the system interacts with another particle or field for the annihilation to produce one photon, as when a positron annihilates with a bound atomic electron, it is possible for only one photon to be emitted, as the nuclear Coulomb field breaks translational symmetry.) The energy of the two photons, or, equivalently, their frequency, may be determined from conservation of four-momentum. Seen another way, the photon can be considered as its own antiparticle. The reverse process, pair production, is the dominant mechanism by which high-energy photons such as gamma rays lose energy while passing through matter. That process is the reverse of "annihilation to one photon" allowed in the electric field of an atomic nucleus.

The classical formulae for the energy and momentum of electromagnetic radiation can be re-expressed in terms of photon events. For example, the pressure of electromagnetic radiation on an object derives from the transfer of photon momentum per unit time and unit area to that object, since pressure is force per unit area and force is the change in momentum per unit time.

Each photon carries two distinct and independent forms of angular momentum of light. The spin angular momentum of light of a particular photon is always either +ħ or −ħ. The light orbital angular momentum of a particular photon can be any integer N, including zero.

Experimental checks on photon mass

Current commonly accepted physical theories imply or assume the photon to be strictly massless. If the photon is not a strictly massless particle, it would not move at the exact speed of light, c, in vacuum. Its speed would be lower and depend on its frequency. Relativity would be unaffected by this; the so-called speed of light, c, would then not be the actual speed at which light moves, but a constant of nature which is the upper bound on speed that any object could theoretically attain in spacetime. Thus, it would still be the speed of spacetime ripples (gravitational waves and gravitons), but it would not be the speed of photons.

If a photon did have non-zero mass, there would be other effects as well. Coulomb's law would be modified and the electromagnetic field would have an extra physical degree of freedom. These effects yield more sensitive experimental probes of the photon mass than the frequency dependence of the speed of light. If Coulomb's law is not exactly valid, then that would allow the presence of an electric field to exist within a hollow conductor when it is subjected to an external electric field. This thus allows one to test Coulomb's law to very high precision. A null result of such an experiment has set a limit of m ≲ 10⁻¹⁴ eV/c².

Sharper upper limits on the speed of light have been obtained in experiments designed to detect effects caused by the galactic vector potential. Although the galactic vector potential is very large because the galactic magnetic field exists on very great length scales, only the magnetic field would be observable if the photon is massless. In the case that the photon has mass, the mass term 1/2m²A_μA^μ would affect the galactic plasma. The fact that no such effects are seen implies an upper bound on the photon mass of m < 3×10⁻²⁷ eV/c². The galactic vector potential can also be probed directly by measuring the torque exerted on a magnetized ring. Such methods were used to obtain the sharper upper limit of 10⁻¹⁸ eV/c² (the equivalent of 1.07×10⁻²⁷ atomic mass units) given by the Particle Data Group.

These sharp limits from the non-observation of the effects caused by the galactic vector potential have been shown to be model-dependent. If the photon mass is generated via the Higgs mechanism then the upper limit of m ≲ 10⁻¹⁴ eV/c² from the test of Coulomb's law is valid.

Photons inside superconductors do develop a nonzero effective rest mass; as a result, electromagnetic forces become short-range inside superconductors.

Historical development

Thomas Young's double-slit experiment in 1801 showed that light can act as a wave, helping to invalidate early particle theories of light.

In most theories up to the eighteenth century, light was pictured as being made up of particles. Since particle models cannot easily account for the refraction, diffraction and birefringence of light, wave theories of light were proposed by René Descartes (1637), Robert Hooke (1665), and Christiaan Huygens (1678); however, particle models remained dominant, chiefly due to the influence of Isaac Newton. In the early nineteenth century, Thomas Young and August Fresnel clearly demonstrated the interference and diffraction of light and by 1850 wave models were generally accepted. In 1865, James Clerk Maxwell's prediction that light was an electromagnetic wave—which was confirmed experimentally in 1888 by Heinrich Hertz's detection of radio waves—seemed to be the final blow to particle models of light.

In 1900, Maxwell's theoretical model of light as oscillating electric and magnetic fields seemed complete. However, several observations could not be explained by any wave model of electromagnetic radiation, leading to the idea that light-energy was packaged into quanta described by E=hν. Later experiments showed that these light-quanta also carry momentum and, thus, can be considered particles: the photon concept was born, leading to a deeper understanding of the electric and magnetic fields themselves.

The Maxwell wave theory, however, does not account for all properties of light. The Maxwell theory predicts that the energy of a light wave depends only on its intensity, not on its frequency; nevertheless, several independent types of experiments show that the energy imparted by light to atoms depends only on the light's frequency, not on its intensity. For example, some chemical reactions are provoked only by light of frequency higher than a certain threshold; light of frequency lower than the threshold, no matter how intense, does not initiate the reaction. Similarly, electrons can be ejected from a metal plate by shining light of sufficiently high frequency on it (the photoelectric effect); the energy of the ejected electron is related only to the light's frequency, not to its intensity.

At the same time, investigations of blackbody radiation carried out over four decades (1860–1900) by various researchers culminated in Max Planck's hypothesis that the energy of any system that absorbs or emits electromagnetic radiation of frequency ν is an integer multiple of an energy quantum E = hν. As shown by Albert Einstein, some form of energy quantization must be assumed to account for the thermal equilibrium observed between matter and electromagnetic radiation; for this explanation of the photoelectric effect, Einstein received the 1921 Nobel Prize in physics.

Since the Maxwell theory of light allows for all possible energies of electromagnetic radiation, most physicists assumed initially that the energy quantization resulted from some unknown constraint on the matter that absorbs or emits the radiation. In 1905, Einstein was the first to propose that energy quantization was a property of electromagnetic radiation itself. Although he accepted the validity of Maxwell's theory, Einstein pointed out that many anomalous experiments could be explained if the energy of a Maxwellian light wave were localized into point-like quanta that move independently of one another, even if the wave itself is spread continuously over space. In 1909 and 1916, Einstein showed that, if Planck's law of black-body radiation is accepted, the energy quanta must also carry momentum p = h/λ, making them full-fledged particles. This photon momentum was observed experimentally by Arthur Compton, for which he received the Nobel Prize in 1927. The pivotal question was then: how to unify Maxwell's wave theory of light with its experimentally observed particle nature? The answer to this question occupied Albert Einstein for the rest of his life, and was solved in quantum electrodynamics and its successor, the Standard Model.

Einstein's light quantum

Unlike Planck, Einstein entertained the possibility that there might be actual physical quanta of light—what we now call photons. He noticed that a light quantum with energy proportional to its frequency would explain a number of troubling puzzles and paradoxes, including an unpublished law by Stokes, the ultraviolet catastrophe, and the photoelectric effect. Stokes's law said simply that the frequency of fluorescent light cannot be greater than the frequency of the light (usually ultraviolet) inducing it. Einstein eliminated the ultraviolet catastrophe by imagining a gas of photons behaving like a gas of electrons that he had previously considered. He was advised by a colleague to be careful how he wrote up this paper, in order to not challenge Planck, a powerful figure in physics, too directly, and indeed the warning was justified, as Planck never forgave him for writing it.

Early objections

Up to 1923, most physicists were reluctant to accept that light itself was quantized. Instead, they tried to explain photon behavior by quantizing only matter, as in the Bohr model of the hydrogen atom (shown here). Even though these semiclassical models were only a first approximation, they were accurate for simple systems and they led to quantum mechanics.

Einstein's 1905 predictions were verified experimentally in several ways in the first two decades of the 20th century, as recounted in Robert Millikan's Nobel lecture. However, before Compton's experiment showed that photons carried momentum proportional to their wave number (1922), most physicists were reluctant to believe that electromagnetic radiation itself might be particulate. (See, for example, the Nobel lectures of Wien, Planck and Millikan.) Instead, there was a widespread belief that energy quantization resulted from some unknown constraint on the matter that absorbed or emitted radiation. Attitudes changed over time. In part, the change can be traced to experiments such as Compton scattering, where it was much more difficult not to ascribe quantization to light itself to explain the observed results.

Even after Compton's experiment, Niels Bohr, Hendrik Kramers and John Slater made one last attempt to preserve the Maxwellian continuous electromagnetic field model of light, the so-called BKS model. To account for the data then available, two drastic hypotheses had to be made:

1. Energy and momentum are conserved only on the average in interactions between matter and radiation, but not in elementary processes such as absorption and emission. This allows one to reconcile the discontinuously changing energy of the atom (the jump between energy states) with the continuous release of energy as radiation.
   
2. Causality is abandoned. For example, spontaneous emissions are merely emissions stimulated by a "virtual" electromagnetic field.

However, refined Compton experiments showed that energy–momentum is conserved extraordinarily well in elementary processes; and also that the jolting of the electron and the generation of a new photon in Compton scattering obey causality to within 10 ps. Accordingly, Bohr and his co-workers gave their model "as honorable a funeral as possible". Nevertheless, the failures of the BKS model inspired Werner Heisenberg in his development of matrix mechanics.

A few physicists persisted in developing semiclassical models in which electromagnetic radiation is not quantized, but matter appears to obey the laws of quantum mechanics. Although the evidence from chemical and physical experiments for the existence of photons was overwhelming by the 1970s, this evidence could not be considered as absolutely definitive; since it relied on the interaction of light with matter, and a sufficiently complete theory of matter could in principle account for the evidence. Nevertheless, all semiclassical theories were refuted definitively in the 1970s and 1980s by photon-correlation experiments. Hence, Einstein's hypothesis that quantization is a property of light itself is considered to be proven.

Wave–particle duality and uncertainty principles

Photons in a Mach–Zehnder interferometer exhibit wave-like interference and particle-like detection at single-photon detectors.

Photons, like all quantum objects, exhibit wave-like and particle-like properties. Their dual wave–particle nature can be difficult to visualize. The photon displays clearly wave-like phenomena such as diffraction and interference on the length scale of its wavelength. For example, a single photon passing through a double-slit experiment exhibits interference phenomena but only if no measure was made at the slit. A single photon passing through a double-slit experiment lands on the screen with a probability distribution given by its interference pattern determined by Maxwell's equations. However, experiments confirm that the photon is not a short pulse of electromagnetic radiation; it does not spread out as it propagates, nor does it divide when it encounters a beam splitter. Rather, the photon seems to be a point-like particle since it is absorbed or emitted as a whole by arbitrarily small systems, systems much smaller than its wavelength, such as an atomic nucleus (≈10⁻¹⁵ m across) or even the point-like electron. Nevertheless, the photon is not a point-like particle whose trajectory is shaped probabilistically by the electromagnetic field, as conceived by Einstein and others; that hypothesis was also refuted by the photon-correlation experiments cited above. According to our present understanding, the electromagnetic field itself is produced by photons, which in turn result from a local gauge symmetry and the laws of quantum field theory.

Heisenberg's thought experiment for locating an electron (shown in blue) with a high-resolution gamma-ray microscope. The incoming gamma ray (shown in green) is scattered by the electron up into the microscope's aperture angle θ. The scattered gamma ray is shown in red. Classical optics shows that the electron position can be resolved only up to an uncertainty Δx that depends on θ and the wavelength λ of the incoming light.

A key element of quantum mechanics is Heisenberg's uncertainty principle, which forbids the simultaneous measurement of the position and momentum of a particle along the same direction. Remarkably, the uncertainty principle for charged, material particles requires the quantization of light into photons, and even the frequency dependence of the photon's energy and momentum.

An elegant illustration of the uncertainty principle is Heisenberg's thought experiment for locating an electron with an ideal microscope. The position of the electron can be determined to within the resolving power of the microscope, which is given by a formula from classical optics

${\displaystyle \Delta x\sim {\frac {\lambda }{\sin \theta }}}$

where θ is the aperture angle of the microscope and λ is the wavelength of the light used to observe the electron. Thus, the position uncertainty ${\displaystyle \Delta x}$ can be made arbitrarily small by reducing the wavelength λ. Even if the momentum of the electron is initially known, the light impinging on the electron will give it a momentum "kick" ${\displaystyle \Delta p}$ of some unknown amount, rendering the momentum of the electron uncertain. If light were not quantized into photons, the uncertainty ${\displaystyle \Delta p}$ could be made arbitrarily small by reducing the light's intensity. In that case, since the wavelength and intensity of light can be varied independently, one could simultaneously determine the position and momentum to arbitrarily high accuracy, violating the uncertainty principle. By contrast, Einstein's formula for photon momentum preserves the uncertainty principle; since the photon is scattered anywhere within the aperture, the uncertainty of momentum transferred equals

${\displaystyle \Delta p\sim p_{\text{photon}}\sin \theta ={\frac {h}{\lambda }}\sin \theta }$

giving the product ${\displaystyle \Delta x\Delta p\,\sim \,h}$, which is Heisenberg's uncertainty principle. Thus, the entire world is quantized; both matter and fields must obey a consistent set of quantum laws, if either one is to be quantized.

The analogous uncertainty principle for photons forbids the simultaneous measurement of the number ${\displaystyle n}$ of photons (see Fock state and the Second quantization section below) in an electromagnetic wave and the phase ${\displaystyle \phi }$ of that wave

${\displaystyle \Delta n\Delta \phi >1}$

Both photons and electrons create analogous interference patterns when passed through a double-slit experiment. For photons, this corresponds to the interference of a Maxwell light wave whereas, for material particles (electron), this corresponds to the interference of the Schrödinger wave equation. Although this similarity might suggest that Maxwell's equations describing the photon's electromagnetic wave are simply Schrödinger's equation for photons, most physicists do not agree. For one thing, they are mathematically different; most obviously, Schrödinger's one equation for the electron solves for a complex field, whereas Maxwell's four equations solve for real fields. More generally, the normal concept of a Schrödinger probability wave function cannot be applied to photons. As photons are massless, they cannot be localized without being destroyed; technically, photons cannot have a position eigenstate ${\displaystyle |\mathbf {r} \rangle }$, and, thus, the normal Heisenberg uncertainty principle ${\displaystyle \Delta x\Delta p>h/2}$ does not pertain to photons. A few substitute wave functions have been suggested for the photon, but they have not come into general use. Instead, physicists generally accept the second-quantized theory of photons described below, quantum electrodynamics, in which photons are quantized excitations of electromagnetic modes.

Another interpretation, that avoids duality, is the De Broglie–Bohm theory: known also as the pilot-wave model. In that theory, the photon is both, wave and particle. "This idea seems to me so natural and simple, to resolve the wave-particle dilemma in such a clear and ordinary way, that it is a great mystery to me that it was so generally ignored", J.S.Bell.

Bose–Einstein model of a photon gas

In 1924, Satyendra Nath Bose derived Planck's law of black-body radiation without using any electromagnetism, but rather by using a modification of coarse-grained counting of phase space. Einstein showed that this modification is equivalent to assuming that photons are rigorously identical and that it implied a "mysterious non-local interaction", now understood as the requirement for a symmetric quantum mechanical state. This work led to the concept of coherent states and the development of the laser. In the same papers, Einstein extended Bose's formalism to material particles (bosons) and predicted that they would condense into their lowest quantum state at low enough temperatures; this Bose–Einstein condensation was observed experimentally in 1995. It was later used by Lene Hau to slow, and then completely stop, light in 1999 and 2001.

The modern view on this is that photons are, by virtue of their integer spin, bosons (as opposed to fermions with half-integer spin). By the spin-statistics theorem, all bosons obey Bose–Einstein statistics (whereas all fermions obey Fermi–Dirac statistics).

Stimulated and spontaneous emission

Stimulated emission (in which photons "clone" themselves) was predicted by Einstein in his kinetic analysis, and led to the development of the laser. Einstein's derivation inspired further developments in the quantum treatment of light, which led to the statistical interpretation of quantum mechanics.

In 1916, Albert Einstein showed that Planck's radiation law could be derived from a semi-classical, statistical treatment of photons and atoms, which implies a link between the rates at which atoms emit and absorb photons. The condition follows from the assumption that functions of the emission and absorption of radiation by the atoms are independent of each other, and that thermal equilibrium is made by way of the radiation's interaction with the atoms. Consider a cavity in thermal equilibrium with all parts of itself and filled with electromagnetic radiation and that the atoms can emit and absorb that radiation. Thermal equilibrium requires that the energy density ${\displaystyle \rho (\nu )}$ of photons with frequency ${\displaystyle \nu }$ (which is proportional to their number density) is, on average, constant in time; hence, the rate at which photons of any particular frequency are emitted must equal the rate at which they absorb them.

Einstein began by postulating simple proportionality relations for the different reaction rates involved. In his model, the rate ${\displaystyle R_{ji}}$ for a system to absorb a photon of frequency ${\displaystyle \nu }$ and transition from a lower energy ${\displaystyle E_{j}}$ to a higher energy ${\displaystyle E_{i}}$ is proportional to the number ${\displaystyle N_{j}}$ of atoms with energy ${\displaystyle E_{j}}$ and to the energy density ${\displaystyle \rho (\nu )}$ of ambient photons of that frequency,

${\displaystyle R_{ji}=N_{j}B_{ji}\rho (\nu )\!}$

where ${\displaystyle B_{ji}}$ is the rate constant for absorption. For the reverse process, there are two possibilities: spontaneous emission of a photon, or the emission of a photon initiated by the interaction of the atom with a passing photon and the return of the atom to the lower-energy state. Following Einstein's approach, the corresponding rate ${\displaystyle R_{ij}}$ for the emission of photons of frequency ${\displaystyle \nu }$ and transition from a higher energy ${\displaystyle E_{i}}$ to a lower energy ${\displaystyle E_{j}}$ is

${\displaystyle R_{ij}=N_{i}A_{ij}+N_{i}B_{ij}\rho (\nu )\!}$

where ${\displaystyle A_{ij}}$ is the rate constant for emitting a photon spontaneously, and ${\displaystyle B_{ij}}$ is the rate constant for emissions in response to ambient photons (induced or stimulated emission). In thermodynamic equilibrium, the number of atoms in state i and those in state j must, on average, be constant; hence, the rates ${\displaystyle R_{ji}}$ and ${\displaystyle R_{ij}}$ must be equal. Also, by arguments analogous to the derivation of Boltzmann statistics, the ratio of ${\displaystyle N_{i}}$ and ${\displaystyle N_{j}}$ is ${\displaystyle g_{i}/g_{j}\exp {(E_{j}-E_{i})/(kT)},}$ where ${\displaystyle g_{i,j}}$ are the degeneracy of the state i and that of j, respectively, ${\displaystyle E_{i,j}}$ their energies, k the Boltzmann constant and T the system's temperature. From this, it is readily derived that ${\displaystyle g_{i}B_{ij}=g_{j}B_{ji}}$ and

${\displaystyle A_{ij}={\frac {8\pi h\nu ^{3}}{c^{3}}}B_{ij}.}$

The A and Bs are collectively known as the Einstein coefficients.

Einstein could not fully justify his rate equations, but claimed that it should be possible to calculate the coefficients ${\displaystyle A_{ij}}$, ${\displaystyle B_{ji}}$ and ${\displaystyle B_{ij}}$ once physicists had obtained "mechanics and electrodynamics modified to accommodate the quantum hypothesis". In fact, in 1926, Paul Dirac derived the ${\displaystyle B_{ij}}$ rate constants by using a semiclassical approach, and, in 1927, succeeded in deriving all the rate constants from first principles within the framework of quantum theory. Dirac's work was the foundation of quantum electrodynamics, i.e., the quantization of the electromagnetic field itself. Dirac's approach is also called second quantization or quantum field theory; earlier quantum mechanical treatments only treat material particles as quantum mechanical, not the electromagnetic field.

Einstein was troubled by the fact that his theory seemed incomplete, since it did not determine the direction of a spontaneously emitted photon. A probabilistic nature of light-particle motion was first considered by Newton in his treatment of birefringence and, more generally, of the splitting of light beams at interfaces into a transmitted beam and a reflected beam. Newton hypothesized that hidden variables in the light particle determined which of the two paths a single photon would take. Similarly, Einstein hoped for a more complete theory that would leave nothing to chance, beginning his separation from quantum mechanics. Ironically, Max Born's probabilistic interpretation of the wave function was inspired by Einstein's later work searching for a more complete theory.

Second quantization and high energy photon interactions

Different electromagnetic modes (such as those depicted here) can be treated as independent simple harmonic oscillators. A photon corresponds to a unit of energy E=hν in its electromagnetic mode.

In 1910, Peter Debye derived Planck's law of black-body radiation from a relatively simple assumption. He correctly decomposed the electromagnetic field in a cavity into its Fourier modes, and assumed that the energy in any mode was an integer multiple of ${\displaystyle h\nu }$, where ${\displaystyle \nu }$ is the frequency of the electromagnetic mode. Planck's law of black-body radiation follows immediately as a geometric sum. However, Debye's approach failed to give the correct formula for the energy fluctuations of blackbody radiation, which were derived by Einstein in 1909.

In 1925, Born, Heisenberg and Jordan reinterpreted Debye's concept in a key way. As may be shown classically, the Fourier modes of the electromagnetic field—a complete set of electromagnetic plane waves indexed by their wave vector k and polarization state—are equivalent to a set of uncoupled simple harmonic oscillators. Treated quantum mechanically, the energy levels of such oscillators are known to be ${\displaystyle E=nh\nu }$, where ${\displaystyle \nu }$ is the oscillator frequency. The key new step was to identify an electromagnetic mode with energy ${\displaystyle E=nh\nu }$ as a state with ${\displaystyle n}$ photons, each of energy ${\displaystyle h\nu }$. This approach gives the correct energy fluctuation formula.

In quantum field theory, the probability of an event is computed by summing the probability amplitude (a complex number) for all possible ways in which the event can occur, as in the Feynman diagram shown here; the probability equals the square of the modulus of the total amplitude.

Dirac took this one step further. He treated the interaction between a charge and an electromagnetic field as a small perturbation that induces transitions in the photon states, changing the numbers of photons in the modes, while conserving energy and momentum overall. Dirac was able to derive Einstein's ${\displaystyle A_{ij}}$ and ${\displaystyle B_{ij}}$ coefficients from first principles, and showed that the Bose–Einstein statistics of photons is a natural consequence of quantizing the electromagnetic field correctly (Bose's reasoning went in the opposite direction; he derived Planck's law of black-body radiation by assuming B–E statistics). In Dirac's time, it was not yet known that all bosons, including photons, must obey Bose–Einstein statistics.

Dirac's second-order perturbation theory can involve virtual photons, transient intermediate states of the electromagnetic field; the static electric and magnetic interactions are mediated by such virtual photons. In such quantum field theories, the probability amplitude of observable events is calculated by summing over all possible intermediate steps, even ones that are unphysical; hence, virtual photons are not constrained to satisfy ${\displaystyle E=pc}$, and may have extra polarization states; depending on the gauge used, virtual photons may have three or four polarization states, instead of the two states of real photons. Although these transient virtual photons can never be observed, they contribute measurably to the probabilities of observable events. Indeed, such second-order and higher-order perturbation calculations can give apparently infinite contributions to the sum. Such unphysical results are corrected for using the technique of renormalization.

Other virtual particles may contribute to the summation as well; for example, two photons may interact indirectly through virtual electron–positron pairs. In fact, such photon–photon scattering (see two-photon physics), as well as electron–photon scattering, is meant to be one of the modes of operations of the planned particle accelerator, the International Linear Collider.

In modern physics notation, the quantum state of the electromagnetic field is written as a Fock state, a tensor product of the states for each electromagnetic mode

${\displaystyle |n_{k_{0}}\rangle \otimes |n_{k_{1}}\rangle \otimes \dots \otimes |n_{k_{n}}\rangle \dots }$

where ${\displaystyle |n_{k_{i}}\rangle }$ represents the state in which ${\displaystyle \,n_{k_{i}}}$ photons are in the mode ${\displaystyle k_{i}}$. In this notation, the creation of a new photon in mode ${\displaystyle k_{i}}$ (e.g., emitted from an atomic transition) is written as ${\displaystyle |n_{k_{i}}\rangle \rightarrow |n_{k_{i}}+1\rangle }$. This notation merely expresses the concept of Born, Heisenberg and Jordan described above, and does not add any physics.

The hadronic properties of the photon

Measurements of the interaction between energetic photons and hadrons show that the interaction is much more intense than expected by the interaction of merely photons with the hadron's electric charge. Furthermore, the interaction of energetic photons with protons is similar to the interaction of photons with neutrons in spite of the fact that the electric charge structures of protons and neutrons are substantially different. A theory called Vector Meson Dominance (VMD) was developed to explain this effect. According to VMD, the photon is a superposition of the pure electromagnetic photon which interacts only with electric charges and vector mesons. However, if experimentally probed at very short distances, the intrinsic structure of the photon is recognized as a flux of quark and gluon components, quasi-free according to asymptotic freedom in QCD and described by the photon structure function. A comprehensive comparison of data with theoretical predictions was presented in a review in 2000.

The photon as a gauge boson

The electromagnetic field can be understood as a gauge field, i.e., as a field that results from requiring that a gauge symmetry holds independently at every position in spacetime. For the electromagnetic field, this gauge symmetry is the Abelian U(1) symmetry of complex numbers of absolute value 1, which reflects the ability to vary the phase of a complex field without affecting observables or real valued functions made from it, such as the energy or the Lagrangian.

The quanta of an Abelian gauge field must be massless, uncharged bosons, as long as the symmetry is not broken; hence, the photon is predicted to be massless, and to have zero electric charge and integer spin. The particular form of the electromagnetic interaction specifies that the photon must have spin ±1; thus, its helicity must be ${\displaystyle \pm \hbar }$. These two spin components correspond to the classical concepts of right-handed and left-handed circularly polarized light. However, the transient virtual photons of quantum electrodynamics may also adopt unphysical polarization states.

In the prevailing Standard Model of physics, the photon is one of four gauge bosons in the electroweak interaction; the other three are denoted W⁺, W⁻ and Z⁰ and are responsible for the weak interaction. Unlike the photon, these gauge bosons have mass, owing to a mechanism that breaks their SU(2) gauge symmetry. The unification of the photon with W and Z gauge bosons in the electroweak interaction was accomplished by Sheldon Glashow, Abdus Salam and Steven Weinberg, for which they were awarded the 1979 Nobel Prize in physics. Physicists continue to hypothesize grand unified theories that connect these four gauge bosons with the eight gluon gauge bosons of quantum chromodynamics; however, key predictions of these theories, such as proton decay, have not been observed experimentally.

Contributions to the mass of a system

The energy of a system that emits a photon is decreased by the energy ${\displaystyle E}$ of the photon as measured in the rest frame of the emitting system, which may result in a reduction in mass in the amount ${\displaystyle {E}/{c^{2}}}$. Similarly, the mass of a system that absorbs a photon is increased by a corresponding amount. As an application, the energy balance of nuclear reactions involving photons is commonly written in terms of the masses of the nuclei involved, and terms of the form ${\displaystyle {E}/{c^{2}}}$ for the gamma photons (and for other relevant energies, such as the recoil energy of nuclei).

This concept is applied in key predictions of quantum electrodynamics (QED, see above). In that theory, the mass of electrons (or, more generally, leptons) is modified by including the mass contributions of virtual photons, in a technique known as renormalization. Such "radiative corrections" contribute to a number of predictions of QED, such as the magnetic dipole moment of leptons, the Lamb shift, and the hyperfine structure of bound lepton pairs, such as muonium and positronium.

Since photons contribute to the stress–energy tensor, they exert a gravitational attraction on other objects, according to the theory of general relativity. Conversely, photons are themselves affected by gravity; their normally straight trajectories may be bent by warped spacetime, as in gravitational lensing, and their frequencies may be lowered by moving to a higher gravitational potential, as in the Pound–Rebka experiment. However, these effects are not specific to photons; exactly the same effects would be predicted for classical electromagnetic waves.

Photons in matter

Light that travels through transparent matter does so at a lower speed than c, the speed of light in a vacuum. For example, photons engage in so many collisions on the way from the core of the sun that radiant energy can take about a million years to reach the surface; however, once in open space, a photon takes only 8.3 minutes to reach Earth. The factor by which the speed is decreased is called the refractive index of the material. In a classical wave picture, the slowing can be explained by the light inducing electric polarization in the matter, the polarized matter radiating new light, and that new light interfering with the original light wave to form a delayed wave. In a particle picture, the slowing can instead be described as a blending of the photon with quantum excitations of the matter to produce quasi-particles known as polariton (other quasi-particles are phonons and excitons); this polariton has a nonzero effective mass, which means that it cannot travel at c. Light of different frequencies may travel through matter at different speeds; this is called dispersion (not to be confused with scattering). In some cases, it can result in extremely slow speeds of light in matter. The effects of photon interactions with other quasi-particles may be observed directly in Raman scattering and Brillouin scattering.

Photons can also be absorbed by nuclei, atoms or molecules, provoking transitions between their energy levels. A classic example is the molecular transition of retinal (C₂₀H₂₈O), which is responsible for vision, as discovered in 1958 by Nobel laureate biochemist George Wald and co-workers. The absorption provokes a cis-trans isomerization that, in combination with other such transitions, is transduced into nerve impulses. The absorption of photons can even break chemical bonds, as in the photodissociation of chlorine; this is the subject of photochemistry.

Technological applications

Photons have many applications in technology. These examples are chosen to illustrate applications of photons per se, rather than general optical devices such as lenses, etc. that could operate under a classical theory of light. The laser is an extremely important application and is discussed above under stimulated emission.

Individual photons can be detected by several methods. The classic photomultiplier tube exploits the photoelectric effect: a photon of sufficient energy strikes a metal plate and knocks free an electron, initiating an ever-amplifying avalanche of electrons. Semiconductor charge-coupled device chips use a similar effect: an incident photon generates a charge on a microscopic capacitor that can be detected. Other detectors such as Geiger counters use the ability of photons to ionize gas molecules contained in the device, causing a detectable change of conductivity of the gas.

Planck's energy formula ${\displaystyle E=h\nu }$ is often used by engineers and chemists in design, both to compute the change in energy resulting from a photon absorption and to determine the frequency of the light emitted from a given photon emission. For example, the emission spectrum of a gas-discharge lamp can be altered by filling it with (mixtures of) gases with different electronic energy level configurations.

Under some conditions, an energy transition can be excited by "two" photons that individually would be insufficient. This allows for higher resolution microscopy, because the sample absorbs energy only in the spectrum where two beams of different colors overlap significantly, which can be made much smaller than the excitation volume of a single beam (see two-photon excitation microscopy). Moreover, these photons cause less damage to the sample, since they are of lower energy.

In some cases, two energy transitions can be coupled so that, as one system absorbs a photon, another nearby system "steals" its energy and re-emits a photon of a different frequency. This is the basis of fluorescence resonance energy transfer, a technique that is used in molecular biology to study the interaction of suitable proteins.

Several different kinds of hardware random number generators involve the detection of single photons. In one example, for each bit in the random sequence that is to be produced, a photon is sent to a beam-splitter. In such a situation, there are two possible outcomes of equal probability. The actual outcome is used to determine whether the next bit in the sequence is "0" or "1".

Recent research

Much research has been devoted to applications of photons in the field of quantum optics. Photons seem well-suited to be elements of an extremely fast quantum computer, and the quantum entanglement of photons is a focus of research. Nonlinear optical processes are another active research area, with topics such as two-photon absorption, self-phase modulation, modulational instability and optical parametric oscillators. However, such processes generally do not require the assumption of photons per se; they may often be modeled by treating atoms as nonlinear oscillators. The nonlinear process of spontaneous parametric down conversion is often used to produce single-photon states. Finally, photons are essential in some aspects of optical communication, especially for quantum cryptography.

Two-photon physics studies interactions between photons, which are rare. In 2018, MIT researchers announced the discovery of bound photon triplets, which may involve polaritons.

Science of photography

From Wikipedia, the free encyclopedia

The science of photography refers to the use of science, such as chemistry and physics, in all aspects of photography. This applies to the camera, its lenses, physical operation of the camera, electronic camera internals, and the process of developing film in order to take and develop pictures properly.

Law of Reciprocity

Exposure ∝ Aperture Area × Exposure Time × Scene Luminance

The law of reciprocity describes how light intensity and duration trade off to make an exposure—it defines the relationship between shutter speed and aperture, for a given total exposure. Changes to any of these elements are often measured in units known as "stops"; a stop is equal to a factor of two.
Halving the amount light exposing the film can be achieved either by:

1. Closing the aperture by one stop
2. Decreasing the shutter time (increasing the shutter speed) by one stop
3. Cutting the scene lighting by half

Likewise, doubling the amount of light exposing the film can be achieved by the opposite of one of these operations.

The luminance of the scene, as measured on a reflected light meter, also affects the exposure proportionately. The amount of light required for proper exposure depends on the film speed; which can be varied in stops or fractions of stops. With either of these changes, the aperture or shutter speed can be adjusted by an equal number of stops to get to a suitable exposure.

Light is most easily controlled through the use of the camera's aperture (measure in f-stops), but it can also be regulated by adjusting the shutter speed. Using faster or slower film is not usually something that can be done quickly, at least using roll film. Large format cameras use individual sheets of film and each sheet could be a different speed. Also, if you're using a larger format camera with a polaroid back, you can switch between backs containing different speed polaroids. Digital cameras can easily adjust the film speed they are simulating by adjusting the exposure index, and many digital cameras can do so automatically in response to exposure measurements.

For example, starting with an exposure of 1/60 at f/16, the depth-of-field could be made shallower by opening up the aperture to f/4, an increase in exposure of 4 stops. To compensate, the shutter speed would need to be increased as well by 4 stops, that is, adjust exposure time down to 1/1000. Closing down the aperture limits the resolution due to the diffraction limit.

The reciprocity law specifies the total exposure, but the response of a photographic material to a constant total exposure may not remain constant for very long exposures in very faint light, such as photographing a starry sky, or very short exposures in very bright light, such as photographing the sun. This is known as reciprocity failure of the material (film, paper, or sensor).

Lenses

A photographic lens is usually composed of several lens elements, which combine to reduce the effects of chromatic aberration, coma, spherical aberration, and other aberrations. A simple example is the three-element Cooke triplet, still in use over a century after it was first designed, but many current photographic lenses are much more complex.

Using a smaller aperture can reduce most, but not all aberrations. They can also be reduced dramatically by using an aspheric element, but these are more complex to grind than spherical or cylindrical lenses. However, with modern manufacturing techniques the extra cost of manufacturing aspherical lenses is decreasing, and small aspherical lenses can now be made by molding, allowing their use in inexpensive consumer cameras. Fresnel lenses are not used in cameras even though they are extremely light and cheap, because they produce poor image quality. The recently developed Fiber-coupled monocentric lens consists of spheres constructed of concentric hemispherical shells of different glasses tied to the focal plane by bundles of optical fibers. Monocentric lenses are also not used in cameras because the technology was just debuted in October 2013 at the Frontiers in Optics Conference in Orlando, Florida.

All lens design is a compromise between numerous factors, not excluding cost. Zoom lenses (i.e. lenses of variable focal length) involve additional compromises and therefore normally do not match the performance of prime lenses.

When a camera lens is focused to project an object some distance away onto the film or detector, the objects that are closer in distance, relative to the distant object, are also approximately in focus. The range of distances that are nearly in focus is called the depth of field. Depth of field generally increases with decreasing aperture diameter (increasing f-number). The unfocused blur outside the depth of field is sometimes used for artistic effect in photography. The subjective appearance of this blur is known as bokeh.

If the camera lens is focused at or beyond its hyperfocal distance, then the depth of field becomes large, covering everything from half the hyperfocal distance to infinity. This effect is used to make "focus free" or fixed-focus cameras.

Motion blur

Motion blur is caused when either the camera or the subject moves during the exposure. This causes a distinctive streaky appearance to the moving object or the entire picture (in the case of camera shake).

Motion blur of background while following the subject

 

Motion blur can be used artistically to create the feeling of speed or motion, as with running water. An example of this is the technique of "panning", where the camera is moved so it follows the subject, which is usually fast moving, such as a car. Done correctly, this will give an image of a clear subject, but the background will have motion blur, giving the feeling of movement. This is one of the more difficult photographic techniques to master, as the movement must be smooth, and at the correct speed. A subject that gets closer or further away from the camera may further cause focusing difficulties.

Light trails

 

Light trails is another photographic effect where motion blur is used. Photographs of the lines of light visible in long exposure photos of roads at night are one example of effect. This is caused by the cars moving along the road during the exposure. The same principle is used to create star trail photographs.

Generally, motion blur is something that is to be avoided, and this can be done in several different ways. The simplest way is to limit the shutter time so that there is very little movement of the image during the time the shutter is open. At longer focal lengths, the same movement of the camera body will cause more motion of the image, so a shorter shutter time is needed. A commonly cited rule of thumb is that the shutter speed in seconds should be about the reciprocal of the 35 mm equivalent focal length of the lens in millimeters. For example, a 50 mm lens should be used at a minimum speed of 1/50 sec, and a 300 mm lens at 1/300 of a second. This can cause difficulties when used in low light scenarios, since exposure also decreases with shutter time.

High speed photography uses very short exposures to prevent blurring of fast moving subjects.

 

Motion blur due to subject movement can usually be prevented by using a faster shutter speed. The exact shutter speed will depend on the speed at which the subject is moving. For example, a very fast shutter speed will be needed to "freeze" the rotors of a helicopter, whereas a slower shutter speed will be sufficient to freeze a runner.

A tripod may be used to avoid motion blur due to camera shake. This will stabilize the camera during the exposure. A tripod is recommended for exposure times more than about 1/15 seconds. There are additional techniques which, in conjunction with use of a tripod, ensure that the camera remains very still. These may employ use of a remote actuator, such as a cable release or infrared remote switch to activate the shutter, so as to avoid the movement normally caused when the shutter release button is pressed directly. The use of a "self timer" (a timed release mechanism that automatically trips the shutter release after an interval of time) can serve the same purpose. Most modern single-lens reflex camera (SLR) have a mirror lock-up feature that eliminates the small amount of shake produced by the mirror flipping up.

Focus

This subject is in sharp focus while the distant background is unfocused.

 

Focus is the tendency for light rays to reach the same place on the image sensor or film, independent of where they pass through the lens. For clear pictures, the focus is adjusted for distance, because at a different object distance the rays reach different parts of the lens with different angles. In modern photography, focusing is often accomplished automatically.

The autofocus system in modern SLRs use a sensor in the mirrorbox to measure contrast. The sensor's signal is analyzed by an application-specific integrated circuit (ASIC), and the ASIC tries to maximize the contrast pattern by moving lens elements. The ASICs in modern cameras also have special algorithms for predicting motion, and other advanced features.

Aberration

Aberrations are the blurring and distorting properties of an optical system. A high quality lens will produce a smaller amount of aberrations.

Spherical aberration occurs due to the increased refraction of light rays that occurs when rays strike a lens, or a reflection of light rays that occurs when rays strike a mirror near its edge in comparison with those that strike nearer the center. This is dependent on the focal length of a spherical lens and the distance from its center. It is compensated by designing a multi-lens system or by using an aspheric lens.

Chromatic aberration is caused by a lens having a different refractive index for different wavelengths of light and the dependence of the optical properties on color. Blue light will generally bend more than red light. There are higher order chromatic aberrations, such as the dependence of magnification on color. Chromatic aberration is compensated by using a lens made out of materials carefully designed to cancel out chromatic aberrations.

Curved focal surface is the dependence of the first order focus on the position on the film or CCD. This can be compensated with a multiple lens optical design, but curving the film has also been used.

Film grain resolution

Strong grain on ISO1600 negative

 

Black-and-white film has a "shiny" side and a "dull" side. The dull side is the emulsion, a gelatin that suspends an array of silver halide crystals. These crystals contain silver grains that determine how sensitive the film is to light exposure, and how fine or grainy the negative the print will look. Larger grains mean faster exposure but a grainier appearance; smaller grains are finer looking but take more exposure to activate. The graininess of film is represented by its ISO factor; generally a multiple of 10 or 100. Lower numbers produce finer grain but slower film, and vice versa.

Diffraction limit

Since light propagates as waves, the patterns it produces on the film are subject to the wave phenomenon known as diffraction, which limits the image resolution to features on the order of several times the wavelength of light. Diffraction is the main effect limiting the sharpness of optical images from lenses that are stopped down to small apertures (high f-numbers), while aberrations are the limiting effect at large apertures (low f-numbers). Since diffraction cannot be eliminated, the best possible lens for a given operating condition (aperture setting) is one that produces an image whose quality is limited only by diffraction. Such a lens is said to be diffraction limited.

The diffraction-limited optical spot size on the CCD or film is proportional to the f-number (about equal to the f-number times the wavelength of light, which is near 0.0005 mm), making the overall detail in a photograph proportional to the size of the film, or CCD divided by the f-number. For a 35 mm camera with f/11, this limit corresponds to about 6,000 resolution elements across the width of the film (36 mm / (11 * 0.0005 mm) = 6,500.

The finite spot size caused by diffraction can also be expressed as a criterion for distinguishing distant objects: two distant point sources can only produce separate images on the film or sensor if their angular separation exceeds the wavelength of light divided by the width of the open aperture of the camera lens.

Contribution to noise (grain)

Quantum efficiency

Light comes in particles and the energy of a light-particle (the photon) is the frequency of the light times Planck's constant. A fundamental property of any photographic method is how it collects the light on its photographic plate or electronic detector.

CCDs and other photodiodes

Photodiodes are back-biased semiconductor diodes, in which an intrinsic layer with very few charge carriers prevents electric currents from flowing. Depending on the material, photons have enough energy to raise one electron from the upper full band to the lowest empty band. The electron and the "hole", or empty space where it was, are then free to move in the electric field and carry current, which can be measured. The fraction of incident photons that produce carrier pairs depends largely on the semiconductor material.

Photomultiplier tubes

Photomultiplier tubes are vacuum phototubes that amplify light by accelerating the photoelectrons to knock more electrons free from a series of electrodes. They are among the most sensitive light detectors but are not well suited to photography.

Aliasing

Aliasing can occur in optical and chemical processing, but it is more common and easily understood in digital processing. It occurs whenever an optical or digital image is sampled or re-sampled at a rate which is too low for its resolution. Some digital cameras and scanners have anti-aliasing filters to reduce aliasing by intentionally blurring the image to match the sampling rate. It is common for film developing equipment used to make prints of different sizes to increase the graininess of the smaller size prints by aliasing.

It is usually desirable to suppress both noise such as grain and detail of the real object that are too small to be represented at the sampling rate.

Surface science

From Wikipedia, the free encyclopedia

STM image of a quinacridone adsorbate. The self-assembled supramolecular chains of the organic semiconductor are adsorbed on a graphite surface.

Surface science is the study of physical and chemical phenomena that occur at the interface of two phases, including solid–liquid interfaces, solid–gas interfaces, solid–vacuum interfaces, and liquid–gas interfaces. It includes the fields of surface chemistry and surface physics. Some related practical applications are classed as surface engineering. The science encompasses concepts such as heterogeneous catalysis, semiconductor device fabrication, fuel cells, self-assembled monolayers, and adhesives. Surface science is closely related to interface and colloid science. Interfacial chemistry and physics are common subjects for both. The methods are different. In addition, interface and colloid science studies macroscopic phenomena that occur in heterogeneous systems due to peculiarities of interfaces.

History

The field of surface chemistry started with heterogeneous catalysis pioneered by Paul Sabatier on hydrogenation and Fritz Haber on the Haber process. Irving Langmuir was also one of the founders of this field, and the scientific journal on surface science, Langmuir, bears his name. The Langmuir adsorption equation is used to model monolayer adsorption where all surface adsorption sites have the same affinity for the adsorbing species. Gerhard Ertl in 1974 described for the first time the adsorption of hydrogen on a palladium surface using a novel technique called LEED. Similar studies with platinum, nickel, and iron  followed. Most recent developments in surface sciences include the 2007 Nobel prize of Chemistry winner Gerhard Ertl's advancements in surface chemistry, specifically his investigation of the interaction between carbon monoxide molecules and platinum surfaces.

Surface chemistry

Surface chemistry can be roughly defined as the study of chemical reactions at interfaces. It is closely related to surface engineering, which aims at modifying the chemical composition of a surface by incorporation of selected elements or functional groups that produce various desired effects or improvements in the properties of the surface or interface. Surface science is of particular importance to the fields of heterogeneous catalysis, electrochemistry, and geochemistry.

Catalysis

The adhesion of gas or liquid molecules to the surface is known as adsorption. This can be due to either chemisorption or physisorption, and the strength of molecular adsorption to a catalyst surface is critically important to the catalyst's performance (see Sabatier principle). However, it is difficult to study these phenomena in real catalyst particles, which have complex structures. Instead, well-defined single crystal surfaces of catalytically active materials such as platinum are often used as model catalysts. Multi-component materials systems are used to study interactions between catalytically active metal particles and supporting oxides; these are produced by growing ultra-thin films or particles on a single crystal surface.

Relationships between the composition, structure, and chemical behavior of these surfaces are studied using ultra-high vacuum techniques, including adsorption and temperature-programmed desorption of molecules, scanning tunneling microscopy, low energy electron diffraction, and Auger electron spectroscopy. Results can be fed into chemical models or used toward the rational design of new catalysts. Reaction mechanisms can also be clarified due to the atomic-scale precision of surface science measurements.

Electrochemistry

The behavior of an electrode-electrolyte interface is affected by the distribution of ions within the electrical double layer. Adsorption and desorption events can be studied at atomically flat single crystal surfaces as a function of applied bias, time, and solution conditions using scanning probe microscopy and surface X-ray scattering. These studies link traditional electrochemical techniques such as cyclic voltammetry to direct observations of interfacial processes.

Geochemistry

Geologic phenomena such as iron cycling and soil contamination are controlled by the interfaces between minerals and their environment. The atomic-scale structure and chemical properties of mineral-solution interfaces are studied using in situ synchrotron X-ray techniques such as X-ray reflectivity, X-ray standing waves, and X-ray absorption spectroscopy as well as scanning probe microscopy. For example, studies of heavy metal or actinide adsorption onto mineral surfaces reveal molecular-scale details of adsorption, enabling more accurate predictions of how these contaminants travel through soils or disrupt natural dissolution-precipitation cycles.

Surface physics

Surface physics can be roughly defined as the study of physical interactions that occur at interfaces. It overlaps with surface chemistry. Some of the things investigated by surface physics include friction, surface states, surface diffusion, surface reconstruction, surface phonons and plasmons, epitaxy and surface enhanced Raman scattering, the emission and tunneling of electrons, spintronics, and the self-assembly of nanostructures on surfaces. In a confined liquid, defined by geometric constraints on a nanoscopic scale, most molecules sense some surface effects, which can result in physical properties grossly deviating from those of the bulk liquid.

Analysis techniques

The study and analysis of surfaces involves both physical and chemical analysis techniques.
Several modern methods probe the topmost 1–10 nm of surfaces exposed to vacuum. These include X-ray photoelectron spectroscopy, Auger electron spectroscopy, low-energy electron diffraction, electron energy loss spectroscopy, thermal desorption spectroscopy, ion scattering spectroscopy, secondary ion mass spectrometry, dual polarization interferometry, and other surface analysis methods included in the list of materials analysis methods. Many of these techniques require vacuum as they rely on the detection of electrons or ions emitted from the surface under study. Moreover, in general ultra high vacuum, in the range of 10⁻⁷ pascal pressure or better, it is necessary to reduce surface contamination by residual gas, by reducing the number of molecules reaching the sample over a given time period. At 0.1 mPa (10⁻⁶ torr) partial pressure of a contaminant and standard temperature, it only takes on the order of 1 second to cover a surface with a one-to-one monolayer of contaminant to surface atoms, so much lower pressures are needed for measurements. This is found by an order of magnitude estimate for the (number) specific surface area of materials and the impingement rate formula from the kinetic theory of gases.

Purely optical techniques can be used to study interfaces under a wide variety of conditions. Reflection-absorption infrared, dual polarisation interferometry, surface enhanced Raman and sum frequency generation spectroscopies can be used to probe solid–vacuum as well as solid–gas, solid–liquid, and liquid–gas surfaces. Multi-Parametric Surface Plasmon Resonance works in solid-gas, solid-liquid, liquid-gas surfaces and can detect even subnanometer layers. It probes the interaction kinetics as well as dynamic structural changes such as liposome collapse or swelling of layers in different pH. Dual Polarization Interferometry is used to quantify the order and disruption in birefringent thin films. This has been used, for example, to study the formation of lipid bilayers and their interaction with membrane proteins.

X-ray scattering and spectroscopy techniques are also used to characterize surfaces and interfaces. While some of these measurements can be performed using laboratory X-ray sources, many require the high intensity and energy tunability of synchrotron radiation. X-ray crystal truncation rods (CTR) and X-ray standing wave (XSW) measurements probe changes in surface and adsorbate structures with sub-Ångström resolution. Surface-extended X-ray absorption fine structure (SEXAFS) measurements reveal the coordination structure and chemical state of adsorbates. Grazing-incidence small angle X-ray scattering (GISAXS) yields the size, shape, and orientation of nanoparticles on surfaces. The crystal structure and texture of thin films can be investigated using grazing-incidence X-ray diffraction (GIXD, GIXRD).

X-ray photoelectron spectroscopy (XPS) is a standard tool for measuring the chemical states of surface species and for detecting the presence of surface contamination. Surface sensitivity is achieved by detecting photoelectrons with kinetic energies of about 10-1000 eV, which have corresponding inelastic mean free paths of only a few nanometers. This technique has been extended to operate at near-ambient pressures (ambient pressure XPS, AP-XPS) to probe more realistic gas-solid and liquid-solid interfaces. Performing XPS with hard X-rays at synchrotron light sources yields photoelectrons with kinetic energies of several keV (hard X-ray photoelectron spectroscopy, HAXPES), enabling access to chemical information from buried interfaces.

Modern physical analysis methods include scanning-tunneling microscopy (STM) and a family of methods descended from it, including atomic force microscopy. These microscopies have considerably increased the ability and desire of surface scientists to measure the physical structure of many surfaces. For example, they make it possible to follow reactions at the solid–gas interface in real space, if those proceed on a time scale accessible by the instrument.

Atom probe

From Wikipedia, the free encyclopedia

 

Visualisation of data obtained from an atom probe, each point represents a reconstructed atom position from detected evaporated ions.

The atom probe was introduced at the 14th Field Emission Symposium in 1967 by Erwin Wilhelm Müller and J. A. Panitz. It combined a field ion microscope with a mass spectrometer having a single particle detection capability and, for the first time, an instrument could “... determine the nature of one single atom seen on a metal surface and selected from neighboring atoms at the discretion of the observer”.

Atom probes are unlike conventional optical or electron microscopes, in that the magnification effect comes from the magnification provided by a highly curved electric field, rather than by the manipulation of radiation paths. The method is destructive in nature removing ions from a sample surface in order to image and identify them, generating magnifications sufficient to observe individual atoms as they are removed from the sample surface. Through coupling of this magnification method with time of flight mass spectrometry, ions evaporated by application of electric pulses can have their mass-to-charge ratio computed.

Through successive evaporation of material, layers of atoms are removed from a specimen, allowing for probing not only of the surface, but also through the material itself. Computer methods are used to rebuild a three-dimensional view of the sample, prior to it being evaporated, providing atomic scale information on the structure of a sample, as well as providing the type atomic species information. The instrument allows the three-dimensional reconstruction of up to billions of atoms from a sharp tip (corresponding to specimen volumes of 10,000-10,000,000 nm³).

Overview

Atom probe samples are shaped to implicitly provide a highly curved electric potential to induce the resultant magnification, as opposed to direct use of lensing, such as via magnetic lenses. Furthermore, in normal operation (as opposed to a field ionization modes) the atom probe does not utilize a secondary source to probe the sample. Rather, the sample is evaporated in a controlled manner (field evaporation) and the evaporated ions are impacted onto a detector, which is typically 10 to 100 cm away.

The samples are required to have a needle geometry and are produced by similar techniques as TEM sample preparation electropolishing, or focused ion beam methods. Since 2006, commercial systems with laser pulsing have become available and this has expanded applications from metallic only specimens into semiconducting, insulating such as ceramics, and even geological materials. Preparation is done, often by hand, to manufacture a tip radius sufficient to induce a high electric field, with radii on the order of 100 nm.

To conduct an atom probe experiment a very sharp needle shaped specimen is placed in an ultra high vacuum chamber. After introduction into the vacuum system, the sample is reduced to cryogenic temperatures (typically 20-100 K) and manipulated such that the needle's point is aimed towards an ion detector. A high voltage is applied to the specimen, and either a laser pulse is applied to the specimen or a voltage pulse (typically 1-2 kV) with pulse repetition rates in the hundreds of kilohertz range is applied to a counter electrode. The application of the pulse to the sample allows for individual atoms at the sample surface to be ejected as an ion from the sample surface at a known time. Typically the pulse amplitude and the high voltage on the specimen are computer controlled to encourage only one atom to ionize at a time, but multiple ionizations are possible. The delay between application of the pulse and detection of the ion(s) at the detector allow for the computation of a mass-to-charge ratio.

Whilst the uncertainty in the atomic mass computed by time-of-flight methods in atom probe is sufficiently small to allow for detection of individual isotopes within a material this uncertainty may still, in some cases, confound definitive identification of atomic species. Effects such as superposition of differing ions with multiple electrons removed, or through the presence of complex species formation during evaporation may cause two or more species to have sufficiently close time-of-flights to make definitive identification impossible.

History

Field ion microscopy

Field ion microscopy is a modification of field emission microscopy where a stream of tunneling electrons is emitted from the apex of a sharp needle-like tip cathode when subjected to a sufficiently high electric field (~3-6 V/nm). The needle is oriented towards a phosphor screen to create a projected image of the work function at the tip apex. The image resolution is limited to (2-2.5 nm), due to quantum mechanical effects and lateral variations in the electron velocity.

In field ion microscopy the tip is cooled by a cryogen and its polarity is reversed. When an imaging gas (usually hydrogen or helium) is introduced at low pressures (< 0.1 Pascal) gas ions in the high electric field at the tip apex are field ionized and produce a projected image of protruding atoms at the tip apex. The image resolution is determined primarily by the temperature of the tip but even at 78 Kelvin atomic resolution is achieved.

10-cm Atom Probe

The 10-cm Atom Probe, invented in 1973 by J. A. Panitz  was a “new and simple atom probe which permits rapid, in depth species identification or the more usual atom-by atom analysis provided by its predecessors ... in an instrument having a volume of less than two liters in which tip movement is unnecessary and the problems of evaporation pulse stability and alignment common to previous designs have been eliminated.” This was accomplished by combining a time of flight (TOF) mass spectrometer with a proximity focussed, dual channel plate detector, an 11.8 cm drift region and a 38° field of view. An FIM image or a desorption image of the atoms removed from the apex of a field emitter tip could be obtained. The 10-cm Atom Probe has been called the progenitor of later atom probes including the commercial instruments.

Imaging Atom Probe

The Imaging Atom-Probe (IAP) was introduced in 1974 by J. A. Panitz. It incorporated the features of the 10-cm Atom-Probe yet “... departs completely from [previous] atom probe philosophy. Rather than attempt to determine the identity of a surface species producing a preselected ion-image spot, we wish to determine the complete crystallographic distribution of a surface species of preselected mass-to-charge ratio. Now suppose that instead of operating the [detector] continuously, it is turned on for a short time coincidentally with the arrival of a preselected species of interest by applying a gate pulse a time T after the evaporation pulse has reached the specimen. If the duration of the gate pulse is shorter than the travel time between adjacent species, only that surface species having the unique travel time T will be detected and its complete crystallographic distribution displayed.”  It was patented in 1975 as the Field Desorption Spectrometer. The Imaging Atom-Probe moniker was coined by A. J. Waugh in 1978 and the instrument was described in detail by J. A. Panitz in the same year.

Atom Probe Tomography (APT)

Modern day atom probe tomography (APT) uses a position-sensitive detector to deduce the lateral location of atoms. The idea of the APT, inspired by J. A. Panitz's Field Desorption Spectrometer patent, was developed by Mike Miller starting in 1983 and culminated with the first prototype in 1986.^[4] Various refinements were made to the instrument, including the use of a so-called position-sensitive (PoS) detector by Alfred Cerezo, Terence Godfrey, and George D. W. Smith at Oxford University in 1988. The Tomographic Atom Probe (TAP), developed by researchers at the University of Rouen in France in 1993, introduced a multichannel timing system and multianode array. Both instruments (PoSAP and TAP) were commercialized by Oxford Nanoscience and CAMECA respectively. Since then, there have been many refinements to increase the field of view, mass and position resolution, and data acquisition rate of the instrument. The Local Electrode Atom Probe was first introduced in 2003 by Imago Scientific Instruments. In 2005, the commercialization of the pulsed laser atom probe (PLAP) expanded the avenues of research from highly conductive materials (metals) to poor conductors (semiconductors like silicon) and even insulating materials. AMETEK acquired CAMECA in 2007 and Imago Scientific Instruments (Madison, WI) in 2010, making the company the sole commercial developer of APTs with more than 90 instruments installed around the world in 2016.

The first few decades of work with APT focused on metals. However, more recent work has been done on semiconductors, ceramic and geologic materials, with some work on biomaterials.^[16] The most advanced study of biological material to date using APT involved analyzing the chemical structure of teeth of the radula of chiton Chaetopleura apiculata. In this study, the use of APT showed chemical maps of organic fibers in the surrounding nano-crystalline magnetite in the chiton teeth, fibers which were often co-located with sodium or magnesium. This has been furthered to study elephant tusks, dentin and potentially human enamel.

Theory

Field evaporation

Field evaporation is an effect that can occur when an atom bonded at the surface of a material is in the presence of a sufficiently high and appropriately directed electric field, where the electric field is the differential of electric potential (voltage) with respect to distance. Once this condition is met, it is sufficient that local bonding at the specimen surface is capable of being overcome by the field, allowing for evaporation of an atom from the surface to which it is otherwise bonded.

Ion flight

Whether evaporated from the material itself, or ionised from the gas, the ions that are evaporated are accelerated by electrostatic force, acquiring most of their energy within a few tip-radii of the sample.

Subsequently, the accelerative force on any given ion is controlled by the electrostatic equation, where n is the ionisation state of the ion, and e is the fundamental electric charge.

${\displaystyle F=ne\nabla \phi }$

This can be equated with the mass of the ion, m, via Newton's law (F=ma):

${\displaystyle ma=q\nabla \phi }$

${\displaystyle a={\frac {q}{m}}\nabla \phi }$

Relativistic effects in the ion flight are usually ignored, as realisable ion speeds are only a very small fraction of the speed of light.

Assuming that the ion is accelerated during a very short interval, the ion can be assumed to be travelling at constant velocity. As the ion will travel from the tip at voltage V₁ to some nominal ground potential, the speed at which the ion is travelling can be estimated by the energy transferred into the ion during (or near) ionisation. Therefore, the ion speed can be computed with the following equation, which relates kinetic energy to energy gain due to the electric field, the negative arising from the loss of electrons forming a net positive charge.

${\displaystyle E={\frac {1}{2}}mU_{\mathrm {ion} }^{2}=-neV_{1}}$

Where U is the ion velocity. Solving for U, the following relation is found:

${\displaystyle U={\sqrt {\frac {2neV_{1}}{m}}}}$

Let's say that for at a certain ionization voltage, a singly charged hydrogen ion acquires a resulting velocity of X ms⁻¹. A singly charged deuterium ion under the sample conditions would have acquired roughly X/1.41 ms⁻¹. If a detector was placed at a distance of 1 m, the ion flight times would be 1/X and 1.41/X s. Thus, the time of the ion arrival can be used to infer the ion type itself, if the evaporation time is known.

From the above equation, it can be re-arranged to show that

${\displaystyle {\frac {m}{n}}=-{\frac {2eV_{1}}{U^{2}}}}$

given a known flight distance. F, for the ion, and a known flight time, t,

${\displaystyle U={\frac {f}{t}}}$

and thus one can substitute these values to obtain the mass-to-charge for the ion.

${\displaystyle {\frac {m}{n}}=-2eV_{1}\left({\frac {t}{f}}\right)^{2}}$

Thus for an ion which traverses a 1 m flight path, across a time of 2000 ns, given an initial accelerating voltage of 5000 V (V in Si units is kg.m^2.s^-3.A^-1) and noting that one amu is 1×10⁻²⁷ kg, the mass-to-charge ratio (more correctly the mass-to-ionisation value ratio) becomes ~3.86 amu/charge. The number of electrons removed, and thus net positive charge on the ion is not known directly, but can be inferred from the histogram (spectrum) of observed ions.

Magnification

The magnification in an atom is due to the projection of ions radially away from the small, sharp tip. Subsequently, in the far field, the ions will be greatly magnified. This magnification is sufficient to observe field variations due to individual atoms, thus allowing in field ion and field evaporation modes for the imaging of single atoms.

The standard projection model for the atom probe is an emitter geometry that is based upon a revolution of a conic section, such as a sphere, hyperboloid or paraboloid. For these tip models, solutions to the field may be approximated or obtained analytically. The magnification for a spherical emitter is inversely proportional to the radius of the tip, given a projection directly onto a spherical screen, the following equation can be obtained geometrically.

${\displaystyle M={\frac {r_{screen}}{r_{tip}}}.}$

Where r_screen is the radius of the detection screen from the tip centre, and r_tip the tip radius. Practical tip to screen distances may range from several centimeters to several meters, with increased detector area required at larger to subtend the same field of view.

Practically speaking, the usable magnification will be limited by several effects, such as lateral vibration of the atoms prior to evaporation.

Whilst the magnification of both the field ion and atom probe microscopes is extremely high, the exact magnification is dependent upon conditions specific to the examined specimen, so unlike for conventional electron microscopes, there is often little direct control on magnification, and furthermore, obtained images may have strongly variable magnifications due to fluctuations in the shape of the electric field at the surface.

Reconstruction

The computational conversion of the ion sequence data, as obtained from a position sensitive detector, to a three-dimensional visualisation of atomic types, is termed "reconstruction". Reconstruction algorithms are typically geometrically based, and have several literature formulations. Most models for reconstruction assume that the tip is a spherical object, and use empirical corrections to stereographic projection to convert detector positions back to a 2D surface embedded in 3D space, R³. By sweeping this surface through R³ as a function of the ion sequence input data, such as via ion-ordering, a volume is generated onto which positions the 2D detector positions can be computed and placed three-dimensional space.

Typically the sweep takes the simple form of an advancement of the surface, such that the surface is expanded in a symmetric manner about its advancement axis, with the advancement rate set by a volume attributed to each ion detected and identified. This causes the final reconstructed volume to assume a rounded-conical shape, similar to a badminton shuttlecock. The detected events thus become a point cloud data with attributed experimentally measured values, such as ion time of flight or experimentally derived quantities, e.g. time of flight or detector data.

This form of data manipulation allows for rapid computer visualisation and analysis, with data presented as point cloud data with additional information, such as each ion's mass to charge (as computed from the velocity equation above), voltage or other auxiliary measured quantity or computation therefrom.

Data features

The canonical feature of atom probe data, is its high spatial resolution in the direction through the material, which has been attributed to an ordered evaporation sequence. This data can therefore image near atomically sharp buried interfaces with the associated chemical information.

The data obtained from the evaporative process is however not without artefacts that form the physical evaporation or ionisation process. A key feature of the evaporation or field ion images is that the data density is highly inhomogeneous, due to the corrugation of the specimen surface at the atomic scale. This corrugation gives rise to strong electric field gradients in the near-tip zone (on the order of an atomic radii or less from the tip), which during ionisation deflects ions away from the electric field normal.

The resultant deflection means that in these regions of high curvature, atomic terraces are belied by a strong anisotropy in the detection density. Where this occurs due to a few atoms on a surface is usually referred to as a "pole", as these are coincident with the crystallographic axes of the specimen (FCC, BCC, HCP) etc. Where the edges of an atomic terrace causes deflection, a low density line is formed and is termed a "zone line".

These poles and zone-lines, whilst inducing fluctuations in data density in the reconstructed datasets, which can prove problematic during post-analysis, are critical for determining information such as angular magnification, as the crystallographic relationships between features are typically well known.

When reconstructing the data, owing to the evaporation of successive layers of material from the sample, the lateral and in-depth reconstruction values are highly anisotropic. Determination of the exact resolution of the instrument is of limited use, as the resolution of the device is set by the physical properties of the material under analysis.

Systems

Many designs have been constructed since the method's inception. Initial field ion microscopes, precursors to modern atom probes, were usually glass blown devices developed by individual research laboratories.

System layout

At a minimum, an atom probe will consist of several key pieces of equipment.

• A vacuum system for maintaining the low pressures (~10⁻⁸ to 10⁻¹⁰ Pa) required, typically a classic 3 chambered UHV design.
• A system for manipulation of samples inside the vacuum, including sample viewing systems.
• A cooling system to reduce atomic motion, such as a helium refrigeration circuit - providing sample temperatures as low as 15K.
• A high voltage system to raise the sample standing voltage near the threshold for field evaporation.
• A high voltage pulsing system, use to create timed field evaporation events
• A counter electrode that can be a simple disk shape (like the EIKOS™, or earlier generation atom probes), or a cone shaped Local Electrode, like on a LEAP® system. The voltage pulse (negative) is typically applied to the counter electrode.
• A detection system for single energetic ions that includes XY position and TOF information.

Optionally, an atom probe may also include laser-optical systems for laser beam targeting and pulsing, if using laser-evaporation methods. In-situ reaction systems, heaters, or plasma treatment may also be employed for some studies as well as pure noble gas introduction for FIM.

Performance

Collectable ion volumes were previously limited to several thousand, or tens of thousands of ionic events. Subsequent electronics and instrumentation development has increased the rate of data accumulation, with datasets of hundreds of million atoms (dataset volumes of 10⁷ nm³). Data collection times vary considerably depending upon the experimental conditions and the number of ions collected. Experiments take from a few minutes, to many hours to complete.

Applications

Metallurgy

Atom probe has typically been employed in the chemical analysis of alloy systems at the atomic level. This has arisen as a result of voltage pulsed atom probes providing good chemical and sufficient spatial information in these materials. Metal samples from large grained alloys may be simple to fabricate, particularly from wire samples, with hand-electropolishing techniques giving good results.

Subsequently, atom probe has been used in the analysis of the chemical composition of a wide range of alloys.

Such data is critical in determining the effect of alloy constituents in a bulk material, identification of solid-state reaction features, such as solid phase precipitates. Such information may not be amenable to analysis by other means (e.g. TEM) owing to the difficulty in generating a three-dimensional dataset with composition.

Semiconductors

Semi-conductor materials are often analysable in atom probe, however sample preparation may be more difficult, and interpretation of results may be more complex, particularly if the semi-conductor contains phases which evaporate at differing electric field strengths.

Applications such as ion implantation may be used to identify the distribution of dopants inside a semi-conducting material, which is increasingly critical in the correct design of modern nanometre scale electronics.

Limitations

• Materials implicitly control achievable spatial resolution.
• Specimen geometry during the analysis is uncontrolled, yet controls projection behaviour, hence there is little control over the magnification. This induces distortions into the computer generated 3D dataset. Features of interest might evaporate in a physically different manner to the bulk sample, altering projection geometry and the magnification of the reconstructed volume. This yields strong spatial distortions in the final image.
• Volume selectability can be limited. Site specific preparation methods, e.g. using Focussed ion beam preparation, although more time consuming, may be used to bypass such limitations.
• Ion overlap in some samples (e.g. between oxygen and sulfur) resulted in ambiguous analysed species. This may be mitigated by selection of experiment temperature or laser input energy to influence the ionisation number (+, ++, 3+ etc.) of the ionised groups. Data analysis can be used in some cases to statistically recover ovelaps.
• Low molecular weight gases (Hydrogen & Helium) may be difficult to be removed from the analysis chamber, and may be adsorbed and emitted from the specimen, even though not present in the original specimen. This may also limit identification of Hydrogen in some samples. For this reason, deuterated samples have been used to overcome limitations.
• Results may be contingent on the parameters used to convert the 2D detected data into 3D. In more problematic materials, correct reconstruction may not be done, due to limited knowledge of the true magnification; particularly if zone or pole regions cannot be observed.