Nuclear structure

From Wikipedia, the free encyclopedia

Understanding the structure of the atomic nucleus is one of the central challenges in nuclear physics.

Models

The liquid drop model

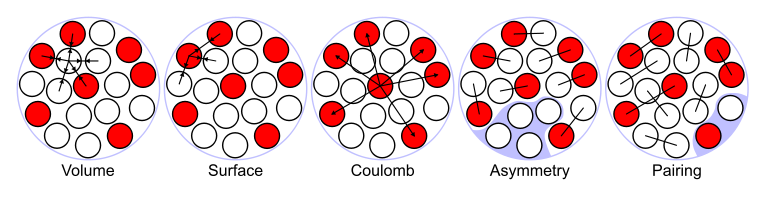
The liquid drop model is one of the first models of nuclear structure, proposed by Carl Friedrich von Weizsäcker in 1935. It describes the nucleus as a semiclassical fluid made up of neutrons and protons, with an internal repulsive electrostatic force proportional to the number of protons. The quantum mechanical nature of these particles appears via the Pauli exclusion principle, which states that no two nucleons of the same kind can be at the same state. Thus the fluid is actually what is known as a Fermi liquid. In this model, the binding energy of a nucleus with ${\displaystyle Z}$ protons and ${\displaystyle N}$ neutrons is given by

${\displaystyle E_{B}=a_{V}A-a_{S}A^{2/3}-a_{C}{\frac {Z^{2}}{A^{1/3}}}-a_{A}{\frac {(N-Z)^{2}}{A}}-\delta (A,Z)}$

where ${\displaystyle A=Z+N}$ is the total number of nucleons (Mass Number). The terms proportional to ${\displaystyle A}$ and ${\displaystyle A^{2/3}}$ represent the volume and surface energy of the liquid drop, the term proportional to ${\displaystyle Z^{2}}$ represents the electrostatic energy, the term proportional to ${\displaystyle (N-Z)^{2}}$ represents the Pauli exclusion principle and the last term ${\displaystyle \delta (A,Z)}$ is the pairing term, which lowers the energy for even numbers of protons or neutrons. The coefficients ${\displaystyle a_{V},a_{S},a_{C},a_{A}}$ and the strength of the pairing term may be estimated theoretically, or fit to data. This simple model reproduces the main features of the binding energy of nuclei.

The assumption of nucleus as a drop of Fermi liquid is still widely used in the form of Finite Range Droplet Model (FRDM), due to the possible good reproduction of nuclear binding energy on the whole chart, with the necessary accuracy for predictions of unknown nuclei.

The shell model

The expression "shell model" is ambiguous in that it refers to two different eras in the state of the art. It was previously used to describe the existence of nucleon shells in the nucleus according to an approach closer to what is now called mean field theory. Nowadays, it refers to a formalism analogous to the configuration interaction formalism used in quantum chemistry. We shall introduce the latter here.

Introduction to the shell concept

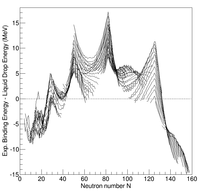
Difference between experimental binding energies and the liquid drop model prediction as a function of neutron number for Z>7

Systematic measurements of the binding energy of atomic nuclei show systematic deviations with respect to those estimated from the liquid drop model. In particular, some nuclei having certain values for the number of protons and/or neutrons are bound more tightly together than predicted by the liquid drop model. These nuclei are called singly/doubly magic. This observation led scientists to assume the existence of a shell structure of nucleons (protons and neutrons) within the nucleus, like that of electrons within atoms.

Indeed, nucleons are quantum objects. Strictly speaking, one should not speak of energies of individual nucleons, because they are all correlated with each other. However, as an approximation one may envision an average nucleus, within which nucleons propagate individually. Owing to their quantum character, they may only occupy discrete energy levels. These levels are by no means uniformly distributed; some intervals of energy are crowded, and some are empty, generating a gap in possible energies. A shell is such a set of levels separated from the other ones by a wide empty gap.

The energy levels are found by solving the Schrödinger equation for a single nucleon moving in the average potential generated by all other nucleons. Each level may be occupied by a nucleon, or empty. Some levels accommodate several different quantum states with the same energy; they are said to be degenerate. This occurs in particular if the average nucleus has some symmetry.

The concept of shells allows one to understand why some nuclei are bound more tightly than others. This is because two nucleons of the same kind cannot be in the same state (Pauli exclusion principle). So the lowest-energy state of the nucleus is one where nucleons fill all energy levels from the bottom up to some level. A nucleus with full shells is exceptionally stable, as will be explained.

As with electrons in the electron shell model, protons in the outermost shell are relatively loosely bound to the nucleus if there are only few protons in that shell, because they are farthest from the center of the nucleus. Therefore, nuclei which have a full outer proton shell will be more tightly bound and have a higher binding energy than other nuclei with a similar total number of protons. All this is also true for neutrons.

Furthermore, the energy needed to excite the nucleus (i.e. moving a nucleon to a higher, previously unoccupied level) is exceptionally high in such nuclei. Whenever this unoccupied level is the next after a full shell, the only way to excite the nucleus is to raise one nucleon across the gap, thus spending a large amount of energy. Otherwise, if the highest occupied energy level lies in a partly filled shell, much less energy is required to raise a nucleon to a higher state in the same shell.

Some evolution of the shell structure observed in stable nuclei is expected away from the valley of stability. For example, observations of unstable isotopes have shown shifting and even a reordering of the single particle levels of which the shell structure is composed. This is sometimes observed as the creation of an island of inversion or in the reduction of excitation energy gaps above the traditional magic numbers.

Basic hypotheses

Some basic hypotheses are made in order to give a precise conceptual framework to the shell model:

• The atomic nucleus is a quantum n-body system.
• The internal motion of nucleons within the nucleus is non-relativistic, and their behavior is governed by the Schrödinger equation.
• Nucleons are considered to be pointlike, without any internal structure.

Brief description of the formalism

The general process used in the shell model calculations is the following. First a Hamiltonian for the nucleus is defined. Usually, for computational practicality, only one- and two-body terms are taken into account in this definition. The interaction is an effective theory: it contains free parameters which have to be fitted with experimental data.

The next step consists in defining a basis of single-particle states, i.e. a set of wavefunctions describing all possible nucleon states. Most of the time, this basis is obtained via a Hartree–Fock computation. With this set of one-particle states, Slater determinants are built, that is, wavefunctions for Z proton variables or N neutron variables, which are antisymmetrized products of single-particle wavefunctions (antisymmetrized meaning that under exchange of variables for any pair of nucleons, the wavefunction only changes sign).

In principle, the number of quantum states available for a single nucleon at a finite energy is finite, say n. The number of nucleons in the nucleus must be smaller than the number of available states, otherwise the nucleus cannot hold all of its nucleons. There are thus several ways to choose Z (or N) states among the n possible. In combinatorial mathematics, the number of choices of Z objects among n is the binomial coefficient C^Z
_n. If n is much larger than Z (or N), this increases roughly like n^Z. Practically, this number becomes so large that every computation is impossible for A=N+Z larger than 8.

To obviate this difficulty, the space of possible single-particle states is divided into a core and a valence shell, by analogy with chemistry. The core is a set of single-particles which are assumed to be inactive, in the sense that they are the well bound lowest-energy states, and that there is no need to reexamine their situation. They do not appear in the Slater determinants, contrary to the states in the valence space, which is the space of all single-particle states not in the core, but possibly to be considered in the choice of the build of the (Z-) N-body wavefunction. The set of all possible Slater determinants in the valence space defines a basis for (Z-) N-body states.

The last step consists in computing the matrix of the Hamiltonian within this basis, and to diagonalize it. In spite of the reduction of the dimension of the basis owing to the fixation of the core, the matrices to be diagonalized reach easily dimensions of the order of 10⁹, and demand specific diagonalization techniques.

The shell model calculations give in general an excellent fit with experimental data. They depend however strongly on two main factors:

• The way to divide the single-particle space into core and valence.
• The effective nucleon–nucleon interaction.

Mean field theories

The independent-particle model

The interaction between nucleons, which is a consequence of strong interactions and binds the nucleons within the nucleus, exhibits the peculiar behaviour of having a finite range: it vanishes when the distance between two nucleons becomes too large; it is attractive at medium range, and repulsive at very small range. This last property correlates with the Pauli exclusion principle according to which two fermions (nucleons are fermions) cannot be in the same quantum state. This results in a very large mean free path predicted for a nucleon within the nucleus.

The main idea of the Independent Particle approach is that a nucleon moves inside a certain potential well (which keeps it bound to the nucleus) independently from the other nucleons. This amounts to replacing a N-body problem (N particles interacting) by N single-body problems. This essential simplification of the problem is the cornerstone of mean field theories. These are also widely used in atomic physics, where electrons move in a mean field due to the central nucleus and the electron cloud itself.

The independent particle model and mean field theories (we shall see that there exist several variants) have a great success in describing the properties of the nucleus starting from an effective interaction or an effective potential, thus are a basic part of atomic nucleus theory. One should also notice that they are modular enough, in that it is quite easy to extend the model to introduce effects such as nuclear pairing, or collective motions of the nucleon like rotation, or vibration, adding the corresponding energy terms in the formalism. This implies that in many representations, the mean field is only a starting point for a more complete description which introduces correlations reproducing properties like collective excitations and nucleon transfer.

Nuclear potential and effective interaction

A large part of the practical difficulties met in mean field theories is the definition (or calculation) of the potential of the mean field itself. One can very roughly distinguish between two approaches:

• The phenomenological approach is a parameterization of the nuclear potential by an appropriate mathematical function. Historically, this procedure was applied with the greatest success by Sven Gösta Nilsson, who used as a potential a (deformed) harmonic oscillator potential. The most recent parameterizations are based on more realistic functions, which account more accurately for scattering experiments, for example. In particular the form known as the Woods–Saxon potential can be mentioned.
• The self-consistent or Hartree–Fock approach aims to deduce mathematically the nuclear potential from an effective nucleon–nucleon interaction. This technique implies a resolution of the Schrödinger equation in an iterative fashion, starting from an ansatz wavefunction and improving it variationally, since the potential depends there upon the wavefunctions to be determined. The latter are written as Slater determinants.

In the case of the Hartree–Fock approaches, the trouble is not to find the mathematical function which describes best the nuclear potential, but that which describes best the nucleon–nucleon interaction. Indeed, in contrast with atomic physics where the interaction is known (it is the Coulomb interaction), the nucleon–nucleon interaction within the nucleus is not known analytically.

There are two main reasons for this fact. First, the strong interaction acts essentially among the quarks forming the nucleons. The nucleon–nucleon interaction in vacuum is a mere consequence of the quark–quark interaction. While the latter is well understood in the framework of the Standard Model at high energies, it is much more complicated in low energies due to color confinement and asymptotic freedom. Thus there is yet no fundamental theory allowing one to deduce the nucleon–nucleon interaction from the quark–quark interaction. Furthermore, even if this problem were solved, there would remain a large difference between the ideal (and conceptually simpler) case of two nucleons interacting in vacuum, and that of these nucleons interacting in the nuclear matter. To go further, it was necessary to invent the concept of effective interaction. The latter is basically a mathematical function with several arbitrary parameters, which are adjusted to agree with experimental data.

Most modern interaction are zero-range so they act only when the two nucleons are in contact, as introduced by Tony Skyrme.

The self-consistent approaches of the Hartree–Fock type

In the Hartree–Fock approach of the n-body problem, the starting point is a Hamiltonian containing n kinetic energy terms, and potential terms. As mentioned before, one of the mean field theory hypotheses is that only the two-body interaction is to be taken into account. The potential term of the Hamiltonian represents all possible two-body interactions in the set of n fermions. It is the first hypothesis.

The second step consists in assuming that the wavefunction of the system can be written as a Slater determinant of one-particle spin-orbitals. This statement is the mathematical translation of the independent-particle model. This is the second hypothesis.

There remains now to determine the components of this Slater determinant, that is, the individual wavefunctions of the nucleons. To this end, it is assumed that the total wavefunction (the Slater determinant) is such that the energy is minimum. This is the third hypothesis.

Technically, it means that one must compute the mean value of the (known) two-body Hamiltonian on the (unknown) Slater determinant, and impose that its mathematical variation vanishes. This leads to a set of equations where the unknowns are the individual wavefunctions: the Hartree–Fock equations. Solving these equations gives the wavefunctions and individual energy levels of nucleons, and so the total energy of the nucleus and its wavefunction.

This short account of the Hartree–Fock method explains why it is called also the variational approach. At the beginning of the calculation, the total energy is a "function of the individual wavefunctions" (a so-called functional), and everything is then made in order to optimize the choice of these wavefunctions so that the functional has a minimum – hopefully absolute, and not only local. To be more precise, there should be mentioned that the energy is a functional of the density, defined as the sum of the individual squared wavefunctions. Let us note also that the Hartree–Fock method is also used in atomic physics and condensed matter physics as Density Functional Theory, DFT.

The process of solving the Hartree–Fock equations can only be iterative, since these are in fact a Schrödinger equation in which the potential depends on the density, that is, precisely on the wavefunctions to be determined. Practically, the algorithm is started with a set of individual grossly reasonable wavefunctions (in general the eigenfunctions of a harmonic oscillator). These allow to compute the density, and therefrom the Hartree–Fock potential. Once this done, the Schrödinger equation is solved anew, and so on. The calculation stops – convergence is reached – when the difference among wavefunctions, or energy levels, for two successive iterations is less than a fixed value. Then the mean field potential is completely determined, and the Hartree–Fock equations become standard Schrödinger equations. The corresponding Hamiltonian is then called the Hartree–Fock Hamiltonian.

The relativistic mean field approaches

Born first in the 1970s with the works of John Dirk Walecka on quantum hadrodynamics, the relativistic models of the nucleus were sharpened up towards the end of the 1980s by P. Ring and coworkers. The starting point of these approaches is the relativistic quantum field theory. In this context, the nucleon interactions occur via the exchange of virtual particles called mesons. The idea is, in a first step, to build a Lagrangian containing these interaction terms. Second, by an application of the least action principle, one gets a set of equations of motion. The real particles (here the nucleons) obey the Dirac equation, whilst the virtual ones (here the mesons) obey the Klein–Gordon equations.

In view of the non-perturbative nature of strong interaction, and also in view of the fact that the exact potential form of this interaction between groups of nucleons is relatively badly known, the use of such an approach in the case of atomic nuclei requires drastic approximations. The main simplification consists in replacing in the equations all field terms (which are operators in the mathematical sense) by their mean value (which are functions). In this way, one gets a system of coupled integro-differential equations, which can be solved numerically, if not analytically.

The interacting boson model

The interacting boson model (IBM) is a model in nuclear physics in which nucleons are represented as pairs, each of them acting as a boson particle, with integral spin of 0, 2 or 4. This makes calculations feasible for larger nuclei. There are several branches of this model - in one of them (IBM-1) one can group all types of nucleons in pairs, in others (for instance - IBM-2) one considers protons and neutrons in pairs separately.

Spontaneous breaking of symmetry in nuclear physics

One of the focal points of all physics is symmetry. The nucleon–nucleon interaction and all effective interactions used in practice have certain symmetries. They are invariant by translation (changing the frame of reference so that directions are not altered), by rotation (turning the frame of reference around some axis), or parity (changing the sense of axes) in the sense that the interaction does not change under any of these operations. Nevertheless, in the Hartree–Fock approach, solutions which are not invariant under such a symmetry can appear. One speaks then of spontaneous symmetry breaking.

Qualitatively, these spontaneous symmetry breakings can be explained in the following way: in the mean field theory, the nucleus is described as a set of independent particles. Most additional correlations among nucleons which do not enter the mean field are neglected. They can appear however by a breaking of the symmetry of the mean field Hamiltonian, which is only approximate. If the density used to start the iterations of the Hartree–Fock process breaks certain symmetries, the final Hartree–Fock Hamiltonian may break these symmetries, if it is advantageous to keep these broken from the point of view of the total energy.

It may also converge towards a symmetric solution. In any case, if the final solution breaks the symmetry, for example, the rotational symmetry, so that the nucleus appears not to be spherical, but elliptic, all configurations deduced from this deformed nucleus by a rotation are just as good solutions for the Hartree–Fock problem. The ground state of the nucleus is then degenerate.

A similar phenomenon happens with the nuclear pairing, which violates the conservation of the number of baryons (see below).

Extensions of the mean field theories

Nuclear pairing phenomenon

The most common extension to mean field theory is the nuclear pairing. Nuclei with an even number of nucleons are systematically more bound than those with an odd one. This implies that each nucleon binds with another one to form a pair, consequently the system cannot be described as independent particles subjected to a common mean field. When the nucleus has an even number of protons and neutrons, each one of them finds a partner. To excite such a system, one must at least use such an energy as to break a pair. Conversely, in the case of odd number of protons or neutrons, there exists an unpaired nucleon, which needs less energy to be excited.

This phenomenon is closely analogous to that of Type 1 superconductivity in solid state physics. The first theoretical description of nuclear pairing was proposed at the end of the 1950s by Aage Bohr, Ben Mottelson, and David Pines (which contributed to the reception of the Nobel Prize in Physics in 1975 by Bohr and Mottelson). It was close to the BCS theory of Bardeen, Cooper and Schrieffer, which accounts for metal superconductivity. Theoretically, the pairing phenomenon as described by the BCS theory combines with the mean field theory: nucleons are both subject to the mean field potential and to the pairing interaction.

The Hartree–Fock–Bogolyubov (HFB) method is a more sophisticated approach, enabling one to consider the pairing and mean field interactions consistently on equal footing. HFB is now the de facto standard in the mean field treatment of nuclear systems.

Symmetry restoration

Peculiarity of mean field methods is the calculation of nuclear property by explicit symmetry breaking. The calculation of the mean field with self-consistent methods (e.g. Hartree-Fock), breaks rotational symmetry, and the calculation of pairing property breaks particle-number.

Several techniques for symmetry restoration by projecting on good quantum numbers have been developed.

Particle vibration coupling

Mean field methods (eventually considering symmetry restoration) are a good approximation for the ground state of the system, even postulating a system of independent particles. Higher-order corrections consider the fact that the particles interact together by the means of correlation. These correlations can be introduced taking into account the coupling of independent particle degrees of freedom, low-energy collective excitation of systems with even number of protons and neutrons.

In these way excited states can be reproduced by the means of random phase approximation (RPA), and eventually consistently calculating also corrections to the ground state (e.g. by the means of nuclear field theory).

Atomic nucleus

From Wikipedia, the free encyclopedia

A model of the atomic nucleus showing it as a compact bundle of the two types of nucleons: protons (red) and neutrons (blue). In this diagram, protons and neutrons look like little balls stuck together, but an actual nucleus (as understood by modern nuclear physics) cannot be explained like this, but only by using quantum mechanics. In a nucleus which occupies a certain energy level (for example, the ground state), each nucleon can be said to occupy a range of locations.

The atomic nucleus is the small, dense region consisting of protons and neutrons at the center of an atom, discovered in 1911 by Ernest Rutherford based on the 1909 Geiger–Marsden gold foil experiment. After the discovery of the neutron in 1932, models for a nucleus composed of protons and neutrons were quickly developed by Dmitri Ivanenko and Werner Heisenberg. An atom is composed of a positively-charged nucleus, with a cloud of negatively-charged electrons surrounding it, bound together by electrostatic force. Almost all of the mass of an atom is located in the nucleus, with a very small contribution from the electron cloud. Protons and neutrons are bound together to form a nucleus by the nuclear force.

The diameter of the nucleus is in the range of 1.7566 fm (1.7566×10⁻¹⁵ m) for hydrogen (the diameter of a single proton) to about 11.7142 fm for the heaviest atom uranium. These dimensions are much smaller than the diameter of the atom itself (nucleus + electron cloud), by a factor of about 26,634 (uranium atomic radius is about 156 pm (156×10⁻¹² m)) to about 60,250 (hydrogen atomic radius is about 52.92 pm).

The branch of physics concerned with the study and understanding of the atomic nucleus, including its composition and the forces which bind it together, is called nuclear physics.

Introduction

History

The nucleus was discovered in 1911, as a result of Ernest Rutherford's efforts to test Thomson's "plum pudding model" of the atom. The electron had already been discovered earlier by J.J. Thomson himself. Knowing that atoms are electrically neutral, Thomson postulated that there must be a positive charge as well. In his plum pudding model, Thomson suggested that an atom consisted of negative electrons randomly scattered within a sphere of positive charge. Ernest Rutherford later devised an experiment with his research partner Hans Geiger and with help of Ernest Marsden, that involved the deflection of alpha particles (helium nuclei) directed at a thin sheet of metal foil. He reasoned that if Thomson's model were correct, the positively charged alpha particles would easily pass through the foil with very little deviation in their paths, as the foil should act as electrically neutral if the negative and positive charges are so intimately mixed as to make it appear neutral. To his surprise, many of the particles were deflected at very large angles. Because the mass of an alpha particle is about 8000 times that of an electron, it became apparent that a very strong force must be present if it could deflect the massive and fast moving alpha particles. He realized that the plum pudding model could not be accurate and that the deflections of the alpha particles could only be explained if the positive and negative charges were separated from each other and that the mass of the atom was a concentrated point of positive charge. This justified the idea of a nuclear atom with a dense center of positive charge and mass.

Etymology

The term nucleus is from the Latin word nucleus, a diminutive of nux ("nut"), meaning the kernel (i.e., the "small nut") inside a watery type of fruit (like a peach). In 1844, Michael Faraday used the term to refer to the "central point of an atom". The modern atomic meaning was proposed by Ernest Rutherford in 1912. The adoption of the term "nucleus" to atomic theory, however, was not immediate. In 1916, for example, Gilbert N. Lewis stated, in his famous article The Atom and the Molecule, that "the atom is composed of the kernel and an outer atom or shell"

Nuclear makeup

A figurative depiction of the helium-4 atom with the electron cloud in shades of gray. In the nucleus, the two protons and two neutrons are depicted in red and blue. This depiction shows the particles as separate, whereas in an actual helium atom, the protons are superimposed in space and most likely found at the very center of the nucleus, and the same is true of the two neutrons. Thus, all four particles are most likely found in exactly the same space, at the central point. Classical images of separate particles fail to model known charge distributions in very small nuclei. A more accurate image is that the spatial distribution of nucleons in a helium nucleus is much closer to the helium electron cloud shown here, although on a far smaller scale, than to the fanciful nucleus image.

The nucleus of an atom consists of neutrons and protons, which in turn are the manifestation of more elementary particles, called quarks, that are held in association by the nuclear strong force in certain stable combinations of hadrons, called baryons. The nuclear strong force extends far enough from each baryon so as to bind the neutrons and protons together against the repulsive electrical force between the positively charged protons. The nuclear strong force has a very short range, and essentially drops to zero just beyond the edge of the nucleus. The collective action of the positively charged nucleus is to hold the electrically negative charged electrons in their orbits about the nucleus. The collection of negatively charged electrons orbiting the nucleus display an affinity for certain configurations and numbers of electrons that make their orbits stable. Which chemical element an atom represents is determined by the number of protons in the nucleus; the neutral atom will have an equal number of electrons orbiting that nucleus. Individual chemical elements can create more stable electron configurations by combining to share their electrons. It is that sharing of electrons to create stable electronic orbits about the nucleus that appears to us as the chemistry of our macro world.

Protons define the entire charge of a nucleus, and hence its chemical identity. Neutrons are electrically neutral, but contribute to the mass of a nucleus to nearly the same extent as the protons. Neutrons can explain the phenomenon of isotopes (same atomic number with different atomic mass.) The main role of neutrons is to reduce electrostatic repulsion inside the nucleus.

Composition and shape

Protons and neutrons are fermions, with different values of the strong isospin quantum number, so two protons and two neutrons can share the same space wave function since they are not identical quantum entities. They are sometimes viewed as two different quantum states of the same particle, the nucleon. Two fermions, such as two protons, or two neutrons, or a proton + neutron (the deuteron) can exhibit bosonic behavior when they become loosely bound in pairs, which have integer spin.
In the rare case of a hypernucleus, a third baryon called a hyperon, containing one or more strange quarks and/or other unusual quark(s), can also share the wave function. However, this type of nucleus is extremely unstable and not found on Earth except in high energy physics experiments.
The neutron has a positively charged core of radius ≈ 0.3 fm surrounded by a compensating negative charge of radius between 0.3 fm and 2 fm. The proton has an approximately exponentially decaying positive charge distribution with a mean square radius of about 0.8 fm.

Nuclei can be spherical, rugby ball-shaped (prolate deformation), discus-shaped (oblate deformation), triaxial (a combination of oblate and prolate deformation) or pear-shaped.

Forces

Nuclei are bound together by the residual strong force (nuclear force). The residual strong force is a minor residuum of the strong interaction which binds quarks together to form protons and neutrons. This force is much weaker between neutrons and protons because it is mostly neutralized within them, in the same way that electromagnetic forces between neutral atoms (such as van der Waals forces that act between two inert gas atoms) are much weaker than the electromagnetic forces that hold the parts of the atoms together internally (for example, the forces that hold the electrons in an inert gas atom bound to its nucleus).

The nuclear force is highly attractive at the distance of typical nucleon separation, and this overwhelms the repulsion between protons due to the electromagnetic force, thus allowing nuclei to exist. However, the residual strong force has a limited range because it decays quickly with distance; thus only nuclei smaller than a certain size can be completely stable. The largest known completely stable nucleus (i.e. stable to alpha, beta, and gamma decay) is lead-208 which contains a total of 208 nucleons (126 neutrons and 82 protons). Nuclei larger than this maximum are unstable and tend to be increasingly short-lived with larger numbers of nucleons. However, bismuth-209 is also stable to beta decay and has the longest half-life to alpha decay of any known isotope, estimated at a billion times longer than the age of the universe.

The residual strong force is effective over a very short range (usually only a few femtometres (fm); roughly one or two nucleon diameters) and causes an attraction between any pair of nucleons. For example, between protons and neutrons to form [NP] deuteron, and also between protons and protons, and neutrons and neutrons.

Halo nuclei and strong force range limits

The effective absolute limit of the range of the strong force is represented by halo nuclei such as lithium-11 or boron-14, in which dineutrons, or other collections of neutrons, orbit at distances of about 10 fm (roughly similar to the 8 fm radius of the nucleus of uranium-238). These nuclei are not maximally dense. Halo nuclei form at the extreme edges of the chart of the nuclides—the neutron drip line and proton drip line—and are all unstable with short half-lives, measured in milliseconds; for example, lithium-11 has a half-life of 8.8 ms.

Halos in effect represent an excited state with nucleons in an outer quantum shell which has unfilled energy levels "below" it (both in terms of radius and energy). The halo may be made of either neutrons [NN, NNN] or protons [PP, PPP]. Nuclei which have a single neutron halo include ¹¹Be and ¹⁹C. A two-neutron halo is exhibited by ⁶He, ¹¹Li, ¹⁷B, ¹⁹B and ²²C. Two-neutron halo nuclei break into three fragments, never two, and are called Borromean nuclei because of this behavior (referring to a system of three interlocked rings in which breaking any ring frees both of the others). ⁸He and ¹⁴Be both exhibit a four-neutron halo. Nuclei which have a proton halo include ⁸B and ²⁶P. A two-proton halo is exhibited by ¹⁷Ne and ²⁷S. Proton halos are expected to be more rare and unstable than the neutron examples, because of the repulsive electromagnetic forces of the excess proton(s).

Nuclear models

Although the standard model of physics is widely believed to completely describe the composition and behavior of the nucleus, generating predictions from theory is much more difficult than for most other areas of particle physics. This is due to two reasons:

• In principle, the physics within a nucleus can be derived entirely from quantum chromodynamics (QCD). In practice however, current computational and mathematical approaches for solving QCD in low-energy systems such as the nuclei are extremely limited. This is due to the phase transition that occurs between high-energy quark matter and low-energy hadronic matter, which renders perturbative techniques unusable, making it difficult to construct an accurate QCD-derived model of the forces between nucleons. Current approaches are limited to either phenomenological models such as the Argonne v18 potential or chiral effective field theory.
• Even if the nuclear force is well constrained, a significant amount of computational power is required to accurately compute the properties of nuclei ab initio. Developments in many-body theory have made this possible for many low mass and relatively stable nuclei, but further improvements in both computational power and mathematical approaches are required before heavy nuclei or highly unstable nuclei can be tackled.

Historically, experiments have been compared to relatively crude models that are necessarily imperfect. None of these models can completely explain experimental data on nuclear structure.

The nuclear radius (R) is considered to be one of the basic quantities that any model must predict. For stable nuclei (not halo nuclei or other unstable distorted nuclei) the nuclear radius is roughly proportional to the cube root of the mass number (A) of the nucleus, and particularly in nuclei containing many nucleons, as they arrange in more spherical configurations:

The stable nucleus has approximately a constant density and therefore the nuclear radius R can be approximated by the following formula,

${\displaystyle R=r_{0}A^{1/3}\,}$

where A = Atomic mass number (the number of protons Z, plus the number of neutrons N) and r₀ = 1.25 fm = 1.25 × 10⁻¹⁵ m. In this equation, the "constant" r₀ varies by 0.2 fm, depending on the nucleus in question, but this is less than 20% change from a constant.

In other words, packing protons and neutrons in the nucleus gives approximately the same total size result as packing hard spheres of a constant size (like marbles) into a tight spherical or almost spherical bag (some stable nuclei are not quite spherical, but are known to be prolate).

Models of nuclear structure include :

Liquid drop model

Early models of the nucleus viewed the nucleus as a rotating liquid drop. In this model, the trade-off of long-range electromagnetic forces and relatively short-range nuclear forces, together cause behavior which resembled surface tension forces in liquid drops of different sizes. This formula is successful at explaining many important phenomena of nuclei, such as their changing amounts of binding energy as their size and composition changes, but it does not explain the special stability which occurs when nuclei have special "magic numbers" of protons or neutrons.
The terms in the semi-empirical mass formula, which can be used to approximate the binding energy of many nuclei, are considered as the sum of five types of energies (see below). Then the picture of a nucleus as a drop of incompressible liquid roughly accounts for the observed variation of binding energy of the nucleus:


Volume energy. When an assembly of nucleons of the same size is packed together into the smallest volume, each interior nucleon has a certain number of other nucleons in contact with it. So, this nuclear energy is proportional to the volume.

Surface energy. A nucleon at the surface of a nucleus interacts with fewer other nucleons than one in the interior of the nucleus and hence its binding energy is less. This surface energy term takes that into account and is therefore negative and is proportional to the surface area.

Coulomb Energy. The electric repulsion between each pair of protons in a nucleus contributes toward decreasing its binding energy.

Asymmetry energy (also called Pauli Energy). An energy associated with the Pauli exclusion principle. Were it not for the Coulomb energy, the most stable form of nuclear matter would have the same number of neutrons as protons, since unequal numbers of neutrons and protons imply filling higher energy levels for one type of particle, while leaving lower energy levels vacant for the other type.

Pairing energy. An energy which is a correction term that arises from the tendency of proton pairs and neutron pairs to occur. An even number of particles is more stable than an odd number.

Shell models and other quantum models

A number of models for the nucleus have also been proposed in which nucleons occupy orbitals, much like the atomic orbitals in atomic physics theory. These wave models imagine nucleons to be either sizeless point particles in potential wells, or else probability waves as in the "optical model", frictionlessly orbiting at high speed in potential wells.
In the above models, the nucleons may occupy orbitals in pairs, due to being fermions, which allows explanation of even/odd Z and N effects well-known from experiments. The exact nature and capacity of nuclear shells differs from those of electrons in atomic orbitals, primarily because the potential well in which the nucleons move (especially in larger nuclei) is quite different from the central electromagnetic potential well which binds electrons in atoms. Some resemblance to atomic orbital models may be seen in a small atomic nucleus like that of helium-4, in which the two protons and two neutrons separately occupy 1s orbitals analogous to the 1s orbital for the two electrons in the helium atom, and achieve unusual stability for the same reason. Nuclei with 5 nucleons are all extremely unstable and short-lived, yet, helium-3, with 3 nucleons, is very stable even with lack of a closed 1s orbital shell. Another nucleus with 3 nucleons, the triton hydrogen-3 is unstable and will decay into helium-3 when isolated. Weak nuclear stability with 2 nucleons {NP} in the 1s orbital is found in the deuteron hydrogen-2, with only one nucleon in each of the proton and neutron potential wells. While each nucleon is a fermion, the {NP} deuteron is a boson and thus does not follow Pauli Exclusion for close packing within shells. Lithium-6 with 6 nucleons is highly stable without a closed second 1p shell orbital. For light nuclei with total nucleon numbers 1 to 6 only those with 5 do not show some evidence of stability. Observations of beta-stability of light nuclei outside closed shells indicate that nuclear stability is much more complex than simple closure of shell orbitals with magic numbers of protons and neutrons.

For larger nuclei, the shells occupied by nucleons begin to differ significantly from electron shells, but nevertheless, present nuclear theory does predict the magic numbers of filled nuclear shells for both protons and neutrons. The closure of the stable shells predicts unusually stable configurations, analogous to the noble group of nearly-inert gases in chemistry. An example is the stability of the closed shell of 50 protons, which allows tin to have 10 stable isotopes, more than any other element. Similarly, the distance from shell-closure explains the unusual instability of isotopes which have far from stable numbers of these particles, such as the radioactive elements 43 (technetium) and 61 (promethium), each of which is preceded and followed by 17 or more stable elements.

There are however problems with the shell model when an attempt is made to account for nuclear properties well away from closed shells. This has led to complex post hoc distortions of the shape of the potential well to fit experimental data, but the question remains whether these mathematical manipulations actually correspond to the spatial deformations in real nuclei. Problems with the shell model have led some to propose realistic two-body and three-body nuclear force effects involving nucleon clusters and then build the nucleus on this basis. Three such cluster models are the 1936 Resonating Group Structure model of John Wheeler, Close-Packed Spheron Model of Linus Pauling and the 2D Ising Model of MacGregor.

Consistency between models

As with the case of superfluid liquid helium, atomic nuclei are an example of a state in which both (1) "ordinary" particle physical rules for volume and (2) non-intuitive quantum mechanical rules for a wave-like nature apply. In superfluid helium, the helium atoms have volume, and essentially "touch" each other, yet at the same time exhibit strange bulk properties, consistent with a Bose–Einstein condensation. The nucleons in atomic nuclei also exhibit a wave-like nature and lack standard fluid properties, such as friction. For nuclei made of hadrons which are fermions, Bose-Einstein condensation does not occur, yet nevertheless, many nuclear properties can only be explained similarly by a combination of properties of particles with volume, in addition to the frictionless motion characteristic of the wave-like behavior of objects trapped in Erwin Schrödinger's quantum orbitals.

Magnetic confinement fusion

From Wikipedia, the free encyclopedia

The reaction chamber of the TCV, an experimental tokamak fusion reactor at École polytechnique fédérale de Lausanne, Lausanne, Switzerland which has been used in research since it was built in 1992. The characteristic torus-shaped chamber is clad with graphite to help withstand the extreme heat (the shape is distorted by the camera's fisheye lens).

Magnetic confinement fusion is an approach to generate thermonuclear fusion power that uses magnetic fields to confine the hot fusion fuel in the form of a plasma. Magnetic confinement is one of two major branches of fusion energy research, the other being inertial confinement fusion. The magnetic approach dates into the 1940s and has seen the majority of development since then. It is usually considered more promising for practical power production.

Fusion reactions combine light atomic nuclei such as hydrogen to form heavier ones such as helium, producing energy. In order to overcome the electrostatic repulsion between the nuclei, they must have a temperature of several tens of millions of degrees, under which conditions they no longer form neutral atoms but exist in the plasma state. In addition, sufficient density and energy confinement are required, as specified by the Lawson criterion.

At these temperatures, no material container could withstand the extreme heat of the plasma. Magnetic confinement fusion attempts to create these conditions by using the electrical conductivity of the plasma to contain it with magnetic fields. The basic concept can be thought of in a fluid picture as a balance between magnetic pressure and plasma pressure, or in terms of individual particles spiralling along magnetic field lines. Developing a suitable arrangement of fields that contain the fuel ions without introducing turbulence or leaking the fuel at a profuse rate has proven to be a difficult problem.

The development of MFE has gone through three distinct phases. In the 1950s it was believed MFE would be relatively easy to achieve, and this developed into a race to build a suitable machine. By the late 1950s, it was clear that turbulence and instabilities in the plasma were a serious problem, and during the 1960s, "the doldrums", effort turned to a better understanding of the physics of plasmas. In 1968, a Soviet team invented the tokamak magnetic confinement device, which demonstrated performance ten times better than the best alternatives. Since then the MFE field has been dominated by the tokamak approach. Construction of a 500-MW power generating fusion plant using this design, the ITER, began in France in 2007 and is scheduled to begin operation 2025.

Magnetic mirrors

A major area of research in the early years of fusion energy research was the magnetic mirror. Most early mirror devices attempted to confine plasma near the focus of a non-planar magnetic field generated in a solenoid with the field strength increased at either end of the tube. In order to escape the confinement area, nuclei had to enter a small annular area near each magnet. It was known that nuclei would escape through this area, but by adding and heating fuel continually it was felt this could be overcome.
In 1954, Edward Teller gave a talk in which he outlined a theoretical problem that suggested the plasma would also quickly escape sideways through the confinement fields. This would occur in any machine with convex magnetic fields, which existed in the centre of the mirror area. Existing machines were having other problems and it was not obvious whether this was occurring. In 1961, a Soviet team conclusively demonstrated this flute instability was indeed occurring, and when a US team stated they were not seeing this issue, the Soviets examined their experiment and noted this was due to a simple instrumentation error.

The Soviet team also introduced a potential solution, in the form of "Ioffe bars". These bent the plasma into a new shape that was concave at all points, avoiding the problem Teller had pointed out. This demonstrated a clear improvement in confinement. A UK team then introduced a simpler arrangement of these magnets they called the "tennis ball", which was taken up in the US as the "baseball". Several baseball series machines were tested and showed much-improved performance. However, theoretical calculations showed that the maximum amount of energy they could produce would be about the same as the energy needed to run the magnets. As a power-producing machine, the mirror appeared to be a dead end.

In the 1970s, a solution was developed. By placing a baseball coil at either end of a large solenoid, the entire assembly could hold a much larger volume of plasma, and thus produce more energy. Plans began to build a large device of this "tandem mirror" design, which became the Mirror Fusion Test Facility (MFTF). Having never tried this layout before, a smaller machine, the Tandem Mirror Experiment (TMX) was built to test this layout. TMX demonstrated a new series of problems that suggested MFTF would not reach its performance goals, and during construction MFTF was modified to MFTF-B. However, due to budget cuts, one day after the construction of MFTF was completed it was mothballed. Mirrors have seen little development since that time.

Toroidal machines

Z-pinch

The first real effort to build a control fusion reactor used the pinch effect in a toroidal container. A large transformer wrapping the container was used to induce a current in the plasma inside. This current creates a magnetic field that squeezes the plasma into a thin ring, thus "pinching" it. The combination of Joule heating by the current and adiabatic heating as it pinches raises the temperature of the plasma to the required range in the tens of millions of degrees Kelvin.

First built in the UK in 1948, and followed by a series of increasingly large and powerful machines in the UK and US, all early machines proved subject to powerful instabilities in the plasma. Notable among them was the kink instability, which caused the pinched ring to thrash about and hit the walls of the container long before it reached the required temperatures. The concept was so simple, however, that herculean effort was expended to address these issues.

This led to the "stabilized pinch" concept, which added external magnets to "give the plasma a backbone" while it compressed. The largest such machine was the UK's ZETA reactor, completed in 1957, which appeared to successfully produce fusion. Only a few months after its public announcement in January 1958, these claims had to be retracted when it was discovered the neutrons being seen were created by new instabilities in the plasma mass. Further studies showed any such design would be beset with similar problems, and research using the z-pinch approach largely ended.

Stellarators

An early attempt to build a magnetic confinement system was the stellarator, introduced by Lyman Spitzer in 1951. Essentially the stellarator consists of a torus that has been cut in half and then attached back together with straight "crossover" sections to form a figure-8. This has the effect of propagating the nuclei from the inside to outside as it orbits the device, thereby cancelling out the drift across the axis, at least if the nuclei orbit fast enough.
Not long after the construction of the earliest figure-8 machines, it was noticed the same effect could be achieved in a completely circular arrangement by adding a second set of helically-wound magnets on either side. This arrangement generated a field that extended only part way into the plasma, which proved to have the significant advantage of adding "shear", which suppressed turbulence in the plasma. However, as larger devices were built on this model, it was seen that plasma was escaping from the system much more rapidly than expected, much more rapidly than could be replaced.

By the mid-1960s it appeared the stellarator approach was a dead end. In addition to the fuel loss problems, it was also calculated that a power-producing machine based on this system would be enormous, the better part of a thousand feet long. When the tokamak was introduced in 1968, interest in the stellarator vanished, and the latest design at Princeton University, the Model C, was eventually converted to the Symmetrical Tokamak.

Stellarators have seen renewed interest since the turn of the millennium as they avoid several problems subsequently found in the tokamak. Newer models have been built, but these remain about two generations behind the latest tokamak designs.

Tokamaks

Tokamak magnetic fields.

In the late 1950s, Soviet researchers noticed that the kink instability would be strongly suppressed if the twists in the path were strong enough that a particle travelled around the circumference of the inside of the chamber more rapidly than around the chamber's length. This would require the pinch current to be reduced and the external stabilizing magnets to be made much stronger.

In 1968 Russian research on the toroidal tokamak was first presented in public, with results that far outstripped existing efforts from any competing design, magnetic or not. Since then the majority of effort in magnetic confinement has been based on the tokamak principle. In the tokamak a current is periodically driven through the plasma itself, creating a field "around" the torus that combines with the toroidal field to produce a winding field in some ways similar to that in a modern stellarator, at least in that nuclei move from the inside to the outside of the device as they flow around it.

In 1991, START was built at Culham, UK, as the first purpose-built spherical tokamak. This was essentially a spheromak with an inserted central rod. START produced impressive results, with β values at approximately 40% - three times that produced by standard tokamaks at the time. The concept has been scaled up to higher plasma currents and larger sizes, with the experiments NSTX (US), MAST (UK) and Globus-M (Russia) currently running. Spherical tokamaks have improved stability properties compared to conventional tokamaks and as such the area is receiving considerable experimental attention. However spherical tokamaks to date have been at low toroidal field and as such are impractical for fusion neutron devices.

Other

Some more novel configurations produced in toroidal machines are the reversed field pinch and the Levitated Dipole Experiment.

Compact toroids

Compact toroids, e.g. the spheromak and the Field-Reversed Configuration, attempt to combine the good confinement of closed magnetic surfaces configurations with the simplicity of machines without a central core. An early experiment of this type in the 1970s was Trisops. (Trisops fired two theta-pinch rings towards each other.)

Magnetic fusion energy

All of these devices have faced considerable problems being scaled up and in their approach toward the Lawson criterion. One researcher has described the magnetic confinement problem in simple terms, likening it to squeezing a balloon – the air will always attempt to "pop out" somewhere else. Turbulence in the plasma has proven to be a major problem, causing the plasma to escape the confinement area, and potentially touch the walls of the container. If this happens, a process known as "sputtering", high-mass particles from the container (often steel and other metals) are mixed into the fusion fuel, lowering its temperature.

In 1997, scientists at the Joint European Torus (JET) facilities in the UK produced 16 megawatts of fusion power. Scientists can now exercise a measure of control over plasma turbulence and resultant energy leakage, long considered an unavoidable and intractable feature of plasmas. There is increased optimism that the plasma pressure above which the plasma disassembles can now be made large enough to sustain a fusion reaction rate acceptable for a power plant. Electromagnetic waves can be injected and steered to manipulate the paths of plasma particles and then to produce the large electrical currents necessary to produce the magnetic fields to confine the plasma.

These and other control capabilities have come from advances in basic understanding of plasma science in such areas as plasma turbulence, plasma macroscopic stability, and plasma wave propagation. Much of this progress has been achieved with a particular emphasis on the tokamak.