Electromagnet

From Wikipedia, the free encyclopedia

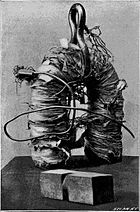
A simple electromagnet consisting of a coil of wire wrapped around an iron core. A core of ferromagnetic material like iron serves to increase the magnetic field created. The strength of magnetic field generated is proportional to the amount of current through the winding.

 

Magnetic field produced by a solenoid (coil of wire). This drawing shows a cross section through the center of the coil. The crosses are wires in which current is moving into the page; the dots are wires in which current is moving up out of the page.

An electromagnet is a type of magnet in which the magnetic field is produced by an electric current. The magnetic field disappears when the current is turned off. Electromagnets usually consist of wire wound into a coil. A current through the wire creates a magnetic field which is concentrated in the hole in the center of the coil. The wire turns are often wound around a magnetic core made from a ferromagnetic or ferrimagnetic material such as iron; the magnetic core concentrates the magnetic flux and makes a more powerful magnet.

The main advantage of an electromagnet over a permanent magnet is that the magnetic field can be quickly changed by controlling the amount of electric current in the winding. However, unlike a permanent magnet that needs no power, an electromagnet requires a continuous supply of current to maintain the magnetic field.

Electromagnets are widely used as components of other electrical devices, such as motors, generators, electromechanical solenoids, relays, loudspeakers, hard disks, MRI machines, scientific instruments, and magnetic separation equipment. Electromagnets are also employed in industry for picking up and moving heavy iron objects such as scrap iron and steel.

History

Sturgeon's electromagnet, 1824

 

One of Henry's electromagnets that could lift

hundreds of pounds, 1830s

 

Closeup of a large Henry electromagnet

Danish scientist Hans Christian Ørsted discovered in 1820 that electric currents create magnetic fields. British scientist William Sturgeon invented the electromagnet in 1824. His first electromagnet was a horseshoe-shaped piece of iron that was wrapped with about 18 turns of bare copper wire (insulated wire didn't exist yet). The iron was varnished to insulate it from the windings. When a current was passed through the coil, the iron became magnetized and attracted other pieces of iron; when the current was stopped, it lost magnetization. Sturgeon displayed its power by showing that although it only weighed seven ounces (roughly 200 grams), it could lift nine pounds (roughly 4 kilos) when the current of a single-cell battery was applied. However, Sturgeon's magnets were weak because the uninsulated wire he used could only be wrapped in a single spaced out layer around the core, limiting the number of turns.

Beginning in 1830, US scientist Joseph Henry systematically improved and popularized the electromagnet. By using wire insulated by silk thread, and inspired by Schweigger's use of multiple turns of wire to make a galvanometer, he was able to wind multiple layers of wire on cores, creating powerful magnets with thousands of turns of wire, including one that could support 2,063 lb (936 kg). The first major use for electromagnets was in telegraph sounders.

The magnetic domain theory of how ferromagnetic cores work was first proposed in 1906 by French physicist Pierre-Ernest Weiss, and the detailed modern quantum mechanical theory of ferromagnetism was worked out in the 1920s by Werner Heisenberg, Lev Landau, Felix Bloch and others.

Uses of electromagnets

Industrial electromagnet lifting scrap iron, 1914

A portative electromagnet is one designed to just hold material in place; an example is a lifting magnet. A tractive electromagnet applies a force and moves something.

Electromagnets are very widely used in electric and electromechanical devices, including:

• Motors and generators
• Transformers
• Relays
• Electric bells and buzzers
• Loudspeakers and headphones
• Actuators such as valves
• Magnetic recording and data storage equipment: tape recorders, VCRs, hard disks
• MRI machines
• Scientific equipment such as mass spectrometers
• Particle accelerators
• Magnetic locks
• Magnetic separation equipment, used for separating magnetic from nonmagnetic material, for example separating ferrous metal from other material in scrap.
• Industrial lifting magnets
• magnetic levitation, used in a maglev train or trains
• Induction heating for cooking, manufacturing, and hyperthermia therapy

Laboratory electromagnet. Produces 2 T field

with 20 A current.

 

Magnet in a mass spectrometer

 

AC electromagnet on the stator of an electric motor

 

Magnets in an electric bell

Simple solenoid

A common tractive electromagnet is a uniformly-wound solenoid and plunger. The solenoid is a coil of wire, and the plunger is made of a material such as soft iron. Applying a current to the solenoid applies a force to the plunger and may make it move. The plunger stops moving when the forces upon it are balanced. For example, the forces are balanced when the plunger is centered in the solenoid.

The maximum uniform pull happens when one end of the plunger is at the middle of the solenoid. An approximation for the force F is

${\displaystyle F=CAnI/l}$

where C is a proportionality constant, A is the cross-sectional area of the plunger, n is the number of turns in the solenoid, I is the current through the solenoid wire, and l is the length of the solenoid. For units using inches, pounds force, and amperes with long, slender, solenoids, the value of C is around 0.009 to 0.010 psi (maximum pull pounds per square inch of plunger cross-sectional area). For example, a 12-inch long coil (l=12 in) with a long plunger of 1-square inch cross section (A=1 in²) and 11,200 ampere-turns (n I=11,200 Aturn) had a maximum pull of 8.75 pounds (corresponding to C=0.0094 psi).

The maximum pull is increased when a magnetic stop is inserted into the solenoid. The stop becomes a magnet that will attract the plunger; it adds little to the solenoid pull when the plunger is far away but dramatically increases the pull when they are close. An approximation for the pull P is

${\displaystyle P=AnI[(nI/l_{\mathrm {a} }^{2}C_{1}^{2})+(C/l)]=(An^{2}I^{2}/l_{\mathrm {a} }^{2}C_{1}^{2})+(CAnI/l)}$

Here l_a is the distance between the end of the stop and the end of the plunger. The additional constant C₁ for units of inches, pounds, and amperes with slender solenoids is about 2660. The second term within the bracket represents the same force as the stop-less solenoid above; the first term represents the attraction between the stop and the plunger.

Some improvements can be made on the basic design. The ends of the stop and plunger are often conical. For example, the plunger may have a pointed end that fits into a matching recess in the stop. The shape makes the solenoid's pull more uniform as a function of separation. Another improvement is to add a magnetic return path around the outside of the solenoid (an "iron-clad solenoid"). The magnetic return path, just as the stop, has little impact until the air gap is small.

Physics

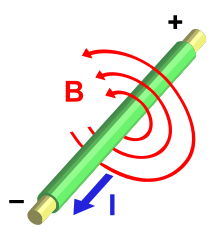
Current (I) through a wire produces a magnetic field (B). The field is oriented according to the right-hand rule.

 

The magnetic field lines of a current-carrying loop of wire pass through the center of the loop, concentrating the field there

An electric current flowing in a wire creates a magnetic field around the wire, due to Ampere's law (see drawing below). To concentrate the magnetic field, in an electromagnet the wire is wound into a coil with many turns of wire lying side by side. The magnetic field of all the turns of wire passes through the center of the coil, creating a strong magnetic field there. A coil forming the shape of a straight tube (a helix) is called a solenoid.

The direction of the magnetic field through a coil of wire can be found from a form of the right-hand rule. If the fingers of the right hand are curled around the coil in the direction of current flow (conventional current, flow of positive charge) through the windings, the thumb points in the direction of the field inside the coil. The side of the magnet that the field lines emerge from is defined to be the north pole.

Much stronger magnetic fields can be produced if a "magnetic core" of a soft ferromagnetic (or ferrimagnetic) material, such as iron, is placed inside the coil. A core can increase the magnetic field to thousands of times the strength of the field of the coil alone, due to the high magnetic permeability μ of the material. This is called a ferromagnetic-core or iron-core electromagnet. However, not all electromagnets use cores, and the very strongest electromagnets, such as superconducting and the very high current electromagnets, cannot use them due to saturation.

Ampere's law

For definitions of the variables below, see box at end of article.

The magnetic field of electromagnets in the general case is given by Ampere's Law:

${\displaystyle \int \mathbf {J} \cdot d\mathbf {A} =\oint \mathbf {H} \cdot d\mathbf {l} }$

which says that the integral of the magnetizing field H around any closed loop of the field is equal to the sum of the current flowing through the loop. Another equation used, that gives the magnetic field due to each small segment of current, is the Biot–Savart law. Computing the magnetic field and force exerted by ferromagnetic materials is difficult for two reasons. First, because the strength of the field varies from point to point in a complicated way, particularly outside the core and in air gaps, where fringing fields and leakage flux must be considered. Second, because the magnetic field B and force are nonlinear functions of the current, depending on the nonlinear relation between B and H for the particular core material used. For precise calculations, computer programs that can produce a model of the magnetic field using the finite element method are employed.

Magnetic core

The material of a magnetic core (often made of iron or steel) is composed of small regions called magnetic domains that act like tiny magnets (see ferromagnetism). Before the current in the electromagnet is turned on, the domains in the iron core point in random directions, so their tiny magnetic fields cancel each other out, and the iron has no large-scale magnetic field. When a current is passed through the wire wrapped around the iron, its magnetic field penetrates the iron, and causes the domains to turn, aligning parallel to the magnetic field, so their tiny magnetic fields add to the wire's field, creating a large magnetic field that extends into the space around the magnet. The effect of the core is to concentrate the field, and the magnetic field passes through the core more easily than it would pass through air.

The larger the current passed through the wire coil, the more the domains align, and the stronger the magnetic field is. Finally, all the domains are lined up, and further increases in current only cause slight increases in the magnetic field: this phenomenon is called saturation.

When the current in the coil is turned off, in the magnetically soft materials that are nearly always used as cores, most of the domains lose alignment and return to a random state and the field disappears. However, some of the alignment persists, because the domains have difficulty turning their direction of magnetization, leaving the core a weak permanent magnet. This phenomenon is called hysteresis and the remaining magnetic field is called remanent magnetism. The residual magnetization of the core can be removed by degaussing. In alternating current electromagnets, such as are used in motors, the core's magnetization is constantly reversed, and the remanence contributes to the motor's losses.

Magnetic circuit – the constant B field approximation

Magnetic field (green) of a typical electromagnet,with the iron core C forming a closed loop with two air gaps G in it.

B – magnetic field in the core

B_F – "fringing fields". In the gaps G the magnetic field lines "bulge" out, so the field strength is less than in the core: B_F < B

B_L – leakage flux; magnetic field lines which don't follow complete magnetic circuit

L – average length of the magnetic circuit used in eq. 1 below. It is the sum of the length L_core in the iron core pieces and the length L_gap in the air gaps G.

Both the leakage flux and the fringing fields get larger as the gaps are increased, reducing the force exerted by the magnet.

In many practical applications of electromagnets, such as motors, generators, transformers, lifting magnets, and loudspeakers, the iron core is in the form of a loop or magnetic circuit, possibly broken by a few narrow air gaps. This is because the magnetic field lines are in the form of closed loops. Iron presents much less "resistance" (reluctance) to the magnetic field than air, so a stronger field can be obtained if most of the magnetic field's path is within the core.

Since most of the magnetic field is confined within the outlines of the core loop, this allows a simplification of the mathematical analysis. See the drawing above. A common simplifying assumption satisfied by many electromagnets, which will be used in this section, is that the magnetic field strength B is constant around the magnetic circuit (within the core and air gaps) and zero outside it. Most of the magnetic field will be concentrated in the core material (C). Within the core the magnetic field (B) will be approximately uniform across any cross section, so if in addition the core has roughly constant area throughout its length, the field in the core will be constant. This just leaves the air gaps (G), if any, between core sections. In the gaps the magnetic field lines are no longer confined by the core, so they 'bulge' out beyond the outlines of the core before curving back to enter the next piece of core material, reducing the field strength in the gap. The bulges (B_F) are called fringing fields. However, as long as the length of the gap is smaller than the cross section dimensions of the core, the field in the gap will be approximately the same as in the core. In addition, some of the magnetic field lines (B_L) will take 'short cuts' and not pass through the entire core circuit, and thus will not contribute to the force exerted by the magnet. This also includes field lines that encircle the wire windings but do not enter the core. This is called leakage flux. Therefore, the equations in this section are valid for electromagnets for which:

1. the magnetic circuit is a single loop of core material, possibly broken by a few air gaps
2. the core has roughly the same cross sectional area throughout its length.
3. any air gaps between sections of core material are not large compared with the cross sectional dimensions of the core.
4. there is negligible leakage flux

The main nonlinear feature of ferromagnetic materials is that the B field saturates at a certain value, which is around 1.6 to 2 teslas (T) for most high permeability core steels. The B field increases quickly with increasing current up to that value, but above that value the field levels off and becomes almost constant, regardless of how much current is sent through the windings. So the maximum strength of the magnetic field possible from an iron core electromagnet is limited to around 1.6 to 2 T.

Magnetic field created by a current

The magnetic field created by an electromagnet is proportional to both the number of turns in the winding, N, and the current in the wire, I, hence this product, NI, in ampere-turns, is given the name magnetomotive force. For an electromagnet with a single magnetic circuit, of which length L_core of the magnetic field path is in the core material and length L_gap is in air gaps, Ampere's Law reduces to:

${\displaystyle NI=H_{\mathrm {core} }L_{\mathrm {core} }+H_{\mathrm {gap} }L_{\mathrm {gap} }\,}$

${\displaystyle NI=B\left({\frac {L_{\mathrm {core} }}{\mu }}+{\frac {L_{\mathrm {gap} }}{\mu _{0}}}\right)\qquad \qquad \qquad \qquad (1)\,}$

where

${\displaystyle \mu =B/H\,}$ is the magnetic permeability of the core material at the particular B field used.

${\displaystyle \mu _{0}=4\pi (10^{-7})\ \mathrm {N} \cdot \mathrm {A} ^{-2}}$ is the permeability of free space (or air); note that ${\displaystyle \mathrm {A} }$ in this definition is amperes.

This is a nonlinear equation, because the permeability of the core, μ, varies with the magnetic field B. For an exact solution, the value of μ at the B value used must be obtained from the core material hysteresis curve. If B is unknown, the equation must be solved by numerical methods. However, if the magnetomotive force is well above saturation, so the core material is in saturation, the magnetic field will be approximately the saturation value B_sat for the material, and won't vary much with changes in NI. For a closed magnetic circuit (no air gap) most core materials saturate at a magnetomotive force of roughly 800 ampere-turns per meter of flux path.

For most core materials, ${\displaystyle \mu _{r}=\mu /\mu _{0}\approx 2000-6000\,}$. So in equation (1) above, the second term dominates. Therefore, in magnetic circuits with an air gap, the strength of the magnetic field B depends strongly on the length of the air gap, and the length of the flux path in the core doesn't matter much. Given an air gap of 1mm, a magnetomotive force of about 796 Ampere-turns is required to produce a magnetic field of 1T.

Force exerted by magnetic field

The force exerted by an electromagnet on a section of core material is:

${\displaystyle F={\frac {B^{2}A}{2\mu _{0}}}\qquad \qquad \qquad \qquad \qquad \qquad (2)\,}$

where ${\displaystyle A}$ is the cross-sectional area of the core. The force equation can be derived from the energy stored in a magnetic field. Energy is force times distance. Rearranging terms yields the equation above.

The 1.6 T limit on the field mentioned above sets a limit on the maximum force per unit core area, or magnetic pressure, an iron-core electromagnet can exert; roughly:

${\displaystyle {\frac {F}{A}}={\frac {B_{sat}^{2}}{2\mu _{0}}}\approx 1000\ \mathrm {kPa} =10^{6}\mathrm {N/m^{2}} =145\ \mathrm {lbf} \cdot \mathrm {in} ^{-2}\,}$

In more intuitive units it's useful to remember that at 1 T the magnetic pressure is approximately 4 atmospheres, or kg/cm².

Given a core geometry, the B field needed for a given force can be calculated from (2); if it comes out to much more than 1.6 T, a larger core must be used.

Closed magnetic circuit

Cross section of lifting electromagnet like that in above photo, showing cylindrical construction. The windings (C) are flat copper strips to withstand the Lorentz force of the magnetic field. The core is formed by the thick iron housing (D) that wraps around the windings.

For a closed magnetic circuit (no air gap), such as would be found in an electromagnet lifting a piece of iron bridged across its poles, equation (1) becomes:

${\displaystyle B={\frac {NI\mu }{L}}\qquad \qquad \qquad \qquad \qquad \qquad (3)\,}$

Substituting into (2), the force is:

${\displaystyle F={\frac {\mu ^{2}N^{2}I^{2}A}{2\mu _{0}L^{2}}}\qquad \qquad \qquad \qquad \qquad (4)\,}$

It can be seen that to maximize the force, a core with a short flux path L and a wide cross-sectional area A is preferred (this also applies to magnets with an air gap). To achieve this, in applications like lifting magnets (see photo above) and loudspeakers a flat cylindrical design is often used. The winding is wrapped around a short wide cylindrical core that forms one pole, and a thick metal housing that wraps around the outside of the windings forms the other part of the magnetic circuit, bringing the magnetic field to the front to form the other pole.

Force between electromagnets

The above methods are applicable to electromagnets with a magnetic circuit and do not apply when a large part of the magnetic field path is outside the core. An example would be a magnet with a straight cylindrical core like the one shown at the top of this article. For electromagnets (or permanent magnets) with well defined 'poles' where the field lines emerge from the core, the force between two electromagnets can be found using the 'Gilbert model' which assumes the magnetic field is produced by fictitious 'magnetic charges' on the surface of the poles, with pole strength m and units of Ampere-turn meter. Magnetic pole strength of electromagnets can be found from:

${\displaystyle m={\frac {NIA}{L}}}$.

The force between two poles is:

${\displaystyle F={\frac {\mu _{0}m_{1}m_{2}}{4\pi r^{2}}}}$.

This model doesn't give the correct magnetic field inside the core and thus gives incorrect results if the pole of one magnet gets too close to another magnet.

Side effects

There are several side effects which occur in electromagnets which must be provided for in their design. These generally become more significant in larger electromagnets.

Ohmic heating

Large aluminum busbars carrying current into the electromagnets at the LNCMI (Laboratoire National des Champs Magnétiques Intenses) high field laboratory.

The only power consumed in a DC electromagnet under steady state conditions is due to the resistance of the windings, and is dissipated as heat. Some large electromagnets require cooling water circulating through pipes in the windings to carry off the waste heat.

Since the magnetic field is proportional to the product NI, the number of turns in the windings N and the current I can be chosen to minimize heat losses, as long as their product is constant. Since the power dissipation, P = I²R, increases with the square of the current but only increases approximately linearly with the number of windings, the power lost in the windings can be minimized by reducing I and increasing the number of turns N proportionally, or using thicker wire to reduce the resistance. For example, halving I and doubling N halves the power loss, as does doubling the area of the wire. In either case, increasing the amount of wire reduces the ohmic losses. For this reason, electromagnets often have a significant thickness of windings.

However, the limit to increasing N or lowering the resistance is that the windings take up more room between the magnet's core pieces. If the area available for the windings is filled up, more turns require going to a smaller diameter of wire, which has higher resistance, which cancels the advantage of using more turns. So in large magnets there is a minimum amount of heat loss that can't be reduced. This increases with the square of the magnetic flux B².

Inductive voltage spikes

An electromagnet has significant inductance, and resists changes in the current through its windings. Any sudden changes in the winding current cause large voltage spikes across the windings. This is because when the current through the magnet is increased, such as when it is turned on, energy from the circuit must be stored in the magnetic field. When it is turned off the energy in the field is returned to the circuit.

If an ordinary switch is used to control the winding current, this can cause sparks at the terminals of the switch. This doesn't occur when the magnet is switched on, because the limited supply voltage causes the current through the magnet and the field energy to increase slowly, but when it is switched off, the energy in the magnetic field is suddenly returned to the circuit, causing a large voltage spike and an arc across the switch contacts, which can damage them. With small electromagnets a capacitor is sometimes used across the contacts, which reduces arcing by temporarily storing the current. More often a diode is used to prevent voltage spikes by providing a path for the current to recirculate through the winding until the energy is dissipated as heat. The diode is connected across the winding, oriented so it is reverse-biased during steady state operation and doesn't conduct. When the supply voltage is removed, the voltage spike forward-biases the diode and the reactive current continues to flow through the winding, through the diode and back into the winding. A diode used in this way is called a freewheeling diode or flyback diode.

Large electromagnets are usually powered by variable current electronic power supplies, controlled by a microprocessor, which prevent voltage spikes by accomplishing current changes slowly, in gentle ramps. It may take several minutes to energize or deenergize a large magnet.

Lorentz forces

In powerful electromagnets, the magnetic field exerts a force on each turn of the windings, due to the Lorentz force ${\displaystyle q\mathbf {v} \times \mathbf {B} \,}$ acting on the moving charges within the wire. The Lorentz force is perpendicular to both the axis of the wire and the magnetic field. It can be visualized as a pressure between the magnetic field lines, pushing them apart. It has two effects on an electromagnet's windings:

• The field lines within the axis of the coil exert a radial force on each turn of the windings, tending to push them outward in all directions. This causes a tensile stress in the wire.
• The leakage field lines between each turn of the coil exert a repulsive force between adjacent turns, tending to push them apart.

The Lorentz forces increase with B². In large electromagnets the windings must be firmly clamped in place, to prevent motion on power-up and power-down from causing metal fatigue in the windings. In the Bitter design, below, used in very high field research magnets, the windings are constructed as flat disks to resist the radial forces, and clamped in an axial direction to resist the axial ones.

Core losses

In alternating current (AC) electromagnets, used in transformers, inductors, and AC motors and generators, the magnetic field is constantly changing. This causes energy losses in their magnetic cores that is dissipated as heat in the core. The losses stem from two processes:

• Eddy currents: From Faraday's law of induction, the changing magnetic field induces circulating electric currents inside nearby conductors, called eddy currents. The energy in these currents is dissipated as heat in the electrical resistance of the conductor, so they are a cause of energy loss. Since the magnet's iron core is conductive, and most of the magnetic field is concentrated there, eddy currents in the core are the major problem. Eddy currents are closed loops of current that flow in planes perpendicular to the magnetic field. The energy dissipated is proportional to the area enclosed by the loop. To prevent them, the cores of AC electromagnets are made of stacks of thin steel sheets, or laminations, oriented parallel to the magnetic field, with an insulating coating on the surface. The insulation layers prevent eddy current from flowing between the sheets. Any remaining eddy currents must flow within the cross-section of each individual lamination, which reduces losses greatly. Another alternative is to use a ferrite core, which is a nonconductor.
• Hysteresis losses: Reversing the direction of magnetization of the magnetic domains in the core material each cycle causes energy loss, because of the coercivity of the material. These losses are called hysteresis. The energy lost per cycle is proportional to the area of the hysteresis loop in the BH graph. To minimize this loss, magnetic cores used in transformers and other AC electromagnets are made of "soft" low coercivity materials, such as silicon steel or soft ferrite.

The energy loss per cycle of the AC current is constant for each of these processes, so the power loss increases linearly with frequency.

High field electromagnets

Superconducting electromagnets

The most powerful electromagnet in the world, the 45 T hybrid Bitter-superconducting magnet at the US National High Magnetic Field Laboratory, Tallahassee, Florida, USA

When a magnetic field higher than the ferromagnetic limit of 1.6 T is needed, superconducting electromagnets can be used. Instead of using ferromagnetic materials, these use superconducting windings cooled with liquid helium, which conduct current without electrical resistance. These allow enormous currents to flow, which generate intense magnetic fields. Superconducting magnets are limited by the field strength at which the winding material ceases to be superconducting. Current designs are limited to 10–20 T, with the current (2017) record of 32 T. The necessary refrigeration equipment and cryostat make them much more expensive than ordinary electromagnets. However, in high power applications this can be offset by lower operating costs, since after startup no power is required for the windings, since no energy is lost to ohmic heating. They are used in particle accelerators and MRI machines.

Bitter electromagnets

Both iron-core and superconducting electromagnets have limits to the field they can produce. Therefore, the most powerful man-made magnetic fields have been generated by air-core nonsuperconducting electromagnets of a design invented by Francis Bitter in 1933, called Bitter electromagnets. Instead of wire windings, a Bitter magnet consists of a solenoid made of a stack of conducting disks, arranged so that the current moves in a helical path through them, with a hole through the center where the maximum field is created. This design has the mechanical strength to withstand the extreme Lorentz forces of the field, which increase with B². The disks are pierced with holes through which cooling water passes to carry away the heat caused by the high current. The strongest continuous field achieved solely with a resistive magnet is 37.5 T as of 31 March 2014, produced by a Bitter electromagnet at the Radboud University High Field Magnet Laboratory in Nijmegen, Holland. The previous record was 35 T. The strongest continuous magnetic field overall, 45 T, was achieved in June 2000 with a hybrid device consisting of a Bitter magnet inside a superconducting magnet.

Explosively pumped flux compression

A hollow tube type of explosively pumped flux compression generator.

The factor limiting the strength of electromagnets is the inability to dissipate the enormous waste heat, so more powerful fields, up to 100 T, have been obtained from resistive magnets by sending brief pulses of high current through them; the inactive period after each pulse allows the heat produced during the pulse to be removed, before the next pulse. The most powerful manmade magnetic fields have been created by using explosives to compress the magnetic field inside an electromagnet as it is pulsed; these are called explosively pumped flux compression generators. The implosion compresses the magnetic field to values of around 1000 T for a few microseconds. While this method may seem very destructive, it is possible to redirect the brunt of the blast radially outwards so that neither the experiment nor the magnetic structure are harmed. These devices are known as destructive pulsed electromagnets. They are used in physics and materials science research to study the properties of materials at high magnetic fields.

Definition of terms

${\displaystyle A\,}$	square meter	cross sectional area of core
${\displaystyle B\,}$	tesla	Magnetic field (Magnetic flux density)
${\displaystyle F\,}$	newton	Force exerted by magnetic field
${\displaystyle H\,}$	ampere per meter	Magnetizing field
${\displaystyle I\,}$	ampere	Current in the winding wire
${\displaystyle L\,}$	meter	Total length of the magnetic field path ${\displaystyle L_{\mathrm {core} }+L_{\mathrm {gap} }\,}$
${\displaystyle L_{\mathrm {core} }\,}$	meter	Length of the magnetic field path in the core material
${\displaystyle L_{\mathrm {gap} }\,}$	meter	Length of the magnetic field path in air gaps
${\displaystyle m_{1},m_{2}\,}$	ampere meter	Pole strength of the electromagnet
${\displaystyle \mu \,}$	newton per square ampere	Permeability of the electromagnet core material
${\displaystyle \mu _{0}\,}$	newton per square ampere	Permeability of free space (or air) = 4π(10−7)
${\displaystyle \mu _{r}\,}$	-	Relative permeability of the electromagnet core material
${\displaystyle N\,}$	-	Number of turns of wire on the electromagnet
${\displaystyle r\,}$	meter	Distance between the poles of two electromagnets

Solenoid

From Wikipedia, the free encyclopedia

An illustration of a solenoid

 

Magnetic field created by a seven-loop solenoid (cross-sectional view) described using field lines.

A solenoid (/ˈsolə.nɔɪd/) (from the French solénoïde, derived in turn from the Greek solen ("pipe, channel") and eidos ("form, shape")) is a coil wound into a tightly packed helix. The term was invented by French physicist André-Marie Ampère to designate a helical coil.

In physics, the term refers to a coil whose length is substantially greater than its diameter, often wrapped around a metallic core, which produces a uniform magnetic field in a volume of space (where some experiment might be carried out) when an electric current is passed through it. A solenoid is a type of electromagnet whose purpose is to generate a controlled magnetic field. If the purpose of the solenoid is instead to impede changes in the electric current, a solenoid can be more specifically classified as an inductor rather than an electromagnet. Not all electromagnets and inductors are solenoids; for example, the first electromagnet, invented in 1824, had a horseshoe rather than a cylindrical solenoid shape.

In engineering, the term may also refer to a variety of transducer devices that convert energy into linear motion. The term is also often used to refer to a solenoid valve, which is an integrated device containing an electromechanical solenoid which actuates either a pneumatic or hydraulic valve, or a solenoid switch, which is a specific type of relay that internally uses an electromechanical solenoid to operate an electrical switch; for example, an automobile starter solenoid, or a linear solenoid, which is an electromechanical solenoid. Solenoid bolts, a type of electronic-mechanical locking mechanism, also exist.

Infinite continuous solenoid

An infinite solenoid is a solenoid with infinite length but finite diameter. Continuous means that the solenoid is not formed by discrete finite-width coils but by infinitely many infinitely-thin coils with no space between them; in this abstraction, the solenoid is often viewed as a cylindrical sheet of conductive material.

Inside

Figure 1: An infinite solenoid with 3 arbitrary Ampèrian loops labeled a, b and c. Integrating over path c demonstrates that the magnetic field inside the solenoid must be radially uniform.

The magnetic field inside an infinitely long solenoid is homogeneous and its strength neither depends on the distance from the axis, nor on the solenoid's cross-sectional area.

This is a derivation of the magnetic flux density around a solenoid that is long enough so that fringe effects can be ignored. In Figure 1, we immediately know that the flux density vector points in the positive z direction inside the solenoid, and in the negative z direction outside the solenoid. We confirm this by applying the right hand grip rule for the field around a wire. If we wrap our right hand around a wire with the thumb pointing in the direction of the current, the curl of the fingers shows how the field behaves. Since we are dealing with a long solenoid, all of the components of the magnetic field not pointing upwards cancel out by symmetry. Outside, a similar cancellation occurs, and the field is only pointing downwards.

Now consider the imaginary loop c that is located inside the solenoid. By Ampère's law, we know that the line integral of B (the magnetic flux density vector) around this loop is zero, since it encloses no electrical currents (it can be also assumed that the circuital electric field passing through the loop is constant under such conditions: a constant or constantly changing current through the solenoid). We have shown above that the field is pointing upwards inside the solenoid, so the horizontal portions of loop c do not contribute anything to the integral. Thus the integral of the up side 1 is equal to the integral of the down side 2. Since we can arbitrarily change the dimensions of the loop and get the same result, the only physical explanation is that the integrands are actually equal, that is, the magnetic field inside the solenoid is radially uniform. Note, though, that nothing prohibits it from varying longitudinally, which in fact it does.

Outside

A similar argument can be applied to the loop a to conclude that the field outside the solenoid is radially uniform or constant. This last result, which holds strictly true only near the centre of the solenoid where the field lines are parallel to its length, is important as it shows that the flux density outside is practically zero since the radii of the field outside the solenoid will tend to infinity.

An intuitive argument can also be used to show that the flux density outside the solenoid is actually zero. Magnetic field lines only exist as loops, they cannot diverge from or converge to a point like electric field lines can. The magnetic field lines follow the longitudinal path of the solenoid inside, so they must go in the opposite direction outside of the solenoid so that the lines can form a loop. However, the volume outside the solenoid is much greater than the volume inside, so the density of magnetic field lines outside is greatly reduced. Now recall that the field outside is constant. In order for the total number of field lines to be conserved, the field outside must go to zero as the solenoid gets longer.

Of course, if the solenoid is constructed as a wire spiral (as often done in practice), then it emanates an outside field the same way as a single wire, due to the current flowing overall down the length of the solenoid.

Quantitative description

Now we can consider the imaginary loop b. Take the line integral of B (the magnetic flux density vector) around the loop of length l. The horizontal components vanish, and the field outside is practically zero, so Ampère's Law gives us

${\displaystyle Bl=\mu _{0}NI,}$

where ${\displaystyle \mu _{0}}$ is the magnetic constant, ${\displaystyle N}$ the number of turns, and ${\displaystyle I}$ the current. From this we get

${\displaystyle B=\mu _{0}{\frac {NI}{l}}.}$

This equation is valid for a solenoid in free space, which means the permeability of the magnetic path is the same as permeability of free space, μ₀.

If the solenoid is immersed in a material with relative permeability μ_r, then the field is increased by that amount:

${\displaystyle B=\mu _{0}\mu _{\mathrm {r} }{\frac {NI}{l}}.}$

In most solenoids, the solenoid is not immersed in a higher permeability material, but rather some portion of the space around the solenoid has the higher permeability material and some is just air (which behaves much like free space). In that scenario, the full effect of the high permeability material is not seen, but there will be an effective (or apparent) permeability μ_eff such that 1 ≤ μ_eff ≤ μ_r.

The inclusion of a ferromagnetic core, such as iron, increases the magnitude of the magnetic flux density in the solenoid and raises the effective permeability of the magnetic path. This is expressed by the formula

${\displaystyle B=\mu _{0}\mu _{\mathrm {eff} }{\frac {NI}{l}}=\mu {\frac {NI}{l}},}$

where μ_eff is the effective or apparent permeability of the core. The effective permeability is a function of the geometric properties of the core and its relative permeability. The terms relative permeability (a property of just the material) and effective permeability (a property of the whole structure) are often confused; they can differ by many orders of magnitude.

For an open magnetic structure, the relationship between the effective permeability and relative permeability is given as follows:

${\displaystyle \mu _{\mathrm {eff} }={\frac {\mu _{r}}{1+k(\mu _{r}-1)}},}$

where k is the demagnetization factor of the core.

Finite continuous solenoid

Magnetic field line and density created by a solenoid with surface current density

A finite solenoid is a solenoid with finite length. Continuous means that the solenoid is not formed by discrete coils but by a sheet of conductive material. We assume the current is uniformly distributed on the surface of the solenoid, with a surface current density K; in cylindrical coordinates:

${\displaystyle {\vec {K}}={\frac {I}{L}}{\hat {\phi }}.}$

The magnetic field can be found using the vector potential, which for a finite solenoid with radius a and length L in cylindrical coordinates ${\displaystyle (\rho ,\phi ,z)}$ is

${\displaystyle A_{\phi }={\frac {\mu _{0}I}{4\pi }}{\frac {1}{L}}{\sqrt {\frac {a}{\rho }}}\left[\zeta k\left({\frac {k^{2}+h^{2}-h^{2}k^{2}}{h^{2}k^{2}}}K(k^{2})-{\frac {1}{k^{2}}}E(k^{2})+{\frac {h^{2}-1}{h^{2}}}\Pi (h^{2},k^{2})\right)\right]_{\zeta _{-}}^{\zeta _{+}},}$

where

${\displaystyle \zeta _{\pm }=z\pm {\frac {L}{2}},}$

${\displaystyle h^{2}={\frac {4a\rho }{(a+\rho )^{2}}},}$

${\displaystyle k^{2}={\frac {4a\rho }{(a+\rho )^{2}+\zeta ^{2}}},}$

${\displaystyle K(m)=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-m\sin ^{2}\theta }}}d\theta ,}$

${\displaystyle E(m)=\int _{0}^{\pi /2}{\sqrt {1-m\sin ^{2}\theta }}d\theta ,}$

${\displaystyle \Pi (n,m)=\int _{0}^{\pi /2}{\frac {1}{(1-n\sin ^{2}\theta ){\sqrt {1-m\sin ^{2}\theta }}}}d\theta .}$

Here, ${\displaystyle K(m)}$, ${\displaystyle E(m)}$, and ${\displaystyle \Pi (n,m)}$ are complete elliptic integrals of the first, second, and third kind.
Using

${\displaystyle {\vec {B}}=\nabla \times {\vec {A}},}$

the magnetic flux density is obtained as

${\displaystyle B_{\rho }={\frac {\mu _{0}I}{4\pi }}{\frac {1}{L}}{\sqrt {\frac {a}{\rho }}}\left[{\frac {k^{2}-2}{k}}K(k^{2})+{\frac {2}{k}}E(k^{2})\right]_{\zeta _{-}}^{\zeta _{+}},}$

${\displaystyle B_{z}=-{\frac {\mu _{0}I}{4\pi }}{\frac {1}{2L}}{\frac {1}{\sqrt {a\rho }}}\left[\zeta k\left(K(k^{2})+{\frac {a-\rho }{a+\rho }}\Pi (h^{2},k^{2})\right)\right]_{\zeta _{-}}^{\zeta _{+}}.}$

Inductance

As shown above, the magnetic flux density ${\displaystyle B}$ within the coil is practically constant and given by

${\displaystyle B=\mu _{0}{\frac {Ni}{l}},}$

where μ₀ is the magnetic constant, ${\displaystyle N}$ the number of turns, ${\displaystyle i}$ the current and ${\displaystyle l}$ the length of the coil. Ignoring end effects, the total magnetic flux through the coil is obtained by multiplying the flux density ${\displaystyle B}$ by the cross-section area ${\displaystyle A}$:

${\displaystyle \Phi =\mu _{0}{\frac {NiA}{l}}.}$

Combining this with the definition of inductance

${\displaystyle L={\frac {N\Phi }{i}},}$

the inductance of a solenoid follows as

${\displaystyle L=\mu _{0}{\frac {N^{2}A}{l}}.}$

A table of inductance for short solenoids of various diameter to length ratios has been calculated by Dellinger, Whittmore, and Ould.

This, and the inductance of more complicated shapes, can be derived from Maxwell's equations. For rigid air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current.

Similar analysis applies to a solenoid with a magnetic core, but only if the length of the coil is much greater than the product of the relative permeability of the magnetic core and the diameter. That limits the simple analysis to low-permeability cores, or extremely long thin solenoids. The presence of a core can be taken into account in the above equations by replacing the magnetic constant μ₀ with μ or μ₀μ_r, where μ represents permeability and μ_r relative permeability. Note that since the permeability of ferromagnetic materials changes with applied magnetic flux, the inductance of a coil with a ferromagnetic core will generally vary with current.

Applications

Electromechanical solenoid

A 1920 explanation of a commercial solenoid used as an electromechanical actuator

Electromechanical solenoids consist of an electromagnetically inductive coil, wound around a movable steel or iron slug (termed the armature). The coil is shaped such that the armature can be moved in and out of the center, altering the coil's inductance and thereby becoming an electromagnet. The armature is used to provide a mechanical force to some mechanism (such as controlling a pneumatic valve). Although typically weak over anything but very short distances, solenoids may be controlled directly by a controller circuit, and thus have very quick reaction times.

The force applied to the armature is proportional to the change in inductance of the coil with respect to the change in position of the armature, and the current flowing through the coil. The force applied to the armature will always move the armature in a direction that increases the coil's inductance.

Electromechanical solenoids are commonly seen in electronic paintball markers, pinball machines, dot matrix printers and fuel injectors. Some residential doorbells use electromechanical solenoids to hit metal chime bars.

Proportional Solenoid - Included in this category of solenoids are the uniquely designed magnetic circuits that effect analog positioning of the solenoid plunger or armature as a function of coil current. These solenoids, whether axial or rotary, employ a flux carrying geometry that both produces a high starting force (torque), and has a section that quickly begins to saturate magnetically. The resulting force (torque) profile as the solenoid progresses through its operational stroke is nearly flat or descends from a high to a lower value. The solenoid can be useful for positioning, stopping mid-stroke, or for low velocity actuation; especially in a closed loop control system. A uni-directional solenoid would actuate against an opposing force or a dual solenoid system would be self cycling. The proportional concept is more fully described in SAE publication 860759 (1986).

Proportional Solenoid Principles - Focusing of the magnetic field and its attendant flux metering, as illustrated in the SAE paper, is required to produce a high starting force at the start of the solenoid stroke and to maintain a level or declining force as the solenoid moves thru its displacement range. This is quite contrary to that experienced with normal diminishing air gap types of solenoids. The focusing of the magnetic field to the working air gap initially produces a high mmf (ampere turns) and relatively low flux level across the air gap. This high product of mmf x flux (read energy) produces a high starting force. As the plunger is incremented (ds) the energy of motion, F∙ds, is extracted from the air gap energy. Inherent with the plunger increment of motion, the air gap permeance increases slightly, the magnetic flux increases, the mmf across the air gap decreases slightly; all of which results in maintaining a high product of mmf x flux. Because of the increased flux level a rise in ampere-turns drops elsewhere in the ferrous circuit (predominately in the pole geometry) causes the reduction of air gap ampere-turns and, therefore, the reduced potential energy of the field at the air gap. Further incrementing of the plunger causes a continuing decrease of the solenoid force thus creating an ideal condition for motion control as controlled by the current to the solenoid coil. The aforementioned pole geometry, having a linearly changing path area, produces a nearly linear change in force. An opposing spring force or a dual ended solenoid (two coils) allows over and back motion control. Closed loop control improves the linearity and stiffness of the system.

Rotary solenoid

The rotary solenoid is an electromechanical device used to rotate a ratcheting mechanism when power is applied. These were used in the 1950s for rotary snap-switch automation in electromechanical controls. Repeated actuation of the rotary solenoid advances the snap-switch forward one position. Two rotary actuators on opposite ends of the rotary snap-switch shaft, can advance or reverse the switch position.

The rotary solenoid has a similar appearance to a linear solenoid, except that the core is mounted in the center of a large flat disk, with two or three inclined grooves cut into the underside of the disk. These grooves align with slots on the solenoid body, with ball bearings in the grooves.

When the solenoid is activated, the core is drawn into the coil, and the disk rotates on the ball bearings in the grooves as it moves towards the coil body. When power is removed, a spring on the disk rotates it back to its starting position, also pulling the core out of the coil.

The rotary solenoid was invented in 1944 by George H. Leland, of Dayton, Ohio, to provide a more reliable and shock/vibration tolerant release mechanism for air-dropped bombs. Previously used linear (axial) solenoids were prone to inadvertent releases. U.S. Patent number 2,496,880 describes the electromagnet and inclined raceways that are the basis of the invention. Leland's engineer, Earl W. Kerman, was instrumental in developing a compatible bomb release shackle that incorporated the rotary solenoid. Bomb shackles of this type are found in a B-29 aircraft fuselage on display at the National Museum of the USAF in Dayton, Ohio. Solenoids of this variety continue to be used in countless modern applications, and are still manufactured under Leland's original brand "Ledex", now owned by Johnson Electric.

Rotary voice coil

A rotary voice coil is a rotational version of a solenoid. Typically the fixed magnet is on the outside, and the coil part moves in an arc controlled by the current flow through the coils. Rotary voice coils are widely employed in devices such as disk drives. The working part of a moving coil meter is also a type of rotary voice coil that pivots around the pointer axis, a hairspring is usually used to provide a weak nearly linear restoring force.

Pneumatic solenoid valve

A pneumatic solenoid valve is a switch for routing air to any pneumatic device, usually an actuator, allowing a relatively small signal to control a large device. It is also the interface between electronic controllers and pneumatic systems.

Hydraulic solenoid valve

Hydraulic solenoid valves are in general similar to pneumatic solenoid valves except that they control the flow of hydraulic fluid (oil), often at around 3000 psi (210 bar, 21 MPa, 21 MN/m²). Hydraulic machinery uses solenoids to control the flow of oil to rams or actuators. Solenoid-controlled valves are often used in irrigation systems, where a relatively weak solenoid opens and closes a small pilot valve, which in turn activates the main valve by applying fluid pressure to a piston or diaphragm that is mechanically coupled to the main valve. Solenoids are also in everyday household items such as washing machines to control the flow and amount of water into the drum.

Transmission solenoids control fluid flow through an automatic transmission and are typically installed in the transmission valve body.

Automobile starter solenoid

In a car or truck, the starter solenoid is part of an automobile starting system. The starter solenoid receives a large electric current from the car battery and a small electric current from the ignition switch. When the ignition switch is turned on (i.e. when the key is turned to start the car), the small electric current forces the starter solenoid to close a pair of heavy contacts, thus relaying the large electric current to the starter motor.

Starter solenoids can also be built into the starter itself, often visible on the outside of the starter. If a starter solenoid receives insufficient power from the battery, it will fail to start the motor, and may produce a rapid 'clicking' or 'clacking' sound. This can be caused by a low or dead battery, by corroded or loose connections in the cable, or by a broken or damaged positive (red) cable from the battery. Any of these will result in some power to the solenoid, but not enough to hold the heavy contacts closed, so the starter motor itself never spins, and the engine doesn't start.