Diagram of orbital motion of a satellite around the earth, showing perpendicular velocity and acceleration (force) vectors.
Classical mechanics describes the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars and galaxies.
If the present state of an object is known it is possible to predict by the laws of classical mechanics how it will move in the future (determinism) and how it has moved in the past (reversibility).
The earliest development of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts employed by and the mathematical methods invented by Isaac Newton and Gottfried Wilhelm Leibniz and others in the 17th century to describe the motion of bodies under the influence of a system of forces.
Later, more abstract methods were developed, leading to the reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances, made predominantly in the 18th and 19th centuries, extend substantially beyond Newton's work, particularly through their use of analytical mechanics. They are, with some modification, also used in all areas of modern physics.
Classical mechanics provides extremely accurate results when studying large objects that are not extremely massive and speeds not approaching the speed of light. When the objects being examined have about the size of an atom diameter, it becomes necessary to introduce the other major sub-field of mechanics: quantum mechanics. To describe velocities that are not small compared to the speed of light, special relativity is needed. In case that objects become extremely massive, General relativity becomes applicable. However, a number of modern sources do include relativistic mechanics into classical physics, which in their view represents classical mechanics in its most developed and accurate form.
Description of the theory
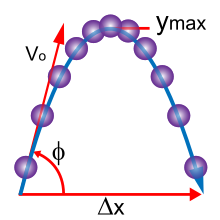
The analysis of projectile motion is a part of classical mechanics.
The following introduces the basic concepts of classical mechanics. For simplicity, it often models real-world objects as point particles (objects with negligible size). The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it. Each of these parameters is discussed in turn.
In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron, is more accurately described by quantum mechanics.) Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom, e.g., a baseball can spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made of a large number of collectively acting point particles. The center of mass of a composite object behaves like a point particle.
Classical mechanics uses common-sense notions of how matter and forces exist and interact. It assumes that matter and energy have definite, knowable attributes such as location in space and speed. Non-relativistic mechanics also assumes that forces act instantaneously).
Position and its derivatives
| position | m |
| angular position/angle | unitless (radian) |
| velocity | m·s−1 |
| angular velocity | s−1 |
| acceleration | m·s−2 |
| angular acceleration | s−2 |
| jerk | m·s−3 |
| "angular jerk" | s−3 |
| specific energy | m2·s−2 |
| absorbed dose rate | m2·s−3 |
| moment of inertia | kg·m2 |
| momentum | kg·m·s−1 |
| angular momentum | kg·m2·s−1 |
| force | kg·m·s−2 |
| torque | kg·m2·s−2 |
| energy | kg·m2·s−2 |
| power | kg·m2·s−3 |
| pressure and energy density | kg·m−1·s−2 |
| surface tension | kg·s−2 |
| spring constant | kg·s−2 |
| irradiance and energy flux | kg·s−3 |
| kinematic viscosity | m2·s−1 |
| dynamic viscosity | kg·m−1·s−1 |
| density (mass density) | kg·m−3 |
| density (weight density) | kg·m−2·s−2 |
| number density | m−3 |
| action | kg·m2·s−1 |
Velocity and speed
The velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time:- .
Mathematically, if the velocity of the first object in the previous discussion is denoted by the vector u = ud and the velocity of the second object by the vector v = ve, where u is the speed of the first object, v is the speed of the second object, and d and e are unit vectors in the directions of motion of each object respectively, then the velocity of the first object as seen by the second object is
Acceleration
The acceleration, or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time):Frames of reference
While the position, velocity and acceleration of a particle can be described with respect to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames.An inertial frame is a frame of reference within which an object interacting with no forces (an idealized situation) appears either at rest or moving uniformly in a straight line. This is the fundamental definition of an inertial frame. These are characterized by the requirement that all forces entering the observer's physical laws originate from identifiable sources caused by fields, such as electro-static field (caused by static electrical charges), electro-magnetic field (caused by moving charges), gravitational field (caused by mass), and so forth.
A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that do not accelerate with respect to distant stars (an extremely distant point) are regarded as good approximations to inertial frames. Non-inertial reference frames accelerate in relation to an existing inertial frame. They form the basis for Einstein's relativity. Due to the relative motion, particles in the non-inertial frame appear to move in ways not explained by forces from existing fields in the reference frame. Hence, it appears that there are other forces that enter the equations of motion solely as a result of the relative acceleration. These forces are referred to as fictitious forces, inertia forces, or pseudo-forces.
Consider two reference frames S and S'. For observers in each of the reference frames an event has space-time coordinates of (x,y,z,t) in frame S and (x',y',z',t') in frame S'. Assuming time is measured the same in all reference frames, and if we require x = x' when t = 0, then the relation between the space-time coordinates of the same event observed from the reference frames S' and S, which are moving at a relative velocity of u in the x direction is:
The transformations have the following consequences:
- v′ = v − u (the velocity v′ of a particle from the perspective of S′ is slower by u than its velocity v from the perspective of S)
- a′ = a (the acceleration of a particle is the same in any inertial reference frame)
- F′ = F (the force on a particle is the same in any inertial reference frame)
- the speed of light is not a constant in classical mechanics, nor does the special position given to the speed of light in relativistic mechanics have a counterpart in classical mechanics.
Forces; Newton's second law
Newton was the first to mathematically express the relationship between force and momentum. Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":As an example, assume that friction is the only force acting on the particle, and that it may be modeled as a function of the velocity of the particle, for example:
Important forces include the gravitational force and the Lorentz force for electromagnetism. In addition, Newton's third law can sometimes be used to deduce the forces acting on a particle: if it is known that particle A exerts a force F on another particle B, it follows that B must exert an equal and opposite reaction force, −F, on A. The strong form of Newton's third law requires that F and −F act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
Work and energy
If a constant force F is applied to a particle that makes a displacement Δr, the work done by the force is defined as the scalar product of the force and displacement vectors:The kinetic energy Ek of a particle of mass m travelling at speed v is given by
The work–energy theorem states that for a particle of constant mass m, the total work W done on the particle as it moves from position r1 to r2 is equal to the change in kinetic energy Ek of the particle:
Beyond Newton's laws
Classical mechanics also describes the more complex motions of extended non-pointlike objects. Euler's laws provide extensions to Newton's laws in this area. The concepts of angular momentum rely on the same calculus used to describe one-dimensional motion. The rocket equation extends the notion of rate of change of an object's momentum to include the effects of an object "losing mass".There are two important alternative formulations of classical mechanics: Lagrangian mechanics and Hamiltonian mechanics. These, and other modern formulations, usually bypass the concept of "force", instead referring to other physical quantities, such as energy, speed and momentum, for describing mechanical systems in generalized coordinates.
The expressions given above for momentum and kinetic energy are only valid when there is no significant electromagnetic contribution. In electromagnetism, Newton's second law for current-carrying wires breaks down unless one includes the electromagnetic field contribution to the momentum of the system as expressed by the Poynting vector divided by c2, where c is the speed of light in free space.
Limits of validity
Domain of validity for Classical Mechanics
Many branches of classical mechanics are simplifications or approximations of more accurate forms; two of the most accurate being general relativity and relativistic statistical mechanics. Geometric optics is an approximation to the quantum theory of light, and does not have a superior "classical" form.
When both quantum mechanics and classical mechanics cannot apply, such as at the quantum level with many degrees of freedom, quantum field theory (QFT) is of use. QFT deals with small distances and large speeds with many degrees of freedom as well as the possibility of any change in the number of particles throughout the interaction. When treating large degrees of freedom at the macroscopic level, statistical mechanics becomes useful. Statistical mechanics describes the behavior of large (but countable) numbers of particles and their interactions as a whole at the macroscopic level. Statistical mechanics is mainly used in thermodynamics for systems that lie outside the bounds of the assumptions of classical thermodynamics. In the case of high velocity objects approaching the speed of light, classical mechanics is enhanced by special relativity. In case that objects become extremely heavy (i.e. their Schwarzschild radius is not negligibly small for a given application), deviations from Newtonian mechanics become apparent and can be quantified by using the Parameterized post-Newtonian formalism. In that case, General relativity (GR) becomes applicable. However, until now there is no theory of Quantum gravity unifying GR and QFT in the sense that it could be used when objects become extremely small and heavy.
The Newtonian approximation to special relativity
In special relativity, the momentum of a particle is given byIf v is very small compared to c, v2/c2 is approximately zero, and so
For example, the relativistic cyclotron frequency of a cyclotron, gyrotron, or high voltage magnetron is given by
The classical approximation to quantum mechanics
The ray approximation of classical mechanics breaks down when the de Broglie wavelength is not much smaller than other dimensions of the system. For non-relativistic particles, this wavelength isAgain, this happens with electrons before it happens with heavier particles. For example, the electrons used by Clinton Davisson and Lester Germer in 1927, accelerated by 54 V, had a wavelength of 0.167 nm, which was long enough to exhibit a single diffraction side lobe when reflecting from the face of a nickel crystal with atomic spacing of 0.215 nm. With a larger vacuum chamber, it would seem relatively easy to increase the angular resolution from around a radian to a milliradian and see quantum diffraction from the periodic patterns of integrated circuit computer memory.
More practical examples of the failure of classical mechanics on an engineering scale are conduction by quantum tunneling in tunnel diodes and very narrow transistor gates in integrated circuits.
Classical mechanics is the same extreme high frequency approximation as geometric optics. It is more often accurate because it describes particles and bodies with rest mass. These have more momentum and therefore shorter De Broglie wavelengths than massless particles, such as light, with the same kinetic energies.
History
The study of the motion of bodies is an ancient one, making classical mechanics one of the oldest and largest subjects in science, engineering and technology,Some Greek philosophers of antiquity, among them Aristotle, founder of Aristotelian physics, may have been the first to maintain the idea that "everything happens for a reason" and that theoretical principles can assist in the understanding of nature. While to a modern reader, many of these preserved ideas come forth as eminently reasonable, there is a conspicuous lack of both mathematical theory and controlled experiment, as we know it. These later became decisive factors in forming modern science, and their early application came to be known as classical mechanics.
In his Elementa super demonstrationem ponderum, medieval mathematician Jordanus de Nemore introduced the concept of "positional gravity" and the use of component forces.
Three stage Theory of impetus according to Albert of Saxony.
The first published causal explanation of the motions of planets was Johannes Kepler's Astronomia nova, published in 1609. He concluded, based on Tycho Brahe's observations on the orbit of Mars, that the planet's orbits were ellipses. This break with ancient thought was happening around the same time that Galileo was proposing abstract mathematical laws for the motion of objects. He may (or may not) have performed the famous experiment of dropping two cannonballs of different weights from the tower of Pisa, showing that they both hit the ground at the same time. The reality of that particular experiment is disputed, but he did carry out quantitative experiments by rolling balls on an inclined plane. His theory of accelerated motion was derived from the results of such experiments and forms a cornerstone of classical mechanics.
Sir Isaac Newton (1643–1727), an influential figure in the history of physics and whose three laws of motion form the basis of classical mechanics
Newton founded his principles of natural philosophy on three proposed laws of motion: the law of inertia, his second law of acceleration (mentioned above), and the law of action and reaction; and hence laid the foundations for classical mechanics. Both Newton's second and third laws were given the proper scientific and mathematical treatment in Newton's Philosophiæ Naturalis Principia Mathematica. Here they are distinguished from earlier attempts at explaining similar phenomena, which were either incomplete, incorrect, or given little accurate mathematical expression. Newton also enunciated the principles of conservation of momentum and angular momentum. In mechanics, Newton was also the first to provide the first correct scientific and mathematical formulation of gravity in Newton's law of universal gravitation. The combination of Newton's laws of motion and gravitation provide the fullest and most accurate description of classical mechanics. He demonstrated that these laws apply to everyday objects as well as to celestial objects. In particular, he obtained a theoretical explanation of Kepler's laws of motion of the planets.
Newton had previously invented the calculus, of mathematics, and used it to perform the mathematical calculations. For acceptability, his book, the Principia, was formulated entirely in terms of the long-established geometric methods, which were soon eclipsed by his calculus. However, it was Leibniz who developed the notation of the derivative and integral preferred today.
Hamilton's greatest contribution is perhaps the reformulation of Newtonian mechanics, now called Hamiltonian mechanics.
Newton, and most of his contemporaries, with the notable exception of Huygens, worked on the assumption that classical mechanics would be able to explain all phenomena, including light, in the form of geometric optics. Even when discovering the so-called Newton's rings (a wave interference phenomenon) he maintained his own corpuscular theory of light.
After Newton, classical mechanics became a principal field of study in mathematics as well as physics. Several re-formulations progressively allowed finding solutions to a far greater number of problems. The first notable re-formulation was in 1788 by Joseph Louis Lagrange. Lagrangian mechanics was in turn re-formulated in 1833 by William Rowan Hamilton.
Some difficulties were discovered in the late 19th century that could only be resolved by more modern physics. Some of these difficulties related to compatibility with electromagnetic theory, and the famous Michelson–Morley experiment. The resolution of these problems led to the special theory of relativity, often still considered a part of classical mechanics.
A second set of difficulties were related to thermodynamics. When combined with thermodynamics, classical mechanics leads to the Gibbs paradox of classical statistical mechanics, in which entropy is not a well-defined quantity. Black-body radiation was not explained without the introduction of quanta. As experiments reached the atomic level, classical mechanics failed to explain, even approximately, such basic things as the energy levels and sizes of atoms and the photo-electric effect. The effort at resolving these problems led to the development of quantum mechanics.
Since the end of the 20th century, classical mechanics in physics has no longer been an independent theory. Instead, classical mechanics is now considered an approximate theory to the more general quantum mechanics. Emphasis has shifted to understanding the fundamental forces of nature as in the Standard model and its more modern extensions into a unified theory of everything. Classical mechanics is a theory useful for the study of the motion of non-quantum mechanical, low-energy particles in weak gravitational fields. Also, it has been extended into the complex domain where complex classical mechanics exhibits behaviors very similar to quantum mechanics.