From Wikipedia, the free encyclopedia
Tests of general relativity serve to establish observational evidence for the
theory of general relativity. The first three tests, proposed by Einstein in 1915, concerned the "anomalous"
precession of the
perihelion of
Mercury, the bending of light in
gravitational fields, and the
gravitational redshift. The precession of Mercury was already known; experiments showing light
bending in line with the predictions of general relativity was found in
1919, with increasing precision measurements done in subsequent tests,
and astrophysical measurement of the gravitational redshift was claimed
to be measured in 1925, although measurements sensitive enough to
actually confirm the theory were not done until 1954. A program of more
accurate tests starting in 1959 tested the various predictions of
general relativity with a further degree of accuracy in the weak
gravitational field limit, severely limiting possible deviations from
the theory.
In the 1970s, additional tests began to be made, starting with
Irwin Shapiro's measurement of the relativistic time delay in radar
signal travel time near the sun. Beginning in 1974,
Hulse,
Taylor and others have studied the behaviour of
binary pulsars
experiencing much stronger gravitational fields than those found in the
Solar System. Both in the weak field limit (as in the Solar System) and
with the stronger fields present in systems of binary pulsars the
predictions of general relativity have been extremely well tested
locally.
In February 2016, the
Advanced LIGO team announced that they had
directly detected gravitational waves from a black hole merger. This discovery, along with additional detections announced in June 2016 and June 2017, tested general relativity in the very strong field limit, observing to date no deviations from theory.
Classical tests
Albert Einstein proposed three tests of general relativity, subsequently called
the classical tests of general relativity, in 1916:
- the perihelion precession of Mercury's orbit
- the deflection of light by the Sun
- the gravitational redshift of light
In the letter to the
London Times
on November 28, 1919, he described the theory of relativity and thanked
his English colleagues for their understanding and testing of his work.
He also mentioned three classical tests with comments:
- "The chief attraction of the theory lies in its logical
completeness. If a single one of the conclusions drawn from it proves
wrong, it must be given up; to modify it without destroying the whole
structure seems to be impossible."
Perihelion precession of Mercury
Transit of Mercury on November 8, 2006 with
sunspots #921, 922, and 923
The perihelion precession of Mercury
Under
Newtonian physics, a two-body system consisting of a lone object orbiting a spherical mass would trace out an
ellipse with the spherical mass at a
focus. The point of closest approach, called the
periapsis (or, because the central body in the Solar System is the Sun,
perihelion),
is fixed. A number of effects in the Solar System cause the perihelia
of planets to precess (rotate) around the Sun. The principal cause is
the presence of other planets which
perturb one another's orbit. Another (much less significant) effect is solar
oblateness.
Mercury
deviates from the precession predicted from these Newtonian effects.
This anomalous rate of precession of the perihelion of Mercury's orbit
was first recognized in 1859 as a problem in
celestial mechanics, by
Urbain Le Verrier.
His reanalysis of available timed observations of transits of Mercury
over the Sun's disk from 1697 to 1848 showed that the actual rate of the
precession disagreed from that predicted from Newton's theory by 38″ (
arc seconds) per
tropical century (later re-estimated at 43″ by
Simon Newcomb in 1882). A number of
ad hoc and ultimately unsuccessful solutions were proposed, but they tended to introduce more problems.
In general relativity, this remaining
precession,
or change of orientation of the orbital ellipse within its orbital
plane, is explained by gravitation being mediated by the curvature of
spacetime. Einstein showed that general relativity
agrees closely with the observed amount of perihelion shift. This was a
powerful factor motivating the adoption of general relativity.
Although earlier measurements of planetary orbits were made using
conventional telescopes, more accurate measurements are now made with
radar. The total observed precession of Mercury is 574.10″±0.65 per century relative to the inertial
ICRF. This precession can be attributed to the following causes:
Sources of the precession of perihelion for Mercury
| Amount (arcsec/Julian century) |
Cause
|
| 532.3035 |
Gravitational tugs of other solar bodies
|
| 0.0286 |
Oblateness of the Sun (quadrupole moment)
|
| 42.9799 |
Gravitoelectric effects (Schwarzschild-like)
|
| −0.0020 |
Lense–Thirring precession
|
| 575.31 |
Total predicted
|
| 574.10±0.65 |
Observed
|
The correction by 42.98″ is 3/2 multiple of classical prediction with
PPN parameters 
. Thus the effect can be fully explained by general relativity. More
recent calculations based on more precise measurements have not
materially changed the situation.
In general relativity the perihelion shift
σ, expressed in radians per revolution, is approximately given by:

where
L is the
semi-major axis,
T is the
orbital period,
c is the speed of light, and
e is the
orbital eccentricity (see:
Two-body problem in general relativity).
The other planets experience perihelion shifts as well, but,
since they are farther from the Sun and have longer periods, their
shifts are lower, and could not be observed accurately until long after
Mercury's. For example, the perihelion shift of Earth's orbit due to
general relativity is of 3.84″ per century, and Venus's is 8.62″. Both
values have now been measured, with results in good agreement with
theory. The
periapsis shift has also now been measured for binary pulsar systems, with
PSR 1913+16 amounting to 4.2º per year. These observations are consistent with general relativity.
It is also possible to measure periapsis shift in binary star systems
which do not contain ultra-dense stars, but it is more difficult to
model the classical effects precisely – for example, the alignment of
the stars' spin to their orbital plane needs to be known and is hard to
measure directly. A few systems, such as
DI Herculis, have been measured as test cases for general relativity.
Deflection of light by the Sun
One of
Eddington's photographs of the 1919
solar eclipse experiment, presented in his 1920 paper announcing its success
Henry Cavendish in 1784 (in an unpublished manuscript) and
Johann Georg von Soldner in 1801 (published in 1804) had pointed out that Newtonian gravity predicts that starlight will bend around a massive object.
The same value as Soldner's was calculated by Einstein in 1911 based on
the equivalence principle alone. However, Einstein noted in 1915 in the
process of completing general relativity, that his (and thus Soldner's)
1911 result is only half of the correct value. Einstein became the
first to calculate the correct value for light bending.
The first observation of light deflection was performed by noting the change in position of
stars as they passed near the Sun on the
celestial sphere. The observations were performed by
Arthur Eddington and his collaborators during the total
solar eclipse of May 29, 1919, when the stars near the Sun (at that time in the constellation
Taurus) could be observed. Observations were made simultaneously in the cities of
Sobral, Ceará, Brazil and in
São Tomé and Príncipe on the west coast of Africa.
The result was considered spectacular news and made the front page of
most major newspapers. It made Einstein and his theory of general
relativity world-famous. When asked by his assistant what his reaction
would have been if general relativity had not been confirmed by
Eddington and Dyson in 1919, Einstein famously made the quip: "Then I
would feel sorry for the dear Lord. The theory is correct anyway."
The early accuracy, however, was poor. The results were argued by some to have been plagued by
systematic error and possibly
confirmation bias, although modern reanalysis of the dataset suggests that Eddington's analysis was accurate. The measurement was repeated by a team from the
Lick Observatory in the
1922 eclipse, with results that agreed with the 1919 results and has been repeated several times since, most notably in 1953 by
Yerkes Observatory astronomers and in 1973 by a team from the
University of Texas. Considerable uncertainty remained in these measurements for almost fifty years, until observations started being made at
radio frequencies.
While the Sun is too close by for an
Einstein ring
to lie outside its corona, such a ring formed by the deflection of
light from distant galaxies has been observed for a nearby star.
Gravitational redshift of light
The gravitational redshift of a light wave as it moves upwards against a gravitational field (caused by the yellow star below).
Einstein predicted the
gravitational redshift of light from the
equivalence principle in 1907, and it was predicted that this effect might be measured in the spectral lines of a
white dwarf star, which has a very high gravitational field. Initial attempts to measure the gravitational redshift of the spectrum of
Sirius-B, were done by
Walter Sydney Adams
in 1925, but the result was criticized as being unusable due to the
contamination from light from the (much brighter) primary star,
Sirius.
The first accurate measurement of the gravitational redshift of a white
dwarf was done by Popper in 1954, measuring a 21 km/sec gravitational
redshift of
40 Eridani B.
The redshift of Sirius B was finally measured by Greenstein
et al.
in 1971, obtaining the value for the gravitational redshift of
89±19 km/sec, with more accurate measurements by the Hubble Space
Telescope showing 80.4±4.8 km/sec.
Tests of special relativity
The general theory of relativity incorporates Einstein's
special theory of relativity, and hence test of special relativity are also testing aspects of general relativity. As a consequence of the
equivalence principle,
Lorentz invariance
holds locally in non-rotating, freely falling reference frames. Experiments related to Lorentz invariance special relativity (that is,
when gravitational effects can be neglected) are described in
tests of special relativity.
Modern tests
The modern era of testing general relativity was ushered in largely at the impetus of
Dicke and
Schiff who laid out a framework for testing general relativity.
They emphasized the importance not only of the classical tests, but of
null experiments, testing for effects which in principle could occur in a
theory of gravitation, but do not occur in general relativity. Other
important theoretical developments included the inception of
alternative theories to general relativity, in particular,
scalar-tensor theories such as the
Brans–Dicke theory; the
parameterized post-Newtonian formalism in which deviations from general relativity can be quantified; and the framework of the
equivalence principle.
Experimentally, new developments in
space exploration,
electronics and
condensed matter physics
have made additional precise experiments possible, such as the
Pound–Rebka experiment, laser interferometry and lunar rangefinding.
Post-Newtonian tests of gravity
Early
tests of general relativity were hampered by the lack of viable
competitors to the theory: it was not clear what sorts of tests would
distinguish it from its competitors. General relativity was the only
known relativistic theory of gravity compatible with special relativity
and observations. Moreover, it is an extremely simple and elegant
theory. This changed with the introduction of
Brans–Dicke theory in 1960. This theory is arguably simpler, as it contains no
dimensionful constants, and is compatible with a version of
Mach's principle and
Dirac's large numbers hypothesis,
two philosophical ideas which have been influential in the history of
relativity. Ultimately, this led to the development of the
parametrized post-Newtonian formalism by
Nordtvedt and
Will,
which parametrizes, in terms of ten adjustable parameters, all the
possible departures from Newton's law of universal gravitation to first
order in the velocity of moving objects (
i.e. to first order in

, where
v is the velocity of an object and
c
is the speed of light). This approximation allows the possible
deviations from general relativity, for slowly moving objects in weak
gravitational fields, to be systematically analyzed. Much effort has
been put into constraining the post-Newtonian parameters, and deviations
from general relativity are at present severely limited.
The experiments testing gravitational lensing and light time
delay limits the same post-Newtonian parameter, the so-called Eddington
parameter γ, which is a straightforward parametrization of the amount of
deflection of light by a gravitational source. It is equal to one for
general relativity, and takes different values in other theories (such
as Brans–Dicke theory). It is the best constrained of the ten
post-Newtonian parameters, but there are other experiments designed to
constrain the others. Precise observations of the perihelion shift of
Mercury constrain other parameters, as do tests of the strong
equivalence principle.
One of the goals of the
BepiColombo
mission to Mercury, is to test the general relativity theory by
measuring the parameters gamma and beta of the parametrized
post-Newtonian formalism with high accuracy. The experiment is part of the Mercury Orbiter Radio science Experiment (MORE). The spacecraft was launched in October 2018 and is expected to enter orbit around Mercury in December 2025.
Gravitational lensing
One of the most important tests is
gravitational lensing.
It has been observed in distant astrophysical sources, but these are
poorly controlled and it is uncertain how they constrain general
relativity. The most precise tests are analogous to Eddington's 1919
experiment: they measure the deflection of radiation from a distant
source by the Sun. The sources that can be most precisely analyzed are
distant
radio sources. In particular, some
quasars
are very strong radio sources. The directional resolution of any
telescope is in principle limited by diffraction; for radio telescopes
this is also the practical limit. An important improvement in obtaining
positional high accuracies (from milli-arcsecond to micro-arcsecond) was
obtained by combining radio telescopes across Earth. The technique is
called
very long baseline interferometry
(VLBI). With this technique radio observations couple the phase
information of the radio signal observed in telescopes separated over
large distances. Recently, these telescopes have measured the deflection
of radio waves by the Sun to extremely high precision, confirming the
amount of deflection predicted by general relativity aspect to the 0.03%
level.
At this level of precision systematic effects have to be carefully
taken into account to determine the precise location of the telescopes
on Earth. Some important effects are Earth's
nutation,
rotation, atmospheric refraction, tectonic displacement and tidal
waves. Another important effect is refraction of the radio waves by the
solar corona. Fortunately, this effect has a characteristic
spectrum,
whereas gravitational distortion is independent of wavelength. Thus,
careful analysis, using measurements at several frequencies, can
subtract this source of error.
The entire sky is slightly distorted due to the gravitational
deflection of light caused by the Sun (the anti-Sun direction excepted).
This effect has been observed by the
European Space Agency astrometric satellite
Hipparcos. It measured the positions of about 10
5 stars. During the full mission about
3.5×106
relative positions have been determined, each to an accuracy of
typically 3 milliarcseconds (the accuracy for an 8–9 magnitude star).
Since the gravitation deflection perpendicular to the Earth–Sun
direction is already 4.07 milliarcseconds, corrections are needed for
practically all stars. Without systematic effects, the error in an
individual observation of 3 milliarcseconds, could be reduced by the
square root of the number of positions, leading to a precision of 0.0016
milliarcseconds. Systematic effects, however, limit the accuracy of the
determination to 0.3% (Froeschlé, 1997).
Launched in 2013, the
Gaia spacecraft will conduct a census of one billion
stars in the
Milky Way
and measure their positions to an accuracy of 24 microarcseconds. Thus
it will also provide stringent new tests of gravitational deflection of
light caused by the
Sun which was predicted by General relativity.
Light travel time delay testing
Irwin I. Shapiro
proposed another test, beyond the classical tests, which could be
performed within the Solar System. It is sometimes called the fourth
"classical" test of
general relativity. He predicted a relativistic time delay (
Shapiro delay) in the round-trip travel time for radar signals reflecting off other planets. The mere curvature of the path of a
photon
passing near the Sun is too small to have an observable delaying effect
(when the round-trip time is compared to the time taken if the photon
had followed a straight path), but general relativity predicts a time
delay that becomes progressively larger when the photon passes nearer to
the Sun due to the
time dilation in the
gravitational potential
of the Sun. Observing radar reflections from Mercury and Venus just
before and after it is eclipsed by the Sun agrees with general
relativity theory at the 5% level. More recently, the
Cassini probe has undertaken a similar experiment which gave agreement with general relativity at the 0.002% level. However, the following detailed studies revealed that the measured value of the PPN parameter gamma is affected by
gravitomagnetic effect caused by the orbital motion of Sun around the
barycenter of the solar system. The gravitomagnetic effect in the
Cassini
radioscience experiment was implicitly postulated by B. Berotti as
having a pure general relativistic origin but its theoretical value has
never been tested in the experiment which effectively makes the
experimental uncertainty in the measured value of gamma actually larger
(by a factor of 10) than 0.002% claimed by B. Berotti and co-authors in
Nature.
Very Long Baseline Interferometry has measured velocity-dependent
(gravitomagnetic) corrections to the Shapiro time delay in the field of
moving Jupiter and Saturn.
The equivalence principle
The equivalence principle, in its simplest form, asserts that the
trajectories of falling bodies in a gravitational field should be
independent of their mass and internal structure, provided they are
small enough not to disturb the environment or be affected by
tidal forces. This idea has been tested to extremely high precision by
Eötvös torsion balance experiments,
which look for a differential acceleration between two test masses.
Constraints on this, and on the existence of a composition-dependent
fifth force or gravitational
Yukawa interaction are very strong, and are discussed under
fifth force and
weak equivalence principle.
A version of the equivalence principle, called the
strong equivalence principle,
asserts that self-gravitation falling bodies, such as stars, planets or
black holes (which are all held together by their gravitational
attraction) should follow the same trajectories in a gravitational
field, provided the same conditions are satisfied. This is called the
Nordtvedt effect and is most precisely tested by the
Lunar Laser Ranging Experiment.
Since 1969, it has continuously measured the distance from several
rangefinding stations on Earth to reflectors on the Moon to
approximately centimeter accuracy. These have provided a strong constraint on several of the other post-Newtonian parameters.
Another part of the strong equivalence principle is the
requirement that Newton's gravitational constant be constant in time,
and have the same value everywhere in the universe. There are many
independent observations limiting the possible variation of Newton's
gravitational constant,
but one of the best comes from lunar rangefinding which suggests that
the gravitational constant does not change by more than one part in 10
11 per year. The constancy of the other constants is discussed in the
Einstein equivalence principle section of the equivalence principle article.
Gravitational redshift
The first of the classical tests discussed above, the
gravitational redshift, is a simple consequence of the
Einstein equivalence principle
and was predicted by Einstein in 1907. As such, it is not a test of
general relativity in the same way as the post-Newtonian tests, because
any theory of gravity obeying the equivalence principle should also
incorporate the gravitational redshift. Nonetheless, confirming the
existence of the effect was an important substantiation of relativistic
gravity, since the absence of gravitational redshift would have strongly
contradicted relativity. The first observation of the gravitational
redshift was the measurement of the shift in the spectral lines from the
white dwarf star
Sirius
B by Adams in 1925, discussed above, and follow-on measurements of
other white dwarfs. Because of the difficulty of the astrophysical
measurement, however, experimental verification using a known
terrestrial source was preferable.
Experimental verification of gravitational redshift using
terrestrial sources took several decades, because it is difficult to
find clocks (to measure
time dilation)
or sources of electromagnetic radiation (to measure redshift) with a
frequency that is known well enough that the effect can be accurately
measured. It was confirmed experimentally for the first time in 1959
using measurements of the change in wavelength of gamma-ray photons
generated with the
Mössbauer effect, which generates radiation with a very narrow line width. The
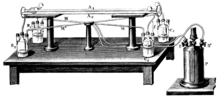
Pound–Rebka experiment measured the relative redshift of two sources situated at the top and bottom of Harvard University's Jefferson tower.
The result was in excellent agreement with general relativity. This was
one of the first precision experiments testing general relativity. The
experiment was later improved to better than the 1% level by Pound and
Snider.
The blueshift of a falling photon can be found by assuming it has an equivalent mass based on its frequency

(where
h is
Planck's constant) along with

,
a result of special relativity. Such simple derivations ignore the fact
that in general relativity the experiment compares clock rates, rather
than energies. In other words, the "higher energy" of the photon after
it falls can be equivalently ascribed to the slower running of clocks
deeper in the gravitational potential well. To fully validate general
relativity, it is important to also show that the rate of arrival of the
photons is greater than the rate at which they are emitted. A very
accurate gravitational redshift experiment, which deals with this issue,
was performed in 1976, where a
hydrogen maser
clock on a rocket was launched to a height of 10,000 km, and its rate
compared with an identical clock on the ground. It tested the
gravitational redshift to 0.007%.
Although the
Global Positioning System
(GPS) is not designed as a test of fundamental physics, it must account
for the gravitational redshift in its timing system, and physicists
have analyzed timing data from the GPS to confirm other tests. When the
first satellite was launched, some engineers resisted the prediction
that a noticeable gravitational time dilation would occur, so the first
satellite was launched without the clock adjustment that was later built
into subsequent satellites. It showed the predicted shift of 38
microseconds per day. This rate of discrepancy is sufficient to
substantially impair function of GPS within hours if not accounted for.
An excellent account of the role played by general relativity in the
design of GPS can be found in Ashby 2003.
Other precision tests of general relativity, not discussed here, are the
Gravity Probe A
satellite, launched in 1976, which showed gravity and velocity affect
the ability to synchronize the rates of clocks orbiting a central mass
and the
Hafele–Keating experiment, which used atomic clocks in circumnavigating aircraft to test general relativity and special relativity together.
Frame-dragging tests
The LAGEOS-1 satellite. (
D=60 cm)
Tests of the
Lense–Thirring precession, consisting of small secular
precessions
of the orbit of a test particle in motion around a central rotating
mass, for example, a planet or a star, have been performed with the
LAGEOS satellites, but many aspects of them remain controversial. The same effect may have been detected in the data of the
Mars Global Surveyor (MGS) spacecraft, a former probe in orbit around
Mars; also such a test raised a debate. First attempts to detect the
Sun's Lense–Thirring effect on the
perihelia of the inner
planets have been recently reported as well. Frame dragging would cause the orbital plane of stars orbiting near a
supermassive black hole to precess about the black hole spin axis. This effect should be detectable within the next few years via
astrometric monitoring of stars at the center of the
Milky Way galaxy. By comparing the rate of orbital precession of two stars on different orbits, it is possible in principle to test the
no-hair theorems of general relativity.
The
Gravity Probe B satellite, launched in 2004 and operated until 2005, detected frame-dragging and the
geodetic effect.
The experiment used four quartz spheres the size of ping pong balls
coated with a superconductor. Data analysis continued through 2011 due
to high noise levels and difficulties in modelling the noise accurately
so that a useful signal could be found. Principal investigators at
Stanford University reported on May 4, 2011, that they had accurately measured the frame dragging effect relative to the distant star
IM Pegasi, and the calculations proved to be in line with the prediction of Einstein's theory. The results, published in
Physical Review Letters measured the
geodetic effect
with an error of about 0.2 percent. The results reported the frame
dragging effect (caused by Earth's rotation) added up to 37
milliarcseconds with an error of about 19 percent. Investigator Francis Everitt explained that a milliarcsecond "is the width of a human hair seen at the distance of 10 miles".
In January 2012,
LARES satellite was launched on a
Vega rocket to measure
Lense–Thirring effect with an accuracy of about 1%, according to its proponents.
This evaluation of the actual accuracy obtainable is a subject of debate.
Tests of the gravitational potential at small distances
It
is possible to test whether the gravitational potential continues with
the inverse square law at very small distances. Tests so far have
focused on a divergence from GR in the form of a
Yukawa potential 
, but no evidence for a potential of this kind has been found. The Yukawa potential with

has been ruled out down to

m.
Strong field tests
The very strong gravitational fields that are present close to
black holes, especially those
supermassive black holes which are thought to power
active galactic nuclei and the more active
quasars,
belong to a field of intense active research. Observations of these
quasars and active galactic nuclei are difficult, and interpretation of
the observations is heavily dependent upon astrophysical models other
than general relativity or competing fundamental
theories of gravitation, but they are qualitatively consistent with the black hole concept as modeled in general relativity.
Binary pulsars
Pulsars are rapidly rotating
neutron stars
which emit regular radio pulses as they rotate. As such they act as
clocks which allow very precise monitoring of their orbital motions.
Observations of pulsars in orbit around other stars have all
demonstrated substantial
periapsis
precessions that cannot be accounted for classically but can be
accounted for by using general relativity. For example, the Hulse–Taylor
binary pulsar PSR B1913+16
(a pair of neutron stars in which one is detected as a pulsar) has an
observed precession of over 4° of arc per year (periastron shift per
orbit only about 10
−6). This precession has been used to compute the masses of the components.
Similarly to the way in which atoms and molecules emit electromagnetic radiation, a gravitating mass that is in
quadrupole type or higher order vibration, or is asymmetric and in rotation, can emit gravitational waves. These
gravitational waves are predicted to travel at the
speed of light.
For example, planets orbiting the Sun constantly lose energy via
gravitational radiation, but this effect is so small that it is unlikely
it will be observed in the near future (Earth radiates about 200 watts of gravitational radiation).
The radiation of gravitational waves has been inferred from the
Hulse–Taylor binary (and other binary pulsars). Precise timing of the pulses shows that the stars orbit only approximately according to
Kepler's Laws: over time they gradually spiral towards each other, demonstrating an
energy loss in close agreement with the predicted energy radiated by gravitational waves. For their discovery of the first binary pulsar and measuring its orbital decay due to gravitational-wave emission,
Hulse and
Taylor won the 1993
Nobel Prize in Physics.
A "double pulsar" discovered in 2003,
PSR J0737-3039, has a periastron precession of 16.90° per year; unlike the Hulse–Taylor binary, both
neutron stars
are detected as pulsars, allowing precision timing of both members of
the system. Due to this, the tight orbit, the fact that the system is
almost edge-on, and the very low transverse velocity of the system as
seen from Earth, J0737−3039 provides by far the best system for
strong-field tests of general relativity known so far. Several distinct
relativistic effects are observed, including orbital decay as in the
Hulse–Taylor system. After observing the system for two and a half
years, four independent tests of general relativity were possible, the
most precise (the Shapiro delay) confirming the general relativity
prediction within 0.05%
(nevertheless the periastron shift per orbit is only about 0.0013% of a
circle and thus it is not a higher-order relativity test).
In 2013, an international team of astronomers reported new data from observing a pulsar-white dwarf system
PSR J0348+0432,
in which they have been able to measure a change in the orbital period
of 8 millionths of a second per year, and confirmed GR predictions in a
regime of extreme gravitational fields never probed before; but there are still some competing theories that would agree with these data.
Direct detection of gravitational waves
A number of
gravitational-wave detectors
have been built with the intent of directly detecting the gravitational
waves emanating from such astronomical events as the merger of two
neutron stars or
black holes. In February 2016, the
Advanced LIGO team announced that they had
directly detected gravitational waves from a stellar
binary black hole merger, with additional detections announced in June 2016, June 2017, and August 2017.
General relativity predicts gravitational waves, as does any
theory of gravitation in which changes in the gravitational field
propagate at a finite speed. Since gravitational waves can be directly detected, it is possible to use them to learn about the Universe. This is
gravitational-wave astronomy. Gravitational-wave astronomy can test general relativity by verifying
that the observed waves are of the form predicted (for example, that
they only have two transverse polarizations), and by checking that
black holes are the objects described by solutions of the
Einstein field equations.
"These amazing observations are the confirmation of a lot of
theoretical work, including Einstein's general theory of relativity,
which predicts gravitational waves," said Stephen Hawking.
Gravitational redshift
Gravitational redshift in light from the
S2 star orbiting the supermassive black hole
Sagittarius A* in the center of the Milky Way has been measured with the
Very Large Telescope using GRAVITY, NACO and SIFONI instruments.
Strong equivalence principle
The
strong equivalence principle of general relativity requires
universality of free fall to apply even to bodies with strong
self-gravity. Direct tests of this principle using Solar System bodies
are limited by the weak self-gravity of the bodies, and tests using
pulsar–white-dwarf binaries have been limited by the weak gravitational
pull of the Milky Way. With the discovery of a triple star system called
PSR J0337+1715,
located about 4,200 light-years from Earth, the strong equivalence
principle can be tested with a high accuracy. This system contains a
neutron star in a 1.6-day orbit with a
white dwarf
star, and the pair in a 327-day orbit with another white dwarf further
away. This system permits a test that compares how the gravitational
pull of the outer white dwarf affects the pulsar, which has strong
self-gravity, and the inner white dwarf. The result shows that the
accelerations of the pulsar and its nearby white-dwarf companion differ
fractionally by no more than 2.6 x 10
−6.
X-ray spectroscopy
This technique is based on the idea that
photon trajectories are modified in the presence of a gravitational body. A very common astrophysical system in the universe is a
black hole surrounded by an
accretion disk.
The radiation from the general neighborhood, including the accretion
disk, is affected by the nature of the central black hole. Assuming
Einstein’s theory is correct, astrophysical black holes are described by
the Kerr metric. (A consequence of the
no-hair theorems.) Thus, by analyzing the radiation from such systems, it is possible to test Einstein’s theory.
Most of the radiation from these black hole - accretion disk systems (e.g.,
black hole binaries and
active galactic nuclei)
arrives in the form of X-rays. When modeled, the radiation is
decomposed into several components. Tests of Einstein’s theory are
possible with the thermal spectrum (only for black hole binaries) and
the reflection spectrum (for both black hole binaries and active
galactic nuclei). The former is not expected to provide strong
constraints, while the latter is much more promising. In both cases, systematic uncertainties might make such tests more challenging.
Cosmological tests
Tests of general relativity on the largest scales are not nearly so stringent as Solar System tests. The earliest such test was prediction and discovery of the
expansion of the universe. In 1922,
Alexander Friedmann found that Einstein equations have non-stationary solutions (even in the presence of the
cosmological constant). In 1927,
Georges Lemaître
showed that static solutions of the Einstein equations, which are
possible in the presence of the cosmological constant, are unstable, and
therefore the static universe envisioned by Einstein could not exist
(it must either expand or contract). Lemaître made an explicit prediction that the universe should expand. He also derived a redshift-distance relationship, which is now known as the
Hubble Law. Later, in 1931, Einstein himself agreed with the results of Friedmann and Lemaître. The expansion of the universe discovered by
Edwin Hubble in 1929 was then considered by many (and continues to be considered by some now) as a direct confirmation of general relativity. In the 1930s, largely due to the work of
E. A. Milne,
it was realised that the linear relationship between redshift and
distance derives from the general assumption of uniformity and isotropy
rather than specifically from general relativity.
However the prediction of a non-static universe was non-trivial, indeed
dramatic, and primarily motivated by general relativity.
Some other cosmological tests include searches for primordial gravitational waves generated during
cosmic inflation, which may be detected in the
cosmic microwave background polarization or by a proposed space-based
gravitational-wave interferometer called the
Big Bang Observer. Other tests at high redshift are constraints on other theories of gravity, and the variation of the gravitational constant since
big bang nucleosynthesis (it varied by no more than 40% since then).
In August 2017, the findings of tests conducted by astronomers using the
European Southern Observatory’s
Very Large Telescope
(VLT), among other instruments, were released, and which positively
demonstrated gravitational effects predicted by Albert Einstein. One of
which tests observed the orbit of the stars circling around
Sagittarius A*,
a black hole about 4 million times as massive as the sun. Einstein’s
theory suggested that large objects bend the space around them, causing
other objects to diverge from the straight lines they would otherwise
follow. Although previous studies have validated Einstein's theory, this
was the first time his theory had been tested on such a gigantic
object.
Gravitational lensing
Astronomers
using the Hubble Space Telescope and the Very Large Telescope has made
the precise test of general relativity on galactic scale. The nearby
galaxy
ESO 325-G004 acts as a strong gravitational lens, distorting light from a distant galaxy behind it to create an
Einstein ring
around its centre. By comparing the mass of ESO 325-G004 (measures from
the motion of stars inside this galaxy) with the curvature of space
around it, the astronomers found that gravity on these astronomical
length-scales behaves as predicted by general relativity.