Agrivoltaics is co-developing the same area of land for both solar photovoltaic power as well as for conventional agriculture. This technique was originally conceived by Adolf Goetzberger and Armin Zastrow in 1981. The coexistence of solar panels and crops implies a sharing of light between these two types of production.
Agrivoltaics has been massively implemented in Japan since 2004 and then, Agrivoltaics has expanded in Asia and Europe. Several crops can benefit from these systems, including fruit production.
Agrivoltaics has been massively implemented in Japan since 2004 and then, Agrivoltaics has expanded in Asia and Europe. Several crops can benefit from these systems, including fruit production.
History
In 1981, Adolf Goetzberger
and Armin Zastrow were the first to propose the concept of a dual use
of arable land for solar energy production and plant cultivation in
order to improve overall production.
They were addressing the ongoing discussion on the competition for the
use of arable land between solar energy production and crop. The light
saturation point is the maximum amount of photons absorbable by a plant
species. As more photons won’t increase to the rate of photosynthesis,
Akira Nagashima suggest to combine PV systems and farming to use the
excess of light. He developed the first prototypes in Japan in 2004.
The term “agrivoltaic“ was used for the first time in a publication in 2011. The concept is known under several names in the world: "agrophotovoltaics" in Germany, "agrovoltaics" in Italy, "solar sharing" in Asia. Facilities such as photovoltaic greenhouses can be considered as agrivoltaic systems.
As one of the objectives of the agricultural systems is to
preserve agricultural land, it is generally considered that agricultural
production in agrivoltaic should not be neglected. The constraints on
agricultural production vary from one country to another according to
the legislation or according to the type of crop and to the objectives
of the agrivoltaic system (optimization of the volume of agricultural
production, quality of agricultural products, energy production...).
Agrivoltaics in the world
Asia
Japan
has been the forerunner in the development of open field agrivoltaics
worldwide since 2004. Between 2004 and 2017, more than 1,000 open field
power plants were developed in Japan.
Japan
In 2004 in Japan, Akira Nagashima developed a demountable structure that he tested on several crops.
Since then, many field projects have been installed in Japan with a
large number of crops (citrus fruits, peanuts, eggplants, cucumbers,
cabbage, rice, vines, mushrooms ...) or livestock.
Removable structures allow farmers to remove or move facilities based
on crop rotations and their needs. Increasingly large plants with
capacities of several MW have been developed since 2004 with permanent
structures and dynamic systems. For example, a 35 MW power plant, installed on 54 ha of crops, was commissioned in 2017.
The shading rate of this plant is 50%, a value higher than the 30%
shading usually used on Japanese agrivoltaic power plants. Farmers
cultivate, among others, ginseng, ashitaba and coriander. Soon, the
island of Ukujima should host a solar power plant of 480 MW, part of
which will be agrivoltaics. The project has been under study since 2013
and the various partners have signed an agreement for the start of
construction in 2019.
To obtain permission to exploit solar panels over crops, Japanese
law requires farmers to maintain at least 80% of agricultural
production.
China
In 2016, the Italian company REM TEC built a 0.5 MWp agrivoltaic power plant in Jinzhai County, Anhui
Province. Chinese companies have developed several GWs of solar power
plants combining agriculture and solar energy production, either
photovoltaic greenhouses or open-field installations. For example, in
August 2016, Panda Green Energy installed solar panels over vineyards in
Turpan, Xinjiang
Uygur Autonomous Region. The 0.2 MW plant was connected to the grid.
The project was audited in October 2017 and the company has received
approval to roll out its system across the country. Projects of several
tens of MW have been deployed. For instance, in 2016, in Jiangxi Province, a 70 MW agrivoltaic plant was installed on agricultural and forestry crops.
For 30 years, the Elion Group has been trying to combat desertification in the Kubuqi region.
Among the techniques used, agrivoltaic systems were installed to
protect crops and produce electricity. Regarding the equipment for the
desert areas, Wan You-Bao patented in 2007 on a shade system to protect
crops in the desert. The shades are equipped with solar panels.
South Korea
South Korea is conducting initial tests of agrivoltaic power plants, drawing on the Japanese example since 2017.
Agrivoltaic is one of the solutions studied to increase the share of
renewable energies in Korea's energy mix. Their goal is to reach 20%
renewable energy in 2030 against 5% in 2017.
India
Projects for isolated sites are being studied by Amity University in Noida, northern India. A study published in 2017 looks at the potential of agrivoltaism for vineyards in India.
The agrivoltaic systems studied in this article consist of solar panels
intercalated between crops to limit shading on plants. This study
suggests that agrivoltaic systems can significantly increase the incomes
of Indian farmers.
Malaysia
The Universiti Putra Malaysia,
which specializes in agronomy, launched experiments in 2015 on
plantations of Orthosiphon stamineus (Java tea). It is a fixed structure
installed on an experimental surface of about 0.4 ha.
Vietnam
Fraunhofer ISE
has deployed their agrivoltaic system on a shrimp farm located in Bac
Liêu in the Mekong Delta. According to this institute, the results of
their pilot project indicate that water consumption has been reduced by
75%. Their system would offer other benefits such as shading for workers
as well as a lower and stable water temperature for better shrimp
growth.
Europe
In Europe in the early 2000s, photovoltaic greenhouses
are emerging. Part of the greenhouse roof is replaced by solar panels.
In Austria and then in Italy, open field agrivoltaic systems appeared
from 2007, followed by France and Germany.
Austria
In 2004, Günter Czaloun proposed a photovoltaic tracking system with a rope rack system. The first prototype is built in South Tyrol
in 2007 on a 0.1 ha area. The cable structure is more than five meters
above ground. A new system was presented at the Intersolar 2017
conference in Munich. This technology is potentially less expensive than
other open field systems because it requires less steel.
Italy
In 2009 and 2011, agrivoltaic systems with fixed panels were installed above vineyards. Experiments showed a slight decrease of the yield and late harvests.
In 2009, the Italian company REM TEC develops a dual-axis solar
tracking system. In 2011 and 2012, REM TEC built several MWp of open
field agrivoltaic power plants. The solar panels are installed 5 m above the ground to operate agricultural machinery. The cover of photovoltaic panels
shadow is less than 15% to minimize the effect on the crops. They are
the first to offer automated integrated shading net systems into the
supporting structure. REM TEC also designs dual-axis solar tracking systems integrated into greenhouse structure. The control of the position of the solar panels would optimize the greenhouse microclimate.
France
Photovoltaic greenhouses
Since the beginning of the 2000s, photovoltaic greenhouses
have been built in France. Photovoltaic greenhouse designers continue
to innovate to improve both agricultural production and power
generation. For instance, the concept of Agrinergie has been developed
by Akuo Energy since 2007. The first power plants consisted of alternation of crops and solar panels. The new power plants are greenhouses.
In 2017, the Tenergie company began the deployment of photovoltaic
greenhouses with an architecture that diffuses light in order to reduce
the contrasts between light bands and shade bands created by solar
panels.
Open field systems
Since 2009, INRA, IRSTEA and Sun'R have been working on the Sun'Agri program. A first prototype installed in the field with fixed panels is built in 2009 on a surface of 0.1 ha in Montpellier. Other prototypes with 1-axis mobile panels were built in 2014
and 2017. The aim of these studies is to manage the microclimate
received by plants and to produce electricity, by optimizing the
position of the panels. and to study how radiation is distributed
between crops and solar panels. The first agrivoltaic plant in the open
field of Sun'R is built in the spring of 2018 in Tresserre in the Pyrénées-Orientales. This plant has a capacity of 2.2 MWp installed on 4.5 ha of vineyards. It will evaluate, on a large scale and in real conditions, the performance of the Sun'Agri system on vineyards.
In 2016, the Agrivolta company specialized on the agrivoltaïcs. After a first prototype built in 2017 in Aix-en-Provence, Agrivolta deployed its system on a plot of the National Research Institute of Horticulture (Astredhor) in Hyères. Agrivolta win several innovation prizes Agrivolta presented its technology at the CES in Las Vegas in January 2018.
Germany
In 2011, the Fraunhofer Institute
ISE started a reaserch project on agrivoltaics. Research continues with
the APV-Resola project, which began in 2015 and is scheduled to end in
2020. A first prototype of 194.4 kWp is being built in 2016 on a 0.5 ha
site belonging to the Hofgemeinschaft Heggelbach cooperative farm in Herdwangen (Baden-Württemberg). They estimate that such structures will be profitable without government fundings after 2022.
Danemark
The Agronomy Department of the Aarhus University has launched a study project of agrivoltaic system on orchards in 2014.
Croatia
In 2017, Work-ing d.o.o installed a 500 kW open field power plant near Virovitica-Podravina. The agronomic studies are supported by the University of Osijek and the agricultural engineering school of Slatina.
The electricity production is used for the irrigation system and
agricultural machinery. At first, shade-adapted cultures will be tested
under the device.
America
USA
In the United States, SolAgra is interested in the concept in collaboration with the Department of Agronomy at the University of California at Davis.
A first poxer plant on 0.4 ha is under development. An area of 2.8 ha
is used as a control. Several types of crops are studied: alfalfa, sorghum, lettuce, spinach, beets, carrots, chard, radishes, potatoes, arugula, mint, turnips, kale, parsley, coriander, beans, peas, shallots, mustard ... Projects for isolated sites are also studied. Experimental systems are being studied by several universities: the Biosphere 2 project at the University of Arizona, the Stockbridge School of Agriculture project (University of Massachusetts at Amherst).
Chile
Three 13
kWp agro-photovoltaic systems were built in Chile in 2017. The goal of
this project, supported by the Metropolitan Region of Santiago, was to
study the plants that can benefit from the shading of the agrivoltaic
system. The electricity produced was used to power agricultural
facilities: cleaning, packaging and cold storage of agricultural
production, incubator for eggs ... One of the systems was installed in a
region with a lot of power outages.
Methods
There are three types of Agrivoltaics
that are being actively researched: solar arrays with space between for
crops, stilted solar array above crops and greenhouse solar array. All three of these systems have several variables used to maximize solar energy absorbed in both the panels and the crops. The main variable taken into account for agrivoltaic
systems is the angle of the solar panels-called the tilt angle. Other
variables taken into account for choosing the location of the agrivoltaic system are the crops chosen, height of the panels, solar irradiation in the area and climate of the area.
Configuration of agrivoltaic systems
There
are different configurations of agrivoltaic devices. Goetzberger and
Zastrow have studied the conditions for optimizing agrivoltaic
installations. Presented in the early 1980s, these conditions still serve as a reference in the definition of agrivoltaic systems:
- Orientation of solar panels in the south for fixed or east-west panels for panels rotating on an axis;
- Sufficient spacing between solar panels for sufficient light transmission to ground crops;
- Elevation of the supporting structure of the solar panels to homogenize the amounts of radiation on the ground.
Experimental facilities often have a control agricultural area. The
control zone is exploited under the same conditions as the agrivoltaic
device in order to study the effects of the device on the development of
crops.
Fixed solar panels over crops
The simplest approach is to install fixed solar panels on agricultural greenhouses, above open fields crops or between open fields crops. It is possible to optimize the installation by modifying the density of solar panels or the inclination of the panels. In Japan,
agrivoltaic systems generally consist of dismountable light structures
with light and small size solar panels to reduce wind resistance.
Dynamic Agrivoltaic
In more elaborate configurations, agrivoltaic system use a tracking system. Solar panels can be controlled to optimize their positioning to improve agricultural production or electricity production.
The first dynamic agrivoltaic devices were developed in Japan. The panels are manually adjustable.
Farmers can modify the position of the solar panels according to the
season or stage of crop development to increase or decrease shading and
power generation. Japanese companies have also developed several more
sophisticated systems. For example, crops grow under systems composed of
tables (25 solar panels) fixed dual axis tracker.
In 2004, Günter Czaloun proposed a photovoltaic tracking system with a rope rack system. Panels can be oriented to improve power generation or shade crops as needed. The first prototype is built in 2007 in Austria. The company REM TEC has deployed several plants equipped with dual axis tracking system in Italy and China. They have also developed an equivalent system used for agricultural greenhouses.
In France, Sun'R and Agrivolta companies are developing single
axis tracking systems. According to these companies, their systems can
be adapgted to the needs of plants. The Sun'R system is east-west axis
tracking system. According to this company, complex models of plant
growth, weather forecasts, calculation and optimization software are
used. The device from Agrivolta is equipped with south-facing solar panels that can be erased by a sliding system.
The Artigianfer company developed a photovoltaic greenhouse whose solar panels are installed on movable shutters. The panels can follow the course of the Sun along an east-west axis.
The difficulty of such systems is to find the mode of operation
to maintain the good balance between the two types of production
according to the goals of the system. Fine control of the panels to
adapt shading to the need of plants requires advanced agronomic skills
to understand the development of plants. Experimental devices are
usually developed in collaboration with research centers.
Effects
The solar panels of Agrivoltaics
affects crops and land they cover in ways more than providing shade.
Two ways are affecting water flow and heat. They also allow for more
revenue per acre to be created. For example, grape farms with appropriate spacing could increase revenue 15 times.
Water Flow
In experiments testing evaporation levels under PVP for shade resistant crops cucumbers and lettuce watered by irrigation, a 14-29% savings in evaporation was found. Agrivoltaics could be used for crops or areas where water efficiency is imperative.
Heat
A study was done on the heat of the land, air and crops under solar panels
for a growing season. It was found that while the air beneath the
panels stayed consistent, the land and plants had lower temperatures
recorded. With rising temperature from climate change this may become important for some food crops.
Advantages
Simulations and studies on Agrivoltaics
indicate electricity and shade-resistant crop production do not
decrease in productivity, allowing both to be simultaneously produced
efficiently. Dinesh et al. found lettuce output was found to be
comparable in Agrivoltaics to monocultures. Agrivoltaics
work best for plants that are shade resistant, with potential
functioning crops being "hog peanut, alfalfa, yam, taro, cassava, sweet
potato" along with lettuce. Simulations performed by Dupraz et al. found the potential of land productivity to increase by 60-70%.
Furthermore, Dinesh et al. found that the value of solar generated
electricity coupled to shade-tolerant crop production created an over
30% increase in economic value from farms deploying agrivoltaic systems
instead of conventional agriculture. It has been postulated that Agrivoltaics would be beneficial for summer crops for the microclimate they create and the side effect of heat and water flow control.
Disadvantages
Shade resistant crops are not typically grown in industrial agricultural systems. For instance, wheat crops do not fare well in a low light environment, meaning they would not work with Agrivoltaics. Agrivoltaics
do not yet work with greenhouses. Greenhouses with half of the roof
covered in panels were simulated, and the resulting crop output reduced
by 64% and panel productivity reduced by 84%.
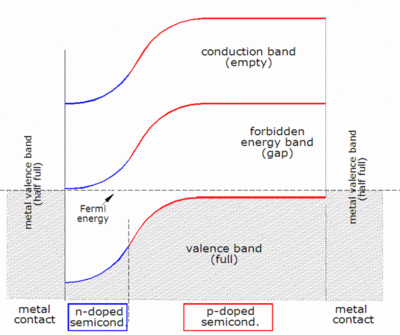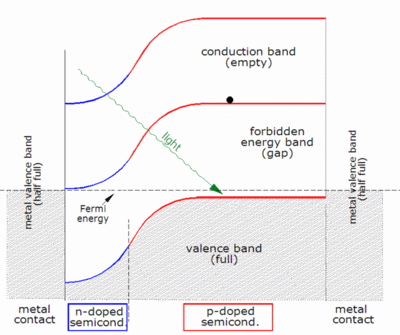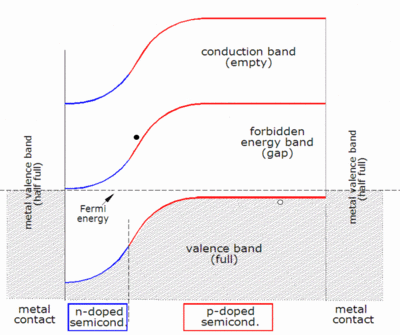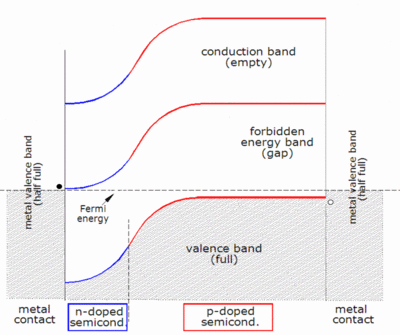





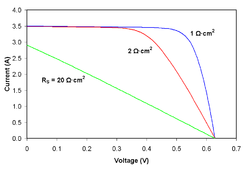
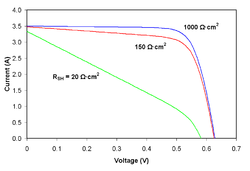
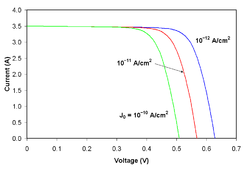
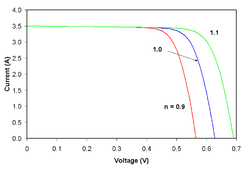
![{\displaystyle I_{D}=I_{0}\left\{\exp \left[{\frac {V_{j}}{nV_{T}}}\right]-1\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b50e360bdf5d4b6a17729bcfddff18aba2151d9)