Medical diagnosis

From Wikipedia, the free encyclopedia

Radiography is an important tool in diagnosis of certain disorders.

Medical diagnosis (abbreviated Dx or D_S) is the process of determining which disease or condition explains a person's symptoms and signs. It is most often referred to as diagnosis with the medical context being implicit. The information required for diagnosis is typically collected from a history and physical examination of the person seeking medical care. Often, one or more diagnostic procedures, such as diagnostic tests, are also done during the process. Sometimes posthumous diagnosis is considered a kind of medical diagnosis. 

Diagnosis is often challenging, because many signs and symptoms are nonspecific. For example, redness of the skin (erythema), by itself, is a sign of many disorders and thus does not tell the healthcare professional what is wrong. Thus differential diagnosis, in which several possible explanations are compared and contrasted, must be performed. This involves the correlation of various pieces of information followed by the recognition and differentiation of patterns. Occasionally the process is made easy by a sign or symptom (or a group of several) that is pathognomonic. 

Diagnosis is a major component of the procedure of a doctor's visit. From the point of view of statistics, the diagnostic procedure involves classification tests.

History

The first recorded examples of medical diagnosis are found in the writings of Imhotep (2630–2611 BC) in ancient Egypt (the Edwin Smith Papyrus). A Babylonian medical textbook, the Diagnostic Handbook written by Esagil-kin-apli (fl.1069–1046 BC), introduced the use of empiricism, logic and rationality in the diagnosis of an illness or disease. Traditional Chinese Medicine, as described in the Yellow Emperor's Inner Canon or Huangdi Neijing, specified four diagnostic methods: inspection, auscultation-olfaction, interrogation, and palpation. Hippocrates was known to make diagnoses by tasting his patients' urine and smelling their sweat.

Medical uses

A diagnosis, in the sense of diagnostic procedure, can be regarded as an attempt at classification of an individual's condition into separate and distinct categories that allow medical decisions about treatment and prognosis to be made. Subsequently, a diagnostic opinion is often described in terms of a disease or other condition, but in the case of a wrong diagnosis, the individual's actual disease or condition is not the same as the individual's diagnosis. 

A diagnostic procedure may be performed by various health care professionals such as a physician, physical therapist, optometrist, healthcare scientist, chiropractor, dentist, podiatrist, nurse practitioner, or physician assistant. This article uses diagnostician as any of these person categories.

A diagnostic procedure (as well as the opinion reached thereby) does not necessarily involve elucidation of the etiology of the diseases or conditions of interest, that is, what caused the disease or condition. Such elucidation can be useful to optimize treatment, further specify the prognosis or prevent recurrence of the disease or condition in the future. 

The initial task is to detect a medical indication to perform a diagnostic procedure. Indications include:

• Detection of any deviation from what is known to be normal, such as can be described in terms of, for example, anatomy (the structure of the human body), physiology (how the body works), pathology (what can go wrong with the anatomy and physiology), psychology (thought and behavior) and human homeostasis (regarding mechanisms to keep body systems in balance). Knowledge of what is normal and measuring of the patient's current condition against those norms can assist in determining the patient's particular departure from homeostasis and the degree of departure, which in turn can assist in quantifying the indication for further diagnostic processing.
• A complaint expressed by a patient.
• The fact that a patient has sought a diagnostician can itself be an indication to perform a diagnostic procedure. For example, in a doctor's visit, the physician may already start performing a diagnostic procedure by watching the gait of the patient from the waiting room to the doctor's office even before she or he has started to present any complaints.

Even during an already ongoing diagnostic procedure, there can be an indication to perform another, separate, diagnostic procedure for another, potentially concomitant, disease or condition. This may occur as a result of an incidental finding of a sign unrelated to the parameter of interest, such as can occur in comprehensive tests such as radiological studies like magnetic resonance imaging or blood test panels that also include blood tests that are not relevant for the ongoing diagnosis.

Procedure

General components which are present in a diagnostic procedure in most of the various available methods include:

• Complementing the already given information with further data gathering, which may include questions of the medical history (potentially from other people close to the patient as well), physical examination and various diagnostic tests.
  A diagnostic test is any kind of medical test performed to aid in the diagnosis or detection of disease. Diagnostic tests can also be used to provide prognostic information on people with established disease.
• Processing of the answers, findings or other results. Consultations with other providers and specialists in the field may be sought.

There are a number of methods or techniques that can be used in a diagnostic procedure, including performing a differential diagnosis or following medical algorithms. In reality, a diagnostic procedure may involve components of multiple methods.

Differential diagnosis

The method of differential diagnosis is based on finding as many candidate diseases or conditions as possible that can possibly cause the signs or symptoms, followed by a process of elimination or at least of rendering the entries more or less probable by further medical tests and other processing until, aiming to reach the point where only one candidate disease or condition remains as probable. The final result may also remain a list of possible conditions, ranked in order of probability or severity. 

The resultant diagnostic opinion by this method can be regarded more or less as a diagnosis of exclusion. Even if it does not result in a single probable disease or condition, it can at least rule out any imminently life-threatening conditions. 

Unless the provider is certain of the condition present, further medical tests, such as medical imaging, are performed or scheduled in part to confirm or disprove the diagnosis but also to document the patient's status and keep the patient's medical history up to date. 

If unexpected findings are made during this process, the initial hypothesis may be ruled out and the provider must then consider other hypotheses.

Pattern recognition

In a pattern recognition method the provider uses experience to recognize a pattern of clinical characteristics. It is mainly based on certain symptoms or signs being associated with certain diseases or conditions, not necessarily involving the more cognitive processing involved in a differential diagnosis. 

This may be the primary method used in cases where diseases are "obvious", or the provider's experience may enable him or her to recognize the condition quickly. Theoretically, a certain pattern of signs or symptoms can be directly associated with a certain therapy, even without a definite decision regarding what is the actual disease, but such a compromise carries a substantial risk of missing a diagnosis which actually has a different therapy so it may be limited to cases where no diagnosis can be made.

Diagnostic criteria

The term diagnostic criteria designates the specific combination of signs, symptoms, and test results that the clinician uses to attempt to determine the correct diagnosis.

Some examples of diagnostic criteria, also known as clinical case definitions, are:

• Amsterdam criteria for hereditary nonpolyposis colorectal cancer
• McDonald criteria for multiple sclerosis
• ACR criteria for systemic lupus erythematosus
• Centor criteria for strep throat

Clinical decision support system

Clinical decision support systems are interactive computer programs designed to assist health professionals with decision-making tasks. The clinician interacts with the software utilizing both the clinician’s knowledge and the software to make a better analysis of the patients data than either human or software could make on their own. Typically the system makes suggestions for the clinician to look through and the clinician picks useful information and removes erroneous suggestions.

Other diagnostic procedure methods

Other methods that can be used in performing a diagnostic procedure include: 

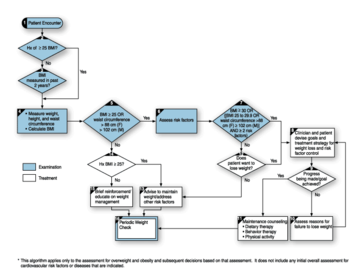
An example of a medical algorithm for assessment and treatment of overweight and obesity.

• Usage of medical algorithms
• An "exhaustive method", in which every possible question is asked and all possible data is collected. This is often referred to as a "diagnostic workup".
• Use of a sensory pill that collects and transmits physiological information after being swallowed.
• Using optical coherence tomography to produce detailed images of the brain or other soft tissue, through a "window" made of zirconia that has been modified to be transparent and implanted in the skull.

Adverse effects

Diagnosis problems are the dominant cause of medical malpractice payments, accounting for 35% of total payments in a study of 25 years of data and 350,000 claims.

Overdiagnosis

Overdiagnosis is the diagnosis of "disease" that will never cause symptoms or death during a patient's lifetime. It is a problem because it turns people into patients unnecessarily and because it can lead to economic waste (overutilization) and treatments that may cause harm. Overdiagnosis occurs when a disease is diagnosed correctly, but the diagnosis is irrelevant. A correct diagnosis may be irrelevant because treatment for the disease is not available, not needed, or not wanted.

Errors

Most people will experience at least one diagnostic error in their lifetime, according to a 2015 report by the National Academies of Sciences, Engineering, and Medicine.

Causes and factors of error in diagnosis are:

• the manifestation of disease are not sufficiently noticeable
• a disease is omitted from consideration
• too much significance is given to some aspect of the diagnosis
• the condition is a rare disease with symptoms suggestive of many other conditions
• the condition has a rare presentation

Lag time

When making a medical diagnosis, a lag time is a delay in time until a step towards diagnosis of a disease or condition is made. Types of lag times are mainly:

• Onset-to-medical encounter lag time, the time from onset of symptoms until visiting a health care provider
• Encounter-to-diagnosis lag time, the time from first medical encounter to diagnosis

Society and culture

Etymology

The plural of diagnosis is diagnoses. The verb is to diagnose, and a person who diagnoses is called a diagnostician. The word diagnosis /daɪ.əɡˈnoʊsɪs/ is derived through Latin from the Greek word διάγνωσις (diágnōsis) from διαγιγνώσκειν (diagignṓskein), meaning "to discern, distinguish".

Medical diagnosis or the actual process of making a diagnosis is a cognitive process. A clinician uses several sources of data and puts the pieces of the puzzle together to make a diagnostic impression. The initial diagnostic impression can be a broad term describing a category of diseases instead of a specific disease or condition. After the initial diagnostic impression, the clinician obtains follow up tests and procedures to get more data to support or reject the original diagnosis and will attempt to narrow it down to a more specific level. Diagnostic procedures are the specific tools that the clinicians use to narrow the diagnostic possibilities.

Social context

Diagnosis can take many forms. It might be a matter of naming the disease, lesion, dysfunction or disability. It might be a management-naming or prognosis-naming exercise. It may indicate either degree of abnormality on a continuum or kind of abnormality in a classification. It’s influenced by non-medical factors such as power, ethics and financial incentives for patient or doctor. It can be a brief summation or an extensive formulation, even taking the form of a story or metaphor. It might be a means of communication such as a computer code through which it triggers payment, prescription, notification, information or advice. It might be pathogenic or salutogenic. It’s generally uncertain and provisional. 

Once a diagnostic opinion has been reached, the provider is able to propose a management plan, which will include treatment as well as plans for follow-up. From this point on, in addition to treating the patient's condition, the provider can educate the patient about the etiology, progression, prognosis, other outcomes, and possible treatments of her or his ailments, as well as providing advice for maintaining health. 

A treatment plan is proposed which may include therapy and follow-up consultations and tests to monitor the condition and the progress of the treatment, if needed, usually according to the medical guidelines provided by the medical field on the treatment of the particular illness. 

Relevant information should be added to the medical record of the patient. 

A failure to respond to treatments that would normally work may indicate a need for review of the diagnosis. 

Nancy McWilliams identifies five reasons that determine the necessity for diagnosis:

1. diagnosis for treatment planning;
2. information contained in it related to prognosis;
3. protecting interests of patients;
4. a diagnosis might help the therapist to empathize with his patient;
5. might reduce the likelihood that some fearful patients will go-by the treatment.

Concepts related to diagnosis

Sub-types of diagnoses include:

• Clinical diagnosis:  A diagnosis made on the basis of medical signs and patient-reported symptoms, rather than diagnostic tests
• Laboratory diagnosis:  A diagnosis based significantly on laboratory reports or test results, rather than the physical examination of the patient. For instance, a proper diagnosis of infectious diseases usually requires both an examination of signs and symptoms, as well as laboratory characteristics of the pathogen involved.
• Radiology diagnosis:  A diagnosis based primarily on the results from medical imaging studies. Greenstick fractures are common radiological diagnoses.
• Principal diagnosis:  The single medical diagnosis that is most relevant to the patient's chief complaint or need for treatment. Many patients have additional diagnoses.
• Admitting diagnosis:  The diagnosis given as the reason why the patient was admitted to the hospital; it may differ from the actual problem or from the discharge diagnoses, which are the diagnoses recorded when the patient is discharged from the hospital.
• Differential diagnosis:  A process of identifying all of the possible diagnoses that could be connected to the signs, symptoms, and lab findings, and then ruling out diagnoses until a final determination can be made.
• Diagnostic criteria:  Designates the combination of signs, symptoms, and test results that the clinician uses to attempt to determine the correct diagnosis. They are standards, normally published by international committees, and they are designed to offer the best sensitivity and specificity possible, respect the presence of a condition, with the state-of-the-art technology.
• Prenatal diagnosis:  Diagnosis work done before birth
• Diagnosis of exclusion:  A medical condition whose presence cannot be established with complete confidence from history, examination or testing. Diagnosis is therefore by elimination of all other reasonable possibilities.
• Dual diagnosis:  The diagnosis of two related, but separate, medical conditions or co-morbidities; the term almost always refers to a diagnosis of a serious mental illness and a substance addiction.
• Self-diagnosis:  The diagnosis or identification of a medical conditions in oneself. Self-diagnosis is very common.
• Remote diagnosis:  A type of telemedicine that diagnoses a patient without being physically in the same room as the patient.
• Nursing diagnosis:  Rather than focusing on biological processes, a nursing diagnosis identifies people's responses to situations in their lives, such as a readiness to change or a willingness to accept assistance.
• Computer-aided diagnosis:  Providing symptoms allows the computer to identify the problem and diagnose the user to the best of its ability. Health screening begins by identifying the part of the body where the symptoms are located; the computer cross-references a database for the corresponding disease and presents a diagnosis.
• Overdiagnosis:  The diagnosis of "disease" that will never cause symptoms, distress, or death during a patient's lifetime
• Wastebasket diagnosis:  A vague, or even completely fake, medical or psychiatric label given to the patient or to the medical records department for essentially non-medical reasons, such as to reassure the patient by providing an official-sounding label, to make the provider look effective, or to obtain approval for treatment. This term is also used as a derogatory label for disputed, poorly described, overused, or questionably classified diagnoses, such as pouchitis and senility, or to dismiss diagnoses that amount to overmedicalization, such as the labeling of normal responses to physical hunger as reactive hypoglycemia.
• Retrospective diagnosis:  The labeling of an illness in a historical figure or specific historical event using modern knowledge, methods and disease classifications.

Mathematical modelling of infectious disease

From Wikipedia, the free encyclopedia

Mathematical models can project how infectious diseases progress to show the likely outcome of an epidemic and help inform public health interventions. Models use some basic assumptions and mathematics to find parameters for various infectious diseases and use those parameters to calculate the effects of different interventions, like mass vaccination programmes. The modelling can help in deciding which intervention/s to avoid and which to trial.

History

The modeling of infectious diseases is a tool which has been used to study the mechanisms by which diseases spread, to predict the future course of an outbreak and to evaluate strategies to control an epidemic.

The first scientist who systematically tried to quantify causes of death was John Graunt in his book Natural and Political Observations made upon the Bills of Mortality, in 1662. The bills he studied were listings of numbers and causes of deaths published weekly. Graunt’s analysis of causes of death is considered the beginning of the “theory of competing risks” which according to Daley and Gani  is “a theory that is now well established among modern epidemiologists”. 

The earliest account of mathematical modelling of spread of disease was carried out in 1766 by Daniel Bernoulli. Trained as a physician, Bernoulli created a mathematical model to defend the practice of inoculating against smallpox. The calculations from this model showed that universal inoculation against smallpox would increase the life expectancy from 26 years 7 months to 29 years 9 months. Daniel Bernoulli's work preceded the modern understanding of germ theory. 

In the early 20th century, William Hamer and Ronald Ross applied the law of mass action to explain epidemic behavior. 

The 1920s saw the emergence of compartmental models. The Kermack–McKendrick epidemic model (1927) and the Reed–Frost epidemic model (1928) both describe the relationship between susceptible, infected and immune individuals in a population. The Kermack–McKendrick epidemic model model was successful in predicting the behavior of outbreaks very similar to that observed in many recorded epidemics.

Assumptions

Models are only as good as the assumptions on which they are based. If a model makes predictions which are out of line with observed results and the mathematics is correct, the initial assumptions must change to make the model useful.

• Rectangular and stationary age distribution, i.e., everybody in the population lives to age L and then dies, and for each age (up to L) there is the same number of people in the population. This is often well-justified for developed countries where there is a low infant mortality and much of the population lives to the life expectancy.
• Homogeneous mixing of the population, i.e., individuals of the population under scrutiny assort and make contact at random and do not mix mostly in a smaller subgroup. This assumption is rarely justified because social structure is widespread. For example, most people in London only make contact with other Londoners. Further, within London then there are smaller subgroups, such as the Turkish community or teenagers (just to give two examples), who mix with each other more than people outside their group. However, homogeneous mixing is a standard assumption to make the mathematics tractable.

Types of epidemic models

Stochastic

"Stochastic" means being or having a random variable. A stochastic model is a tool for estimating probability distributions of potential outcomes by allowing for random variation in one or more inputs over time. Stochastic models depend on the chance variations in risk of exposure, disease and other illness dynamics.

Deterministic

When dealing with large populations, as in the case of tuberculosis, deterministic or compartmental mathematical models are often used. In a deterministic model, individuals in the population are assigned to different subgroups or compartments, each representing a specific stage of the epidemic. Letters such as M, S, E, I, and R are often used to represent different stages. 

The transition rates from one class to another are mathematically expressed as derivatives, hence the model is formulated using differential equations. While building such models, it must be assumed that the population size in a compartment is differentiable with respect to time and that the epidemic process is deterministic. In other words, the changes in population of a compartment can be calculated using only the history that was used to develop the model.

Reproduction number

The basic reproduction number (denoted by R₀) is a measure of how transferrable a disease is. It is the average number of people that a single infectious person will infect over the course of their infection. This quantity determines whether the infection will spread exponentially, die out, or remain constant: if R₀ > 1, then each person on average infects more than one other person so the disease will spread; if R₀ < 1, then each person infects less than one person on average so the disease will die out; and if R₀ = 1, then each person will infect exactly one other person, so the disease will become endemic: it will move throughout the population but not increase or decrease. 

The basic reproduction number can be computed as a ratio of known rates over time: if an infectious individual contacts β other people per unit time, if all of those people are assumed to contract the disease, and if the disease has a mean infectious period of 1/γ, then the basic reproduction number is just R₀ = β/γ. Some diseases have multiple possible latency periods, in which case the reproduction number for the disease overall is the sum of the reproduction number for each transition time into the disease. For example, Blower et al. model two forms of tuberculosis infection: in the fast case, the symptoms show up immediately after exposure; in the slow case, the symptoms develop years after the initial exposure (endogenous reactivation). The overall reproduction number is the sum of the two forms of contraction: R₀ = R₀^FAST + R₀^SLOW.

Endemic steady state

An infectious disease is said to be endemic when it can be sustained in a population without the need for external inputs. This means that, on average, each infected person is infecting exactly one other person (any more and the number of people infected will grow exponentially and there will be an epidemic, any less and the disease will die out). In mathematical terms, that is:

${\displaystyle \ R_{0}\ =1.}$

The basic reproduction number (R₀) of the disease, assuming everyone is susceptible, multiplied by the proportion of the population that is actually susceptible (S) must be one (since those who are not susceptible do not feature in our calculations as they cannot contract the disease). Notice that this relation means that for a disease to be in the endemic steady state, the higher the basic reproduction number, the lower the proportion of the population susceptible must be, and vice versa.

Assume the rectangular stationary age distribution and let also the ages of infection have the same distribution for each birth year. Let the average age of infection be A, for instance when individuals younger than A are susceptible and those older than A are immune (or infectious). Then it can be shown by an easy argument that the proportion of the population that is susceptible is given by:

${\displaystyle S={\frac {A}{L}}.}$

But the mathematical definition of the endemic steady state can be rearranged to give:

${\displaystyle S={\frac {1}{R_{0}}}.}$

Therefore, due to the transitive property:

${\displaystyle {\frac {1}{R_{0}}}={\frac {A}{L}}\Rightarrow R_{0}={\frac {L}{A}}.}$

This provides a simple way to estimate the parameter R₀ using easily available data. 

For a population with an exponential age distribution,

${\displaystyle R_{0}=1+{\frac {L}{A}}.}$

This allows for the basic reproduction number of a disease given A and L in either type of population distribution.

Modelling epidemics

The SIR model is one of the more basic models used for modelling epidemics. There are a large number of modifications to the model.

The SIR model

In 1927, W. O. Kermack and A. G. McKendrick created a model in which they considered a fixed population with only three compartments: susceptible, ${\displaystyle S(t)}$; infected, ${\displaystyle I(t)}$; and removed, ${\displaystyle R(t)}$. The compartments used for this model consist of three classes:

• ${\displaystyle S(t)}$ is used to represent the number of individuals not yet infected with the disease at time t, or those susceptible to the disease.
• ${\displaystyle I(t)}$ denotes the number of individuals who have been infected with the disease and are capable of spreading the disease to those in the susceptible category.
• ${\displaystyle R(t)}$ is the compartment used for those individuals who have been infected and then removed from the disease, either due to immunization or due to death. Those in this category are not able to be infected again or to transmit the infection to others.

The flow of this model may be considered as follows:

${\displaystyle {\color {blue}{{\mathcal {S}}\rightarrow {\mathcal {I}}\rightarrow {\mathcal {R}}}}}$

Using a fixed population, ${\displaystyle N=S(t)+I(t)+R(t)}$, Kermack and McKendrick derived the following equations:

${\displaystyle {\frac {dS}{dt}}=-{\frac {\beta SI}{N}}}$

${\displaystyle {\frac {dI}{dt}}={\frac {\beta SI}{N}}-\gamma I}$

${\displaystyle {\frac {dR}{dt}}=\gamma I}$

Several assumptions were made in the formulation of these equations: First, an individual in the population must be considered as having an equal probability as every other individual of contracting the disease with a rate of ${\displaystyle \beta }$, which is considered the contact or infection rate of the disease. Therefore, an infected individual makes contact and is able to transmit the disease with ${\displaystyle \beta N}$ others per unit time and the fraction of contacts by an infected with a susceptible is ${\displaystyle S/N}$. The number of new infections in unit time per infective then is ${\displaystyle \beta N(S/N)}$, giving the rate of new infections (or those leaving the susceptible category) as ${\displaystyle \beta N(S/N)I=\beta SI}$. For the second and third equations, consider the population leaving the susceptible class as equal to the number entering the infected class. However, a number equal to the fraction (${\displaystyle \gamma }$ which represents the mean recovery/death rate, or ${\displaystyle 1/\gamma }$ the mean infective period) of infectives are leaving this class per unit time to enter the removed class. These processes which occur simultaneously are referred to as the Law of Mass Action, a widely accepted idea that the rate of contact between two groups in a population is proportional to the size of each of the groups concerned. Finally, it is assumed that the rate of infection and recovery is much faster than the time scale of births and deaths and therefore, these factors are ignored in this model.

Steady state solutions

The expected duration of susceptibility will be${\textstyle E[min(T_{L}|T_{S})]}$where ${\textstyle T_{L}}$reflects the time alive (life expectancy) and ${\textstyle T_{S}}$reflects the time in the susceptible state before becoming infected, which can be simplified to: 

${\displaystyle E[min(T_{L}|T_{S})]=\int _{0}^{\inf[}exp^{-(\mu +\delta )}={\frac {1}{\mu +\delta }}}$,

such that the number of susceptible persons is the number entering the susceptible compartment ${\textstyle \mu N}$times the duration of susceptibility: 

${\displaystyle S={\frac {\mu N}{\mu +\lambda }}}$.

Analogously, the steady-state number of infected persons is the number entering the infected state from the susceptible state (number susceptible, times rate of infection ${\textstyle \lambda ={\frac {\beta I}{N}}}$, times the duration of infectiousness ${\textstyle {\frac {1}{\mu +v}}}$: 

${\displaystyle I={\frac {\mu N}{\mu +\lambda }}\lambda {\frac {1}{\mu +v}}}$.

Other compartmental models

There are a large number of modifications of the SIR model, including those that include births and deaths, where upon recovery there is no immunity (SIS model), where immunity lasts only for a short period of time (SIRS), where there is a latent period of the disease where the person is not infectious (SEIS and SEIR), and where infants can be born with immunity (MSIR).

Infectious disease dynamics

Mathematical models need to integrate the increasing volume of data being generated on host-pathogen interactions. Many theoretical studies of the population dynamics, structure and evolution of infectious diseases of plants and animals, including humans, are concerned with this problem.

Research topics include:

• transmission, spread and control of infection
• epidemiological networks
• spatial epidemiology
• persistence of pathogens within hosts
• intra-host dynamics
• immuno-epidemiology
• virulence
• Strain (biology) structure and interactions
• antigenic shift
• phylodynamics
• pathogen population genetics
• evolution and spread of resistance
• role of host genetic factors
• statistical and mathematical tools and innovations
• role and identification of infection reservoirs

Mathematics of mass vaccination

If the proportion of the population that is immune exceeds the herd immunity level for the disease, then the disease can no longer persist in the population. Thus, if this level can be exceeded by vaccination, the disease can be eliminated. An example of this being successfully achieved worldwide is the global smallpox eradication, with the last wild case in 1977. The WHO is carrying out a similar vaccination campaign to eradicate polio.

The herd immunity level will be denoted q. Recall that, for a stable state:

${\displaystyle \ R_{0}\cdot S=1.}$

 

In turn,

 

${\displaystyle R_{0}={\frac {N}{S}}={\frac {\mu NE(T_{L})}{\mu NE[min(T_{L},T_{S})}}={\frac {E(T_{L})}{E[min(T_{L},T_{S})]}}}$,

 

which is approximately:

 

${\displaystyle {\frac {E(T_{L})}{E(T_{S})}}=1+{\frac {\lambda }{\mu }}={\frac {\beta N}{v}}}$.

S will be (1 − q), since q is the proportion of the population that is immune and q + S must equal one (since in this simplified model, everyone is either susceptible or immune). Then:

${\displaystyle \ R_{0}\cdot (1-q)=1,}$

${\displaystyle 1-q={\frac {1}{R_{0}}},}$

${\displaystyle q=1-{\frac {1}{R_{0}}}.}$

Remember that this is the threshold level. If the proportion of immune individuals exceeds this level due to a mass vaccination programme, the disease will die out. 

We have just calculated the critical immunisation threshold (denoted q_c). It is the minimum proportion of the population that must be immunised at birth (or close to birth) in order for the infection to die out in the population.

${\displaystyle q_{c}=1-{\frac {1}{R_{0}}}}$.

 

Because the fraction of the final size of the population p that is never infected can be defined as:

 

${\displaystyle \lim _{t->\inf }S(t)=\exp ^{-\int _{0}^{\inf }{\lambda (t)dt}}=1-p}$.

 

Hence,

 

${\displaystyle p=1-\exp ^{-\int _{0}^{\inf }{\beta I(t)dt}}=1-\exp ^{-R_{0}p}}$.

 

Solving for ${\displaystyle \ R_{0}}$, we obtain:

 

${\displaystyle {R_{0}}={\frac {-ln(1-p)}{p}}}$.

When mass vaccination cannot exceed the herd immunity

If the vaccine used is insufficiently effective or the required coverage cannot be reached (for example due to popular resistance), the programme may fail to exceed q_c. Such a programme can, however, disturb the balance of the infection without eliminating it, often causing unforeseen problems. 

Suppose that a proportion of the population q (where q < q_c) is immunised at birth against an infection with R₀>1. The vaccination programme changes R₀ to R_q where

${\displaystyle \ R_{q}=R_{0}(1-q)}$

This change occurs simply because there are now fewer susceptibles in the population who can be infected. R_q is simply R₀ minus those that would normally be infected but that cannot be now since they are immune. 

As a consequence of this lower basic reproduction number, the average age of infection A will also change to some new value A_q in those who have been left unvaccinated. 

Recall the relation that linked R₀, A and L. Assuming that life expectancy has not changed, now:

${\displaystyle \ R_{q}={\frac {L}{A_{q}}},}$

${\displaystyle \ A_{q}={\frac {L}{R_{q}}}={\frac {L}{R_{0}(1-q)}}.}$

But R₀ = L/A so:

${\displaystyle \ {A_{q}}={\frac {L}{(L/A)(1-q)}}={\frac {AL}{L(1-q)}}={\frac {A}{1-q}}.}$

Thus the vaccination programme will raise the average age of infection, another mathematical justification for a result that might have been intuitively obvious. Unvaccinated individuals now experience a reduced force of infection due to the presence of the vaccinated group. 

However, it is important to consider this effect when vaccinating against diseases that are more severe in older people. A vaccination programme against such a disease that does not exceed q_c may cause more deaths and complications than there were before the programme was brought into force as individuals will be catching the disease later in life. These unforeseen outcomes of a vaccination programme are called perverse effects.

When mass vaccination exceeds the herd immunity

If a vaccination programme causes the proportion of immune individuals in a population to exceed the critical threshold for a significant length of time, transmission of the infectious disease in that population will stop. This is known as elimination of the infection and is different from eradication.

Elimination

Interruption of endemic transmission of an infectious disease, which occurs if each infected individual infects less than one other, is achieved by maintaining vaccination coverage to keep the proportion of immune individuals above the critical immunisation threshold.

Eradication

Reduction of infective organisms in the wild worldwide to zero. So far, this has only been achieved for smallpox and rinderpest. To get to eradication, elimination in all world regions must be achieved.