Group theory

From Wikipedia, the free encyclopedia

The popular puzzle Rubik's cube invented in 1974 by Ernő Rubik has been used as an illustration of permutation groups.

 

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. 

Various physical systems, such as crystals and the hydrogen atom, may be modeled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also central to public key cryptography. 

One of the most important mathematical achievements of the 20th century was the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 1980, that culminated in a complete classification of finite simple groups.

Main classes of groups

The range of groups being considered has gradually expanded from finite permutation groups and special examples of matrix groups to abstract groups that may be specified through a presentation by generators and relations.

Permutation groups

The first class of groups to undergo a systematic study was permutation groups. Given any set X and a collection G of bijections of X into itself (known as permutations) that is closed under compositions and inverses, G is a group acting on X. If X consists of n elements and G consists of all permutations, G is the symmetric group S_n; in general, any permutation group G is a subgroup of the symmetric group of X. An early construction due to Cayley exhibited any group as a permutation group, acting on itself (X = G) by means of the left regular representation. 

In many cases, the structure of a permutation group can be studied using the properties of its action on the corresponding set. For example, in this way one proves that for n ≥ 5, the alternating group A_n is simple, i.e. does not admit any proper normal subgroups. This fact plays a key role in the impossibility of solving a general algebraic equation of degree n ≥ 5 in radicals.

Matrix groups

The next important class of groups is given by matrix groups, or linear groups. Here G is a set consisting of invertible matrices of given order n over a field K that is closed under the products and inverses. Such a group acts on the n-dimensional vector space Kⁿ by linear transformations. This action makes matrix groups conceptually similar to permutation groups, and the geometry of the action may be usefully exploited to establish properties of the group G.

Transformation groups

Permutation groups and matrix groups are special cases of transformation groups: groups that act on a certain space X preserving its inherent structure. In the case of permutation groups, X is a set; for matrix groups, X is a vector space. The concept of a transformation group is closely related with the concept of a symmetry group: transformation groups frequently consist of all transformations that preserve a certain structure. 

The theory of transformation groups forms a bridge connecting group theory with differential geometry. A long line of research, originating with Lie and Klein, considers group actions on manifolds by homeomorphisms or diffeomorphisms. The groups themselves may be discrete or continuous.

Abstract groups

Most groups considered in the first stage of the development of group theory were "concrete", having been realized through numbers, permutations, or matrices. It was not until the late nineteenth century that the idea of an abstract group as a set with operations satisfying a certain system of axioms began to take hold. A typical way of specifying an abstract group is through a presentation by generators and relations,

${\displaystyle G=\langle S|R\rangle .}$

A significant source of abstract groups is given by the construction of a factor group, or quotient group, G/H, of a group G by a normal subgroup H. Class groups of algebraic number fields were among the earliest examples of factor groups, of much interest in number theory. If a group G is a permutation group on a set X, the factor group G/H is no longer acting on X; but the idea of an abstract group permits one not to worry about this discrepancy. 

The change of perspective from concrete to abstract groups makes it natural to consider properties of groups that are independent of a particular realization, or in modern language, invariant under isomorphism, as well as the classes of group with a given such property: finite groups, periodic groups, simple groups, solvable groups, and so on. Rather than exploring properties of an individual group, one seeks to establish results that apply to a whole class of groups. The new paradigm was of paramount importance for the development of mathematics: it foreshadowed the creation of abstract algebra in the works of Hilbert, Emil Artin, Emmy Noether, and mathematicians of their school.

Groups with additional structure

An important elaboration of the concept of a group occurs if G is endowed with additional structure, notably, of a topological space, differentiable manifold, or algebraic variety. If the group operations m (multiplication) and i (inversion),

${\displaystyle m:G\times G\to G,(g,h)\mapsto gh,\quad i:G\to G,g\mapsto g^{-1},}$

are compatible with this structure, that is, they are continuous, smooth or regular (in the sense of algebraic geometry) maps, then G is a topological group, a Lie group, or an algebraic group.

The presence of extra structure relates these types of groups with other mathematical disciplines and means that more tools are available in their study. Topological groups form a natural domain for abstract harmonic analysis, whereas Lie groups (frequently realized as transformation groups) are the mainstays of differential geometry and unitary representation theory. Certain classification questions that cannot be solved in general can be approached and resolved for special subclasses of groups. Thus, compact connected Lie groups have been completely classified. There is a fruitful relation between infinite abstract groups and topological groups: whenever a group Γ can be realized as a lattice in a topological group G, the geometry and analysis pertaining to G yield important results about Γ. A comparatively recent trend in the theory of finite groups exploits their connections with compact topological groups (profinite groups): for example, a single p-adic analytic group G has a family of quotients which are finite p-groups of various orders, and properties of G translate into the properties of its finite quotients.

Branches of group theory

Finite group theory

During the twentieth century, mathematicians investigated some aspects of the theory of finite groups in great depth, especially the local theory of finite groups and the theory of solvable and nilpotent groups. As a consequence, the complete classification of finite simple groups was achieved, meaning that all those simple groups from which all finite groups can be built are now known.

During the second half of the twentieth century, mathematicians such as Chevalley and Steinberg also increased our understanding of finite analogs of classical groups, and other related groups. One such family of groups is the family of general linear groups over finite fields. Finite groups often occur when considering symmetry of mathematical or physical objects, when those objects admit just a finite number of structure-preserving transformations. The theory of Lie groups, which may be viewed as dealing with "continuous symmetry", is strongly influenced by the associated Weyl groups. These are finite groups generated by reflections which act on a finite-dimensional Euclidean space. The properties of finite groups can thus play a role in subjects such as theoretical physics and chemistry.

Representation of groups

Saying that a group G acts on a set X means that every element of G defines a bijective map on the set X in a way compatible with the group structure. When X has more structure, it is useful to restrict this notion further: a representation of G on a vector space V is a group homomorphism:

${\displaystyle \rho :G\to \operatorname {GL} (V),}$

where GL(V) consists of the invertible linear transformations of V. In other words, to every group element g is assigned an automorphism ρ(g) such that ρ(g) ∘ ρ(h) = ρ(gh) for any h in G. 

This definition can be understood in two directions, both of which give rise to whole new domains of mathematics. On the one hand, it may yield new information about the group G: often, the group operation in G is abstractly given, but via ρ, it corresponds to the multiplication of matrices, which is very explicit. On the other hand, given a well-understood group acting on a complicated object, this simplifies the study of the object in question. For example, if G is finite, it is known that V above decomposes into irreducible parts. These parts in turn are much more easily manageable than the whole V (via Schur's lemma). 

Given a group G, representation theory then asks what representations of G exist. There are several settings, and the employed methods and obtained results are rather different in every case: representation theory of finite groups and representations of Lie groups are two main subdomains of the theory. The totality of representations is governed by the group's characters. For example, Fourier polynomials can be interpreted as the characters of U(1), the group of complex numbers of absolute value 1, acting on the L²-space of periodic functions.

Lie theory

A Lie group is a group that is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure. Lie groups are named after Sophus Lie, who laid the foundations of the theory of continuous transformation groups. The term groupes de Lie first appeared in French in 1893 in the thesis of Lie’s student Arthur Tresse, page 3.

Lie groups represent the best-developed theory of continuous symmetry of mathematical objects and structures, which makes them indispensable tools for many parts of contemporary mathematics, as well as for modern theoretical physics. They provide a natural framework for analyzing the continuous symmetries of differential equations, in much the same way as permutation groups are used in Galois theory for analyzing the discrete symmetries of algebraic equations. An extension of Galois theory to the case of continuous symmetry groups was one of Lie's principal motivations.

Combinatorial and geometric group theory

Groups can be described in different ways. Finite groups can be described by writing down the group table consisting of all possible multiplications g • h. A more compact way of defining a group is by generators and relations, also called the presentation of a group. Given any set F of generators ${\displaystyle \{g_{i}\}_{i\in I}}$, the free group generated by F surjects onto the group G. The kernel of this map is called the subgroup of relations, generated by some subset D. The presentation is usually denoted by ${\displaystyle \langle F\mid D\rangle .}$ For example, the group presentation ${\displaystyle \langle a,b\mid aba^{-1}b^{-1}\rangle }$ describes a group which is isomorphic to ${\displaystyle \mathbb {Z} \times \mathbb {Z} .}$ A string consisting of generator symbols and their inverses is called a word. 

Combinatorial group theory studies groups from the perspective of generators and relations. It is particularly useful where finiteness assumptions are satisfied, for example finitely generated groups, or finitely presented groups (i.e. in addition the relations are finite). The area makes use of the connection of graphs via their fundamental groups. For example, one can show that every subgroup of a free group is free.

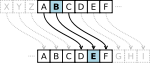
There are several natural questions arising from giving a group by its presentation. The word problem asks whether two words are effectively the same group element. By relating the problem to Turing machines, one can show that there is in general no algorithm solving this task. Another, generally harder, algorithmically insoluble problem is the group isomorphism problem, which asks whether two groups given by different presentations are actually isomorphic. For example, the group with presentation ${\displaystyle \langle x,y\mid xyxyx=e\rangle ,}$ is isomorphic to the additive group Z of integers, although this may not be immediately apparent.

The Cayley graph of 〈 x, y ∣ 〉, the free group of rank 2.

Geometric group theory attacks these problems from a geometric viewpoint, either by viewing groups as geometric objects, or by finding suitable geometric objects a group acts on. The first idea is made precise by means of the Cayley graph, whose vertices correspond to group elements and edges correspond to right multiplication in the group. Given two elements, one constructs the word metric given by the length of the minimal path between the elements. A theorem of Milnor and Svarc then says that given a group G acting in a reasonable manner on a metric space X, for example a compact manifold, then G is quasi-isometric (i.e. looks similar from a distance) to the space X.

Connection of groups and symmetry

Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This occurs in many cases, for example

1. If X is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups.
2. If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (an isometry). The corresponding group is called isometry group of X.
3. If instead angles are preserved, one speaks of conformal maps. Conformal maps give rise to Kleinian groups, for example.
4. Symmetries are not restricted to geometrical objects, but include algebraic objects as well. For instance, the equation ${\displaystyle x^{2}-3=0}$ has the two solutions ${\displaystyle {\sqrt {3}}}$ and ${\displaystyle -{\sqrt {3}}}$. In this case, the group that exchanges the two roots is the Galois group belonging to the equation. Every polynomial equation in one variable has a Galois group, that is a certain permutation group on its roots.

The axioms of a group formalize the essential aspects of symmetry. Symmetries form a group: they are closed because if you take a symmetry of an object, and then apply another symmetry, the result will still be a symmetry. The identity keeping the object fixed is always a symmetry of an object. Existence of inverses is guaranteed by undoing the symmetry and the associativity comes from the fact that symmetries are functions on a space, and composition of functions are associative.

Frucht's theorem says that every group is the symmetry group of some graph. So every abstract group is actually the symmetries of some explicit object.

The saying of "preserving the structure" of an object can be made precise by working in a category. Maps preserving the structure are then the morphisms, and the symmetry group is the automorphism group of the object in question.

Applications of group theory

Applications of group theory abound. Almost all structures in abstract algebra are special cases of groups. Rings, for example, can be viewed as abelian groups (corresponding to addition) together with a second operation (corresponding to multiplication). Therefore, group theoretic arguments underlie large parts of the theory of those entities.

Galois theory

Galois theory uses groups to describe the symmetries of the roots of a polynomial (or more precisely the automorphisms of the algebras generated by these roots). The fundamental theorem of Galois theory provides a link between algebraic field extensions and group theory. It gives an effective criterion for the solvability of polynomial equations in terms of the solvability of the corresponding Galois group. For example, S₅, the symmetric group in 5 elements, is not solvable which implies that the general quintic equation cannot be solved by radicals in the way equations of lower degree can. The theory, being one of the historical roots of group theory, is still fruitfully applied to yield new results in areas such as class field theory.

Algebraic topology

Algebraic topology is another domain which prominently associates groups to the objects the theory is interested in. There, groups are used to describe certain invariants of topological spaces. They are called "invariants" because they are defined in such a way that they do not change if the space is subjected to some deformation. For example, the fundamental group "counts" how many paths in the space are essentially different. The Poincaré conjecture, proved in 2002/2003 by Grigori Perelman, is a prominent application of this idea. The influence is not unidirectional, though. For example, algebraic topology makes use of Eilenberg–MacLane spaces which are spaces with prescribed homotopy groups. Similarly algebraic K-theory relies in a way on classifying spaces of groups. Finally, the name of the torsion subgroup of an infinite group shows the legacy of topology in group theory. 

A torus. Its abelian group structure is induced from the map C → C/Z + τZ, where τ is a parameter living in the upper half plane.

 

The cyclic group Z₂₆ underlies Caesar's cipher.

Algebraic geometry and cryptography

Algebraic geometry and cryptography likewise uses group theory in many ways. Abelian varieties have been introduced above. The presence of the group operation yields additional information which makes these varieties particularly accessible. They also often serve as a test for new conjectures. The one-dimensional case, namely elliptic curves is studied in particular detail. They are both theoretically and practically intriguing. Very large groups of prime order constructed in elliptic curve cryptography serve for public-key cryptography. Cryptographical methods of this kind benefit from the flexibility of the geometric objects, hence their group structures, together with the complicated structure of these groups, which make the discrete logarithm very hard to calculate. One of the earliest encryption protocols, Caesar's cipher, may also be interpreted as a (very easy) group operation. In another direction, toric varieties are algebraic varieties acted on by a torus. Toroidal embeddings have recently led to advances in algebraic geometry, in particular resolution of singularities.

Algebraic number theory

Algebraic number theory is a special case of group theory, thereby following the rules of the latter. For example, Euler's product formula

${\displaystyle {\begin{aligned}\sum _{n\geq 1}{\frac {1}{n^{s}}}&=\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}\\\end{aligned}}\!}$

captures the fact that any integer decomposes in a unique way into primes. The failure of this statement for more general rings gives rise to class groups and regular primes, which feature in Kummer's treatment of Fermat's Last Theorem.

Harmonic analysis

Analysis on Lie groups and certain other groups is called harmonic analysis. Haar measures, that is, integrals invariant under the translation in a Lie group, are used for pattern recognition and other image processing techniques.

Combinatorics

In combinatorics, the notion of permutation group and the concept of group action are often used to simplify the counting of a set of objects; see in particular Burnside's lemma. 

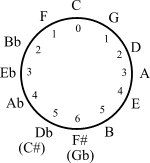
The circle of fifths may be endowed with a cyclic group structure

Music

The presence of the 12-periodicity in the circle of fifths yields applications of elementary group theory in musical set theory.

Physics

In physics, groups are important because they describe the symmetries which the laws of physics seem to obey. According to Noether's theorem, every continuous symmetry of a physical system corresponds to a conservation law of the system. Physicists are very interested in group representations, especially of Lie groups, since these representations often point the way to the "possible" physical theories. Examples of the use of groups in physics include the Standard Model, gauge theory, the Lorentz group, and the Poincaré group.

Chemistry and materials science

In chemistry and materials science, groups are used to classify crystal structures, regular polyhedra, and the symmetries of molecules. The assigned point groups can then be used to determine physical properties (such as chemical polarity and chirality), spectroscopic properties (particularly useful for Raman spectroscopy, infrared spectroscopy, circular dichroism spectroscopy, magnetic circular dichroism spectroscopy, UV/Vis spectroscopy, and fluorescence spectroscopy), and to construct molecular orbitals. 

Molecular symmetry is responsible for many physical and spectroscopic properties of compounds and provides relevant information about how chemical reactions occur. In order to assign a point group for any given molecule, it is necessary to find the set of symmetry operations present on it. The symmetry operation is an action, such as a rotation around an axis or a reflection through a mirror plane. In other words, it is an operation that moves the molecule such that it is indistinguishable from the original configuration. In group theory, the rotation axes and mirror planes are called "symmetry elements". These elements can be a point, line or plane with respect to which the symmetry operation is carried out. The symmetry operations of a molecule determine the specific point group for this molecule. 

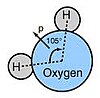
Water molecule with symmetry axis

 

In chemistry, there are five important symmetry operations. The identity operation (E) consists of leaving the molecule as it is. This is equivalent to any number of full rotations around any axis. This is a symmetry of all molecules, whereas the symmetry group of a chiral molecule consists of only the identity operation. Rotation around an axis (C_n) consists of rotating the molecule around a specific axis by a specific angle. For example, if a water molecule rotates 180° around the axis that passes through the oxygen atom and between the hydrogen atoms, it is in the same configuration as it started. In this case, n = 2, since applying it twice produces the identity operation. Other symmetry operations are: reflection, inversion and improper rotation (rotation followed by reflection).

Statistical mechanics

Group theory can be used to resolve the incompleteness of the statistical interpretations of mechanics developed by Willard Gibbs, relating to the summing of an infinite number of probabilities to yield a meaningful solution.

History

Group theory has three main historical sources: number theory, the theory of algebraic equations, and geometry. The number-theoretic strand was begun by Leonhard Euler, and developed by Gauss's work on modular arithmetic and additive and multiplicative groups related to quadratic fields. Early results about permutation groups were obtained by Lagrange, Ruffini, and Abel in their quest for general solutions of polynomial equations of high degree. Évariste Galois coined the term "group" and established a connection, now known as Galois theory, between the nascent theory of groups and field theory. In geometry, groups first became important in projective geometry and, later, non-Euclidean geometry. Felix Klein's Erlangen program proclaimed group theory to be the organizing principle of geometry. 

Galois, in the 1830s, was the first to employ groups to determine the solvability of polynomial equations. Arthur Cayley and Augustin Louis Cauchy pushed these investigations further by creating the theory of permutation groups. The second historical source for groups stems from geometrical situations. In an attempt to come to grips with possible geometries (such as euclidean, hyperbolic or projective geometry) using group theory, Felix Klein initiated the Erlangen program. Sophus Lie, in 1884, started using groups (now called Lie groups) attached to analytic problems. Thirdly, groups were, at first implicitly and later explicitly, used in algebraic number theory.

The different scope of these early sources resulted in different notions of groups. The theory of groups was unified starting around 1880. Since then, the impact of group theory has been ever growing, giving rise to the birth of abstract algebra in the early 20th century, representation theory, and many more influential spin-off domains. The classification of finite simple groups is a vast body of work from the mid 20th century, classifying all the finite simple groups.

Quantum spacetime

From Wikipedia, the free encyclopedia

In mathematical physics, the concept of quantum spacetime is a generalization of the usual concept of spacetime in which some variables that ordinarily commute are assumed not to commute and form a different Lie algebra. The choice of that algebra still varies from theory to theory. As a result of this change some variables that are usually continuous may become discrete. Often only such discrete variables are called "quantized"; usage varies. The idea of quantum spacetime was proposed in the early days of quantum theory by Heisenberg and Ivanenko as a way to eliminate infinities from quantum field theory. The germ of the idea passed from Heisenberg to Rudolf Peierls, who noted that electrons in a magnetic field can be regarded as moving in a quantum space-time, and to Robert Oppenheimer, who carried it to Hartland Snyder, who published the first concrete example. Snyder's Lie algebra was made simple by C. N. Yang in the same year.

Physical reasons have been given to believe that physical spacetime is a quantum spacetime. In quantum mechanics position and momentum variables ${\displaystyle x,p}$ are already noncommutative, obey the Heisenberg uncertainty principle, and are continuous. Because of the Heisenberg uncertainty relations, greater energy is needed to probe smaller distances. Ultimately, according to gravity theory, the probing particles form black holes that destroy what was to be measured. The process cannot be repeated, so it cannot be counted as a measurement. This limited measurability led many to expect that our usual picture of continuous commutative spacetime breaks down at Planck scale distances, if not sooner.

Again, physical spacetime is expected to be quantum because physical coordinates are already slightly noncommutative. The astronomical coordinates of a star are modified by gravitational fields between us and the star, as in the deflection of light by the sun, one of the classic tests of general relativity. Therefore, the coordinates actually depend on gravitational field variables. According to quantum theories of gravity these field variables do not commute; therefore coordinates that depend on them likely do not commute.

Both arguments are based on pure gravity and quantum theory, and they limit the measurement of time by the only time constant in pure quantum gravity, the Planck time. Our instruments, however, are not purely gravitational but are made of particles. They may set a more severe, larger, limit than the Planck time.

Quantum spacetimes are often described mathematically using the noncommutative geometry of Connes, quantum geometry, or quantum groups.

Any noncommutative algebra with at least four generators could be interpreted as a quantum spacetime, but the following desiderata have been suggested:

• Local Lorentz group and Poincaré group symmetries should be retained, possibly in a generalised form. Their generalization often takes the form of a quantum group acting on the quantum spacetime algebra.
• The algebra might plausibly arise in an effective description of quantum gravity effects in some regime of that theory. For example, a physical parameter ${\displaystyle \lambda }$, perhaps the Planck length, might control the deviation from commutative classical spacetime, so that ordinary Lorentzian spacetime arises as ${\displaystyle \lambda \to 0}$.
• There might be a notion of quantum differential calculus on the quantum spacetime algebra, compatible with the (quantum) symmetry and preferably reducing to the usual differential calculus as ${\displaystyle \lambda \to 0}$.

This would permit wave equations for particles and fields and facilitate predictions for experimental deviations from classical spacetime physics that can then be tested experimentally.

• The Lie algebra should be semisimple. This makes it easier to formulate a finite theory.

Several models were found in the 1990s more or less meeting most of the above criteria.

Bicrossproduct model spacetime

The bicrossproduct model spacetime was introduced by Shahn Majid and Henri Ruegg and has Lie algebra relations

${\displaystyle [x_{i},x_{j}]=0,\quad [x_{i},t]=i\lambda x_{i}}$

for the spatial variables ${\displaystyle x_{i}}$ and the time variable ${\displaystyle t}$. Here ${\displaystyle \lambda }$ has dimensions of time and is therefore expected to be something like the Planck time. The Poincaré group here is correspondingly deformed, now to a certain bicrossproduct quantum group with the following characteristic features. 

Orbits for the action of the Lorentz group on momentum space in the construction of the bicrossproduct model in units of ${\displaystyle \lambda ^{-1}}$. Mass-shell hyperboloids are `squashed' into a cylinder.

 

The momentum generators ${\displaystyle p_{i}}$ commute among themselves but addition of momenta, reflected in the quantum group structure, is deformed (momentum space becomes a non-abelian group). Meanwhile, the Lorentz group generators enjoy their usual relations among themselves but act non-linearly on the momentum space. The orbits for this action are depicted in the figure as a cross-section of ${\displaystyle p_{0}}$ against one of the ${\displaystyle p_{i}}$. The on-shell region describing particles in the upper center of the image would normally be hyperboloids but these are now `squashed' into the cylinder

${\displaystyle {\sqrt {p_{1}^{2}+p_{2}^{2}+p_{3}^{2}}}<\lambda ^{-1}\,}$

in simplified units. The upshot is that Lorentz-boosting a momentum will never increase it above the Planck momentum. The existence of a highest momentum scale or lowest distance scale fits the physical picture. This squashing comes from the non-linearity of the Lorentz boost and is an endemic feature of bicrossproduct quantum groups known since their introduction in 1988. Some physicists dub the bicrossproduct model doubly special relativity, since it sets an upper limit to both speed and momentum. 

Another consequence of the squashing is that the propagation of particles is deformed, even of light, leading to a variable speed of light. This prediction requires the particular ${\displaystyle p_{0},p_{i}}$ to be the physical energy and spatial momentum (as opposed to some other function of them). Arguments for this identification were provided in 1999 by Giovanni Amelino-Camelia and Majid through a study of plane waves for a quantum differential calculus in the model. They take the form

${\displaystyle e^{i\sum _{i}p_{i}x_{i}}e^{ip_{0}t}\,}$

in other words a form which is sufficiently close to classical that one might plausibly believe the interpretation. At the moment such wave analysis represents the best hope to obtain physically testable predictions from the model. 

Prior to this work there were a number of unsupported claims to make predictions from the model based solely on the form of the Poincaré quantum group. There were also claims based on an earlier ${\displaystyle \kappa }$-Poincaré quantum group introduced by Jurek Lukierski and co-workers which should be viewed as an important precursor to the bicrossproduct one, albeit without the actual quantum spacetime and with different proposed generators for which the above picture does not apply. The bicrossproduct model spacetime has also been called ${\displaystyle \kappa }$-deformed spacetime with ${\displaystyle \kappa =\lambda ^{-1}}$.

q-Deformed spacetime

This model was introduced independently by a team working under Julius Wess in 1990 and by Majid and coworkers in a series of papers on braided matrices starting a year later. The point of view in the second approach is that usual Minkowski spacetime has a nice description via Pauli matrices as the space of 2 x 2 hermitian matrices. In quantum group theory and using braided monoidal category methods one has a natural q-version of this defined here for real values of ${\displaystyle q}$ as a `braided hermitian matrix' of generators and relations

${\displaystyle {\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}={\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}^{\dagger },\quad \beta \alpha =q^{2}\alpha \beta ,\ [\alpha ,\delta ]=0,\ [\beta ,\gamma ]=(1-q^{-2})\alpha (\delta -\alpha ),\ [\delta ,\beta ]=(1-q^{-2})\alpha \beta }$

These relations say that the generators commute as ${\displaystyle q\to 1}$ thereby recovering usual Minkowski space. One can work with more familiar variables ${\displaystyle x,y,z,t}$ as linear combinations of these. In particular, time

${\displaystyle t={\text{Trace}}_{q}{\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}=q\delta +q^{-1}\alpha }$

is given by a natural braided trace of the matrix and commutes with the other generators (so this model has a very different flavour from the bicrossproduct one). The braided-matrix picture also leads naturally to a quantity

${\displaystyle {\det }_{q}{\begin{pmatrix}\alpha &\beta \\\gamma &\delta \end{pmatrix}}=\alpha \delta -q^{2}\gamma \beta }$

which as ${\displaystyle q\to 1}$ returns us the usual Minkowski distance (this translates to a metric in the quantum differential geometry). The parameter ${\displaystyle q=e^{\lambda }}$ or ${\displaystyle q=e^{i\lambda }}$ is dimensionless and ${\displaystyle \lambda }$ is thought to be a ratio of the Planck scale and the cosmological length. That is, there are indications that this model relates to quantum gravity with non-zero cosmological constant, the choice of ${\displaystyle q}$ depending on whether this is positive or negative. We have described the mathematically better understood but perhaps less physically justified positive case here. 

A full understanding of this model requires (and was concurrent with the development of) a full theory of `braided linear algebra' for such spaces. The momentum space for the theory is another copy of the same algebra and there is a certain `braided addition' of momentum on it expressed as the structure of a braided Hopf algebra or quantum group in a certain braided monoidal category). This theory by 1993 had provided the corresponding ${\displaystyle q}$-deformed Poincaré group as generated by such translations and ${\displaystyle q}$-Lorentz transformations, completing the interpretation as a quantum spacetime.

In the process it was discovered that the Poincaré group not only had to be deformed but had to be extended to include dilations of the quantum spacetime. For such a theory to be exact we would need all particles in the theory to be massless, which is consistent with experiment as masses of elementary particles are indeed vanishingly small compared to the Planck mass. If current thinking in cosmology is correct then this model is more appropriate, but it is significantly more complicated and for this reason its physical predictions have yet to be worked out.

Fuzzy or spin model spacetime

This refers in modern usage to the angular momentum algebra

${\displaystyle [x_{1},x_{2}]=2i\lambda x_{3},\ [x_{2},x_{3}]=2i\lambda x_{1},\ [x_{3},x_{1}]=2i\lambda x_{2}}$

familiar from quantum mechanics but interpreted in this context as coordinates of a quantum space or spacetime. These relations were proposed by Roger Penrose in his earliest spin network theory of space. It is a toy model of quantum gravity in 3 spacetime dimensions (not the physical 4) with a Euclidean (not the physical Minkowskian) signature. It was again proposed in this context by Gerardus 't Hooft. A further development including a quantum differential calculus and an action of a certain `quantum double' quantum group as deformed Euclidean group of motions was given by Majid and E. Batista.

A striking feature of the noncommutative geometry here is that the smallest covariant quantum differential calculus has one dimension higher than expected, namely 4, suggesting that the above can also be viewed as the spatial part of a 4-dimensional quantum spacetime. The model should not be confused with fuzzy spheres which are finite-dimensional matrix algebras which one can think of as spheres in the spin model spacetime of fixed radius.

Heisenberg model spacetimes

The quantum spacetime of Hartland Snyder proposes that

${\displaystyle [x_{\mu },x_{\nu }]=iM_{\mu \nu }}$

where the ${\displaystyle M_{\mu \nu }}$ generate the Lorentz group. This quantum spacetime and that of C. N. Yang entail a radical unification of spacetime, energy-momentum, and angular momentum. 

The idea was revived in a modern context by Sergio Doplicher, Klaus Fredenhagen and John Roberts in 1995 by letting ${\displaystyle M_{\mu \nu }}$ simply be viewed as some function of ${\displaystyle x_{\mu }}$ as defined by the above relation, and any relations involving it viewed as higher order relations among the ${\displaystyle x_{\mu }}$. The Lorentz symmetry is arranged so as to transform the indices as usual and without being deformed.

An even simpler variant of this model is to let ${\displaystyle M}$ here be a numerical antisymmetric tensor, in which context it is usually denoted ${\displaystyle \theta }$, so the relations are ${\displaystyle [x_{\mu },x_{\nu }]=i\theta _{\mu \nu }}$. In even dimensions ${\displaystyle D}$, any nondegenerate such theta can be transformed to a normal form in which this really is just the Heisenberg algebra but the difference that the variables are being proposed as those of spacetime. This proposal was for a time quite popular because of its familiar form of relations and because it has been argued that it emerges from the theory of open strings landing on D-branes, see noncommutative quantum field theory and Moyal plane. However, it should be realised that this D-brane lives in some of the higher spacetime dimensions in the theory and hence it is not our physical spacetime that string theory suggests to be effectively quantum in this way. You also have to subscribe to D-branes as an approach to quantum gravity in the first place. Even when posited as quantum spacetime it is hard to obtain physical predictions and one reason for this is that if ${\displaystyle \theta }$ is a tensor then by dimensional analysis it should have dimensions of length${\displaystyle {}^{2}}$, and if this length is speculated to be the Planck length then the effects would be even harder to ever detect than for other models.

Noncommutative extensions to spacetime

Although not quantum spacetime in the sense above, another use of noncommutative geometry is to tack on `noncommutative extra dimensions' at each point of ordinary spacetime. Instead of invisible curled up extra dimensions as in string theory, Alain Connes and coworkers have argued that the coordinate algebra of this extra part should be replaced by a finite-dimensional noncommutative algebra. For a certain reasonable choice of this algebra, its representation and extended Dirac operator, one is able to recover the Standard Model of elementary particles. In this point of view the different kinds of matter particles are manifestations of geometry in these extra noncommutative directions. Connes's first works here date from 1989 but has been developed considerably since then. Such an approach can theoretically be combined with quantum spacetime as above.