Blaise Pascal

From Wikipedia, the free encyclopedia

Blaise Pascal
Painting of Blaise Pascal made by François II Quesnel for Gérard Edelinck in 1691
Born	19 June 1623 Clermont-Ferrand, Auvergne, France
Died	19 August 1662 (aged 39) Paris, France
Residence	France
Nationality	French
Era	17th-century philosophy
Region	Western philosophy
School	Jansenism
Main interests	Theology Mathematics Philosophy Physics
Notable ideas	Pascal's Wager Pascal's triangle Pascal's law Pascal's theorem

Blaise Pascal was a French mathematician, physicist, inventor, writer and Catholic theologian. He was a child prodigy who was educated by his father, a tax collector in Rouen. Pascal's earliest work was in the natural and applied sciences where he made important contributions to the study of fluids, and clarified the concepts of pressure and vacuum by generalising the work of Evangelista Torricelli. Pascal also wrote in defence of the scientific method.

In 1642, while still a teenager, he started some pioneering work on calculating machines. After three years of effort and 50 prototypes, he built 20 finished machines (called Pascal's calculators and later Pascalines) over the following 10 years, establishing him as one of the first two inventors of the mechanical calculator.

Pascal was an important mathematician, helping create two major new areas of research: he wrote a significant treatise on the subject of projective geometry at the age of 16, and later corresponded with Pierre de Fermat on probability theory, strongly influencing the development of modern economics and social science. Following Galileo Galilei and Torricelli, in 1647, he rebutted Aristotle's followers who insisted that nature abhors a vacuum. Pascal's results caused many disputes before being accepted.

In 1646, he and his sister Jacqueline identified with the religious movement within Catholicism known by its detractors as Jansenism. Following a religious experience in late 1654, he began writing influential works on philosophy and theology. His two most famous works date from this period: the Lettres provinciales and the Pensées, the former set in the conflict between Jansenists and Jesuits. In that year, he also wrote an important treatise on the arithmetical triangle. Between 1658 and 1659, he wrote on the cycloid and its use in calculating the volume of solids.

Throughout his life, Pascal was in frail health, especially after the age of 18; he died just two months after his 39th birthday.

Early life and education

Pascal was born in Clermont-Ferrand, which is in France's Auvergne region. He lost his mother, Antoinette Begon, at the age of three. His father, Étienne Pascal (1588–1651), who also had an interest in science and mathematics, was a local judge and member of the "Noblesse de Robe". Pascal had two sisters, the younger Jacqueline and the elder Gilberte.

In 1631, five years after the death of his wife, Étienne Pascal moved with his children to Paris. The newly arrived family soon hired Louise Delfault, a maid who eventually became an instrumental member of the family. Étienne, who never remarried, decided that he alone would educate his children, for they all showed extraordinary intellectual ability, particularly his son Blaise. The young Pascal showed an amazing aptitude for mathematics and science.

Portrait of Pascal

 

Particularly of interest to Pascal was a work of Desargues on conic sections. Following Desargues' thinking, the 16-year-old Pascal produced, as a means of proof, a short treatise on what was called the "Mystic Hexagram", Essai pour les coniques ("Essay on Conics") and sent it—his first serious work of mathematics—to Père Mersenne in Paris; it is known still today as Pascal's theorem. It states that if a hexagon is inscribed in a circle (or conic) then the three intersection points of opposite sides lie on a line (called the Pascal line). 

Pascal's work was so precocious that Descartes was convinced that Pascal's father had written it. When assured by Mersenne that it was, indeed, the product of the son and not the father, Descartes dismissed it with a sniff: "I do not find it strange that he has offered demonstrations about conics more appropriate than those of the ancients," adding, "but other matters related to this subject can be proposed that would scarcely occur to a 16-year-old child."

In France at that time offices and positions could be—and were—bought and sold. In 1631, Étienne sold his position as second president of the Cour des Aides for 65,665 livres. The money was invested in a government bond which provided, if not a lavish, then certainly a comfortable income which allowed the Pascal family to move to, and enjoy, Paris. But in 1638 Richelieu, desperate for money to carry on the Thirty Years' War, defaulted on the government's bonds. Suddenly Étienne Pascal's worth had dropped from nearly 66,000 livres to less than 7,300. 

An early Pascaline on display at the Musée des Arts et Métiers, Paris

 

Like so many others, Étienne was eventually forced to flee Paris because of his opposition to the fiscal policies of Cardinal Richelieu, leaving his three children in the care of his neighbour Madame Sainctot, a great beauty with an infamous past who kept one of the most glittering and intellectual salons in all France. It was only when Jacqueline performed well in a children's play with Richelieu in attendance that Étienne was pardoned. In time, Étienne was back in good graces with the cardinal and in 1639 had been appointed the king's commissioner of taxes in the city of Rouen—a city whose tax records, thanks to uprisings, were in utter chaos. 

In 1642, in an effort to ease his father's endless, exhausting calculations, and recalculations, of taxes owed and paid (into which work the young Pascal had been recruited), Pascal, not yet 19, constructed a mechanical calculator capable of addition and subtraction, called Pascal's calculator or the Pascaline. Of the eight Pascalines known to have survived, four are held by the Musée des Arts et Métiers in Paris and one more by the Zwinger museum in Dresden, Germany, exhibit two of his original mechanical calculators. Although these machines are pioneering forerunners to a further 400 years of development of mechanical methods of calculation, and in a sense to the later field of computer engineering, the calculator failed to be a great commercial success. Partly because it was still quite cumbersome to use in practice, but probably primarily because it was extraordinarily expensive, the Pascaline became little more than a toy, and a status symbol, for the very rich both in France and elsewhere in Europe. Pascal continued to make improvements to his design through the next decade, and he refers to some 50 machines that were built to his design.

Contributions to mathematics

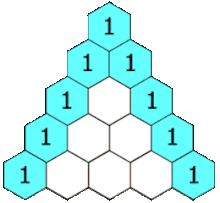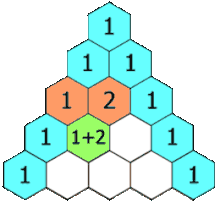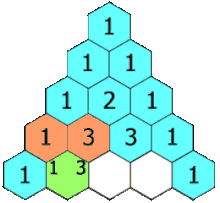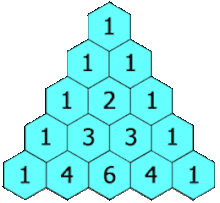
Pascal's triangle. Each number is the sum of the two directly above it. The triangle demonstrates many mathematical properties in addition to showing binomial coefficients

 

Pascal continued to influence mathematics throughout his life. His Traité du triangle arithmétique ("Treatise on the Arithmetical Triangle") of 1653 described a convenient tabular presentation for binomial coefficients, now called Pascal's triangle. The triangle can also be represented: 

	0	1	2	3	4	5	6
0	1	1	1	1	1	1	1
1	1	2	3	4	5	6
2	1	3	6	10	15
3	1	4	10	20
4	1	5	15
5	1	6
6	1

He defines the numbers in the triangle by recursion: Call the number in the (m + 1)th row and (n + 1)th column t_mn. Then t_mn = t_m–1,n + t_m,n–1, for m = 0, 1, 2, ... and n = 0, 1, 2, ... The boundary conditions are t_m,−1 = 0, t_−1,n = 0 for m = 1, 2, 3, ... and n = 1, 2, 3, ... The generator t₀₀ = 1. Pascal concludes with the proof,

${\displaystyle t_{mn}={\frac {(m+n)(m+n-1)\cdots (m+1)}{n(n-1)\cdots 1}}.}$

In 1654, he proved Pascal's identity relating the sums of the p-th powers of the first n positive integers for p = 0, 1, 2, ..., k.

In 1654, prompted by his friend the Chevalier de Méré, he corresponded with Pierre de Fermat on the subject of gambling problems, and from that collaboration was born the mathematical theory of probabilities. The specific problem was that of two players who want to finish a game early and, given the current circumstances of the game, want to divide the stakes fairly, based on the chance each has of winning the game from that point. From this discussion, the notion of expected value was introduced. Pascal later (in the Pensées) used a probabilistic argument, Pascal's Wager, to justify belief in God and a virtuous life. The work done by Fermat and Pascal into the calculus of probabilities laid important groundwork for Leibniz' formulation of the calculus.

After a religious experience in 1654, Pascal mostly gave up work in mathematics.

Philosophy of mathematics

Pascal's major contribution to the philosophy of mathematics came with his De l'Esprit géométrique ("Of the Geometrical Spirit"), originally written as a preface to a geometry textbook for one of the famous "Petites-Ecoles de Port-Royal" ("Little Schools of Port-Royal"). The work was unpublished until over a century after his death. Here, Pascal looked into the issue of discovering truths, arguing that the ideal of such a method would be to found all propositions on already established truths. At the same time, however, he claimed this was impossible because such established truths would require other truths to back them up—first principles, therefore, cannot be reached. Based on this, Pascal argued that the procedure used in geometry was as perfect as possible, with certain principles assumed and other propositions developed from them. Nevertheless, there was no way to know the assumed principles to be true. 

Pascal also used De l'Esprit géométrique to develop a theory of definition. He distinguished between definitions which are conventional labels defined by the writer and definitions which are within the language and understood by everyone because they naturally designate their referent. The second type would be characteristic of the philosophy of essentialism. Pascal claimed that only definitions of the first type were important to science and mathematics, arguing that those fields should adopt the philosophy of formalism as formulated by Descartes. 

In De l'Art de persuader ("On the Art of Persuasion"), Pascal looked deeper into geometry's axiomatic method, specifically the question of how people come to be convinced of the axioms upon which later conclusions are based. Pascal agreed with Montaigne that achieving certainty in these axioms and conclusions through human methods is impossible. He asserted that these principles can be grasped only through intuition, and that this fact underscored the necessity for submission to God in searching out truths.

Contributions to the physical sciences

An illustration of the (apocryphal) Pascal's barrel experiment

 

Pascal's work in the fields of the study of hydrodynamics and hydrostatics centered on the principles of hydraulic fluids. His inventions include the hydraulic press (using hydraulic pressure to multiply force) and the syringe. He proved that hydrostatic pressure depends not on the weight of the fluid but on the elevation difference. He demonstrated this principle by attaching a thin tube to a barrel full of water and filling the tube with water up to the level of the third floor of a building. This caused the barrel to leak, in what became known as Pascal's barrel experiment.

By 1647, Pascal had learned of Evangelista Torricelli's experimentation with barometers. Having replicated an experiment that involved placing a tube filled with mercury upside down in a bowl of mercury, Pascal questioned what force kept some mercury in the tube and what filled the space above the mercury in the tube. At the time, most scientists contended that, rather than a vacuum, some invisible matter was present. This was based on the Aristotelian notion that creation was a thing of substance, whether visible or invisible; and that this substance was forever in motion. Furthermore, "Everything that is in motion must be moved by something," Aristotle declared. Therefore, to the Aristotelian trained scientists of Pascal's time, a vacuum was an impossibility. How so? As proof it was pointed out:

• Light passed through the so-called "vacuum" in the glass tube.
• Aristotle wrote how everything moved, and must be moved by something.
• Therefore, since there had to be an invisible "something" to move the light through the glass tube, there was no vacuum in the tube. Not in the glass tube or anywhere else. Vacuums – the absence of any and everything – were simply an impossibility.

Following more experimentation in this vein, in 1647 Pascal produced Experiences nouvelles touchant le vide ("New experiments with the vacuum"), which detailed basic rules describing to what degree various liquids could be supported by air pressure. It also provided reasons why it was indeed a vacuum above the column of liquid in a barometer tube. This work was followed by Récit de la grande expérience de l'équilibre des liqueurs ("Account of the great experiment on equilibrium in liquids") published in 1648. 

The Torricellian vacuum found that air pressure is equal to the weight of 30 inches of mercury. If air has a finite weight, Earth's atmosphere must have a maximum height. Pascal reasoned that if true, air pressure on a high mountain must be less than at a lower altitude. He lived near the Puy de Dôme mountain, 4,790 feet (1,460 m) tall, but his health was poor so could not climb it. On 19 September 1648, after many months of Pascal's friendly but insistent prodding, Florin Périer, husband of Pascal's elder sister Gilberte, was finally able to carry out the fact-finding mission vital to Pascal's theory. The account, written by Périer, reads:

The weather was chancy last Saturday...[but] around five o'clock that morning...the Puy-de-Dôme was visible...so I decided to give it a try. Several important people of the city of Clermont had asked me to let them know when I would make the ascent...I was delighted to have them with me in this great work...
...at eight o'clock we met in the gardens of the Minim Fathers, which has the lowest elevation in town....First I poured 16 pounds of quicksilver...into a vessel...then took several glass tubes...each four feet long and hermetically sealed at one end and opened at the other...then placed them in the vessel [of quicksilver]...I found the quick silver stood at 26" and 3​¹⁄₂ lines above the quicksilver in the vessel...I repeated the experiment two more times while standing in the same spot...[they] produced the same result each time...
I attached one of the tubes to the vessel and marked the height of the quicksilver and...asked Father Chastin, one of the Minim Brothers...to watch if any changes should occur through the day...Taking the other tube and a portion of the quick silver...I walked to the top of Puy-de-Dôme, about 500 fathoms higher than the monastery, where upon experiment...found that the quicksilver reached a height of only 23" and 2 lines...I repeated the experiment five times with care...each at different points on the summit...found the same height of quicksilver...in each case...

Pascal replicated the experiment in Paris by carrying a barometer up to the top of the bell tower at the church of Saint-Jacques-de-la-Boucherie, a height of about 50 metres. The mercury dropped two lines. 

In the face of criticism that some invisible matter must exist in Pascal's empty space, Pascal, in his reply to Estienne Noel, gave one of the 17th century's major statements on the scientific method, which is a striking anticipation of the idea popularised by Karl Popper that scientific theories are characterised by their falsifiability: "In order to show that a hypothesis is evident, it does not suffice that all the phenomena follow from it; instead, if it leads to something contrary to a single one of the phenomena, that suffices to establish its falsity." His insistence on the existence of the vacuum also led to conflict with other prominent scientists, including Descartes. 

Pascal introduced a primitive form of roulette and the roulette wheel in his search for a perpetual motion machine.

Adult life, religion, philosophy, and literature

For after all what is man in nature? A nothing in relation to infinity, all in relation to nothing, a central point between nothing and all and infinitely far from understanding either. The ends of things and their beginnings are impregnably concealed from him in an impenetrable secret. He is equally incapable of seeing the nothingness out of which he was drawn and the infinite in which he is engulfed.

Blaise Pascal, Pensées No. 72

Religious conversion

Pascal studying the cycloid, by Augustin Pajou, 1785, Louvre

 

In the winter of 1646, Pascal's 58-year-old father broke his hip when he slipped and fell on an icy street of Rouen; given the man's age and the state of medicine in the 17th century, a broken hip could be a very serious condition, perhaps even fatal. Rouen was home to two of the finest doctors in France: Monsieur Doctor Deslandes and Monsieur Doctor de La Bouteillerie. The elder Pascal "would not let anyone other than these men attend him...It was a good choice, for the old man survived and was able to walk again..." But treatment and rehabilitation took three months, during which time La Bouteillerie and Deslandes had become regular visitors. 

Both men were followers of Jean Guillebert, proponent of a splinter group from Catholic teaching known as Jansenism. This still fairly small sect was making surprising inroads into the French Catholic community at that time. It espoused rigorous Augustinism. Blaise spoke with the doctors frequently, and after their successful treatment of his father, borrowed from them works by Jansenist authors. In this period, Pascal experienced a sort of "first conversion" and began to write on theological subjects in the course of the following year. 

Pascal fell away from this initial religious engagement and experienced a few years of what some biographers have called his "worldly period" (1648–54). His father died in 1651 and left his inheritance to Pascal and his sister Jacqueline, for whom Pascal acted as conservator. Jacqueline announced that she would soon become a postulant in the Jansenist convent of Port-Royal. Pascal was deeply affected and very sad, not because of her choice, but because of his chronic poor health; he needed her just as she had needed him.

Suddenly there was war in the Pascal household. Blaise pleaded with Jacqueline not to leave, but she was adamant. He commanded her to stay, but that didn't work, either. At the heart of this was...Blaise's fear of abandonment...if Jacqueline entered Port-Royal, she would have to leave her inheritance behind...[but] nothing would change her mind.

By the end of October in 1651, a truce had been reached between brother and sister. In return for a healthy annual stipend, Jacqueline signed over her part of the inheritance to her brother. Gilberte had already been given her inheritance in the form of a dowry. In early January, Jacqueline left for Port-Royal. On that day, according to Gilberte concerning her brother, "He retired very sadly to his rooms without seeing Jacqueline, who was waiting in the little parlor..." In early June 1653, after what must have seemed like endless badgering from Jacqueline, Pascal formally signed over the whole of his sister's inheritance to Port-Royal, which, to him, "had begun to smell like a cult." With two thirds of his father's estate now gone, the 29-year-old Pascal was now consigned to genteel poverty. 

For a while, Pascal pursued the life of a bachelor. During visits to his sister at Port-Royal in 1654, he displayed contempt for affairs of the world but was not drawn to God.

Brush with death

On 23 November 1654, between 10:30 and 12:30 at night, Pascal had an intense religious vision and immediately recorded the experience in a brief note to himself which began: "Fire. God of Abraham, God of Isaac, God of Jacob, not of the philosophers and the scholars..." and concluded by quoting Psalm 119:16: "I will not forget thy word. Amen." He seems to have carefully sewn this document into his coat and always transferred it when he changed clothes; a servant discovered it only by chance after his death. This piece is now known as the Memorial. The story of the carriage accident as having led to the experience described in the Memorial is disputed by some scholars. His belief and religious commitment revitalized, Pascal visited the older of two convents at Port-Royal for a two-week retreat in January 1655. For the next four years, he regularly travelled between Port-Royal and Paris. It was at this point immediately after his conversion when he began writing his first major literary work on religion, the Provincial Letters.

The Provincial Letters

Beginning in 1656–57, Pascal published his memorable attack on casuistry, a popular ethical method used by Catholic thinkers in the early modern period (especially the Jesuits, and in particular Antonio Escobar). Pascal denounced casuistry as the mere use of complex reasoning to justify moral laxity and all sorts of sins. The 18-letter series was published between 1656 and 1657 under the pseudonym Louis de Montalte and incensed Louis XIV. The king ordered that the book be shredded and burnt in 1660. In 1661, in the midsts of the formulary controversy, the Jansenist school at Port-Royal was condemned and closed down; those involved with the school had to sign a 1656 papal bull condemning the teachings of Jansen as heretical. The final letter from Pascal, in 1657, had defied Alexander VII himself. Even Pope Alexander, while publicly opposing them, nonetheless was persuaded by Pascal's arguments. 

Aside from their religious influence, the Provincial Letters were popular as a literary work. Pascal's use of humor, mockery, and vicious satire in his arguments made the letters ripe for public consumption, and influenced the prose of later French writers like Voltaire and Jean-Jacques Rousseau.

Charles Perrault wrote of the Letters: "Everything is there—purity of language, nobility of thought, solidity in reasoning, finesse in raillery, and throughout an agrément not to be found anywhere else."

The Pensées

Pascal's most influential theological work, referred to posthumously as the Pensées ("Thoughts"), was not completed before his death. It was to have been a sustained and coherent examination and defense of the Christian faith, with the original title Apologie de la religion Chrétienne ("Defense of the Christian Religion"). The first version of the numerous scraps of paper found after his death appeared in print as a book in 1669 titled Pensées de M. Pascal sur la religion, et sur quelques autres sujets ("Thoughts of M. Pascal on religion, and on some other subjects") and soon thereafter became a classic. One of the Apologie's main strategies was to use the contradictory philosophies of skepticism and stoicism, personalized by Montaigne on one hand, and Epictetus on the other, in order to bring the unbeliever to such despair and confusion that he would embrace God.

Pascal's Pensées is widely considered to be a masterpiece, and a landmark in French prose. When commenting on one particular section (Thought #72), Sainte-Beuve praised it as the finest pages in the French language. Will Durant hailed the Pensées as "the most eloquent book in French prose".

Last works and death

Pascal's epitaph in Saint-Étienne-du-Mont, where he was buried

 

T. S. Eliot described him during this phase of his life as "a man of the world among ascetics, and an ascetic among men of the world." Pascal's ascetic lifestyle derived from a belief that it was natural and necessary for a person to suffer. In 1659, Pascal fell seriously ill. During his last years, he frequently tried to reject the ministrations of his doctors, saying, "Sickness is the natural state of Christians."

Louis XIV suppressed the Jansenist movement at Port-Royal in 1661. In response, Pascal wrote one of his final works, Écrit sur la signature du formulaire ("Writ on the Signing of the Form"), exhorting the Jansenists not to give in. Later that year, his sister Jacqueline died, which convinced Pascal to cease his polemics on Jansenism. Pascal's last major achievement, returning to his mechanical genius, was inaugurating perhaps the first bus line, the carrosses à cinq sols, moving passengers within Paris in a carriage with many seats. 

In 1662, Pascal's illness became more violent, and his emotional condition had severely worsened since his sister's death. Aware that his health was fading quickly, he sought a move to the hospital for incurable diseases, but his doctors declared that he was too unstable to be carried. In Paris on 18 August 1662, Pascal went into convulsions and received extreme unction. He died the next morning, his last words being "May God never abandon me," and was buried in the cemetery of Saint-Étienne-du-Mont.

An autopsy performed after his death revealed grave problems with his stomach and other organs of his abdomen, along with damage to his brain. Despite the autopsy, the cause of his poor health was never precisely determined, though speculation focuses on tuberculosis, stomach cancer, or a combination of the two. The headaches which afflicted Pascal are generally attributed to his brain lesion.

Legacy

Death mask of Blaise Pascal.

 

In honour of his scientific contributions, the name Pascal has been given to the SI unit of pressure, to a programming language, and Pascal's law (an important principle of hydrostatics), and as mentioned above, Pascal's triangle and Pascal's wager still bear his name. 

Pascal's development of probability theory was his most influential contribution to mathematics. Originally applied to gambling, today it is extremely important in economics, especially in actuarial science. John Ross writes, "Probability theory and the discoveries following it changed the way we regard uncertainty, risk, decision-making, and an individual's and society's ability to influence the course of future events." However, it should be noted that Pascal and Fermat, though doing important early work in probability theory, did not develop the field very far. Christiaan Huygens, learning of the subject from the correspondence of Pascal and Fermat, wrote the first book on the subject. Later figures who continued the development of the theory include Abraham de Moivre and Pierre-Simon Laplace. 

In literature, Pascal is regarded as one of the most important authors of the French Classical Period and is read today as one of the greatest masters of French prose. His use of satire and wit influenced later polemicists. The content of his literary work is best remembered for its strong opposition to the rationalism of René Descartes and simultaneous assertion that the main countervailing philosophy, empiricism, was also insufficient for determining major truths. 

In France, prestigious annual awards, Blaise Pascal Chairs are given to outstanding international scientists to conduct their research in the Ile de France region. One of the Universities of Clermont-Ferrand, France – Université Blaise Pascal – is named after him. The University of Waterloo, Ontario, Canada, holds an annual math contest named in his honour.

Pascalian theology has grown out of his perspective that we are, according to Wood, "born into a duplicitous world that shapes us into duplicitous subjects and so we find it easy to reject God continually and deceive ourselves about our own sinfulness".

Roberto Rossellini directed a filmed biopic, Blaise Pascal, which originally aired on Italian television in 1971. Pascal was a subject of the first edition of the 1984 BBC Two documentary, Sea of Faith, presented by Don Cupitt. 

In 2014, Nvidia announced its new Pascal microarchitecture, which is named for Pascal. The first graphics cards featuring Pascal were released in 2016. 

The 2017 game Nier: Automata has multiple characters named after famous philosophers; one of these is a sentient pacifistic machine named Pascal, who serves as a major supporting character. Pascal creates a village for machines to live peacefully with the androids they're at war with and acts as a parental figure for other machines trying to adapt to their newly-found individuality.

Works

• Essai pour les coniques [Essay on conics] (1639)
• Experiences nouvelles touchant le vide [New experiments with the vacuum] (1647)
• Récit de la grande expérience de l'équilibre des liqueurs [Account of the great experiment on equilibrium in liquids] (1648)
• Traité du triangle arithmétique [Treatise on the arithmetic triangle] (1653)
• Lettres provinciales [The provincial letters] (1656–57)
• De l'Esprit géométrique [On the geometrical spirit] (1657 or 1658)
• Écrit sur la signature du formulaire (1661)
• Traité du triangle arithmétique (Treatise on arithmetical triangle) (written c. 1654; publ. 1665)
• Pensées [Thoughts] (incomplete at death; publ. 1670)

Nonlinear system

From Wikipedia, the free encyclopedia

In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the unknown variables or functions that appear in them. Systems can be defined as nonlinear, regardless of whether known linear functions appear in the equations. In particular, a differential equation is linear if it is linear in terms of the unknown function and its derivatives, even if nonlinear in terms of the other variables appearing in it.

As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such as solitons, chaos,^[10] and singularities are hidden by linearization. It follows that some aspects of the dynamic behavior of a nonlinear system can appear to be counterintuitive, unpredictable or even chaotic. Although such chaotic behavior may resemble random behavior, it is in fact not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout. This nonlinearity is one of the reasons why accurate long-term forecasts are impossible with current technology.

Some authors use the term nonlinear science for the study of nonlinear systems. This is disputed by others:

Using a term like nonlinear science is like referring to the bulk of zoology as the study of non-elephant animals.

— Stanislaw Ulam

Definition

In mathematics, a linear map (or linear function) ${\displaystyle f(x)}$ is one which satisfies both of the following properties:

• Additivity or superposition principle: ${\displaystyle \textstyle f(x+y)=f(x)+f(y);}$
• Homogeneity: ${\displaystyle \textstyle f(\alpha x)=\alpha f(x).}$

Additivity implies homogeneity for any rational α, and, for continuous functions, for any real α. For a complex α, homogeneity does not follow from additivity. For example, an antilinear map is additive but not homogeneous. The conditions of additivity and homogeneity are often combined in the superposition principle

${\displaystyle f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)}$

An equation written as

${\displaystyle f(x)=C}$

is called linear if ${\displaystyle f(x)}$ is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if ${\displaystyle C=0}$. 

The definition ${\displaystyle f(x)=C}$ is very general in that ${\displaystyle x}$ can be any sensible mathematical object (number, vector, function, etc.), and the function ${\displaystyle f(x)}$ can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If ${\displaystyle f(x)}$ contains differentiation with respect to ${\displaystyle x}$, the result will be a differential equation.

Nonlinear algebraic equations

Nonlinear algebraic equations, which are also called polynomial equations, are defined by equating polynomials to zero. For example,

${\displaystyle x^{2}+x-1=0\,.}$

For a single polynomial equation, root-finding algorithms can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However, systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry, a difficult branch of modern mathematics. It is even difficult to decide whether a given algebraic system has complex solutions. Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations are now well understood and efficient methods exist for solving them.

Nonlinear recurrence relations

A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related nonlinear system identification and analysis procedures. These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains.

Nonlinear differential equations

A system of differential equations is said to be nonlinear if it is not a linear system. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics and the Lotka–Volterra equations in biology. 

One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions.

Ordinary differential equations

First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation

${\displaystyle {\frac {du}{dx}}=-u^{2}}$

has ${\displaystyle u={\frac {1}{x+C}}}$ as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as

${\displaystyle {\frac {du}{dx}}+u^{2}=0}$

and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u² term were replaced with u, the problem would be linear (the exponential decay problem). 

Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed-form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered. 

Common methods for the qualitative analysis of nonlinear ordinary differential equations include:

• Examination of any conserved quantities, especially in Hamiltonian systems
• Examination of dissipative quantities (see Lyapunov function) analogous to conserved quantities
• Linearization via Taylor expansion
• Change of variables into something easier to study
• Bifurcation theory
• Perturbation methods (can be applied to algebraic equations too)

Partial differential equations

The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable. 

Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation. 

Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations.

Pendula

Illustration of a pendulum

 

Linearizations of a pendulum

A classic, extensively studied nonlinear problem is the dynamics of a pendulum under the influence of gravity. Using Lagrangian mechanics, it may be shown that the motion of a pendulum can be described by the dimensionless nonlinear equation

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+\sin(\theta )=0}$

where gravity points "downwards" and ${\displaystyle \theta }$ is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use ${\displaystyle d\theta /dt}$ as an integrating factor, which would eventually yield

${\displaystyle \int {\frac {d\theta }{\sqrt {C_{0}+2\cos(\theta )}}}=t+C_{1}}$

which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary unless ${\displaystyle C_{0}=2}$). 

Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at ${\displaystyle \theta =0}$, called the small angle approximation, is

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+\theta =0}$

since ${\displaystyle \sin(\theta )\approx \theta }$ for ${\displaystyle \theta \approx 0}$. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at ${\displaystyle \theta =\pi }$, corresponding to the pendulum being straight up:

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+\pi -\theta =0}$

since ${\displaystyle \sin(\theta )\approx \pi -\theta }$ for ${\displaystyle \theta \approx \pi }$. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that ${\displaystyle |\theta |}$ will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state. 

One more interesting linearization is possible around ${\displaystyle \theta =\pi /2}$, around which ${\displaystyle \sin(\theta )\approx 1}$:

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+1=0.}$

This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact) phase portraits and approximate periods.

Types of nonlinear dynamic behaviors

• Amplitude death – any oscillations present in the system cease due to some kind of interaction with other system or feedback by the same system
• Chaos – values of a system cannot be predicted indefinitely far into the future, and fluctuations are aperiodic
• Multistability – the presence of two or more stable states
• Solitons – self-reinforcing solitary waves

Examples of nonlinear equations

• Algebraic Riccati equation
• Ball and beam system
• Bellman equation for optimal policy
• Boltzmann equation
• Colebrook equation
• General relativity
• Ginzburg–Landau theory
• Ishimori equation
• Kadomtsev–Petviashvili equation
• Korteweg–de Vries equation
• Landau–Lifshitz–Gilbert equation
• Liénard equation
• Navier–Stokes equations of fluid dynamics
• Nonlinear optics
• Nonlinear Schrödinger equation
• Power-flow study
• Richards equation for unsaturated water flow
• Self-balancing unicycle
• Sine-Gordon equation
• Van der Pol oscillator
• Vlasov equation