Abundance of the chemical elements

From Wikipedia, the free encyclopedia

 

The abundance of the chemical elements is a measure of the occurrence of the chemical elements relative to all other elements in a given environment. Abundance is measured in one of three ways: by the mass-fraction (the same as weight fraction); by the mole-fraction (fraction of atoms by numerical count, or sometimes fraction of molecules in gases); or by the volume-fraction. Volume-fraction is a common abundance measure in mixed gases such as planetary atmospheres, and is similar in value to molecular mole-fraction for gas mixtures at relatively low densities and pressures, and ideal gas mixtures. Most abundance values in this article are given as mass-fractions.

 

For example, the abundance of oxygen in pure water can be measured in two ways: the mass fraction is about 89%, because that is the fraction of water's mass which is oxygen. However, the mole-fraction is 33.3333...% because only 1 atom of 3 in water, H₂O, is oxygen. As another example, looking at the mass-fraction abundance of hydrogen and helium in both the Universe as a whole and in the atmospheres of gas-giant planets such as Jupiter, it is 74% for hydrogen and 23–25% for helium; while the (atomic) mole-fraction for hydrogen is 92%, and for helium is 8%, in these environments. Changing the given environment to Jupiter's outer atmosphere, where hydrogen is diatomic while helium is not, changes the molecular mole-fraction (fraction of total gas molecules), as well as the fraction of atmosphere by volume, of hydrogen to about 86%, and of helium to 13%.

The abundance of chemical elements in the universe is dominated by the large amounts of hydrogen and helium which were produced in the Big Bang. Remaining elements, making up only about 2% of the universe, were largely produced by supernovae and certain red giant stars. Lithium, beryllium and boron are rare because although they are produced by nuclear fusion, they are then destroyed by other reactions in the stars. The elements from carbon to iron are relatively more common in the universe because of the ease of making them in supernova nucleosynthesis. Elements of higher atomic number than iron (element 26) become progressively more rare in the universe, because they increasingly absorb stellar energy in being produced. Elements with even atomic numbers are generally more common than their neighbors in the periodic table, also due to favorable energetics of formation.

The abundance of elements in the Sun and outer planets is similar to that in the universe. Due to solar heating, the elements of Earth and the inner rocky planets of the Solar System have undergone an additional depletion of volatile hydrogen, helium, neon, nitrogen, and carbon (which volatilizes as methane). The crust, mantle, and core of the Earth show evidence of chemical segregation plus some sequestration by density. Lighter silicates of aluminum are found in the crust, with more magnesium silicate in the mantle, while metallic iron and nickel compose the core. The abundance of elements in specialized environments, such as atmospheres, or oceans, or the human body, are primarily a product of chemical interactions with the medium in which they reside.

Universe

Ten most common elements in the Milky Way Galaxy estimated spectroscopically

Z	Element	Mass fraction (ppm)
1	Hydrogen	739,000
2	Helium	240,000
8	Oxygen	10,400
6	Carbon	4,600
10	Neon	1,340
26	Iron	1,090
7	Nitrogen	960
14	Silicon	650
12	Magnesium	580
16	Sulfur	440

The elements – that is, ordinary (baryonic) matter made of protons, neutrons, and electrons, are only a small part of the content of the Universe. Cosmological observations suggest that only 4.6% of the universe's energy (including the mass contributed by energy, E = mc² ↔ m = E / c²) comprises the visible baryonic matter that constitutes stars, planets, and living beings. The rest is thought to be made up of dark energy (68%) and dark matter (27%). These are forms of matter and energy believed to exist on the basis of scientific theory and observational deductions, but they have not been directly observed and their nature is not well understood. 

Most standard (baryonic) matter is found in intergalactic gas, stars, and interstellar clouds, in the form of atoms or ions (plasma), although it can be found in degenerate forms in extreme astrophysical settings, such as the high densities inside white dwarfs and neutron stars. 

Hydrogen is the most abundant element in the Universe; helium is second. However, after this, the rank of abundance does not continue to correspond to the atomic number; oxygen has abundance rank 3, but atomic number 8. All others are substantially less common. 

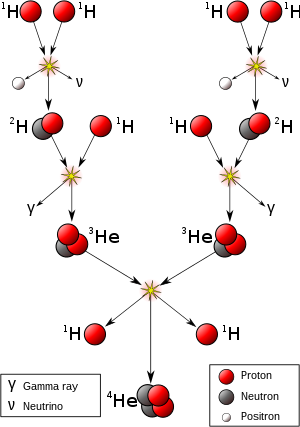
The abundance of the lightest elements is well predicted by the standard cosmological model, since they were mostly produced shortly (i.e., within a few hundred seconds) after the Big Bang, in a process known as Big Bang nucleosynthesis. Heavier elements were mostly produced much later, inside of stars. 

Hydrogen and helium are estimated to make up roughly 74% and 24% of all baryonic matter in the universe respectively. Despite comprising only a very small fraction of the universe, the remaining "heavy elements" can greatly influence astronomical phenomena. Only about 2% (by mass) of the Milky Way galaxy's disk is composed of heavy elements. 

These other elements are generated by stellar processes. In astronomy, a "metal" is any element other than hydrogen or helium. This distinction is significant because hydrogen and helium are the only elements that were produced in significant quantities in the Big Bang. Thus, the metallicity of a galaxy or other object is an indication of stellar activity, after the Big Bang. 

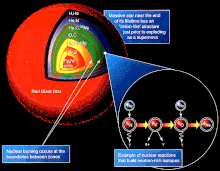
In general, elements up to iron are made in large stars in the process of becoming supernovae. Iron-56 is particularly common, since it is the most stable element that can easily be made from alpha particles (being a product of decay of radioactive nickel-56, ultimately made from 14 helium nuclei). Elements heavier than iron are made in energy-absorbing processes in large stars, and their abundance in the universe (and on Earth) generally decreases with increasing atomic number. 

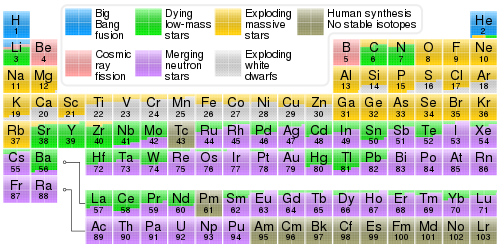
Periodic table showing the cosmogenic origin of each element.

Solar system

Most abundant nuclides
in the Solar System

Nuclide	A	Mass fraction in parts per million	Atom fraction in parts per million
Hydrogen-1	1	705,700	909,964
Helium-4	4	275,200	88,714
Oxygen-16	16	9,592	477
Carbon-12	12	3,032	326
Nitrogen-14	14	1,105	102
Neon-20	20	1,548	100
Other nuclides:		3,879	149
Silicon-28	28	653	30
Magnesium-24	24	513	28
Iron-56	56	1,169	27
Sulfur-32	32	396	16
Helium-3	3	35	15
Hydrogen-2	2	23	15
Neon-22	22	208	12
Magnesium-26	26	79	4
Carbon-13	13	37	4
Magnesium-25	25	69	4
Aluminium-27	27	58	3
Argon-36	36	77	3
Calcium-40	40	60	2
Sodium-23	23	33	2
Iron-54	54	72	2
Silicon-29	29	34	2
Nickel-58	58	49	1
Silicon-30	30	23	1
Iron-57	57	28	1

The above graph (note log scale) shows abundance of elements in the Solar System. The table shows the twelve most common elements in our galaxy (estimated spectroscopically), as measured in parts per million, by mass. Nearby galaxies that have evolved along similar lines have a corresponding enrichment of elements heavier than hydrogen and helium. The more distant galaxies are being viewed as they appeared in the past, so their abundances of elements appear closer to the primordial mixture. Since physical laws and processes are uniform throughout the universe, however, it is expected that these galaxies will likewise have evolved similar abundances of elements. 

The abundance of elements is in keeping with their origin from the Big Bang and nucleosynthesis in a number of progenitor supernova stars. Very abundant hydrogen and helium are products of the Big Bang, while the next three elements are rare since they had little time to form in the Big Bang and are not made in stars (they are, however, produced in small quantities by breakup of heavier elements in interstellar dust, as a result of impact by cosmic rays). 

Beginning with carbon, elements have been produced in stars by buildup from alpha particles (helium nuclei), resulting in an alternatingly larger abundance of elements with even atomic numbers (these are also more stable). The effect of odd-numbered chemical elements generally being more rare in the universe was empirically noticed in 1914, and is known as the Oddo-Harkins rule. 

Estimated abundances of the chemical elements in the Solar System (logarithmic scale).

Relation to nuclear binding energy

Loose correlations have been observed between estimated elemental abundances in the universe and the nuclear binding energy curve. Roughly speaking, the relative stability of various atomic nuclides has exerted a strong influence on the relative abundance of elements formed in the Big Bang, and during the development of the universe thereafter. See the article about nucleosynthesis for the explanation on how certain nuclear fusion processes in stars (such as carbon burning, etc.) create the elements heavier than hydrogen and helium. 

A further observed peculiarity is the jagged alternation between relative abundance and scarcity of adjacent atomic numbers in the elemental abundance curve, and a similar pattern of energy levels in the nuclear binding energy curve. This alternation is caused by the higher relative binding energy (corresponding to relative stability) of even atomic numbers compared with odd atomic numbers and is explained by the Pauli Exclusion Principle. The semi-empirical mass formula (SEMF), also called Weizsäcker's formula or the Bethe-Weizsäcker mass formula, gives a theoretical explanation of the overall shape of the curve of nuclear binding energy.

Earth

The Earth formed from the same cloud of matter that formed the Sun, but the planets acquired different compositions during the formation and evolution of the solar system. In turn, the natural history of the Earth caused parts of this planet to have differing concentrations of the elements. 

The mass of the Earth is approximately 5.98×10²⁴ kg. In bulk, by mass, it is composed mostly of iron (32.1%), oxygen (30.1%), silicon (15.1%), magnesium (13.9%), sulfur (2.9%), nickel (1.8%), calcium (1.5%), and aluminium (1.4%); with the remaining 1.2% consisting of trace amounts of other elements.

The bulk composition of the Earth by elemental-mass is roughly similar to the gross composition of the solar system, with the major differences being that Earth is missing a great deal of the volatile elements hydrogen, helium, neon, and nitrogen, as well as carbon which has been lost as volatile hydrocarbons. The remaining elemental composition is roughly typical of the "rocky" inner planets, which formed in the thermal zone where solar heat drove volatile compounds into space. The Earth retains oxygen as the second-largest component of its mass (and largest atomic-fraction), mainly from this element being retained in silicate minerals which have a very high melting point and low vapor pressure.

Crust

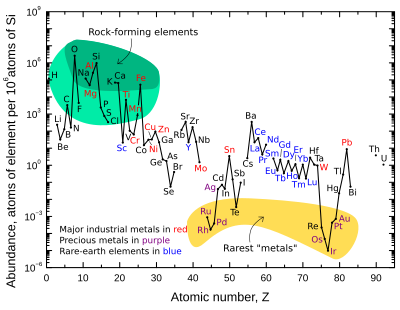
Abundance (atom fraction) of the chemical elements in Earth's upper continental crust as a function of atomic number. The rarest elements in the crust (shown in yellow) are rare due to a combination of factors: all but 1 of them are the densest siderophiles (iron-loving) elements in the Goldschmidt classification of elements, meaning they have a tendency to mix well with iron, depleting them by being relocated deeper into the Earth's core. Their abundance in meteoroids is higher. Additionally, tellurium has been depleted from the crust due to formation of volatile hydrides.

 

The mass-abundance of the nine most abundant elements in the Earth's crust is approximately: oxygen 46%, silicon 28%, aluminum 8.2%, iron 5.6%, calcium 4.2%, sodium 2.5%, magnesium 2.4%, potassium 2.0%, and titanium 0.61%. Other elements occur at less than 0.15%. For a complete list, see abundance of elements in Earth's crust. 

The graph above illustrates the relative atomic-abundance of the chemical elements in Earth's upper continental crust— the part that is relatively accessible for measurements and estimation.

Many of the elements shown in the graph are classified into (partially overlapping) categories:

1. rock-forming elements (major elements in green field, and minor elements in light green field);
2. rare earth elements (lanthanides, La-Lu, and Y; labeled in blue);
3. major industrial metals (global production >~3×10⁷ kg/year; labeled in red);
4. precious metals (labeled in purple);
5. the nine rarest "metals" — the six platinum group elements plus Au, Re, and Te (a metalloid) — in the yellow field. These are rare in the crust from being soluble in iron and thus concentrated in the Earth's core.

Note that there are two breaks where the unstable (radioactive) elements technetium (atomic number 43) and promethium (atomic number 61) would be. These elements are surrounded by stable elements, yet both have relatively short half lives (~ 4 million years and ~ 18 years respectively). These are thus extremely rare, since any primordial initial fractions of these in pre-Solar System materials have long since decayed. These two elements are now only produced naturally through the spontaneous fission of very heavy radioactive elements (for example, uranium, thorium, or the trace amounts of plutonium that exist in uranium ores), or by the interaction of certain other elements with cosmic rays. Both technetium and promethium have been identified spectroscopically in the atmospheres of stars, where they are produced by ongoing nucleosynthetic processes. 

There are also breaks in the abundance graph where the six noble gases would be, since they are not chemically bound in the Earth's crust, and they are only generated by decay chains from radioactive elements in the crust, and are therefore extremely rare there. 

The eight naturally occurring very rare, highly radioactive elements (polonium, astatine, francium, radium, actinium, protactinium, neptunium, and plutonium) are not included, since any of these elements that were present at the formation of the Earth have decayed away eons ago, and their quantity today is negligible and is only produced from the radioactive decay of uranium and thorium.

Oxygen and silicon are notably the most common elements in the crust. On Earth and in rocky planets in general, silicon and oxygen are far more common than their cosmic abundance. The reason is that they combine with each other to form silicate minerals. In this way, they are the lightest of all of the two-percent "astronomical metals" (i.e., non-hydrogen and helium elements) to form a solid that is refractory to the Sun's heat, and thus cannot boil away into space. All elements lighter than oxygen have been removed from the crust in this way.

Rare-earth elements

"Rare" earth elements is a historical misnomer. The persistence of the term reflects unfamiliarity rather than true rarity. The more abundant rare earth elements are similarly concentrated in the crust compared to commonplace industrial metals such as chromium, nickel, copper, zinc, molybdenum, tin, tungsten, or lead. The two least abundant rare earth elements (thulium and lutetium) are nearly 200 times more common than gold. However, in contrast to the ordinary base and precious metals, rare earth elements have very little tendency to become concentrated in exploitable ore deposits. Consequently, most of the world's supply of rare earth elements comes from only a handful of sources. Furthermore, the rare earth metals are all quite chemically similar to each other, and they are thus quite difficult to separate into quantities of the pure elements. 

Differences in abundances of individual rare earth elements in the upper continental crust of the Earth represent the superposition of two effects, one nuclear and one geochemical. First, the rare earth elements with even atomic numbers (₅₈Ce, ₆₀Nd, ...) have greater cosmic and terrestrial abundances than the adjacent rare earth elements with odd atomic numbers (₅₇La, ₅₉Pr, ...). Second, the lighter rare earth elements are more incompatible (because they have larger ionic radii) and therefore more strongly concentrated in the continental crust than the heavier rare earth elements. In most rare earth ore deposits, the first four rare earth elements – lanthanum, cerium, praseodymium, and neodymium – constitute 80% to 99% of the total amount of rare earth metal that can be found in the ore.

Mantle

The mass-abundance of the eight most abundant elements in the Earth's mantle is approximately: oxygen 45%, magnesium 23%, silicon 22%, iron 5.8%, calcium 2.3%, aluminum 2.2%, sodium 0.3%, potassium 0.3%. 

The mantle differs in elemental composition from the crust in having a great deal more magnesium and significantly more iron, while having much less aluminum and sodium.

Core

Due to mass segregation, the core of the Earth is believed to be primarily composed of iron (88.8%), with smaller amounts of nickel (5.8%), sulfur (4.5%), and less than 1% trace elements.

Ocean

The most abundant elements in the ocean by proportion of mass in percent are oxygen (85.84), hydrogen (10.82), chlorine (1.94), sodium (1.08), magnesium (0.1292), sulfur (0.091), calcium (0.04), potassium (0.04), bromine (0.0067), carbon (0.0028), and boron (0.00043).

Atmosphere

The order of elements by volume-fraction (which is approximately molecular mole-fraction) in the atmosphere is nitrogen (78.1%), oxygen (20.9%), argon (0.96%), followed by (in uncertain order) carbon and hydrogen because water vapor and carbon dioxide, which represent most of these two elements in the air, are variable components. Sulfur, phosphorus, and all other elements are present in significantly lower proportions. 

According to the abundance curve graph (above right), argon, a significant if not major component of the atmosphere, does not appear in the crust at all. This is because the atmosphere has a far smaller mass than the crust, so argon remaining in the crust contributes little to mass-fraction there, while at the same time buildup of argon in the atmosphere has become large enough to be significant.

Human body

By mass, human cells consist of 65–90% water (H₂O), and a significant portion of the remainder is composed of carbon-containing organic molecules. Oxygen therefore contributes a majority of a human body's mass, followed by carbon. Almost 99% of the mass of the human body is made up of six elements: hydrogen (H), carbon (C), nitrogen (N), oxygen (O), calcium (Ca), and phosphorus (P). The next 0.75% is made up of the next five elements: potassium (K), sulfur (S), chlorine (Cl), sodium (Na), and magnesium (Mg). CHNOPS for short. Only 17 elements are known for certain to be necessary to human life, with one additional element (fluorine) thought to be helpful for tooth enamel strength. A few more trace elements may play some role in the health of mammals. Boron and silicon are notably necessary for plants but have uncertain roles in animals. The elements aluminium and silicon, although very common in the earth's crust, are conspicuously rare in the human body.

Below is a periodic table highlighting nutritional elements.

Nutritional elements in the periodic table

H

He

Li

Be

B

C

N

O

F

Ne

Na

Mg

Al

Si

P

S

Cl

Ar

K

Ca

Sc

Ti

V

Cr

Mn

Fe

Co

Ni

Cu

Zn

Ga

Ge

As

Se

Br

Kr

Rb

Sr

Y

Zr

Nb

Mo

Tc

Ru

Rh

Pd

Ag

Cd

In

Sn

Sb

Te

I

Xe

Cs

Ba

La

*

Hf

Ta

W

Re

Os

Ir

Pt

Au

Hg

Tl

Pb

Bi

Po

At

Rn

Fr

Ra

Ac

**

Rf

Db

Sg

Bh

Hs

Mt

Ds

Rg

Cn

Nh

Fl

Mc

Lv

Ts

Og

*

Ce

Pr

Nd

Pm

Sm

Eu

Gd

Tb

Dy

Ho

Er

Tm

Yb

Lu

**

Th

Pa

U

Np

Pu

Am

Cm

Bk

Cf

Es

Fm

Md

No

Lr

The four basic organic elements

Quantity elements

Essential trace elements

Deemed essential trace element by U.S., not by European Union

Suggested function from deprivation effects or active metabolic handling, but no clearly-identified biochemical function in humans

Limited circumstantial evidence for trace benefits or biological action in mammals

No evidence for biological action in mammals, but essential in some lower organisms. (In the case of lanthanum, the definition of an essential nutrient as being indispensable and irreplaceable is not completely applicable due to the extreme similarity of the lanthanides. Thus Ce, Pr, and Nd may be substituted for La without ill effects for organisms using La, and the smaller Sm, Eu, and Gd may also be similarly substituted but cause slower growth.)

Stellar nucleosynthesis

From Wikipedia, the free encyclopedia

Stellar nucleosynthesis is the theory explaining the creation (nucleosynthesis) of chemical elements by nuclear fusion reactions between atoms within stars. Stellar nucleosynthesis has occurred continuously since the original creation of hydrogen, helium and lithium during the Big Bang. It is a highly predictive theory that today yields excellent agreement between calculations based upon it and the observed abundances of the elements. It explains why the observed abundances of elements in the universe grow over time and why some elements and their isotopes are much more abundant than others. The theory was initially proposed by Fred Hoyle in 1946, who later refined it in 1954. Further advances were made, especially to nucleosynthesis by neutron capture of the elements heavier than iron, by Margaret Burbidge, Geoffrey Burbidge, William Alfred Fowler and Hoyle in their famous 1957 B²FH paper, which became one of the most heavily cited papers in astrophysics history.

 

Stars evolve because of changes in their composition (the abundance of their constituent elements) over their lifespans, first by burning hydrogen (main sequence star), then helium (red giant star), and progressively burning higher elements. However, this does not by itself significantly alter the abundances of elements in the universe as the elements are contained within the star. Later in its life, a low-mass star will slowly eject its atmosphere via stellar wind, forming a planetary nebula, while a higher–mass star will eject mass via a sudden catastrophic event called a supernova. The term supernova nucleosynthesis is used to describe the creation of elements during the evolution and explosion of a pre-supernova massive star (12–35 times the mass of the sun). Those massive stars are the most prolific source of new isotopes from carbon (Z = 6) to nickel (Z = 28).

The advanced sequence of burning fuels is driven by gravitational collapse and its associated heating, resulting in the subsequent burning of carbon, oxygen and silicon. However, most of the nucleosynthesis in the mass range A = 28–56 (from silicon to nickel) is actually caused by the upper layers of the star collapsing onto the core, creating a compressional shock wave rebounding outward. The shock front briefly raises temperatures by roughly 50%, thereby causing furious burning for about a second. This final burning in massive stars, called explosive nucleosynthesis or supernova nucleosynthesis, is the final epoch of stellar nucleosynthesis.

A stimulus to the development of the theory of nucleosynthesis was the discovery of variations in the abundances of elements found in the universe. The need for a physical description was already inspired by the relative abundances of isotopes of the chemical elements in the solar system. Those abundances, when plotted on a graph as a function of atomic number of the element, have a jagged sawtooth shape that varies by factors of tens of millions. This suggested a natural process that is not random. A second stimulus to understanding the processes of stellar nucleosynthesis occurred during the 20th century, when it was realized that the energy released from nuclear fusion reactions accounted for the longevity of the Sun as a source of heat and light.

History

In 1920, Arthur Eddington proposed that stars obtained their energy from nuclear fusion of hydrogen to form helium and also raised the possibility that the heavier elements are produced in stars.

 

In 1920, Arthur Eddington, on the basis of the precise measurements of atomic masses by F.W. Aston and a preliminary suggestion by Jean Perrin, proposed that stars obtained their energy from nuclear fusion of hydrogen to form helium and raised the possibility that the heavier elements are produced in stars. This was a preliminary step toward the idea of nucleosynthesis. In 1928, George Gamow derived what is now called the Gamow factor, a quantum-mechanical formula that gave the probability of bringing two nuclei sufficiently close for the strong nuclear force to overcome the Coulomb barrier. The Gamow factor was used in the decade that followed by Atkinson and Houtermans and later by Gamow himself and Edward Teller to derive the rate at which nuclear reactions would proceed at the high temperatures believed to exist in stellar interiors. 

In 1939, in a paper entitled "Energy Production in Stars", Hans Bethe analyzed the different possibilities for reactions by which hydrogen is fused into helium. He defined two processes that he believed to be the sources of energy in stars. The first one, the proton–proton chain reaction, is the dominant energy source in stars with masses up to about the mass of the Sun. The second process, the carbon–nitrogen–oxygen cycle, which was also considered by Carl Friedrich von Weizsäcker in 1938, is more important in more massive main-sequence stars. These works concerned the energy generation capable of keeping stars hot. A clear physical description of the proton–proton chain and of the CNO cycle appears in a 1968 textbook. Bethe's two papers did not address the creation of heavier nuclei, however. That theory was begun by Fred Hoyle in 1946 with his argument that a collection of very hot nuclei would assemble thermodynamically into iron. Hoyle followed that in 1954 with a large paper describing how advanced fusion stages within massive stars would synthesize the elements from carbon to iron in mass. This is the first work of stellar nucleosynthesis. It and Hoyle's 1954 paper provided the roadmap to how the most abundant elements on Earth had been synthesized within stars from their initial hydrogen and helium, making clear how those abundant elements increased their galactic abundances as the galaxy aged. 

Hoyle's theory was expanded to other processes, beginning with the publication of a review paper in 1957 by Burbidge, Burbidge, Fowler and Hoyle (commonly referred to as the B²FH paper). This review paper collected and refined earlier research into a heavily cited picture that gave promise of accounting for the observed relative abundances of the elements; but it did not itself enlarge Hoyle's 1954 picture for the origin of primary nuclei as much as many assumed, except in the understanding of nucleosynthesis of those elements heavier than iron by neutron capture. Significant improvements were made by Alastair G. W. Cameron and by Donald D. Clayton. Cameron presented his own independent approach (following Hoyle's approach for the most part) of nucleosynthesis. He introduced computers into time-dependent calculations of evolution of nuclear systems. Clayton calculated the first time-dependent models of the S-process and of the R-process, as well as of the burning of silicon into the abundant alpha-particle nuclei and iron-group elements, and discovered radiogenic chronologies for determining the age of the elements. The entire research field expanded rapidly in the 1970s.

Cross section of a supergiant showing nucleosynthesis and elements formed.

Key reactions

A version of the periodic table indicating the origins – including stellar nucleosynthesis – of the elements. Elements above 94 are manmade and are not included.

 

The most important reactions in stellar nucleosynthesis:

• Hydrogen fusion:
  • Deuterium fusion
  • The proton–proton chain
  • The carbon–nitrogen–oxygen cycle
• Helium fusion:
  • The triple-alpha process
  • The alpha process
• Fusion of heavier elements:
  • Lithium burning: a process found most commonly in brown dwarfs
  • Carbon-burning process
  • Neon-burning process
  • Oxygen-burning process
  • Silicon-burning process
• Production of elements heavier than iron:
  • Neutron capture:
    • The R-process
    • The S-process
  • Proton capture:
    • The Rp-process
    • The P-process
  • Photodisintegration

Hydrogen fusion

Proton–proton chain reaction

 

CNO-I cycle  The helium nucleus is released at the top-left step.

 

Hydrogen fusion (nuclear fusion of four protons to form a helium-4 nucleus) is the dominant process that generates energy in the cores of main-sequence stars. It is also called "hydrogen burning", which should not be confused with the chemical combustion of hydrogen in an oxidizing atmosphere. There are two predominant processes by which stellar hydrogen fusion occurs: proton-proton chain and the carbon-nitrogen-oxygen (CNO) cycle. Ninety percent of all stars, with the exception of white dwarfs, are fusing hydrogen by these two processes. 

In the cores of lower-mass main-sequence stars such as the Sun, the dominant energy production process is the proton–proton chain reaction. This creates a helium-4 nucleus through a sequence of chain reactions that begin with the fusion of two protons to form a deuterium nucleus (one proton plus one neutron) along with an ejected positron and neutrino. In each complete fusion cycle, the proton–proton chain reaction releases about 26.2 MeV. The proton–proton chain reaction cycle is relatively insensitive to temperature; a 10% rise of temperature would increase energy production by this method by 46%, hence, this hydrogen fusion process can occur in up to a third of the star's radius and occupy half the star's mass. For stars above 35% of the Sun's mass, the energy flux toward the surface is sufficiently low and energy transfer from the core region remains by radiative heat transfer, rather than by convective heat transfer. As a result, there is little mixing of fresh hydrogen into the core or fusion products outward. 

In higher-mass stars, the dominant energy production process is the CNO cycle, which is a catalytic cycle that uses nuclei of carbon, nitrogen and oxygen as intermediaries and in the end produces a helium nucleus as with the proton-proton chain. During a complete CNO cycle, 25.0 MeV of energy is released. The difference in energy production of this cycle, compared to the proton–proton chain reaction, is accounted for by the energy lost through neutrino emission. The CNO cycle is very temperature sensitive, a 10% rise of temperature would produce a 350% rise in energy production. About 90% of the CNO cycle energy generation occurs within the inner 15% of the star's mass, hence it is strongly concentrated at the core. This results in such an intense outward energy flux that convective energy transfer become more important than does radiative transfer. As a result, the core region becomes a convection zone, which stirs the hydrogen fusion region and keeps it well mixed with the surrounding proton-rich region. This core convection occurs in stars where the CNO cycle contributes more than 20% of the total energy. As the star ages and the core temperature increases, the region occupied by the convection zone slowly shrinks from 20% of the mass down to the inner 8% of the mass. Our Sun produces 10% of its energy from the CNO cycle. 

The type of hydrogen fusion process that dominates in a star is determined by the temperature dependency differences between the two reactions. The proton–proton chain reaction starts at temperatures about 4×10⁶ K, making it the dominant fusion mechanism in smaller stars. A self-maintaining CNO chain requires a higher temperature of approximately 16×10⁶ K, but thereafter it increases more rapidly in efficiency as the temperature rises, than does the proton-proton reaction. Above approximately 17×10⁶ K, the CNO cycle becomes the dominant source of energy. This temperature is achieved in the cores of main sequence stars with at least 1.3 times the mass of the Sun. The Sun itself has a core temperature of about 15.7×10⁶ K. As a main sequence star ages, the core temperature will rise, resulting in a steadily increasing contribution from its CNO cycle.

Helium fusion

Main sequence stars accumulate helium in their cores as a result of hydrogen fusion, but the core does not become hot enough to initiate helium fusion. Helium fusion first begins when a star leaves the red giant branch after accumulating sufficient helium in its core to ignite it. In stars around the mass of the sun, this begins at the tip of the red giant branch with a helium flash from a degenerate helium core and the star moves to the horizontal branch where it burns helium in its core. More massive stars ignite helium in their cores without a flash and execute a blue loop before reaching the asymptotic giant branch. Despite the name, stars on a blue loop from the red giant branch are typically not blue in color, but are rather yellow giants, possibly Cepheid variables. They fuse helium until the core is largely carbon and oxygen. The most massive stars become supergiants when they leave the main sequence and quickly start helium fusion as they become red supergiants. After helium is exhausted in the core of a star, it will continue in a shell around the carbon-oxygen core.

In all cases, helium is fused to carbon via the triple-alpha process. This can then form oxygen, neon, and heavier elements via the alpha process. In this way, the alpha process preferentially produces elements with even numbers of protons by the capture of helium nuclei. Elements with odd numbers of protons are formed by other fusion pathways.

Reaction rate

The reaction rate per volume between species A and B, having number densities n_A,B is given by:

${\displaystyle {\frac {r}{V}}=n_{A}\,n_{B}\,\langle \sigma (v)\,v\rangle }$

where σ(v) is the cross section at relative velocity v, and averaging is performed over all velocities.

Semi-classically, the cross section is proportional to ${\displaystyle \pi \,\lambda ^{2}}$, where ${\displaystyle \lambda =h/p}$ is the de Broglie wavelength. Thus semi-classically the cross section is proportional to ${\displaystyle {\frac {m}{E}}}$. 

However, since the reaction involves quantum tunneling, there is an exponential damping at low energies that depends on Gamow factor E_G, giving:

${\displaystyle \sigma (E)={\frac {S(E)}{E}}e^{-{\sqrt {\frac {E_{G}}{E}}}}}$

where S(E) depends on the details of the nuclear interaction.

One then integrates over all energies to get the total reaction rate, using the Maxwell–Boltzmann distribution and the relation :

${\displaystyle {\frac {r}{V}}=n_{A}\,n_{B}\int _{0}^{\infty }{\frac {S(E)}{E}}\,e^{-{\sqrt {\frac {E_{G}}{E}}}}{\frac {2}{{\sqrt {\pi }}(kT)^{3/2}}}E^{1/2}e^{-E/kT}\,{\sqrt {\frac {2E}{m_{R}}}}dE}$

where ${\displaystyle m_{R}={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}}$ is the reduced mass.

Since this integration has an exponential damping at high energies of the form ${\displaystyle \sim e^{-{\frac {E}{kT}}}}$ and at high energies from the Gamow factor, the integral almost vanished everywhere except around the peak, called Gamow peak, at E₀, where:

${\displaystyle {\frac {\partial }{\partial E}}\left(-{\sqrt {\frac {E_{G}}{E}}}-{\frac {E}{kT}}\right)\,=\,0}$

Thus:

${\displaystyle E_{0}=\left({\sqrt {E_{G}}}\,kT/2\right)^{2/3}}$

The exponent can then be approximated around E₀ as:

${\displaystyle e^{-{\frac {E}{kT}}-{\sqrt {\frac {E_{G}}{E}}}}\approx e^{-{\frac {3E_{0}}{kT}}}\cdot exp\left(-{\frac {(E-E_{0})^{2}}{4E_{0}kT/3}}\right)}$

And the reaction rate is approximated as:

${\displaystyle {\frac {r}{V}}\approx n_{A}\,n_{B}\,{\frac {4{\sqrt {2}}}{\sqrt {3m_{R}}}}\,{\sqrt {E_{0}}}{\frac {S(E_{0})}{kT}}e^{-{\frac {3E_{0}}{kT}}}}$

Values of S(E₀) are typically 10^-3-10³ in units of keV*b, but are damped by a huge factor when involving a beta decay, due to the relation between the intermediate bound state (e.g. diproton) half-life and the beta decay half-life , as in the proton–proton chain reaction. Note that typical core temperatures in main-sequence stars give kT of the order of keV. 

Thus, the limiting reaction in the CNO cycle, proton capture by ¹⁴
₇N
, has S(E₀) ~ S(0) = 3.5 keV b, while the limiting reaction in the proton-proton chain reaction, the creation of deuterium from two protons, has a much lower S(E₀) ~ S(0) = 4*10^-22 keV b. Incidentally, since the former reaction has a much higher Gamow factor, and due to the relative abundance of elements in typical stars, the two reaction rates are equal at a temperature value that is within the core temperature ranges of main-sequence stars.