European science in the Middle Ages

From Wikipedia, the free encyclopedia

For most medieval scholars, who believed that God created the universe according to geometric and harmonic principles, science – particularly geometry and astronomy – was linked directly to the divine. To seek these principles, therefore, would be to seek God.

 

European science in the Middle Ages comprised the study of nature, mathematics and natural philosophy in medieval Europe. Following the fall of the Western Roman Empire and the decline in knowledge of Greek, Christian Western Europe was cut off from an important source of ancient learning. Although a range of Christian clerics and scholars from Isidore and Bede to Buridan and Oresme maintained the spirit of rational inquiry, Western Europe would see a period of scientific decline during the Early Middle Ages. However, by the time of the High Middle Ages, the region had rallied and was on its way to once more taking the lead in scientific discovery. Scholarship and scientific discoveries of the Late Middle Ages laid the groundwork for the Scientific Revolution of the Early Modern Period. 

According to Pierre Duhem, who founded the academic study of medieval science as a critique of the Enlightenment-positivist theory of a 17th-century anti-Aristotelian and anticlerical scientific revolution, the various conceptual origins of that alleged revolution lay in the 12th to 14th centuries, in the works of churchmen such as Aquinas and Buridan.

In the context of this article, "Western Europe" refers to the European cultures bound together by the Roman Catholic Church and the Latin language.

Western Europe

As Roman imperial authority effectively ended in the West during the 5th century, Western Europe entered the Middle Ages with great difficulties that affected the continent's intellectual production dramatically. Most classical scientific treatises of classical antiquity written in Greek were unavailable, leaving only simplified summaries and compilations. Nonetheless, Roman and early medieval scientific texts were read and studied, contributing to the understanding of nature as a coherent system functioning under divinely established laws that could be comprehended in the light of reason. This study continued through the Early Middle Ages, and with the Renaissance of the 12th century, interest in this study was revitalized through the translation of Greek and Arabic scientific texts. Scientific study further developed within the emerging medieval universities, where these texts were studied and elaborated, leading to new insights into the phenomena of the universe. These advances are virtually unknown to the lay public of today, partly because most theories advanced in medieval science are today obsolete, and partly because of the caricature of Middle Ages as a supposedly "Dark Age" which placed "the word of religious authorities over personal experience and rational activity."

Early Middle Ages (AD 476–1000)

In the ancient world, Greek had been the primary language of science. Even under the Roman Empire, Latin texts drew extensively on Greek work, some pre-Roman, some contemporary; while advanced scientific research and teaching continued to be carried on in the Hellenistic side of the empire, in Greek. Late Roman attempts to translate Greek writings into Latin had limited success.

As the knowledge of Greek declined during the transition to the Middle Ages, the Latin West found itself cut off from its Greek philosophical and scientific roots. Most scientific inquiry came to be based on information gleaned from sources which were often incomplete and posed serious problems of interpretation. Latin-speakers who wanted to learn about science only had access to books by such Roman writers as Calcidius, Macrobius, Martianus Capella, Boethius, Cassiodorus, and later Latin encyclopedists. Much had to be gleaned from non-scientific sources: Roman surveying manuals were read for what geometry was included.

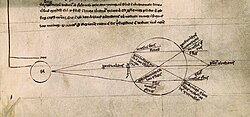
Ninth century diagram of the observed and computed positions of the seven planets on 18 March 816.

 

De-urbanization reduced the scope of education and by the 6th century teaching and learning moved to monastic and cathedral schools, with the center of education being the study of the Bible. Education of the laity survived modestly in Italy, Spain, and the southern part of Gaul, where Roman influences were most long-lasting. In the 7th century, learning began to emerge in Ireland and the Celtic lands, where Latin was a foreign language and Latin texts were eagerly studied and taught.

The leading scholars of the early centuries were clergymen for whom the study of nature was but a small part of their interest. They lived in an atmosphere which provided little institutional support for the disinterested study of natural phenomena. The study of nature was pursued more for practical reasons than as an abstract inquiry: the need to care for the sick led to the study of medicine and of ancient texts on drugs, the need for monks to determine the proper time to pray led them to study the motion of the stars, the need to compute the date of Easter led them to study and teach rudimentary mathematics and the motions of the Sun and Moon. Modern readers may find it disconcerting that sometimes the same works discuss both the technical details of natural phenomena and their symbolic significance.

Around 800, Charles the Great, assisted by the English monk Alcuin of York, undertook what has become known as the Carolingian Renaissance, a program of cultural revitalization and educational reform. The chief scientific aspect of Charlemagne's educational reform concerned the study and teaching of astronomy, both as a practical art that clerics required to compute the date of Easter and as a theoretical discipline. From the year 787 on, decrees were issued recommending the restoration of old schools and the founding of new ones throughout the empire. Institutionally, these new schools were either under the responsibility of a monastery, a cathedral or a noble court. 

The scientific work of the period after Charlemagne was not so much concerned with original investigation as it was with the active study and investigation of ancient Roman scientific texts. This investigation paved the way for the later effort of Western scholars to recover and translate ancient Greek texts in philosophy and the sciences.

High Middle Ages (AD 1000–1300)

The translation of Greek and Arabic works allowed the full development of Christian philosophy and the method of scholasticism.

 

Beginning around the year 1050, European scholars built upon their existing knowledge by seeking out ancient learning in Greek and Arabic texts which they translated into Latin. They encountered a wide range of classical Greek texts, some of which had earlier been translated into Arabic, accompanied by commentaries and independent works by Islamic thinkers.

Gerard of Cremona is a good example: an Italian who traveled to Spain to copy a single text, he stayed on to translate some seventy works. His biography describes how he came to Toledo: "He was trained from childhood at centers of philosophical study and had come to a knowledge of all that was known to the Latins; but for love of the Almagest, which he could not find at all among the Latins, he went to Toledo; there, seeing the abundance of books in Arabic on every subject and regretting the poverty of the Latins in these things, he learned the Arabic language, in order to be able to translate." 

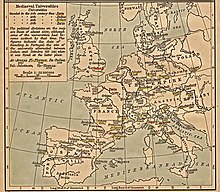
Map of medieval universities. They started a new infrastructure which was needed for scientific communities.

 

This period also saw the birth of medieval universities, which benefited materially from the translated texts and provided a new infrastructure for scientific communities. Some of these new universities were registered as an institution of international excellence by the Holy Roman Empire, receiving the title of Studium Generale. Most of the early Studia Generali were found in Italy, France, England, and Spain, and these were considered the most prestigious places of learning in Europe. This list quickly grew as new universities were founded throughout Europe. As early as the 13th century, scholars from a Studium Generale were encouraged to give lecture courses at other institutes across Europe and to share documents, and this led to the current academic culture seen in modern European universities. 

The rediscovery of the works of Aristotle allowed the full development of the new Christian philosophy and the method of scholasticism. By 1200 there were reasonably accurate Latin translations of the main works of Aristotle, Euclid, Ptolemy, Archimedes, and Galen—that is, of all the intellectually crucial ancient authors except Plato. Also, many of the medieval Arabic and Jewish key texts, such as the main works of Avicenna, Averroes and Maimonides now became available in Latin. During the 13th century, scholastics expanded the natural philosophy of these texts by commentaries (associated with teaching in the universities) and independent treatises. Notable among these were the works of Robert Grosseteste, Roger Bacon, John of Sacrobosco, Albertus Magnus, and Duns Scotus. 

Scholastics believed in empiricism and supporting Roman Catholic doctrines through secular study, reason, and logic. The most famous was Thomas Aquinas (later declared a "Doctor of the Church"), who led the move away from the Platonic and Augustinian and towards Aristotelianism (although natural philosophy was not his main concern). Meanwhile, precursors of the modern scientific method can be seen already in Grosseteste's emphasis on mathematics as a way to understand nature and in the empirical approach admired by Roger Bacon. 

Optical diagram showing light being refracted by a spherical glass container full of water (from Roger Bacon, De multiplicatione specierum).

 

Grosseteste was the founder of the famous Oxford Franciscan school. He built his work on Aristotle's vision of the dual path of scientific reasoning. Concluding from particular observations into a universal law, and then back again: from universal laws to prediction of particulars. Grosseteste called this "resolution and composition". Further, Grosseteste said that both paths should be verified through experimentation in order to verify the principals. These ideas established a tradition that carried forward to Padua and Galileo Galilei in the 17th century. 

Under the tuition of Grosseteste and inspired by the writings of Arab alchemists who had preserved and built upon Aristotle's portrait of induction, Bacon described a repeating cycle of observation, hypothesis, experimentation, and the need for independent verification. He recorded the manner in which he conducted his experiments in precise detail so that others could reproduce and independently test his results - a cornerstone of the scientific method, and a continuation of the work of researchers like Al Battani. 

Bacon and Grosseteste conducted investigations into optics, although much of it was similar to what was being done at the time by Arab scholars. Bacon did make a major contribution to the development of science in medieval Europe by writing to the Pope to encourage the study of natural science in university courses and compiling several volumes recording the state of scientific knowledge in many fields at the time. He described the possible construction of a telescope, but there is no strong evidence of his having made one.

Late Middle Ages (AD 1300–1500)

The first half of the 14th century saw the scientific work of great thinkers. The logic studies by William of Occam led him to postulate a specific formulation of the principle of parsimony, known today as Occam's razor. This principle is one of the main heuristics used by modern science to select between two or more underdetermined theories, though it is only fair to point out that this principle was employed explicitly by both Aquinas and Aristotle before him. 

As Western scholars became more aware (and more accepting) of controversial scientific treatises of the Byzantine and Islamic Empires these readings sparked new insights and speculation. The works of the early Byzantine scholar John Philoponus inspired Western scholars such as Jean Buridan to question the received wisdom of Aristotle's mechanics. Buridan developed the theory of impetus which was a step towards the modern concept of inertia. Buridan anticipated Isaac Newton when he wrote: 

Galileo's demonstration of the law of the space traversed in case of uniformly varied motion – as Oresme had demonstrated centuries earlier.

. . . after leaving the arm of the thrower, the projectile would be moved by an impetus given to it by the thrower and would continue to be moved as long as the impetus remained stronger than the resistance, and would be of infinite duration were it not diminished and corrupted by a contrary force resisting it or by something inclining it to a contrary motion.

Thomas Bradwardine and his partners, the Oxford Calculators of Merton College, Oxford, distinguished kinematics from dynamics, emphasizing kinematics, and investigating instantaneous velocity. They formulated the mean speed theorem: a body moving with constant velocity travels distance and time equal to an accelerated body whose velocity is half the final speed of the accelerated body. They also demonstrated this theorem—the essence of "The Law of Falling Bodies"—long before Galileo, who has gotten the credit for this.

In his turn, Nicole Oresme showed that the reasons proposed by the physics of Aristotle against the movement of the Earth were not valid and adduced the argument of simplicity for the theory that the Earth moves, and not the heavens. Despite this argument in favor of the Earth's motion, Oresme fell back on the commonly held opinion that "everyone maintains, and I think myself, that the heavens do move and not the earth."

The historian of science Ronald Numbers notes that the modern scientific assumption of methodological naturalism can be also traced back to the work of these medieval thinkers:

By the late Middle Ages the search for natural causes had come to typify the work of Christian natural philosophers. Although characteristically leaving the door open for the possibility of direct divine intervention, they frequently expressed contempt for soft-minded contemporaries who invoked miracles rather than searching for natural explanations. The University of Paris cleric Jean Buridan (a. 1295–ca. 1358), described as "perhaps the most brilliant arts master of the Middle Ages," contrasted the philosopher’s search for "appropriate natural causes" with the common folk’s erroneous habit of attributing unusual astronomical phenomena to the supernatural. In the fourteenth century the natural philosopher Nicole Oresme (ca. 1320–82), who went on to become a Roman Catholic bishop, admonished that, in discussing various marvels of nature, "there is no reason to take recourse to the heavens, the last refuge of the weak, or demons, or to our glorious God as if He would produce these effects directly, more so than those effects whose causes we believe are well known to us."

However, a series of events that would be known as the Crisis of the Late Middle Ages was under its way. When came the Black Death of 1348, it sealed a sudden end to the previous period of massive scientific change. The plague killed a third of the people in Europe, especially in the crowded conditions of the towns, where the heart of innovations lay. Recurrences of the plague and other disasters caused a continuing decline of population for a century.

Renaissance (15th century)

Leonardo da Vinci's Vitruvian Man.

 

The 15th century saw the beginning of the cultural movement of the Renaissance. The rediscovery of Greek scientific texts, both ancient and medieval, was accelerated as the Byzantine Empire fell to the Ottoman Turks and many Byzantine scholars sought refuge in the West, particularly Italy. 

Also, the invention of printing was to have great effect on European society: the facilitated dissemination of the printed word democratized learning and allowed a faster propagation of new ideas. 

When the Renaissance moved to Northern Europe that science would be revived, by figures as Copernicus, Francis Bacon, and Descartes (though Descartes is often described as an early Enlightenment thinker, rather than a late Renaissance one).

Byzantine and Islamic influences

Byzantine interactions

Byzantine science played an important role in the transmission of classical knowledge to the Islamic world and to Renaissance Italy, and also in the transmission of medieval Arabic knowledge to Renaissance Italy. Its rich historiographical tradition preserved ancient knowledge upon which splendid art, architecture, literature and technological achievements were built. 

Byzantine scientists preserved and continued the legacy of the great Ancient Greek mathematicians and put mathematics in practice. In early Byzantium (5th to 7th century) the architects and mathematicians Isidore of Miletus and Anthemius of Tralles used complex mathematical formulas to construct the great “Hagia Sophia” temple, a magnificent technological breakthrough for its time and for centuries afterwards due to its striking geometry, bold design and height. In late Byzantium (9th to 12th century) mathematicians like Michael Psellos considered mathematics as a way to interpret the world. 

John Philoponus, a Byzantine scholar in the 500s, was the first person to systematically question Aristotle's teaching of physics. This served as an inspiration for Galileo Galilei ten centuries later as Galileo cited Philoponus substantially in his works when Galileo also argued why Aristotelian physics was flawed during the Scientific Revolution.

Islamic interactions

A Westerner and an Arab learning geometry in the 15th century.

 

The Byzantine Empire initially provided the medieval Islamic world with Ancient Greek texts on astronomy and mathematics for translation into Arabic. Later with the emerging of the Muslim world, Byzantine scientists such as Gregory Choniades translated Arabic texts on Islamic astronomy, mathematics and science into Medieval Greek, including the works of Ja'far ibn Muhammad Abu Ma'shar al-Balkhi, Ibn Yunus, al-Khazini, Muhammad ibn Mūsā al-Khwārizmī, and Nasīr al-Dīn al-Tūsī among others. There were also some Byzantine scientists who used Arabic transliterations to describe certain scientific concepts instead of the equivalent Ancient Greek terms (such as the use of the Arabic talei instead of the Ancient Greek horoscopus). Byzantine science thus played an important role in not only transmitting ancient Greek knowledge to Western Europe and the Islamic world, but in also transmitting Islamic knowledge to Western Europe. Byzantine scientists also became acquainted with Sassanid and Indian astronomy through citations in some Arabic works.

Conservation of energy

From Wikipedia, the free encyclopedia

In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be conserved over time. This law means that energy can neither be created nor destroyed; rather, it can only be transformed or transferred from one form to another. For instance, chemical energy is converted to kinetic energy when a stick of dynamite explodes. If one adds up all the forms of energy that were released in the explosion, such as the kinetic energy and potential energy of the pieces, as well as heat and sound, one will get the exact decrease of chemical energy in the combustion of the dynamite. Classically, conservation of energy was distinct from conservation of mass; however, special relativity showed that mass is related to energy and vice versa by E = mc², and science now takes the view that mass–energy is conserved.

 

Conservation of energy can be rigorously proven by Noether's theorem as a consequence of continuous time translation symmetry; that is, from the fact that the laws of physics do not change over time.

A consequence of the law of conservation of energy is that a perpetual motion machine of the first kind cannot exist, that is to say, no system without an external energy supply can deliver an unlimited amount of energy to its surroundings. For systems which do not have time translation symmetry, it may not be possible to define conservation of energy. Examples include curved spacetimes in general relativity or time crystals in condensed matter physics.

History

Gottfried Leibniz

 

Ancient philosophers as far back as Thales of Miletus c. 550 BCE had inklings of the conservation of some underlying substance of which everything is made. However, there is no particular reason to identify this with what we know today as "mass-energy" (for example, Thales thought it was water). Empedocles (490–430 BCE) wrote that in this universal system, composed of four roots (earth, air, water, fire), "nothing comes to be or perishes"; instead, these elements suffer continual rearrangement.

In 1605, Simon Stevinus was able to solve a number of problems in statics based on the principle that perpetual motion was impossible.

In 1639, Galileo published his analysis of several situations—including the celebrated "interrupted pendulum"—which can be described (in modern language) as conservatively converting potential energy to kinetic energy and back again. Essentially, he pointed out that the height a moving body rises is equal to the height from which it falls, and used this observation to infer the idea of inertia. The remarkable aspect of this observation is that the height to which a moving body ascends on a frictionless surface does not depend on the shape of the surface. 

In 1669, Christiaan Huygens published his laws of collision. Among the quantities he listed as being invariant before and after the collision of bodies were both the sum of their linear momentums as well as the sum of their kinetic energies. However, the difference between elastic and inelastic collision was not understood at the time. This led to the dispute among later researchers as to which of these conserved quantities was the more fundamental. In his Horologium Oscillatorium, he gave a much clearer statement regarding the height of ascent of a moving body, and connected this idea with the impossibility of a perpetual motion. Huygens' study of the dynamics of pendulum motion was based on a single principle: that the center of gravity of a heavy object cannot lift itself.

The fact that kinetic energy is scalar, unlike linear momentum which is a vector, and hence easier to work with did not escape the attention of Gottfried Wilhelm Leibniz. It was Leibniz during 1676–1689 who first attempted a mathematical formulation of the kind of energy which is connected with motion (kinetic energy). Using Huygens' work on collision, Leibniz noticed that in many mechanical systems (of several masses, m_i each with velocity v_i),

${\displaystyle \sum _{i}m_{i}v_{i}^{2}}$

was conserved so long as the masses did not interact. He called this quantity the vis viva or living force of the system. The principle represents an accurate statement of the approximate conservation of kinetic energy in situations where there is no friction. Many physicists at that time, such as Newton, held that the conservation of momentum, which holds even in systems with friction, as defined by the momentum:

${\displaystyle \,\!\sum _{i}m_{i}v_{i}}$

was the conserved vis viva. It was later shown that both quantities are conserved simultaneously, given the proper conditions such as an elastic collision. 

In 1687, Isaac Newton published his Principia, which was organized around the concept of force and momentum. However, the researchers were quick to recognize that the principles set out in the book, while fine for point masses, were not sufficient to tackle the motions of rigid and fluid bodies. Some other principles were also required. 

Daniel Bernoulli

 

The law of conservation of vis viva was championed by the father and son duo, Johann and Daniel Bernoulli. The former enunciated the principle of virtual work as used in statics in its full generality in 1715, while the latter based his Hydrodynamica, published in 1738, on this single conservation principle. Daniel's study of loss of vis viva of flowing water led him to formulate the Bernoulli's principle, which relates the loss to be proportional to the change in hydrodynamic pressure. Daniel also formulated the notion of work and efficiency for hydraulic machines; and he gave a kinetic theory of gases, and linked the kinetic energy of gas molecules with the temperature of the gas.

This focus on the vis viva by the continental physicists eventually led to the discovery of stationarity principles governing mechanics, such as the D'Alembert's principle, Lagrangian, and Hamiltonian formulations of mechanics. 

Émilie du Châtelet (1706 – 1749) proposed and tested the hypothesis of the conservation of total energy, as distinct from momentum. Inspired by the theories of Gottfried Leibniz, she repeated and publicized an experiment originally devised by Willem 's Gravesande in 1722 in which balls were dropped from different heights into a sheet of soft clay. Each ball's kinetic energy - as indicated by the quantity of material displaced - was shown to be proportional to the square of the velocity. The deformation of the clay was found to be directly proportional to the height the balls were dropped from, equal to the initial potential energy. Earlier workers, including Newton and Voltaire, had all believed that "energy" (so far as they understood the concept at all) was not distinct from momentum and therefore proportional to velocity. According to this understanding, the deformation of the clay should have been proportional to the square root of the height from which the balls were dropped from. In classical physics the correct formula is ${\displaystyle E_{k}={\frac {1}{2}}mv^{2}}$, where ${\displaystyle E_{k}}$ is the kinetic energy of an object, ${\displaystyle m}$ its mass and ${\displaystyle v}$ its speed. On this basis, Châtelet proposed that energy must always have the same dimensions in any form, which is necessary to be able to relate it in different forms (kinetic, potential, heat…).

Engineers such as John Smeaton, Peter Ewart, Carl Holtzmann, Gustave-Adolphe Hirn and Marc Seguin recognized that conservation of momentum alone was not adequate for practical calculation and made use of Leibniz's principle. The principle was also championed by some chemists such as William Hyde Wollaston. Academics such as John Playfair were quick to point out that kinetic energy is clearly not conserved. This is obvious to a modern analysis based on the second law of thermodynamics, but in the 18th and 19th centuries the fate of the lost energy was still unknown. 

Gradually it came to be suspected that the heat inevitably generated by motion under friction was another form of vis viva. In 1783, Antoine Lavoisier and Pierre-Simon Laplace reviewed the two competing theories of vis viva and caloric theory. Count Rumford's 1798 observations of heat generation during the boring of cannons added more weight to the view that mechanical motion could be converted into heat, and (as importantly) that the conversion was quantitative and could be predicted (allowing for a universal conversion constant between kinetic energy and heat). Vis viva then started to be known as energy, after the term was first used in that sense by Thomas Young in 1807. 

Gaspard-Gustave Coriolis

 

The recalibration of vis viva to

${\displaystyle {\frac {1}{2}}\sum _{i}m_{i}v_{i}^{2}}$

which can be understood as converting kinetic energy to work, was largely the result of Gaspard-Gustave Coriolis and Jean-Victor Poncelet over the period 1819–1839. The former called the quantity quantité de travail (quantity of work) and the latter, travail mécanique (mechanical work), and both championed its use in engineering calculation. 

In a paper Über die Natur der Wärme(German "On the Nature of Heat/Warmth"), published in the Zeitschrift für Physik in 1837, Karl Friedrich Mohr gave one of the earliest general statements of the doctrine of the conservation of energy in the words: "besides the 54 known chemical elements there is in the physical world one agent only, and this is called Kraft [energy or work]. It may appear, according to circumstances, as motion, chemical affinity, cohesion, electricity, light and magnetism; and from any one of these forms it can be transformed into any of the others."

Mechanical equivalent of heat

A key stage in the development of the modern conservation principle was the demonstration of the mechanical equivalent of heat. The caloric theory maintained that heat could neither be created nor destroyed, whereas conservation of energy entails the contrary principle that heat and mechanical work are interchangeable. 

In the middle of the eighteenth century, Mikhail Lomonosov, a Russian scientist, postulated his corpusculo-kinetic theory of heat, which rejected the idea of a caloric. Through the results of empirical studies, Lomonosov came to the conclusion that heat was not transferred through the particles of the caloric fluid. 

In 1798, Count Rumford (Benjamin Thompson) performed measurements of the frictional heat generated in boring cannons, and developed the idea that heat is a form of kinetic energy; his measurements refuted caloric theory, but were imprecise enough to leave room for doubt. 

James Prescott Joule

 

The mechanical equivalence principle was first stated in its modern form by the German surgeon Julius Robert von Mayer in 1842. Mayer reached his conclusion on a voyage to the Dutch East Indies, where he found that his patients' blood was a deeper red because they were consuming less oxygen, and therefore less energy, to maintain their body temperature in the hotter climate. He discovered that heat and mechanical work were both forms of energy and in 1845, after improving his knowledge of physics, he published a monograph that stated a quantitative relationship between them.

Joule's apparatus for measuring the mechanical equivalent of heat. A descending weight attached to a string causes a paddle immersed in water to rotate.

 

Meanwhile, in 1843, James Prescott Joule independently discovered the mechanical equivalent in a series of experiments. In the most famous, now called the "Joule apparatus", a descending weight attached to a string caused a paddle immersed in water to rotate. He showed that the gravitational potential energy lost by the weight in descending was equal to the internal energy gained by the water through friction with the paddle. 

Over the period 1840–1843, similar work was carried out by engineer Ludwig A. Colding, although it was little known outside his native Denmark. 

Both Joule's and Mayer's work suffered from resistance and neglect but it was Joule's that eventually drew the wider recognition. 

For the dispute between Joule and Mayer over priority, see Mechanical equivalent of heat: Priority.

In 1844, William Robert Grove postulated a relationship between mechanics, heat, light, electricity and magnetism by treating them all as manifestations of a single "force" (energy in modern terms). In 1846, Grove published his theories in his book The Correlation of Physical Forces. In 1847, drawing on the earlier work of Joule, Sadi Carnot and Émile Clapeyron, Hermann von Helmholtz arrived at conclusions similar to Grove's and published his theories in his book Über die Erhaltung der Kraft (On the Conservation of Force, 1847). The general modern acceptance of the principle stems from this publication.

In 1850, William Rankine first used the phrase the law of the conservation of energy for the principle.

In 1877, Peter Guthrie Tait claimed that the principle originated with Sir Isaac Newton, based on a creative reading of propositions 40 and 41 of the Philosophiae Naturalis Principia Mathematica. This is now regarded as an example of Whig history.

Mass–energy equivalence

Matter is composed of such things as atoms, electrons, neutrons, and protons. It has intrinsic or rest mass. In the limited range of recognized experience of the nineteenth century it was found that such rest mass is conserved. Einstein's 1905 theory of special relativity showed that it corresponds to an equivalent amount of rest energy. This means that it can be converted to or from equivalent amounts of other (non-material) forms of energy, for example kinetic energy, potential energy, and electromagnetic radiant energy. When this happens, as recognized in twentieth century experience, rest mass is not conserved, unlike the total mass or total energy. All forms of energy contribute to the total mass and total energy. 

For example, an electron and a positron each have rest mass. They can perish together, converting their combined rest energy into photons having electromagnetic radiant energy, but no rest mass. If this occurs within an isolated system that does not release the photons or their energy into the external surroundings, then neither the total mass nor the total energy of the system will change. The produced electromagnetic radiant energy contributes just as much to the inertia (and to any weight) of the system as did the rest mass of the electron and positron before their demise. Likewise, non-material forms of energy can perish into matter, which has rest mass. 

Thus, conservation of energy (total, including material or rest energy), and conservation of mass (total, not just rest), each still holds as an (equivalent) law. In the 18th century these had appeared as two seemingly-distinct laws.

Conservation of energy in beta decay

The discovery in 1911 that electrons emitted in beta decay have a continuous rather than a discrete spectrum appeared to contradict conservation of energy, under the then-current assumption that beta decay is the simple emission of an electron from a nucleus. This problem was eventually resolved in 1933 by Enrico Fermi who proposed the correct description of beta-decay as the emission of both an electron and an antineutrino, which carries away the apparently missing energy.

First law of thermodynamics

For a closed thermodynamic system, the first law of thermodynamics may be stated as:

${\displaystyle \delta Q=\mathrm {d} U+\delta W}$, or equivalently, ${\displaystyle \mathrm {d} U=\delta Q-\delta W,}$

where ${\displaystyle \delta Q}$ is the quantity of energy added to the system by a heating process, ${\displaystyle \delta W}$ is the quantity of energy lost by the system due to work done by the system on its surroundings and ${\displaystyle \mathrm {d} U}$ is the change in the internal energy of the system.

The δ's before the heat and work terms are used to indicate that they describe an increment of energy which is to be interpreted somewhat differently than the ${\displaystyle \mathrm {d} U}$ increment of internal energy (see Inexact differential). Work and heat refer to kinds of process which add or subtract energy to or from a system, while the internal energy ${\displaystyle U}$ is a property of a particular state of the system when it is in unchanging thermodynamic equilibrium. Thus the term "heat energy" for ${\displaystyle \delta Q}$ means "that amount of energy added as the result of heating" rather than referring to a particular form of energy. Likewise, the term "work energy" for ${\displaystyle \delta W}$ means "that amount of energy lost as the result of work". Thus one can state the amount of internal energy possessed by a thermodynamic system that one knows is presently in a given state, but one cannot tell, just from knowledge of the given present state, how much energy has in the past flowed into or out of the system as a result of its being heated or cooled, nor as the result of work being performed on or by the system. 

Entropy is a function of the state of a system which tells of limitations of the possibility of conversion of heat into work. 

For a simple compressible system, the work performed by the system may be written:

${\displaystyle \delta W=P\,\mathrm {d} V,}$

where ${\displaystyle P}$ is the pressure and ${\displaystyle dV}$ is a small change in the volume of the system, each of which are system variables. In the fictive case in which the process is idealized and infinitely slow, so as to be called quasi-static, and regarded as reversible, the heat being transferred from a source with temperature infinitesimally above the system temperature, then the heat energy may be written

${\displaystyle \delta Q=T\,\mathrm {d} S,}$

where ${\displaystyle T}$ is the temperature and ${\displaystyle \mathrm {d} S}$ is a small change in the entropy of the system. Temperature and entropy are variables of state of a system. 

If an open system (in which mass may be exchanged with the environment) has several walls such that the mass transfer is through rigid walls separate from the heat and work transfers, then the first law may be written:

${\displaystyle \mathrm {d} U=\delta Q-\delta W+u'\,dM,\,}$

where ${\displaystyle dM}$ is the added mass and ${\displaystyle u'}$ is the internal energy per unit mass of the added mass, measured in the surroundings before the process.

Noether's theorem

Emmy Noether (1882-1935) was an influential mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics.

 

The conservation of energy is a common feature in many physical theories. From a mathematical point of view it is understood as a consequence of Noether's theorem, developed by Emmy Noether in 1915 and first published in 1918. The theorem states every continuous symmetry of a physical theory has an associated conserved quantity; if the theory's symmetry is time invariance then the conserved quantity is called "energy". The energy conservation law is a consequence of the shift symmetry of time; energy conservation is implied by the empirical fact that the laws of physics do not change with time itself. Philosophically this can be stated as "nothing depends on time per se". In other words, if the physical system is invariant under the continuous symmetry of time translation then its energy (which is canonical conjugate quantity to time) is conserved. Conversely, systems which are not invariant under shifts in time (an example, systems with time dependent potential energy) do not exhibit conservation of energy – unless we consider them to exchange energy with another, external system so that the theory of the enlarged system becomes time invariant again. Conservation of energy for finite systems is valid in such physical theories as special relativity and quantum theory (including QED) in the flat space-time.

Relativity

With the discovery of special relativity by Henri Poincaré and Albert Einstein, energy was proposed to be one component of an energy-momentum 4-vector. Each of the four components (one of energy and three of momentum) of this vector is separately conserved across time, in any closed system, as seen from any given inertial reference frame. Also conserved is the vector length (Minkowski norm), which is the rest mass for single particles, and the invariant mass for systems of particles (where momenta and energy are separately summed before the length is calculated—see the article on invariant mass). 

The relativistic energy of a single massive particle contains a term related to its rest mass in addition to its kinetic energy of motion. In the limit of zero kinetic energy (or equivalently in the rest frame) of a massive particle, or else in the center of momentum frame for objects or systems which retain kinetic energy, the total energy of particle or object (including internal kinetic energy in systems) is related to its rest mass or its invariant mass via the famous equation ${\displaystyle E=mc^{2}}$. 

Thus, the rule of conservation of energy over time in special relativity continues to hold, so long as the reference frame of the observer is unchanged. This applies to the total energy of systems, although different observers disagree as to the energy value. Also conserved, and invariant to all observers, is the invariant mass, which is the minimal system mass and energy that can be seen by any observer, and which is defined by the energy–momentum relation. 

In general relativity, energy–momentum conservation is not well-defined except in certain special cases. Energy-momentum is typically expressed with the aid of a stress–energy–momentum pseudotensor. However, since pseudotensors are not tensors, they do not transform cleanly between reference frames. If the metric under consideration is static (that is, does not change with time) or asymptotically flat (that is, at an infinite distance away spacetime looks empty), then energy conservation holds without major pitfalls. In practice, some metrics such as the Friedmann–Lemaître–Robertson–Walker metric do not satisfy these constraints and energy conservation is not well defined. The theory of general relativity leaves open the question of whether there is a conservation of energy for the entire universe.

Quantum theory

In quantum mechanics, energy of a quantum system is described by a self-adjoint (or Hermitian) operator called the Hamiltonian, which acts on the Hilbert space (or a space of wave functions) of the system. If the Hamiltonian is a time-independent operator, emergence probability of the measurement result does not change in time over the evolution of the system. Thus the expectation value of energy is also time independent. The local energy conservation in quantum field theory is ensured by the quantum Noether's theorem for energy-momentum tensor operator. Note that due to the lack of the (universal) time operator in quantum theory, the uncertainty relations for time and energy are not fundamental in contrast to the position-momentum uncertainty principle, and merely holds in specific cases. Energy at each fixed time can in principle be exactly measured without any trade-off in precision forced by the time-energy uncertainty relations. Thus the conservation of energy in time is a well defined concept even in quantum mechanics.