Ernest Rutherford was a New Zealand physicist who came to be known as the father of nuclear physics. Encyclopædia Britannica considers him to be the greatest experimentalist since Michael Faraday (1791–1867).
In early work, Rutherford discovered the concept of radioactive half-life, the radioactive element radon, and differentiated and named alpha and beta radiation. This work was performed at McGill University in Montreal, Canada. It is the basis for the Nobel Prize in Chemistry he was awarded in 1908 "for his investigations into the disintegration of the elements, and the chemistry of radioactive substances", for which he was the first Canadian and Oceanian Nobel laureate.
Rutherford moved in 1907 to the Victoria University of Manchester (today University of Manchester) in the UK, where he and Thomas Royds proved that alpha radiation is helium nuclei. Rutherford performed his most famous work after he became a Nobel laureate. In 1911, although he could not prove that it was positive or negative, he theorized that atoms have their charge concentrated in a very small nucleus, and thereby pioneered the Rutherford model of the atom, through his discovery and interpretation of Rutherford scattering by the gold foil experiment of Hans Geiger and Ernest Marsden. He performed the first artificially induced nuclear reaction in 1917 in experiments where nitrogen nuclei were bombarded with alpha particles. As a result, he discovered the emission of a subatomic particle which, in 1919, he called the "hydrogen atom" but, in 1920, he more accurately named the proton.
Rutherford became Director of the Cavendish Laboratory at the University of Cambridge in 1919. Under his leadership the neutron was discovered by James Chadwick in 1932 and in the same year the first experiment to split the nucleus in a fully controlled manner was performed by students working under his direction, John Cockcroft and Ernest Walton. After his death in 1937, he was honoured by being interred with the greatest scientists of the United Kingdom, near Sir Isaac Newton's tomb in Westminster Abbey. The chemical element rutherfordium (element 104) was named after him in 1997.
Biography
Early life and education
Rutherford aged 21
Ernest Rutherford was the son of James Rutherford, a farmer, and his wife Martha Thompson, originally from Hornchurch, Essex, England. James had emigrated to New Zealand from Perth, Scotland, "to raise a little flax and a lot of children". Ernest was born at Brightwater, near Nelson, New Zealand. His first name was mistakenly spelled 'Earnest' when his birth was registered. Rutherford's mother Martha Thompson was a schoolteacher.
He studied at Havelock School and then Nelson College and won a scholarship to study at Canterbury College, University of New Zealand, where he participated in the debating society and played rugby. After gaining his BA, MA
and BSc, and doing two years of research during which he invented a new
form of radio receiver, in 1895 Rutherford was awarded an 1851 Research Fellowship from the Royal Commission for the Exhibition of 1851, to travel to England for postgraduate study at the Cavendish Laboratory, University of Cambridge.
He was among the first of the 'aliens' (those without a Cambridge
degree) allowed to do research at the university, under the leadership
of J. J. Thomson,
which aroused jealousies from the more conservative members of the
Cavendish fraternity. With Thomson's encouragement, he managed to detect
radio waves at half a mile and briefly held the world record for the
distance over which electromagnetic waves could be detected, though when
he presented his results at the British Association meeting in 1896, he discovered he had been outdone by another lecturer, by the name of Marconi.
In 1898, Thomson recommended Rutherford for a position at McGill University in Montreal, Canada. He was to replace Hugh Longbourne Callendar who held the chair of Macdonald Professor of physics and was coming to Cambridge. Rutherford was accepted, which meant that in 1900 he could marry Mary Georgina Newton (1876–1954) to whom he had become engaged before leaving New Zealand; they married at St Paul's Anglican Church, Papanui in Christchurch, they had one daughter, Eileen Mary (1901–1930), who married Ralph Fowler. In 1901, he gained a DSc from the University of New Zealand. In 1907, Rutherford returned to Britain to take the chair of physics at the Victoria University of Manchester.
Later years and honours
He was knighted in 1914. During World War I, he worked on a top secret project to solve the practical problems of submarine detection by sonar. In 1916, he was awarded the Hector Memorial Medal.
In 1919, he returned to the Cavendish succeeding J. J. Thomson as the
Cavendish professor and Director. Under him, Nobel Prizes were awarded
to James Chadwick for discovering the neutron (in 1932), John Cockcroft and Ernest Walton for an experiment which was to be known as splitting the atom using a particle accelerator, and Edward Appleton for demonstrating the existence of the ionosphere. In 1925, Rutherford pushed calls to the Government of New Zealand to support education and research, which led to the formation of the Department of Scientific and Industrial Research (DSIR) in the following year. Between 1925 and 1930, he served as President of the Royal Society, and later as president of the Academic Assistance Council which helped almost 1,000 university refugees from Germany. He was appointed to the Order of Merit in the 1925 New Year Honours and raised to the peerage as Baron Rutherford of Nelson, of Cambridge in the County of Cambridge in 1931,
a title that became extinct upon his unexpected death in 1937. In 1933,
Rutherford was one of the two inaugural recipients of the T. K. Sidey Medal, set up by the Royal Society of New Zealand as an award for outstanding scientific research.
Lord Rutherford's grave in Westminster Abbey
For some time before his death, Rutherford had a small hernia,
which he had neglected to have fixed, and it became strangulated,
causing him to be violently ill. Despite an emergency operation in
London, he died four days afterwards of what physicians termed
"intestinal paralysis", at Cambridge. After cremation at Golders Green Crematorium, he was given the high honour of burial in Westminster Abbey, near Isaac Newton and other illustrious British scientists.
Scientific research
Ernest Rutherford at McGill University in 1905
At Cambridge, Rutherford started to work with J. J. Thomson on the conductive effects of X-rays on gases, work which led to the discovery of the electron which Thomson presented to the world in 1897. Hearing of Becquerel's experience with uranium, Rutherford started to explore its radioactivity,
discovering two types that differed from X-rays in their penetrating
power. Continuing his research in Canada, he coined the terms alpha ray and beta ray in 1899 to describe the two distinct types of radiation. He then discovered that thorium
gave off a gas which produced an emanation which was itself radioactive
and would coat other substances. He found that a sample of this
radioactive material of any size invariably took the same amount of time
for half the sample to decay – its "half-life" (11½ minutes in this case).
From 1900 to 1903, he was joined at McGill by the young chemist Frederick Soddy (Nobel Prize in Chemistry,
1921) for whom he set the problem of identifying the thorium
emanations. Once he had eliminated all the normal chemical reactions,
Soddy suggested that it must be one of the inert gases, which they named
thoron (later found to be an isotope of radon).
They also found another type of thorium they called Thorium X, and kept
on finding traces of helium. They also worked with samples of "Uranium
X" from William Crookes and radium from Marie Curie.
In 1903, they published their "Law of Radioactive Change," to
account for all their experiments. Until then, atoms were assumed to be
the indestructible basis of all matter and although Curie had suggested
that radioactivity was an atomic phenomenon, the idea of the atoms of
radioactive substances breaking up was a radically new idea. Rutherford
and Soddy demonstrated that radioactivity involved the spontaneous
disintegration of atoms into other, as yet, unidentified matter. The Nobel Prize in Chemistry 1908
was awarded to Ernest Rutherford "for his investigations into the
disintegration of the elements, and the chemistry of radioactive
substances".
In 1903, Rutherford considered a type of radiation discovered (but not named) by French chemist Paul Villard in 1900, as an emission from radium,
and realised that this observation must represent something different
from his own alpha and beta rays, due to its very much greater
penetrating power. Rutherford therefore gave this third type of
radiation the name of gamma ray. All three of Rutherford's terms are in standard use today – other types of radioactive decay have since been discovered, but Rutherford's three types are among the most common.
In Manchester, he continued to work with alpha radiation. In conjunction with Hans Geiger, he developed zinc sulfide scintillation screens
and ionisation chambers to count alphas. By dividing the total charge
they produced by the number counted, Rutherford decided that the charge
on the alpha was two. In late 1907, Ernest Rutherford and Thomas Royds allowed alphas to penetrate a very thin window into an evacuated tube. As they sparked the tube into discharge,
the spectrum obtained from it changed, as the alphas accumulated in the
tube. Eventually, the clear spectrum of helium gas appeared, proving
that alphas were at least ionised helium atoms, and probably helium
nuclei.
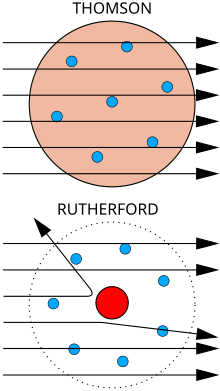
Gold foil experiment
Top: Expected results: alpha particles passing through the plum pudding model of the atom undisturbed. Bottom: Observed results: a small portion of the particles were deflected, indicating a small, concentrated charge. Note that the image is not to scale; in reality the nucleus is vastly smaller than the electron shell.
Rutherford performed his most famous work after receiving the Nobel prize in 1908. Along with Hans Geiger and Ernest Marsden in 1909, he carried out the Geiger–Marsden experiment, which demonstrated the nuclear nature of atoms by deflecting alpha particles
passing through a thin gold foil. Rutherford was inspired to ask Geiger
and Marsden in this experiment to look for alpha particles with very
high deflection angles, of a type not expected from any theory of matter
at that time. Such deflections, though rare, were found, and proved to
be a smooth but high-order function of the deflection angle. It was
Rutherford's interpretation of this data that led him to formulate the Rutherford model of the atom in 1911 – that a very small charged nucleus, containing much of the atom's mass, was orbited by low-mass electrons.
In 1919–1920, Rutherford found that nitrogen and other light
elements ejected a proton (Rutherford said "a hydrogen atom" rather than
"a proton") when hit with α (alpha) particles.
This result showed Rutherford that hydrogen nuclei were a part of
nitrogen nuclei (and by inference, probably other nuclei as well). Such a
construction had been suspected for many years on the basis of atomic
weights which were whole numbers of that of hydrogen.
Hydrogen was known to be the lightest element, and its nuclei
presumably the lightest nuclei. Now, because of all these
considerations, Rutherford decided that a hydrogen nucleus was possibly a
fundamental building block of all nuclei, and also possibly a new
fundamental particle as well, since nothing was known from the nucleus
that was lighter. Thus, confirming and extending the work of Wilhelm Wien who in 1898 discovered the proton in streams of ionized gas, Rutherford postulated the hydrogen nucleus to be a new particle in 1920, which he dubbed the proton.
In 1921, while working with Niels Bohr (who postulated that electrons moved in specific orbits), Rutherford theorized about the existence of neutrons, (which he had christened in his 1920 Bakerian Lecture), which could somehow compensate for the repelling effect of the positive charges of protons by causing an attractive nuclear force
and thus keep the nuclei from flying apart from the repulsion between
protons. The only alternative to neutrons was the existence of "nuclear
electrons" which would counteract some of the proton charges in the
nucleus, since by then it was known that nuclei had about twice the mass
that could be accounted for if they were simply assembled from hydrogen
nuclei (protons). But how these nuclear electrons could be trapped in
the nucleus, was a mystery.
Rutherford's theory of neutrons was proved in 1932 by his associate James Chadwick,
who recognized neutrons immediately when they were produced by other
scientists and later himself, in bombarding beryllium with alpha
particles. In 1935, Chadwick was awarded the Nobel Prize in Physics for
this discovery.
Legacy
A plaque commemorating Rutherford's presence at the University of Manchester
Nuclear physics
Rutherford's research, and work done under him as laboratory
director, established the nuclear structure of the atom and the
essential nature of radioactive decay as a nuclear process. Patrick Blackett, a research fellow working under Rutherford, using natural alpha particles, demonstrated induced nuclear transmutation. Rutherford's team later, using protons from an accelerator, demonstrated artificially-induced nuclear reactions and transmutation. He is known as the father of nuclear physics. Rutherford died too early to see Leó Szilárd's idea of controlled nuclear chain reactions
come into being. However, a speech of Rutherford's about his
artificially-induced transmutation in lithium, printed in 12 September
1933 London paper The Times, was reported by Szilárd to have been his inspiration for thinking of the possibility of a controlled energy-producing nuclear chain reaction. Szilard had this idea while walking in London, on the same day.
Rutherford's speech touched on the 1932 work of his students John Cockcroft and Ernest Walton
in "splitting" lithium into alpha particles by bombardment with protons
from a particle accelerator they had constructed. Rutherford realized
that the energy released from the split lithium atoms was enormous, but
he also realized that the energy needed for the accelerator, and its
essential inefficiency in splitting atoms in this fashion, made the
project an impossibility as a practical source of energy
(accelerator-induced fission of light elements remains too inefficient
to be used in this way, even today). Rutherford's speech in part, read:
We might in these processes obtain very much more energy than the proton supplied, but on the average we could not expect to obtain energy in this way. It was a very poor and inefficient way of producing energy, and anyone who looked for a source of power in the transformation of the atoms was talking moonshine. But the subject was scientifically interesting because it gave insight into the atoms.
Items named in honour of Rutherford's life and work
A statue of a young Ernest Rutherford at his memorial in Brightwater, New Zealand.
- Scientific discoveries
- The element rutherfordium, Rf, Z=104. (1997)
- The rutherford (Rd), an obsolete unit of radioactivity equivalent to one megabecquerel.
- Institutions
- Rutherford Appleton Laboratory, a scientific research laboratory near Didcot, Oxfordshire.
- Rutherford College, Auckland, a school in Auckland, New Zealand
- Rutherford College, Kent, a college at the University of Kent in Canterbury, England
- Rutherford Institute for Innovation at the University of Cambridge
- Rutherford Intermediate School, Wanganui, New Zealand
- Rutherford Hall, a hall of residence at Loughborough University
- Awards
- Rutherford Medal, the highest science medal awarded by the Royal Society of New Zealand
- Rutherford Award at Thomas Carr College for excellence in Victorian Certificate of Education chemistry, Australia.
- Rutherford Memorial Medal is an award for research in the fields of physics and chemistry by the Royal Society of Canada.
- Rutherford Medal and Prize is awarded once every two years by the Institute of Physics for "distinguished research in nuclear physics or nuclear technology".
- Rutherford Memorial Lecture is an international lecture tour under the auspices of the Royal Society created under the Rutherford Memorial Scheme in 1952.
- Buildings
- Rutherford House, a boarding house at Nelson College
- Rutherford Hotel, Nelson's largest hotel, which incorporates the Rutherford Cafe and Bar
- The physics and chemistry building at the University of Canterbury, New Zealand
- Rochester and Rutherford Hall at the University of Canterbury, New Zealand
- Rutherford House, the primary building of Victoria University of Wellington's Pipitea Campus, originally the headquarters of the New Zealand Electricity Department, in Wellington, New Zealand.
- Rutherford building at Bedford Modern School.
- A building of the modern Cavendish Laboratory at the University of Cambridge
- The Ernest Rutherford Physics Building at McGill University, Montreal
- The Coupland Building at the University of Manchester, where Rutherford worked, was renamed "The Rutherford Building" in 2006.
- The Rutherford lecture theatre in the Schuster Laboratory at the University of Manchester
- Major streets
- Lord Rutherford Road (the location of his birthplace in Brightwater, New Zealand)
- Rutherford Street, a major thoroughfare in central Nelson, New Zealand
- Rutherford Close, a residential street in Abingdon, Oxfordshire
- Rutherford Road in the biotechnology district of Carlsbad, California
- Rutherford Road, commercial/residential street in Vaughan, Ontario, Canada
- Other
- Rutherford Park, a sports ground in Nelson, New Zealand
- The Rutherford Memorial at the site of his birth in Brightwater, New Zealand
- His image is on the obverse of the New Zealand one hundred-dollar note (since 1992).
- The Rutherford Foundation, a charitable trust set up by the Royal Society of New Zealand to support research in science and technology.
- Rutherford House, at Macleans College, Auckland, New Zealand
- Rutherford House, at Hillcrest High School, Hamilton, New Zealand
- Rutherford House, at Rotorua Intermediate School, Rotorua, New Zealand
- Rutherford House, at Rangiora High School
- The crater Rutherford on the Moon, and the crater Rutherford on the planet Mars
- Ernest Rutherford was the subject of a play by Stuart Hoar.
- On the side of the Mond Laboratory on the site of the original Cavendish Laboratory in Cambridge, there is an engraving in Rutherford's memory in the form of a crocodile, this being the nickname given to him by its commissioner, his colleague Peter Kapitza.
- Rutherford rocket engine, an engine developed in New Zealand by Rocket Lab and the first to use the electric pump feed cycle.
- His image is depicted in the stained glass window of the Presbyterian chapel at Lindisfarne College in Hastings, New Zealand. The window, unveiled in 2007, is dedicated to the college's concept of men with supreme content of character, and depicts Rutherford along with Charles Upham, Edmund Hillary, and John Rangihau as iconic examples.
Incidences of cancer at Rutherford's former laboratory
The Coupland Building at Manchester University, at which Rutherford conducted many of his experiments, has been the subject of a cancer cluster investigation. There has been a statistically high incidence of pancreatic cancer, brain cancer, and motor neuron disease
occurring in and around Rutherford's former laboratories and, since
1984, a total of six workers have been stricken with these ailments. In
2009, an independent commission concluded that the very slightly
elevated levels of various radiation related to Rutherford's experiments
decades earlier are not the likely cause of such cancers and ruled the
illnesses a coincidence.
Rutherford Nitrogen-to-Oxygen Transmutation Myth
A long-standing myth existed, at least as early as 1948,
running at least to 2017, that Rutherford was the first scientist to
observe and report an artificial transmutation of a stable element into
another element; nitrogen into oxygen. It was thought by many people to
be one of Rutherford's greatest accomplishments.
The New Zealand government even commemorated a stamp in honor of its
belief that that the nitrogen-to-oxygen discovery belonged to
Rutherford.
In fact, Rutherford did detect the ejected proton in 1919 and
interpreted it as evidence for disintegration of the nitrogen nucleus
(to lighter nuclei). However, Blackett identified the true reaction in
1925 and showed that the actual product is oxygen. Rutherford therefore
recognized "that the nucleus may increase rather than diminish in mass
as the result of collisions in which the proton is expelled."
Beginning in 2017, many scientific institutions corrected their
versions of this history to indicate that the discovery credit for the
reaction belongs to Patrick Blackett who identified the oxygen product.
These institutions included the U.S. Department of Energy Office of
History and Heritage Resources, the American Institute of Physics Center for History of Physics, Imperial College London, Faculty of Natural Sciences, and the University of Cambridge, Department of Physics.
Rutherford later claimed to have discovered the occurrence of a
transmutation reaction but not to have identified the oxygen product.
The earliest known instance of this attribution is an article written by
Rutherford in the McGill News, September 1932 and reprinted in the
Journal of the Royal Astronomical Society of Canada in 1933.
In this article, Rutherford, writing about himself in the third person,
claimed the discovery as his own "Rutherford, in 1919, bombarded
nitrogen gas with swift alpha particles from radioactive substances and
found that high-speed hydrogen nuclei, or free protons as we now term
them, were liberated. … This was the first time that definite evidence
had been obtained that an atom could be transmuted by artificial
methods…"
Rutherford made the same claim the following year. On October 11,
1933, he gave a lecture, broadcast by the British Broadcasting
Corporation, called “The Transmutation of the Atom.” A transcript of the
lecture was published in The Scientific Monthly in January 1934.
Rutherford wrote "The first successful experiments in transmutation are
comparatively recent, dating back to the year 1919. … I made in 1919
some experiments to test whether any evidence of transformation could be
obtained when alpha particles were used to bombard matter. … This was
the first time that definite evidence was obtained that an atom could be
transformed by artificial methods."
Rutherford never explicitly claimed that the transmutation of
nitrogen resulted in oxygen in his experiments. In these 1933 and 1934
claims, he simply claimed that he had transmuted an atom. After Blackett
performed the first experiments to obtain the first definite evidence
that the nitrogen atom was transmuted into oxygen in 1925, and with the
help of Rutherford's 1933-1934 claims that he was the first to obtain
"definite evidence" for transmuting an atom, the scientific community,
with very few exceptions, assumed for the next 84 years that the
nitrogen-to-oxygen discovery belonged to Rutherford.