Edward Bernard's "Orbis eruditi", comparing all known alphabets as of 1689
An alphabet is a standardized set of basic written symbols or graphemes (called letters) that represent the phonemes of certain spoken languages. Not all writing systems represent language in this way; in a syllabary, each character represents a syllable, for instance, and logographic systems use characters to represent words, morphemes, or other semantic units).
The first fully phonemic script, the Proto-Canaanite script, later known as the Phoenician alphabet, is considered to be the first alphabet, and is the ancestor of most modern alphabets, including Arabic, Greek, Latin, Cyrillic, Hebrew, and possibly Brahmic. Peter T. Daniels, however, distinguishes an abugida or alphasyllabary, a set of graphemes that represent consonantal base letters which diacritics modify to represent vowels (as in Devanagari and other South Asian scripts), an abjad, in which letters predominantly or exclusively represent consonants (as in the original Phoenician, Hebrew or Arabic), and an "alphabet", a set of graphemes that represent both vowels and consonants. In this narrow sense of the word the first "true" alphabet was the Greek alphabet, which was developed on the basis of the earlier Phoenician alphabet.
Of the dozens of alphabets in use today, the most popular is the Latin alphabet, which was derived from the Greek, and which many languages modify by adding letters formed using diacritical marks. While most alphabets have letters composed of lines (linear writing), there are also exceptions such as the alphabets used in Braille. The Khmer alphabet (for Cambodian) is the longest, with 74 letters.
Alphabets are usually associated with a standard ordering of letters. This makes them useful for purposes of collation, specifically by allowing words to be sorted in alphabetical order. It also means that their letters can be used as an alternative method of "numbering" ordered items, in such contexts as numbered lists and number placements.
Etymology
The English word alphabet came into Middle English from the Late Latin word alphabetum, which in turn originated in the Greek ἀλφάβητος (alphabētos). The Greek word was made from the first two letters, alpha(α) and beta(β). The names for the Greek letters came from the first two letters of the Phoenician alphabet; aleph, which also meant ox, and bet, which also meant house.
Sometimes, like in the alphabet song in English, the term "ABCs" is used instead of the word "alphabet" (Now I know my ABCs...). "Knowing one's ABCs", in general, can be used as a metaphor for knowing the basics about anything.
History
A Specimen of typeset fonts and languages, by William Caslon, letter founder; from the 1728 Cyclopaedia
Ancient Northeast African and Middle Eastern scripts
The history of the alphabet started in ancient Egypt. Egyptian writing had a set of some 24 hieroglyphs that are called uniliterals, to represent syllables that begin with a single consonant
of their language, plus a vowel (or no vowel) to be supplied by the
native speaker. These glyphs were used as pronunciation guides for logograms, to write grammatical inflections, and, later, to transcribe loan words and foreign names.
A specimen of Proto-Sinaitic script, one of the earliest (if not the very first) phonemic scripts
In the Middle Bronze Age, an apparently "alphabetic" system known as the Proto-Sinaitic script appears in Egyptian turquoise mines in the Sinai peninsula
dated to circa the 15th century BC, apparently left by Canaanite
workers. In 1999, John and Deborah Darnell discovered an even earlier
version of this first alphabet at Wadi el-Hol dated to circa 1800 BC and
showing evidence of having been adapted from specific forms of Egyptian
hieroglyphs that could be dated to circa 2000 BC, strongly suggesting
that the first alphabet had been developed about that time. Based on letter appearances and names, it is believed to be based on Egyptian hieroglyphs.
This script had no characters representing vowels, although originally
it probably was a syllabary, but unneeded symbols were discarded. An
alphabetic cuneiform script with 30 signs including three that indicate the following vowel was invented in Ugarit before the 15th century BC. This script was not used after the destruction of Ugarit.
The Proto-Sinaitic script eventually developed into the Phoenician alphabet, which is conventionally called "Proto-Canaanite" before ca. 1050 BC. The oldest text in Phoenician script is an inscription on the sarcophagus of King Ahiram. This script is the parent script of all western alphabets. By the tenth century, two other forms can be distinguished, namely Canaanite and Aramaic. The Aramaic gave rise to the Hebrew script. The South Arabian alphabet, a sister script to the Phoenician alphabet, is the script from which the Ge'ez alphabet (an abugida) is descended. Vowelless alphabets are called abjads, currently exemplified in scripts including Arabic, Hebrew, and Syriac.
The omission of vowels was not always a satisfactory solution and some
"weak" consonants are sometimes used to indicate the vowel quality of a
syllable (matres lectionis). These letters have a dual function since they are also used as pure consonants.
The Proto-Sinaitic or Proto-Canaanite script and the Ugaritic script were the first scripts with a limited number of signs, in contrast to the other widely used writing systems at the time, Cuneiform, Egyptian hieroglyphs, and Linear B. The Phoenician script was probably the first phonemic script
and it contained only about two dozen distinct letters, making it a
script simple enough for common traders to learn. Another advantage of
Phoenician was that it could be used to write down many different
languages, since it recorded words phonemically.
Illustration from Acta Eruditorum, 1741
The script was spread by the Phoenicians across the Mediterranean.
In Greece, the script was modified to add vowels, giving rise to the
ancestor of all alphabets in the West. It was the first alphabet in
which vowels have independent letter forms separate from those of
consonants. The Greeks chose letters representing sounds that did not
exist in Greek to represent vowels. Vowels are significant in the Greek
language, and the syllabical Linear B script that was used by the Mycenaean
Greeks from the 16th century BC had 87 symbols, including 5 vowels. In
its early years, there were many variants of the Greek alphabet, a
situation that caused many different alphabets to evolve from it.
European alphabets
The Greek alphabet, in its Euboean form, was carried over by Greek colonists to the Italian peninsula, where it gave rise to a variety of alphabets used to write the Italic languages. One of these became the Latin alphabet,
which was spread across Europe as the Romans expanded their empire.
Even after the fall of the Roman state, the alphabet survived in
intellectual and religious works. It eventually became used for the
descendant languages of Latin (the Romance languages) and then for most of the other languages of Europe.
Some adaptations of the Latin alphabet are augmented with ligatures, such as æ in Danish and Icelandic and Ȣ in Algonquian; by borrowings from other alphabets, such as the thorn þ in Old English and Icelandic, which came from the Futhark runes; and by modifying existing letters, such as the eth ð of Old English and Icelandic, which is a modified d. Other alphabets only use a subset of the Latin alphabet, such as Hawaiian, and Italian, which uses the letters j, k, x, y and w only in foreign words.
Another notable script is Elder Futhark, which is believed to have evolved out of one of the Old Italic alphabets. Elder Futhark gave rise to a variety of alphabets known collectively as the Runic alphabets.
The Runic alphabets were used for Germanic languages from AD 100 to the
late Middle Ages. Its usage is mostly restricted to engravings on stone
and jewelry, although inscriptions have also been found on bone and
wood. These alphabets have since been replaced with the Latin alphabet,
except for decorative usage for which the runes remained in use until
the 20th century.
The Old Hungarian script
is a contemporary writing system of the Hungarians. It was in use
during the entire history of Hungary, albeit not as an official writing
system. From the 19th century it once again became more and more
popular.
The Glagolitic alphabet was the initial script of the liturgical language Old Church Slavonic and became, together with the Greek uncial script, the basis of the Cyrillic script.
Cyrillic is one of the most widely used modern alphabetic scripts, and
is notable for its use in Slavic languages and also for other languages
within the former Soviet Union. Cyrillic alphabets include the Serbian, Macedonian, Bulgarian, Russian, Belarusian and Ukrainian. The Glagolitic alphabet is believed to have been created by Saints Cyril and Methodius, while the Cyrillic alphabet was invented by Clement of Ohrid, who was their disciple. They feature many letters that appear to have been borrowed from or influenced by the Greek alphabet and the Hebrew alphabet.
The longest European alphabet is the Latin-derived Slovak alphabet which has 46 letters.
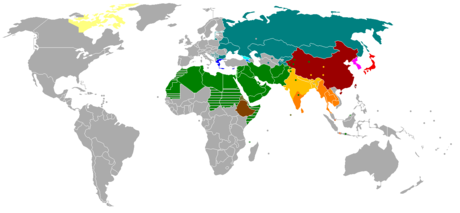
Asian alphabets
Beyond the logographic Chinese writing, many phonetic scripts are in existence in Asia. The Arabic alphabet, Hebrew alphabet, Syriac alphabet, and other abjads of the Middle East are developments of the Aramaic alphabet.
Most alphabetic scripts of India and Eastern Asia are descended from the Brahmi script, which is often believed to be a descendant of Aramaic.
Zhuyin on a cell phone
In Korea, the Hangul alphabet was created by Sejong the Great. Hangul is a unique alphabet: it is a featural alphabet,
where many of the letters are designed from a sound's place of
articulation (P to look like the widened mouth, L to look like the
tongue pulled in, etc.); its design was planned by the government of the
day; and it places individual letters in syllable clusters with equal
dimensions, in the same way as Chinese characters, to allow for mixed-script writing (one syllable always takes up one type-space no matter how many letters get stacked into building that one sound-block).
Zhuyin (sometimes called Bopomofo) is a semi-syllabary used to phonetically transcribe Mandarin Chinese in the Republic of China. After the later establishment of the People's Republic of China and its adoption of Hanyu Pinyin, the use of Zhuyin today is limited, but it is still widely used in Taiwan
where the Republic of China still governs. Zhuyin developed out of a
form of Chinese shorthand based on Chinese characters in the early 1900s
and has elements of both an alphabet and a syllabary. Like an alphabet
the phonemes of syllable initials are represented by individual symbols, but like a syllabary the phonemes of the syllable finals are not; rather, each possible final (excluding the medial glide) is represented by its own symbol. For example, luan is represented as ㄌㄨㄢ (l-u-an), where the last symbol ㄢ represents the entire final -an. While Zhuyin is not used as a mainstream writing system, it is still often used in ways similar to a romanization system—that is, for aiding in pronunciation and as an input method for Chinese characters on computers and cellphones.
European alphabets, especially Latin and Cyrillic, have been
adapted for many languages of Asia. Arabic is also widely used,
sometimes as an abjad (as with Urdu and Persian) and sometimes as a complete alphabet (as with Kurdish and Uyghur).
Types
The term "alphabet" is used by linguists and paleographers in both a wide and a narrow sense. In the wider sense, an alphabet is a script that is segmental at the phoneme
level—that is, it has separate glyphs for individual sounds and not for
larger units such as syllables or words. In the narrower sense, some
scholars distinguish "true" alphabets from two other types of segmental
script, abjads and abugidas.
These three differ from each other in the way they treat vowels: abjads
have letters for consonants and leave most vowels unexpressed; abugidas
are also consonant-based, but indicate vowels with diacritics
to or a systematic graphic modification of the consonants. In alphabets
in the narrow sense, on the other hand, consonants and vowels are
written as independent letters. The earliest known alphabet in the wider sense is the Wadi el-Hol script, believed to be an abjad, which through its successor Phoenician is the ancestor of modern alphabets, including Arabic, Greek, Latin (via the Old Italic alphabet), Cyrillic (via the Greek alphabet) and Hebrew (via Aramaic).
Examples of present-day abjads are the Arabic and Hebrew scripts; true alphabets include Latin, Cyrillic, and Korean hangul; and abugidas are used to write Tigrinya, Amharic, Hindi, and Thai. The Canadian Aboriginal syllabics
are also an abugida rather than a syllabary as their name would imply,
since each glyph stands for a consonant that is modified by rotation to
represent the following vowel. (In a true syllabary, each
consonant-vowel combination would be represented by a separate glyph.)
All three types may be augmented with syllabic glyphs. Ugaritic, for example, is basically an abjad, but has syllabic letters for /ʔa, ʔi, ʔu/. (These are the only time vowels are indicated.) Cyrillic is basically a true alphabet, but has syllabic letters for /ja, je, ju/ (я, е, ю); Coptic has a letter for /ti/. Devanagari is typically an abugida augmented with dedicated letters for initial vowels, though some traditions use अ as a zero consonant as the graphic base for such vowels.
The boundaries between the three types of segmental scripts are not always clear-cut. For example, Sorani Kurdish is written in the Arabic script,
which is normally an abjad. However, in Kurdish, writing the vowels is
mandatory, and full letters are used, so the script is a true alphabet.
Other languages may use a Semitic abjad with mandatory vowel diacritics,
effectively making them abugidas. On the other hand, the Phagspa script of the Mongol Empire was based closely on the Tibetan abugida, but all vowel marks were written after the preceding consonant rather than as diacritic marks. Although short a
was not written, as in the Indic abugidas, one could argue that the
linear arrangement made this a true alphabet. Conversely, the vowel
marks of the Tigrinya abugida and the Amharic abugida
(ironically, the original source of the term "abugida") have been so
completely assimilated into their consonants that the modifications are
no longer systematic and have to be learned as a syllabary rather than
as a segmental script. Even more extreme, the Pahlavi abjad eventually
became logographic.
Thus the primary classification of alphabets reflects how they treat vowels. For tonal languages,
further classification can be based on their treatment of tone, though
names do not yet exist to distinguish the various types. Some alphabets
disregard tone entirely, especially when it does not carry a heavy
functional load, as in Somali
and many other languages of Africa and the Americas. Such scripts are
to tone what abjads are to vowels. Most commonly, tones are indicated
with diacritics, the way vowels are treated in abugidas. This is the
case for Vietnamese (a true alphabet) and Thai (an abugida). In Thai, tone is determined primarily by the choice of consonant, with diacritics for disambiguation. In the Pollard script,
an abugida, vowels are indicated by diacritics, but the placement of
the diacritic relative to the consonant is modified to indicate the
tone. More rarely, a script may have separate letters for tones, as is
the case for Hmong and Zhuang.
For most of these scripts, regardless of whether letters or diacritics
are used, the most common tone is not marked, just as the most common
vowel is not marked in Indic abugidas; in Zhuyin not only is one of the tones unmarked, but there is a diacritic to indicate lack of tone, like the virama of Indic.
The number of letters in an alphabet can be quite small. The Book Pahlavi script, an abjad, had only twelve letters at one point, and may have had even fewer later on. Today the Rotokas alphabet has only twelve letters. (The Hawaiian alphabet is sometimes claimed to be as small, but it actually consists of 18 letters, including the ʻokina and five long vowels. However, Hawaiian Braille
has only 13 letters.) While Rotokas has a small alphabet because it has
few phonemes to represent (just eleven), Book Pahlavi was small because
many letters had been conflated—that is, the graphic
distinctions had been lost over time, and diacritics were not developed
to compensate for this as they were in Arabic, another script that lost many of its distinct letter shapes. For example, a comma-shaped letter represented g, d, y, k, or j. However, such apparent simplifications can perversely make a script more complicated. In later Pahlavi papyri,
up to half of the remaining graphic distinctions of these twelve
letters were lost, and the script could no longer be read as a sequence
of letters at all, but instead each word had to be learned as a
whole—that is, they had become logograms as in Egyptian Demotic.
A Venn diagram showing the Greek (left), Cyrillic (bottom) and Latin (right) alphabets, which share many of the same letters, although they have different pronunciations
The largest segmental script is probably an abugida, Devanagari. When written in Devanagari, Vedic Sanskrit has an alphabet of 53 letters, including the visarga mark for final aspiration and special letters for kš and jñ,
though one of the letters is theoretical and not actually used. The
Hindi alphabet must represent both Sanskrit and modern vocabulary, and
so has been expanded to 58 with the khutma letters (letters with a
dot added) to represent sounds from Persian and English. Thai has a
total of 59 symbols, consisting of 44 consonants, 13 vowels and 2
syllabics, not including 4 diacritics for tone marks and one for vowel
length.
The largest known abjad is Sindhi, with 51 letters. The largest alphabets in the narrow sense include Kabardian and Abkhaz (for Cyrillic), with 58 and 56 letters, respectively, and Slovak (for the Latin script), with 46. However, these scripts either count di- and tri-graphs as separate letters, as Spanish did with ch and ll until recently, or uses diacritics like Slovak č.
The Georgian alphabet (Georgian: ანბანი Anbani)
is an alphabetic writing system. With 33 letters, it is the largest
true alphabet where each letter is graphically independent. The original Georgian alphabet had 38 letters but 5 letters were removed in 19th century by Ilia Chavchavadze.
The Georgian alphabet is much closer to Greek than the other Caucasian
alphabets. The letter order parallels the Greek, with the consonants
without a Greek equivalent organized at the end of the alphabet. The
origins of the alphabet are still unknown. Some Armenian and Western
scholars believe it was created by Mesrop Mashtots (Armenian: Մեսրոպ
Մաշտոց Mesrop Maštoc') also known as Mesrob the Vartabed, who was an
early medieval Armenian linguist, theologian, statesman and hymnologist,
best known for inventing the Armenian alphabet c. 405 AD; other Georgian and Western scholars are against this theory.
Syllabaries typically contain 50 to 400 glyphs, and the glyphs of
logographic systems typically number from the many hundreds into the
thousands. Thus a simple count of the number of distinct symbols is an
important clue to the nature of an unknown script.
The Armenian alphabet (Armenian: Հայոց գրեր Hayots grer or Հայոց այբուբեն Hayots aybuben)
is a graphically unique alphabetical writing system that has been used
to write the Armenian language. It was created in year 405 A.D.
originally contained 36 letters. Two more letters, օ (o) and ֆ (f), were
added in the Middle Ages. During the 1920s orthography reform, a new
letter և (capital ԵՎ) was added, which was a ligature before ե+ւ, while
the letter Ւ ւ was discarded and reintroduced as part of a new letter ՈՒ
ու (which was a digraph before).
Old Georgian alphabet inscription on Monastery gate
The Armenian script's directionality is horizontal left-to-right, like the Latin and Greek alphabets. It also uses bicameral script like those. The Armenian word for "alphabet" is այբուբեն aybuben (Armenian pronunciation: [ɑjbubɛn]), named after the first two letters of the Armenian alphabet Ա այբ ayb and Բ բեն ben.
Alphabetical order
Alphabets often come to be associated with a standard ordering of their letters, which can then be used for purposes of collation—namely for the listing of words and other items in what is called alphabetical order.
The basic ordering of the Latin alphabet (A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z), which is derived from the Northwest Semitic "Abgad" order,
is well established, although languages using this alphabet have
different conventions for their treatment of modified letters (such as
the French é, à, and ô) and of certain combinations of letters (multigraphs). In French, these are not considered to be additional letters for the purposes of collation. However, in Icelandic, the accented letters such as á, í, and ö
are considered distinct letters representing different vowel sounds
from the sounds represented by their unaccented counterparts. In
Spanish, ñ is considered a separate letter, but accented vowels such as á and é are not. The ll and ch were also considered single letters, but in 1994 the Real Academia Española changed the collating order so that ll is between lk and lm in the dictionary and ch is between cg and ci, and in 2010 the tenth congress of the Association of Spanish Language Academies changed it so they were no longer letters at all.
In German, words starting with sch- (which spells the German phoneme /ʃ/) are inserted between words with initial sca- and sci- (all incidentally loanwords) instead of appearing after initial sz, as though it were a single letter—in contrast to several languages such as Albanian, in which dh-, ë-, gj-, ll-, rr-, th-, xh- and zh- (all representing phonemes and considered separate single letters) would follow the letters d, e, g, l, n, r, t, x and z respectively, as well as Hungarian and Welsh. Further, German words with umlaut are collated ignoring the umlaut—contrary to Turkish that adopted the graphemes ö and ü, and where a word like tüfek, would come after tuz, in the dictionary. An exception is the German telephone directory where umlauts are sorted like ä = ae since names such as Jäger also appear with the spelling Jaeger, and are not distinguished in the spoken language.
The Danish and Norwegian alphabets end with æ—ø—å, whereas the Swedish and Finnish ones conventionally put å—ä—ö at the end.
It is unknown whether the earliest alphabets had a defined sequence. Some alphabets today, such as the Hanuno'o script, are learned one letter at a time, in no particular order, and are not used for collation where a definite order is required. However, a dozen Ugaritic tablets from the fourteenth century BC preserve the alphabet in two sequences. One, the ABCDE order later used in Phoenician, has continued with minor changes in Hebrew, Greek, Armenian, Gothic, Cyrillic, and Latin; the other, HMĦLQ, was used in southern Arabia and is preserved today in Ethiopic. Both orders have therefore been stable for at least 3000 years.
Runic used an unrelated Futhark sequence, which was later simplified. Arabic uses its own sequence, although Arabic retains the traditional abjadi order for numbering.
The Brahmic family of alphabets used in India use a unique order based on phonology:
The letters are arranged according to how and where they are produced
in the mouth. This organization is used in Southeast Asia, Tibet, Korean
hangul, and even Japanese kana, which is not an alphabet.
Names of letters
The Phoenician letter names, in which each letter was associated with a word that begins with that sound (acrophony), continue to be used to varying degrees in Samaritan, Aramaic, Syriac, Hebrew, Greek and Arabic.
The names were abandoned in Latin, which instead referred to the letters by adding a vowel (usually e) before or after the consonant; the two exceptions were Y and Z, which were borrowed from the Greek alphabet rather than Etruscan, and were known as Y Graeca "Greek Y" (pronounced I Graeca "Greek I") and zeta (from Greek)—this discrepancy was inherited by many European languages, as in the term zed for Z in all forms of English other than American English. Over time names sometimes shifted or were added, as in double U for W ("double V" in French), the English name for Y, and American zee for Z. Comparing names in English and French gives a clear reflection of the Great Vowel Shift: A, B, C and D are pronounced /eɪ, biː, siː, diː/ in today's English, but in contemporary French they are /a, be, se, de/.
The French names (from which the English names are derived) preserve
the qualities of the English vowels from before the Great Vowel Shift.
By contrast, the names of F, L, M, N and S (/ɛf, ɛl, ɛm, ɛn, ɛs/) remain the same in both languages, because "short" vowels were largely unaffected by the Shift.
In Cyrillic originally the letters were given names based on
Slavic words; this was later abandoned as well in favor of a system
similar to that used in Latin.
Letters of Armenian alphabet also have distinct letter names.
Orthography and pronunciation
When an alphabet is adopted or developed to represent a given language, an orthography generally comes into being, providing rules for the spelling
of words in that language. In accordance with the principle on which
alphabets are based, these rules will generally map letters of the
alphabet to the phonemes (significant sounds) of the spoken language. In a perfectly phonemic orthography
there would be a consistent one-to-one correspondence between the
letters and the phonemes, so that a writer could predict the spelling of
a word given its pronunciation, and a speaker would always know the
pronunciation of a word given its spelling, and vice versa. However this
ideal is not usually achieved in practice; some languages (such as Spanish and Finnish) come close to it, while others (such as English) deviate from it to a much larger degree.
The pronunciation of a language often evolves independently of
its writing system, and writing systems have been borrowed for languages
they were not designed for, so the degree to which letters of an
alphabet correspond to phonemes of a language varies greatly from one
language to another and even within a single language.
Languages may fail to achieve a one-to-one correspondence between letters and sounds in any of several ways:
- A language may represent a given phoneme by a combination of letters rather than just a single letter. Two-letter combinations are called digraphs and three-letter groups are called trigraphs. German uses the tetragraphs (four letters) "tsch" for the phoneme [tʃ] and (in a few borrowed words) "dsch" for [dʒ]. Kabardian also uses a tetragraph for one of its phonemes, namely "кхъу". Two letters representing one sound occur in several instances in Hungarian as well (where, for instance, cs stands for [tʃ], sz for [s], zs for [ʒ], dzs for [dʒ]).
- A language may represent the same phoneme with two or more different letters or combinations of letters. An example is modern Greek which may write the phoneme [i] in six different ways: ⟨ι⟩, ⟨η⟩, ⟨υ⟩, ⟨ει⟩, ⟨οι⟩, and ⟨υι⟩ (though the last is rare).
- A language may spell some words with unpronounced letters that exist for historical or other reasons. For example, the spelling of the Thai word for "beer" [เบียร์] retains a letter for the final consonant "r" present in the English word it was borrowed from, but silences it.
- Pronunciation of individual words may change according to the presence of surrounding words in a sentence (sandhi).
- Different dialects of a language may use different phonemes for the same word.
- A language may use different sets of symbols or different rules for distinct sets of vocabulary items, such as the Japanese hiragana and katakana syllabaries, or the various rules in English for spelling words from Latin and Greek, or the original Germanic vocabulary.
National languages sometimes elect to address the problem of dialects
by simply associating the alphabet with the national standard. Some
national languages like Finnish, Armenian, Turkish, Russian, Serbo-Croatian (Serbian, Croatian and Bosnian) and Bulgarian
have a very regular spelling system with a nearly one-to-one
correspondence between letters and phonemes. Strictly speaking, these
national languages lack a word corresponding to the verb "to spell"
(meaning to split a word into its letters), the closest match being a
verb meaning to split a word into its syllables. Similarly, the Italian verb corresponding to 'spell (out)', compitare, is unknown to many Italians because spelling is usually trivial, as Italian spelling is highly phonemic. In standard Spanish,
one can tell the pronunciation of a word from its spelling, but not
vice versa, as certain phonemes can be represented in more than one way,
but a given letter is consistently pronounced. French, with its silent letters and its heavy use of nasal vowels and elision,
may seem to lack much correspondence between spelling and
pronunciation, but its rules on pronunciation, though complex, are
actually consistent and predictable with a fair degree of accuracy.
At the other extreme are languages such as English, where the
pronunciations of many words simply have to be memorized as they do not
correspond to the spelling in a consistent way. For English, this is
partly because the Great Vowel Shift
occurred after the orthography was established, and because English has
acquired a large number of loanwords at different times, retaining
their original spelling at varying levels. Even English has general,
albeit complex, rules that predict pronunciation from spelling, and
these rules are successful most of the time; rules to predict spelling
from the pronunciation have a higher failure rate.
Sometimes, countries have the written language undergo a spelling reform
to realign the writing with the contemporary spoken language. These can
range from simple spelling changes and word forms to switching the
entire writing system itself, as when Turkey switched from the Arabic alphabet to a Latin-based Turkish alphabet.
The standard system of symbols used by linguists to represent sounds in any language, independently of orthography, is called the International Phonetic Alphabet.