| Sedimentary rock | |
 Combustion of oil shale | |
| Composition | |
|---|---|
| Primary | |
| Secondary | |
Oil shale is an organic-rich fine-grained sedimentary rock containing kerogen (a solid mixture of organic chemical compounds) from which liquid hydrocarbons can be produced, called shale oil (not to be confused with tight oil—crude oil occurring naturally in shales). Shale oil is a substitute for conventional crude oil; however, extracting shale oil from oil shale is more costly than the production of conventional crude oil both financially and in terms of its environmental impact. Deposits of oil shale occur around the world, including major deposits in the United States. A 2016 estimate of global deposits set the total world resources of oil shale equivalent of 6.05 trillion barrels (962 billion cubic metres) of oil in place.
Heating oil shale to a sufficiently high temperature causes the chemical process of pyrolysis to yield a vapor. Upon cooling the vapor, the liquid shale oil—an unconventional oil—is separated from combustible oil-shale gas (the term shale gas can also refer to gas occurring naturally in shales). Oil shale can also be burned directly in furnaces as a low-grade fuel for power generation and district heating or used as a raw material in chemical and construction-materials processing.
Oil shale gains attention as a potential abundant source of oil whenever the price of crude oil rises. At the same time, oil-shale mining and processing raise a number of environmental concerns, such as land use, waste disposal, water use, waste-water management, greenhouse-gas emissions and air pollution. Estonia and China have well-established oil shale industries, and Brazil, Germany, and Russia also utilize oil shale.
General composition of oil shales constitutes inorganic matrix, bitumens, and kerogen. Oil shales differ from oil-bearing shales, shale deposits that contain petroleum (tight oil) that is sometimes produced from drilled wells. Examples of oil-bearing shales are the Bakken Formation, Pierre Shale, Niobrara Formation, and Eagle Ford Formation.
Geology
Oil shale, an organic-rich sedimentary rock, belongs to the group of sapropel fuels. It does not have a definite geological definition nor a specific chemical formula, and its seams do not always have discrete boundaries. Oil shales vary considerably in their mineral content, chemical composition, age, type of kerogen, and depositional history and not all oil shales would necessarily be classified as shales in the strict sense. According to the petrologist Adrian C. Hutton of the University of Wollongong, oil shales are not "geological nor geochemically distinctive rock but rather 'economic' term." Their common defining feature is low solubility in low-boiling organic solvents and generation of liquid organic products on thermal decomposition.
Oil shale differs from bitumen-impregnated rocks (oil sands and petroleum reservoir rocks), humic coals and carbonaceous shale. While oil sands do originate from the biodegradation of oil, heat and pressure have not (yet) transformed the kerogen in oil shale into petroleum, that means that its maturation does not exceed early mesocatagenetic.
General composition of oil shales constitutes inorganic matrix, bitumens, and kerogen. While the bitumen portion of oil shales is soluble in carbon disulfide, kerogen portion is insoluble in carbon disulfide and may contain iron, vanadium, nickel, molybdenum, and uranium. Oil shale contains a lower percentage of organic matter than coal. In commercial grades of oil shale the ratio of organic matter to mineral matter lies approximately between 0.75:5 and 1.5:5. At the same time, the organic matter in oil shale has an atomic ratio of hydrogen to carbon (H/C) approximately 1.2 to 1.8 times lower than for crude oil and about 1.5 to 3 times higher than for coals. The organic components of oil shale derive from a variety of organisms, such as the remains of algae, spores, pollen, plant cuticles and corky fragments of herbaceous and woody plants, and cellular debris from other aquatic and land plants. Some deposits contain significant fossils; Germany's Messel Pit has the status of a Unesco World Heritage Site. The mineral matter in oil shale includes various fine-grained silicates and carbonates. Inorganic matrix can contain quartz, feldspars, clays (mainly illite and chlorite), carbonates (calcite and dolomites), pyrite and some other minerals.
Geologists can classify oil shales on the basis of their composition as carbonate-rich shales, siliceous shales, or cannel shales.
Another classification, known as the van Krevelen diagram, assigns kerogen types, depending on the hydrogen, carbon, and oxygen content of oil shales' original organic matter. The most commonly used classification of oil shales, developed between 1987 and 1991 by Adrian C. Hutton, adapts petrographic terms from coal terminology. This classification designates oil shales as terrestrial, lacustrine (lake-bottom-deposited), or marine (ocean bottom-deposited), based on the environment of the initial biomass deposit. Known oil shales are predominantly aquatic (marine, lacustrine) origin. Hutton's classification scheme has proven useful in estimating the yield and composition of the extracted oil.
Resource
As source rocks for most conventional oil reservoirs, oil shale deposits are found in all world oil provinces, although most of them are too deep to be exploited economically. As with all oil and gas resources, analysts distinguish between oil shale resources and oil shale reserves. "Resources" refers to all oil shale deposits, while "reserves", represents those deposits from which producers can extract oil shale economically using existing technology. Since extraction technologies develop continuously, planners can only estimate the amount of recoverable kerogen. Although resources of oil shale occur in many countries, only 33 countries possess known deposits of possible economic value. Well-explored deposits, potentially classifiable as reserves, include the Green River deposits in the western United States, the Tertiary deposits in Queensland, Australia, deposits in Sweden and Estonia, the El-Lajjun deposit in Jordan, and deposits in France, Germany, Brazil, China, southern Mongolia and Russia. These deposits have given rise to expectations of yielding at least 40 liters of shale oil per tonne of oil shale, using the Fischer Assay.
A 2016 estimate set the total world resources of oil shale equivalent to yield of 6.05 trillion barrels (962 billion cubic metres) of shale oil, with the largest resource deposits in the United States accounting more than 80% of the world total resource. For comparison, at the same time the world's proven oil reserves are estimated to be 1.6976 trillion barrels (269.90 billion cubic metres). The largest deposits in the world occur in the United States in the Green River Formation, which covers portions of Colorado, Utah, and Wyoming; about 70% of this resource lies on land owned or managed by the United States federal government. Deposits in the United States constitute more than 80% of world resources; other significant resource holders being China, Russia, and Brazil.
History
Humans have used oil shale as a fuel since prehistoric times, since it generally burns without any processing. Around 3000 BC, "rock oil" was used in Mesopotamia for road construction and making architectural adhesives. Britons of the Iron Age also used to polish it and form it into ornaments.
In the 10th century, the Arab physician Masawaih al-Mardini (Mesue the Younger) described a method of extraction of oil from "some kind of bituminous shale". The first patent for extracting oil from oil shale was British Crown Patent 330 granted in 1694 to three persons named Martin Eele, Thomas Hancock and William Portlock who had "found a way to extract and make great quantities of pitch, tarr, and oyle out of a sort of stone."
Modern industrial mining of oil shale began in 1837 in Autun, France, followed by exploitation in Scotland, Germany, and several other countries.
Operations during the 19th century focused on the production of kerosene, lamp oil, and paraffin; these products helped supply the growing demand for lighting that arose during the Industrial Revolution. Fuel oil, lubricating oil and grease, and ammonium sulfate were also produced. The European oil-shale industry expanded immediately before World War I due to limited access to conventional petroleum resources and to the mass production of automobiles and trucks, which accompanied an increase in gasoline consumption.
Although the Estonian and Chinese oil-shale industries continued to grow after World War II, most other countries abandoned their projects due to high processing costs and the availability of cheaper petroleum. Following the 1973 oil crisis, world production of oil shale reached a peak of 46 million tonnes in 1980 before falling to about 16 million tonnes in 2000, due to competition from cheap conventional petroleum in the 1980s.
On 2 May 1982, known in some circles as "Black Sunday", Exxon canceled its US$5 billion Colony Shale Oil Project near Parachute, Colorado because of low oil-prices and increased expenses, laying off more than 2,000 workers and leaving a trail of home-foreclosures and small-business bankruptcies. In 1986, President Ronald Reagan signed into law the Consolidated Omnibus Budget Reconciliation Act of 1985 which among other things abolished the United States' Synthetic Liquid Fuels Program.
The global oil-shale industry began to revive at the beginning of the 21st century. In 2003, an oil-shale development program restarted in the United States. Authorities introduced a commercial leasing program permitting the extraction of oil shale and oil sands on federal lands in 2005, in accordance with the Energy Policy Act of 2005.
Industry
As of 2008, industry uses oil shale in Brazil, China, Estonia and to some extent in Germany, and Russia. Several additional countries started assessing their reserves or had built experimental production plants, while others had phased out their oil shale industry. Oil shale serves for oil production in Estonia, Brazil, and China; for power generation in Estonia, China, and Germany; for cement production in Estonia, Germany, and China; and for use in chemical industries in China, Estonia, and Russia.
As of 2009, 80% of oil shale used globally is extracted in Estonia, mainly due to the Oil-shale-fired power plants. Oil-shale-fired power plants occur in Estonia, which has an installed capacity of 2,967 megawatts (MW), China (12 MW), and Germany (9.9 MW). Israel, Romania and Russia have in the past run power plants fired by oil shale, but have shut them down or switched to other fuel sources such as natural gas. Jordan and Egypt plan to construct power plants fired by oil shale, while Canada and Turkey plan to burn oil shale along with coal for power generation. Oil shale serves as the main fuel for power generation only in Estonia, where 90.3% of country's electrical generation in 2016 was produced from oil shale.
According to the World Energy Council, in 2008 the total production of shale oil from oil shale was 930,000 tonnes, equal to 17,700 barrels per day (2,810 m3/d), of which China produced 375,000 tonnes, Estonia 355,000 tonnes, and Brazil 200,000 tonnes. In comparison, production of the conventional oil and natural gas liquids in 2008 amounted 3.95 billion tonnes or 82.1 million barrels per day (13.1×106 m3/d).
Extraction and processing
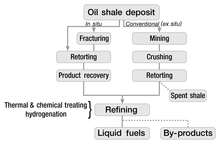
Most exploitation of oil shale involves mining followed by shipping elsewhere, after which one can burn the shale directly to generate electricity, or undertake further processing. The most common methods of surface mining involve open pit mining and strip mining. These procedures remove most of the overlying material to expose the deposits of oil shale, and become practical when the deposits occur near the surface. Underground mining of oil shale, which removes less of the overlying material, employs the room-and-pillar method.
The extraction of the useful components of oil shale usually takes place above ground (ex-situ processing), although several newer technologies perform this underground (on-site or in-situ processing). In either case, the chemical process of pyrolysis converts the kerogen in the oil shale to shale oil (synthetic crude oil) and oil shale gas. Most conversion technologies involve heating shale in the absence of oxygen to a temperature at which kerogen decomposes (pyrolyses) into gas, condensable oil, and a solid residue. This usually takes place between 450 °C (842 °F) and 500 °C (932 °F). The process of decomposition begins at relatively low temperatures (300 °C or 572 °F), but proceeds more rapidly and more completely at higher temperatures.
In-situ processing involves heating the oil shale underground. Such technologies can potentially extract more oil from a given area of land than ex-situ processes, since they can access the material at greater depths than surface mines can. Several companies have patented methods for in-situ retorting. However, most of these methods remain in the experimental phase. One can distinguish true in-situ processes (TIS) and modified in-situ processes (MIS). True in-situ processes do not involve mining the oil shale. Modified in-situ processes involve removing part of the oil shale and bringing it to the surface for modified in-situ retorting in order to create permeability for gas flow in a rubble chimney. Explosives rubblize the oil-shale deposit.
Hundreds of patents for oil shale retorting technologies exist; however, only a few dozen have undergone testing. By 2006, only four technologies remained in commercial use: Kiviter, Galoter, Fushun, and Petrosix.
Applications and products
Industry can use oil shale as a fuel for thermal power-plants, burning it (like coal) to drive steam turbines; some of these plants employ the resulting heat for district heating of homes and businesses. In addition to its use as a fuel, oil shale may also serve in the production of specialty carbon fibers, adsorbent carbons, carbon black, phenols, resins, glues, tanning agents, mastic, road bitumen, cement, bricks, construction and decorative blocks, soil-additives, fertilizers, rock-wool insulation, glass, and pharmaceutical products. However, oil shale use for production of these items remains small or only in its experimental stages. Some oil shales yield sulfur, ammonia, alumina, soda ash, uranium, and nahcolite as shale-oil extraction byproducts. Between 1946 and 1952, a marine type of Dictyonema shale served for uranium production in Sillamäe, Estonia, and between 1950 and 1989 Sweden used alum shale for the same purposes. Oil shale gas has served as a substitute for natural gas, but as of 2009, producing oil shale gas as a natural-gas substitute remained economically infeasible.
The shale oil derived from oil shale does not directly substitute for crude oil in all applications. It may contain higher concentrations of olefins, oxygen, and nitrogen than conventional crude oil. Some shale oils may have higher sulfur or arsenic content. By comparison with West Texas Intermediate, the benchmark standard for crude oil in the futures-contract market, the Green River shale oil sulfur content ranges from near 0% to 4.9% (in average 0.76%), where West Texas Intermediate's sulfur content has a maximum of 0.42%. The sulfur content in shale oil from Jordan's oil shales may rise even up to 9.5%. The arsenic content, for example, becomes an issue for Green River formation oil shale. The higher concentrations of these materials means that the oil must undergo considerable upgrading (hydrotreating) before serving as oil-refinery feedstock. Above-ground retorting processes tended to yield a lower API gravity shale oil than the in situ processes. Shale oil serves best for producing middle-distillates such as kerosene, jet fuel, and diesel fuel. Worldwide demand for these middle distillates, particularly for diesel fuels, increased rapidly in the 1990s and 2000s. However, appropriate refining processes equivalent to hydrocracking can transform shale oil into a lighter-range hydrocarbon (gasoline).
Economics
The amount of economically recoverable oil shale is unknown. The various attempts to develop oil shale deposits have succeeded only when the cost of shale-oil production in a given region comes in below the price of crude oil or its other substitutes. According to a survey conducted by the RAND Corporation, the cost of producing a barrel of oil at a surface retorting complex in the United States (comprising a mine, retorting plant, upgrading plant, supporting utilities, and spent shale reclamation), would range between US$70–95 ($440–600/m3, adjusted to 2005 values). This estimate considers varying levels of kerogen quality and extraction efficiency. In order to run a profitable operation, the price of crude oil would need to remain above these levels. The analysis also discusses the expectation that processing costs would drop after the establishment of the complex. The hypothetical unit would see a cost reduction of 35–70% after producing its first 500 million barrels (79 million cubic metres). Assuming an increase in output of 25 thousand barrels per day (4.0×103 m3/d) during each year after the start of commercial production, RAND predicts the costs would decline to $35–48 per barrel ($220–300/m3) within 12 years. After achieving the milestone of 1 billion barrels (160 million cubic metres), its costs would decline further to $30–40 per barrel ($190–250/m3). Some commentators compare the proposed American oil-shale industry to the Athabasca oil-sands industry (the latter enterprise generated over 1 million barrels (160,000 cubic metres) of oil per day in late 2007), stating that "the first-generation facility is the hardest, both technically and economically".
In 2005, Royal Dutch Shell announced that its in-situ process could become competitive for oil prices over $30 per barrel ($190/m3). A 2004 report by the United States Department of Energy stated that both the Shell technology and technology used in the Stuart Oil Shale Project could be competitive at prices above $25 per barrel, and that the Viru Keemia Grupp expected full-scale production to be economical at prices above $18 per barrel ($130/m3).
To increase efficiency when retorting oil shale, researchers have proposed and tested several co-pyrolysis processes.
A 1972 publication in the journal Pétrole Informations (ISSN 0755-561X) compared shale-based oil production unfavorably with coal liquefaction. The article portrayed coal liquefaction as less expensive, generating more oil, and creating fewer environmental impacts than extraction from oil shale. It cited a conversion ratio of 650 liters (170 U.S. gal; 140 imp gal) of oil per one ton of coal, as against 150 liters (40 U.S. gal; 33 imp gal) of shale oil per one ton of oil shale.
A critical measure of the viability of oil shale as an energy source lies in the ratio of the energy produced by the shale to the energy used in its mining and processing, a ratio known as "Energy Returned on Energy Invested" (EROEI). A 1984 study estimated the EROEI of the various known oil-shale deposits as varying between 0.7–13.3 although known oil-shale extraction development projects assert an EROEI between 3 and 10. According to the World Energy Outlook 2010, the EROEI of ex-situ processing is typically 4 to 5 while of in-situ processing it may be even as low as 2. However, according to the IEA most of used energy can be provided by burning the spent shale or oil-shale gas.
The water needed in the oil shale retorting process offers an additional economic consideration: this may pose a problem in areas with water scarcity.
Environmental considerations
Mining oil shale involves a number of environmental impacts, more pronounced in surface mining than in underground mining. These include acid drainage induced by the sudden rapid exposure and subsequent oxidation of formerly buried materials, the introduction of metals including mercury into surface-water and groundwater, increased erosion, sulfur-gas emissions, and air pollution caused by the production of particulates during processing, transport, and support activities. In 2002, about 97% of air pollution, 86% of total waste and 23% of water pollution in Estonia came from the power industry, which uses oil shale as the main resource for its power production.
Oil-shale extraction can damage the biological and recreational value of land and the ecosystem in the mining area. Combustion and thermal processing generate waste material. In addition, the atmospheric emissions from oil shale processing and combustion include carbon dioxide, a greenhouse gas. Environmentalists oppose production and usage of oil shale, as it creates even more greenhouse gases than conventional fossil fuels. Experimental in situ conversion processes and carbon capture and storage technologies may reduce some of these concerns in the future, but at the same time they may cause other problems, including groundwater pollution. Among the water contaminants commonly associated with oil shale processing are oxygen and nitrogen heterocyclic hydrocarbons. Commonly detected examples include quinoline derivatives, pyridine, and various alkyl homologues of pyridine (picoline, lutidine).
Water concerns are sensitive issues in arid regions, such as the western US and Israel's Negev Desert, where plans exist to expand oil-shale extraction despite a water shortage. Depending on technology, above-ground retorting uses between one and five barrels of water per barrel of produced shale-oil. A 2008 programmatic environmental impact statement issued by the US Bureau of Land Management stated that surface mining and retort operations produce 2 to 10 U.S. gallons (7.6 to 37.9 l; 1.7 to 8.3 imp gal) of waste water per 1 short ton (0.91 t) of processed oil shale. In situ processing, according to one estimate, uses about one-tenth as much water.
Environmental activists, including members of Greenpeace, have organized strong protests against the oil shale industry. In one result, Queensland Energy Resources put the proposed Stuart Oil Shale Project in Australia on hold in 2004.
Extraterrestrial oil shale
Some comets contain "massive amounts of an organic material almost identical to high grade oil shale," the equivalent of cubic kilometers of such mixed with other material; for instance, corresponding hydrocarbons were detected in a probe fly-by through the tail of Comet Halley during 1986.