Superfluid helium-4

From Wikipedia, the free encyclopedia

Superfluid helium-4 is the superfluid form of helium-4, an isotope of the element helium. A superfluid is a state of matter in which matter behaves like a fluid with zero viscosity. The substance, which looks like a normal liquid, flows without friction past any surface, which allows it to continue to circulate over obstructions and through pores in containers which hold it, subject only to its own inertia.

The formation of the superfluid is known to be related to the formation of a Bose–Einstein condensate. This is made obvious by the fact that superfluidity occurs in liquid helium-4 at far higher temperatures than it does in helium-3. Each atom of helium-4 is a boson particle, by virtue of its zero spin. Helium-3, however, is a fermion particle, which can form bosons only by pairing with itself at much lower temperatures, in a process similar to the electron pairing in superconductivity.

History

Known as a major facet in the study of quantum hydrodynamics and macroscopic quantum phenomena, the superfluidity effect was discovered by Pyotr Kapitsa and John F. Allen, and Don Misener in 1937. It has since been described through phenomenological and microscopic theories.

In the 1950s, Hall and Vinen performed experiments establishing the existence of quantized vortex lines in superfluid helium. In the 1960s, Rayfield and Reif established the existence of quantized vortex rings. Packard has observed the intersection of vortex lines with the free surface of the fluid, and Avenel and Varoquaux have studied the Josephson effect in superfluid helium-4. In 2006, a group at the University of Maryland visualized quantized vortices by using small tracer particles of solid hydrogen.

In the early 2000s, physicists created a Fermionic condensate from pairs of ultra-cold fermionic atoms. Under certain conditions, fermion pairs form diatomic molecules and undergo Bose–Einstein condensation. At the other limit, the fermions (most notably superconducting electrons) form Cooper pairs which also exhibit superfluidity. This work with ultra-cold atomic gases has allowed scientists to study the region in between these two extremes, known as the BEC-BCS crossover.

Supersolids may also have been discovered in 2004 by physicists at Penn State University. When helium-4 is cooled below about 200 mK under high pressures, a fraction (≈1%) of the solid appears to become superfluid. By quench cooling or lengthening the annealing time, thus increasing or decreasing the defect density respectively, it was shown, via torsional oscillator experiment, that the supersolid fraction could be made to range from 20% to completely non-existent. This suggested that the supersolid nature of helium-4 is not intrinsic to helium-4 but a property of helium-4 and disorder. Some emerging theories posit that the supersolid signal observed in helium-4 was actually an observation of either a superglass state or intrinsically superfluid grain boundaries in the helium-4 crystal.

Applications

Recently in the field of chemistry, superfluid helium-4 has been successfully used in spectroscopic techniques as a quantum solvent. Referred to as superfluid helium droplet spectroscopy (SHeDS), it is of great interest in studies of gas molecules, as a single molecule solvated in a superfluid medium allows a molecule to have effective rotational freedom, allowing it to behave similarly to how it would in the "gas" phase. Droplets of superfluid helium also have a characteristic temperature of about 0.4 K which cools the solvated molecule(s) to its ground or nearly ground rovibronic state.

Superfluids are also used in high-precision devices such as gyroscopes, which allow the measurement of some theoretically predicted gravitational effects (for an example, see Gravity Probe B).

The Infrared Astronomical Satellite IRAS, launched in January 1983 to gather infrared data was cooled by 73 kilograms of superfluid helium, maintaining a temperature of 1.6 K (−271.55 °C). When used in conjunction with helium-3, temperatures as low as 40 mK are routinely achieved in extreme low temperature experiments. The helium-3, in liquid state at 3.2 K, can be evaporated into the superfluid helium-4, where it acts as a gas due to the latter's properties as a Bose–Einstein condensate. This evaporation pulls energy from the overall system, which can be pumped out in a way completely analogous to normal refrigeration techniques.

Superfluid-helium technology is used to extend the temperature range of cryocoolers to lower temperatures. So far the limit is 1.19 K, but there is a potential to reach 0.7 K.

Properties

Superfluids, such as helium-4 below the lambda point, exhibit many unusual properties. A superfluid acts as if it were a mixture of a normal component, with all the properties of a normal fluid, and a superfluid component. The superfluid component has zero viscosity and zero entropy. Application of heat to a spot in superfluid helium results in a flow of the normal component which takes care of the heat transport at relatively high velocity (up to 20 cm/s) which leads to a very high effective thermal conductivity.

Film flow

Many ordinary liquids, like alcohol or petroleum, creep up solid walls, driven by their surface tension. Liquid helium also has this property, but, in the case of He-II, the flow of the liquid in the layer is not restricted by its viscosity but by a critical velocity which is about 20 cm/s. This is a fairly high velocity so superfluid helium can flow relatively easily up the wall of containers, over the top, and down to the same level as the surface of the liquid inside the container, in a siphon effect as illustrated in figure 4. In a container, lifted above the liquid level, it forms visible droplets as seen in figure 5. It was, however, observed, that the flow through nanoporous membrane becomes restricted if the pore diameter is less than 0.7 nm (i.e. roughly three times the classical diameter of helium atom), suggesting the unusual hydrodynamic properties of He arise at larger scale than in the classical liquid helium.

Rotation

Another fundamental property becomes visible if a superfluid is placed in a rotating container. Instead of rotating uniformly with the container, the rotating state consists of quantized vortices. That is, when the container is rotated at speeds below the first critical angular velocity, the liquid remains perfectly stationary. Once the first critical angular velocity is reached, the superfluid will form a vortex. The vortex strength is quantized, that is, a superfluid can only spin at certain "allowed" values. Rotation in a normal fluid, like water, is not quantized. If the rotation speed is increased more and more quantized vortices will be formed which arrange in nice patterns similar to the Abrikosov lattice in a superconductor.

Comparison with helium-3

Although the phenomenologies of the superfluid states of helium-4 and helium-3 are very similar, the microscopic details of the transitions are very different. Helium-4 atoms are bosons, and their superfluidity can be understood in terms of the Bose–Einstein statistics that they obey. Specifically, the superfluidity of helium-4 can be regarded as a consequence of Bose–Einstein condensation in an interacting system. On the other hand, helium-3 atoms are fermions, and the superfluid transition in this system is described by a generalization of the BCS theory of superconductivity. In it, Cooper pairing takes place between atoms rather than electrons, and the attractive interaction between them is mediated by spin fluctuations rather than phonons. A unified description of superconductivity and superfluidity is possible in terms of gauge symmetry breaking.

Macroscopic theory

Thermodynamics

Fig. 1. Phase diagram of ⁴He. In this diagram is also given the λ-line.

 

Fig. 2. Heat capacity of liquid ⁴He at saturated vapor pressure as function of the temperature. The peak at T=2.17 K marks a (second-order) phase transition.

 

Fig. 3. Temperature dependence of the relative superfluid and normal components ρ_n/ρ and ρ_s/ρ as functions of T.

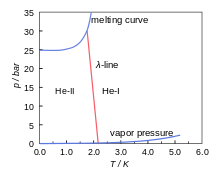
Figure 1 is the phase diagram of ⁴He. It is a pressure-temperature (p-T) diagram indicating the solid and liquid regions separated by the melting curve (between the liquid and solid state) and the liquid and gas region, separated by the vapor-pressure line. This latter ends in the critical point where the difference between gas and liquid disappears. The diagram shows the remarkable property that ⁴He is liquid even at absolute zero. ⁴He is only solid at pressures above 25 bar.

Figure 1 also shows the λ-line. This is the line that separates two fluid regions in the phase diagram indicated by He-I and He-II. In the He-I region the helium behaves like a normal fluid; in the He-II region the helium is superfluid.

The name lambda-line comes from the specific heat – temperature plot which has the shape of the Greek letter λ. See figure 2, which shows a peak at 2.172 K, the so-called λ-point of ⁴He.

Below the lambda line the liquid can be described by the so-called two-fluid model. It behaves as if it consists of two components: a normal component, which behaves like a normal fluid, and a superfluid component with zero viscosity and zero entropy. The ratios of the respective densities ρ_n/ρ and ρ_s/ρ, with ρ_n (ρ_s) the density of the normal (superfluid) component, and ρ (the total density), depends on temperature and is represented in figure 3. By lowering the temperature, the fraction of the superfluid density increases from zero at T_λ to one at zero kelvins. Below 1 K the helium is almost completely superfluid.

It is possible to create density waves of the normal component (and hence of the superfluid component since ρ_n + ρ_s = constant) which are similar to ordinary sound waves. This effect is called second sound. Due to the temperature dependence of ρ_n (figure 3) these waves in ρ_n are also temperature waves.

Fig. 4. Helium II will "creep" along surfaces in order to find its own level – after a short while, the levels in the two containers will equalize. The Rollin film also covers the interior of the larger container; if it were not sealed, the helium II would creep out and escape.

 

Fig. 5. The liquid helium is in the superfluid phase. As long as it remains superfluid, it creeps up the wall of the cup as a thin film. It comes down on the outside, forming a drop which will fall into the liquid below. Another drop will form – and so on – until the cup is empty.

Superfluid hydrodynamics

The equation of motion for the superfluid component, in a somewhat simplified form, is given by Newton's law

${\displaystyle {\vec {F}}=M_{4}{\frac {\mathrm {d} {\vec {v}}_{s}}{\mathrm {d} t}}.}$

The mass M₄ is the molar mass of ⁴He, and ${\displaystyle {\vec {v}}_{s}}$ is the velocity of the superfluid component. The time derivative is the so-called hydrodynamic derivative, i.e. the rate of increase of the velocity when moving with the fluid. In the case of superfluid ⁴He in the gravitational field the force is given by

${\displaystyle {\vec {F}}=-{\vec {\nabla }}(\mu +M_{4}gz).}$

In this expression μ is the molar chemical potential, g the gravitational acceleration, and z the vertical coordinate. Thus we get

${\displaystyle M_{4}{\frac {\mathrm {d} {\vec {v}}_{s}}{\mathrm {d} t}}=-{\vec {\nabla }}(\mu +M_{4}gz).}$

(1)

Eq. (1) only holds if v_s is below a certain critical value, which usually is determined by the diameter of the flow channel.

In classical mechanics the force is often the gradient of a potential energy. Eq. (1) shows that, in the case of the superfluid component, the force contains a term due to the gradient of the chemical potential. This is the origin of the remarkable properties of He-II such as the fountain effect.

Fig. 6. Integration path for calculating μ at arbitrary p and T.

 

Fig. 7. Demonstration of the fountain pressure. The two vessels are connected by a superleak through which only the superfluid component can pass.

 

Fig. 8. Demonstration of the fountain effect. A capillary tube is “closed” at one end by a superleak and is placed into a bath of superfluid helium and then heated. The helium flows up through the tube and squirts like a fountain.

Fountain pressure

In order to rewrite Eq.(1) in more familiar form we use the general formula

${\displaystyle \mathrm {d} \mu =V_{m}\mathrm {d} p-S_{m}\mathrm {d} T.}$

(2)

Here S_m is the molar entropy and V_m the molar volume. With Eq.(2) μ(p,T) can be found by a line integration in the p-T plane. First we integrate from the origin (0,0) to (p,0), so at T =0. Next we integrate from (p,0) to (p,T), so with constant pressure (see figure 6). In the first integral dT=0 and in the second dp=0. With Eq.(2) we obtain

${\displaystyle \mu (p,T)=\mu (0,0)+\int _{0}^{p}V_{m}(p^{\prime },0)\mathrm {d} p^{\prime }-\int _{0}^{T}S_{m}(p,T^{\prime })\mathrm {d} T^{\prime }.}$

(3)

We are interested only in cases where p is small so that V_m is practically constant. So

${\displaystyle \int _{0}^{p}V_{m}(p^{\prime },0)\mathrm {d} p^{\prime }=V_{m0}p}$

(4)

where V_m0 is the molar volume of the liquid at T =0 and p =0. The other term in Eq.(3) is also written as a product of V_m0 and a quantity p_f which has the dimension of pressure

${\displaystyle \int _{0}^{T}S_{m}(p,T^{\prime })\mathrm {d} T^{\prime }=V_{m0}p_{f}.}$

(5)

The pressure p_f is called the fountain pressure. It can be calculated from the entropy of ⁴He which, in turn, can be calculated from the heat capacity. For T =T_λ the fountain pressure is equal to 0.692 bar. With a density of liquid helium of 125 kg/m³ and g = 9.8 m/s² this corresponds with a liquid-helium column of 56 meter height. So, in many experiments, the fountain pressure has a bigger effect on the motion of the superfluid helium than gravity.

With Eqs.(4) and (5), Eq.(3) obtains the form

${\displaystyle \mu (p,T)=\mu _{0}+V_{m0}(p-p_{f}).}$

(6)

Substitution of Eq.(6) in (1) gives

${\displaystyle \rho _{0}{\frac {\mathrm {d} {\vec {v}}_{s}}{\mathrm {d} t}}=-{\vec {\nabla }}(p+\rho _{0}gz-p_{f}).}$

(7)

with ρ₀ = M₄/V_m0 the density of liquid ⁴He at zero pressure and temperature.

Eq.(7) shows that the superfluid component is accelerated by gradients in the pressure and in the gravitational field, as usual, but also by a gradient in the fountain pressure.

So far Eq.(5) has only mathematical meaning, but in special experimental arrangements p_f can show up as a real pressure. Figure 7 shows two vessels both containing He-II. The left vessel is supposed to be at zero kelvins (T_l=0) and zero pressure (p_l = 0). The vessels are connected by a so-called superleak. This is a tube, filled with a very fine powder, so the flow of the normal component is blocked. However, the superfluid component can flow through this superleak without any problem (below a critical velocity of about 20 cm/s). In the steady state v_s=0 so Eq.(7) implies

${\displaystyle p_{l}+\rho _{0}gz_{l}-p_{fl}=p_{r}+\rho _{0}gz_{r}-p_{fr}}$

(8)

where the index l (r) applies to the left (right) side of the superleak. In this particular case p_l = 0, z_l = z_r, and p_fl = 0 (since T_l = 0). Consequently,

${\displaystyle 0=p_{r}-p_{fr}.}$

This means that the pressure in the right vessel is equal to the fountain pressure at T_r.

In an experiment, arranged as in figure 8, a fountain can be created. The fountain effect is used to drive the circulation of ³He in dilution refrigerators.

Fig. 9. Transport of heat by a counterflow of the normal and superfluid components of He-II

Heat transport

Figure 9 depicts a heat-conduction experiment between two temperatures T_H and T_L connected by a tube filled with He-II. When heat is applied to the hot end a pressure builds up at the hot end according to Eq.(7). This pressure drives the normal component from the hot end to the cold end according to

${\displaystyle \Delta p=-\eta _{n}Z{\dot {V}}_{n}.}$

(9)

Here η_n is the viscosity of the normal component, Z some geometrical factor, and ${\displaystyle {\dot {V}}_{n}}$ the volume flow. The normal flow is balanced by a flow of the superfluid component from the cold to the hot end. At the end sections a normal to superfluid conversion takes place and vice versa. So heat is transported, not by heat conduction, but by convection. This kind of heat transport is very effective, so the thermal conductivity of He-II is very much better than the best materials. The situation is comparable with heat pipes where heat is transported via gas–liquid conversion. The high thermal conductivity of He-II is applied for stabilizing superconducting magnets such as in the Large Hadron Collider at CERN.

Microscropic theory

Landau two-fluid approach

L. D. Landau's phenomenological and semi-microscopic theory of superfluidity of helium-4 earned him the Nobel Prize in physics, in 1962. Assuming that sound waves are the most important excitations in helium-4 at low temperatures, he showed that helium-4 flowing past a wall would not spontaneously create excitations if the flow velocity was less than the sound velocity. In this model, the sound velocity is the "critical velocity" above which superfluidity is destroyed. (Helium-4 actually has a lower flow velocity than the sound velocity, but this model is useful to illustrate the concept.) Landau also showed that the sound wave and other excitations could equilibrate with one another and flow separately from the rest of the helium-4, which is known as the "condensate".

From the momentum and flow velocity of the excitations he could then define a "normal fluid" density, which is zero at zero temperature and increases with temperature. At the so-called Lambda temperature, where the normal fluid density equals the total density, the helium-4 is no longer superfluid.

To explain the early specific heat data on superfluid helium-4, Landau posited the existence of a type of excitation he called a "roton", but as better data became available he considered that the "roton" was the same as a high momentum version of sound.

The Landau theory does not elaborate on the microscopic structure of the superfluid component of liquid helium. The first attempts to create a microscopic theory of the superfluid component itself were done by London and subsequently, Tisza. Other microscopical models have been proposed by different authors. Their main objective is to derive the form of the inter-particle potential between helium atoms in superfluid state from first principles of quantum mechanics. To date, a number of models of this kind have been proposed, including: models with vortex rings, hard-sphere models, and Gaussian cluster theories.

Vortex ring model

Landau thought that vorticity entered superfluid helium-4 by vortex sheets, but such sheets have since been shown to be unstable. Lars Onsager and, later independently, Feynman showed that vorticity enters by quantized vortex lines. They also developed the idea of quantum vortex rings. Arie Bijl in the 1940s, and Richard Feynman around 1955, developed microscopic theories for the roton, which was shortly observed with inelastic neutron experiments by Palevsky. Later on, Feynman admitted that his model gives only qualitative agreement with experiment.

Hard-sphere models

The models are based on the simplified form of the inter-particle potential between helium-4 atoms in the superfluid phase. Namely, the potential is assumed to be of the hard-sphere type. In these models the famous Landau (roton) spectrum of excitations is qualitatively reproduced.

Gaussian cluster approach

This is a two-scale approach which describes the superfluid component of liquid helium-4. It consists of two nested models linked via parametric space. The short-wavelength part describes the interior structure of the fluid element using a non-perturbative approach based on the Logarithmic Schrödinger equation; it suggests the Gaussian-like behaviour of the element's interior density and interparticle interaction potential. The long-wavelength part is the quantum many-body theory of such elements which deals with their dynamics and interactions. The approach provides a unified description of the phonon, maxon and roton excitations, and has noteworthy agreement with experiment: with one essential parameter to fit one reproduces at high accuracy the Landau roton spectrum, sound velocity and structure factor of superfluid helium-4. This model utilizes the general theory of quantum Bose liquids with logarithmic nonlinearities which is based on introducing a dissipative-type contribution to energy related to the quantum Everett–Hirschman entropy function.

Physics beyond the Standard Model

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Physics_beyond_the_Standard_Model 

 

Beyond the Standard Model
Simulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons

Physics beyond the Standard Model (BSM) refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the inability to explain the fundamental parameters of the standard model, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy. Another problem lies within the mathematical framework of the Standard Model itself: the Standard Model is inconsistent with that of general relativity, and one or both theories break down under certain conditions, such as spacetime singularities like the Big Bang and black hole event horizons.

Theories that lie beyond the Standard Model include various extensions of the standard model through supersymmetry, such as the Minimal Supersymmetric Standard Model (MSSM) and Next-to-Minimal Supersymmetric Standard Model (NMSSM), and entirely novel explanations, such as string theory, M-theory, and extra dimensions. As these theories tend to reproduce the entirety of current phenomena, the question of which theory is the right one, or at least the "best step" towards a Theory of Everything, can only be settled via experiments, and is one of the most active areas of research in both theoretical and experimental physics.

Problems with the Standard Model

Despite being the most successful theory of particle physics to date, the Standard Model is not perfect. A large share of the published output of theoretical physicists consists of proposals for various forms of "Beyond the Standard Model" new physics proposals that would modify the Standard Model in ways subtle enough to be consistent with existing data, yet address its imperfections materially enough to predict non-Standard Model outcomes of new experiments that can be proposed.

The Standard Model of elementary particles + hypothetical Graviton

Phenomena not explained

The Standard Model is inherently an incomplete theory. There are fundamental physical phenomena in nature that the Standard Model does not adequately explain:

• Gravity. The standard model does not explain gravity. The approach of simply adding a graviton to the Standard Model does not recreate what is observed experimentally without other modifications, as yet undiscovered, to the Standard Model. Moreover, the Standard Model is widely considered to be incompatible with the most successful theory of gravity to date, general relativity.
• Dark matter. Cosmological observations tell us the standard model explains about 5% of the energy present in the universe. About 26% should be dark matter, which would behave just like other matter, but which only interacts weakly (if at all) with the Standard Model fields. Yet, the Standard Model does not supply any fundamental particles that are good dark matter candidates.
• Dark energy. The remaining 69% of universe's energy should consist of the so-called dark energy, a constant energy density for the vacuum. Attempts to explain dark energy in terms of vacuum energy of the standard model lead to a mismatch of 120 orders of magnitude.
• Neutrino masses. According to the standard model, neutrinos are massless particles. However, neutrino oscillation experiments have shown that neutrinos do have mass. Mass terms for the neutrinos can be added to the standard model by hand, but these lead to new theoretical problems. For example, the mass terms need to be extraordinarily small and it is not clear if the neutrino masses would arise in the same way that the masses of other fundamental particles do in the Standard Model.
• Matter–antimatter asymmetry. The universe is made out of mostly matter. However, the standard model predicts that matter and antimatter should have been created in (almost) equal amounts if the initial conditions of the universe did not involve disproportionate matter relative to antimatter. Yet, there is no mechanism in the Standard Model to sufficiently explain this asymmetry.

Experimental results not explained

No experimental result is accepted as definitively contradicting the Standard Model at the 5 σ level, widely considered to be the threshold of a discovery in particle physics. Because every experiment contains some degree of statistical and systemic uncertainty, and the theoretical predictions themselves are also almost never calculated exactly and are subject to uncertainties in measurements of the fundamental constants of the Standard Model (some of which are tiny and others of which are substantial), it is to be expected that some of the hundreds of experimental tests of the Standard Model will deviate from it to some extent, even if there were no new physics to be discovered.

At any given moment there are several experimental results standing that significantly differ from a Standard Model-based prediction. In the past, many of these discrepancies have been found to be statistical flukes or experimental errors that vanish as more data has been collected, or when the same experiments were conducted more carefully. On the other hand, any physics beyond the Standard Model would necessarily first appear in experiments as a statistically significant difference between an experiment and the theoretical prediction. The task is to determine which is the case.

In each case, physicists seek to determine if a result is merely a statistical fluke or experimental error on the one hand, or a sign of new physics on the other. More statistically significant results cannot be mere statistical flukes but can still result from experimental error or inaccurate estimates of experimental precision. Frequently, experiments are tailored to be more sensitive to experimental results that would distinguish the Standard Model from theoretical alternatives.

Some of the most notable examples include the following:

• Anomalous magnetic dipole moment of muon – the experimentally measured value of muon's anomalous magnetic dipole moment (muon "g − 2") is significantly different from the Standard Model prediction.
• B meson decay etc. – results from a BaBar experiment may suggest a surplus over Standard Model predictions of a type of particle decay ( B  →  D^(*)  τ⁻  ν_τ ). In this, an electron and positron collide, resulting in a B meson and an antimatter B meson, which then decays into a D meson and a tau lepton as well as a tau antineutrino. While the level of certainty of the excess (3.4 σ in statistical jargon) is not enough to declare a break from the Standard Model, the results are a potential sign of something amiss and are likely to affect existing theories, including those attempting to deduce the properties of Higgs bosons. In 2015, LHCb reported observing a 2.1 σ excess in the same ratio of branching fractions. The Belle experiment also reported an excess. In 2017 a meta analysis of all available data reported a 5 σ deviation from SM.

Theoretical predictions not observed

Observation at particle colliders of all of the fundamental particles predicted by the Standard Model has been confirmed. The Higgs boson is predicted by the Standard Model's explanation of the Higgs mechanism, which describes how the weak SU(2) gauge symmetry is broken and how fundamental particles obtain mass; it was the last particle predicted by the Standard Model to be observed. On July 4, 2012, CERN scientists using the Large Hadron Collider announced the discovery of a particle consistent with the Higgs boson, with a mass of about 126 GeV/c². A Higgs boson was confirmed to exist on March 14, 2013, although efforts to confirm that it has all of the properties predicted by the Standard Model are ongoing.

A few hadrons (i.e. composite particles made of quarks) whose existence is predicted by the Standard Model, which can be produced only at very high energies in very low frequencies have not yet been definitively observed, and "glueballs" (i.e. composite particles made of gluons) have also not yet been definitively observed. Some very low frequency particle decays predicted by the Standard Model have also not yet been definitively observed because insufficient data is available to make a statistically significant observation.

Unexplained relations

• Koide formula - an unexplained empirical equation discovered by Yoshio Koide in 1981. It relates the masses of the three charged leptons: ${\displaystyle Q={\frac {m_{e}+m_{\mu }+m_{\tau }}{{\big (}{\sqrt {m_{e}}}+{\sqrt {m_{\mu }}}+{\sqrt {m_{\tau }}}{\big )}^{2}}}=0.666661(7)\approx {\frac {2}{3}}}$. Standard Model does not predict masses of leptons (they are free parameters of the theory). However, the value of Koide formula being equal to 2/3 within experimental errors of measured lepton masses suggests existence of theory which is able to predict lepton masses.

• CKM matrix, if interpreted as a rotation matrix in a 3-dimensional vector space, "rotates" vector composed of square roots of down-type quark masses ${\displaystyle ({\sqrt {m_{d}}},{\sqrt {m_{s}}},{\sqrt {m_{b}}}{\big )}}$ into vector of square roots of up-type quark masses ${\displaystyle ({\sqrt {m_{u}}},{\sqrt {m_{c}}},{\sqrt {m_{t}}}{\big )}}$, up to vector lengths. 

Theoretical problems

Some features of the standard model are added in an ad hoc way. These are not problems per se (i.e. the theory works fine with these ad hoc features), but they imply a lack of understanding. These ad hoc features have motivated theorists to look for more fundamental theories with fewer parameters. Some of the ad hoc features are:

• Hierarchy problem – the standard model introduces particle masses through a process known as spontaneous symmetry breaking caused by the Higgs field. Within the standard model, the mass of the Higgs gets some very large quantum corrections due to the presence of virtual particles (mostly virtual top quarks). These corrections are much larger than the actual mass of the Higgs. This means that the bare mass parameter of the Higgs in the standard model must be fine tuned in such a way that almost completely cancels the quantum corrections. This level of fine-tuning is deemed unnatural by many theorists.
• Number of parameters – the standard model depends on 19 numerical parameters. Their values are known from experiment, but the origin of the values is unknown. Some theorists have tried to find relations between different parameters, for example, between the masses of particles in different generations or calculating particle masses, such as in asymptotic safety scenarios.
• Quantum triviality – suggests that it may not be possible to create a consistent quantum field theory involving elementary scalar Higgs particles. This is sometimes called the Landau pole problem.
• Strong CP problem – theoretically it can be argued that the standard model should contain a term that breaks CP symmetry—relating matter to antimatter—in the strong interaction sector. Experimentally, however, no such violation has been found, implying that the coefficient of this term is very close to zero. This fine tuning is also considered unnatural.

Grand unified theories

The standard model has three gauge symmetries; the colour SU(3), the weak isospin SU(2), and the weak hypercharge U(1) symmetry, corresponding to the three fundamental forces. Due to renormalization the coupling constants of each of these symmetries vary with the energy at which they are measured. Around 10¹⁶ GeV these couplings become approximately equal. This has led to speculation that above this energy the three gauge symmetries of the standard model are unified in one single gauge symmetry with a simple gauge group, and just one coupling constant. Below this energy the symmetry is spontaneously broken to the standard model symmetries. Popular choices for the unifying group are the special unitary group in five dimensions SU(5) and the special orthogonal group in ten dimensions SO(10).

Theories that unify the standard model symmetries in this way are called Grand Unified Theories (or GUTs), and the energy scale at which the unified symmetry is broken is called the GUT scale. Generically, grand unified theories predict the creation of magnetic monopoles in the early universe, and instability of the proton. Neither of these have been observed, and this absence of observation puts limits on the possible GUTs.

Supersymmetry

Supersymmetry extends the Standard Model by adding another class of symmetries to the Lagrangian. These symmetries exchange fermionic particles with bosonic ones. Such a symmetry predicts the existence of supersymmetric particles, abbreviated as sparticles, which include the sleptons, squarks, neutralinos and charginos. Each particle in the Standard Model would have a superpartner whose spin differs by 1/2 from the ordinary particle. Due to the breaking of supersymmetry, the sparticles are much heavier than their ordinary counterparts; they are so heavy that existing particle colliders may not be powerful enough to produce them.

Neutrinos

In the standard model, neutrinos have exactly zero mass. This is a consequence of the standard model containing only left-handed neutrinos. With no suitable right-handed partner, it is impossible to add a renormalizable mass term to the standard model. Measurements however indicated that neutrinos spontaneously change flavour, which implies that neutrinos have a mass. These measurements only give the mass differences between the different flavours. The best constraint on the absolute mass of the neutrinos comes from precision measurements of tritium decay, providing an upper limit 2 eV, which makes them at least five orders of magnitude lighter than the other particles in the standard model. This necessitates an extension of the standard model, which not only needs to explain how neutrinos get their mass, but also why the mass is so small.

One approach to add masses to the neutrinos, the so-called seesaw mechanism, is to add right-handed neutrinos and have these couple to left-handed neutrinos with a Dirac mass term. The right-handed neutrinos have to be sterile, meaning that they do not participate in any of the standard model interactions. Because they have no charges, the right-handed neutrinos can act as their own anti-particles, and have a Majorana mass term. Like the other Dirac masses in the standard model, the neutrino Dirac mass is expected to be generated through the Higgs mechanism, and is therefore unpredictable. The standard model fermion masses differ by many orders of magnitude; the Dirac neutrino mass has at least the same uncertainty. On the other hand, the Majorana mass for the right-handed neutrinos does not arise from the Higgs mechanism, and is therefore expected to be tied to some energy scale of new physics beyond the standard model, for example the Planck scale. Therefore, any process involving right-handed neutrinos will be suppressed at low energies. The correction due to these suppressed processes effectively gives the left-handed neutrinos a mass that is inversely proportional to the right-handed Majorana mass, a mechanism known as the see-saw. The presence of heavy right-handed neutrinos thereby explains both the small mass of the left-handed neutrinos and the absence of the right-handed neutrinos in observations. However, due to the uncertainty in the Dirac neutrino masses, the right-handed neutrino masses can lie anywhere. For example, they could be as light as keV and be dark matter, they can have a mass in the LHC energy range and lead to observable lepton number violation, or they can be near the GUT scale, linking the right-handed neutrinos to the possibility of a grand unified theory.

The mass terms mix neutrinos of different generations. This mixing is parameterized by the PMNS matrix, which is the neutrino analogue of the CKM quark mixing matrix. Unlike the quark mixing, which is almost minimal, the mixing of the neutrinos appears to be almost maximal. This has led to various speculations of symmetries between the various generations that could explain the mixing patterns. The mixing matrix could also contain several complex phases that break CP invariance, although there has been no experimental probe of these. These phases could potentially create a surplus of leptons over anti-leptons in the early universe, a process known as leptogenesis. This asymmetry could then at a later stage be converted in an excess of baryons over anti-baryons, and explain the matter-antimatter asymmetry in the universe.

The light neutrinos are disfavored as an explanation for the observation of dark matter, due to considerations of large-scale structure formation in the early universe. Simulations of structure formation show that they are too hot—i.e. their kinetic energy is large compared to their mass—while formation of structures similar to the galaxies in our universe requires cold dark matter. The simulations show that neutrinos can at best explain a few percent of the missing dark matter. However, the heavy sterile right-handed neutrinos are a possible candidate for a dark matter WIMP.

Preon models

Several preon models have been proposed to address the unsolved problem concerning the fact that there are three generations of quarks and leptons. Preon models generally postulate some additional new particles which are further postulated to be able to combine to form the quarks and leptons of the standard model. One of the earliest preon models was the Rishon model.

To date, no preon model is widely accepted or fully verified.

Theories of everything

Theoretical physics continues to strive toward a theory of everything, a theory that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle.

In practical terms the immediate goal in this regard is to develop a theory which would unify the Standard Model with General Relativity in a theory of quantum gravity. Additional features, such as overcoming conceptual flaws in either theory or accurate prediction of particle masses, would be desired. The challenges in putting together such a theory are not just conceptual - they include the experimental aspects of the very high energies needed to probe exotic realms.

Several notable attempts in this direction are supersymmetry, loop quantum gravity, and string theory.

Supersymmetry

Main article: supersymmetry

Loop quantum gravity

Main article: loop quantum gravity

Theories of quantum gravity such as loop quantum gravity and others are thought by some to be promising candidates to the mathematical unification of quantum field theory and general relativity, requiring less drastic changes to existing theories. However recent work places stringent limits on the putative effects of quantum gravity on the speed of light, and disfavours some current models of quantum gravity.

String theory

Extensions, revisions, replacements, and reorganizations of the Standard Model exist in attempt to correct for these and other issues. String theory is one such reinvention, and many theoretical physicists think that such theories are the next theoretical step toward a true Theory of Everything.

Among the numerous variants of string theory, M-theory, whose mathematical existence was first proposed at a String Conference in 1995 by Edward Witten, is believed by many to be a proper "ToE" candidate, notably by physicists Brian Greene and Stephen Hawking. Though a full mathematical description is not yet known, solutions to the theory exist for specific cases. Recent works have also proposed alternate string models, some of which lack the various harder-to-test features of M-theory (e.g. the existence of Calabi–Yau manifolds, many extra dimensions, etc.) including works by well-published physicists such as Lisa Randall.

Strong interaction

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Strong_interaction

 

The nucleus of a helium atom. The two protons have the same charge, but still stay together due to the residual nuclear force

 

Standard Model of particle physics
Elementary particles of the Standard Model

In nuclear physics and particle physics, the strong interaction is the mechanism responsible for the strong nuclear force, and is one of the four known fundamental interactions, with the others being electromagnetism, the weak interaction, and gravitation. At the range of 10⁻¹⁵ m (1 femtometer), the strong force is approximately 137 times as strong as electromagnetism, a million times as strong as the weak interaction, and 10³⁸ times as strong as gravitation. The strong nuclear force holds most ordinary matter together because it confines quarks into hadron particles such as the proton and neutron. In addition, the strong force binds these neutrons and protons to create atomic nuclei. Most of the mass of a common proton or neutron is the result of the strong force field energy; the individual quarks provide only about 1% of the mass of a proton.

The strong interaction is observable at two ranges and mediated by two force carriers. On a larger scale (about 1 to 3 fm), it is the force (carried by mesons) that binds protons and neutrons (nucleons) together to form the nucleus of an atom. On the smaller scale (less than about 0.8 fm, the radius of a nucleon), it is the force (carried by gluons) that holds quarks together to form protons, neutrons, and other hadron particles. In the latter context, it is often known as the color force. The strong force inherently has such a high strength that hadrons bound by the strong force can produce new massive particles. Thus, if hadrons are struck by high-energy particles, they give rise to new hadrons instead of emitting freely moving radiation (gluons). This property of the strong force is called color confinement, and it prevents the free "emission" of the strong force: instead, in practice, jets of massive particles are produced.

In the context of atomic nuclei, the same strong interaction force (that binds quarks within a nucleon) also binds protons and neutrons together to form a nucleus. In this capacity it is called the nuclear force (or residual strong force). So the residuum from the strong interaction within protons and neutrons also binds nuclei together. As such, the residual strong interaction obeys a distance-dependent behavior between nucleons that is quite different from that when it is acting to bind quarks within nucleons. Additionally, distinctions exist in the binding energies of the nuclear force of nuclear fusion vs nuclear fission. Nuclear fusion accounts for most energy production in the Sun and other stars. Nuclear fission allows for decay of radioactive elements and isotopes, although it is often mediated by the weak interaction. Artificially, the energy associated with the nuclear force is partially released in nuclear power and nuclear weapons, both in uranium or plutonium-based fission weapons and in fusion weapons like the hydrogen bomb.

The strong interaction is mediated by the exchange of massless particles called gluons that act between quarks, antiquarks, and other gluons. Gluons are thought to interact with quarks and other gluons by way of a type of charge called color charge. Color charge is analogous to electromagnetic charge, but it comes in three types (±red, ±green, ±blue) rather than one, which results in a different type of force, with different rules of behavior. These rules are detailed in the theory of quantum chromodynamics (QCD), which is the theory of quark–gluon interactions.

History

Before the 1970s, physicists were uncertain as to how the atomic nucleus was bound together. It was known that the nucleus was composed of protons and neutrons and that protons possessed positive electric charge, while neutrons were electrically neutral. By the understanding of physics at that time, positive charges would repel one another and the positively charged protons should cause the nucleus to fly apart. However, this was never observed. New physics was needed to explain this phenomenon.

A stronger attractive force was postulated to explain how the atomic nucleus was bound despite the protons' mutual electromagnetic repulsion. This hypothesized force was called the strong force, which was believed to be a fundamental force that acted on the protons and neutrons that make up the nucleus.

It was later discovered that protons and neutrons were not fundamental particles, but were made up of constituent particles called quarks. The strong attraction between nucleons was the side-effect of a more fundamental force that bound the quarks together into protons and neutrons. The theory of quantum chromodynamics explains that quarks carry what is called a color charge, although it has no relation to visible color. Quarks with unlike color charge attract one another as a result of the strong interaction, and the particle that mediates this was called the gluon.

Behavior of the strong force

The fundamental couplings of the strong interaction, from left to right: gluon radiation, gluon splitting and gluon self-coupling.

The word strong is used since the strong interaction is the "strongest" of the four fundamental forces. At a distance of 1 femtometer (1 fm = 10⁻¹⁵ meters) or less, its strength is around 137 times that of the electromagnetic force, some 10⁶ times as great as that of the weak force, and about 10³⁸ times that of gravitation.

The strong force is described by quantum chromodynamics (QCD), a part of the standard model of particle physics. Mathematically, QCD is a non-Abelian gauge theory based on a local (gauge) symmetry group called SU(3).

The force carrier particle of the strong interaction is the gluon, a massless boson. Unlike the photon in electromagnetism, which is neutral, the gluon carries a color charge. Quarks and gluons are the only fundamental particles that carry non-vanishing color charge, and hence they participate in strong interactions only with each other. The strong force is the expression of the gluon interaction with other quark and gluon particles.

All quarks and gluons in QCD interact with each other through the strong force. The strength of interaction is parameterized by the strong coupling constant. This strength is modified by the gauge color charge of the particle, a group theoretical property.

The strong force acts between quarks. Unlike all other forces (electromagnetic, weak, and gravitational), the strong force does not diminish in strength with increasing distance between pairs of quarks. After a limiting distance (about the size of a hadron) has been reached, it remains at a strength of about 10,000 newtons (N), no matter how much farther the distance between the quarks. As the separation between the quarks grows, the energy added to the pair creates new pairs of matching quarks between the original two; hence it is impossible to create separate quarks. The explanation is that the amount of work done against a force of 10,000 newtons is enough to create particle–antiparticle pairs within a very short distance of that interaction. The very energy added to the system required to pull two quarks apart would create a pair of new quarks that will pair up with the original ones. In QCD, this phenomenon is called color confinement; as a result only hadrons, not individual free quarks, can be observed. The failure of all experiments that have searched for free quarks is considered to be evidence of this phenomenon.

The elementary quark and gluon particles involved in a high energy collision are not directly observable. The interaction produces jets of newly created hadrons that are observable. Those hadrons are created, as a manifestation of mass–energy equivalence, when sufficient energy is deposited into a quark–quark bond, as when a quark in one proton is struck by a very fast quark of another impacting proton during a particle accelerator experiment. However, quark–gluon plasmas have been observed.

Residual strong force

Contrary to the description above of distance independence, in the post-Big Bang universe it is not the case that every quark in the universe attracts every other quark. Color confinement implies that the strong force acts without distance-diminishment only between pairs of quarks, and that in compact collections of bound quarks (hadrons), the net color-charge of the quarks essentially cancels out, resulting in a limit of the action of the color-forces: From distances approaching or greater than the radius of a proton, compact collections of color-interacting quarks (hadrons) collectively appear to have effectively no color-charge, or "colorless", and the strong force is therefore nearly absent between those hadrons. However, the cancellation is not quite perfect, and a residual force (described below) remains. This residual force does diminish rapidly with distance, and is thus very short-range (effectively a few femtometers). It manifests as a force between the "colorless" hadrons, and is sometimes known as the strong nuclear force or simply nuclear force.

An animation of the nuclear force (or residual strong force) interaction between a proton and a neutron. The small colored double circles are gluons, which can be seen binding the proton and neutron together. These gluons also hold the quark/antiquark combination called the pion together, and thus help transmit a residual part of the strong force even between colorless hadrons. Anticolors are shown as per this diagram.

The nuclear force acts between hadrons, known as mesons and baryons. This "residual strong force", acting indirectly, transmits gluons that form part of the virtual π and ρ mesons, which, in turn, transmit the force between nucleons that holds the nucleus (beyond protium) together.

The residual strong force is thus a minor residuum of the strong force that binds quarks together into protons and neutrons. This same force is much weaker between neutrons and protons, because it is mostly neutralized within them, in the same way that electromagnetic forces between neutral atoms (van der Waals forces) are much weaker than the electromagnetic forces that hold electrons in association with the nucleus, forming the atoms.

Unlike the strong force itself, the residual strong force, does diminish in strength, and it in fact diminishes rapidly with distance. The decrease is approximately as a negative exponential power of distance, though there is no simple expression known for this; see Yukawa potential. The rapid decrease with distance of the attractive residual force and the less-rapid decrease of the repulsive electromagnetic force acting between protons within a nucleus, causes the instability of larger atomic nuclei, such as all those with atomic numbers larger than 82 (the element lead).

Although the nuclear force is weaker than strong interaction itself, it is still highly energetic: transitions produce gamma rays. The mass of a nucleus is significantly different from the summed masses of the individual nucleons. This mass defect is due to the potential energy associated with the nuclear force. Differences between mass defects power nuclear fusion and nuclear fission.

Unification

The so-called Grand Unified Theories (GUT) aim to describe the strong interaction and the electroweak interaction as aspects of a single force, similarly to how the electromagnetic and weak interactions were unified by the Glashow–Weinberg–Salam model into the electroweak interaction. The strong interaction has a property called asymptotic freedom, wherein the strength of the strong force diminishes at higher energies (or temperatures). The theorized energy where its strength becomes equal to the electroweak interaction is the grand unification energy. However, no Grand Unified Theory has yet been successfully formulated to describe this process, and Grand Unification remains an unsolved problem in physics.

If GUT is correct, after the Big Bang and during the electroweak epoch of the universe, the electroweak force separated from the strong force. Accordingly, a grand unification epoch is hypothesized to have existed prior to this.