From Wikipedia, the free encyclopedia
Machine learning (ML) is the study of computer algorithms that improve automatically through experience and by the use of data. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as "training data", in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.
A subset of machine learning is closely related to computational statistics, which focuses on making predictions using computers; but not all machine learning is statistical learning. The study of mathematical optimization delivers methods, theory and application domains to the field of machine learning. Data mining is a related field of study, focusing on exploratory data analysis through unsupervised learning. In its application across business problems, machine learning is also referred to as predictive analytics.
Overview
Machine
learning involves computers discovering how they can perform tasks
without being explicitly programmed to do so. It involves computers
learning from data provided so that they carry out certain tasks. For
simple tasks assigned to computers, it is possible to program algorithms
telling the machine how to execute all steps required to solve the
problem at hand; on the computer's part, no learning is needed. For more
advanced tasks, it can be challenging for a human to manually create
the needed algorithms. In practice, it can turn out to be more effective
to help the machine develop its own algorithm, rather than having human
programmers specify every needed step.
The discipline of machine learning employs various approaches to
teach computers to accomplish tasks where no fully satisfactory
algorithm is available. In cases where vast numbers of potential answers
exist, one approach is to label some of the correct answers as valid.
This can then be used as training data for the computer to improve the
algorithm(s) it uses to determine correct answers. For example, to train
a system for the task of digital character recognition, the MNIST dataset of handwritten digits has often been used.
History and relationships to other fields
The term machine learning was coined in 1959 by Arthur Samuel, an American IBMer and pioneer in the field of computer gaming and artificial intelligence.
A representative book of the machine learning research during the 1960s
was the Nilsson's book on Learning Machines, dealing mostly with
machine learning for pattern classification. Interest related to pattern recognition continued into the 1970s, as described by Duda and Hart in 1973. In 1981 a report was given on using teaching strategies so that a neural network learns to recognize 40 characters (26 letters, 10 digits, and 4 special symbols) from a computer terminal.
Tom M. Mitchell
provided a widely quoted, more formal definition of the algorithms
studied in the machine learning field: "A computer program is said to
learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E." This definition of the tasks in which machine learning is concerned offers a fundamentally operational definition rather than defining the field in cognitive terms. This follows Alan Turing's proposal in his paper "Computing Machinery and Intelligence",
in which the question "Can machines think?" is replaced with the
question "Can machines do what we (as thinking entities) can do?".
Modern day machine learning has two objectives, one is to
classify data based on models which have been developed, the other
purpose is to make predictions for future outcomes based on these
models. A hypothetical algorithm specific to classifying data may use
computer vision of moles coupled with supervised learning in order to
train it to classify the cancerous moles. Where as, a machine learning
algorithm for stock trading may inform the trader of future potential
predictions.
Artificial intelligence
Machine learning as subfield of AI
Part of machine learning as subfield of AI or part of AI as subfield of machine learning
As a scientific endeavor, machine learning grew out of the quest for artificial intelligence. In the early days of AI as an academic discipline,
some researchers were interested in having machines learn from data.
They attempted to approach the problem with various symbolic methods, as
well as what was then termed "neural networks"; these were mostly perceptrons and other models that were later found to be reinventions of the generalized linear models of statistics. Probabilistic reasoning was also employed, especially in automated medical diagnosis.
However, an increasing emphasis on the logical, knowledge-based approach
caused a rift between AI and machine learning. Probabilistic systems
were plagued by theoretical and practical problems of data acquisition
and representation. By 1980, expert systems had come to dominate AI, and statistics was out of favor. Work on symbolic/knowledge-based learning did continue within AI, leading to inductive logic programming, but the more statistical line of research was now outside the field of AI proper, in pattern recognition and information retrieval. Neural networks research had been abandoned by AI and computer science around the same time. This line, too, was continued outside the AI/CS field, as "connectionism", by researchers from other disciplines including Hopfield, Rumelhart and Hinton. Their main success came in the mid-1980s with the reinvention of backpropagation.
Machine learning (ML), reorganized as a separate field, started
to flourish in the 1990s. The field changed its goal from achieving
artificial intelligence to tackling solvable problems of a practical
nature. It shifted focus away from the symbolic approaches it had inherited from AI, and toward methods and models borrowed from statistics and probability theory.
As of 2020, many sources continue to assert that machine learning remains a subfield of AI.
The main disagreement is whether all of ML is part of AI, as this would
mean that anyone using ML could claim they are using AI. Others have
the view that not all of ML is part of AI where only an 'intelligent' subset of ML is part of AI.
The question to what is the difference between ML and AI is answered by Judea Pearl in The Book of Why.
Accordingly ML learns and predicts based on passive observations,
whereas AI implies an agent interacting with the environment to learn
and take actions that maximize its chance of successfully achieving its
goals.
Data mining
Machine learning and data mining often employ the same methods and overlap significantly, but while machine learning focuses on prediction, based on known properties learned from the training data, data mining focuses on the discovery of (previously) unknown properties in the data (this is the analysis step of knowledge discovery
in databases). Data mining uses many machine learning methods, but with
different goals; on the other hand, machine learning also employs data
mining methods as "unsupervised learning" or as a preprocessing step to
improve learner accuracy. Much of the confusion between these two
research communities (which do often have separate conferences and
separate journals, ECML PKDD
being a major exception) comes from the basic assumptions they work
with: in machine learning, performance is usually evaluated with respect
to the ability to reproduce known knowledge, while in knowledge discovery and data mining (KDD) the key task is the discovery of previously unknown
knowledge. Evaluated with respect to known knowledge, an uninformed
(unsupervised) method will easily be outperformed by other supervised
methods, while in a typical KDD task, supervised methods cannot be used
due to the unavailability of training data.
Optimization
Machine learning also has intimate ties to optimization: many learning problems are formulated as minimization of some loss function
on a training set of examples. Loss functions express the discrepancy
between the predictions of the model being trained and the actual
problem instances (for example, in classification, one wants to assign a
label to instances, and models are trained to correctly predict the
pre-assigned labels of a set of examples).
Generalization
The
difference between optimization and machine learning arises from the
goal of generalization: while optimization algorithms can minimize the
loss on a training set, machine learning is concerned with minimizing
the loss on unseen samples. Characterizing the generalization of various
learning algorithms is an active topic of current research, especially
for deep learning algorithms.
Statistics
Machine learning and statistics are closely related fields in terms of methods, but distinct in their principal goal: statistics draws population inferences from a sample, while machine learning finds generalizable predictive patterns. According to Michael I. Jordan, the ideas of machine learning, from methodological principles to theoretical tools, have had a long pre-history in statistics. He also suggested the term data science as a placeholder to call the overall field.
Leo Breiman distinguished two statistical modeling paradigms: data model and algorithmic model, wherein "algorithmic model" means more or less the machine learning algorithms like Random forest.
Some statisticians have adopted methods from machine learning, leading to a combined field that they call statistical learning.
Theory
A core objective of a learner is to generalize from its experience.
Generalization in this context is the ability of a learning machine to
perform accurately on new, unseen examples/tasks after having
experienced a learning data set. The training examples come from some
generally unknown probability distribution (considered representative of
the space of occurrences) and the learner has to build a general model
about this space that enables it to produce sufficiently accurate
predictions in new cases.
The computational analysis of machine learning algorithms and their performance is a branch of theoretical computer science known as computational learning theory.
Because training sets are finite and the future is uncertain, learning
theory usually does not yield guarantees of the performance of
algorithms. Instead, probabilistic bounds on the performance are quite
common. The bias–variance decomposition is one way to quantify generalization error.
For the best performance in the context of generalization, the
complexity of the hypothesis should match the complexity of the function
underlying the data. If the hypothesis is less complex than the
function, then the model has under fitted the data. If the complexity of
the model is increased in response, then the training error decreases.
But if the hypothesis is too complex, then the model is subject to overfitting and generalization will be poorer.
In addition to performance bounds, learning theorists study the
time complexity and feasibility of learning. In computational learning
theory, a computation is considered feasible if it can be done in polynomial time. There are two kinds of time complexity
results. Positive results show that a certain class of functions can be
learned in polynomial time. Negative results show that certain classes
cannot be learned in polynomial time.
Approaches
Machine learning approaches are traditionally divided into three broad
categories, depending on the nature of the "signal" or "feedback"
available to the learning system:
- Supervised learning:
The computer is presented with example inputs and their desired
outputs, given by a "teacher", and the goal is to learn a general rule
that maps inputs to outputs.
- Unsupervised learning:
No labels are given to the learning algorithm, leaving it on its own to
find structure in its input. Unsupervised learning can be a goal in
itself (discovering hidden patterns in data) or a means towards an end (feature learning).
- Reinforcement learning: A computer program interacts with a dynamic environment in which it must perform a certain goal (such as driving a vehicle
or playing a game against an opponent). As it navigates its problem
space, the program is provided feedback that's analogous to rewards,
which it tries to maximize.
Supervised learning
A
support-vector machine is a supervised learning model that divides the data into regions separated by a
linear boundary. Here, the linear boundary divides the black circles from the white.
Supervised learning algorithms build a mathematical model of a set of
data that contains both the inputs and the desired outputs. The data is known as training data,
and consists of a set of training examples. Each training example has
one or more inputs and the desired output, also known as a supervisory
signal. In the mathematical model, each training example is represented
by an array or vector, sometimes called a feature vector, and the training data is represented by a matrix. Through iterative optimization of an objective function, supervised learning algorithms learn a function that can be used to predict the output associated with new inputs.
An optimal function will allow the algorithm to correctly determine the
output for inputs that were not a part of the training data. An
algorithm that improves the accuracy of its outputs or predictions over
time is said to have learned to perform that task.
Types of supervised learning algorithms include active learning, classification and regression.
Classification algorithms are used when the outputs are restricted to a
limited set of values, and regression algorithms are used when the
outputs may have any numerical value within a range. As an example, for a
classification algorithm that filters emails, the input would be an
incoming email, and the output would be the name of the folder in which
to file the email.
Similarity learning
is an area of supervised machine learning closely related to regression
and classification, but the goal is to learn from examples using a
similarity function that measures how similar or related two objects
are. It has applications in ranking, recommendation systems, visual identity tracking, face verification, and speaker verification.
Unsupervised learning
Unsupervised learning algorithms take a set of data that contains
only inputs, and find structure in the data, like grouping or clustering
of data points. The algorithms, therefore, learn from test data that
has not been labeled, classified or categorized. Instead of responding
to feedback, unsupervised learning algorithms identify commonalities in
the data and react based on the presence or absence of such
commonalities in each new piece of data. A central application of
unsupervised learning is in the field of density estimation in statistics, such as finding the probability density function. Though unsupervised learning encompasses other domains involving summarizing and explaining data features.
Cluster analysis is the assignment of a set of observations into subsets (called clusters)
so that observations within the same cluster are similar according to
one or more predesignated criteria, while observations drawn from
different clusters are dissimilar. Different clustering techniques make
different assumptions on the structure of the data, often defined by
some similarity metric and evaluated, for example, by internal compactness, or the similarity between members of the same cluster, and separation, the difference between clusters. Other methods are based on estimated density and graph connectivity.
Semi-supervised learning
Semi-supervised learning falls between unsupervised learning (without any labeled training data) and supervised learning
(with completely labeled training data). Some of the training examples
are missing training labels, yet many machine-learning researchers have
found that unlabeled data, when used in conjunction with a small amount
of labeled data, can produce a considerable improvement in learning
accuracy.
In weakly supervised learning,
the training labels are noisy, limited, or imprecise; however, these
labels are often cheaper to obtain, resulting in larger effective
training sets.
Reinforcement learning
Reinforcement learning is an area of machine learning concerned with how software agents ought to take actions
in an environment so as to maximize some notion of cumulative reward.
Due to its generality, the field is studied in many other disciplines,
such as game theory, control theory, operations research, information theory, simulation-based optimization, multi-agent systems, swarm intelligence, statistics and genetic algorithms. In machine learning, the environment is typically represented as a Markov decision process (MDP). Many reinforcement learning algorithms use dynamic programming techniques.
Reinforcement learning algorithms do not assume knowledge of an exact
mathematical model of the MDP, and are used when exact models are
infeasible. Reinforcement learning algorithms are used in autonomous
vehicles or in learning to play a game against a human opponent.
Dimensionality Reduction
The
Dimensionality reduction is a process of reducing the number of random
variables under the consideration by obtaining a set of principal
variables.
In other words, it is a process of reducing the dimension of your
feature set also called no of features. Most of the dimensionality
reduction techniques can be considered as either feature elimination or
extraction.
One of the popular method of dimensionality reduction is called as
principal component analysis.
- Principal Component Analysis (PCA)
The PCA involves changing higher dimensional data (eg. 3D) to a
smaller space (eg. 2D). This results in a smaller dimension of data, (2D
instead of 3D) while keeping all original variables in the model
without changing the data.
Other types
Other
approaches have been developed which don't fit neatly into this
three-fold categorisation, and sometimes more than one is used by the
same machine learning system. For example topic modeling, meta learning.
As of 2020, deep learning has become the dominant approach for much ongoing work in the field of machine learning.
Self learning
Self-learning as a machine learning paradigm was introduced in 1982 along with a neural network capable of self-learning named crossbar adaptive array (CAA).
It is a learning with no external rewards and no external teacher
advice. The CAA self-learning algorithm computes, in a crossbar fashion,
both decisions about actions and emotions (feelings) about consequence
situations. The system is driven by the interaction between cognition
and emotion.
The self-learning algorithm updates a memory matrix W =||w(a,s)|| such
that in each iteration executes the following machine learning routine:
In situation s perform an action a;
Receive consequence situation s’;
Compute emotion of being in consequence situation v(s’);
Update crossbar memory w’(a,s) = w(a,s) + v(s’).
It is a system with only one input, situation s, and only one output,
action (or behavior) a. There is neither a separate reinforcement input
nor an advice input from the environment. The backpropagated value
(secondary reinforcement) is the emotion toward the consequence
situation. The CAA exists in two environments, one is the behavioral
environment where it behaves, and the other is the genetic environment,
wherefrom it initially and only once receives initial emotions about
situations to be encountered in the behavioral environment. After
receiving the genome (species) vector from the genetic environment, the
CAA learns a goal-seeking behavior, in an environment that contains both
desirable and undesirable situations.
Feature learning
Several learning algorithms aim at discovering better representations of the inputs provided during training. Classic examples include principal components analysis
and cluster analysis. Feature learning algorithms, also called
representation learning algorithms, often attempt to preserve the
information in their input but also transform it in a way that makes it
useful, often as a pre-processing step before performing classification
or predictions. This technique allows reconstruction of the inputs
coming from the unknown data-generating distribution, while not being
necessarily faithful to configurations that are implausible under that
distribution. This replaces manual feature engineering, and allows a machine to both learn the features and use them to perform a specific task.
Feature learning can be either supervised or unsupervised. In
supervised feature learning, features are learned using labeled input
data. Examples include artificial neural networks, multilayer perceptrons, and supervised dictionary learning. In unsupervised feature learning, features are learned with unlabeled input data. Examples include dictionary learning, independent component analysis, autoencoders, matrix factorization and various forms of clustering.
Manifold learning algorithms attempt to do so under the constraint that the learned representation is low-dimensional. Sparse coding
algorithms attempt to do so under the constraint that the learned
representation is sparse, meaning that the mathematical model has many
zeros. Multilinear subspace learning algorithms aim to learn low-dimensional representations directly from tensor representations for multidimensional data, without reshaping them into higher-dimensional vectors. Deep learning
algorithms discover multiple levels of representation, or a hierarchy
of features, with higher-level, more abstract features defined in terms
of (or generating) lower-level features. It has been argued that an
intelligent machine is one that learns a representation that
disentangles the underlying factors of variation that explain the
observed data.
Feature learning is motivated by the fact that machine learning
tasks such as classification often require input that is mathematically
and computationally convenient to process. However, real-world data such
as images, video, and sensory data has not yielded to attempts to
algorithmically define specific features. An alternative is to discover
such features or representations through examination, without relying on
explicit algorithms.
Sparse dictionary learning
Sparse dictionary learning is a feature learning method where a training example is represented as a linear combination of basis functions, and is assumed to be a sparse matrix. The method is strongly NP-hard and difficult to solve approximately. A popular heuristic method for sparse dictionary learning is the K-SVD
algorithm. Sparse dictionary learning has been applied in several
contexts. In classification, the problem is to determine the class to
which a previously unseen training example belongs. For a dictionary
where each class has already been built, a new training example is
associated with the class that is best sparsely represented by the
corresponding dictionary. Sparse dictionary learning has also been
applied in image de-noising. The key idea is that a clean image patch can be sparsely represented by an image dictionary, but the noise cannot.
Anomaly detection
In data mining,
anomaly detection, also known as outlier detection, is the
identification of rare items, events or observations which raise
suspicions by differing significantly from the majority of the data. Typically, the anomalous items represent an issue such as bank fraud, a structural defect, medical problems or errors in a text. Anomalies are referred to as outliers, novelties, noise, deviations and exceptions.
In particular, in the context of abuse and network intrusion
detection, the interesting objects are often not rare objects, but
unexpected bursts of inactivity. This pattern does not adhere to the
common statistical definition of an outlier as a rare object, and many
outlier detection methods (in particular, unsupervised algorithms) will
fail on such data unless it has been aggregated appropriately. Instead, a
cluster analysis algorithm may be able to detect the micro-clusters
formed by these patterns.
Three broad categories of anomaly detection techniques exist.
Unsupervised anomaly detection techniques detect anomalies in an
unlabeled test data set under the assumption that the majority of the
instances in the data set are normal, by looking for instances that seem
to fit least to the remainder of the data set. Supervised anomaly
detection techniques require a data set that has been labeled as
"normal" and "abnormal" and involves training a classifier (the key
difference to many other statistical classification problems is the
inherently unbalanced nature of outlier detection). Semi-supervised
anomaly detection techniques construct a model representing normal
behavior from a given normal training data set and then test the
likelihood of a test instance to be generated by the model.
Robot learning
In developmental robotics, robot learning
algorithms generate their own sequences of learning experiences, also
known as a curriculum, to cumulatively acquire new skills through
self-guided exploration and social interaction with humans. These robots
use guidance mechanisms such as active learning, maturation, motor synergies and imitation.
Association rules
Association rule learning is a rule-based machine learning
method for discovering relationships between variables in large
databases. It is intended to identify strong rules discovered in
databases using some measure of "interestingness".
Rule-based machine learning is a general term for any machine
learning method that identifies, learns, or evolves "rules" to store,
manipulate or apply knowledge. The defining characteristic of a
rule-based machine learning algorithm is the identification and
utilization of a set of relational rules that collectively represent the
knowledge captured by the system. This is in contrast to other machine
learning algorithms that commonly identify a singular model that can be
universally applied to any instance in order to make a prediction. Rule-based machine learning approaches include learning classifier systems, association rule learning, and artificial immune systems.
Based on the concept of strong rules, Rakesh Agrawal, Tomasz Imieliński
and Arun Swami introduced association rules for discovering
regularities between products in large-scale transaction data recorded
by point-of-sale (POS) systems in supermarkets. For example, the rule  found in the sales data of a supermarket would indicate that if a
customer buys onions and potatoes together, they are likely to also buy
hamburger meat. Such information can be used as the basis for decisions
about marketing activities such as promotional pricing or product placements. In addition to market basket analysis, association rules are employed today in application areas including Web usage mining, intrusion detection, continuous production, and bioinformatics. In contrast with sequence mining, association rule learning typically does not consider the order of items either within a transaction or across transactions.
found in the sales data of a supermarket would indicate that if a
customer buys onions and potatoes together, they are likely to also buy
hamburger meat. Such information can be used as the basis for decisions
about marketing activities such as promotional pricing or product placements. In addition to market basket analysis, association rules are employed today in application areas including Web usage mining, intrusion detection, continuous production, and bioinformatics. In contrast with sequence mining, association rule learning typically does not consider the order of items either within a transaction or across transactions.
Learning classifier systems (LCS) are a family of rule-based
machine learning algorithms that combine a discovery component,
typically a genetic algorithm, with a learning component, performing either supervised learning, reinforcement learning, or unsupervised learning. They seek to identify a set of context-dependent rules that collectively store and apply knowledge in a piecewise manner in order to make predictions.
Inductive logic programming (ILP) is an approach to rule-learning using logic programming
as a uniform representation for input examples, background knowledge,
and hypotheses. Given an encoding of the known background knowledge and a
set of examples represented as a logical database of facts, an ILP
system will derive a hypothesized logic program that entails all positive and no negative examples. Inductive programming
is a related field that considers any kind of programming language for
representing hypotheses (and not only logic programming), such as functional programs.
Inductive logic programming is particularly useful in bioinformatics and natural language processing. Gordon Plotkin and Ehud Shapiro laid the initial theoretical foundation for inductive machine learning in a logical setting.
Shapiro built their first implementation (Model Inference System) in
1981: a Prolog program that inductively inferred logic programs from
positive and negative examples. The term inductive here refers to philosophical induction, suggesting a theory to explain observed facts, rather than mathematical induction, proving a property for all members of a well-ordered set.
Models
Performing machine learning involves creating a model,
which is trained on some training data and then can process additional
data to make predictions. Various types of models have been used and
researched for machine learning systems.
Artificial neural networks
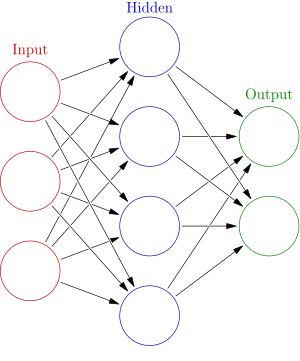
An artificial neural network is an interconnected group of nodes, akin to the vast network of
neurons in a
brain. Here, each circular node represents an
artificial neuron and an arrow represents a connection from the output of one artificial neuron to the input of another.
Artificial neural networks (ANNs), or connectionist systems, are computing systems vaguely inspired by the biological neural networks that constitute animal brains.
Such systems "learn" to perform tasks by considering examples,
generally without being programmed with any task-specific rules.
An ANN is a model based on a collection of connected units or nodes called "artificial neurons", which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain,
can transmit information, a "signal", from one artificial neuron to
another. An artificial neuron that receives a signal can process it and
then signal additional artificial neurons connected to it. In common ANN
implementations, the signal at a connection between artificial neurons
is a real number,
and the output of each artificial neuron is computed by some non-linear
function of the sum of its inputs. The connections between artificial
neurons are called "edges". Artificial neurons and edges typically have a
weight
that adjusts as learning proceeds. The weight increases or decreases
the strength of the signal at a connection. Artificial neurons may have a
threshold such that the signal is only sent if the aggregate signal
crosses that threshold. Typically, artificial neurons are aggregated
into layers. Different layers may perform different kinds of
transformations on their inputs. Signals travel from the first layer
(the input layer) to the last layer (the output layer), possibly after
traversing the layers multiple times.
The original goal of the ANN approach was to solve problems in the same way that a human brain would. However, over time, attention moved to performing specific tasks, leading to deviations from biology. Artificial neural networks have been used on a variety of tasks, including computer vision, speech recognition, machine translation, social network filtering, playing board and video games and medical diagnosis.
Deep learning
consists of multiple hidden layers in an artificial neural network.
This approach tries to model the way the human brain processes light and
sound into vision and hearing. Some successful applications of deep
learning are computer vision and speech recognition.
Decision trees
Decision tree learning uses a decision tree as a predictive model
to go from observations about an item (represented in the branches) to
conclusions about the item's target value (represented in the leaves).
It is one of the predictive modeling approaches used in statistics, data
mining, and machine learning. Tree models where the target variable can
take a discrete set of values are called classification trees; in these
tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels. Decision trees where the target variable can take continuous values (typically real numbers)
are called regression trees. In decision analysis, a decision tree can
be used to visually and explicitly represent decisions and decision making. In data mining, a decision tree describes data, but the resulting classification tree can be an input for decision making.
Support-vector machines
Support-vector machines (SVMs), also known as support-vector networks, are a set of related supervised learning
methods used for classification and regression. Given a set of training
examples, each marked as belonging to one of two categories, an SVM
training algorithm builds a model that predicts whether a new example
falls into one category or the other. An SVM training algorithm is a non-probabilistic, binary, linear classifier, although methods such as Platt scaling
exist to use SVM in a probabilistic classification setting. In addition
to performing linear classification, SVMs can efficiently perform a
non-linear classification using what is called the kernel trick, implicitly mapping their inputs into high-dimensional feature spaces.
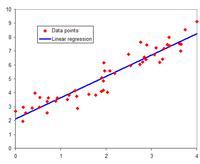
Illustration of linear regression on a data set.
Regression analysis
Regression analysis encompasses a large variety of statistical
methods to estimate the relationship between input variables and their
associated features. Its most common form is linear regression, where a single line is drawn to best fit the given data according to a mathematical criterion such as ordinary least squares. The latter is often extended by regularization (mathematics) methods to mitigate overfitting and bias, as in ridge regression. When dealing with non-linear problems, go-to models include polynomial regression (for example, used for trendline fitting in Microsoft Excel), logistic regression (often used in statistical classification) or even kernel regression, which introduces non-linearity by taking advantage of the kernel trick to implicitly map input variables to higher-dimensional space.
Bayesian networks
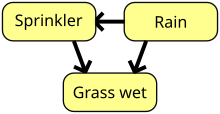
A
simple Bayesian network. Rain influences whether the sprinkler is
activated, and both rain and the sprinkler influence whether the grass
is wet.
A Bayesian network, belief network, or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional independence with a directed acyclic graph
(DAG). For example, a Bayesian network could represent the
probabilistic relationships between diseases and symptoms. Given
symptoms, the network can be used to compute the probabilities of the
presence of various diseases. Efficient algorithms exist that perform inference and learning. Bayesian networks that model sequences of variables, like speech signals or protein sequences, are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.
Genetic algorithms
A genetic algorithm (GA) is a search algorithm and heuristic technique that mimics the process of natural selection, using methods such as mutation and crossover to generate new genotypes
in the hope of finding good solutions to a given problem. In machine
learning, genetic algorithms were used in the 1980s and 1990s. Conversely, machine learning techniques have been used to improve the performance of genetic and evolutionary algorithms.
Training models
Usually,
machine learning models require a lot of data in order for them to
perform well. Usually, when training a machine learning model, one needs
to collect a large, representative sample of data from a training set.
Data from the training set can be as varied as a corpus of text, a
collection of images, and data collected from individual users of a
service. Overfitting
is something to watch out for when training a machine learning model.
Trained models derived from biased data can result in skewed or
undesired predictions. Algorithmic bias is a potential result from data not fully prepared for training.
Federated learning
Federated learning is an adapted form of distributed artificial intelligence
to training machine learning models that decentralizes the training
process, allowing for users' privacy to be maintained by not needing to
send their data to a centralized server. This also increases efficiency
by decentralizing the training process to many devices. For example, Gboard
uses federated machine learning to train search query prediction models
on users' mobile phones without having to send individual searches back
to Google.
Applications
There are many applications for machine learning, including:
In 2006, the media-services provider Netflix held the first "Netflix Prize"
competition to find a program to better predict user preferences and
improve the accuracy of its existing Cinematch movie recommendation
algorithm by at least 10%. A joint team made up of researchers from AT&T Labs-Research in collaboration with the teams Big Chaos and Pragmatic Theory built an ensemble model to win the Grand Prize in 2009 for $1 million.
Shortly after the prize was awarded, Netflix realized that viewers'
ratings were not the best indicators of their viewing patterns
("everything is a recommendation") and they changed their recommendation
engine accordingly.
In 2010 The Wall Street Journal wrote about the firm Rebellion Research
and their use of machine learning to predict the financial crisis. In 2012, co-founder of Sun Microsystems, Vinod Khosla,
predicted that 80% of medical doctors' jobs would be lost in the next
two decades to automated machine learning medical diagnostic software.
In 2014, it was reported that a machine learning algorithm had been
applied in the field of art history to study fine art paintings and that
it may have revealed previously unrecognized influences among artists. In 2019 Springer Nature published the first research book created using machine learning. In 2020, machine learning technology was used to help make diagnoses and aid researchers in developing a cure for COVID-19. Machine learning is recently applied to predict the green behavior of human-being.
Recently, machine learning technology is also applied to optimise
smartphone's performance and thermal behaviour based on the user's
interaction with the phone.
Limitations
Although
machine learning has been transformative in some fields,
machine-learning programs often fail to deliver expected results.
Reasons for this are numerous: lack of (suitable) data, lack of access
to the data, data bias, privacy problems, badly chosen tasks and
algorithms, wrong tools and people, lack of resources, and evaluation
problems.
In 2018, a self-driving car from Uber failed to detect a pedestrian, who was killed after a collision. Attempts to use machine learning in healthcare with the IBM Watson system failed to deliver even after years of time and billions of dollars invested.
Machine learning has been used as a strategy to update the
evidence related to systematic review and increased reviewer burden
related to the growth of biomedical literature. While it has improved
with training sets, it has not yet developed sufficiently to reduce the
workload burden without limiting the necessary sensitivity for the
findings research themselves.
Bias
Machine learning approaches in particular can suffer from different
data biases. A machine learning system trained specifically on current
customers may not be able to predict the needs of new customer groups
that are not represented in the training data. When trained on man-made
data, machine learning is likely to pick up the constitutional and
unconscious biases already present in society. Language models learned from data have been shown to contain human-like biases. Machine learning systems used for criminal risk assessment have been found to be biased against black people. In 2015, Google photos would often tag black people as gorillas,
and in 2018 this still was not well resolved, but Google reportedly was
still using the workaround to remove all gorillas from the training
data, and thus was not able to recognize real gorillas at all. Similar issues with recognizing non-white people have been found in many other systems. In 2016, Microsoft tested a chatbot that learned from Twitter, and it quickly picked up racist and sexist language. Because of such challenges, the effective use of machine learning may take longer to be adopted in other domains. Concern for fairness
in machine learning, that is, reducing bias in machine learning and
propelling its use for human good is increasingly expressed by
artificial intelligence scientists, including Fei-Fei Li,
who reminds engineers that "There’s nothing artificial about AI...It’s
inspired by people, it’s created by people, and—most importantly—it
impacts people. It is a powerful tool we are only just beginning to
understand, and that is a profound responsibility.”
Model assessments
Classification of machine learning models can be validated by accuracy estimation techniques like the holdout
method, which splits the data in a training and test set
(conventionally 2/3 training set and 1/3 test set designation) and
evaluates the performance of the training model on the test set. In
comparison, the K-fold-cross-validation
method randomly partitions the data into K subsets and then K
experiments are performed each respectively considering 1 subset for
evaluation and the remaining K-1 subsets for training the model. In
addition to the holdout and cross-validation methods, bootstrap, which samples n instances with replacement from the dataset, can be used to assess model accuracy.
In addition to overall accuracy, investigators frequently report sensitivity and specificity meaning True Positive Rate (TPR) and True Negative Rate (TNR) respectively. Similarly, investigators sometimes report the false positive rate (FPR) as well as the false negative rate (FNR). However, these rates are ratios that fail to reveal their numerators and denominators. The total operating characteristic
(TOC) is an effective method to express a model's diagnostic ability.
TOC shows the numerators and denominators of the previously mentioned
rates, thus TOC provides more information than the commonly used receiver operating characteristic (ROC) and ROC's associated area under the curve (AUC).
Ethics
Machine learning poses a host of ethical questions. Systems which are trained on datasets collected with biases may exhibit these biases upon use (algorithmic bias), thus digitizing cultural prejudices.
For example, in 1988, the UK's Commission for Racial Equality found
that St. George's Medical School had been using a computer program
trained from data of previous admissions staff and this program had
denied nearly 60 candidates who were found to be either women or had
non-European sounding names.
Using job hiring data from a firm with racist hiring policies may lead
to a machine learning system duplicating the bias by scoring job
applicants by similarity to previous successful applicants.
Responsible collection of data and documentation of algorithmic rules used by a system thus is a critical part of machine learning.
AI can be well-equipped to make decisions in technical fields,
which rely heavily on data and historical information. These decisions
rely on objectivity and logical reasoning. Because human languages contain biases, machines trained on language corpora will necessarily also learn these biases.
Other forms of ethical challenges, not related to personal
biases, are seen in health care. There are concerns among health care
professionals that these systems might not be designed in the public's
interest but as income-generating machines.
This is especially true in the United States where there is a
long-standing ethical dilemma of improving health care, but also
increasing profits. For example, the algorithms could be designed to
provide patients with unnecessary tests or medication in which the
algorithm's proprietary owners hold stakes. There is potential for
machine learning in health care to provide professionals an additional
tool to diagnose, medicate, and plan recovery paths for patients, but
this requires these biases to be mitigated.
Hardware
Since
the 2010s, advances in both machine learning algorithms and computer
hardware have led to more efficient methods for training deep neural
networks (a particular narrow subdomain of machine learning) that
contain many layers of non-linear hidden units. By 2019, graphic processing units (GPUs), often with AI-specific enhancements, had displaced CPUs as the dominant method of training large-scale commercial cloud AI. OpenAI
estimated the hardware compute used in the largest deep learning
projects from AlexNet (2012) to AlphaZero (2017), and found a
300,000-fold increase in the amount of compute required, with a
doubling-time trendline of 3.4 months.