Parallel computing

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Parallel_computing 

IBM's Blue Gene/P massively parallel supercomputer

Parallel computing is a type of computation in which many calculations or processes are carried out simultaneously. Large problems can often be divided into smaller ones, which can then be solved at the same time. There are several different forms of parallel computing: bit-level, instruction-level, data, and task parallelism. Parallelism has long been employed in high-performance computing, but has gained broader interest due to the physical constraints preventing frequency scaling. As power consumption (and consequently heat generation) by computers has become a concern in recent years, parallel computing has become the dominant paradigm in computer architecture, mainly in the form of multi-core processors.

Parallel computing is closely related to concurrent computing—they are frequently used together, and often conflated, though the two are distinct: it is possible to have parallelism without concurrency (such as bit-level parallelism), and concurrency without parallelism (such as multitasking by time-sharing on a single-core CPU). In parallel computing, a computational task is typically broken down into several, often many, very similar sub-tasks that can be processed independently and whose results are combined afterwards, upon completion. In contrast, in concurrent computing, the various processes often do not address related tasks; when they do, as is typical in distributed computing, the separate tasks may have a varied nature and often require some inter-process communication during execution.

Parallel computers can be roughly classified according to the level at which the hardware supports parallelism, with multi-core and multi-processor computers having multiple processing elements within a single machine, while clusters, MPPs, and grids use multiple computers to work on the same task. Specialized parallel computer architectures are sometimes used alongside traditional processors, for accelerating specific tasks.

In some cases parallelism is transparent to the programmer, such as in bit-level or instruction-level parallelism, but explicitly parallel algorithms, particularly those that use concurrency, are more difficult to write than sequential ones, because concurrency introduces several new classes of potential software bugs, of which race conditions are the most common. Communication and synchronization between the different subtasks are typically some of the greatest obstacles to getting optimal parallel program performance.

A theoretical upper bound on the speed-up of a single program as a result of parallelization is given by Amdahl's law.

Background

Traditionally, computer software has been written for serial computation. To solve a problem, an algorithm is constructed and implemented as a serial stream of instructions. These instructions are executed on a central processing unit on one computer. Only one instruction may execute at a time—after that instruction is finished, the next one is executed.

Parallel computing, on the other hand, uses multiple processing elements simultaneously to solve a problem. This is accomplished by breaking the problem into independent parts so that each processing element can execute its part of the algorithm simultaneously with the others. The processing elements can be diverse and include resources such as a single computer with multiple processors, several networked computers, specialized hardware, or any combination of the above. Historically parallel computing was used for scientific computing and the simulation of scientific problems, particularly in the natural and engineering sciences, such as meteorology. This led to the design of parallel hardware and software, as well as high performance computing.

Frequency scaling was the dominant reason for improvements in computer performance from the mid-1980s until 2004. The runtime of a program is equal to the number of instructions multiplied by the average time per instruction. Maintaining everything else constant, increasing the clock frequency decreases the average time it takes to execute an instruction. An increase in frequency thus decreases runtime for all compute-bound programs. However, power consumption P by a chip is given by the equation P = C × V ² × F, where C is the capacitance being switched per clock cycle (proportional to the number of transistors whose inputs change), V is voltage, and F is the processor frequency (cycles per second). Increases in frequency increase the amount of power used in a processor. Increasing processor power consumption led ultimately to Intel's May 8, 2004 cancellation of its Tejas and Jayhawk processors, which is generally cited as the end of frequency scaling as the dominant computer architecture paradigm.

To deal with the problem of power consumption and overheating the major central processing unit (CPU or processor) manufacturers started to produce power efficient processors with multiple cores. The core is the computing unit of the processor and in multi-core processors each core is independent and can access the same memory concurrently. Multi-core processors have brought parallel computing to desktop computers. Thus parallelisation of serial programmes has become a mainstream programming task. In 2012 quad-core processors became standard for desktop computers, while servers have 10 and 12 core processors. From Moore's law it can be predicted that the number of cores per processor will double every 18–24 months. This could mean that after 2020 a typical processor will have dozens or hundreds of cores.

An operating system can ensure that different tasks and user programmes are run in parallel on the available cores. However, for a serial software programme to take full advantage of the multi-core architecture the programmer needs to restructure and parallelise the code. A speed-up of application software runtime will no longer be achieved through frequency scaling, instead programmers will need to parallelise their software code to take advantage of the increasing computing power of multicore architectures.

Amdahl's law and Gustafson's law

A graphical representation of Amdahl's law. The speedup of a program from parallelization is limited by how much of the program can be parallelized. For example, if 90% of the program can be parallelized, the theoretical maximum speedup using parallel computing would be 10 times no matter how many processors are used.

Assume that a task has two independent parts, A and B. Part B takes roughly 25% of the time of the whole computation. By working very hard, one may be able to make this part 5 times faster, but this only reduces the time for the whole computation by a little. In contrast, one may need to perform less work to make part A be twice as fast. This will make the computation much faster than by optimizing part B, even though part B's speedup is greater by ratio, (5 times versus 2 times).

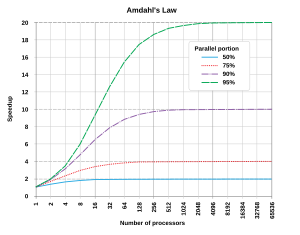
Optimally, the speedup from parallelization would be linear—doubling the number of processing elements should halve the runtime, and doubling it a second time should again halve the runtime. However, very few parallel algorithms achieve optimal speedup. Most of them have a near-linear speedup for small numbers of processing elements, which flattens out into a constant value for large numbers of processing elements.

The potential speedup of an algorithm on a parallel computing platform is given by Amdahl's law

${\displaystyle S_{\text{latency}}(s)={\frac {1}{1-p+{\frac {p}{s}}}},}$

where

• S_latency is the potential speedup in latency of the execution of the whole task;
• s is the speedup in latency of the execution of the parallelizable part of the task;
• p is the percentage of the execution time of the whole task concerning the parallelizable part of the task before parallelization.

Since S_latency < 1/(1 - p), it shows that a small part of the program which cannot be parallelized will limit the overall speedup available from parallelization. A program solving a large mathematical or engineering problem will typically consist of several parallelizable parts and several non-parallelizable (serial) parts. If the non-parallelizable part of a program accounts for 10% of the runtime (p = 0.9), we can get no more than a 10 times speedup, regardless of how many processors are added. This puts an upper limit on the usefulness of adding more parallel execution units. "When a task cannot be partitioned because of sequential constraints, the application of more effort has no effect on the schedule. The bearing of a child takes nine months, no matter how many women are assigned."

A graphical representation of Gustafson's law

Amdahl's law only applies to cases where the problem size is fixed. In practice, as more computing resources become available, they tend to get used on larger problems (larger datasets), and the time spent in the parallelizable part often grows much faster than the inherently serial work. In this case, Gustafson's law gives a less pessimistic and more realistic assessment of parallel performance:

${\displaystyle S_{\text{latency}}(s)=1-p+sp.}$

Both Amdahl's law and Gustafson's law assume that the running time of the serial part of the program is independent of the number of processors. Amdahl's law assumes that the entire problem is of fixed size so that the total amount of work to be done in parallel is also independent of the number of processors, whereas Gustafson's law assumes that the total amount of work to be done in parallel varies linearly with the number of processors.

Dependencies

Understanding data dependencies is fundamental in implementing parallel algorithms. No program can run more quickly than the longest chain of dependent calculations (known as the critical path), since calculations that depend upon prior calculations in the chain must be executed in order. However, most algorithms do not consist of just a long chain of dependent calculations; there are usually opportunities to execute independent calculations in parallel.

Let P_i and P_j be two program segments. Bernstein's conditions describe when the two are independent and can be executed in parallel. For P_i, let I_i be all of the input variables and O_i the output variables, and likewise for P_j. P_i and P_j are independent if they satisfy

${\displaystyle I_{j}\cap O_{i}=\varnothing ,}$

${\displaystyle I_{i}\cap O_{j}=\varnothing ,}$

${\displaystyle O_{i}\cap O_{j}=\varnothing .}$

Violation of the first condition introduces a flow dependency, corresponding to the first segment producing a result used by the second segment. The second condition represents an anti-dependency, when the second segment produces a variable needed by the first segment. The third and final condition represents an output dependency: when two segments write to the same location, the result comes from the logically last executed segment.

Consider the following functions, which demonstrate several kinds of dependencies:

1: function Dep(a, b)
2: c := a * b
3: d := 3 * c
4: end function

In this example, instruction 3 cannot be executed before (or even in parallel with) instruction 2, because instruction 3 uses a result from instruction 2. It violates condition 1, and thus introduces a flow dependency.

1: function NoDep(a, b)
2: c := a * b
3: d := 3 * b
4: e := a + b
5: end function

In this example, there are no dependencies between the instructions, so they can all be run in parallel.

Bernstein's conditions do not allow memory to be shared between different processes. For that, some means of enforcing an ordering between accesses is necessary, such as semaphores, barriers or some other synchronization method.

Race conditions, mutual exclusion, synchronization, and parallel slowdown

Subtasks in a parallel program are often called threads. Some parallel computer architectures use smaller, lightweight versions of threads known as fibers, while others use bigger versions known as processes. However, "threads" is generally accepted as a generic term for subtasks. Threads will often need synchronized access to an object or other resource, for example when they must update a variable that is shared between them. Without synchronization, the instructions between the two threads may be interleaved in any order. For example, consider the following program:

Thread A	Thread B
1A: Read variable V	1B: Read variable V
2A: Add 1 to variable V	2B: Add 1 to variable V
3A: Write back to variable V	3B: Write back to variable V

If instruction 1B is executed between 1A and 3A, or if instruction 1A is executed between 1B and 3B, the program will produce incorrect data. This is known as a race condition. The programmer must use a lock to provide mutual exclusion. A lock is a programming language construct that allows one thread to take control of a variable and prevent other threads from reading or writing it, until that variable is unlocked. The thread holding the lock is free to execute its critical section (the section of a program that requires exclusive access to some variable), and to unlock the data when it is finished. Therefore, to guarantee correct program execution, the above program can be rewritten to use locks:

Thread A	Thread B
1A: Lock variable V	1B: Lock variable V
2A: Read variable V	2B: Read variable V
3A: Add 1 to variable V	3B: Add 1 to variable V
4A: Write back to variable V	4B: Write back to variable V
5A: Unlock variable V	5B: Unlock variable V

One thread will successfully lock variable V, while the other thread will be locked out—unable to proceed until V is unlocked again. This guarantees correct execution of the program. Locks may be necessary to ensure correct program execution when threads must serialize access to resources, but their use can greatly slow a program and may affect its reliability.

Locking multiple variables using non-atomic locks introduces the possibility of program deadlock. An atomic lock locks multiple variables all at once. If it cannot lock all of them, it does not lock any of them. If two threads each need to lock the same two variables using non-atomic locks, it is possible that one thread will lock one of them and the second thread will lock the second variable. In such a case, neither thread can complete, and deadlock results.

Many parallel programs require that their subtasks act in synchrony. This requires the use of a barrier. Barriers are typically implemented using a lock or a semaphore. One class of algorithms, known as lock-free and wait-free algorithms, altogether avoids the use of locks and barriers. However, this approach is generally difficult to implement and requires correctly designed data structures.

Not all parallelization results in speed-up. Generally, as a task is split up into more and more threads, those threads spend an ever-increasing portion of their time communicating with each other or waiting on each other for access to resources. Once the overhead from resource contention or communication dominates the time spent on other computation, further parallelization (that is, splitting the workload over even more threads) increases rather than decreases the amount of time required to finish. This problem, known as parallel slowdown, can be improved in some cases by software analysis and redesign.

Fine-grained, coarse-grained, and embarrassing parallelism

Applications are often classified according to how often their subtasks need to synchronize or communicate with each other. An application exhibits fine-grained parallelism if its subtasks must communicate many times per second; it exhibits coarse-grained parallelism if they do not communicate many times per second, and it exhibits embarrassing parallelism if they rarely or never have to communicate. Embarrassingly parallel applications are considered the easiest to parallelize.

Flynn's taxonomy

Michael J. Flynn created one of the earliest classification systems for parallel (and sequential) computers and programs, now known as Flynn's taxonomy. Flynn classified programs and computers by whether they were operating using a single set or multiple sets of instructions, and whether or not those instructions were using a single set or multiple sets of data.

Flynn's taxonomy
Single data stream
SISD MISD
Multiple data streams
SIMD MIMD
SIMD Subcategories
Array Processing (SIMT) Pipelined Processing (Packed SIMD) Associative Processing (Predicated/Masked SIMD)
See also
SPMD MPMD

The single-instruction-single-data (SISD) classification is equivalent to an entirely sequential program. The single-instruction-multiple-data (SIMD) classification is analogous to doing the same operation repeatedly over a large data set. This is commonly done in signal processing applications. Multiple-instruction-single-data (MISD) is a rarely used classification. While computer architectures to deal with this were devised (such as systolic arrays), few applications that fit this class materialized. Multiple-instruction-multiple-data (MIMD) programs are by far the most common type of parallel programs.

According to David A. Patterson and John L. Hennessy, "Some machines are hybrids of these categories, of course, but this classic model has survived because it is simple, easy to understand, and gives a good first approximation. It is also—perhaps because of its understandability—the most widely used scheme."

Types of parallelism

Bit-level parallelism

From the advent of very-large-scale integration (VLSI) computer-chip fabrication technology in the 1970s until about 1986, speed-up in computer architecture was driven by doubling computer word size—the amount of information the processor can manipulate per cycle. Increasing the word size reduces the number of instructions the processor must execute to perform an operation on variables whose sizes are greater than the length of the word. For example, where an 8-bit processor must add two 16-bit integers, the processor must first add the 8 lower-order bits from each integer using the standard addition instruction, then add the 8 higher-order bits using an add-with-carry instruction and the carry bit from the lower order addition; thus, an 8-bit processor requires two instructions to complete a single operation, where a 16-bit processor would be able to complete the operation with a single instruction.

Historically, 4-bit microprocessors were replaced with 8-bit, then 16-bit, then 32-bit microprocessors. This trend generally came to an end with the introduction of 32-bit processors, which has been a standard in general-purpose computing for two decades. Not until the early 2000s, with the advent of x86-64 architectures, did 64-bit processors become commonplace.

Instruction-level parallelism

A canonical processor without pipeline. It takes five clock cycles to complete one instruction and thus the processor can issue subscalar performance (IPC = 0.2 < 1).

A computer program is, in essence, a stream of instructions executed by a processor. Without instruction-level parallelism, a processor can only issue less than one instruction per clock cycle (IPC < 1). These processors are known as subscalar processors. These instructions can be re-ordered and combined into groups which are then executed in parallel without changing the result of the program. This is known as instruction-level parallelism. Advances in instruction-level parallelism dominated computer architecture from the mid-1980s until the mid-1990s.

A canonical five-stage pipelined processor. In the best case scenario, it takes one clock cycle to complete one instruction and thus the processor can issue scalar performance (IPC = 1).

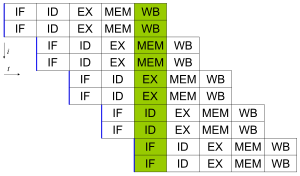
All modern processors have multi-stage instruction pipelines. Each stage in the pipeline corresponds to a different action the processor performs on that instruction in that stage; a processor with an N-stage pipeline can have up to N different instructions at different stages of completion and thus can issue one instruction per clock cycle (IPC = 1). These processors are known as scalar processors. The canonical example of a pipelined processor is a RISC processor, with five stages: instruction fetch (IF), instruction decode (ID), execute (EX), memory access (MEM), and register write back (WB). The Pentium 4 processor had a 35-stage pipeline.

A canonical five-stage pipelined processor with two execution units. In the best case scenario, it takes one clock cycle to complete two instructions and thus the processor can issue superscalar performance (IPC = 2 > 1).

Most modern processors also have multiple execution units. They usually combine this feature with pipelining and thus can issue more than one instruction per clock cycle (IPC > 1). These processors are known as superscalar processors. Superscalar processors differ from multi-core processors in that the several execution units are not entire processors (i.e. processing units). Instructions can be grouped together only if there is no data dependency between them. Scoreboarding and the Tomasulo algorithm (which is similar to scoreboarding but makes use of register renaming) are two of the most common techniques for implementing out-of-order execution and instruction-level parallelism.

Task parallelism

Task parallelisms is the characteristic of a parallel program that "entirely different calculations can be performed on either the same or different sets of data". This contrasts with data parallelism, where the same calculation is performed on the same or different sets of data. Task parallelism involves the decomposition of a task into sub-tasks and then allocating each sub-task to a processor for execution. The processors would then execute these sub-tasks concurrently and often cooperatively. Task parallelism does not usually scale with the size of a problem.

Superword level parallelism

Superword level parallelism is a vectorization technique based on loop unrolling and basic block vectorization. It is distinct from loop vectorization algorithms in that it can exploit parallelism of inline code, such as manipulating coordinates, color channels or in loops unrolled by hand.

Hardware

Memory and communication

Main memory in a parallel computer is either shared memory (shared between all processing elements in a single address space), or distributed memory (in which each processing element has its own local address space). Distributed memory refers to the fact that the memory is logically distributed, but often implies that it is physically distributed as well. Distributed shared memory and memory virtualization combine the two approaches, where the processing element has its own local memory and access to the memory on non-local processors. Accesses to local memory are typically faster than accesses to non-local memory. On the supercomputers, distributed shared memory space can be implemented using the programming model such as PGAS. This model allows processes on one compute node to transparently access the remote memory of another compute node. All compute nodes are also connected to an external shared memory system via high-speed interconnect, such as Infiniband, this external shared memory system is known as burst buffer, which is typically built from arrays of non-volatile memory physically distributed across multiple I/O nodes.

A logical view of a non-uniform memory access (NUMA) architecture. Processors in one directory can access that directory's memory with less latency than they can access memory in the other directory's memory.

Computer architectures in which each element of main memory can be accessed with equal latency and bandwidth are known as uniform memory access (UMA) systems. Typically, that can be achieved only by a shared memory system, in which the memory is not physically distributed. A system that does not have this property is known as a non-uniform memory access (NUMA) architecture. Distributed memory systems have non-uniform memory access.

Computer systems make use of caches—small and fast memories located close to the processor which store temporary copies of memory values (nearby in both the physical and logical sense). Parallel computer systems have difficulties with caches that may store the same value in more than one location, with the possibility of incorrect program execution. These computers require a cache coherency system, which keeps track of cached values and strategically purges them, thus ensuring correct program execution. Bus snooping is one of the most common methods for keeping track of which values are being accessed (and thus should be purged). Designing large, high-performance cache coherence systems is a very difficult problem in computer architecture. As a result, shared memory computer architectures do not scale as well as distributed memory systems do.

Processor–processor and processor–memory communication can be implemented in hardware in several ways, including via shared (either multiported or multiplexed) memory, a crossbar switch, a shared bus or an interconnect network of a myriad of topologies including star, ring, tree, hypercube, fat hypercube (a hypercube with more than one processor at a node), or n-dimensional mesh.

Parallel computers based on interconnected networks need to have some kind of routing to enable the passing of messages between nodes that are not directly connected. The medium used for communication between the processors is likely to be hierarchical in large multiprocessor machines.

Classes of parallel computers

Parallel computers can be roughly classified according to the level at which the hardware supports parallelism. This classification is broadly analogous to the distance between basic computing nodes. These are not mutually exclusive; for example, clusters of symmetric multiprocessors are relatively common.

Multi-core computing

A multi-core processor is a processor that includes multiple processing units (called "cores") on the same chip. This processor differs from a superscalar processor, which includes multiple execution units and can issue multiple instructions per clock cycle from one instruction stream (thread); in contrast, a multi-core processor can issue multiple instructions per clock cycle from multiple instruction streams. IBM's Cell microprocessor, designed for use in the Sony PlayStation 3, is a prominent multi-core processor. Each core in a multi-core processor can potentially be superscalar as well—that is, on every clock cycle, each core can issue multiple instructions from one thread.

Simultaneous multithreading (of which Intel's Hyper-Threading is the best known) was an early form of pseudo-multi-coreism. A processor capable of concurrent multithreading includes multiple execution units in the same processing unit—that is it has a superscalar architecture—and can issue multiple instructions per clock cycle from multiple threads. Temporal multithreading on the other hand includes a single execution unit in the same processing unit and can issue one instruction at a time from multiple threads.

Symmetric multiprocessing

A symmetric multiprocessor (SMP) is a computer system with multiple identical processors that share memory and connect via a bus. Bus contention prevents bus architectures from scaling. As a result, SMPs generally do not comprise more than 32 processors. Because of the small size of the processors and the significant reduction in the requirements for bus bandwidth achieved by large caches, such symmetric multiprocessors are extremely cost-effective, provided that a sufficient amount of memory bandwidth exists.

Distributed computing

A distributed computer (also known as a distributed memory multiprocessor) is a distributed memory computer system in which the processing elements are connected by a network. Distributed computers are highly scalable. The terms "concurrent computing", "parallel computing", and "distributed computing" have a lot of overlap, and no clear distinction exists between them. The same system may be characterized both as "parallel" and "distributed"; the processors in a typical distributed system run concurrently in parallel.

Cluster computing

A Beowulf cluster

A cluster is a group of loosely coupled computers that work together closely, so that in some respects they can be regarded as a single computer. Clusters are composed of multiple standalone machines connected by a network. While machines in a cluster do not have to be symmetric, load balancing is more difficult if they are not. The most common type of cluster is the Beowulf cluster, which is a cluster implemented on multiple identical commercial off-the-shelf computers connected with a TCP/IP Ethernet local area network. Beowulf technology was originally developed by Thomas Sterling and Donald Becker. 87% of all Top500 supercomputers are clusters. The remaining are Massively Parallel Processors, explained below.

Because grid computing systems (described below) can easily handle embarrassingly parallel problems, modern clusters are typically designed to handle more difficult problems—problems that require nodes to share intermediate results with each other more often. This requires a high bandwidth and, more importantly, a low-latency interconnection network. Many historic and current supercomputers use customized high-performance network hardware specifically designed for cluster computing, such as the Cray Gemini network. As of 2014, most current supercomputers use some off-the-shelf standard network hardware, often Myrinet, InfiniBand, or Gigabit Ethernet.

Massively parallel computing

A cabinet from IBM's Blue Gene/L massively parallel supercomputer

A massively parallel processor (MPP) is a single computer with many networked processors. MPPs have many of the same characteristics as clusters, but MPPs have specialized interconnect networks (whereas clusters use commodity hardware for networking). MPPs also tend to be larger than clusters, typically having "far more" than 100 processors. In an MPP, "each CPU contains its own memory and copy of the operating system and application. Each subsystem communicates with the others via a high-speed interconnect."

IBM's Blue Gene/L, the fifth fastest supercomputer in the world according to the June 2009 TOP500 ranking, is an MPP.

Grid computing

Grid computing is the most distributed form of parallel computing. It makes use of computers communicating over the Internet to work on a given problem. Because of the low bandwidth and extremely high latency available on the Internet, distributed computing typically deals only with embarrassingly parallel problems. Many distributed computing applications have been created, of which SETI@home and Folding@home are the best-known examples.

Most grid computing applications use middleware (software that sits between the operating system and the application to manage network resources and standardize the software interface). The most common distributed computing middleware is the Berkeley Open Infrastructure for Network Computing (BOINC). Often, distributed computing software makes use of "spare cycles", performing computations at times when a computer is idling.

Specialized parallel computers

Within parallel computing, there are specialized parallel devices that remain niche areas of interest. While not domain-specific, they tend to be applicable to only a few classes of parallel problems.

Reconfigurable computing with field-programmable gate arrays

Reconfigurable computing is the use of a field-programmable gate array (FPGA) as a co-processor to a general-purpose computer. An FPGA is, in essence, a computer chip that can rewire itself for a given task.

FPGAs can be programmed with hardware description languages such as VHDL or Verilog. However, programming in these languages can be tedious. Several vendors have created C to HDL languages that attempt to emulate the syntax and semantics of the C programming language, with which most programmers are familiar. The best known C to HDL languages are Mitrion-C, Impulse C, DIME-C, and Handel-C. Specific subsets of SystemC based on C++ can also be used for this purpose.

AMD's decision to open its HyperTransport technology to third-party vendors has become the enabling technology for high-performance reconfigurable computing. According to Michael R. D'Amour, Chief Operating Officer of DRC Computer Corporation, "when we first walked into AMD, they called us 'the socket stealers.' Now they call us their partners."

General-purpose computing on graphics processing units (GPGPU)

Nvidia's Tesla GPGPU card

General-purpose computing on graphics processing units (GPGPU) is a fairly recent trend in computer engineering research. GPUs are co-processors that have been heavily optimized for computer graphics processing. Computer graphics processing is a field dominated by data parallel operations—particularly linear algebra matrix operations.

In the early days, GPGPU programs used the normal graphics APIs for executing programs. However, several new programming languages and platforms have been built to do general purpose computation on GPUs with both Nvidia and AMD releasing programming environments with CUDA and Stream SDK respectively. Other GPU programming languages include BrookGPU, PeakStream, and RapidMind. Nvidia has also released specific products for computation in their Tesla series. The technology consortium Khronos Group has released the OpenCL specification, which is a framework for writing programs that execute across platforms consisting of CPUs and GPUs. AMD, Apple, Intel, Nvidia and others are supporting OpenCL.

Application-specific integrated circuits

Several application-specific integrated circuit (ASIC) approaches have been devised for dealing with parallel applications.

Because an ASIC is (by definition) specific to a given application, it can be fully optimized for that application. As a result, for a given application, an ASIC tends to outperform a general-purpose computer. However, ASICs are created by UV photolithography. This process requires a mask set, which can be extremely expensive. A mask set can cost over a million US dollars. (The smaller the transistors required for the chip, the more expensive the mask will be.) Meanwhile, performance increases in general-purpose computing over time (as described by Moore's law) tend to wipe out these gains in only one or two chip generations. High initial cost, and the tendency to be overtaken by Moore's-law-driven general-purpose computing, has rendered ASICs unfeasible for most parallel computing applications. However, some have been built. One example is the PFLOPS RIKEN MDGRAPE-3 machine which uses custom ASICs for molecular dynamics simulation.

Vector processors

The Cray-1 is a vector processor

A vector processor is a CPU or computer system that can execute the same instruction on large sets of data. Vector processors have high-level operations that work on linear arrays of numbers or vectors. An example vector operation is A = B × C, where A, B, and C are each 64-element vectors of 64-bit floating-point numbers. They are closely related to Flynn's SIMD classification.

Cray computers became famous for their vector-processing computers in the 1970s and 1980s. However, vector processors—both as CPUs and as full computer systems—have generally disappeared. Modern processor instruction sets do include some vector processing instructions, such as with Freescale Semiconductor's AltiVec and Intel's Streaming SIMD Extensions (SSE).

Software

Parallel programming languages

Concurrent programming languages, libraries, APIs, and parallel programming models (such as algorithmic skeletons) have been created for programming parallel computers. These can generally be divided into classes based on the assumptions they make about the underlying memory architecture—shared memory, distributed memory, or shared distributed memory. Shared memory programming languages communicate by manipulating shared memory variables. Distributed memory uses message passing. POSIX Threads and OpenMP are two of the most widely used shared memory APIs, whereas Message Passing Interface (MPI) is the most widely used message-passing system API. One concept used in programming parallel programs is the future concept, where one part of a program promises to deliver a required datum to another part of a program at some future time.

CAPS entreprise and Pathscale are also coordinating their effort to make hybrid multi-core parallel programming (HMPP) directives an open standard called OpenHMPP. The OpenHMPP directive-based programming model offers a syntax to efficiently offload computations on hardware accelerators and to optimize data movement to/from the hardware memory. OpenHMPP directives describe remote procedure call (RPC) on an accelerator device (e.g. GPU) or more generally a set of cores. The directives annotate C or Fortran codes to describe two sets of functionalities: the offloading of procedures (denoted codelets) onto a remote device and the optimization of data transfers between the CPU main memory and the accelerator memory.

The rise of consumer GPUs has led to support for compute kernels, either in graphics APIs (referred to as compute shaders), in dedicated APIs (such as OpenCL), or in other language extensions.

Automatic parallelization

Automatic parallelization of a sequential program by a compiler is the "holy grail" of parallel computing, especially with the aforementioned limit of processor frequency. Despite decades of work by compiler researchers, automatic parallelization has had only limited success.

Mainstream parallel programming languages remain either explicitly parallel or (at best) partially implicit, in which a programmer gives the compiler directives for parallelization. A few fully implicit parallel programming languages exist—SISAL, Parallel Haskell, SequenceL, System C (for FPGAs), Mitrion-C, VHDL, and Verilog.

Application checkpointing

As a computer system grows in complexity, the mean time between failures usually decreases. Application checkpointing is a technique whereby the computer system takes a "snapshot" of the application—a record of all current resource allocations and variable states, akin to a core dump—; this information can be used to restore the program if the computer should fail. Application checkpointing means that the program has to restart from only its last checkpoint rather than the beginning. While checkpointing provides benefits in a variety of situations, it is especially useful in highly parallel systems with a large number of processors used in high performance computing.

Algorithmic methods

As parallel computers become larger and faster, we are now able to solve problems that had previously taken too long to run. Fields as varied as bioinformatics (for protein folding and sequence analysis) and economics (for mathematical finance) have taken advantage of parallel computing. Common types of problems in parallel computing applications include:

• Dense linear algebra
• Sparse linear algebra
• Spectral methods (such as Cooley–Tukey fast Fourier transform)
• N-body problems (such as Barnes–Hut simulation)
• structured grid problems (such as Lattice Boltzmann methods)
• Unstructured grid problems (such as found in finite element analysis)
• Monte Carlo method
• Combinational logic (such as brute-force cryptographic techniques)
• Graph traversal (such as sorting algorithms)
• Dynamic programming
• Branch and bound methods
• Graphical models (such as detecting hidden Markov models and constructing Bayesian networks)
• Finite-state machine simulation

Fault tolerance

Parallel computing can also be applied to the design of fault-tolerant computer systems, particularly via lockstep systems performing the same operation in parallel. This provides redundancy in case one component fails, and also allows automatic error detection and error correction if the results differ. These methods can be used to help prevent single-event upsets caused by transient errors. Although additional measures may be required in embedded or specialized systems, this method can provide a cost-effective approach to achieve n-modular redundancy in commercial off-the-shelf systems.

History

ILLIAC IV, "the most infamous of supercomputers"

The origins of true (MIMD) parallelism go back to Luigi Federico Menabrea and his Sketch of the Analytic Engine Invented by Charles Babbage.

In April 1958, Stanley Gill (Ferranti) discussed parallel programming and the need for branching and waiting. Also in 1958, IBM researchers John Cocke and Daniel Slotnick discussed the use of parallelism in numerical calculations for the first time. Burroughs Corporation introduced the D825 in 1962, a four-processor computer that accessed up to 16 memory modules through a crossbar switch. In 1967, Amdahl and Slotnick published a debate about the feasibility of parallel processing at American Federation of Information Processing Societies Conference. It was during this debate that Amdahl's law was coined to define the limit of speed-up due to parallelism.

In 1969, Honeywell introduced its first Multics system, a symmetric multiprocessor system capable of running up to eight processors in parallel. C.mmp, a multi-processor project at Carnegie Mellon University in the 1970s, was among the first multiprocessors with more than a few processors. The first bus-connected multiprocessor with snooping caches was the Synapse N+1 in 1984.

SIMD parallel computers can be traced back to the 1970s. The motivation behind early SIMD computers was to amortize the gate delay of the processor's control unit over multiple instructions. In 1964, Slotnick had proposed building a massively parallel computer for the Lawrence Livermore National Laboratory. His design was funded by the US Air Force, which was the earliest SIMD parallel-computing effort, ILLIAC IV. The key to its design was a fairly high parallelism, with up to 256 processors, which allowed the machine to work on large datasets in what would later be known as vector processing. However, ILLIAC IV was called "the most infamous of supercomputers", because the project was only one-fourth completed, but took 11 years and cost almost four times the original estimate. When it was finally ready to run its first real application in 1976, it was outperformed by existing commercial supercomputers such as the Cray-1.

Biological brain as massively parallel computer

In the early 1970s, at the MIT Computer Science and Artificial Intelligence Laboratory, Marvin Minsky and Seymour Papert started developing the Society of Mind theory, which views the biological brain as massively parallel computer. In 1986, Minsky published The Society of Mind, which claims that “mind is formed from many little agents, each mindless by itself”. The theory attempts to explain how what we call intelligence could be a product of the interaction of non-intelligent parts. Minsky says that the biggest source of ideas about the theory came from his work in trying to create a machine that uses a robotic arm, a video camera, and a computer to build with children's blocks.

Similar models (which also view the biological brain as a massively parallel computer, i.e., the brain is made up of a constellation of independent or semi-independent agents) were also described by:

• Thomas R. Blakeslee,
• Michael S. Gazzaniga,
• Robert E. Ornstein,
• Ernest Hilgard,
• Michio Kaku,
• George Ivanovich Gurdjieff,
• Neurocluster Brain Model.

 

Connectome (book)

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Connectome_(book) 

 

Connectome: How the Brain's Wiring Makes Us Who We Are

Author	Sebastian Seung
Subject	Connectomics, Neuroscience
Publisher	Houghton Mifflin Harcourt
Publication date	2012
Pages	384
ISBN	978-0547508184 (hardcover)

Connectome: How the Brain's Wiring Makes Us Who We Are (2012) is a book by Sebastian Seung. It introduces basic concepts in neuroscience and then elaborates on the field of connectomics, i.e., how to scan, decode, compare, and understand patterns in brain connectivity. The book concludes with musings on cryonics and mind uploading. It was selected by The Wall Street Journal as Top Ten Nonfiction of 2012.

Book outline

Introduction

Seung frames the idea of connectomics and argues that "You are more than your genes. You are your connectome."

Ch. 1: Genius and Madness

Seung introduces the 19th-century idea of phrenology and its modern-day counterpart, which he calls "neo-phrenology", i.e., the idea that sizes of brain regions play a role in intelligence (e.g., Einstein's enlarged inferior parietal lobule) or mental disorders (e.g., schizophrenia and autism). That said, Seung emphasizes that these size correlations only show up for large samples and can't necessarily predict what will happen in any individual's brain.

Ch. 2: Border Disputes

Seung discusses localization maps of the brain that attempt to confine particular functions to particular regions. For instance, phantom-limb pain is hypothesized to result when brain regions formerly devoted to the now-missing lower arm become occupied for use by the upper arm and face. Hence, stimulation of the upper arm or face produces what feels like pain in the missing lower arm.

In contrast to brain localization is the theory of equipotentiality, that any brain region has the potential to perform any function.

Ch. 3: No Neuron Is an Island

Seung discusses basic cell-level neuroscience, including the structure of neurons and their neurites, as well as a "weighted voting model" of neuronal firing in which a neuron fires when the weighted sum of excitatory minus inhibitory inputs exceeds a threshold.

Ch. 4: Neurons All the Way Down

Seung explores how hierarchical neural networks can encode concepts (e.g., Jennifer Aniston) as compositions of simpler parts and how these concepts can be linked in one's mind when connections are formed between them, either bidirectionally with cell assemblies or unidirectionally with synaptic chains.

Ch. 5: The Assembly of Memories

Seung discusses theories of memory formation, including basic Hebbian plasticity and the more speculative neural Darwinism. According to the "dual trace" theory of memory, short-term memory can take the form of persistent spiking among a cell assembly, while long-term memories can be stored in persistent connections. It's useful to have both types of memory because of a "stability-plasticity dilemma", which is a concept familiar in computers that use both RAM and hard drive storage.

Ch. 6: The Forestry of the Genes

Seung discusses how many psychological traits and disorders are at least partly genetic. (He quotes Eric Turkheimer's First Law of Behavior Genetics: "All human behavioral traits are heritable.") He elaborates on some of the mechanisms by which genes influence neural development and can lead to neural disorders.

Ch. 7: Renewing Our Potential

To what extent are the first three years of development a crucial window after which brain traits cannot be reversed? And to what extent do brains remain plastic throughout life? Seung discusses evidence on both sides to show that the truth is a little bit of both.

Ch. 8: Seeing Is Believing

Seung discusses how advances in technologies to see the brain have driven neuroscience progress—in the long run arguably more than the immediate neuroscientific advances that these technologies enabled.

Ch. 9: Following the Trail

"If connectomics experiences sustained exponential progress, then finding entire human connectomes will become easy well before the end of the twenty-first century."

Sebastian Seung, Connectome, p. 169

Seung reviews the history of mapping the Caenorhabditis elegans connectome by Sydney Brenner and colleagues, published in 1986. The process required immense manual labor, but connectome mapping is speeding up due to automation with artificial intelligence and intelligence amplification.

Ch. 10: Carving

Seung discusses ways of dividing up the brain into regions. Korbinian Brodmann based his Brodmann areas on uniformity of cortical layers within each area. Santiago Ramón y Cajal tried to identify types of neurons based on their shapes. Seung himself proposes to divide brain regions based on what other regions they generally connect to. He says this might often coincide with Brodmann's or Cajal's divisions, but if we ultimately care about connectivity, Seung's classification would be most directly relevant.

Ch. 11: Codebreaking

Seung discusses decoding memories from neural connections. As an example potentially feasible in the near/medium term, he suggests the HVC region in birds, which may store their songs in a roughly analogous way as a compact disc stores Beethoven music.

Ch. 12: Comparing

Seung discusses how to look at differences among brains based on differences in connectivity. This can be approximated at a coarse level using diffusion MRI or at more fine-grained levels using connectome maps.

Ch. 13: Changing

Seung examines how connectomics may in the future help identify neurological problems before they become serious and inform development of drugs or gene therapies for connectopathies.

Ch. 14: To Freeze or to Pickle?

Seung examines the efforts of the Alcor Life Extension Foundation to offer some chance of immortality by cryonics. He compares preservation in liquid nitrogen with a plastination approach that, unlike Alcor's method, requires "no special maintenance".

Ch. 15: Save As ...

Seung explores the idea of mind uploading and associated philosophical implications, such as using an analogue of the Turing test to determine if a simulation has sufficient fidelity to appear as the real "you" to outsiders, as well as whether you would subjectively feel the upload to be "you" on the inside relative to your stored self-model. Seung discusses the idea that thinking of ourselves as information—as not neurons per se but as the connections of neurons—can be seen as a new conception of the soul. He suggests that transhumanism can give spiritual purpose to a seemingly cold, material universe: "transhumanism lends meaning to lives that were robbed of it by science" (p. 273).

Reactions

Abigail Zuger characterized Connectome as a book arguing that we are more than just our genes. She adds: "it is a testament to Dr. Seung's remarkable clarity of exposition that the reader is swept along with his enthusiasm". Terry Sejnowski echoed this sentiment about the book's style: "With the first-person flavour of James Watson's Double Helix - an account of how DNA's structure was discovered - Connectome gives a sense of the excitement on the cutting edge of neuroscience."

Susan Okie affirms that "Seung is a clear, lively writer who chooses vivid examples," though she expresses skepticism about the "science-fiction fantasy that, one day, a human being's connectome could be simulated and 'uploaded' onto a computer".

Daniel Levitin praised Connectome as "the best lay book on brain science I've ever read." He says it is "witty and exceptionally clear" and includes "the equivalent of a college course on neuroscience". That said, Levitin raised the caveat that a person's connectome by itself isn't the whole story of who that person is, because beyond understanding neural wiring, "we also need to know the precise chemical soup du jour in the brain" as well as the update rules for how experiences change brain connections.^[5]

"Even though we have known the connectome of the nematode worm for 25 years, we are far from reading its mind. We don't yet understand how its nerve cells work."

Christof Koch

Christof Koch said: "Treating the connectome as the be-all and end-all of brain function has its problems. ....The book is well illustrated and sourced with an ending that is both engaging and idiosyncratic." But like Levitin, Koch felt that the connectome by itself is missing some pieces of the picture and that not all brain diseases are diseases of connectivity. Other possible problems may arise from "Faults in synaptic transmission and in processes inside neurons and the glial cells that support them".

 

Human Connectome Project

From Wikipedia, the free encyclopedia

The Human Connectome Project (HCP) is a five-year project sponsored by sixteen components of the National Institutes of Health, split between two consortia of research institutions. The project was launched in July 2009 as the first of three Grand Challenges of the NIH's Blueprint for Neuroscience Research. On September 15, 2010, the NIH announced that it would award two grants: $30 million over five years to a consortium led by Washington University in Saint Louis and the University of Minnesota, with strong contributions from Oxford University (FMRIB) and $8.5 million over three years to a consortium led by Harvard University, Massachusetts General Hospital and the University of California Los Angeles.

The goal of the Human Connectome Project is to build a "network map" (connectome) that will shed light on the anatomical and functional connectivity within the healthy human brain, as well as to produce a body of data that will facilitate research into brain disorders such as dyslexia, autism, Alzheimer's disease, and schizophrenia.

WU-Minn-Oxford consortium

The WU-Minn-Oxford consortium developed improved MRI instrumentation, image acquisition and image analysis methods for mapping the connectivity in the human brain at spatial resolutions significantly better than previously available; using these methods, WU-Minn-Oxford consortium collected a large amount of MRI and behavioral data on 1,200 healthy adults — twin pairs and their siblings from 300 families - using a special 3 Tesla MRI instrument. In addition, it scanned 184 subjects from this pool at 7 Tesla, with higher spatial resolution. The data are being analyzed to show the anatomical and functional connections between parts of the brain for each individual, and will be related to behavioral test data. Comparing the connectomes and genetic data of genetically identical twins with fraternal twins will reveal the relative contributions of genes and environment in shaping brain circuitry and pinpoint relevant genetic variation. The maps will also shed light on how brain networks are organized.

Using a combination of non-invasive imaging technologies, including resting-state fMRI and task-based functional MRI, MEG and EEG, and diffusion MRI, the WU-Minn will be mapping connectomes at the macro scale — mapping large brain systems that can be divided into anatomically and functionally distinct areas, rather than mapping individual neurons.

Dozens of investigators and researchers from nine institutions have contributed to this project. Research institutions include: Washington University in Saint Louis, the Center for Magnetic Resonance Research at the University of Minnesota, Oxford University, Saint Louis University, Indiana University, D'Annunzio University of Chieti–Pescara, Ernst Strungmann Institute, Warwick University, Advanced MRI Technologies, and the University of California at Berkeley.

The data that results from this research is being made publicly available in an open-source web-accessible neuroinformatics platform.

MGH/Harvard-UCLA consortium

The MGH/Harvard-UCLA consortium will focus on optimizing MRI technology for imaging the brain’s structural connections using diffusion MRI, with a goal of increasing spatial resolution, quality, and speed. Diffusion MRI, employed in both projects, maps the brain's fibrous long distance connections by tracking the motion of water. Water diffusion patterns in different types of cells allow the detection of different types of tissues. Using this imaging method, the long extensions of neurons, called white matter, can be seen in sharp relief.

The new scanner built at the MGH Martinos Center for this project is "4 to 8 times as powerful as conventional systems, enabling imaging of human neuroanatomy with greater sensitivity than was previously possible." The scanner has a maximum gradient strength of 300 mT/m and a slew rate of 200 T/m/s, with b-values tested up to 20,000. For comparison, a standard gradient is 45 mT/m, with a b-value of 700.

Behavioral testing and measurement

To understand the relationship between brain connectivity and behavior better, the Human Connectome Project will use a reliable and well-validated battery of measures that assess a wide range of human functions. The core of its battery is the tools and methods developed by the NIH Toolbox for Assessment of Neurological and Behavioral function.

Research

The Human Connectome Project has grown into a large group of research teams. These teams make use of the style of brain scanning developed by the Project. The studies usually include using large groups of participants, scanning many angles of participants' brains, and carefully documenting the location of the structures in each participant's brain. Studies affiliated with the Human Connectome Project are currently cataloged by the Connectome Coordination Facility. The studies fall into three categories: Healthy Adult Connectomes, Lifespan Connectome Data, and Connectomes Related to Human Disease. Under each of these categories are research groups working on specific questions.

Healthy Adult Connectomes

The Human Connectome Project Young Adult study made data on the brain connections of 1100 healthy young adults available to the scientific community. Scientists have used data from the study to support theories about which areas of the brain communicate with one another. For example, one study used data from the project to show that the amygdala, a part of the brain essential for emotional processing, is connected to the parts of the brain that receive information from the senses and plan movement. Another study showed that healthy individuals who had a high tendency to experience anxious or depressed mood had fewer connections between the amygdala and a number of brain areas related to attention.

Lifespan Connectome Data

There are currently four research groups collecting data on connections in the brains of populations other than young adults. The purpose of these groups is to determine ordinary brain connectivity during infancy, childhood, adolescence, and aging. Scientists will use the data from these research groups in the same manner in which they have used data from the Human Connectome Project Young Adult study.

Connectomes Related to Human Disease

Fourteen research groups investigate how connections in the brain change during the course of a particular disease. Four of the groups focus on Alzheimer's disease or dementia. Alzheimer's disease and dementia are diseases that begin during aging. Memory loss and cognitive impairment mark the progression of these diseases. While scientists consider Alzheimer's disease to be a disease with a specific cause, dementia actually describes symptoms which could be attributed to a number of causes. Two other research groups investigate how diseases that disrupt vision change connectivity in the brain. Another four of the research groups focus on anxiety disorders and major depressive disorder, psychological disorders that result in abnormal emotional regulation. Two more of the research groups focus on the effects of psychosis, a symptom of some psychological disorders in which an individual perceives reality differently than others do. One of the teams researches epilepsy, a disease characterized by seizures. Finally, one research team is documenting the brain connections of the Amish people, a religious and ethnic group that has high rates of some psychological disorders.

Although theories have been put forth about the way brain connections change in the diseases under investigation, many of these theories have been supported by data from healthy populations. For example, an analysis of the brains of healthy individuals supported the theory that individuals with anxiety disorders and depression have less connectivity between their emotional centers and the areas that govern attention. By collecting data specifically from individuals with these diseases, researchers hope to have a more certain idea of how brain connections in these individuals change over time.

Status

The project has yet to be officially declared complete.

Connectome

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Connectome 

 

White matter tracts within a human brain, as visualized by MRI tractography

Rendering of a group connectome based on 20 subjects. Anatomical fibers that constitute the white matter architecture of the human brain are visualized color-coded by traversing direction (xyz-directions mapping to RGB colors respectively). Visualization of fibers was done using TrackVis software.

A connectome (/kəˈnɛktoʊm/) is a comprehensive map of neural connections in the brain, and may be thought of as its "wiring diagram". More broadly, a connectome would include the mapping of all neural connections within an organism's nervous system.

The production and study of connectomes, known as connectomics, may range in scale from a detailed map of the full set of neurons and synapses within part or all of the nervous system of an organism to a macro scale description of the functional and structural connectivity between all cortical areas and subcortical structures. The term "connectome" is used primarily in scientific efforts to capture, map, and understand the organization of neural interactions within the brain.

Research has successfully constructed the full connectome of one animal: the roundworm Caenorhabditis elegans, beginning with the first electron micrographs published by White, Brenner et al., 1986. Based on this seminal work, the first ever connectome (then called "neural circuitry database" by the authors) for C. elegans was published in book form with accompanying floppy disks by Achacoso and Yamamoto in 1992, with the very first paper on the computer representation of its connectome presented and published three years earlier in 1989 by Achacoso at the Symposium on Computer Application in Medical Care (SCAMC). The C. elegans connectome was later revised and expanded across development. Partial connectomes of a mouse retina and mouse primary visual cortex have also been successfully constructed. Other reconstructions, such as a 12-terabyte dataset by Bock et al. from 2011, are publicly available through NeuroData and other services.

The ultimate goal of connectomics is to map the human brain. This effort is pursued by the Human Connectome Project, sponsored by the National Institutes of Health (NIH), whose focus is to build a network map of the human brain in healthy, living adults. Whereas the already mapped roundworm has a total of 302 neurons in its brain, a human has 86 billion.

Origin and usage of the term

In 2005, Dr. Olaf Sporns at Indiana University and Dr. Patric Hagmann at Lausanne University Hospital independently and simultaneously suggested the term "connectome" to refer to a map of the neural connections within the brain. This term was directly inspired by the ongoing effort to sequence the human genetic code—to build a genome.

"Connectomics" (Hagmann, 2005) has been defined as the science concerned with assembling and analyzing connectome data sets.

In their 2005 paper, "The Human Connectome, a structural description of the human brain", Sporns et al. wrote:

To understand the functioning of a network, one must know its elements and their interconnections. The purpose of this article is to discuss research strategies aimed at a comprehensive structural description of the network of elements and connections forming the human brain. We propose to call this dataset the human "connectome," and we argue that it is fundamentally important in cognitive neuroscience and neuropsychology. The connectome will significantly increase our understanding of how functional brain states emerge from their underlying structural substrate, and will provide new mechanistic insights into how brain function is affected if this structural substrate is disrupted.

In his 2005 Ph.D. thesis, From diffusion MRI to brain connectomics, Hagmann wrote:

It is clear that, like the genome, which is much more than just a juxtaposition of genes, the set of all neuronal connections in the brain is much more than the sum of their individual components. The genome is an entity it-self, as it is from the subtle gene interaction that [life] emerges. In a similar manner, one could consider the brain connectome, set of all neuronal connections, as one single entity, thus emphasizing the fact that the huge brain neuronal communication capacity and computational power critically relies on this subtle and incredibly complex connectivity architecture.

Pathways through cerebral white matter can be charted by histological dissection and staining, by degeneration methods, and by axonal tracing. Axonal tracing methods form the primary basis for the systematic charting of long-distance pathways into extensive, species-specific anatomical connection matrices between gray matter regions. Landmark studies have included the areas and connections of the visual cortex of the macaque (Felleman and Van Essen, 1991) and the thalamocortical system in the feline brain (Scannell et al., 1999). The development of neuroinformatics databases for anatomical connectivity allow for continual updating and refinement of such anatomical connection maps. The online macaque cortex connectivity tool CoCoMac (Kötter, 2004) and the temporal lobe connectome of the rat are prominent examples of such a database.

In the human brain, the significance of the connectome stems from the realization that the structure and function of the human brain are intricately linked, through multiple levels and modes of brain connectivity. There are strong natural constraints on which neurons or neural populations can interact, or how strong or direct their interactions are. Indeed, the foundation of human cognition lies in the pattern of dynamic interactions shaped by the connectome.

However, structure-function relationships in the brain are unlikely to reduce to simple one-to-one mappings. In fact, the connectome can evidently support a great number of variable dynamic states, depending on current sensory inputs, global brain state, learning and development. Some changes in functional state may involve rapid changes of structural connectivity at the synaptic level, as has been elucidated by two-photon imaging experiments showing the rapid appearance and disappearance of dendritic spines (Bonhoeffer and Yuste, 2002).

Despite such complex and variable structure-function mappings, the connectome is an indispensable basis for the mechanistic interpretation of dynamic brain data, from single-cell recordings to functional neuroimaging.

The term "connectome" was more recently popularized by Sebastian Seung's I am my Connectome speech given at the 2010 TED conference, which discusses the high-level goals of mapping the human connectome, as well as ongoing efforts to build a three-dimensional neural map of brain tissue at the microscale. In 2012, Seung published the book Connectome: How the Brain's Wiring Makes Us Who We Are.

At multiple scales

Brain networks can be defined at different levels of scale, corresponding to levels of spatial resolution in brain imaging (Kötter, 2007, Sporns, 2010). These scales can be roughly categorized as microscale, mesoscale and macroscale. Ultimately, it may be possible to join connectomic maps obtained at different scales into a single hierarchical map of the neural organization of a given species that ranges from single neurons to populations of neurons to larger systems like cortical areas. Given the methodological uncertainties involved in inferring connectivity from the primary experimental data, and given that there are likely to be large differences in the connectomes of different individuals, any unified map will likely rely on probabilistic representations of connectivity data (Sporns et al., 2005).

Mapping the connectome at the "microscale" (micrometer resolution) means building a complete map of the neural systems, neuron-by-neuron. The challenge of doing this becomes obvious: the number of neurons comprising the brain easily ranges into the billions in more complex organisms. The human cerebral cortex alone contains on the order of 10¹⁰ neurons linked by 10¹⁴ synaptic connections. By comparison, the number of base-pairs in a human genome is 3×10⁹. A few of the main challenges of building a human connectome at the microscale today include: data collection would take years given current technology, machine vision tools to annotate the data remain in their infancy, and are inadequate, and neither theory nor algorithms are readily available for the analysis of the resulting brain-graphs. To address the data collection issues, several groups are building high-throughput serial electron microscopes (Kasthuri et al., 2009; Bock et al. 2011). To address the machine-vision and image-processing issues, the Open Connectome Project is alg-sourcing (algorithm outsourcing) this hurdle. Finally, statistical graph theory is an emerging discipline which is developing sophisticated pattern recognition and inference tools to parse these brain-graphs (Goldenberg et al., 2009).

A "mesoscale" connectome corresponds to a spatial resolution of hundreds of micrometers. Rather than attempt to map each individual neuron, a connectome at the mesoscale would attempt to capture anatomically and/or functionally distinct neuronal populations, formed by local circuits (e.g. cortical columns) that link hundreds or thousands of individual neurons. This scale still presents a very ambitious technical challenge at this time and can only be probed on a small scale with invasive techniques or very high field magnetic resonance imaging (MRI) on a local scale.

A connectome at the macroscale (millimeter resolution) attempts to capture large brain systems that can be parcellated into anatomically distinct modules (areas, parcels or nodes), each having a distinct pattern of connectivity. Connectomic databases at the mesoscale and macroscale may be significantly more compact than those at cellular resolution, but they require effective strategies for accurate anatomical or functional parcellation of the neural volume into network nodes (for complexities see, e.g., Wallace et al., 2004).

Mapping at the cellular level

Current non-invasive imaging techniques cannot capture the brain's activity on a neuron-by-neuron level. Mapping the connectome at the cellular level in vertebrates currently requires post-mortem (after death) microscopic analysis of limited portions of brain tissue. Non-optical techniques that rely on high-throughput DNA sequencing have been proposed recently by Anthony Zador (CSHL).

Traditional histological circuit-mapping approaches rely on imaging and include light-microscopic techniques for cell staining, injection of labeling agents for tract tracing, or chemical brain preservation, staining and reconstruction of serially sectioned tissue blocks via electron microscopy (EM). Each of these classical approaches has specific drawbacks when it comes to deployment for connectomics. The staining of single cells, e.g. with the Golgi stain, to trace cellular processes and connectivity suffers from the limited resolution of light-microscopy as well as difficulties in capturing long-range projections. Tract tracing, often described as the "gold standard" of neuroanatomy for detecting long-range pathways across the brain, generally only allows the tracing of fairly large cell populations and single axonal pathways. EM reconstruction was successfully used for the compilation of the C. elegans connectome (White et al., 1986). However, applications to larger tissue blocks of entire nervous systems have traditionally had difficulty with projections that span longer distances.

Recent advances in mapping neural connectivity at the cellular level offer significant new hope for overcoming the limitations of classical techniques and for compiling cellular connectome data sets (Livet et al., 2007; Lichtman et al., 2008). Using Brainbow, a combinatorial color labeling method based on the stochastic expression of several fluorescent proteins, Jeff W. Lichtman and colleagues were able to mark individual neurons with one of over 100 distinct colors. The labeling of individual neurons with a distinguishable hue then allows the tracing and reconstruction of their cellular structure including long processes within a block of tissue.

In March 2011, the journal Nature published a pair of articles on micro-connectomes: Bock et al. and Briggman et al. In both articles, the authors first characterized the functional properties of a small subset of cells, and then manually traced a subset of the processes emanating from those cells to obtain a partial subgraph. In alignment with the principles of open science, the authors of Bock et al. (2011) have released their data for public access. The full resolution 12 terabyte dataset from Bock et al. is available at NeuroData. In 2012, a citizen science project called EyeWire began attempting to crowdsource the mapping of the connectome through an interactive game. Independently, important topologies of functional interactions among several hundred cells are also gradually going to be declared (Shimono and Beggs, 2014). Scaling up ultrastructural circuit mapping to the whole mouse brain is currently underway (Mikula, 2012). An alternative approach to mapping connectivity was recently proposed by Zador and colleagues (Zador et al., 2012). Zador's technique, called BOINC (barcoding of individual neuronal connections) uses high-throughput DNA sequencing to map neural circuits. Briefly, the approach consists of labelling each neuron with a unique DNA barcode, transferring barcodes between synaptically coupled neurons (for example using Suid herpesvirus 1, SuHV1), and fusion of barcodes to represent a synaptic pair. This approach has the potential to be cheap, fast, and extremely high-throughput.

In 2016, the Intelligence Advanced Research Projects Activity of the United States government launched MICrONS, a five-year, multi-institute project to map one cubic millimeter of rodent visual cortex, as part of the BRAIN Initiative. Though only a small volume of biological tissue, this project will yield one of the largest micro-scale connectomics datasets currently in existence.

Mapping at the macro scale

Established methods of brain research, such as axonal tracing, provided early avenues for building connectome data sets. However, more recent advances in living subjects has been made by the use of non-invasive imaging technologies such as diffusion-weighted magnetic resonance imaging (DW-MRI) and functional magnetic resonance imaging (fMRI). The first, when combined with tractography allows reconstruction of the major fiber bundles in the brain. The second allows the researcher to capture the brain's network activity (either at rest or while performing directed tasks), enabling the identification of structurally and anatomically distinct areas of the brain that are functionally connected.

Notably, the goal of the Human Connectome Project, led by the WU-Minn consortium, is to build a structural and functional map of the healthy human brain at the macro scale, using a combination of multiple imaging technologies and resolutions.

Recent advances in connectivity mapping

Tractographic reconstruction of neural connections via DTI

Throughout the 2000s, several investigators have attempted to map the large-scale structural architecture of the human cerebral cortex. One attempt exploited cross-correlations in cortical thickness or volume across individuals (He et al., 2007). Such gray-matter thickness correlations have been postulated as indicators for the presence of structural connections. A drawback of the approach is that it provides highly indirect information about cortical connection patterns and requires data from large numbers of individuals to derive a single connection data set across a subject group. Other investigators have attempted to build whole-brain connection matrices from DW-MRI imaging data.

The Blue Brain Project is attempting to reconstruct the entire mouse connectome using a diamond knife sharpened to an atomic edge, and electron microscopy for imaging tissue slices.

Primary challenge for macroscale connectomics: determining parcellations of the brain

The initial explorations in macroscale human connectomics were done using either equally sized regions or anatomical regions with unclear relationship to the underlying functional organization of the brain (e.g. gyral and sulcal-based regions). While much can be learned from these approaches, it is highly desirable to parcellate the brain into functionally distinct parcels: brain regions with distinct architectonics, connectivity, function, and/or topography (Felleman and Van Essen, 1991). Accurate parcellation allows each node in the macroscale connectome to be more informative by associating it with a distinct connectivity pattern and functional profile. Parcellation of localized areas of cortex have been accomplished using diffusion tractography (Beckmann et al. 2009) and functional connectivity (Nelson et al. 2010) to non-invasively measure connectivity patterns and define cortical areas based on distinct connectivity patterns. Such analyses may best be done on a whole brain scale and by integrating non-invasive modalities. Accurate whole brain parcellation may lead to more accurate macroscale connectomes for the normal brain, which can then be compared to disease states.

Plasticity of the connectome

At the beginning of the connectome project, it was thought that the connections between neurons were unchangeable once established and that only individual synapses could be altered. However, recent evidence suggests that connectivity is also subject to change, termed neuroplasticity. There are two ways that the brain can rewire: formation and removal of synapses in an established connection or formation or removal of entire connections between neurons. Both mechanisms of rewiring are useful for learning completely novel tasks that may require entirely new connections between regions of the brain. However, the ability of the brain to gain or lose entire connections poses an issue for mapping a universal species connectome. Although rewiring happens on different scales, from microscale to macroscale, each scale does not occur in isolation. For example, in the C. elegans connectome, the total number of synapses increases 5-fold from birth to adulthood, changing both local and global network properties.

Microscale rewiring

Microscale rewiring is the formation or removal of synaptic connections between two neurons and can be studied with longitudinal two-photon imaging. Dendritic spines on pyramidal neurons can be shown forming within days following sensory experience and learning. Changes can even be seen within five hours on apical tufts of layer five pyramidal neurons in the primary motor cortex after a seed reaching task in primates.

Mesoscale rewiring

Rewiring at the mesoscale involves studying the presence or absence of entire connections between neurons. Evidence for this level of rewiring comes from observations that local circuits form new connections as a result of experience-dependent plasticity in the visual cortex. Additionally, the number of local connections between pyramidal neurons in the primary somatosensory cortex increases following altered whisker sensory experience in rodents.

Macroscale rewiring

Evidence for macroscale rewiring mostly comes from research on grey and white matter density, which could indicate new connections or changes in axon density. Direct evidence for this level of rewiring comes from primate studies, using viral tracing to map the formation of connections. Primates that were taught to use novel tools developed new connections between the interparietal cortex and higher visual areas of the brain. Further viral tracing studies have provided evidence that macroscale rewiring occurs in adult animals during associative learning. However, it is not likely that long-distance neural connections undergo extensive rewiring in adults. Small changes in an already established nerve tract are likely what is observed in macroscale rewiring.

Mapping functional connectivity to complement anatomical connectivity

Using fMRI in the resting state and during tasks, functions of the connectome circuits are being studied. Just as detailed road maps of the Earth's surface do not tell us much about the kind of vehicles that travel those roads or what cargo they are hauling, to understand how neural structures result in specific functional behavior such as consciousness, it is necessary to build theories that relate functions to anatomical connectivity. However, the bond between structural and functional connectivity is not straightforward. Computational models of whole-brain network dynamics are valuable tools to investigate the role of the anatomical network in shaping functional connectivity. In particular, computational models can be used to predict the dynamic effect of lesions in the connectome.

As a network or graph

The connectome can be studied as a network by means of network science and graph theory. In case of a micro-scale connectome, the nodes of this network (or graph) are the neurons, and the edges correspond to the synapses between those neurons. For the macro-scale connectome, the nodes correspond to the ROIs (regions of interest), while the edges of the graph are derived from the axons interconnecting those areas. Thus connectomes are sometimes referred to as brain graphs, as they are indeed graphs in a mathematical sense which describe the connections in the brain (or, in a broader sense, the whole nervous system).

One group of researchers (Iturria-Medina et al., 2008) has constructed connectome data sets using diffusion tensor imaging (DTI) followed by the derivation of average connection probabilities between 70–90 cortical and basal brain gray matter areas. All networks were found to have small-world attributes and "broad-scale" degree distributions. An analysis of betweenness centrality in these networks demonstrated high centrality for the precuneus, the insula, the superior parietal and the superior frontal cortex. Another group (Gong et al. 2008) has applied DTI to map a network of anatomical connections between 78 cortical regions. This study also identified several hub regions in the human brain, including the precuneus and the superior frontal gyrus.

Hagmann et al. (2007) constructed a connection matrix from fiber densities measured between homogeneously distributed and equal-sized ROIs numbering between 500 and 4000. A quantitative analysis of connection matrices obtained for approximately 1,000 ROIs and approximately 50,000 fiber pathways from two subjects demonstrated an exponential (one-scale) degree distribution as well as robust small-world attributes for the network. The data sets were derived from diffusion spectrum imaging (DSI) (Wedeen, 2005), a variant of diffusion-weighted imaging that is sensitive to intra-voxel heterogeneities in diffusion directions caused by crossing fiber tracts and thus allows more accurate mapping of axonal trajectories than other diffusion imaging approaches (Wedeen, 2008). The combination of whole-head DSI datasets acquired and processed according to the approach developed by Hagmann et al. (2007) with the graph analysis tools conceived initially for animal tracing studies (Sporns, 2006; Sporns, 2007) allow a detailed study of the network structure of human cortical connectivity (Hagmann et al., 2008). The human brain network was characterized using a broad array of network analysis methods including core decomposition, modularity analysis, hub classification and centrality. Hagmann et al. presented evidence for the existence of a structural core of highly and mutually interconnected brain regions, located primarily in posterior medial and parietal cortex. The core comprises portions of the posterior cingulate cortex, the precuneus, the cuneus, the paracentral lobule, the isthmus of the cingulate, the banks of the superior temporal sulcus, and the inferior and superior parietal cortex, all located in both cerebral hemispheres.

A subfield of connectomics deals with the comparison of the brain graphs of multiple subjects. It is possible to build a consensus graph such the Budapest Reference Connectome by allowing only edges that are present in at least ${\displaystyle k}$ connectomes, for a selectable ${\displaystyle k}$ parameter. The Budapest Reference Connectome has led the researchers to the discovery of the Consensus Connectome Dynamics of the human brain graphs. The edges appeared in all of the brain graphs form a connected subgraph around the brainstem. By allowing gradually less frequent edges, this core subgraph grows continuously, as a shrub. The growth dynamics may reflect the individual brain development and provide an opportunity to direct some edges of the human consensus brain graph.

Alternatively, local difference which are statistically significantly different among groups have attracted more attention as they highlight specific connections and therefore shed more light on specific brain traits or pathology. Hence, algorithms to find local difference between graph populations have also been introduced (e.g. to compare case versus control groups). Those can be found by using either an adjusted t-test, or a sparsity model, with the aim of finding statistically significant connections which are different among those groups.

The possible causes of the difference between individual connectomes were also investigated. Indeed, it has been found that the macro-scale connectomes of women contain significantly more edges than those of men, and a larger portion of the edges in the connectomes of women run between the two hemispheres. In addition, connectomes generally exhibit a small-world character, with overall cortical connectivity decreasing with age. The aim of the as of 2015 ongoing HCP Lifespan Pilot Project is to identify connectome differences between 6 age groups (4–6, 8–9, 14–15, 25–35, 45–55, 65–75).

More recently, connectograms have been used to visualize full-brain data by placing cortical areas around a circle, organized by lobe. Inner circles then depict cortical metrics on a color scale. White matter fiber connections in DTI data are then drawn between these cortical regions and weighted by fractional anisotropy and strength of the connection. Such graphs have even been used to analyze the damage done to the famous traumatic brain injury patient Phineas Gage.

Statistical graph theory is an emerging discipline which is developing sophisticated pattern recognition and inference tools to parse these brain graphs (Goldenberg et al., 2009).

Recent research studied the brain as a signed network and indicated that hubness in positive and negative subnetworks increases the stability of the brain network. It highlighted the role of negative functional connections that are paid less attention to.