Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, to compare the duration of events or the intervals between them, and to quantify rates of change of quantities in material reality or in the conscious experience. Time is often referred to as a fourth dimension, along with three spatial dimensions.
Time has long been an important subject of study in religion, philosophy, and science, but defining it in a manner applicable to all fields without circularity has consistently eluded scholars. Nevertheless, diverse fields such as business, industry, sports, the sciences, and the performing arts all incorporate some notion of time into their respective measuring systems.
Time in physics is operationally defined as "what a clock reads".
The physical nature of time is addressed by general relativity with respect to events in space-time. Examples of events are the collision of two particles, the explosion of a supernova, or the arrival of a rocket ship. Every event can be assigned four numbers representing its time and position (the event's coordinates). However, the numerical values are different for different observers. In general relativity, the question of what time it is now only has meaning relative to a particular observer. Distance and time are intimately related and the time required for light to travel a specific distance is the same for all observers, as first publicly demonstrated by Michelson and Morley. General relativity does not address the nature of time for extremely small intervals where quantum mechanics holds. At this time, there is no generally accepted theory of quantum general relativity.
Time is one of the seven fundamental physical quantities in both the International System of Units (SI) and International System of Quantities. The SI base unit of time is the second. Time is used to define other quantities – such as velocity – so defining time in terms of such quantities would result in circularity of definition. An operational definition of time, wherein one says that observing a certain number of repetitions of one or another standard cyclical event (such as the passage of a free-swinging pendulum) constitutes one standard unit such as the second, is highly useful in the conduct of both advanced experiments and everyday affairs of life. To describe observations of an event, a location (position in space) and time are typically noted.
The operational definition of time does not address what the fundamental nature of it is. It does not address why events can happen forward and backward in space, whereas events only happen in the forward progress of time. Investigations into the relationship between space and time led physicists to define the spacetime continuum. General relativity is the primary framework for understanding how spacetime works. Through advances in both theoretical and experimental investigations of space-time, it has been shown that time can be distorted and dilated, particularly at the edges of black holes.
Temporal measurement has occupied scientists and technologists, and was a prime motivation in navigation and astronomy. Periodic events and periodic motion have long served as standards for units of time. Examples include the apparent motion of the sun across the sky, the phases of the moon, the swing of a pendulum, and the beat of a heart. Currently, the international unit of time, the second, is defined by measuring the electronic transition frequency of caesium atoms. Time is also of significant social importance, having economic value ("time is money") as well as personal value, due to an awareness of the limited time in each day and in human life spans.
There are many systems for determining what time it is, including the Global Positioning System, other satellite systems, Coordinated Universal Time and mean solar time. In general, the numbers obtained from different time systems differ from one another.
Measurement
Generally speaking, methods of temporal measurement, or chronometry, take two distinct forms: the calendar, a mathematical tool for organising intervals of time, and the clock, a physical mechanism that counts the passage of time. In day-to-day life, the clock is consulted for periods less than a day whereas the calendar is consulted for periods longer than a day. Increasingly, personal electronic devices display both calendars and clocks simultaneously. The number (as on a clock dial or calendar) that marks the occurrence of a specified event as to hour or date is obtained by counting from a fiducial epoch – a central reference point.
History of the calendar
Artifacts from the Paleolithic suggest that the moon was used to reckon time as early as 6,000 years ago. Lunar calendars were among the first to appear, with years of either 12 or 13 lunar months (either 354 or 384 days). Without intercalation to add days or months to some years, seasons quickly drift in a calendar based solely on twelve lunar months. Lunisolar calendars have a thirteenth month added to some years to make up for the difference between a full year (now known to be about 365.24 days) and a year of just twelve lunar months. The numbers twelve and thirteen came to feature prominently in many cultures, at least partly due to this relationship of months to years. Other early forms of calendars originated in Mesoamerica, particularly in ancient Mayan civilization. These calendars were religiously and astronomically based, with 18 months in a year and 20 days in a month, plus five epagomenal days at the end of the year.
The reforms of Julius Caesar in 45 BC put the Roman world on a solar calendar. This Julian calendar was faulty in that its intercalation still allowed the astronomical solstices and equinoxes to advance against it by about 11 minutes per year. Pope Gregory XIII introduced a correction in 1582; the Gregorian calendar was only slowly adopted by different nations over a period of centuries, but it is now by far the most commonly used calendar around the world.
During the French Revolution, a new clock and calendar were invented in an attempt to de-Christianize time and create a more rational system in order to replace the Gregorian calendar. The French Republican Calendar's days consisted of ten hours of a hundred minutes of a hundred seconds, which marked a deviation from the base 12 (duodecimal) system used in many other devices by many cultures. The system was abolished in 1806.
History of other devices
A large variety of devices have been invented to measure time. The study of these devices is called horology.
An Egyptian device that dates to c. 1500 BC, similar in shape to a bent T-square, measured the passage of time from the shadow cast by its crossbar on a nonlinear rule. The T was oriented eastward in the mornings. At noon, the device was turned around so that it could cast its shadow in the evening direction.
A sundial uses a gnomon to cast a shadow on a set of markings calibrated to the hour. The position of the shadow marks the hour in local time. The idea to separate the day into smaller parts is credited to Egyptians because of their sundials, which operated on a duodecimal system. The importance of the number 12 is due to the number of lunar cycles in a year and the number of stars used to count the passage of night.
The most precise timekeeping device of the ancient world was the water clock, or clepsydra, one of which was found in the tomb of Egyptian pharaoh Amenhotep I. They could be used to measure the hours even at night but required manual upkeep to replenish the flow of water. The ancient Greeks and the people from Chaldea (southeastern Mesopotamia) regularly maintained timekeeping records as an essential part of their astronomical observations. Arab inventors and engineers, in particular, made improvements on the use of water clocks up to the Middle Ages. In the 11th century, Chinese inventors and engineers invented the first mechanical clocks driven by an escapement mechanism.
The hourglass uses the flow of sand to measure the flow of time. They were used in navigation. Ferdinand Magellan used 18 glasses on each ship for his circumnavigation of the globe (1522).
Incense sticks and candles were, and are, commonly used to measure time in temples and churches across the globe. Waterclocks, and later, mechanical clocks, were used to mark the events of the abbeys and monasteries of the Middle Ages. Richard of Wallingford (1292–1336), abbot of St. Alban's abbey, famously built a mechanical clock as an astronomical orrery about 1330.
Great advances in accurate time-keeping were made by Galileo Galilei and especially Christiaan Huygens with the invention of pendulum-driven clocks along with the invention of the minute hand by Jost Burgi.
The English word clock probably comes from the Middle Dutch word klocke which, in turn, derives from the medieval Latin word clocca, which ultimately derives from Celtic and is cognate with French, Latin, and German words that mean bell. The passage of the hours at sea was marked by bells and denoted the time (see ship's bell). The hours were marked by bells in abbeys as well as at sea.
Clocks can range from watches to more exotic varieties such as the Clock of the Long Now. They can be driven by a variety of means, including gravity, springs, and various forms of electrical power, and regulated by a variety of means such as a pendulum.
Alarm clocks first appeared in ancient Greece around 250 BC with a water clock that would set off a whistle. This idea was later mechanized by Levi Hutchins and Seth E. Thomas.
A chronometer is a portable timekeeper that meets certain precision standards. Initially, the term was used to refer to the marine chronometer, a timepiece used to determine longitude by means of celestial navigation, a precision firstly achieved by John Harrison. More recently, the term has also been applied to the chronometer watch, a watch that meets precision standards set by the Swiss agency COSC.
The most accurate timekeeping devices are atomic clocks, which are accurate to seconds in many millions of years, and are used to calibrate other clocks and timekeeping instruments.
Atomic clocks use the frequency of electronic transitions in certain atoms to measure the second. One of the atoms used is caesium, most modern atomic clocks probe caesium with microwaves to determine the frequency of these electron vibrations. Since 1967, the International System of Measurements bases its unit of time, the second, on the properties of caesium atoms. SI defines the second as 9,192,631,770 cycles of the radiation that corresponds to the transition between two electron spin energy levels of the ground state of the 133Cs atom.
Today, the Global Positioning System in coordination with the Network Time Protocol can be used to synchronize timekeeping systems across the globe.
In medieval philosophical writings, the atom was a unit of time referred to as the smallest possible division of time. The earliest known occurrence in English is in Byrhtferth's Enchiridion (a science text) of 1010–1012, where it was defined as 1/564 of a momentum (1½ minutes), and thus equal to 15/94 of a second. It was used in the computus, the process of calculating the date of Easter.
As of May 2010, the smallest time interval uncertainty in direct measurements is on the order of 12 attoseconds (1.2 × 10−17 seconds), about 3.7 × 1026 Planck times.
Units
The second (s) is the SI base unit. A minute (min) is 60 seconds in length, and an hour is 60 minutes or 3600 seconds in length. A day is usually 24 hours or 86,400 seconds in length; however, the duration of a calendar day can vary due to Daylight saving time and Leap seconds.
Definitions and standards
The Mean Solar Time system defines the second as 1/86,400 of the mean solar day, which is the year-average of the solar day. The solar day is the time interval between two successive solar noons, i.e., the time interval between two successive passages of the Sun across the local meridian. The local meridian is an imaginary line that runs from celestial north pole to celestial south pole passing directly over the head of the observer. At the local meridian, the Sun reaches its highest point on its daily arc across the sky.
In 1874 the British Association for the Advancement of Science introduced the CGS (centimetre/gramme/second system) combining fundamental units of length, mass and time. The second is "elastic", because tidal friction is slowing the earth's rotation rate. For use in calculating ephemerides of celestial motion, therefore, in 1952 astronomers introduced the "ephemeris second", currently defined as
the fraction 1/31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time.
The CGS system has been superseded by the Système international. The SI base unit for time is the SI second. The International System of Quantities, which incorporates the SI, also defines larger units of time equal to fixed integer multiples of one second (1 s), such as the minute, hour and day. These are not part of the SI, but may be used alongside the SI. Other units of time such as the month and the year are not equal to fixed multiples of 1 s, and instead exhibit significant variations in duration.
The official SI definition of the second is as follows:
The second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom.
At its 1997 meeting, the CIPM affirmed that this definition refers to a caesium atom in its ground state at a temperature of 0 K.
The current definition of the second, coupled with the current definition of the meter, is based on the special theory of relativity, which affirms our spacetime to be a Minkowski space. The definition of the second in mean solar time, however, is unchanged.
UTC
While in theory, the concept of a single worldwide universal time-scale may have been conceived of many centuries ago, in practicality the technical ability to create and maintain such a time-scale did not become possible until the mid-19th century. The timescale adopted was Greenwich Mean Time, created in 1847. A few countries have replaced it with Coordinated Universal Time, UTC.
History of development
With the advent of the industrial revolution, a greater understanding and agreement on the nature of time itself became increasingly necessary and helpful. In 1847 in Britain, Greenwich Mean Time (GMT) was first created for use by the British railways, the British navy, and the British shipping industry. Using telescopes, GMT was calibrated to the mean solar time at the Royal Observatory, Greenwich in the UK.
As international commerce continued to increase throughout Europe, in order to achieve a more efficiently functioning modern society, an agreed-upon, and highly accurate international standard of time measurement became necessary. In order to find or determine such a time-standard, three steps had to be followed:
- An internationally agreed-upon time-standard had to be defined.
- This new time-standard then had to be consistently and accurately measured.
- The new time-standard then had to be freely shared and distributed around the world.
The development of what is now known as UTC time began as a collaboration between 41 nations, officially agreed and signed at the International Meridian Conference, in Washington D.C. in 1884. At this conference, the local mean solar time at the Royal Observatory, Greenwich in England was chosen to define the "universal day", counted from 0 hours at Greenwich mean midnight. This agreed with the civil Greenwich Mean Time used on the island of Great Britain since 1847. In contrast, astronomical GMT began at mean noon, i.e. astronomical day X began at noon of civil day X. The purpose of this was to keep one night's observations under one date. The civil system was adopted as of 0 hours (civil) 1 January 1925. Nautical GMT began 24 hours before astronomical GMT, at least until 1805 in the Royal Navy, but persisted much later elsewhere because it was mentioned at the 1884 conference. In 1884, the Greenwich meridian was used for two-thirds of all charts and maps as their Prime Meridian.
Among the 41 nations represented at the conference, the advanced time-technologies that had already come into use in Britain were fundamental components of the agreed method of arriving at a universal and agreed international time. In 1928 Greenwich Mean Time was rebranded for scientific purposes by the International Astronomical Union as Universal Time (UT). This was to avoid confusion with the previous system in which the day had begun at noon. As the general public had always begun the day at midnight, the timescale continued to be presented to them as Greenwich Mean Time. By 1956, universal time had been split into various versions: UT2, which smoothed for polar motion and seasonal effects, was presented to the public as Greenwich Mean Time. Later, UT1 (which smooths only for polar motion) became the default form of UT used by astronomers and hence the form used in navigation, sunrise and sunset and moonrise and moonset tables where the name Greenwich Mean Time continues to be employed. Greenwich Mean Time is also the preferred method of describing the timescale used by legislators. Even to the present day, UT is still based on an international telescopic system. Observations at the Greenwich Observatory itself ceased in 1954, though the location is still used as the basis for the coordinate system. Because the rotational period of Earth is not perfectly constant, the duration of a second would vary if calibrated to a telescope-based standard like GMT, where the second is defined as 1/86 400 of the mean solar day.
Until 1960, the methods and definitions of time-keeping that had been laid out at the International Meridian Conference proved to be adequate to meet the time tracking needs of science. Still, with the advent of the "electronic revolution" in the latter half of the 20th century, the technologies that had been available at the time of the Convention of the Metre proved to be in need of further refinement in order to meet the needs of the ever-increasing precision that the "electronic revolution" had begun to require.
Ephemeris second
An invariable second (the "ephemeris second") had been defined, use of which removed the errors in ephemerides resulting from the use of the variable mean solar second as the time argument. In 1960 this ephemeris second was made the basis of the "coordinated universal time" which was being derived from atomic clocks. It is a specified fraction of the mean tropical year as at 1900 and, being based on historical telescope observations, corresponds roughly to the mean solar second of the early nineteenth century.
SI second
In 1967 a further step was taken with the introduction of the SI second, essentially the ephemeris second as measured by atomic clocks and formally defined in atomic terms. The SI second (Standard Internationale second) is based directly on the measurement of the atomic-clock observation of the frequency oscillation of caesium atoms. It is the basis of all atomic timescales, e.g. coordinated universal time, GPS time, International Atomic Time, etc. Atomic clocks do not measure nuclear decay rates (a common misconception) but rather measure a certain natural vibrational frequency of caesium-133. Coordinated universal time is subject to one constraint which does not affect the other atomic timescales. As it has been adopted as the civil timescale by some countries (most countries have opted to retain mean solar time) it is not permitted to deviate from GMT by more than 0.9 second. This is achieved by the occasional insertion of a leap second.
Current application
Most countries use mean solar time. Australia, Canada (Quebec only), Colombia, France, Germany, New Zealand, Papua New Guinea (Bougainville only), Paraguay, Portugal, Switzerland, the United States and Venezuela use UTC. However, UTC is widely used by the scientific community in countries where mean solar time is official. UTC time is based on the SI second, which was first defined in 1967, and is based on the use of atomic clocks. Some other less used but closely related time-standards include International Atomic Time (TAI), Terrestrial Time, and Barycentric Dynamical Time.
Between 1967 and 1971, UTC was periodically adjusted by fractional amounts of a second in order to adjust and refine for variations in mean solar time, with which it is aligned. After 1 January 1972, UTC time has been defined as being offset from atomic time by a whole number of seconds, changing only when a leap second is added to keep radio-controlled clocks synchronized with the rotation of the Earth.
The Global Positioning System also broadcasts a very precise time signal worldwide, along with instructions for converting GPS time to UTC. GPS-time is based on, and regularly synchronized with or from, UTC-time.
The surface of the Earth is split up into a number of time zones. Most time zones are exactly one hour apart, and by convention compute their local time as an offset from GMT. For example, time zones at sea are based on GMT. In many locations (but not at sea) these offsets vary twice yearly due to daylight saving time transitions.
Conversions
These conversions are accurate at the millisecond level for time systems based on the rotation of the Earth (UT1 and TT). Conversions between atomic time systems (TAI, GPS, and UTC) are accurate at the microsecond level.
| System | Description | UT1 | UTC | TT | TAI | GPS |
|---|---|---|---|---|---|---|
| UT1 | Mean Solar Time | UT1 | UTC = UT1 – DUT1 | TT = UT1 + 32.184 s + LS – DUT1 | TAI = UT1 – DUT1 + LS | GPS = UT1 – DUT1 + LS – 19 s |
| UTC | Civil Time | UT1 = UTC + DUT1 | UTC | TT = UTC + 32.184 s + LS | TAI = UTC + LS | GPS = UTC + LS – 19 s |
| TT | Terrestrial (Ephemeris) Time | UT1 = TT – 32.184 s – LS + DUT1 | UTC = TT – 32.184 s – LS | TT | TAI = TT – 32.184 s | GPS = TT – 51.184 s |
| TAI | Atomic Time | UT1 = TAI + DUT1 – LS | UTC = TAI – LS | TT = TAI + 32.184 s | TAI | GPS = TAI – 19 s |
| GPS | GPS Time | UT1 = GPS + DUT1 – LS + 19 s | UTC = GPS – LS + 19 s | TT = GPS + 51.184 s | TAI = GPS + 19 s | GPS |
Definitions:
- LS = TAI – UTC = Leap Seconds from TAI to UTC
- DUT1 = UT1 – UTC from UT1 to UTC or http://maia.usno.navy.mil/search/search.html
Sidereality
Unlike solar time, which is relative to the apparent position of the Sun, sidereal time is the measurement of time relative to that of a distant star. In astronomy, sidereal time is used to predict when a star will reach its highest point in the sky. Due to Earth's orbital motion around the Sun, a mean solar day is about 3 minutes 56 seconds longer than a mean sidereal day, or 1⁄366 more than a mean sidereal day.
Chronology
Another form of time measurement consists of studying the past. Events in the past can be ordered in a sequence (creating a chronology), and can be put into chronological groups (periodization). One of the most important systems of periodization is the geologic time scale, which is a system of periodizing the events that shaped the Earth and its life. Chronology, periodization, and interpretation of the past are together known as the study of history.
Terminology
The term "time" is generally used for many close but different concepts, including:
- instant as an object – one point on the time axes. Being an object, it has no value;
- date as a quantity characterising an instant. As a quantity, it has a value which may be expressed in a variety of ways, for example "2014-04-26T09:42:36,75" in ISO standard format, or more colloquially such as "today, 9:42 a.m.";
- time interval as an object – part of the time axes limited by two instants. Being an object, it has no value;
- duration as a quantity characterizing a time interval. As a quantity, it has a value, such as a number of minutes, or may be described in terms of the quantities (such as times and dates) of its beginning and end.
Philosophy
Religion
Linear and cyclical
Ancient cultures such as Incan, Mayan, Hopi, and other Native American Tribes – plus the Babylonians, ancient Greeks, Hinduism, Buddhism, Jainism, and others – have a concept of a wheel of time: they regard time as cyclical and quantic, consisting of repeating ages that happen to every being of the Universe between birth and extinction.
In general, the Islamic and Judeo-Christian world-view regards time as linear and directional, beginning with the act of creation by God. The traditional Christian view sees time ending, teleologically, with the eschatological end of the present order of things, the "end time".
In the Old Testament book Ecclesiastes, traditionally ascribed to Solomon (970–928 BC), time (as the Hebrew word עידן, זמן iddan (age, as in "Ice age") zĕman(time) is often translated) was traditionally regarded as a medium for the passage of predestined events. (Another word, زمان" זמן" zamān, meant time fit for an event, and is used as the modern Arabic, Persian, and Hebrew equivalent to the English word "time".)
Time in Greek mythology
The Greek language denotes two distinct principles, Chronos and Kairos. The former refers to numeric, or chronological, time. The latter, literally "the right or opportune moment", relates specifically to metaphysical or Divine time. In theology, Kairos is qualitative, as opposed to quantitative.
In Greek mythology, Chronos (ancient Greek: Χρόνος) is identified as the Personification of Time. His name in Greek means "time" and is alternatively spelled Chronus (Latin spelling) or Khronos. Chronos is usually portrayed as an old, wise man with a long, gray beard, such as "Father Time". Some English words whose etymological root is khronos/chronos include chronology, chronometer, chronic, anachronism, synchronise, and chronicle.
Time in Kabbalah
According to Kabbalists, "time" is a paradox and an illusion. Both the future and the past are recognised to be combined and simultaneously present.
In Western philosophy
Two contrasting viewpoints on time divide prominent philosophers. One view is that time is part of the fundamental structure of the universe – a dimension independent of events, in which events occur in sequence. Isaac Newton subscribed to this realist view, and hence it is sometimes referred to as Newtonian time. The opposing view is that time does not refer to any kind of "container" that events and objects "move through", nor to any entity that "flows", but that it is instead part of a fundamental intellectual structure (together with space and number) within which humans sequence and compare events. This second view, in the tradition of Gottfried Leibniz and Immanuel Kant, holds that time is neither an event nor a thing, and thus is not itself measurable nor can it be travelled.
Furthermore, it may be that there is a subjective component to time, but whether or not time itself is "felt", as a sensation, or is a judgment, is a matter of debate.
In Philosophy, time was questioned throughout the centuries; what time is and if it is real or not. Ancient Greek philosophers asked if time was linear or cyclical and if time was endless or finite. These philosophers had different ways of explaining time; for instance, ancient Indian philosophers had something called the Wheel of Time. It is believed that there was repeating ages over the lifespan of the universe. This led to beliefs like cycles of rebirth and reincarnation. The Greek philosophers believe that the universe was infinite, and was an illusion to humans. Plato believed that time was made by the Creator at the same instant as the heavens. He also says that time is a period of motion of the heavenly bodies. Aristotle believed that time correlated to movement, that time did not exist on its own but was relative to motion of objects. he also believed that time was related to the motion of celestial bodies; the reason that humans can tell time was because of orbital periods and therefore there was a duration on time.
The Vedas, the earliest texts on Indian philosophy and Hindu philosophy dating back to the late 2nd millennium BC, describe ancient Hindu cosmology, in which the universe goes through repeated cycles of creation, destruction and rebirth, with each cycle lasting 4,320 million years. Ancient Greek philosophers, including Parmenides and Heraclitus, wrote essays on the nature of time. Plato, in the Timaeus, identified time with the period of motion of the heavenly bodies. Aristotle, in Book IV of his Physica defined time as 'number of movement in respect of the before and after'.
In Book 11 of his Confessions, St. Augustine of Hippo ruminates on the nature of time, asking, "What then is time? If no one asks me, I know: if I wish to explain it to one that asketh, I know not." He begins to define time by what it is not rather than what it is, an approach similar to that taken in other negative definitions. However, Augustine ends up calling time a "distention" of the mind (Confessions 11.26) by which we simultaneously grasp the past in memory, the present by attention, and the future by expectation.
Isaac Newton believed in absolute space and absolute time; Leibniz believed that time and space are relational. The differences between Leibniz's and Newton's interpretations came to a head in the famous Leibniz–Clarke correspondence.
Philosophers in the 17th and 18th century questioned if time was real and absolute, or if it was an intellectual concept that humans use to understand and sequence events. These questions lead to realism vs anti-realism; the realists believed that time is a fundamental part of the universe, and be perceived by events happening in a sequence, in a dimension. Isaac Newton said that we are merely occupying time, he also says that humans can only understand relative time. Relative time is a measurement of objects in motion. The anti-realists believed that time is merely a convenient intellectual concept for humans to understand events. This means that time was useless unless there were objects that it could interact with, this was called relational time. René Descartes, John Locke, and David Hume said that one's mind needs to acknowledge time, in order to understand what time is. Immanuel Kant believed that we can not know what something is unless we experience it first hand.
Time is not an empirical concept. For neither co-existence nor succession would be perceived by us, if the representation of time did not exist as a foundation a priori. Without this presupposition, we could not represent to ourselves that things exist together at one and the same time, or at different times, that is, contemporaneously, or in succession.
Immanuel Kant, Critique of Pure Reason (1781), trans. Vasilis Politis (London: Dent., 1991), p.54.
Immanuel Kant, in the Critique of Pure Reason, described time as an a priori intuition that allows us (together with the other a priori intuition, space) to comprehend sense experience. With Kant, neither space nor time are conceived as substances, but rather both are elements of a systematic mental framework that necessarily structures the experiences of any rational agent, or observing subject. Kant thought of time as a fundamental part of an abstract conceptual framework, together with space and number, within which we sequence events, quantify their duration, and compare the motions of objects. In this view, time does not refer to any kind of entity that "flows," that objects "move through," or that is a "container" for events. Spatial measurements are used to quantify the extent of and distances between objects, and temporal measurements are used to quantify the durations of and between events. Time was designated by Kant as the purest possible schema of a pure concept or category.
Henri Bergson believed that time was neither a real homogeneous medium nor a mental construct, but possesses what he referred to as Duration. Duration, in Bergson's view, was creativity and memory as an essential component of reality.
According to Martin Heidegger we do not exist inside time, we are time. Hence, the relationship to the past is a present awareness of having been, which allows the past to exist in the present. The relationship to the future is the state of anticipating a potential possibility, task, or engagement. It is related to the human propensity for caring and being concerned, which causes "being ahead of oneself" when thinking of a pending occurrence. Therefore, this concern for a potential occurrence also allows the future to exist in the present. The present becomes an experience, which is qualitative instead of quantitative. Heidegger seems to think this is the way that a linear relationship with time, or temporal existence, is broken or transcended. We are not stuck in sequential time. We are able to remember the past and project into the future – we have a kind of random access to our representation of temporal existence; we can, in our thoughts, step out of (ecstasis) sequential time.
Modern era philosophers asked: is time real or unreal, is time happening all at once or a duration, If time tensed or tenseless, and is there a future to be? There is a theory called the tenseless or B-theory; this theory says that any tensed terminology can be replaced with tenseless terminology. For example, "we will win the game" can be replaced with "we do win the game", taking out the future tense. On the other hand, there is a theory called the tense or A-theory; this theory says that our language has tense verbs for a reason and that the future can not be determined. There is also something called imaginary time, this was from Stephen Hawking, he says that space and imaginary time are finite but have no boundaries. Imaginary time is not real or unreal, it is something that is hard to visualize. Philosophers can agree that physical time exists outside of the human mind and is objective, and psychological time is mind-dependent and subjective.
Unreality
In 5th century BC Greece, Antiphon the Sophist, in a fragment preserved from his chief work On Truth, held that: "Time is not a reality (hypostasis), but a concept (noêma) or a measure (metron)." Parmenides went further, maintaining that time, motion, and change were illusions, leading to the paradoxes of his follower Zeno. Time as an illusion is also a common theme in Buddhist thought.
J. M. E. McTaggart's 1908 The Unreality of Time argues that, since every event has the characteristic of being both present and not present (i.e., future or past), that time is a self-contradictory idea.
These arguments often center on what it means for something to be unreal. Modern physicists generally believe that time is as real as space – though others, such as Julian Barbour in his book The End of Time, argue that quantum equations of the universe take their true form when expressed in the timeless realm containing every possible now or momentary configuration of the universe, called "platonia" by Barbour.
A modern philosophical theory called presentism views the past and the future as human-mind interpretations of movement instead of real parts of time (or "dimensions") which coexist with the present. This theory rejects the existence of all direct interaction with the past or the future, holding only the present as tangible. This is one of the philosophical arguments against time travel. This contrasts with eternalism (all time: present, past and future, is real) and the growing block theory (the present and the past are real, but the future is not).
Physical definition
Until Einstein's reinterpretation of the physical concepts associated with time and space in 1907, time was considered to be the same everywhere in the universe, with all observers measuring the same time interval for any event. Non-relativistic classical mechanics is based on this Newtonian idea of time.
Einstein, in his special theory of relativity, postulated the constancy and finiteness of the speed of light for all observers. He showed that this postulate, together with a reasonable definition for what it means for two events to be simultaneous, requires that distances appear compressed and time intervals appear lengthened for events associated with objects in motion relative to an inertial observer.
The theory of special relativity finds a convenient formulation in Minkowski spacetime, a mathematical structure that combines three dimensions of space with a single dimension of time. In this formalism, distances in space can be measured by how long light takes to travel that distance, e.g., a light-year is a measure of distance, and a meter is now defined in terms of how far light travels in a certain amount of time. Two events in Minkowski spacetime are separated by an invariant interval, which can be either space-like, light-like, or time-like. Events that have a time-like separation cannot be simultaneous in any frame of reference, there must be a temporal component (and possibly a spatial one) to their separation. Events that have a space-like separation will be simultaneous in some frame of reference, and there is no frame of reference in which they do not have a spatial separation. Different observers may calculate different distances and different time intervals between two events, but the invariant interval between the events is independent of the observer (and his or her velocity).
Classical mechanics
In non-relativistic classical mechanics, Newton's concept of "relative, apparent, and common time" can be used in the formulation of a prescription for the synchronization of clocks. Events seen by two different observers in motion relative to each other produce a mathematical concept of time that works sufficiently well for describing the everyday phenomena of most people's experience. In the late nineteenth century, physicists encountered problems with the classical understanding of time, in connection with the behavior of electricity and magnetism. Einstein resolved these problems by invoking a method of synchronizing clocks using the constant, finite speed of light as the maximum signal velocity. This led directly to the conclusion that observers in motion relative to one another measure different elapsed times for the same event.
Spacetime
Time has historically been closely related with space, the two together merging into spacetime in Einstein's special relativity and general relativity. According to these theories, the concept of time depends on the spatial reference frame of the observer, and the human perception, as well as the measurement by instruments such as clocks, are different for observers in relative motion. For example, if a spaceship carrying a clock flies through space at (very nearly) the speed of light, its crew does not notice a change in the speed of time on board their vessel because everything traveling at the same speed slows down at the same rate (including the clock, the crew's thought processes, and the functions of their bodies). However, to a stationary observer watching the spaceship fly by, the spaceship appears flattened in the direction it is traveling and the clock on board the spaceship appears to move very slowly.
On the other hand, the crew on board the spaceship also perceives the observer as slowed down and flattened along the spaceship's direction of travel, because both are moving at very nearly the speed of light relative to each other. Because the outside universe appears flattened to the spaceship, the crew perceives themselves as quickly traveling between regions of space that (to the stationary observer) are many light years apart. This is reconciled by the fact that the crew's perception of time is different from the stationary observer's; what seems like seconds to the crew might be hundreds of years to the stationary observer. In either case, however, causality remains unchanged: the past is the set of events that can send light signals to an entity and the future is the set of events to which an entity can send light signals.
Dilation
Einstein showed in his thought experiments that people travelling at different speeds, while agreeing on cause and effect, measure different time separations between events, and can even observe different chronological orderings between non-causally related events. Though these effects are typically minute in the human experience, the effect becomes much more pronounced for objects moving at speeds approaching the speed of light. Subatomic particles exist for a well-known average fraction of a second in a lab relatively at rest, but when travelling close to the speed of light they are measured to travel farther and exist for much longer than when at rest. According to the special theory of relativity, in the high-speed particle's frame of reference, it exists, on the average, for a standard amount of time known as its mean lifetime, and the distance it travels in that time is zero, because its velocity is zero. Relative to a frame of reference at rest, time seems to "slow down" for the particle. Relative to the high-speed particle, distances seem to shorten. Einstein showed how both temporal and spatial dimensions can be altered (or "warped") by high-speed motion.
Einstein (The Meaning of Relativity): "Two events taking place at the points A and B of a system K are simultaneous if they appear at the same instant when observed from the middle point, M, of the interval AB. Time is then defined as the ensemble of the indications of similar clocks, at rest relative to K, which register the same simultaneously."
Einstein wrote in his book, Relativity, that simultaneity is also relative, i.e., two events that appear simultaneous to an observer in a particular inertial reference frame need not be judged as simultaneous by a second observer in a different inertial frame of reference.
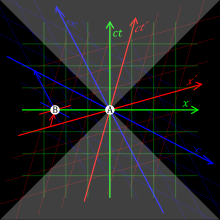
Relativistic versus Newtonian

The animations visualise the different treatments of time in the Newtonian and the relativistic descriptions. At the heart of these differences are the Galilean and Lorentz transformations applicable in the Newtonian and relativistic theories, respectively.
In the figures, the vertical direction indicates time. The horizontal direction indicates distance (only one spatial dimension is taken into account), and the thick dashed curve is the spacetime trajectory ("world line") of the observer. The small dots indicate specific (past and future) events in spacetime.
The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how in both pictures the view of spacetime changes when the observer accelerates.
In the Newtonian description these changes are such that time is absolute: the movements of the observer do not influence whether an event occurs in the 'now' (i.e., whether an event passes the horizontal line through the observer).
However, in the relativistic description the observability of events is absolute: the movements of the observer do not influence whether an event passes the "light cone" of the observer. Notice that with the change from a Newtonian to a relativistic description, the concept of absolute time is no longer applicable: events move up and down in the figure depending on the acceleration of the observer.
Arrow
Time appears to have a direction – the past lies behind, fixed and immutable, while the future lies ahead and is not necessarily fixed. Yet for the most part, the laws of physics do not specify an arrow of time, and allow any process to proceed both forward and in reverse. This is generally a consequence of time being modelled by a parameter in the system being analysed, where there is no "proper time": the direction of the arrow of time is sometimes arbitrary. Examples of this include the cosmological arrow of time, which points away from the Big Bang, CPT symmetry, and the radiative arrow of time, caused by light only travelling forwards in time (see light cone). In particle physics, the violation of CP symmetry implies that there should be a small counterbalancing time asymmetry to preserve CPT symmetry as stated above. The standard description of measurement in quantum mechanics is also time asymmetric (see Measurement in quantum mechanics). The second law of thermodynamics states that entropy must increase over time (see Entropy). This can be in either direction – Brian Greene theorizes that, according to the equations, the change in entropy occurs symmetrically whether going forward or backward in time. So entropy tends to increase in either direction, and our current low-entropy universe is a statistical aberration, in a similar manner as tossing a coin often enough that eventually heads will result ten times in a row. However, this theory is not supported empirically in local experiment.
Quantization
Time quantization is a hypothetical concept. In the modern established physical theories (the Standard Model of Particles and Interactions and General Relativity) time is not quantized.
Planck time (~ 5.4 × 10−44 seconds) is the unit of time in the system of natural units known as Planck units. Current established physical theories are believed to fail at this time scale, and many physicists expect that the Planck time might be the smallest unit of time that could ever be measured, even in principle. Tentative physical theories that describe this time scale exist; see for instance loop quantum gravity.
Travel
Time travel is the concept of moving backwards or forwards to different points in time, in a manner analogous to moving through space, and different from the normal "flow" of time to an earthbound observer. In this view, all points in time (including future times) "persist" in some way. Time travel has been a plot device in fiction since the 19th century. Travelling backwards or forwards in time has never been verified as a process, and doing so presents many theoretical problems and contradictive logic which to date have not been overcome. Any technological device, whether fictional or hypothetical, that is used to achieve time travel is known as a time machine.
A central problem with time travel to the past is the violation of causality; should an effect precede its cause, it would give rise to the possibility of a temporal paradox. Some interpretations of time travel resolve this by accepting the possibility of travel between branch points, parallel realities, or universes.
Another solution to the problem of causality-based temporal paradoxes is that such paradoxes cannot arise simply because they have not arisen. As illustrated in numerous works of fiction, free will either ceases to exist in the past or the outcomes of such decisions are predetermined. As such, it would not be possible to enact the grandfather paradox because it is a historical fact that one's grandfather was not killed before his child (one's parent) was conceived. This view does not simply hold that history is an unchangeable constant, but that any change made by a hypothetical future time traveller would already have happened in his or her past, resulting in the reality that the traveller moves from. More elaboration on this view can be found in the Novikov self-consistency principle.
Perception
The specious present refers to the time duration wherein one's perceptions are considered to be in the present. The experienced present is said to be 'specious' in that, unlike the objective present, it is an interval and not a durationless instant. The term specious present was first introduced by the psychologist E.R. Clay, and later developed by William James.
Biopsychology
The brain's judgment of time is known to be a highly distributed system, including at least the cerebral cortex, cerebellum and basal ganglia as its components. One particular component, the suprachiasmatic nuclei, is responsible for the circadian (or daily) rhythm, while other cell clusters appear capable of shorter-range (ultradian) timekeeping.
Psychoactive drugs can impair the judgment of time. Stimulants can lead both humans and rats to overestimate time intervals, while depressants can have the opposite effect. The level of activity in the brain of neurotransmitters such as dopamine and norepinephrine may be the reason for this. Such chemicals will either excite or inhibit the firing of neurons in the brain, with a greater firing rate allowing the brain to register the occurrence of more events within a given interval (speed up time) and a decreased firing rate reducing the brain's capacity to distinguish events occurring within a given interval (slow down time).
Mental chronometry is the use of response time in perceptual-motor tasks to infer the content, duration, and temporal sequencing of cognitive operations.
Early childhood education
Children's expanding cognitive abilities allow them to understand time more clearly. Two- and three-year-olds' understanding of time is mainly limited to "now and not now". Five- and six-year-olds can grasp the ideas of past, present, and future. Seven- to ten-year-olds can use clocks and calendars.
Alterations
In addition to psychoactive drugs, judgments of time can be altered by temporal illusions (like the kappa effect), age, and hypnosis. The sense of time is impaired in some people with neurological diseases such as Parkinson's disease and attention deficit disorder.
Psychologists assert that time seems to go faster with age, but the literature on this age-related perception of time remains controversial. Those who support this notion argue that young people, having more excitatory neurotransmitters, are able to cope with faster external events.
Spatial conceptualization
Although time is regarded as an abstract concept, there is increasing evidence that time is conceptualized in the mind in terms of space. That is, instead of thinking about time in a general, abstract way, humans think about time in a spatial way and mentally organize it as such. Using space to think about time allows humans to mentally organize temporal events in a specific way.
This spatial representation of time is often represented in the mind as a Mental Time Line (MTL). Using space to think about time allows humans to mentally organize temporal order. These origins are shaped by many environmental factors––for example, literacy appears to play a large role in the different types of MTLs, as reading/writing direction provides an everyday temporal orientation that differs from culture to culture. In western cultures, the MTL may unfold rightward (with the past on the left and the future on the right) since people read and write from left to right. Western calendars also continue this trend by placing the past on the left with the future progressing toward the right. Conversely, Arabic, Farsi, Urdu and Israeli-Hebrew speakers read from right to left, and their MTLs unfold leftward (past on the right with future on the left), and evidence suggests these speakers organize time events in their minds like this as well.
This linguistic evidence that abstract concepts are based in spatial concepts also reveals that the way humans mentally organize time events varies across cultures––that is, a certain specific mental organization system is not universal. So, although Western cultures typically associate past events with the left and future events with the right according to a certain MTL, this kind of horizontal, egocentric MTL is not the spatial organization of all cultures. Although most developed nations use an egocentric spatial system, there is recent evidence that some cultures use an allocentric spatialization, often based on environmental features.
A recent study of the indigenous Yupno people of Papua New Guinea focused on the directional gestures used when individuals used time-related words. When speaking of the past (such as "last year" or "past times"), individuals gestured downhill, where the river of the valley flowed into the ocean. When speaking of the future, they gestured uphill, toward the source of the river. This was common regardless of which direction the person faced, revealing that the Yupno people may use an allocentric MTL, in which time flows uphill.
A similar study of the Pormpuraawans, an aboriginal group in Australia, revealed a similar distinction in which when asked to organize photos of a man aging "in order," individuals consistently placed the youngest photos to the east and the oldest photos to the west, regardless of which direction they faced. This directly clashed with an American group that consistently organized the photos from left to right. Therefore, this group also appears to have an allocentric MTL, but based on the cardinal directions instead of geographical features.
The wide array of distinctions in the way different groups think about time leads to the broader question that different groups may also think about other abstract concepts in different ways as well, such as causality and number.
Use
In sociology and anthropology, time discipline is the general name given to social and economic rules, conventions, customs, and expectations governing the measurement of time, the social currency and awareness of time measurements, and people's expectations concerning the observance of these customs by others. Arlie Russell Hochschild and Norbert Elias have written on the use of time from a sociological perspective.
The use of time is an important issue in understanding human behavior, education, and travel behavior. Time-use research is a developing field of study. The question concerns how time is allocated across a number of activities (such as time spent at home, at work, shopping, etc.). Time use changes with technology, as the television or the Internet created new opportunities to use time in different ways. However, some aspects of time use are relatively stable over long periods of time, such as the amount of time spent traveling to work, which despite major changes in transport, has been observed to be about 20–30 minutes one-way for a large number of cities over a long period.
Time management is the organization of tasks or events by first estimating how much time a task requires and when it must be completed, and adjusting events that would interfere with its completion so it is done in the appropriate amount of time. Calendars and day planners are common examples of time management tools.
Sequence of events
A sequence of events, or series of events, is a sequence of items, facts, events, actions, changes, or procedural steps, arranged in time order (chronological order), often with causality relationships among the items. Because of causality, cause precedes effect, or cause and effect may appear together in a single item, but effect never precedes cause. A sequence of events can be presented in text, tables, charts, or timelines. The description of the items or events may include a timestamp. A sequence of events that includes the time along with place or location information to describe a sequential path may be referred to as a world line.
Uses of a sequence of events include stories, historical events (chronology), directions and steps in procedures, and timetables for scheduling activities. A sequence of events may also be used to help describe processes in science, technology, and medicine. A sequence of events may be focused on past events (e.g., stories, history, chronology), on future events that must be in a predetermined order (e.g., plans, schedules, procedures, timetables), or focused on the observation of past events with the expectation that the events will occur in the future (e.g., processes, projections). The use of a sequence of events occurs in fields as diverse as machines (cam timer), documentaries (Seconds From Disaster), law (choice of law), finance (directional-change intrinsic time), computer simulation (discrete event simulation), and electric power transmission (sequence of events recorder). A specific example of a sequence of events is the timeline of the Fukushima Daiichi nuclear disaster.