Gulf Stream

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Gulf_Stream 

Surface temperatures in the western North Atlantic. The North American landmass is black and dark blue (cold), while the Gulf Stream is red (warm). Source: NASA

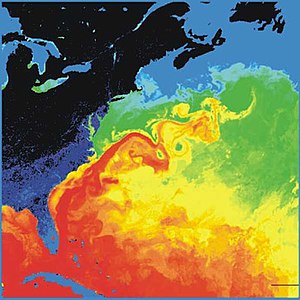
The Gulf Stream, together with its northern extension the North Atlantic Drift, is a warm and swift Atlantic ocean current that originates in the Gulf of Mexico and stretches to the tip of Florida and follows the eastern coastlines of the United States and Newfoundland before crossing the Atlantic Ocean as the North Atlantic Current. The process of western intensification causes the Gulf Stream to be a northwards accelerating current off the east coast of North America. At about 40°0′N 30°0′W, it splits in two, with the northern stream, the North Atlantic Drift, crossing to Northern Europe and the southern stream, the Canary Current, recirculating off West Africa.

The Gulf Stream influences the climate of the east coast of North America from Florida to Newfoundland and the west coast of Europe. Although there has been recent debate, there is consensus that the climate of Western Europe and Northern Europe is warmer than other areas of similar latitude because of the North Atlantic Current. It is part of the North Atlantic Gyre. Its presence has led to the development of strong cyclones of all types, both within the atmosphere and within the ocean. The Gulf Stream is also a significant potential source of renewable power generation.

History

Benjamin Franklin's chart of the Gulf Stream printed in London in 1769

European discovery of the Gulf Stream dates to the 1512 expedition of Juan Ponce de León, after which it became widely used by Spanish ships sailing from the Caribbean to Spain. A summary of Ponce de León's voyage log on April 22, 1513, noted, "A current such that, although they had great wind, they could not proceed forwards, but backwards and it seems that they were proceeding well; at the end, it was known that the current was more powerful than the wind."

Benjamin Franklin became interested in the North Atlantic Ocean circulation patterns. In 1768, while in England, Franklin heard a curious complaint from the Colonial Board of Customs: Why did it take British packets several weeks longer to reach New York from England than it took an average American merchant ship to reach Newport, Rhode Island, despite the merchant ships leaving from London and having to sail down the River Thames and then the length of the English Channel before they sailed across the Atlantic, while the packets left from Falmouth in Cornwall?

Franklin asked Timothy Folger, a Nantucket Island whaling captain, for an answer. Folger explained that merchant ships routinely crossed the current—which was identified by whale behaviour, measurement of the water's temperature, and changes in the water's colour—while the mail packet captains ran against it. Franklin had Folger sketch the path of the current on a chart of the Atlantic and add notes on how to avoid the current when sailing from England to America. Franklin then forwarded the chart to Anthony Todd, secretary of the British Post Office. Franklin's Gulf Stream chart was printed in 1769 in London, but it was mostly ignored by British sea captains. A copy of the chart was printed in Paris circa 1770–1773, and a third version was published by Franklin in Philadelphia in 1786.

Properties

The Gulf Stream proper is a western-intensified current, driven largely by wind stress. The North Atlantic Drift, in contrast, is largely driven by thermohaline circulation. In 1958, oceanographer Henry Stommel noted that "very little water from the Gulf of Mexico is actually in the stream". By carrying warm water northeast across the Atlantic, it makes Western Europe and especially Northern Europe warmer and milder than it otherwise would be.

Formation and behaviour

Evolution of the Gulf Stream to the west of Ireland continuing as the North Atlantic Current

A river of sea water, called the Atlantic North Equatorial Current, flows westwards off the coast of Central Africa. When this current interacts with the northeastern coast of South America, the current forks into two branches. One passes into the Caribbean Sea, while a second, the Antilles Current, flows north and east of the West Indies. These two branches rejoin north of the Straits of Florida.

The trade winds blow westwards in the tropics, and the westerlies blow eastwards at mid-latitudes. This wind pattern applies a stress to the subtropical ocean surface with negative curl across the north Atlantic Ocean. The resulting Sverdrup transport is equatorward.

Because of the conservation of potential vorticity caused by the northwards-moving winds on the subtropical ridge's western periphery and the increased relative vorticity of northwards moving water, transport is balanced by a narrow, accelerating polewards current. This flows along the western boundary of the ocean basin, outweighing the effects of friction with the western boundary current, and is known as the Labrador Current. The conservation of potential vorticity also causes bends along the Gulf Stream, which occasionally break off as the Gulf Stream's position shifts, forming separate warm and cold eddies. This overall process is known as western intensification, causes currents on the western boundary of an ocean basin, such as the Gulf Stream, to be stronger than those on the eastern boundary.

As a consequence, the resulting Gulf Stream is a strong ocean current. It transports water at a rate of 30 million cubic metres per second (30 sverdrups) through the Florida Straits. As it passes south of Newfoundland, this rate increases to 150 sverdrups. The volume of the Gulf Stream dwarfs all rivers that empty into the Atlantic combined, which total 0.6 sverdrups. It is weaker, however, than the Antarctic Circumpolar Current. Given the strength and proximity of the Gulf Stream, beaches along the East Coast of the United States may be more vulnerable to large sea-level anomalies, which significantly impact rates of coastal erosion.

The Gulf Stream is typically 100 kilometres (62 mi) wide and 800 metres (2,600 ft) to 1,200 metres (3,900 ft) deep. The current velocity is fastest near the surface, with the maximum speed typically about 2.5 metres per second (5.6 mph). As it travels north, the warm water transported by the Gulf Stream undergoes evaporative cooling. The cooling is wind-driven: wind moving over the water causes evaporation, cooling the water and increasing its salinity and density. When sea ice forms, salts are left out of the ice, a process known as brine exclusion. These two processes produce water that is denser and colder (or more precisely, water that is still liquid at a lower temperature). In the North Atlantic Ocean, the water becomes so dense that it begins to sink down through less salty and less dense water. (The convective action is similar to a lava lamp.) This downdraft of cold, dense water becomes a part of the North Atlantic Deep Water, a southgoing stream. Very little seaweed lies within the current, although seaweed lies in clusters to its east.

In April 2018, two studies published in Nature  found the Gulf Stream to be at its weakest for at least 1,600 years.

Localized effects

The Gulf Stream is influential on the climate of the Florida peninsula. The portion off the Florida coast, referred to as the Florida Current, maintains an average water temperature of at least 24 °C (75 °F) during the winter. East winds moving over this warm water move warm air from over the Gulf Stream inland, helping to keep temperatures milder across the state than elsewhere across the Southeastern United States during the winter. Also, the Gulf Stream's proximity to Nantucket, Massachusetts adds to its biodiversity, because it is the northern limit for southern varieties of plant life, and the southern limit for northern plant species, Nantucket being warmer during winter than the mainland.

The North Atlantic Current of the Gulf Stream, along with similar warm air currents, helps keep Ireland and the western coast of Great Britain a couple of degrees warmer than the east. However, the difference is most dramatic in the western coastal islands of Scotland. A noticeable effect of the Gulf Stream and the strong westerly winds (driven by the warm water of the Gulf Stream) on Europe occurs along the Norwegian coast. Northern parts of Norway lie close to the Arctic zone, most of which is covered with ice and snow in winter. However, almost all of Norway's coast remains free of ice and snow throughout the year. The warming effect provided by the Gulf Stream has allowed fairly large settlements to be developed and maintained on the coast of Northern Norway, including Tromsø, the third largest city north of the Arctic Circle. Weather systems warmed by the Gulf Stream drift into Northern Europe, also warming the climate behind the Scandinavian mountains.

Effect on cyclone formation

Hurricane Sandy intensifying along the axis of the Gulf Stream in 2012.

The warm water and temperature contrast along the edge of the Gulf Stream often increase the intensity of cyclones, tropical or otherwise. Tropical cyclone generation normally requires water temperatures in excess of 26.5 °C (79.7 °F). Tropical cyclone formation is common over the Gulf Stream, especially in the month of July. Storms travel westwards through the Caribbean and then either move in a northwards direction and curve towards the eastern coast of the United States or stay on a north-westwards track and enter the Gulf of Mexico. Such storms have the potential to create strong winds and extensive damage to the United States' Southeast Coastal Areas. Hurricane Sandy in 2012 was a recent example of a hurricane passing over the Gulf Stream and gaining strength.

Strong extratropical cyclones have been shown to deepen significantly along a shallow frontal zone, forced by the Gulf Stream, during the cold season. Subtropical cyclones also tend to generate near the Gulf Stream. 75 percent of such systems documented between 1951 and 2000 formed near this warm water current, with two annual peaks of activity occurring during the months of May and October. Cyclones within the ocean form under the Gulf Stream, extending as deep as 3,500 metres (11,500 ft) beneath the ocean's surface.

Possible renewable power source

The theoretical maximum energy dissipation from the Gulf Stream by turbines is in the range of 20–60 GW. One suggestion, which could theoretically supply power comparable to several nuclear power plants, would deploy a field of underwater turbines placed 300 metres (980 ft) under the centre of the core of the Gulf Stream. Ocean thermal energy could also be harnessed to produce electricity using the temperature difference between cold deep water and warm surface water.

Gulf Stream Rings

See main article: Cold Core Ring, Warm Core Ring

The Gulf Stream periodically forms rings resulting from a meander of the Gulf Stream being closed off from an alternate route distinctive from that meander, creating an independent eddy. Of these eddies, there are two types: cold core rings, which rotate cyclonically, and warm core rings, which rotate anti cyclonically. These rings have the capacity to transport the distinct biological, chemical, and physical properties of their originating waters to the new waters into which they travel.

 

Atlantic meridional overturning circulation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Atlantic_meridional_overturning_circulation 

Topographic map of the Nordic Seas and subpolar basins with surface currents (solid curves) and deep currents (dashed curves) that form a portion of the Atlantic meridional overturning circulation. Colors of curves indicate approximate temperatures.

The Atlantic meridional overturning circulation (AMOC) is the zonally integrated component of surface and deep currents in the Atlantic Ocean. It is characterized by a northward flow of warm, salty water in the upper layers of the Atlantic, and a southward flow of colder, deep waters that are part of the thermohaline circulation. These "limbs" are linked by regions of overturning in the Nordic and Labrador Seas and the Southern Ocean. The AMOC is an important component of the Earth's climate system, and is a result of both atmospheric and thermohaline drivers.

General

AMOC in relation to the global thermohaline circulation (animation)

Northward surface flow transports a substantial amount of heat energy from the tropics and Southern Hemisphere toward the North Atlantic, where the heat is lost to the atmosphere due to the strong temperature gradient. Upon losing its heat, the water becomes denser and sinks. This densification links the warm, surface limb with the cold, deep return limb at regions of convection in the Nordic and Labrador Seas. The limbs are also linked in regions of upwelling, where a divergence of surface waters causes Ekman suction and an upward flux of deep water.

AMOC consists of upper and lower cells. The upper cell consists of northward surface flow as well as southward return flow of North Atlantic Deep Water (NADW). The lower cell represents northward flow of dense Antarctic Bottom Water (AABW) – this bathes the abyssal ocean.

AMOC exerts a major control on North Atlantic sea level, particularly along the Northeast Coast of North America. Exceptional AMOC weakening during the winter of 2009–10 has been implicated in a damaging 13 cm sea level rise along the New York coastline.

There may be two stable states of the AMOC: a strong circulation (as seen over recent millenia) and a weak circulation mode, as suggested by atmosphere-ocean coupled general circulation models and Earth systems models of intermediate complexity. A number of Earth system models do not identify this bistability, however.

AMOC and climate

The net northward heat transport in the Atlantic is unique among global oceans, and is responsible for the relative warmth of the Northern Hemisphere. AMOC carries up to 25% of the northward global atmosphere-ocean heat transport in the northern hemisphere. This is generally thought to ameliorate the climate of Northwest Europe, although this effect is the subject of debate.

As well as acting as a heat pump and high-latitude heat sink, AMOC is the largest carbon sink in the Northern Hemisphere, sequestering ∼0.7 PgC/year. This sequestration has significant implications for evolution of anthropogenic global warming – especially with respect to the recent and projected future decline in AMOC vigour.

Recent decline

Paleoclimate reconstructions support the hypothesis that AMOC has undergone exceptional weakening in the last 150 years compared to the previous 1500 years, as well as a weakening of around 15% since the mid-twentieth century. Direct observations of the strength of the AMOC have been available only since 2004 from the in situ mooring array at 26°N in the Atlantic, leaving only indirect evidence of the previous AMOC behavior. While climate models predict a weakening of AMOC under global warming scenarios, the magnitude of observed and reconstructed weakening is out of step with model predictions. Observed decline in the period 2004–2014 was of a factor 10 higher than that predicted by climate models participating in Phase 5 of the Coupled Model Intercomparison Project (CMIP5). While observations of Labrador Sea outflow showed no negative trend from 1997–2009, this period is likely an atypical and weakened state. As well as an underestimation of the magnitude of decline, grain size analysis has revealed a discrepancy in the modeled timing of AMOC decline after the Little Ice Age.

A February 2021 study in Nature Geoscience reported that the preceding millennium had seen an unprecedented weakening of the AMOC, an indication that the change was caused by human actions. Its co-author said that AMOC had already slowed by about 15%, with impacts now being seen: "In 20 to 30 years it is likely to weaken further, and that will inevitably influence our weather, so we would see an increase in storms and heatwaves in Europe, and sea level rises on the east coast of the US."

An August 2021 study in Nature Climate Change analysed eight independent AMOC indices and concluded that the system is approaching collapse.

Impacts of AMOC decline

The impacts of the decline and potential shutdown of the AMOC could include losses in agricultural output, ecosystem changes, and the triggering of other climate tipping points.

Regions of overturning

Convection and return flow in the Nordic Seas

Low air temperatures at high latitudes cause substantial sea-air heat flux, driving a density increase and convection in the water column. Open ocean convection occurs in deep plumes and is particularly strong in winter when the sea-air temperature difference is largest. Of the 6 sverdrup (Sv) of dense water that flows southward over the GSR (Greenland-Scotland Ridge), 3 Sv does so via the Denmark Strait forming Denmark Strait Overflow Water (DSOW). 0.5-1 Sv flows over the Iceland-Faroe ridge and the remaining 2–2.5 Sv returns through the Faroe-Shetland Channel; these two flows form Iceland Scotland Overflow Water (ISOW). The majority of flow over the Faroe-Shetland ridge flows through the Faroe-Bank channel and soon joins that which flowed over the Iceland-Faroe ridge, to flow southward at depth along the Eastern flank of the Reykjanes Ridge. As ISOW overflows the GSR (Greenland-Scotland Ridge), it turbulently entrains intermediate density waters such as Sub-Polar Mode water and Labrador Sea Water. This grouping of water-masses then moves geostrophically southward along the East flank of Reykjanes Ridge, through the Charlie Gibbs Fracture Zone and then northward to join DSOW. These waters are sometimes referred to as Nordic Seas Overflow Water (NSOW). NSOW flows cyclonically following the surface route of the SPG (sub-polar gyre) around the Labrador Sea and further entrains Labrador Sea Water (LSW).

Convection is known to be suppressed at these high latitudes by sea-ice cover. Floating sea ice "caps" the surface, reducing the ability for heat to move from the sea to the air. This in turn reduces convection and deep return flow from the region. The summer Arctic sea ice cover has undergone dramatic retreat since satellite records began in 1979, amounting to a loss of almost 30% of the September ice cover in 39 years. Climate model simulations suggest that rapid and sustained September Arctic ice loss is likely in future 21st century climate projections.

Convection and entrainment in the Labrador Sea

Characteristically fresh LSW is formed at intermediate depths by deep convection in the central Labrador Sea, particularly during winter storms. This convection is not deep enough to penetrate into the NSOW layer which forms the deep waters of the Labrador Sea. LSW joins NSOW to move southward out of the Labrador Sea: while NSOW easily passes under the NAC at the North-West Corner, some LSW is retained. This diversion and retention by the SPG explains its presence and entrainment near the GSR (Greenland-Scotland Ridge) overflows. Most of the diverted LSW however splits off before the CGFZ (Charlie-Gibbs Fracture Zone) and remains in the western SPG. LSW production is highly dependent on sea-air heat flux and yearly production typically ranges from 3–9 Sv. ISOW is produced in proportion to the density gradient across the Iceland-Scotland Ridge and as such is sensitive to LSW production which affects the downstream density.  More indirectly, increased LSW production is associated with a strengthened SPG and hypothesised to be anticorrelated with ISOW.  This interplay confounds any simple extension of a reduction in individual overflow waters to a reduction in AMOC. LSW production is understood to have been minimal prior to the 8.2 ka event, with the SPG thought to have existed before in a weakened, non-convective state.

Atlantic upwelling

For reasons of conservation of mass, the global ocean system must upwell an equal volume of water to that downwelled. Upwelling in the Atlantic itself occurs mostly due to coastal and equatorial upwelling mechanisms.

Coastal upwelling occurs as a result of Ekman transport along the interface between land and a wind-driven current. In the Atlantic, this particularly occurs around the Canary Current and Benguela Current. Upwelling in these two regions has been modelled to be in antiphase, an effect known as "upwelling see-saw".

Equatorial upwelling generally occurs due to atmospheric forcing and divergence due to the opposing direction of the Coriolis force either side of the equator. The Atlantic features more complex mechanisms such as migration of the thermocline, particularly in the Eastern Atlantic.

Southern Ocean upwelling

North Atlantic Deep Water is primarily upwelled at the southern end of the Atlantic transect, in the Southern Ocean. This upwelling comprises the majority of upwelling normally associated with AMOC, and links it with the global circulation. On a global scale, observations suggest 80% of deepwater upwells in the Southern Ocean.

This upwelling supplies large quantities of nutrients to the surface, which supports biological activity. Surface supply of nutrients is critical to the ocean's functioning as a carbon sink on long timescales. Furthermore, upwelled water has low concentrations of dissolved carbon, as the water is typically 1000 years old and has not been sensitive to anthropogenic CO2 increases in the atmosphere. Because of its low carbon concentration, this upwelling functions as a carbon sink. Variability in the carbon sink over the observational period has been closely studied and debated. The size of the sink is understood to have decreased until 2002, and then increased until 2012.

After upwelling, the water is understood to take one of two pathways: water surfacing near to sea-ice generally forms dense bottomwater and is committed to AMOC's lower cell; water surfacing at lower latitudes moves further northward due to Ekman transport and is committed to the upper cell.

AMOC stability

Atlantic overturning is not a static feature of global circulation, but rather a sensitive function of temperature and salinity distributions as well as atmospheric forcings. Paleoceanographic reconstructions of AMOC vigour and configuration have revealed significant variations over geologic time complementing variation observed on shorter scales.

Reconstructions of a “shutdown” or “Heinrich” mode of the North Atlantic have fuelled concerns about a future collapse of the overturning circulation due to global climate change. While this possibility is described by the IPCC as “unlikely” for the 21st century, a one-word verdict conceals significant debate and uncertainty about the prospect. The physics of a shutdown would be underpinned by the Stommel Bifurcation, where increased freshwater forcing or warmer surface waters would lead to a sudden reduction in overturning from which the forcing must be substantially reduced before restart is possible.

An AMOC shutdown would be fuelled by two positive feedbacks, the accumulation of both freshwater and heat in areas of downwelling. AMOC exports freshwater from the North Atlantic, and a reduction in overturning would freshen waters and inhibit downwelling. Similar to its export of freshwater, AMOC also partitions heat in the deep-ocean in a global warming regime – it is possible that a weakened AMOC would lead to increasing global temperatures and further stratification and slowdown. However, this effect would be tempered by a concomitant reduction in warm water transport to the North Atlantic under a weakened AMOC, a negative feedback on the system.

As well as paleoceanographic reconstruction, the mechanism and likelihood of collapse has been investigated using climate models. Earth Models of Intermediate Complexity (EMICs) have historically predicted a modern AMOC to have multiple equilibria, characterised as warm, cold and shutdown modes. This is in contrast to more comprehensive models, which bias towards a stable AMOC characterised by a single equilibrium. However, doubt is cast upon this stability by a modelled northward freshwater flux which is at odds with observations. An unphysical northward flux in models acts as a negative feedback on overturning and falsely biases towards stability.

To complicate the issue of positive and negative feedbacks on temperature and salinity, the wind-driven component of AMOC is still not fully constrained. A relatively larger role of atmospheric forcing would lead to less dependency on the thermohaline factors listed above, and would render AMOC less vulnerable to temperature and salinity changes under global warming.

While a shutdown is deemed “unlikely” by the IPCC, a weakening over the 21st century is assessed as “very likely” and previous weakenings have been observed in several records. The cause of future weakening in models is a combination of surface freshening due to changing precipitation patterns in the North Atlantic and glacial melt, and greenhouse-gas induced warming from increased radiative forcing. One model suggests that an increase of 1.2 degrees at the pole would very likely weaken AMOC.

Parallel postulate

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Parallel_postulate 

 

If the sum of the interior angles α and β is less than 180°, the two straight lines, produced indefinitely, meet on that side.

In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:

If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

This postulate does not specifically talk about parallel lines; it is only a postulate related to parallelism. Euclid gave the definition of parallel lines in Book I, Definition 23 just before the five postulates.

Euclidean geometry is the study of geometry that satisfies all of Euclid's axioms, including the parallel postulate.

The postulate was long considered to be obvious or inevitable, but proofs were elusive. Eventually it was discovered that inverting the postulate gave valid, albeit different geometries. A geometry where the parallel postulate does not hold is known as a non-Euclidean geometry. Geometry that is independent of Euclid's fifth postulate (i.e., only assumes the modern equivalent of the first four postulates) is known as absolute geometry (or sometimes "neutral geometry").

Equivalent properties

Probably the best known equivalent of Euclid's parallel postulate, contingent on his other postulates, is Playfair's axiom, named after the Scottish mathematician John Playfair, which states:

In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.

This axiom by itself is not logically equivalent to the Euclidean parallel postulate since there are geometries in which one is true and the other is not. However, in the presence of the remaining axioms which give Euclidean geometry, each of these can be used to prove the other, so they are equivalent in the context of absolute geometry.

Many other statements equivalent to the parallel postulate have been suggested, some of them appearing at first to be unrelated to parallelism, and some seeming so self-evident that they were unconsciously assumed by people who claimed to have proven the parallel postulate from Euclid's other postulates. These equivalent statements include:

1. There is at most one line that can be drawn parallel to another given one through an external point. (Playfair's axiom)
2. The sum of the angles in every triangle is 180° (triangle postulate).
3. There exists a triangle whose angles add up to 180°.
4. The sum of the angles is the same for every triangle.
5. There exists a pair of similar, but not congruent, triangles.
6. Every triangle can be circumscribed.
7. If three angles of a quadrilateral are right angles, then the fourth angle is also a right angle.
8. There exists a quadrilateral in which all angles are right angles, that is, a rectangle.
9. There exists a pair of straight lines that are at constant distance from each other.
10. Two lines that are parallel to the same line are also parallel to each other.
11. In a right-angled triangle, the square of the hypotenuse equals the sum of the squares of the other two sides (Pythagoras' Theorem).
12. The Law of cosines, a generalization of Pythagoras' Theorem.
13. There is no upper limit to the area of a triangle. (Wallis axiom)
14. The summit angles of the Saccheri quadrilateral are 90°.
15. If a line intersects one of two parallel lines, both of which are coplanar with the original line, then it also intersects the other. (Proclus' axiom)

However, the alternatives which employ the word "parallel" cease appearing so simple when one is obliged to explain which of the four common definitions of "parallel" is meant – constant separation, never meeting, same angles where crossed by some third line, or same angles where crossed by any third line – since the equivalence of these four is itself one of the unconsciously obvious assumptions equivalent to Euclid's fifth postulate. In the list above, it is always taken to refer to non-intersecting lines. For example, if the word "parallel" in Playfair's axiom is taken to mean 'constant separation' or 'same angles where crossed by any third line', then it is no longer equivalent to Euclid's fifth postulate, and is provable from the first four (the axiom says 'There is at most one line...', which is consistent with there being no such lines). However, if the definition is taken so that parallel lines are lines that do not intersect, or that have some line intersecting them in the same angles, Playfair's axiom is contextually equivalent to Euclid's fifth postulate and is thus logically independent of the first four postulates. Note that the latter two definitions are not equivalent, because in hyperbolic geometry the second definition holds only for ultraparallel lines.

History

For two thousand years, many attempts were made to prove the parallel postulate using Euclid's first four postulates. The main reason that such a proof was so highly sought after was that, unlike the first four postulates, the parallel postulate is not self-evident. If the order the postulates were listed in the Elements is significant, it indicates that Euclid included this postulate only when he realised he could not prove it or proceed without it. Many attempts were made to prove the fifth postulate from the other four, many of them being accepted as proofs for long periods until the mistake was found. Invariably the mistake was assuming some 'obvious' property which turned out to be equivalent to the fifth postulate (Playfair's axiom). Although known from the time of Proclus, this became known as Playfair's Axiom after John Playfair wrote a famous commentary on Euclid in 1795 in which he proposed replacing Euclid's fifth postulate by his own axiom.

Proclus (410–485) wrote a commentary on The Elements where he comments on attempted proofs to deduce the fifth postulate from the other four; in particular, he notes that Ptolemy had produced a false 'proof'. Proclus then goes on to give a false proof of his own. However, he did give a postulate which is equivalent to the fifth postulate.

Ibn al-Haytham (Alhazen) (965-1039), an Arab mathematician, made an attempt at proving the parallel postulate using a proof by contradiction, in the course of which he introduced the concept of motion and transformation into geometry. He formulated the Lambert quadrilateral, which Boris Abramovich Rozenfeld names the "Ibn al-Haytham–Lambert quadrilateral", and his attempted proof contains elements similar to those found in Lambert quadrilaterals and Playfair's axiom.

The Persian mathematician, astronomer, philosopher, and poet Omar Khayyám (1050–1123), attempted to prove the fifth postulate from another explicitly given postulate (based on the fourth of the five principles due to the Philosopher (Aristotle), namely, "Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge." He derived some of the earlier results belonging to elliptical geometry and hyperbolic geometry, though his postulate excluded the latter possibility. The Saccheri quadrilateral was also first considered by Omar Khayyám in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid. Unlike many commentators on Euclid before and after him (including Giovanni Girolamo Saccheri), Khayyám was not trying to prove the parallel postulate as such but to derive it from his equivalent postulate. He recognized that three possibilities arose from omitting Euclid's fifth postulate; if two perpendiculars to one line cross another line, judicious choice of the last can make the internal angles where it meets the two perpendiculars equal (it is then parallel to the first line). If those equal internal angles are right angles, we get Euclid's fifth postulate, otherwise, they must be either acute or obtuse. He showed that the acute and obtuse cases led to contradictions using his postulate, but his postulate is now known to be equivalent to the fifth postulate.

Nasir al-Din al-Tusi (1201–1274), in his Al-risala al-shafiya'an al-shakk fi'l-khutut al-mutawaziya (Discussion Which Removes Doubt about Parallel Lines) (1250), wrote detailed critiques of the parallel postulate and on Khayyám's attempted proof a century earlier. Nasir al-Din attempted to derive a proof by contradiction of the parallel postulate. He also considered the cases of what are now known as elliptical and hyperbolic geometry, though he ruled out both of them.

Euclidean, elliptical and hyperbolic geometry. The Parallel Postulate is satisfied only for models of Euclidean geometry.

Nasir al-Din's son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), wrote a book on the subject in 1298, based on his father's later thoughts, which presented one of the earliest arguments for a non-Euclidean hypothesis equivalent to the parallel postulate. "He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the Elements." His work was published in Rome in 1594 and was studied by European geometers. This work marked the starting point for Saccheri's work on the subject which opened with a criticism of Sadr al-Din's work and the work of Wallis.

Giordano Vitale (1633-1711), in his book Euclide restituo (1680, 1686), used the Khayyam-Saccheri quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant. Girolamo Saccheri (1667-1733) pursued the same line of reasoning more thoroughly, correctly obtaining absurdity from the obtuse case (proceeding, like Euclid, from the implicit assumption that lines can be extended indefinitely and have infinite length), but failing to refute the acute case (although he managed to wrongly persuade himself that he had).

In 1766 Johann Lambert wrote, but did not publish, Theorie der Parallellinien in which he attempted, as Saccheri did, to prove the fifth postulate. He worked with a figure that today we call a Lambert quadrilateral, a quadrilateral with three right angles (can be considered half of a Saccheri quadrilateral). He quickly eliminated the possibility that the fourth angle is obtuse, as had Saccheri and Khayyám, and then proceeded to prove many theorems under the assumption of an acute angle. Unlike Saccheri, he never felt that he had reached a contradiction with this assumption. He had proved the non-Euclidean result that the sum of the angles in a triangle increases as the area of the triangle decreases, and this led him to speculate on the possibility of a model of the acute case on a sphere of imaginary radius. He did not carry this idea any further.

Where Khayyám and Saccheri had attempted to prove Euclid's fifth by disproving the only possible alternatives, the nineteenth century finally saw mathematicians exploring those alternatives and discovering the logically consistent geometries which result. In 1829, Nikolai Ivanovich Lobachevsky published an account of acute geometry in an obscure Russian journal (later re-published in 1840 in German). In 1831, János Bolyai included, in a book by his father, an appendix describing acute geometry, which, doubtlessly, he had developed independently of Lobachevsky. Carl Friedrich Gauss had also studied the problem, but he did not publish any of his results. Upon hearing of Bolyai's results in a letter from Bolyai's father, Farkas Bolyai, Gauss stated:

"If I commenced by saying that I am unable to praise this work, you would certainly be surprised for a moment. But I cannot say otherwise. To praise it would be to praise myself. Indeed the whole contents of the work, the path taken by your son, the results to which he is led, coincide almost entirely with my meditations, which have occupied my mind partly for the last thirty or thirty-five years."

The resulting geometries were later developed by Lobachevsky, Riemann and Poincaré into hyperbolic geometry (the acute case) and elliptic geometry (the obtuse case). The independence of the parallel postulate from Euclid's other axioms was finally demonstrated by Eugenio Beltrami in 1868.

Converse of Euclid's parallel postulate

The converse of the parallel postulate: If the sum of the two interior angles equals 180°, then the lines are parallel and will never intersect.

Euclid did not postulate the converse of his fifth postulate, which is one way to distinguish Euclidean geometry from elliptic geometry. The Elements contains the proof of an equivalent statement (Book I, Proposition 27): If a straight line falling on two straight lines make the alternate angles equal to one another, the straight lines will be parallel to one another. As De Morgan pointed out, this is logically equivalent to (Book I, Proposition 16). These results do not depend upon the fifth postulate, but they do require the second postulate which is violated in elliptic geometry.

Criticism

Attempts to logically prove the parallel postulate, rather than the eighth axiom, were criticized by Arthur Schopenhauer in The World as Will and Idea. However, the argument used by Schopenhauer was that the postulate is evident by perception, not that it was not a logical consequence of the other axioms.

Decomposition of the parallel postulate

The parallel postulate is equivalent, as shown in, to the conjunction of the Lotschnittaxiom and of Aristotle's axiom. The former states that the perpendiculars to the sides of a right angle intersect, while the latter states that there is no upper bound for the lengths of the distances from the leg of an angle to the other leg. As shown in, the parallel postulate is equivalent to the conjunction of the following incidence-geometric forms of the Lotschnittaxiom and of Aristotle's axiom:

Given three parallel lines, there is a line that intersects all three of them.

Given a line a and two distinct intersecting lines m and n, each different from a, there exists a line g which intersects a and m, but not n.

 

Euclid's Elements

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Euclid%27s_Elements 

 

Elements

Title page of Sir Henry Billingsley's first English version of Euclid's Elements, 1570
Author	Euclid
Language	Ancient Greek
Subject	Euclidean geometry, elementary number theory, incommensurable lines
Genre	Mathematics
Publication date	c. 300 BC
Pages	13 books

The Elements (Ancient Greek: Στοιχεῖον Stoikheîon) is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt c. 300 BC. It is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. Elements is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19th century.

Euclid's Elements has been referred to as the most successful and influential textbook ever written. It was one of the very earliest mathematical works to be printed after the invention of the printing press and has been estimated to be second only to the Bible in the number of editions published since the first printing in 1482, the number reaching well over one thousand. For centuries, when the quadrivium was included in the curriculum of all university students, knowledge of at least part of Euclid's Elements was required of all students. Not until the 20th century, by which time its content was universally taught through other school textbooks, did it cease to be considered something all educated people had read.

Geometry emerged as an indispensable part of the standard education of the English gentleman in the eighteenth century; by the Victorian period it was also becoming an important part of the education of artisans, children at Board Schools, colonial subjects and, to a rather lesser degree, women. The standard textbook for this purpose was none other than Euclid's The Elements.

History

A fragment of Euclid's Elements on part of the Oxyrhynchus papyri

Basis in earlier work

An illumination from a manuscript based on Adelard of Bath's translation of the Elements, c. 1309–1316; Adelard's is the oldest surviving translation of the Elements into Latin, done in the 12th-century work and translated from Arabic.

Scholars believe that the Elements is largely a compilation of propositions based on books by earlier Greek mathematicians.

Proclus (412–485 AD), a Greek mathematician who lived around seven centuries after Euclid, wrote in his commentary on the Elements: "Euclid, who put together the Elements, collecting many of Eudoxus' theorems, perfecting many of Theaetetus', and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors".

Pythagoras (c. 570–495 BC) was probably the source for most of books I and II, Hippocrates of Chios (c. 470–410 BC, not the better known Hippocrates of Kos) for book III, and Eudoxus of Cnidus (c. 408–355 BC) for book V, while books IV, VI, XI, and XII probably came from other Pythagorean or Athenian mathematicians. The Elements may have been based on an earlier textbook by Hippocrates of Chios, who also may have originated the use of letters to refer to figures.

Transmission of the text

In the 4th century AD, Theon of Alexandria produced an edition of Euclid which was so widely used that it became the only surviving source until François Peyrard's 1808 discovery at the Vatican of a manuscript not derived from Theon's. This manuscript, the Heiberg manuscript, is from a Byzantine workshop around 900 and is the basis of modern editions. Papyrus Oxyrhynchus 29 is a tiny fragment of an even older manuscript, but only contains the statement of one proposition.

Although Euclid was known to Cicero, for instance, no record exists of the text having been translated into Latin prior to Boethius in the fifth or sixth century. The Arabs received the Elements from the Byzantines around 760; this version was translated into Arabic under Harun al Rashid (c. 800). The Byzantine scholar Arethas commissioned the copying of one of the extant Greek manuscripts of Euclid in the late ninth century. Although known in Byzantium, the Elements was lost to Western Europe until about 1120, when the English monk Adelard of Bath translated it into Latin from an Arabic translation.

Euclidis – Elementorum libri XV Paris, Hieronymum de Marnef & Guillaume Cavelat, 1573 (second edition after the 1557 ed.); in 8:350, (2)pp. THOMAS–STANFORD, Early Editions of Euclid's Elements, n°32. Mentioned in T.L. Heath's translation. Private collection Hector Zenil.

The first printed edition appeared in 1482 (based on Campanus of Novara's 1260 edition), and since then it has been translated into many languages and published in about a thousand different editions. Theon's Greek edition was recovered in 1533. In 1570, John Dee provided a widely respected "Mathematical Preface", along with copious notes and supplementary material, to the first English edition by Henry Billingsley.

Copies of the Greek text still exist, some of which can be found in the Vatican Library and the Bodleian Library in Oxford. The manuscripts available are of variable quality, and invariably incomplete. By careful analysis of the translations and originals, hypotheses have been made about the contents of the original text (copies of which are no longer available).

Ancient texts which refer to the Elements itself, and to other mathematical theories that were current at the time it was written, are also important in this process. Such analyses are conducted by J. L. Heiberg and Sir Thomas Little Heath in their editions of the text.

Also of importance are the scholia, or annotations to the text. These additions, which often distinguished themselves from the main text (depending on the manuscript), gradually accumulated over time as opinions varied upon what was worthy of explanation or further study.

Influence

A page with marginalia from the first printed edition of Elements, printed by Erhard Ratdolt in 1482

The Elements is still considered a masterpiece in the application of logic to mathematics. In historical context, it has proven enormously influential in many areas of science. Scientists Nicolaus Copernicus, Johannes Kepler, Galileo Galilei, Albert Einstein and Sir Isaac Newton were all influenced by the Elements, and applied their knowledge of it to their work. Mathematicians and philosophers, such as Thomas Hobbes, Baruch Spinoza, Alfred North Whitehead, and Bertrand Russell, have attempted to create their own foundational "Elements" for their respective disciplines, by adopting the axiomatized deductive structures that Euclid's work introduced.

The austere beauty of Euclidean geometry has been seen by many in western culture as a glimpse of an otherworldly system of perfection and certainty. Abraham Lincoln kept a copy of Euclid in his saddlebag, and studied it late at night by lamplight; he related that he said to himself, "You never can make a lawyer if you do not understand what demonstrate means; and I left my situation in Springfield, went home to my father's house, and stayed there till I could give any proposition in the six books of Euclid at sight". Edna St. Vincent Millay wrote in her sonnet "Euclid alone has looked on Beauty bare", "O blinding hour, O holy, terrible day, When first the shaft into his vision shone Of light anatomized!". Albert Einstein recalled a copy of the Elements and a magnetic compass as two gifts that had a great influence on him as a boy, referring to the Euclid as the "holy little geometry book".

The success of the Elements is due primarily to its logical presentation of most of the mathematical knowledge available to Euclid. Much of the material is not original to him, although many of the proofs are his. However, Euclid's systematic development of his subject, from a small set of axioms to deep results, and the consistency of his approach throughout the Elements, encouraged its use as a textbook for about 2,000 years. The Elements still influences modern geometry books. Furthermore, its logical, axiomatic approach and rigorous proofs remain the cornerstone of mathematics.

In modern mathematics

One of the most notable influences of Euclid on modern mathematics is the discussion of the parallel postulate. In Book I, Euclid lists five postulates, the fifth of which stipulates

If a line segment intersects two straight lines forming two interior angles on the same side that sum to less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.

The different versions of the parallel postulate result in different geometries.

This postulate plagued mathematicians for centuries due to its apparent complexity compared with the other four postulates. Many attempts were made to prove the fifth postulate based on the other four, but they never succeeded. Eventually in 1829, mathematician Nikolai Lobachevsky published a description of acute geometry (or hyperbolic geometry), a geometry which assumed a different form of the parallel postulate. It is in fact possible to create a valid geometry without the fifth postulate entirely, or with different versions of the fifth postulate (elliptic geometry). If one takes the fifth postulate as a given, the result is Euclidean geometry.

Contents

• Book 1 contains 5 postulates (including the famous parallel postulate) and 5 common notions, and covers important topics of plane geometry such as the Pythagorean theorem, equality of angles and areas, parallelism, the sum of the angles in a triangle, and the construction of various geometric figures.
• Book 2 contains a number of lemmas concerning the equality of rectangles and squares, sometimes referred to as "geometric algebra", and concludes with a construction of the golden ratio and a way of constructing a square equal in area to any rectilineal plane figure.
• Book 3 deals with circles and their properties: finding the center, inscribed angles, tangents, the power of a point, Thales' theorem.
• Book 4 constructs the incircle and circumcircle of a triangle, as well as regular polygons with 4, 5, 6, and 15 sides.
• Book 5, on proportions of magnitudes, gives the highly sophisticated theory of proportion probably developed by Eudoxus, and proves properties such as "alternation" (if a : b :: c : d, then a : c :: b : d).
• Book 6 applies proportions to plane geometry, especially the construction and recognition of similar figures.
• Book 7 deals with elementary number theory: divisibility, prime numbers and their relation to composite numbers, Euclid's algorithm for finding the greatest common divisor, finding the least common multiple.
• Book 8 deals with the construction and existence of geometric sequences of integers.
• Book 9 applies the results of the preceding two books and gives the infinitude of prime numbers and the construction of all even perfect numbers.
• Book 10 proves the irrationality of the square roots of non-square integers (e.g. ${\displaystyle {\sqrt {2}}}$) and classifies the square roots of incommensurable lines into thirteen disjoint categories. Euclid here introduces the term "irrational", which has a different meaning than the modern concept of irrational numbers. He also gives a formula to produce Pythagorean triples.
• Book 11 generalizes the results of book 6 to solid figures: perpendicularity, parallelism, volumes and similarity of parallelepipeds.
• Book 12 studies the volumes of cones, pyramids, and cylinders in detail by using the method of exhaustion, a precursor to integration, and shows, for example, that the volume of a cone is a third of the volume of the corresponding cylinder. It concludes by showing that the volume of a sphere is proportional to the cube of its radius (in modern language) by approximating its volume by a union of many pyramids.
• Book 13 constructs the five regular Platonic solids inscribed in a sphere and compares the ratios of their edges to the radius of the sphere.

Summary Contents of Euclid's Elements

Book	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII	XIII	Totals
Definitions	23	2	11	7	18	4	22	-	-	16	28	-	-	131
Postulates	5	-	-	-	-	-	-	-	-	-	-	-	-	5
Common Notions	5	-	-	-	-	-	-	-	-	-	-	-	-	5
Propositions	48	14	37	16	25	33	39	27	36	115	39	18	18	465

Euclid's method and style of presentation

• "To draw a straight line from any point to any point."
• "To describe a circle with any center and distance."

Euclid, Elements, Book I, Postulates 1 & 3.

An animation showing how Euclid constructed a hexagon (Book IV, Proposition 15). Every two-dimensional figure in the Elements can be constructed using only a compass and straightedge.

 

Codex Vaticanus 190

Euclid's axiomatic approach and constructive methods were widely influential.

Many of Euclid's propositions were constructive, demonstrating the existence of some figure by detailing the steps he used to construct the object using a compass and straightedge. His constructive approach appears even in his geometry's postulates, as the first and third postulates stating the existence of a line and circle are constructive. Instead of stating that lines and circles exist per his prior definitions, he states that it is possible to 'construct' a line and circle. It also appears that, for him to use a figure in one of his proofs, he needs to construct it in an earlier proposition. For example, he proves the Pythagorean theorem by first inscribing a square on the sides of a right triangle, but only after constructing a square on a given line one proposition earlier.

As was common in ancient mathematical texts, when a proposition needed proof in several different cases, Euclid often proved only one of them (often the most difficult), leaving the others to the reader. Later editors such as Theon often interpolated their own proofs of these cases.

Propositions plotted with lines connected from Axioms on the top and other preceding propositions, labelled by book.

Euclid's presentation was limited by the mathematical ideas and notations in common currency in his era, and this causes the treatment to seem awkward to the modern reader in some places. For example, there was no notion of an angle greater than two right angles, the number 1 was sometimes treated separately from other positive integers, and as multiplication was treated geometrically he did not use the product of more than 3 different numbers. The geometrical treatment of number theory may have been because the alternative would have been the extremely awkward Alexandrian system of numerals.

The presentation of each result is given in a stylized form, which, although not invented by Euclid, is recognized as typically classical. It has six different parts: First is the 'enunciation', which states the result in general terms (i.e., the statement of the proposition). Then comes the 'setting-out', which gives the figure and denotes particular geometrical objects by letters. Next comes the 'definition' or 'specification', which restates the enunciation in terms of the particular figure. Then the 'construction' or 'machinery' follows. Here, the original figure is extended to forward the proof. Then, the 'proof' itself follows. Finally, the 'conclusion' connects the proof to the enunciation by stating the specific conclusions drawn in the proof, in the general terms of the enunciation.

No indication is given of the method of reasoning that led to the result, although the Data does provide instruction about how to approach the types of problems encountered in the first four books of the Elements. Some scholars have tried to find fault in Euclid's use of figures in his proofs, accusing him of writing proofs that depended on the specific figures drawn rather than the general underlying logic, especially concerning Proposition II of Book I. However, Euclid's original proof of this proposition, is general, valid, and does not depend on the figure used as an example to illustrate one given configuration.

Criticism

Euclid's list of axioms in the Elements was not exhaustive, but represented the principles that were the most important. His proofs often invoke axiomatic notions which were not originally presented in his list of axioms. Later editors have interpolated Euclid's implicit axiomatic assumptions in the list of formal axioms.

For example, in the first construction of Book 1, Euclid used a premise that was neither postulated nor proved: that two circles with centers at the distance of their radius will intersect in two points. Later, in the fourth construction, he used superposition (moving the triangles on top of each other) to prove that if two sides and their angles are equal, then they are congruent; during these considerations he uses some properties of superposition, but these properties are not described explicitly in the treatise. If superposition is to be considered a valid method of geometric proof, all of geometry would be full of such proofs. For example, propositions I.2 and I.3 can be proved trivially by using superposition.

Mathematician and historian W. W. Rouse Ball put the criticisms in perspective, remarking that "the fact that for two thousand years [the Elements] was the usual text-book on the subject raises a strong presumption that it is not unsuitable for that purpose."

Apocrypha

It was not uncommon in ancient times to attribute to celebrated authors works that were not written by them. It is by these means that the apocryphal books XIV and XV of the Elements were sometimes included in the collection. The spurious Book XIV was probably written by Hypsicles on the basis of a treatise by Apollonius. The book continues Euclid's comparison of regular solids inscribed in spheres, with the chief result being that the ratio of the surfaces of the dodecahedron and icosahedron inscribed in the same sphere is the same as the ratio of their volumes, the ratio being

$${\displaystyle {\sqrt {\frac {10}{3(5-{\sqrt {5}})}}}={\sqrt {\frac {5+{\sqrt {5}}}{6}}}.}$$

The spurious Book XV was probably written, at least in part, by Isidore of Miletus. This book covers topics such as counting the number of edges and solid angles in the regular solids, and finding the measure of dihedral angles of faces that meet at an edge.