| Astrodynamics |
|---|
 |
The Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum.
where:
- is delta-v – the maximum change of velocity of the vehicle (with no external forces acting).
- is the initial total mass, including propellant, a.k.a. wet mass.
- is the final total mass without propellant, a.k.a. dry mass.
- is the effective exhaust velocity, where:
- is the specific impulse in dimension of time.
- is standard gravity.
- is the natural logarithm function.
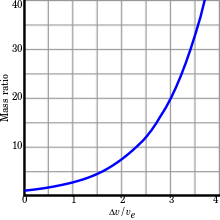
Given the effective exhaust velocity (determined by a rocket motor's design), a desired delta-v (for example, escape velocity), and a given dry mass , the equation can be used to find the required wet mass :
So the necessary wet mass grows exponentially with the desired delta-v, as illustrated in a chart above.
History
The equation is named after Russian scientist Konstantin Tsiolkovsky (Russian: Константин Циолковский) who independently derived it and published it in his 1903 work.
The equation had been derived earlier by the British mathematician William Moore in 1810, and later published in a separate book in 1813.
Robert Goddard in America independently developed the equation in 1912 when he began his research to improve rocket engines for possible space flight. Hermann Oberth in Europe independently derived the equation about 1920 as he studied the feasibility of space travel.
While the derivation of the rocket equation is a straightforward calculus exercise, Tsiolkovsky is honored as being the first to apply it to the question of whether rockets could achieve speeds necessary for space travel.
Derivation
Most popular derivation
In the following derivation, "the rocket" is taken to mean "the rocket and all of its unexpended propellant".
Newton's second law of motion relates external forces () to the change in linear momentum of the whole system (including rocket and exhaust) as follows:
where is the momentum of the rocket at time :
and is the momentum of the rocket and exhausted mass at time :
and where, with respect to the observer:
is the velocity of the rocket at time is the velocity of the rocket at time is the velocity of the mass added to the exhaust (and lost by the rocket) during time is the mass of the rocket at time is the mass of the rocket at time
The velocity of the exhaust in the observer frame is related to the velocity of the exhaust in the rocket frame by (since exhaust velocity is in the negative direction)
Solving yields:
and, using , since ejecting a positive results in a decrease in mass in time,
If there are no external forces then (conservation of linear momentum) and
Assuming is constant, this may be integrated as follows:
This then yields
or equivalently
- or
or
where is the initial total mass including propellant, the final mass, and the velocity of the rocket exhaust with respect to the rocket (the specific impulse, or, if measured in time, that multiplied by gravity-on-Earth acceleration).
The value is the total working mass of propellant expended.
(delta v) is the integration over time of the magnitude of the acceleration produced by using the rocket engine (what would be the actual acceleration if external forces were absent). In free space, for the case of acceleration in the direction of the velocity, this is the increase of the speed. In the case of an acceleration in opposite direction (deceleration) it is the decrease of the speed. Of course gravity and drag also accelerate the vehicle, and they can add or subtract to the change in velocity experienced by the vehicle. Hence delta-v may not always be the actual change in speed or velocity of the vehicle.
Other derivations
Impulse-based
The equation can also be derived from the basic integral of acceleration in the form of force (thrust) over mass. By representing the delta-v equation as the following:
where T is thrust, is the initial (wet) mass and is the initial mass minus the final (dry) mass,
and realising that the integral of a resultant force over time is total impulse, assuming thrust is the only force involved,
The integral is found to be:
Realising that impulse over the change in mass is equivalent to force over propellant mass flow rate (p), which is itself equivalent to exhaust velocity,
the integral can be equated to
Acceleration-based
Imagine a rocket at rest in space with no forces exerted on it (Newton's First Law of Motion). From the moment its engine is started (clock set to 0) the rocket expels gas mass at a constant mass flow rate R (kg/s) and at exhaust velocity relative to the rocket ve (m/s). This creates a constant force F propelling the rocket that is equal to R × ve. The rocket is subject to a constant force, but its total mass is decreasing steadily because it is expelling gas. According to Newton's Second Law of Motion, its acceleration at any time t is its propelling force F divided by its current mass m:
Now, the mass of fuel the rocket initially has on board is equal to m0 – mf. For the constant mass flow rate R it will therefore take a time T = (m0 – mf)/R to burn all this fuel. Integrating both sides of the equation with respect to time from 0 to T (and noting that R = dm/dt allows a substitution on the right), we obtain
Limit of finite mass "pellet" expulsion
The rocket equation can also be derived as the limiting case of the speed change for a rocket that expels its fuel in the form of pellets consecutively, as , with an effective exhaust speed such that the mechanical energy gained per unit fuel mass is given by .
In the rocket's center-of-mass frame, if a pellet of mass is ejected at speed and the remaining mass of the rocket is , the amount of energy converted to increase the rocket's and pellet's kinetic energy is
- .
Using momentum conservation in the rocket's frame just prior to ejection, , from which we find
- .
Let be the initial fuel mass fraction on board and the initial fueled-up mass of the rocket. Divide the total mass of fuel into discrete pellets each of mass . The remaining mass of the rocket after ejecting pellets is then . The overall speed change after ejecting pellets is the sum
Notice that for large the last term in the denominator and can be neglected to give
- where and .
As this Riemann sum becomes the definite integral
- , since the remaining mass of the rocket is .
Special relativity
If special relativity is taken into account, the following equation can be derived for a relativistic rocket, with again standing for the rocket's final velocity (after expelling all its reaction mass and being reduced to a rest mass of ) in the inertial frame of reference where the rocket started at rest (with the rest mass including fuel being initially), and standing for the speed of light in a vacuum:
Writing as allows this equation to be rearranged as
Then, using the identity (here "exp" denotes the exponential function; see also Natural logarithm as well as the "power" identity at Logarithmic identities) and the identity (see Hyperbolic function), this is equivalent to
Terms of the equation
Delta-v
Delta-v (literally "change in velocity"), symbolised as Δv and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse that is needed to perform a maneuver such as launching from, or landing on a planet or moon, or an in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of the vehicle.
Delta-v is produced by reaction engines, such as rocket engines and is proportional to the thrust per unit mass, and burn time, and is used to determine the mass of propellant required for the given manoeuvre through the rocket equation.
For multiple manoeuvres, delta-v sums linearly.
For interplanetary missions delta-v is often plotted on a porkchop plot which displays the required mission delta-v as a function of launch date.
Mass fraction
In aerospace engineering, the propellant mass fraction is the portion of a vehicle's mass which does not reach the destination, usually used as a measure of the vehicle's performance. In other words, the propellant mass fraction is the ratio between the propellant mass and the initial mass of the vehicle. In a spacecraft, the destination is usually an orbit, while for aircraft it is their landing location. A higher mass fraction represents less weight in a design. Another related measure is the payload fraction, which is the fraction of initial weight that is payload.
Effective exhaust velocity
The effective exhaust velocity is often specified as a specific impulse and they are related to each other by:
where
- is the specific impulse in seconds,
- is the specific impulse measured in m/s, which is the same as the effective exhaust velocity measured in m/s (or ft/s if g is in ft/s2),
- is the standard gravity, 9.80665 m/s2 (in Imperial units 32.174 ft/s2).
Applicability
The rocket equation captures the essentials of rocket flight physics in a single short equation. It also holds true for rocket-like reaction vehicles whenever the effective exhaust velocity is constant, and can be summed or integrated when the effective exhaust velocity varies. The rocket equation only accounts for the reaction force from the rocket engine; it does not include other forces that may act on a rocket, such as aerodynamic or gravitational forces. As such, when using it to calculate the propellant requirement for launch from (or powered descent to) a planet with an atmosphere, the effects of these forces must be included in the delta-V requirement (see Examples below). In what has been called "the tyranny of the rocket equation", there is a limit to the amount of payload that the rocket can carry, as higher amounts of propellant increment the overall weight, and thus also increase the fuel consumption. The equation does not apply to non-rocket systems such as aerobraking, gun launches, space elevators, launch loops, tether propulsion or light sails.
The rocket equation can be applied to orbital maneuvers in order to determine how much propellant is needed to change to a particular new orbit, or to find the new orbit as the result of a particular propellant burn. When applying to orbital maneuvers, one assumes an impulsive maneuver, in which the propellant is discharged and delta-v applied instantaneously. This assumption is relatively accurate for short-duration burns such as for mid-course corrections and orbital insertion maneuvers. As the burn duration increases, the result is less accurate due to the effect of gravity on the vehicle over the duration of the maneuver. For low-thrust, long duration propulsion, such as electric propulsion, more complicated analysis based on the propagation of the spacecraft's state vector and the integration of thrust are used to predict orbital motion.
Examples
Assume an exhaust velocity of 4,500 meters per second (15,000 ft/s) and a of 9,700 meters per second (32,000 ft/s) (Earth to LEO, including to overcome gravity and aerodynamic drag).
- Single-stage-to-orbit rocket: = 0.884, therefore 88.4% of the initial total mass has to be propellant. The remaining 11.6% is for the engines, the tank, and the payload.
- Two-stage-to-orbit: suppose that the first stage should provide a of 5,000 meters per second (16,000 ft/s); = 0.671, therefore 67.1% of the initial total mass has to be propellant to the first stage. The remaining mass is 32.9%. After disposing of the first stage, a mass remains equal to this 32.9%, minus the mass of the tank and engines of the first stage. Assume that this is 8% of the initial total mass, then 24.9% remains. The second stage should provide a of 4,700 meters per second (15,000 ft/s); = 0.648, therefore 64.8% of the remaining mass has to be propellant, which is 16.2% of the original total mass, and 8.7% remains for the tank and engines of the second stage, the payload, and in the case of a space shuttle, also the orbiter. Thus together 16.7% of the original launch mass is available for all engines, the tanks, and payload.
Stages
In the case of sequentially thrusting rocket stages, the equation applies for each stage, where for each stage the initial mass in the equation is the total mass of the rocket after discarding the previous stage, and the final mass in the equation is the total mass of the rocket just before discarding the stage concerned. For each stage the specific impulse may be different.
For example, if 80% of the mass of a rocket is the fuel of the first stage, and 10% is the dry mass of the first stage, and 10% is the remaining rocket, then
With three similar, subsequently smaller stages with the same for each stage, we have
and the payload is 10% × 10% × 10% = 0.1% of the initial mass.
A comparable SSTO rocket, also with a 0.1% payload, could have a mass of 11.1% for fuel tanks and engines, and 88.8% for fuel. This would give
If the motor of a new stage is ignited before the previous stage has been discarded and the simultaneously working motors have a different specific impulse (as is often the case with solid rocket boosters and a liquid-fuel stage), the situation is more complicated.















































![{\displaystyle ~\Delta v=v_{f}-v_{0}=-v_{\text{e}}\left[\ln m_{f}-\ln m_{0}\right]=~v_{\text{e}}\ln \left({\frac {m_{0}}{m_{f}}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6b3f9376e3f80de022939656d53c9fdb0f5a881)

























![{\displaystyle {\frac {m_{0}}{m_{1}}}=\left[{\frac {1+{\frac {\Delta v}{c}}}{1-{\frac {\Delta v}{c}}}}\right]^{\frac {c}{2v_{\text{e}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/506b68f3ef6f9d1d236a2f4ab7bfbf995189b937)



![{\displaystyle R^{\frac {2v_{\text{e}}}{c}}=\exp \left[{\frac {2v_{\text{e}}}{c}}\ln R\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aeb10ab0edcb00338caa4424cde4d2c993ba881)











