Tsiolkovsky rocket equation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation 

 

A chart that shows a rocket's mass ratios plotted against its final velocity calculated using Tsiolkovsky's rocket equation.

Astrodynamics

The Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity can thereby move due to the conservation of momentum.

${\displaystyle \Delta v=v_{\text{e}}\ln {\frac {m_{0}}{m_{f}}}=I_{\text{sp}}g_{0}\ln {\frac {m_{0}}{m_{f}}},}$

where:

${\displaystyle \Delta v\ }$ is delta-v – the maximum change of velocity of the vehicle (with no external forces acting).

${\displaystyle m_{0}}$ is the initial total mass, including propellant, a.k.a. wet mass.

${\displaystyle m_{f}}$ is the final total mass without propellant, a.k.a. dry mass.

${\displaystyle v_{\text{e}}=I_{\text{sp}}g_{0}}$ is the effective exhaust velocity, where:

${\displaystyle I_{\text{sp}}}$ is the specific impulse in dimension of time.

${\displaystyle g_{0}}$ is standard gravity.

${\displaystyle \ln }$ is the natural logarithm function.

Given the effective exhaust velocity ${\displaystyle v_{\text{e}}}$ (determined by a rocket motor's design), a desired delta-v (for example, escape velocity), and a given dry mass ${\displaystyle m_{f}}$, the equation can be used to find the required wet mass ${\displaystyle m_{0}}$:

${\displaystyle m_{0}=m_{f}e^{\frac {\Delta v}{v_{\text{e}}}}.}$

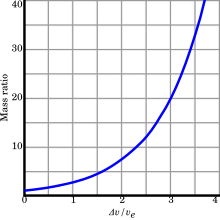
So the necessary wet mass grows exponentially with the desired delta-v, as illustrated in a chart above.

History

The equation is named after Russian scientist Konstantin Tsiolkovsky (Russian: Константин Циолковский) who independently derived it and published it in his 1903 work.

The equation had been derived earlier by the British mathematician William Moore in 1810, and later published in a separate book in 1813.

Robert Goddard in America independently developed the equation in 1912 when he began his research to improve rocket engines for possible space flight. Hermann Oberth in Europe independently derived the equation about 1920 as he studied the feasibility of space travel.

While the derivation of the rocket equation is a straightforward calculus exercise, Tsiolkovsky is honored as being the first to apply it to the question of whether rockets could achieve speeds necessary for space travel.

Derivation

Most popular derivation

Consider the following:

In the following derivation, "the rocket" is taken to mean "the rocket and all of its unexpended propellant".

Newton's second law of motion relates external forces (${\displaystyle F_{i}\,}$) to the change in linear momentum of the whole system (including rocket and exhaust) as follows:

${\displaystyle \sum F_{i}=\lim _{\Delta t\to 0}{\frac {P_{2}-P_{1}}{\Delta t}}}$

where ${\displaystyle P_{1}\,}$ is the momentum of the rocket at time ${\displaystyle t=0}$:

${\displaystyle P_{1}=\left({m+\Delta m}\right)V}$

and ${\displaystyle P_{2}\,}$ is the momentum of the rocket and exhausted mass at time ${\displaystyle t=\Delta t\,}$:

${\displaystyle P_{2}=m\left(V+\Delta V\right)+\Delta mV_{\text{e}}}$

and where, with respect to the observer:

${\displaystyle V\,}$ is the velocity of the rocket at time ${\displaystyle t=0}$

${\displaystyle V+\Delta V\,}$ is the velocity of the rocket at time ${\displaystyle t=\Delta t\,}$

${\displaystyle V_{\text{e}}\,}$ is the velocity of the mass added to the exhaust (and lost by the rocket) during time ${\displaystyle \Delta t\,}$

${\displaystyle m+\Delta m\,}$ is the mass of the rocket at time ${\displaystyle t=0}$

${\displaystyle m\,}$ is the mass of the rocket at time ${\displaystyle t=\Delta t\,}$

The velocity of the exhaust ${\displaystyle V_{\text{e}}}$ in the observer frame is related to the velocity of the exhaust in the rocket frame ${\displaystyle v_{\text{e}}}$ by (since exhaust velocity is in the negative direction)

${\displaystyle V_{\text{e}}=V-v_{\text{e}}}$

Solving yields:

${\displaystyle P_{2}-P_{1}=m\Delta V+v_{\text{e}}\Delta m\,}$

and, using ${\displaystyle dm=-\Delta m}$, since ejecting a positive ${\displaystyle \Delta m}$ results in a decrease in mass in time,

${\displaystyle \sum F_{i}=m{\frac {dV}{dt}}-v_{\text{e}}{\frac {dm}{dt}}}$

If there are no external forces then ${\displaystyle \sum F_{i}=0}$ (conservation of linear momentum) and

${\displaystyle m{\frac {dV}{dt}}=v_{\text{e}}{\frac {dm}{dt}}}$

Assuming ${\displaystyle v_{\text{e}}\,}$ is constant, this may be integrated as follows:

${\displaystyle \int _{V}^{V+\Delta V}\,\mathrm {d} V={v_{e}}\int _{m_{0}}^{m_{f}}{\frac {1}{m}}\,\mathrm {d} m}$

This then yields

${\displaystyle \Delta V=-v_{\text{e}}\ln {\frac {m_{0}}{m_{f}}}}$

or equivalently

${\displaystyle m_{f}=m_{0}e^{-\Delta V\ /v_{\text{e}}}}$      or     

${\displaystyle m_{0}=m_{f}e^{\Delta V/v_{\text{e}}}}$      or      ${\displaystyle m_{0}-m_{f}=m_{f}\left(e^{\Delta V/v_{\text{e}}}-1\right)}$

where ${\displaystyle m_{0}}$ is the initial total mass including propellant, ${\displaystyle m_{f}}$ the final mass, and ${\displaystyle v_{\text{e}}}$ the velocity of the rocket exhaust with respect to the rocket (the specific impulse, or, if measured in time, that multiplied by gravity-on-Earth acceleration).

The value ${\displaystyle m_{0}-m_{f}}$ is the total working mass of propellant expended.

${\displaystyle \Delta V\,}$ (delta v) is the integration over time of the magnitude of the acceleration produced by using the rocket engine (what would be the actual acceleration if external forces were absent). In free space, for the case of acceleration in the direction of the velocity, this is the increase of the speed. In the case of an acceleration in opposite direction (deceleration) it is the decrease of the speed. Of course gravity and drag also accelerate the vehicle, and they can add or subtract to the change in velocity experienced by the vehicle. Hence delta-v may not always be the actual change in speed or velocity of the vehicle.

Other derivations

Impulse-based

The equation can also be derived from the basic integral of acceleration in the form of force (thrust) over mass. By representing the delta-v equation as the following:

${\displaystyle \Delta v=\int _{t_{0}}^{t_{f}}{\frac {|T|}{{m_{0}}-{t}\Delta {m}}}~dt}$

where T is thrust, ${\displaystyle m_{0}}$ is the initial (wet) mass and ${\displaystyle \Delta m}$ is the initial mass minus the final (dry) mass,

and realising that the integral of a resultant force over time is total impulse, assuming thrust is the only force involved,

${\displaystyle \int _{t_{0}}^{t_{f}}F~dt=J}$

The integral is found to be:

${\displaystyle J~{\frac {\ln({m_{0}})-\ln({m_{f}})}{\Delta m}}}$

Realising that impulse over the change in mass is equivalent to force over propellant mass flow rate (p), which is itself equivalent to exhaust velocity,

${\displaystyle {\frac {J}{\Delta m}}={\frac {F}{p}}=V_{\rm {exh}}}$

the integral can be equated to

${\displaystyle \Delta v=V_{\rm {exh}}~\ln \left({\frac {m_{0}}{m_{f}}}\right)}$

Acceleration-based

Imagine a rocket at rest in space with no forces exerted on it (Newton's First Law of Motion). From the moment its engine is started (clock set to 0) the rocket expels gas mass at a constant mass flow rate R (kg/s) and at exhaust velocity relative to the rocket v_e (m/s). This creates a constant force F propelling the rocket that is equal to R × v_e. The rocket is subject to a constant force, but its total mass is decreasing steadily because it is expelling gas. According to Newton's Second Law of Motion, its acceleration at any time t is its propelling force F divided by its current mass m:

${\displaystyle ~a={\frac {dv}{dt}}=-{\frac {F}{m(t)}}=-{\frac {Rv_{\text{e}}}{m(t)}}}$

Now, the mass of fuel the rocket initially has on board is equal to m₀ – m_f. For the constant mass flow rate R it will therefore take a time T = (m₀ – m_f)/R to burn all this fuel. Integrating both sides of the equation with respect to time from 0 to T (and noting that R = dm/dt allows a substitution on the right), we obtain

${\displaystyle ~\Delta v=v_{f}-v_{0}=-v_{\text{e}}\left[\ln m_{f}-\ln m_{0}\right]=~v_{\text{e}}\ln \left({\frac {m_{0}}{m_{f}}}\right).}$

Limit of finite mass "pellet" expulsion

The rocket equation can also be derived as the limiting case of the speed change for a rocket that expels its fuel in the form of ${\displaystyle N}$ pellets consecutively, as ${\displaystyle N\rightarrow \infty }$, with an effective exhaust speed ${\displaystyle v_{\rm {eff}}}$ such that the mechanical energy gained per unit fuel mass is given by ${\displaystyle {\tfrac {1}{2}}v_{\rm {eff}}^{2}}$.

In the rocket's center-of-mass frame, if a pellet of mass ${\displaystyle m_{p}}$ is ejected at speed ${\displaystyle u}$ and the remaining mass of the rocket is ${\displaystyle m}$, the amount of energy converted to increase the rocket's and pellet's kinetic energy is

${\displaystyle {\tfrac {1}{2}}m_{p}v_{\rm {eff}}^{2}={\tfrac {1}{2}}m_{p}u^{2}+{\tfrac {1}{2}}m(\Delta v)^{2}}$.

Using momentum conservation in the rocket's frame just prior to ejection, ${\displaystyle u=\Delta v{\tfrac {m}{m_{p}}}}$, from which we find

${\displaystyle \Delta v=v_{\rm {eff}}{\frac {mp}{\sqrt {m(m+m_{p})}}}}$.

Let ${\displaystyle \phi }$ be the initial fuel mass fraction on board and ${\displaystyle m_{0}}$ the initial fueled-up mass of the rocket. Divide the total mass of fuel ${\displaystyle \phi m_{0}}$ into ${\displaystyle N}$ discrete pellets each of mass ${\displaystyle m_{p}=\phi m_{0}/N}$. The remaining mass of the rocket after ejecting ${\displaystyle j}$ pellets is then ${\displaystyle m_{0}(1-j\phi /N)}$. The overall speed change after ejecting ${\displaystyle j}$ pellets is the sum 

${\displaystyle \Delta v=v_{\rm {eff}}\sum _{j=1}^{j=N}{\frac {\phi /N}{\sqrt {(1-j\phi /N)(1-j\phi /N+\phi /N)}}}}$

Notice that for large ${\displaystyle N}$ the last term in the denominator ${\displaystyle \phi /N\ll 1}$ and can be neglected to give

${\displaystyle \Delta v\approx v_{\rm {eff}}\sum _{j=1}^{j=N}{\frac {\phi /N}{1-j\phi /N}}=v_{\rm {eff}}\sum _{j=1}^{j=N}{\frac {\Delta x}{1-x_{j}}}}$ where ${\displaystyle \Delta x={\frac {\phi }{N}}}$ and ${\displaystyle x_{j}={\frac {j\phi }{N}}}$.

As ${\displaystyle N\rightarrow \infty }$ this Riemann sum becomes the definite integral

${\displaystyle \lim _{N\to \infty }\Delta v=v_{\rm {eff}}\int _{0}^{\phi }{\frac {dx}{1-x}}=v_{\rm {eff}}\ln {\frac {1}{1-\phi }}=v_{\rm {eff}}\ln {\frac {m_{0}}{m_{f}}}}$, since the remaining mass of the rocket is ${\displaystyle m_{f}=m_{0}(1-\phi )}$.

Special relativity

If special relativity is taken into account, the following equation can be derived for a relativistic rocket, with ${\displaystyle \Delta v}$ again standing for the rocket's final velocity (after expelling all its reaction mass and being reduced to a rest mass of ${\displaystyle m_{1}}$) in the inertial frame of reference where the rocket started at rest (with the rest mass including fuel being ${\displaystyle m_{0}}$ initially), and ${\displaystyle c}$ standing for the speed of light in a vacuum:

${\displaystyle {\frac {m_{0}}{m_{1}}}=\left[{\frac {1+{\frac {\Delta v}{c}}}{1-{\frac {\Delta v}{c}}}}\right]^{\frac {c}{2v_{\text{e}}}}}$

Writing ${\displaystyle {\frac {m_{0}}{m_{1}}}}$ as ${\displaystyle R}$ allows this equation to be rearranged as

${\displaystyle {\frac {\Delta v}{c}}={\frac {R^{\frac {2v_{\text{e}}}{c}}-1}{R^{\frac {2v_{\text{e}}}{c}}+1}}}$

Then, using the identity ${\displaystyle R^{\frac {2v_{\text{e}}}{c}}=\exp \left[{\frac {2v_{\text{e}}}{c}}\ln R\right]}$ (here "exp" denotes the exponential function; see also Natural logarithm as well as the "power" identity at Logarithmic identities) and the identity ${\displaystyle \tanh x={\frac {e^{2x}-1}{e^{2x}+1}}}$ (see Hyperbolic function), this is equivalent to

${\displaystyle \Delta v=c\tanh \left({\frac {v_{\text{e}}}{c}}\ln {\frac {m_{0}}{m_{1}}}\right)}$

Terms of the equation

Delta-v

Main article: Delta-v

Delta-v (literally "change in velocity"), symbolised as Δv and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse that is needed to perform a maneuver such as launching from, or landing on a planet or moon, or an in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of the vehicle.

Delta-v is produced by reaction engines, such as rocket engines and is proportional to the thrust per unit mass, and burn time, and is used to determine the mass of propellant required for the given manoeuvre through the rocket equation.

For multiple manoeuvres, delta-v sums linearly.

For interplanetary missions delta-v is often plotted on a porkchop plot which displays the required mission delta-v as a function of launch date.

Mass fraction

Main article: Propellant mass fraction

In aerospace engineering, the propellant mass fraction is the portion of a vehicle's mass which does not reach the destination, usually used as a measure of the vehicle's performance. In other words, the propellant mass fraction is the ratio between the propellant mass and the initial mass of the vehicle. In a spacecraft, the destination is usually an orbit, while for aircraft it is their landing location. A higher mass fraction represents less weight in a design. Another related measure is the payload fraction, which is the fraction of initial weight that is payload.

Effective exhaust velocity

Main article: Effective exhaust velocity

The effective exhaust velocity is often specified as a specific impulse and they are related to each other by:

${\displaystyle v_{\text{e}}=g_{0}I_{\text{sp}},}$

where

${\displaystyle I_{\text{sp}}}$ is the specific impulse in seconds,

${\displaystyle v_{\text{e}}}$ is the specific impulse measured in m/s, which is the same as the effective exhaust velocity measured in m/s (or ft/s if g is in ft/s²),

${\displaystyle g_{0}}$ is the standard gravity, 9.80665 m/s² (in Imperial units 32.174 ft/s²).

Applicability

The rocket equation captures the essentials of rocket flight physics in a single short equation. It also holds true for rocket-like reaction vehicles whenever the effective exhaust velocity is constant, and can be summed or integrated when the effective exhaust velocity varies. The rocket equation only accounts for the reaction force from the rocket engine; it does not include other forces that may act on a rocket, such as aerodynamic or gravitational forces. As such, when using it to calculate the propellant requirement for launch from (or powered descent to) a planet with an atmosphere, the effects of these forces must be included in the delta-V requirement (see Examples below). In what has been called "the tyranny of the rocket equation", there is a limit to the amount of payload that the rocket can carry, as higher amounts of propellant increment the overall weight, and thus also increase the fuel consumption. The equation does not apply to non-rocket systems such as aerobraking, gun launches, space elevators, launch loops, tether propulsion or light sails.

The rocket equation can be applied to orbital maneuvers in order to determine how much propellant is needed to change to a particular new orbit, or to find the new orbit as the result of a particular propellant burn. When applying to orbital maneuvers, one assumes an impulsive maneuver, in which the propellant is discharged and delta-v applied instantaneously. This assumption is relatively accurate for short-duration burns such as for mid-course corrections and orbital insertion maneuvers. As the burn duration increases, the result is less accurate due to the effect of gravity on the vehicle over the duration of the maneuver. For low-thrust, long duration propulsion, such as electric propulsion, more complicated analysis based on the propagation of the spacecraft's state vector and the integration of thrust are used to predict orbital motion.

Examples

Assume an exhaust velocity of 4,500 meters per second (15,000 ft/s) and a ${\displaystyle \Delta v}$ of 9,700 meters per second (32,000 ft/s) (Earth to LEO, including ${\displaystyle \Delta v}$ to overcome gravity and aerodynamic drag).

• Single-stage-to-orbit rocket: ${\displaystyle 1-e^{-9.7/4.5}}$ = 0.884, therefore 88.4% of the initial total mass has to be propellant. The remaining 11.6% is for the engines, the tank, and the payload.
• Two-stage-to-orbit: suppose that the first stage should provide a ${\displaystyle \Delta v}$ of 5,000 meters per second (16,000 ft/s); ${\displaystyle 1-e^{-5.0/4.5}}$ = 0.671, therefore 67.1% of the initial total mass has to be propellant to the first stage. The remaining mass is 32.9%. After disposing of the first stage, a mass remains equal to this 32.9%, minus the mass of the tank and engines of the first stage. Assume that this is 8% of the initial total mass, then 24.9% remains. The second stage should provide a ${\displaystyle \Delta v}$ of 4,700 meters per second (15,000 ft/s); ${\displaystyle 1-e^{-4.7/4.5}}$ = 0.648, therefore 64.8% of the remaining mass has to be propellant, which is 16.2% of the original total mass, and 8.7% remains for the tank and engines of the second stage, the payload, and in the case of a space shuttle, also the orbiter. Thus together 16.7% of the original launch mass is available for all engines, the tanks, and payload.

Stages

In the case of sequentially thrusting rocket stages, the equation applies for each stage, where for each stage the initial mass in the equation is the total mass of the rocket after discarding the previous stage, and the final mass in the equation is the total mass of the rocket just before discarding the stage concerned. For each stage the specific impulse may be different.

For example, if 80% of the mass of a rocket is the fuel of the first stage, and 10% is the dry mass of the first stage, and 10% is the remaining rocket, then

${\displaystyle {\begin{aligned}\Delta v\ &=v_{\text{e}}\ln {100 \over 100-80}\\&=v_{\text{e}}\ln 5\\&=1.61v_{\text{e}}.\\\end{aligned}}}$

With three similar, subsequently smaller stages with the same ${\displaystyle v_{\text{e}}}$ for each stage, we have

${\displaystyle \Delta v\ =3v_{\text{e}}\ln 5\ =4.83v_{\text{e}}}$

and the payload is 10% × 10% × 10% = 0.1% of the initial mass.

A comparable SSTO rocket, also with a 0.1% payload, could have a mass of 11.1% for fuel tanks and engines, and 88.8% for fuel. This would give

${\displaystyle \Delta v\ =v_{\text{e}}\ln(100/11.2)\ =2.19v_{\text{e}}.}$

If the motor of a new stage is ignited before the previous stage has been discarded and the simultaneously working motors have a different specific impulse (as is often the case with solid rocket boosters and a liquid-fuel stage), the situation is more complicated.

Common misconceptions

When viewed as a variable-mass system, a rocket cannot be directly analyzed with Newton's second law of motion because the law is valid for constant-mass systems only. It can cause confusion that the Tsiolkovsky rocket equation looks similar to the relativistic force equation ${\displaystyle F=dp/dt=m\;dv/dt+v\;dm/dt}$. Using this formula with ${\displaystyle m(t)}$ as the varying mass of the rocket seems to derive the Tsiolkovsky rocket equation, but this derivation is not correct. Notice that the effective exhaust velocity ${\displaystyle v_{\text{e}}}$ does not even appear in this formula.

Ecotax

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Ecotax 

An ecotax (short for ecological taxation) is a tax levied on activities which are considered to be harmful to the environment and is intended to promote environmentally friendly activities via economic incentives. Such a policy can complement or avert the need for regulatory (command and control) approaches. Often, an ecotax policy proposal may attempt to maintain overall tax revenue by proportionately reducing other taxes (e.g. taxes on human labor and renewable resources); such proposals are known as a green tax shift towards ecological taxation. Ecotaxes address the failure of free markets to consider environmental impacts.

Ecotaxes are examples of Pigouvian taxes, which are taxes that attempt to make the private parties involved feel the social burden of their actions. An example might be philosopher Thomas Pogge's proposed Global Resources Dividend.

Taxes affected

Examples of taxes which could be lowered or eliminated by a green tax shift are:

• Payroll, income, and, to a lesser extent, sales taxes.
• Corporate taxes (taxes on investment and entrepreneurship).
• Property taxes on buildings and other infrastructure.

Examples of ecotaxes which could be implemented or increased are:

• Carbon taxes on the use of fossil fuels by greenhouse gases produced. Old hydrocarbon taxes don't penalize green house gas (GHG) production.
• Duties on imported goods containing significant non-ecological energy input (to a level necessary to treat fairly local manufacturers)
• Severance taxes on the extraction of mineral, energy, and forestry products.
• License fees for camping, hiking, fishing and hunting and associated equipment.
• Specific taxes on technologies and products which are associated with substantial negative externalities.
• Waste disposal taxes and refundable fees.
• Steering taxes on effluents, pollution and other hazardous wastes.
• Site value taxes on the unimproved value of land.

Economic frameworks and strategies employing tax shifting

The object of a green tax shift is often to implement a "full cost accounting" or "true cost accounting", using fiscal policy to internalize market distorting externalities, which leads to sustainable wealth creation. The broader measures required for this are also sometimes called ecological fiscal reform, especially in Canada, where the government has generally employed this terminology. In some countries the name is eco-social market economy.

Tax shifting usually includes balancing taxation levels to be revenue-neutral for government and to maintain overall progressiveness. It also usually includes measures to protect the most vulnerable, such as raising the minimum income to file income tax at all, or an increase to pension and social assistance levels to offset increased costs of fuel consumption.

Basic economic theory recognizes the existence of externalities and their potential negative effects. To the extent that green taxes correct for externalities such as pollution, they correspond with mainstream economic theory. In practice, however, setting the correct taxation level or the tax collection system needed to do so is difficult, and may lead to further distortions or unintended consequences.

Taxes on consumption may take the "feebate" approach advocated by Amory Lovins, in which additional fees on less sustainable products—such as sport utility vehicles—are pooled to fund subsidies on more sustainable alternatives, such as hybrid electric vehicles.

However, they may simply act as incentives to change habits and make capital investments in newer more efficient vehicles or appliances or to upgrade buildings. Small changes in corporate tax rates for instance can radically change return on investment of capital projects, especially if the averted costs of future fossil fuel use are taken into account.

The same logic applies to major consumer purchases. A "green mortgage" such as a Location Efficient Mortgage, for example, recognizes that persons who do not drive cars and live generally energy-efficient lifestyles pay far less per month than others and accordingly have more to pay a heftier mortgage bill with. This justifies lending them much more money to upgrade a house to use even less energy overall. The result is a bank taking more per month from a consumer's income as utilities and car insurance companies take less, and housing stock upgraded to use the minimum energy feasible with current technology.

Aside from energy, the refits will generally be those required to be maximally accommodating to telework, permaculture gardens (for example green roofs), and a lifestyle that is generally localized in the community not based on commuting. The last, especially, raises real state valuations for not only the neighborhood but the entire surrounding region. Consumers living sustainable lifestyles in upgraded housing will generally be unwilling to drive around aimlessly shopping, for instance, to save a few dollars on their purchases. Instead, they'll stay nearer to home and create jobs in grocery delivery and small organic grocers, spending substantially less money on gasoline and car operation costs even if they pay more for food.

Progressive or regressive?

Some green tax shift proposals have been criticized as being fiscally regressive (a tax with an average tax rate that decreases as the taxpayer's income increases). Taxing negative externalities usually entails exerting a burden on consumption, and since the poor consume more and save or invest less as a share of their income, so that any shift towards consumption taxes can be regressive. In 2004, research by the Policy Studies Institute and Joseph Rowntree Foundation indicated that flat rate taxes on domestic rubbish, energy, water and transport use would have a relatively higher impact on poorer households.

However, conventional regulatory approaches can affect prices in much the same way, while lacking the revenue-recycling potential of ecotaxes. Moreover, correctly assessing distributive impact of any tax shift requires an analysis of the specific instrument design features. For example, tax revenue could be redistributed on a per capita basis as part of a basic income scheme; in this case, the poorest would gain what the average citizen pays as ecotaxes, minus their own small contribution (no car, small apartment, ...). This design would be highly progressive. Alternatively, an ecotax can have a "lifeline" design, in which modest consumption levels are priced relatively low (even zero, in the case of water), and higher consumption levels are priced at a higher rate. Furthermore, an ecotax policy package can include revenue recycling to reduce or eliminate any regressivity; an increase in an ecotax could be more than offset by a decrease in a (regressive) payroll or consumption tax. Some proponents claim a second benefit of increased employment or lower health care costs as the market and society adjust to the new fiscal policy (these claims, as with the claim "tax cuts create jobs," are often difficult to prove or disprove even after the fact).

Furthermore, pollution and other forms of environmental harm are often felt more acutely by the poor, who cannot "buy their way out" of being receptors of air pollution, water pollution, etc. Such losses, although externalities, have real economic welfare impacts. Thus by reducing environmental harm, such instruments have a progressive effect.

Ecotax policies enacted

An ecotax has been enacted in Germany by means of three laws in 1998, 1999 and 2002. The first introduced a tax on electricity and petroleum, at variable rates based on environmental considerations; renewable sources of electricity were not taxed. The second adjusted the taxes to favor efficient conventional power plants. The third increased the tax on petroleum. At the same time, income taxes were reduced proportionally so that the total tax burden remained constant.

The regional government of Balearic Islands (then held by an ecosocialist coalition) established an ecotax in 1999. The Balearic Island suffer a high human pressure from tourism, that at the same time provides the main source of income. The tax (€1.00 per person per day) would be paid by visitors staying at tourist resorts. This was criticized by the conservative opposition as contrary to business interests, and they abolished the tax in 2003 after seizing back the government.

A variety of ecotaxes (often called "severance taxes") have been enacted by various states in the United States. The Supreme Court of the United States held in Commonwealth Edison Co. v. Montana, 453 U.S. 609 (1981), that in the absence of federal law to the contrary, states may set ecotaxes as high as they wish without violating the Commerce Clause or the Supremacy Clause of the United States Constitution.

Registration taxes

The Netherlands, Portugal, Canada, Spain and Finland have introduced differentiations into their car registration taxes to encourage car buyers to opt for the cleanest car models.

In the Netherlands, the new registration taxes, payable when a car is sold to its first buyer, can earn the owner of a hybrid a discount up to €6000. Spain reduced taxes for cars that produced less CO₂ (some of which will be exempted), while the more consuming, like SUVs and 4WDs saw their taxes increased.

Austria has had a registration tax based on fuel consumption for several years.

Worldwide implementation

United Kingdom

In 1993, the conservative government introduced the Fuel Price Escalator, featuring a small but steady increase of fuel taxes, as proposed by Weizsäcker and Jesinghaus in 1992. The FPE was stopped in 2000, following nationwide protests; while fuel was relatively cheap in 1993, fuel prices were then among the highest in Europe. Under the 1997–2007 Labour government, despite Gordon Brown’s promise to the contrary, green taxes as a percentage of overall taxes had actually fallen from 9.4% to 7.7%, according to calculations by Friends of the Earth.

In a 2006 proposal, the U.K.'s then-Environment Secretary David Miliband had the government in discussions on the use of various green taxes to reduce climate-changing pollution. Of the proposed taxes, which were meant to be revenue-neutral, Miliband stated: "They're not fundamentally there to raise revenue."

Miliband provided additional comments on their need, saying: "Changing people's behaviour is only achieved by "market forces and price signals", and "As our understanding of climate change increases, it is clear more needs to be done."

Ukraine

Starting in 1999, the Ukrainian government has been collecting an ecological tax, officially known as Environmental Pollution Fee (Ukrainian: Збір за забруднення навколишнього природного середовища), which is collected from all polluting entities, whether it's one-time or ongoing pollution and regardless of whether the polluting act was legal or illegal at the time.

India

The Ministry of Environment and Forests, Government of India, asked Madras School of Economics, Chennai, to undertake a study of taxes on polluting inputs and outputs in 2001. Raja Chelliah, Paul Appasamy, U.Sankar and Rita Pandey (Academic Foundation, 2007, New Delhi) recommended eco taxes on coal, automobiles, chlorine, phosphate detergents, chemical pesticides, chemical fertilizers, lead acid batteries and plastics. See Ecotaxes on polluting inputs and outputs, Academic Foundation, New Delhi,2007. The Finance Minister introduced a coal cess at the rate of Rs 50 per ton in 2010.

France

The French government shared its intentions to establish a new fee on plane tickets with the purpose to fund environment-friendly alternatives, such as eco-friendly transport infrastructure, including rail. The proposed tax would range between 1.50 euros ($1.7) and 18 euros ($20) and apply to most flights departing in France. The French government expects the new tax to raise over 180 million euros ($200 million) from 2020.

Polluter pays principle

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Polluter_pays_principle 

In environmental law, the polluter pays principle is enacted to make the party responsible for producing pollution responsible for paying for the damage done to the natural environment. It is regarded as a regional custom because of the strong support it has received in most Organisation for Economic Co-operation and Development (OECD) and European Union countries. It is a fundamental principle in US environmental law.

History

According to the French historian of the environment Jean-Baptiste Fressoz, financial compensation (not named "polluter pays principle" at that time) is already the regulation principle of pollution favoured by industrials in the nineteenth century. He wrote that: "This principle, which is now offered as a new solution, actually accompanied the process of industrialisation, and was intended by the manufacturers themselves."

Applications in environmental law

The polluter pays principle underpins environmental policy such as an ecotax, which, if enacted by government, deters and essentially reduces greenhouse gas emissions. This principle is based on the fact that as much as pollution is unavoidable, the person or industry that is responsible for the pollution must pay some money for the rehabilitation of the polluted environment.

Australia

The state of New South Wales in Australia has included the polluter pay principle with the other principles of ecologically sustainable development in the objectives of the Environment Protection Authority.

European Union

The polluter pays principle is set out in the Treaty on the Functioning of the European Union and Directive 2004/35/EC of the European Parliament and of the Council of 21 April 2004 on environmental liability with regard to the prevention and remedying of environmental damage is based on this principle. The directive entered into force on 30 April 2004; member states were allowed three years to transpose the directive into their domestic law and by July 2010 all member states had completed this.

France

In France, the Charter for the Environment contains a formulation of the polluter pays principle (article 4):

Everyone shall be required, in the conditions provided for by law, to contribute to the making good of any damage he or she may have caused to the environment.

Ghana

In Ghana, the polluter pays principle was adopted in 2011.

Sweden

The polluter pays principle is also known as extended producer responsibility (EPR). This is a concept that was probably first described by Thomas Lindhqvist for the Swedish government in 1990. EPR seeks to shift the responsibility of dealing with waste from governments (and thus, taxpayers and society at large) to the entities producing it. In effect, it internalised the cost of waste disposal into the cost of the product, theoretically meaning that the producers will improve the waste profile of their products, thus decreasing waste and increasing possibilities for reuse and recycling.

The Organisation for Economic Co-operation and Development defines extended producer responsibility as:

a concept where manufacturers and importers of products should bear a significant degree of responsibility for the environmental impacts of their products throughout the product life-cycle, including upstream impacts inherent in the selection of materials for the products, impacts from manufacturers’ production process itself, and downstream impacts from the use and disposal of the products. Producers accept their responsibility when designing their products to minimise life-cycle environmental impacts, and when accepting legal, physical or socio-economic responsibility for environmental impacts that cannot be eliminated by design.

Switzerland

The waste management in Switzerland is based on the polluter pays principle. Bin bags (for municipal solid waste) are taxed with pay-per-bag fees in three quarters of the communes (and the recycling rate doubled in twenty years).

United Kingdom

Part IIA of the Environmental Protection Act 1990 established the operation of the polluter pays principle. This was further built upon by The Environmental Damage (Prevention and Remediation) Regulations 2009 (for England) and the Environmental Damage (Prevention and Remediation) (Wales) Regulations 2009 (for Wales).

United States

The principle is employed in all of the major US pollution control laws: Clean Air Act, Clean Water Act, Resource Conservation and Recovery Act (solid waste and hazardous waste management), and Superfund (cleanup of abandoned waste sites).

Some eco-taxes underpinned by the polluter pays principle include:

• the Gas Guzzler Tax for motor vehicles
• Corporate Average Fuel Economy (CAFE), a "polluter pays" fine.
• the Superfund law requires polluters to pay for cleanup of hazardous waste sites, when the polluters can be identified.

In 2003, an amendment was passed negating the "polluter pays" provision of the Florida Constitution.

Limitations of polluter pays principle

The US Environmental Protection Agency (EPA) has observed that the polluter pays principle has typically not been fully implemented in US laws and programs. For example, drinking water and sewage treatment services are subsidized and there are limited mechanisms in place to fully assess polluters for treatment costs.

Zimbabwe

The Zimbabwe Environmental Management Act of 2002 prohibits the discharge of pollutants into the environment. In line with the "Polluter Pays" principle, the Act requires a polluter to meet the cost of decontaminating the polluted environment.

In international environmental law

In international environmental law it is mentioned in the principle 16 of the Rio Declaration on Environment and Development of 1992.