Isomer

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Isomer

In chemistry, isomers are molecules or polyatomic ions with identical molecular formulas — that is, same number of atoms of each element — but distinct arrangements of atoms in space. Isomerism is existence or possibility of isomers.

Isomers do not necessarily share similar chemical or physical properties. Two main forms of isomerism are structural or constitutional isomerism, in which bonds between the atoms differ; and stereoisomerism or spatial isomerism, in which the bonds are the same but the relative positions of the atoms differ.

Isomeric relationships form a hierarchy. Two chemicals might be the same constitutional isomer, but upon deeper analysis be stereoisomers of each other. Two molecules that are the same stereoisomer as each other might be in different conformational forms or be different isotopologues. The depth of analysis depends on the field of study or the chemical and physical properties of interest.

The English word "isomer" (/ˈaɪsəmər/) is a back-formation from "isomeric", which was borrowed through German isomerisch from Swedish isomerisk; which in turn was coined from Greek ἰσόμερoς isómeros, with roots isos = "equal", méros = "part".

Types of isomers.

Structural isomers

Main article: Structural isomer

Structural isomers have the same number of atoms of each element (hence the same molecular formula), but the atoms are connected in distinct ways.

Example: C
₃H
₈O

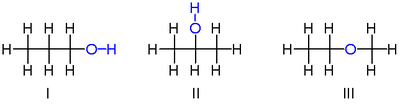
For example, there are three distinct compounds with the molecular formula ${\displaystyle {\ce {C3H8O}}}$:

The first two isomers shown of ${\displaystyle {\ce {C3H8O}}}$ are propanols, that is, alcohols derived from propane. Both have a chain of three carbon atoms connected by single bonds, with the remaining carbon valences being filled by seven hydrogen atoms and by a hydroxyl group ${\displaystyle {\ce {-OH}}}$ comprising the oxygen atom bound to a hydrogen atom. These two isomers differ on which carbon the hydroxyl is bound to: either to an extremity of the carbon chain propan-1-ol (1-propanol, n-propyl alcohol, n-propanol; I) or to the middle carbon propan-2-ol (2-propanol, isopropyl alcohol, isopropanol; II). These can be described by the condensed structural formulas ${\displaystyle {\ce {H3C-CH2-CH2OH}}}$ and ${\displaystyle {\ce {H3C-CH(OH)-CH3}}}$.

The third isomer of ${\displaystyle {\ce {C3H8O}}}$ is the ether methoxyethane (ethyl-methyl-ether; III). Unlike the other two, it has the oxygen atom connected to two carbons, and all eight hydrogens bonded directly to carbons. It can be described by the condensed formula ${\displaystyle {\ce {H3C-O-CH2-CH3}}}$.

The alcohol "3-propanol" is not another isomer, since the difference between it and 1-propanol is not real; it is only the result of an arbitrary choice in the ordering of the carbons along the chain. For the same reason, "ethoxymethane" is not another isomer.

1-Propanol and 2-propanol are examples of positional isomers, which differ by the position at which certain features, such as double bonds or functional groups, occur on a "parent" molecule (propane, in that case).

Example: C
₃H
₄

There are also three structural isomers of the hydrocarbon ${\displaystyle {\ce {C3H4}}}$:

I Propadiene	II Propyne	III Cyclopropene

In two of the isomers, the three carbon atoms are connected in an open chain, but in one of them (propadiene or allene; I) the carbons are connected by two double bonds, while in the other (propyne or methylacetylene, II) they are connected by a single bond and a triple bond. In the third isomer (cyclopropene; III) the three carbons are connected into a ring by two single bonds and a double bond. In all three, the remaining valences of the carbon atoms are satisfied by the four hydrogens.

Again, note that there is only one structural isomer with a triple bond, because the other possible placement of that bond is just drawing the three carbons in a different order. For the same reason, there is only one cyclopropene, not three.

Tautomers

Tautomers are structural isomers which readily interconvert, so that two or more species co-exist in equilibrium such as

${\displaystyle {\ce {H-X-Y=Z <=> X=Y-Z-H}}}$. 

Important examples are keto-enol tautomerism and the equilibrium between neutral and zwitterionic forms of an amino acid.

Resonance forms

The structure of some molecules is sometimes described as a resonance between several apparently different structural isomers. The classical example is 1,2-methylbenzene (o-xylene), which is often described as a mix of the two apparently distinct structural isomers:

However, neither of these two structures describes a real compound; they are fictions devised as a way to describe (by their "averaging" or "resonance") the actual delocalized bonding of o-xylene, which is the single isomer of ${\displaystyle {\ce {C8H10}}}$ with a benzene core and two methyl groups in adjacent positions.

Stereoisomers

Main article: Stereoisomerism

Stereoisomers have the same atoms or isotopes connected by bonds of the same type, but differ in their shapes — the relative positions of those atoms in space — apart from rotations and translations.

In theory, one can imagine any special arrangement of the atoms of a molecule or ion to be gradually changed to any other arrangement in infinitely many ways, by moving each atom along an appropriate path. However, changes in the positions of atoms will generally change the internal energy of a molecule, which is determined by the angles between bonds in each atom and by the distances between atoms (whether they are bonded or not).

A conformational isomer is an arrangement of the atoms of the molecule or ion for which the internal energy is a local minimum; that is, an arrangement such that any small changes in the positions of the atoms will increase the internal energy, and hence result in forces that tend to push the atoms back to the original positions. Changing the shape of the molecule from such an energy minimum ${\displaystyle {\ce {A}}}$ to another energy minimum ${\displaystyle {\ce {B}}}$ will therefore require going through configurations that have higher energy than ${\displaystyle {\ce {A}}}$ and ${\displaystyle {\ce {B}}}$. That is, a conformation isomer is separated from any other isomer by an energy barrier: the amount that must be temporarily added to the internal energy of the molecule in order to go through all the intermediate conformations along the "easiest" path (the one that minimizes that amount).

Molecular models of cyclohexane in boat and chair conformations. The carbon atoms are colored amber or blue according to whether they lie above or below the mean plane of the ring. The C–C bonds on the ring are light green.

A classic example of conformational isomerism is cyclohexane. Alkanes generally have minimum energy when the ${\displaystyle {\ce {C-C-C}}}$ angles are close to 110 degrees. Conformations of the cyclohexane molecule with all six carbon atoms on the same plane have a higher energy, because some or all the ${\displaystyle {\ce {C-C-C}}}$ angles must be far from that value (120 degrees for a regular hexagon). Thus the conformations which are local energy minima have the ring twisted in space, according to one of two patterns known as chair (with the carbons alternately above and below their mean plane) and boat (with two opposite carbons above the plane, and the other four below it).

If the energy barrier between two conformational isomers is low enough, it may be overcome by the random inputs of thermal energy that the molecule gets from interactions with the environment or from its own vibrations. In that case, the two isomers may as well be considered a single isomer, depending on the temperature and the context. For example, the two conformations of cyclohexane convert to each other quite rapidly at room temperature (in the liquid state), so that they are usually treated as a single isomer in chemistry.

In some cases, the barrier can be crossed by quantum tunneling of the atoms themselves. This last phenomenon prevents the separation of stereoisomers of fluorochloroamine ${\displaystyle {\ce {NHFCl}}}$ or hydrogen peroxide ${\displaystyle {\ce {H2O2}}}$, because the two conformations with minimum energy interconvert in a few picoseconds even at very low temperatures.

Conversely, the energy barrier may be so high that the easiest way to overcome it would require temporarily breaking and then reforming or more bonds of the molecule. In that case, the two isomers usually are stable enough to be isolated and treated as distinct substances. These isomers are then said to be different configurational isomers or "configurations" of the molecule, not just two different conformations. (However, one should be aware that the terms "conformation" and "configuration" are largely synonymous outside of chemistry, and their distinction may be controversial even among chemists.)

Interactions with other molecules of the same or different compounds (for example, through hydrogen bonds) can significantly change the energy of conformations of a molecule. Therefore, the possible isomers of a compound in solution or in its liquid and solid phases many be very different from those of an isolated molecule in vacuum. Even in the gas phase, some compounds like acetic acid will exist mostly in the form of dimers or larger groups of molecules, whose configurations may be different from those of the isolated molecule.

Enantiomers

Two compounds are said to be enantiomers if their molecules are mirror images of each other, that cannot be made to coincide only by rotations or translations — like a left hand and a right hand. The two shapes are said to be chiral.

A classical example is bromochlorofluoromethane (${\displaystyle {\ce {CHFClBr}}}$). The two enantiomers can be distinguished, for example, by whether the path ${\displaystyle {\ce {F->Cl->Br}}}$ turns clockwise or counterclockwise as seen from the hydrogen atom. In order to change one conformation to the other, at some point those four atoms would have to lie on the same plane — which would require severely straining or breaking their bonds to the carbon atom. The corresponding energy barrier between the two conformations is so high that there is practically no conversion between them at room temperature, and they can be regarded as different configurations.

The compound chlorofluoromethane ${\displaystyle {\ce {CH2ClF}}}$, in contrast, is not chiral: the mirror image of its molecule is also obtained by a half-turn about a suitable axis.

Another example of a chiral compound is 2,3-pentadiene ${\displaystyle {\ce {H3C-CH=C=CH-CH3}}}$ a hydrocarbon that contains two overlapping double bonds. The double bonds are such that the three middle carbons are in a straight line, while the first three and last three lie on perpendicular planes. The molecule and its mirror image are not superimposable, even though the molecule has an axis of symmetry. The two enantiomers can be distinguished, for example, by the right-hand rule. This type of isomerism is called axial isomerism.

Enantiomers behave identically in chemical reactions, except when reacted with chiral compounds or in the presence of chiral catalysts, such as most enzymes. For this latter reason, the two enantiomers of most chiral compounds usually have markedly different effects and roles in living organisms. In biochemistry and food science, the two enantiomers of a chiral molecule — such as glucose — are usually identified, and treated as very different substances.

Each enantiomer of a chiral compound typically rotates the plane of polarized light that passes through it. The rotation has the same magnitude but opposite senses for the two isomers, and can be a useful way of distinguishing and measuring their concentration in a solution. For this reason, enantiomers were formerly called "optical isomers". However, this term is ambiguous and is discouraged by the IUPAC.

Stereoisomers that are not enantiomers are called diastereomers. Some diastereomers may contain chiral center, some not.

Some enantiomer pairs (such as those of trans-cyclooctene) can be interconverted by internal motions that change bond lengths and angles only slightly. Other pairs (such as CHFClBr) cannot be interconverted without breaking bonds, and therefore are different configurations.

Cis-trans isomerism

A double bond between two carbon atoms forces the remaining four bonds (if they are single) to lie on the same plane, perpendicular to the plane of the bond as defined by its π orbital. If the two bonds on each carbon connect to different atoms, two distinct conformations are possible, that differ from each other by a twist of 180 degrees of one of the carbons about the double bond.

The classical example is dichloroethene ${\displaystyle {\ce {C2H2Cl2}}}$, specifically the structural isomer ${\displaystyle {\ce {Cl-HC=CH-Cl}}}$ that has one chlorine bonded to each carbon. It has two conformational isomers, with the two chlorines on the same side or on opposite sides of the double bond's plane. They are traditionally called cis (from Latin meaning "on this side of") and trans ("on the other side of"), respectively; or Z and E in the IUPAC recommended nomenclature. Conversion between these two forms usually requires temporarily breaking bonds (or turning the double bond into a single bond), so the two are considered different configurations of the molecule.

More generally, cis–trans isomerism (formerly called "geometric isomerism") occurs in molecules where the relative orientation of two distinguishable functional groups is restricted by a somewhat rigid framework of other atoms.

For example, in the cyclic alcohol inositol ${\displaystyle {\ce {(CHOH)6}}}$ (a six-fold alcohol of cyclohexane), the six-carbon cyclic backbone largely prevents the hydroxyl ${\displaystyle {\ce {-OH}}}$ and the hydrogen ${\displaystyle {\ce {-H}}}$ on each carbon from switching places. Therefore, one has different configurational isomers depending on whether each hydroxyl is on "this side" or "the other side" of the ring's mean plane. Discounting isomers that are equivalent under rotations, there are nine isomers that differ by this criterion, and behave as different stable substances (two of them being enantiomers of each other). The most common one in nature (myo-inositol) has the hydroxyls on carbons 1, 2, 3 and 5 on the same side of that plane, and can therefore be called cis-1,2,3,5-trans-4,6-cyclohexanehexol. And each of these cis-trans isomers can possibly have stable "chair" or "boat" conformations (although the barriers between these are significantly lower than those between different cis-trans isomers).

The two isomeric complexes, cisplatin and transplatin, are examples of square planar MX₂Y₂ molecules with M = Pt.

Cis and trans isomers also occur in inorganic coordination compounds, such as square planar ${\displaystyle {\ce {MX2Y2}}}$ complexes and octahedral ${\displaystyle {\ce {MX4Y2}}}$ complexes.

For more complex organic molecules, the cis and trans labels are ambiguous. The IUPAC recommends a more precise labeling scheme, based on the CIP priorities for the bonds at each carbon atom.

Centers with non-equivalent bonds

More generally, atoms or atom groups that can form three or more non-equivalent single bonds (such as the transition metals in coordination compounds) may give rise to multiple stereoisomers when different atoms or groups are attached at those positions. The same is true if a center with six or more equivalent bonds has two or more substituents.

For instance, in the compound ${\displaystyle {\ce {PF4Cl}}}$, the bonds from the phosphorus atom to the five halogens have approximately trigonal bipyramidal geometry. Thus two stereoisomers with that formula are possible, depending on whether the chlorine atom occupies one of the two "axial" positions, or one of the three "equatorial" positions.

For the compound ${\displaystyle {\ce {PF3Cl2}}}$, three isomers are possible, with zero, one, or two chlorines in the axial positions.

As another example, a complex with a formula like ${\displaystyle {\ce {MX3Y3}}}$, where the central atom M forms six bonds with octahedral geometry, has at least two facial–meridional isomers, depending on whether the three ${\displaystyle {\ce {X}}}$ bonds (and thus also the three ${\displaystyle {\ce {Y}}}$ bonds) are directed at the three corners of one face of the octahedron (fac isomer), or lie on the same equatorial or "meridian" plane of it (mer isomer).

Rotamers and atropisomers

Two parts of a molecule that are connected by just one single bond can rotate about that bond. While the bond itself is indifferent to that rotation, attractions and repulsions between the atoms in the two parts normally cause the energy of the whole molecule to vary (and possibly also the two parts to deform) depending on the relative angle of rotation φ between the two parts. Then there will be one or more special values of φ for which the energy is at a local minimum. The corresponding conformations of the molecule are called rotational isomers or rotamers.

Thus, for example, in an ethane molecule ${\displaystyle {\ce {H3C-CH3}}}$, all the bond angles and length are narrowly constrained, except that the two methyl groups can independently rotate about the ${\displaystyle {\ce {C-C}}}$ axis. Thus, even if those angles and distances are assumed fixed, there are infinitely many conformations for the ethane molecule, that differ by the relative angle φ of rotation between the two groups. The feeble repulsion between the hydrogen atoms in the two methyl groups causes the energy to minimized for three specific values of φ, 120° apart. In those configurations, the six planes ${\displaystyle {\ce {H-C-C}}}$ or ${\displaystyle {\ce {C-C-H}}}$ are 60° apart. Discounting rotations of the whole molecule, that configuration is a single isomer — the so-called staggered conformation.

Rotation between the two halves of the molecule 1,2-dichloroethane (${\displaystyle {\ce {ClH2C-CH2Cl}}}$ also has three local energy minima, but they have different energies due to differences between the ${\displaystyle {\ce {H-H}}}$, ${\displaystyle {\ce {Cl-Cl}}}$, and ${\displaystyle {\ce {H-Cl}}}$ interactions. There are therefore three rotamers: a trans isomer where the two chlorines are on the same plane as the two carbons, but with oppositely directed bonds; and two gauche isomers, mirror images of each other, where the two ${\displaystyle {\ce {-CH2Cl}}}$ groups are rotated about 109° from that position. The computed energy difference between trans and gauche is ~1.5 kcal/mol, the barrier for the ~109° rotation from trans to gauche is ~5 kcal/mol, and that of the ~142° rotation from one gauche to its enantiomer is ~8 kcal/mol. The situation for butane is similar, but with sightly lower gauche energies and barriers.

If the two parts of the molecule connected by a single bond are bulky or charged, the energy barriers may be much higher. For example, in the compound biphenyl — two phenyl groups connected by a single bond — the repulsion between hydrogen atoms closest to the central single bond gives the fully planar conformation, with the two rings on the same plane, a higher energy than conformations where the two rings are skewed. In the gas phase, the molecule has therefore at least two rotamers, with the ring planes twisted by ±47°, which are mirror images of each other. The barrier between them is rather low (~8 kJ/mol). This steric hindrance effect is more pronounced when those four hydrogens are replaced by larger atoms or groups, like chlorines or carboxyls. If the barrier is high enough for the two rotamers to be separated as stable compounds at room temperature, they are called atropisomers.

Topoisomers

Large molecules may have isomers that differ by the topology of their overall arrangement in space, even if there is no specific geometric constraint that separate them. For example, long chains may be twisted to form topologically distinct knots, with interconversion prevented by bulky substituents or cycle closing (as in circular DNA and RNA plasmids). Some knots may come in mirror-image enantiomer pairs. Such forms are called topological isomers or topoisomers.

Also, two or more such molecules may be bound together in a catenane by such topological linkages, even if there is no chemical bond between them. If the molecules are large enough, the linking may occur in multiple topologically distinct ways, constituting different isomers. Cage compounds, such as helium enclosed in dodecahedrane (He@C
₂₀H
₂₀) and carbon peapods, are a similar type of topological isomerism involving molecules with large internal voids with restricted or no openings.

Isotopes and spin

Isotopomers

Different isotopes of the same element can be considered as different kinds of atoms when enumerating isomers of a molecule or ion. The replacement of one or more atoms by their isotopes can create multiple structural isomers and/or stereoisomers from a single isomer.

For example, replacing two atoms of common hydrogen (${\displaystyle {\ce {^1 H}}}$) by deuterium (${\displaystyle {\ce {^2 H}}}$, or ${\displaystyle {\ce {D}}}$) on an ethane molecule yields two distinct structural isomers, depending on whether the substitutions are both on the same carbon (1,1-dideuteroethane, ${\displaystyle {\ce {HD2C-CH3}}}$) or one on each carbon (1,2-dideuteroethane, ${\displaystyle {\ce {DH2C-CDH2}}}$); as if the substituent was chlorine instead of deuterium. The two compounds do not interconvert easily and have different properties, such as their microwave spectrum.

Another example would be substituting one atom of deuterium for one of the hydrogens in chlorofluoromethane (${\displaystyle {\ce {CH2ClF}}}$). While the original compound is not chiral and has a single isomer, the substitution creates a pair of chiral enantiomers of ${\displaystyle {\ce {CHDClF}}}$, which could be distinguished (at least in theory) by their optical activity.

When two isomers would be identical if all isotopes of each element were replaced by a single isotope, they are described as isotopomers or isotopic isomers. In the above two examples if all ${\displaystyle {\ce {D}}}$ were replaced by ${\displaystyle {\ce {H}}}$, the two dideuteroethanes would both become ethane and the two deuterochlorofluoromethanes would both become ${\displaystyle {\ce {CH2ClF}}}$.

The concept of isotopomers is different from isotopologs or isotopic homologs, which differ in their isotopic composition. For example, ${\displaystyle {\ce {C2H5D}}}$ and ${\displaystyle {\ce {C2H4D2}}}$ are isotopologues and not isotopomers, and are therefore not isomers of each other.

Spin isomers

Another type of isomerism based on nuclear properties is spin isomerism, where molecules differ only in the relative spins of the constituent atomic nuclei. This phenomenon is significant for molecular hydrogen, which can be partially separated into two spin isomers: parahydrogen, with the spins of the two nuclei pointing in opposite ways, and orthohydrogen, where the spins point the same way.

Ionization and electronic excitation

The same isomer can also be in different excited states, that differ by the quantum state of their electrons. For example, the oxygen molecule can be in the triplet state or one of two singlet states. These are not considered different isomers, since such molecules usually decay spontaneously to their lowest-energy excitation state in a relatively short time scale.

Likewise, polyatomic ions and molecules that differ only by the addition or removal of electrons, like oxygen ${\displaystyle {\ce {O2}}}$or the peroxide ion ${\displaystyle {\ce {O2^2-}}}$ are not considered isomers.

Isomerization

Main article: Isomerization

Isomerization is the process by which one molecule is transformed into another molecule that has exactly the same atoms, but the atoms are rearranged. In some molecules and under some conditions, isomerization occurs spontaneously. Many isomers are equal or roughly equal in bond energy, and so exist in roughly equal amounts, provided that they can interconvert relatively freely, that is the energy barrier between the two isomers is not too high. When the isomerization occurs intramolecularly, it is considered a rearrangement reaction.

An example of an organometallic isomerization is the production of decaphenylferrocene, [(η⁵-C₅Ph₅)₂Fe] from its linkage isomer.

Synthesis of fumaric acid

Industrial synthesis of fumaric acid proceeds via the cis-trans isomerization of maleic acid:

Topoisomerases are enzymes that can cut and reform circular DNA and thus change its topology.

Medicinal chemistry

Isomers having distinct biological properties are common; for example, the placement of methyl groups. In substituted xanthines, theobromine, found in chocolate, is a vasodilator with some effects in common with caffeine; but, if one of the two methyl groups is moved to a different position on the two-ring core, the isomer is theophylline, which has a variety of effects, including bronchodilation and anti-inflammatory action. Another example of this occurs in the phenethylamine-based stimulant drugs. Phentermine is a non-chiral compound with a weaker effect than that of amphetamine. It is used as an appetite-reducing medication and has mild or no stimulant properties. However, an alternate atomic arrangement gives dextromethamphetamine, which is a stronger stimulant than amphetamine.

In medicinal chemistry and biochemistry, enantiomers are a special concern because they may possess distinct biological activity. Many preparative procedures afford a mixture of equal amounts of both enantiomeric forms. In some cases, the enantiomers are separated by chromatography using chiral stationary phases. They may also be separated through the formation of diastereomeric salts. In other cases, enantioselective synthesis have been developed.

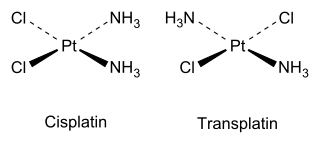
As an inorganic example, cisplatin (see structure above) is an important drug used in cancer chemotherapy, whereas the trans isomer (transplatin) has no useful pharmacological activity.

History

Isomerism was first observed in 1827, when Friedrich Wöhler prepared silver cyanate and discovered that, although its elemental composition of ${\displaystyle {\ce {AgCNO}}}$ was identical to silver fulminate (prepared by Justus von Liebig the previous year), its properties were distinct. This finding challenged the prevailing chemical understanding of the time, which held that chemical compounds could be distinct only when their elemental compositions differ. (We now know that the bonding structures of fulminate and cyanate can be approximately described as ${\displaystyle {\ce {O- N+}}}$≡${\displaystyle {\ce {C-}}}$ and ${\displaystyle {\ce {O=C=N-}}}$, respectively.)

Additional examples were found in succeeding years, such as Wöhler's 1828 discovery that urea has the same atomic composition (${\displaystyle {\ce {CH4N2O}}}$) as the chemically distinct ammonium cyanate. (Their structures are now known to be ${\displaystyle {\ce {(H2N-)2C=O}}}$ and ${\displaystyle {\ce {[NH+4][O=C=N^{-}]}}}$, respectively.) In 1830 Jöns Jacob Berzelius introduced the term isomerism to describe the phenomenon.

In 1848, Louis Pasteur observed that tartaric acid crystals came into two kinds of shapes that were mirror images of each other. Separating the crystals by hand, he obtained two version of tartaric acid, each of which would crystallize in only one of the two shapes, and rotated the plane of polarized light to the same degree but in opposite directions.

Twin prime

From Wikipedia, the free encyclopedia

Jump to navigation Jump to search

A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair (41, 43). In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or prime pair.

Twin primes become increasingly rare as one examines larger ranges, in keeping with the general tendency of gaps between adjacent primes to become larger as the numbers themselves get larger. However, it is unknown whether there are infinitely many twin primes (the so-called twin prime conjecture) or if there is a largest pair. The breakthrough work of Yitang Zhang in 2013, as well as work by James Maynard, Terence Tao and others, has made substantial progress towards proving that there are infinitely many twin primes, but at present this remains unsolved.

Properties

Usually the pair (2, 3) is not considered to be a pair of twin primes. Since 2 is the only even prime, this pair is the only pair of prime numbers that differ by one; thus twin primes are as closely spaced as possible for any other two primes.

The first few twin prime pairs are:

(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), … OEIS: A077800.

Five is the only prime that belongs to two pairs, as every twin prime pair greater than ${\displaystyle (3,5)}$ is of the form ${\displaystyle (6n-1,6n+1)}$ for some natural number n; that is, the number between the two primes is a multiple of 6. As a result, the sum of any pair of twin primes (other than 3 and 5) is divisible by 12.

Brun's theorem

Main article: Brun's theorem

In 1915, Viggo Brun showed that the sum of reciprocals of the twin primes was convergent. This famous result, called Brun's theorem, was the first use of the Brun sieve and helped initiate the development of modern sieve theory. The modern version of Brun's argument can be used to show that the number of twin primes less than N does not exceed

${\displaystyle {\frac {CN}{(\log N)^{2}}}}$

for some absolute constant C > 0. In fact, it is bounded above by

${\displaystyle {\frac {C'N}{(\log N)^{2}}}\left(1+O\left({\frac {\log \log N}{\log N}}\right)\right),}$

where ${\displaystyle C'=8C_{2}}$, where C₂ is the twin prime constant, given below.

Twin prime conjecture

The question of whether there exist infinitely many twin primes has been one of the great open questions in number theory for many years. This is the content of the twin prime conjecture, which states that there are infinitely many primes p such that p + 2 is also prime. In 1849, de Polignac made the more general conjecture that for every natural number k, there are infinitely many primes p such that p + 2k is also prime. The case k = 1 of de Polignac's conjecture is the twin prime conjecture.

A stronger form of the twin prime conjecture, the Hardy–Littlewood conjecture (see below), postulates a distribution law for twin primes akin to the prime number theorem.

On April 17, 2013, Yitang Zhang announced a proof that for some integer N that is less than 70 million, there are infinitely many pairs of primes that differ by N. Zhang's paper was accepted by Annals of Mathematics in early May 2013. Terence Tao subsequently proposed a Polymath Project collaborative effort to optimize Zhang's bound. As of April 14, 2014, one year after Zhang's announcement, the bound has been reduced to 246. Further, assuming the Elliott–Halberstam conjecture and its generalized form, the Polymath project wiki states that the bound has been reduced to 12 and 6, respectively. These improved bounds were discovered using a different approach that was simpler than Zhang's and was discovered independently by James Maynard and Terence Tao. This second approach also gave bounds for the smallest f(m) needed to guarantee that infinitely many intervals of width f(m) contain at least m primes.

A strengthening of Goldbach’s conjecture, if proved, would also prove there is an infinite number of twin primes.

Other theorems weaker than the twin prime conjecture

In 1940, Paul Erdős showed that there is a constant c < 1 and infinitely many primes p such that (p′ − p) < (c ln p) where p′ denotes the next prime after p. What this means is that we can find infinitely many intervals that contain two primes (p,p′) as long as we let these intervals grow slowly in size as we move to bigger and bigger primes. Here, "grow slowly" means that the length of these intervals can grow logarithmically. This result was successively improved; in 1986 Helmut Maier showed that a constant c < 0.25 can be used. In 2004 Daniel Goldston and Cem Yıldırım showed that the constant could be improved further to c = 0.085786… In 2005, Goldston, János Pintz and Yıldırım established that c can be chosen to be arbitrarily small, i.e.

${\displaystyle \liminf _{n\to \infty }{\frac {p_{n+1}-p_{n}}{\log p_{n}}}=0.}$

On the other hand, this result does not rule out that there may not be infinitely many intervals that contain two primes if we only allow the intervals to grow in size as, for example, c ln ln p.

By assuming the Elliott–Halberstam conjecture or a slightly weaker version, they were able to show that there are infinitely many n such that at least two of n, n + 2, n + 6, n + 8, n + 12, n + 18, or n + 20 are prime. Under a stronger hypothesis they showed that for infinitely many n, at least two of n, n + 2, n + 4, and n + 6 are prime.

The result of Yitang Zhang,

${\displaystyle \liminf _{n\to \infty }(p_{n+1}-p_{n})<N\;{\text{ with }}\;N=7\times 10^{7},}$

is a major improvement on the Goldston–Graham–Pintz–Yıldırım result. The Polymath Project optimization of Zhang's bound and the work of Maynard have reduced the bound to N = 246.

Conjectures

First Hardy–Littlewood conjecture

The Hardy–Littlewood conjecture (named after G. H. Hardy and John Littlewood) is a generalization of the twin prime conjecture. It is concerned with the distribution of prime constellations, including twin primes, in analogy to the prime number theorem. Let π₂(x) denote the number of primes p ≤ x such that p + 2 is also prime. Define the twin prime constant C₂ as

${\displaystyle C_{2}=\prod _{\textstyle {p\;{\rm {prime}} \atop p\geq 3}}\left(1-{\frac {1}{(p-1)^{2}}}\right)\approx 0.660161815846869573927812110014\dots }$

(here the product extends over all prime numbers p ≥ 3). Then a special case of the first Hardy-Littlewood conjecture is that

${\displaystyle \pi _{2}(x)\sim 2C_{2}{\frac {x}{(\ln x)^{2}}}\sim 2C_{2}\int _{2}^{x}{dt \over (\ln t)^{2}}}$

in the sense that the quotient of the two expressions tends to 1 as x approaches infinity. (The second ~ is not part of the conjecture and is proven by integration by parts.)

The conjecture can be justified (but not proven) by assuming that 1 / ln t describes the density function of the prime distribution. This assumption, which is suggested by the prime number theorem, implies the twin prime conjecture, as shown in the formula for π₂(x) above.

The fully general first Hardy–Littlewood conjecture on prime k-tuples (not given here) implies that the second Hardy–Littlewood conjecture is false.

This conjecture has been extended by Dickson's conjecture.

Polignac's conjecture

Polignac's conjecture from 1849 states that for every positive even natural number k, there are infinitely many consecutive prime pairs p and p′ such that p′ − p = k (i.e. there are infinitely many prime gaps of size k). The case k = 2 is the twin prime conjecture. The conjecture has not yet been proven or disproven for any specific value of k, but Zhang's result proves that it is true for at least one (currently unknown) value of k. Indeed, if such a k did not exist, then for any positive even natural number N there are at most finitely many n such that p_n+1 − p_n = m for all m < N and so for n large enough we have p_n+1 − p_n > N, which would contradict Zhang's result.

Large twin primes

Beginning in 2007, two distributed computing projects, Twin Prime Search and PrimeGrid, have produced several record-largest twin primes. As of September 2018, the current largest twin prime pair known is 2996863034895 · 2^1290000 ± 1, with 388,342 decimal digits. It was discovered in September 2016.

There are 808,675,888,577,436 twin prime pairs below 10¹⁸.

An empirical analysis of all prime pairs up to 4.35 · 10¹⁵ shows that if the number of such pairs less than x is f(x)·x/(log x)² then f(x) is about 1.7 for small x and decreases towards about 1.3 as x tends to infinity. The limiting value of f(x) is conjectured to equal twice the twin prime constant (OEIS: A114907) (not to be confused with Brun's constant), according to the Hardy–Littlewood conjecture.

Other elementary properties

Every third odd number is divisible by 3, which requires that no three successive odd numbers can be prime unless one of them is 3. Five is therefore the only prime that is part of two twin prime pairs. The lower member of a pair is by definition a Chen prime.

It has been proven that the pair (m, m + 2) is a twin prime if and only if

${\displaystyle 4((m-1)!+1)\equiv -m{\pmod {m(m+2)}}.}$

If m − 4 or m + 6 is also prime then the three primes are called a prime triplet.

For a twin prime pair of the form (6n − 1, 6n + 1) for some natural number n > 1, n must have units digit 0, 2, 3, 5, 7, or 8 (OEIS: A002822).

Isolated prime

An isolated prime (also known as single prime or non-twin prime) is a prime number p such that neither p − 2 nor p + 2 is prime. In other words, p is not part of a twin prime pair. For example, 23 is an isolated prime, since 21 and 25 are both composite.

The first few isolated primes are

2, 23, 37, 47, 53, 67, 79, 83, 89, 97, ... OEIS: A007510

It follows from Brun's theorem that almost all primes are isolated in the sense that the ratio of the number of isolated primes less than a given threshold n and the number of all primes less than n tends to 1 as n tends to infinity.

Goldbach's conjecture

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Goldbach%27s_conjecture 

 

Goldbach's conjecture

Letter from Goldbach to Euler dated on 7 June 1742 (Latin-German)
Field	Number theory
Conjectured by	Christian Goldbach
Conjectured in	1742
Open problem	Yes
Consequences	Goldbach's weak conjecture

Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even whole number greater than 2 is the sum of two prime numbers.

The conjecture has been shown to hold for all integers less than 4 × 10¹⁸, but remains unproven despite considerable effort.

History

On 7 June 1742, the German mathematician Christian Goldbach wrote a letter to Leonhard Euler (letter XLIII), in which he proposed the following conjecture:

Every integer that can be written as the sum of two primes can also be written as the sum of as many primes as one wishes, until all terms are units.

Goldbach was following the now-abandoned convention of considering 1 to be a prime number, so that a sum of units would indeed be a sum of primes. He then proposed a second conjecture in the margin of his letter, which implies the first:

... eine jede Zahl, die grösser ist als 2, ein aggregatum trium numerorum primorum sey.
Every integer greater than 2 can be written as the sum of three primes.

Euler replied in a letter dated 30 June 1742 and reminded Goldbach of an earlier conversation they had had ("... so Ew vormals mit mir communicirt haben ..."), in which Goldbach had remarked that the first of those two conjectures would follow from the statement

Every positive even integer can be written as the sum of two primes.

This is in fact equivalent to his second, marginal conjecture. In the letter dated 30 June 1742, Euler stated:

Dass ... ein jeder numerus par eine summa duorum primorum sey, halte ich für ein ganz gewisses theorema, ungeachtet ich dasselbe nicht demonstriren kann.
That ... every even integer is a sum of two primes, I regard as a completely certain theorem, although I cannot prove it.

Each of the three conjectures above has a natural analog in terms of the modern definition of a prime, under which 1 is excluded. A modern version of the first conjecture is:

Every integer that can be written as the sum of two primes can also be written as the sum of as many primes as one wishes, until either all terms are two (if the integer is even) or one term is three and all other terms are two (if the integer is odd).

A modern version of the marginal conjecture is:

Every integer greater than 5 can be written as the sum of three primes.

And a modern version of Goldbach's older conjecture of which Euler reminded him is:

Every even integer greater than 2 can be written as the sum of two primes.

These modern versions might not be entirely equivalent to the corresponding original statements. For example, if there were an even integer ${\displaystyle N=p+1}$ larger than 4, for ${\displaystyle p}$ a prime, that could not be expressed as the sum of two primes in the modern sense, then it would be a counterexample to the modern version of the third conjecture (without being a counterexample to the original version). The modern version is thus probably stronger (but in order to confirm that, one would have to prove that the first version, freely applied to any positive even integer ${\displaystyle n}$, could not possibly rule out the existence of such a specific counterexample ${\displaystyle N}$). In any case, the modern statements have the same relationships with each other as the older statements did. That is, the second and third modern statements are equivalent, and either implies the first modern statement.

The third modern statement (equivalent to the second) is the form in which the conjecture is usually expressed today. It is also known as the "strong", "even", or "binary" Goldbach conjecture. A weaker form of the second modern statement, known as "Goldbach's weak conjecture", the "odd Goldbach conjecture", or the "ternary Goldbach conjecture," asserts that

Every odd integer greater than 7 can be written as the sum of three odd primes.

A proof for the weak conjecture was proposed in 2013 by Harald Helfgott. Helfgott's proof has not yet appeared in a peer-reviewed publication, though was accepted for publication in the Annals of Mathematics Studies series in 2015, and has been undergoing further review and revision since. The weak conjecture would be a corollary of the strong conjecture: if n – 3 is a sum of two primes, then n is a sum of three primes. However, the converse implication and thus the strong Goldbach conjecture remain unproven.

Verified results

For small values of n, the strong Goldbach conjecture (and hence the weak Goldbach conjecture) can be verified directly. For instance, in 1938, Nils Pipping laboriously verified the conjecture up to n ≤ 10⁵. With the advent of computers, many more values of n have been checked; T. Oliveira e Silva ran a distributed computer search that has verified the conjecture for n ≤ 4 × 10¹⁸ (and double-checked up to 4 × 10¹⁷) as of 2013. One record from this search is that 3325581707333960528 is the smallest number that cannot be written as a sum of two primes where one is smaller than 9781.

Heuristic justification

Statistical considerations that focus on the probabilistic distribution of prime numbers present informal evidence in favour of the conjecture (in both the weak and strong forms) for sufficiently large integers: the greater the integer, the more ways there are available for that number to be represented as the sum of two or three other numbers, and the more "likely" it becomes that at least one of these representations consists entirely of primes.

Number of ways to write an even number n as the sum of two primes (4 ≤ n ≤ 1,000), (sequence A002375 in the OEIS)

 

Number of ways to write an even number n as the sum of two primes (4 ≤ n ≤ 1000000)

A very crude version of the heuristic probabilistic argument (for the strong form of the Goldbach conjecture) is as follows. The prime number theorem asserts that an integer m selected at random has roughly a ${\displaystyle 1/\ln m}$ chance of being prime. Thus if n is a large even integer and m is a number between 3 and n/2, then one might expect the probability of m and n − m simultaneously being prime to be ${\displaystyle 1{\big /}{\big [}\ln m\,\ln(n-m){\big ]}}$. If one pursues this heuristic, one might expect the total number of ways to write a large even integer n as the sum of two odd primes to be roughly

${\displaystyle \sum _{m=3}^{n/2}{\frac {1}{\ln m}}{\frac {1}{\ln(n-m)}}\approx {\frac {n}{2(\ln n)^{2}}}.}$

Since ${\displaystyle \ln n\ll {\sqrt {n}}}$, this quantity goes to infinity as n increases, and we would expect that every large even integer has not just one representation as the sum of two primes, but in fact very many such representations.

This heuristic argument is actually somewhat inaccurate, because it assumes that the events of m and n − m being prime are statistically independent of each other. For instance, if m is odd, then n − m is also odd, and if m is even, then n − m is even, a non-trivial relation because, besides the number 2, only odd numbers can be prime. Similarly, if n is divisible by 3, and m was already a prime distinct from 3, then n − m would also be coprime to 3 and thus be slightly more likely to be prime than a general number. Pursuing this type of analysis more carefully, G. H. Hardy and John Edensor Littlewood in 1923 conjectured (as part of their Hardy–Littlewood prime tuple conjecture) that for any fixed c ≥ 2, the number of representations of a large integer n as the sum of c primes ${\displaystyle n=p_{1}+\cdots +p_{c}}$ with ${\displaystyle p_{1}\leq \cdots \leq p_{c}}$ should be asymptotically equal to

${\displaystyle \left(\prod _{p}{\frac {p\gamma _{c,p}(n)}{(p-1)^{c}}}\right)\int _{2\leq x_{1}\leq \cdots \leq x_{c}:x_{1}+\cdots +x_{c}=n}{\frac {dx_{1}\cdots dx_{c-1}}{\ln x_{1}\cdots \ln x_{c}}},}$

where the product is over all primes p, and ${\displaystyle \gamma _{c,p}(n)}$ is the number of solutions to the equation ${\displaystyle n=q_{1}+\cdots +q_{c}\mod p}$ in modular arithmetic, subject to the constraints ${\displaystyle q_{1},\ldots ,q_{c}\neq 0\mod p}$. This formula has been rigorously proven to be asymptotically valid for c ≥ 3 from the work of Ivan Matveevich Vinogradov, but is still only a conjecture when ${\displaystyle c=2}$. In the latter case, the above formula simplifies to 0 when n is odd, and to

${\displaystyle 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right)\int _{2}^{n}{\frac {dx}{(\ln x)^{2}}}\approx 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right){\frac {n}{(\ln n)^{2}}}}$

when n is even, where ${\displaystyle \Pi _{2}}$ is Hardy–Littlewood's twin prime constant

${\displaystyle \Pi _{2}:=\prod _{\textstyle {p\;{\rm {prime}} \atop p\geq 3}}\left(1-{\frac {1}{(p-1)^{2}}}\right)\approx 0.660161815846869573927812110014\dots }$

This is sometimes known as the extended Goldbach conjecture. The strong Goldbach conjecture is in fact very similar to the twin prime conjecture, and the two conjectures are believed to be of roughly comparable difficulty.

The Goldbach partition functions shown here can be displayed as histograms, which illustrate the above equations. See Goldbach's comet for more information.

Goldbach's comet also suggests that there are tight upper and lower bounds on the number of representatives, and that the modulo 6 of 2n plays a part in the number of representations.

The number of representations is about ${\displaystyle n\ln n}$, from ${\displaystyle 2n=p+c}$ and the Prime Number Theorem. If each c is composite, then it must have a prime factor less than or equal to the square root of ${\displaystyle 2n}$, by the method outlined in trial division.

This leads to an expectation of ${\displaystyle {\frac {n\ln n}{\sqrt {2n}}}={\sqrt {\frac {n}{2}}}\ln n}$ representations.

Rigorous results

The strong Goldbach conjecture is much more difficult than the weak Goldbach conjecture. Using Vinogradov's method, Nikolai Chudakov, Johannes van der Corput, and Theodor Estermann showed that almost all even numbers can be written as the sum of two primes (in the sense that the fraction of even numbers which can be so written tends towards 1). In 1930, Lev Schnirelmann proved that any natural number greater than 1 can be written as the sum of not more than C prime numbers, where C is an effectively computable constant; see Schnirelmann density. Schnirelmann's constant is the lowest number C with this property. Schnirelmann himself obtained C < 800000. This result was subsequently enhanced by many authors, such as Olivier Ramaré, who in 1995 showed that every even number n ≥ 4 is in fact the sum of at most 6 primes. The best known result currently stems from the proof of the weak Goldbach conjecture by Harald Helfgott, which directly implies that every even number n ≥ 4 is the sum of at most 4 primes.

In 1924, Hardy and Littlewood showed under the assumption of the generalized Riemann hypothesis that the number of even numbers up to X violating the Goldbach conjecture is much less than ${\displaystyle X^{(1/2)+c}}$ for small c.

Chen Jingrun showed in 1973 using the methods of sieve theory that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime (the product of two primes). See Chen's theorem for further information.

In 1975, Hugh Montgomery and Robert Charles Vaughan showed that "most" even numbers are expressible as the sum of two primes. More precisely, they showed that there exist positive constants c and C such that for all sufficiently large numbers N, every even number less than N is the sum of two primes, with at most ${\displaystyle CN^{1-c}}$ exceptions. In particular, the set of even integers that are not the sum of two primes has density zero.

In 1951, Yuri Linnik proved the existence of a constant K such that every sufficiently large even number is the sum of two primes and at most K powers of 2. Roger Heath-Brown and Jan-Christoph Schlage-Puchta found in 2002 that K = 13 works.

Related problems

Although Goldbach's conjecture implies that every positive integer greater than one can be written as a sum of at most three primes, it is not always possible to find such a sum using a greedy algorithm that uses the largest possible prime at each step. The Pillai sequence tracks the numbers requiring the largest number of primes in their greedy representations.

Similar problems to Goldbach's conjecture exist in which primes are replaced by other particular sets of numbers, such as the squares:

• It was proven by Lagrange that every positive integer is the sum of four squares. See Waring's problem and the related Waring–Goldbach problem on sums of powers of primes.
• Hardy and Littlewood listed as their Conjecture I: "Every large odd number (n > 5) is the sum of a prime and the double of a prime" (Mathematics Magazine, 66.1 (1993): 45–47). This conjecture is known as Lemoine's conjecture and is also called Levy's conjecture.
• The Goldbach conjecture for practical numbers, a prime-like sequence of integers, was stated by Margenstern in 1984, and proved by Melfi in 1996: every even number is a sum of two practical numbers.
• A strengthening of the Goldbach conjecture proposed by Harvey Dubner states that every even integer greater than 4,208 is the sum of two twin primes. Only 34 even integers less than 4,208 are not the sum of two twin primes. Dubner has verified computationally that this list is complete up to 2×10¹⁰. A proof of this stronger conjecture would not only imply Goldbach's conjecture, but also the twin prime conjecture.

In popular culture

Goldbach's Conjecture (Chinese: 哥德巴赫猜想) is the title of the biography of Chinese mathematician and number theorist Chen Jingrun, written by Xu Chi.

The conjecture is a central point in the plot of the 1992 novel Uncle Petros and Goldbach's Conjecture by Greek author Apostolos Doxiadis, in the short story "Sixty Million Trillion Combinations" by Isaac Asimov and also in the 2008 mystery novel No One You Know by Michelle Richmond.

Goldbach's conjecture is part of the plot of the 2007 Spanish film Fermat's Room.