Probability theory

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Probability_theory 

 

Part of a series on statistics
Probability theory
Probability Axioms Determinism System Indeterminism Randomness
Probability space Sample space Event Collectively exhaustive events Elementary event Mutual exclusivity Outcome Singleton Experiment Bernoulli trial Probability distribution Bernoulli distribution Binomial distribution Normal distribution Probability measure Random variable Bernoulli process Continuous or discrete Expected value Markov chain Observed value Random walk Stochastic process
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram

Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability theory describing such behaviour are the law of large numbers and the central limit theorem.

As a mathematical foundation for statistics, probability theory is essential to many human activities that involve quantitative analysis of data. Methods of probability theory also apply to descriptions of complex systems given only partial knowledge of their state, as in statistical mechanics or sequential estimation. A great discovery of twentieth-century physics was the probabilistic nature of physical phenomena at atomic scales, described in quantum mechanics. 

History of probability

Main article: History of probability

The modern mathematical theory of probability has its roots in attempts to analyze games of chance by Gerolamo Cardano in the sixteenth century, and by Pierre de Fermat and Blaise Pascal in the seventeenth century (for example the "problem of points"). Christiaan Huygens published a book on the subject in 1657. In the 19th century, what is considered the classical definition of probability was completed by Pierre Laplace.

Initially, probability theory mainly considered discrete events, and its methods were mainly combinatorial. Eventually, analytical considerations compelled the incorporation of continuous variables into the theory.

This culminated in modern probability theory, on foundations laid by Andrey Nikolaevich Kolmogorov. Kolmogorov combined the notion of sample space, introduced by Richard von Mises, and measure theory and presented his axiom system for probability theory in 1933. This became the mostly undisputed axiomatic basis for modern probability theory; but, alternatives exist, such as the adoption of finite rather than countable additivity by Bruno de Finetti.

Treatment

Most introductions to probability theory treat discrete probability distributions and continuous probability distributions separately. The measure theory-based treatment of probability covers the discrete, continuous, a mix of the two, and more.

Motivation

Consider an experiment that can produce a number of outcomes. The set of all outcomes is called the sample space of the experiment. The power set of the sample space (or equivalently, the event space) is formed by considering all different collections of possible results. For example, rolling an honest die produces one of six possible results. One collection of possible results corresponds to getting an odd number. Thus, the subset {1,3,5} is an element of the power set of the sample space of die rolls. These collections are called events. In this case, {1,3,5} is the event that the die falls on some odd number. If the results that actually occur fall in a given event, that event is said to have occurred.

Probability is a way of assigning every "event" a value between zero and one, with the requirement that the event made up of all possible results (in our example, the event {1,2,3,4,5,6}) be assigned a value of one. To qualify as a probability distribution, the assignment of values must satisfy the requirement that if you look at a collection of mutually exclusive events (events that contain no common results, e.g., the events {1,6}, {3}, and {2,4} are all mutually exclusive), the probability that any of these events occurs is given by the sum of the probabilities of the events.

The probability that any one of the events {1,6}, {3}, or {2,4} will occur is 5/6. This is the same as saying that the probability of event {1,2,3,4,6} is 5/6. This event encompasses the possibility of any number except five being rolled. The mutually exclusive event {5} has a probability of 1/6, and the event {1,2,3,4,5,6} has a probability of 1, that is, absolute certainty.

When doing calculations using the outcomes of an experiment, it is necessary that all those elementary events have a number assigned to them. This is done using a random variable. A random variable is a function that assigns to each elementary event in the sample space a real number. This function is usually denoted by a capital letter. In the case of a die, the assignment of a number to a certain elementary events can be done using the identity function. This does not always work. For example, when flipping a coin the two possible outcomes are "heads" and "tails". In this example, the random variable X could assign to the outcome "heads" the number "0" (${\displaystyle X(heads)=0}$) and to the outcome "tails" the number "1" (${\displaystyle X(tails)=1}$).

Discrete probability distributions

Main article: Discrete probability distribution

 

The Poisson distribution, a discrete probability distribution.

Discrete probability theory deals with events that occur in countable sample spaces.

Examples: Throwing dice, experiments with decks of cards, random walk, and tossing coins

Classical definition: Initially the probability of an event to occur was defined as the number of cases favorable for the event, over the number of total outcomes possible in an equiprobable sample space: see Classical definition of probability.

For example, if the event is "occurrence of an even number when a die is rolled", the probability is given by ${\displaystyle {\tfrac {3}{6}}={\tfrac {1}{2}}}$, since 3 faces out of the 6 have even numbers and each face has the same probability of appearing.

Modern definition: The modern definition starts with a finite or countable set called the sample space, which relates to the set of all possible outcomes in classical sense, denoted by ${\displaystyle \Omega }$. It is then assumed that for each element ${\displaystyle x\in \Omega \,}$, an intrinsic "probability" value ${\displaystyle f(x)\,}$ is attached, which satisfies the following properties:

1. ${\displaystyle f(x)\in [0,1]{\mbox{ for all }}x\in \Omega \,;}$
2. ${\displaystyle \sum _{x\in \Omega }f(x)=1\,.}$

That is, the probability function f(x) lies between zero and one for every value of x in the sample space Ω, and the sum of f(x) over all values x in the sample space Ω is equal to 1. An event is defined as any subset ${\displaystyle E\,}$ of the sample space ${\displaystyle \Omega \,}$. The probability of the event ${\displaystyle E\,}$ is defined as

${\displaystyle P(E)=\sum _{x\in E}f(x)\,.}$

So, the probability of the entire sample space is 1, and the probability of the null event is 0.

The function ${\displaystyle f(x)\,}$ mapping a point in the sample space to the "probability" value is called a probability mass function abbreviated as pmf. The modern definition does not try to answer how probability mass functions are obtained; instead, it builds a theory that assumes their existence.

Continuous probability distributions

Main article: Continuous probability distribution

 

The normal distribution, a continuous probability distribution.

Continuous probability theory deals with events that occur in a continuous sample space.

Classical definition: The classical definition breaks down when confronted with the continuous case. See Bertrand's paradox.

Modern definition: If the sample space of a random variable X is the set of real numbers (${\displaystyle \mathbb {R} }$) or a subset thereof, then a function called the cumulative distribution function (or cdf) ${\displaystyle F\,}$ exists, defined by ${\displaystyle F(x)=P(X\leq x)\,}$. That is, F(x) returns the probability that X will be less than or equal to x.

The cdf necessarily satisfies the following properties.

1. ${\displaystyle F\,}$ is a monotonically non-decreasing, right-continuous function;
2. ${\displaystyle \lim _{x\rightarrow -\infty }F(x)=0\,;}$
3. ${\displaystyle \lim _{x\rightarrow \infty }F(x)=1\,.}$

If ${\displaystyle F\,}$ is absolutely continuous, i.e., its derivative exists and integrating the derivative gives us the cdf back again, then the random variable X is said to have a probability density function or pdf or simply density ${\displaystyle f(x)={\frac {dF(x)}{dx}}\,.}$

For a set ${\displaystyle E\subseteq \mathbb {R} }$, the probability of the random variable X being in ${\displaystyle E\,}$ is

${\displaystyle P(X\in E)=\int _{x\in E}dF(x)\,.}$

In case the probability density function exists, this can be written as

${\displaystyle P(X\in E)=\int _{x\in E}f(x)\,dx\,.}$

Whereas the pdf exists only for continuous random variables, the cdf exists for all random variables (including discrete random variables) that take values in ${\displaystyle \mathbb {R} \,.}$

These concepts can be generalized for multidimensional cases on ${\displaystyle \mathbb {R} ^{n}}$ and other continuous sample spaces.

Measure-theoretic probability theory

The raison d'être of the measure-theoretic treatment of probability is that it unifies the discrete and the continuous cases, and makes the difference a question of which measure is used. Furthermore, it covers distributions that are neither discrete nor continuous nor mixtures of the two.

An example of such distributions could be a mix of discrete and continuous distributions—for example, a random variable that is 0 with probability 1/2, and takes a random value from a normal distribution with probability 1/2. It can still be studied to some extent by considering it to have a pdf of ${\displaystyle (\delta [x]+\varphi (x))/2}$, where ${\displaystyle \delta [x]}$ is the Dirac delta function.

Other distributions may not even be a mix, for example, the Cantor distribution has no positive probability for any single point, neither does it have a density. The modern approach to probability theory solves these problems using measure theory to define the probability space:

Given any set ${\displaystyle \Omega \,}$ (also called sample space) and a σ-algebra ${\displaystyle {\mathcal {F}}\,}$ on it, a measure ${\displaystyle P\,}$ defined on ${\displaystyle {\mathcal {F}}\,}$ is called a probability measure if ${\displaystyle P(\Omega )=1.\,}$

If ${\displaystyle {\mathcal {F}}\,}$ is the Borel σ-algebra on the set of real numbers, then there is a unique probability measure on ${\displaystyle {\mathcal {F}}\,}$ for any cdf, and vice versa. The measure corresponding to a cdf is said to be induced by the cdf. This measure coincides with the pmf for discrete variables and pdf for continuous variables, making the measure-theoretic approach free of fallacies.

The probability of a set ${\displaystyle E\,}$ in the σ-algebra ${\displaystyle {\mathcal {F}}\,}$ is defined as

${\displaystyle P(E)=\int _{\omega \in E}\mu _{F}(d\omega )\,}$

where the integration is with respect to the measure ${\displaystyle \mu _{F}\,}$ induced by ${\displaystyle F\,.}$

Along with providing better understanding and unification of discrete and continuous probabilities, measure-theoretic treatment also allows us to work on probabilities outside ${\displaystyle \mathbb {R} ^{n}}$, as in the theory of stochastic processes. For example, to study Brownian motion, probability is defined on a space of functions.

When it's convenient to work with a dominating measure, the Radon-Nikodym theorem is used to define a density as the Radon-Nikodym derivative of the probability distribution of interest with respect to this dominating measure. Discrete densities are usually defined as this derivative with respect to a counting measure over the set of all possible outcomes. Densities for absolutely continuous distributions are usually defined as this derivative with respect to the Lebesgue measure. If a theorem can be proved in this general setting, it holds for both discrete and continuous distributions as well as others; separate proofs are not required for discrete and continuous distributions.

Classical probability distributions

Main article: Probability distributions

Certain random variables occur very often in probability theory because they well describe many natural or physical processes. Their distributions, therefore, have gained special importance in probability theory. Some fundamental discrete distributions are the discrete uniform, Bernoulli, binomial, negative binomial, Poisson and geometric distributions. Important continuous distributions include the continuous uniform, normal, exponential, gamma and beta distributions.

Convergence of random variables

Main article: Convergence of random variables

In probability theory, there are several notions of convergence for random variables. They are listed below in the order of strength, i.e., any subsequent notion of convergence in the list implies convergence according to all of the preceding notions.

Weak convergence

A sequence of random variables ${\displaystyle X_{1},X_{2},\dots ,\,}$ converges weakly to the random variable ${\displaystyle X\,}$ if their respective cumulative distribution functions ${\displaystyle F_{1},F_{2},\dots \,}$ converge to the cumulative distribution function ${\displaystyle F\,}$ of ${\displaystyle X\,}$, wherever ${\displaystyle F\,}$ is continuous. Weak convergence is also called convergence in distribution.

Most common shorthand notation: ${\displaystyle \displaystyle X_{n}\,{\xrightarrow {\mathcal {D}}}\,X}$

Convergence in probability

The sequence of random variables ${\displaystyle X_{1},X_{2},\dots \,}$ is said to converge towards the random variable ${\displaystyle X\,}$ in probability if ${\displaystyle \lim _{n\rightarrow \infty }P\left(\left|X_{n}-X\right|\geq \varepsilon \right)=0}$ for every ε > 0.

Most common shorthand notation: ${\displaystyle \displaystyle X_{n}\,{\xrightarrow {P}}\,X}$

Strong convergence

The sequence of random variables ${\displaystyle X_{1},X_{2},\dots \,}$ is said to converge towards the random variable ${\displaystyle X\,}$ strongly if ${\displaystyle P(\lim _{n\rightarrow \infty }X_{n}=X)=1}$. Strong convergence is also known as almost sure convergence.

Most common shorthand notation: ${\displaystyle \displaystyle X_{n}\,{\xrightarrow {\mathrm {a.s.} }}\,X}$

As the names indicate, weak convergence is weaker than strong convergence. In fact, strong convergence implies convergence in probability, and convergence in probability implies weak convergence. The reverse statements are not always true.

Law of large numbers

Main article: Law of large numbers

Common intuition suggests that if a fair coin is tossed many times, then roughly half of the time it will turn up heads, and the other half it will turn up tails. Furthermore, the more often the coin is tossed, the more likely it should be that the ratio of the number of heads to the number of tails will approach unity. Modern probability theory provides a formal version of this intuitive idea, known as the law of large numbers. This law is remarkable because it is not assumed in the foundations of probability theory, but instead emerges from these foundations as a theorem. Since it links theoretically derived probabilities to their actual frequency of occurrence in the real world, the law of large numbers is considered as a pillar in the history of statistical theory and has had widespread influence.

The law of large numbers (LLN) states that the sample average

${\displaystyle {\overline {X}}_{n}={\frac {1}{n}}{\sum _{k=1}^{n}X_{k}}}$

of a sequence of independent and identically distributed random variables ${\displaystyle X_{k}}$ converges towards their common expectation ${\displaystyle \mu }$, provided that the expectation of ${\displaystyle |X_{k}|}$ is finite.

It is in the different forms of convergence of random variables that separates the weak and the strong law of large numbers

Weak law: ${\displaystyle \displaystyle {\overline {X}}_{n}\,{\xrightarrow {P}}\,\mu }$ for ${\displaystyle n\to \infty }$

Strong law: ${\displaystyle \displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathrm {a.\,s.} }}\,\mu }$ for ${\displaystyle n\to \infty .}$

It follows from the LLN that if an event of probability p is observed repeatedly during independent experiments, the ratio of the observed frequency of that event to the total number of repetitions converges towards p.

For example, if ${\displaystyle Y_{1},Y_{2},...\,}$ are independent Bernoulli random variables taking values 1 with probability p and 0 with probability 1-p, then ${\displaystyle {\textrm {E}}(Y_{i})=p}$ for all i, so that ${\displaystyle {\bar {Y}}_{n}}$ converges to p almost surely.

Central limit theorem

Main article: Central limit theorem

The central limit theorem (CLT) explains the ubiquitous occurrence of the normal distribution in nature, and this theorem, according to David Williams, "is one of the great results of mathematics."

The theorem states that the average of many independent and identically distributed random variables with finite variance tends towards a normal distribution irrespective of the distribution followed by the original random variables. Formally, let ${\displaystyle X_{1},X_{2},\dots \,}$ be independent random variables with mean ${\displaystyle \mu }$ and variance ${\displaystyle \sigma ^{2}>0.\,}$ Then the sequence of random variables

${\displaystyle Z_{n}={\frac {\sum _{i=1}^{n}(X_{i}-\mu )}{\sigma {\sqrt {n}}}}\,}$

converges in distribution to a standard normal random variable.

For some classes of random variables, the classic central limit theorem works rather fast, as illustrated in the Berry–Esseen theorem. For example, the distributions with finite first, second, and third moment from the exponential family; on the other hand, for some random variables of the heavy tail and fat tail variety, it works very slowly or may not work at all: in such cases one may use the Generalized Central Limit Theorem (GCLT).

IQ classification

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/IQ_classification 

 

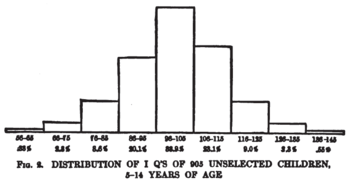
Score distribution chart for sample of 905 children tested on 1916 Stanford–Binet Test

IQ classification is the practice by IQ test publishers of labeling IQ score ranges with category names such as "superior" or "average".

The current scoring method for all IQ tests is the "deviation IQ". In this method, an IQ score of 100 means that the test-taker's performance on the test is at the median level of performance in the sample of test-takers of about the same age as was used to norm the test. An IQ score of 115 means performance one standard deviation above the median, a score of 85 performance, one standard deviation below the median, and so on. Deviation IQs are now used for standard scoring of all IQ tests in large part because they allow a consistent definition of IQ for both children and adults. By the current "deviation IQ" definition of IQ test standard scores, about two-thirds of all test-takers obtain scores from 85 to 115, and about 5 percent of the population scores above 125.

Lewis Terman and other early developers of IQ tests noticed that most child IQ scores come out to approximately the same number regardless of testing procedure. All IQ tests show a slight variation in scores even when the same person takes the same test over and over again. IQ scores also slightly differ for a test-taker taking tests from more than one publisher at the same age. The various test publishers do not use uniform names or definitions for IQ score classifications.

Even before IQ tests were invented, there were attempts to classify people into intelligence categories by observing their behavior in daily life. Those other forms of behavioral observation are still important for validating classifications based primarily on IQ test scores. Both intelligence classification by observation of behavior outside the testing room and classification by IQ testing depend on the definition of "intelligence" used in a particular case and on the reliability and error of estimation in the classification procedure.

Differences in individual IQ classification

IQ scores can differ to some degree for the same person on different IQ tests, so a person does not always belong to the same IQ score range each time the person is tested. (IQ score table data and pupil pseudonyms adapted from description of KABC-II norming study cited in Kaufman 2009.)

Pupil	KABC-II	WISC-III	WJ-III
Asher	90	95	111
Brianna	125	110	105
Colin	100	93	101
Danica	116	127	118
Elpha	93	105	93
Fritz	106	105	105
Georgi	95	100	90
Hector	112	113	103
Imelda	104	96	97
Jose	101	99	86
Keoku	81	78	75
Leo	116	124	102

IQ tests generally are reliable enough that most people 10 years of age and older have similar IQ scores throughout life. Still, some individuals score very differently when taking the same test at different times or when taking more than one kind of IQ test at the same age. For example, many children in the famous longitudinal Genetic Studies of Genius begun in 1921 by Lewis Terman showed declines in IQ as they grew up. Terman recruited school pupils based on referrals from teachers, and gave them his Stanford–Binet IQ test. Children with an IQ above 140 by that test were included in the study. There were 643 children in the main study group. When the students who could be contacted again (503 students) were retested at high school age, they were found to have dropped 9 IQ points on average in Stanford–Binet IQ. More than two dozen children dropped by 15 IQ points and six by 25 points or more. Yet parents of those children thought that the children were still as bright as ever, or even brighter.

Because all IQ tests have error of measurement in the test-taker's IQ score, a test-giver should always inform the test-taker of the confidence interval around the score obtained on a given occasion of taking each test. IQ scores are ordinal scores and are not expressed in an interval measurement unit. Besides the inherent error band around any IQ test score because tests are a "sample racks of learned behavior", IQ scores can also be misleading because test-givers fail to follow standardized administration and scoring procedures. In cases of test-giver mistakes, the usual result is that tests are scored too leniently, giving the test-taker a higher IQ score than the test-taker's performance justifies. Some test-givers err by showing a "halo effect", with low-IQ individuals receiving IQ scores even lower than if standardized procedures were followed, while high-IQ individuals receive inflated IQ scores.

IQ classifications for individuals also vary because category labels for IQ score ranges are specific to each brand of test. The test publishers do not have a uniform practice of labeling IQ score ranges, nor do they have a consistent practice of dividing up IQ score ranges into categories of the same size or with the same boundary scores. Thus psychologists should specify which test was given when reporting a test-taker's IQ. Psychologists and IQ test authors recommend that psychologists adopt the terminology of each test publisher when reporting IQ score ranges.

IQ classifications from IQ testing are not the last word on how a test-taker will do in life, nor are they the only information to be considered for placement in school or job-training programs. There is still a dearth of information about how behavior differs between persons with differing IQ scores. For placement in school programs, for medical diagnosis, and for career advising, factors other than IQ must also be part of an individual assessment.

The lesson here is that classification systems are necessarily arbitrary and change at the whim of test authors, government bodies, or professional organizations. They are statistical concepts and do not correspond in any real sense to the specific capabilities of any particular person with a given IQ. The classification systems provide descriptive labels that may be useful for communication purposes in a case report or conference, and nothing more.

— Alan S. Kaufman and Elizabeth O. Lichtenberger, Assessing Adolescent and Adult Intelligence (2006)

IQ classification tables for current tests

There are a variety of individually administered IQ tests in use in the English-speaking world. Not all report test results as "IQ", but most now report a standard score with a median score level of 100. When a test-taker scores higher or lower than the median score, the score is indicated as 15 standard score points higher or lower for each standard deviation difference higher or lower in the test-taker's performance on the test item content.

Wechsler Intelligence Scales

Main article: Wechsler Adult Intelligence Scale

See also: Wechsler Intelligence Scale for Children and Wechsler Preschool and Primary Scale of Intelligence

The Wechsler intelligence scales were originally developed from earlier intelligence scales by David Wechsler. The first Wechsler test published was the Wechsler–Bellevue Scale in 1939. The Wechsler IQ tests for children and for adults are the most frequently used individual IQ tests in the English-speaking world and in their translated versions are perhaps the most widely used IQ tests worldwide. The Wechsler tests have long been regarded as the "gold standard" in IQ testing. The Wechsler Adult Intelligence Scale—Fourth Edition (WAIS–IV) was published in 2008 by The Psychological Corporation. The Wechsler Intelligence Scale for Children—Fifth Edition (WISC–V) was published in 2014 by The Psychological Corporation, and the Wechsler Preschool and Primary Scale of Intelligence—Fourth Edition (WPPSI–IV) was published in 2012 by The Psychological Corporation. Like all current IQ tests, the Wechsler tests report a "deviation IQ" as the standard score for the full-scale IQ, with the norming sample median raw score defined as IQ 100 and a score one standard deviation higher defined as IQ 115 (and one deviation lower defined as IQ 85).

Current Wechsler (WAIS–IV, WPPSI–IV) IQ classification

IQ Range ("deviation IQ")	IQ Classification
130 and above	Very Superior
120–129	Superior
110–119	High Average
90–109	Average
80–89	Low Average
70–79	Borderline
69 and below	Extremely Low

Wechsler Intelligence Scale for Children–Fifth Edition (WISC-V) IQ classification

IQ Range ("deviation IQ")	IQ Classification
130 and above	Extremely High
120–129	Very High
110–119	High Average
90–109	Average
80–89	Low Average
70–79	Very Low
69 and below	Extremely Low

Psychologists have proposed alternative language for Wechsler IQ classifications. The term "borderline", which implies being very close to being intellectually disabled, is replaced in the alternative system by a term that doesn't imply a medical diagnosis.

Alternate Wechsler IQ Classifications (after Groth-Marnat 2009)

Corresponding IQ Range	Classifications	More value-neutral terms
130+	Very superior	Upper extreme
120–129	Superior	Well above average
110–119	High average	High average
90–109	Average	Average
80–89	Low average	Low average
70–79	Borderline	Well below average
69 and below	Extremely low	Lower extreme

Stanford–Binet Intelligence Scale Fifth Edition

Main article: Stanford–Binet Intelligence Scales

The current fifth edition of the Stanford–Binet scales (SB5) was developed by Gale H. Roid and published in 2003 by Riverside Publishing. Unlike scoring on previous versions of the Stanford–Binet test, SB5 IQ scoring is deviation scoring in which each standard deviation up or down from the norming sample median score is 15 points from the median score, IQ 100, just like the standard scoring on the Wechsler tests.

Stanford–Binet Fifth Edition (SB5) classification

IQ Range ("deviation IQ")	IQ Classification
144+	Very gifted or highly advanced
130–144	Gifted or very advanced
120–129	Superior
110–119	High average
90–109	Average
80–89	Low average
70–79	Borderline impaired or delayed
55–69	Mildly impaired or delayed
40–54	Moderately impaired or delayed

Woodcock–Johnson Test of Cognitive Abilities

Main article: Woodcock–Johnson Tests of Cognitive Abilities

The Woodcock–Johnson a III NU Tests of Cognitive Abilities (WJ III NU) was developed by Richard W. Woodcock, Kevin S. McGrew and Nancy Mather and published in 2007 by Riverside. The WJ III classification terms are not applied.

Woodcock–Johnson R

IQ Score	WJ III Classification
131 and above	Very superior
121 to 130	Superior
111 to 120	High Average
90 to 110	Average
80 to 89	Low Average
70 to 79	Low
69 and below	Very Low

Kaufman Tests

The Kaufman Adolescent and Adult Intelligence Test was developed by Alan S. Kaufman and Nadeen L. Kaufman and published in 1993 by American Guidance Service. Kaufman test scores "are classified in a symmetrical, nonevaluative fashion", in other words the score ranges for classification are just as wide above the median as below the median, and the classification labels do not purport to assess individuals.

KAIT 1993 IQ classification

130 and above	Upper Extreme
120–129	Well Above Average
110–119	Above average
90–109	Average
80–89	Below Average
70–79	Well Below Average
69 and below	Lower Extreme

 

Main article: Kaufman Assessment Battery for Children

The Kaufman Assessment Battery for Children, Second Edition was developed by Alan S. Kaufman and Nadeen L. Kaufman and published in 2004 by American Guidance Service.

KABC-II 2004 Descriptive Categories

Range of Standard Scores	Name of Category
131–160	Upper Extreme
116–130	Above Average
85–115	Average Range
70–84	Below Average
40–69	Lower Extreme

Cognitive Assessment System

Main article: Cognitive Assessment System

The Das-Naglieri Cognitive Assessment System test was developed by Jack Naglieri and J. P. Das and published in 1997 by Riverside.

Cognitive Assessment System 1997 full scale score classification

Standard Scores	Classification
130 and above	Very Superior
120–129	Superior
110–119	High Average
90–109	Average
80–89	Low Average
70–79	Below Average
69 and below	Well Below Average

Differential Ability Scales

Main article: Differential Ability Scales

The Differential Ability Scales Second Edition (DAS–II) was developed by Colin D. Elliott and published in 2007 by Psychological Corporation. The DAS-II is a test battery given individually to children, normed for children from ages two years and six months through seventeen years and eleven months. It was normed on 3,480 noninstitutionalized, English-speaking children in that age range. The DAS-II yields a General Conceptual Ability (GCA) score scaled like an IQ score with the median standard score set at 100 and 15 standard score points for each standard deviation up or down from the median. The lowest possible GCA score on DAS–II is 30, and the highest is 170.

DAS-II 2007 GCA classification

GCA	General Conceptual Ability Classification
≥ 130	Very high
120–129	High
110–119	Above average
90–109	Average
80–89	Below average
70–79	Low
≤ 69	Very low

Reynolds Intellectual Ability Scales

Reynolds Intellectual Ability Scales (RIAS) were developed by Cecil Reynolds and Randy Kamphaus. The RIAS was published in 2003 by Psychological Assessment Resources.

RIAS 2003 Scheme of Verbal Descriptors of Intelligence Test Performance

Intelligence test score range	Verbal descriptor
≥ 130	Significantly above average
120–129	Moderately above average
110–119	Above average
90–109	Average
80–89	Below average
70–79	Moderately below average
≤ 69	Significantly below average

Historical IQ classification tables

Reproduction of an item from the 1908 Binet–Simon intelligence scale, showing three pairs of pictures, about which the tested child was asked, "Which of these two faces is the prettier?" Reproduced from the article "A Practical Guide for Administering the Binet–Simon Scale for Measuring Intelligence" by J. E. Wallace Wallin in the March 1911 issue of the journal The Psychological Clinic (volume 5 number 1), public domain.

Lewis Terman, developer of the Stanford–Binet Intelligence Scales, based his English-language Stanford–Binet IQ test on the French-language Binet–Simon test developed by Alfred Binet. Terman believed his test measured the "general intelligence" construct advocated by Charles Spearman (1904). Terman differed from Binet in reporting scores on his test in the form of intelligence quotient ("mental age" divided by chronological age) scores after the 1912 suggestion of German psychologist William Stern. Terman chose the category names for score levels on the Stanford–Binet test. When he first chose classification for score levels, he relied partly on the usage of earlier authors who wrote, before the existence of IQ tests, on topics such as individuals unable to care for themselves in independent adult life. Terman's first version of the Stanford–Binet was based on norming samples that included only white, American-born subjects, mostly from California, Nevada, and Oregon.

Terman's Stanford–Binet original (1916) classification

IQ Range ("ratio IQ")	IQ Classification
Above 140	"Near" genius or genius
120–140	Very superior intelligence
110–120	Superior intelligence
90–110	Normal, or average, intelligence
80–90	Dullness, rarely classifiable as feeble-mindedness
70–80	Border-line deficiency, sometimes classifiable as dullness, often as feeble-mindedness
Below 70	Definite feeble-mindedness

Rudolph Pintner proposed a set of classification terms in his 1923 book Intelligence Testing: Methods and Results. Pintner commented that psychologists of his era, including Terman, went about "the measurement of an individual's general ability without waiting for an adequate psychological definition." Pintner retained these terms in the 1931 second edition of his book.

Pintner 1923 IQ classification

IQ Range ("ratio IQ")	IQ Classification
130 and above	Very Superior
120–129	Very Bright
110–119	Bright
90–109	Normal
80–89	Backward
70–79	Borderline

Albert Julius Levine and Louis Marks proposed a broader set of categories in their 1928 book Testing Intelligence and Achievement. Some of the entries came from contemporary terms for people with intellectual disability.

Levine and Marks 1928 IQ classification

IQ Range ("ratio IQ")	IQ Classification
175 and over	Precocious
150–174	Very superior
125–149	Superior
115–124	Very bright
105–114	Bright
95–104	Average
85–94	Dull
75–84	Borderline
50–74	Morons
25–49	Imbeciles
0–24	Idiots

The second revision (1937) of the Stanford–Binet test retained "quotient IQ" scoring, despite earlier criticism of that method of reporting IQ test standard scores. The term "genius" was no longer used for any IQ score range. The second revision was normed only on children and adolescents (no adults), and only "American-born white children".

Terman's Stanford–Binet Second Revision (1937) classification

IQ Range ("ratio IQ")	IQ Classification
140 and over	Very superior
120–139	Superior
110–119	High average
90–109	Normal or average
80–89	Low average
70–79	Borderline defective
Below 70	Mentally defective

A data table published later as part of the manual for the 1960 Third Revision (Form L-M) of the Stanford–Binet test reported score distributions from the 1937 second revision standardization group.

Score Distribution of Stanford–Binet 1937 Standardization Group

IQ Range ("ratio IQ")	Percent of Group
160–169	0.03
150–159	0.2
140–149	1.1
130–139	3.1
120–129	8.2
110–119	18.1
100–109	23.5
90–99	23.0
80–89	14.5
70–79	5.6
60–69	2.0
50–59	0.4
40–49	0.2
30–39	0.03

David Wechsler, developer of the Wechsler–Bellevue Scale of 1939 (which was later developed into the Wechsler Adult Intelligence Scale) popularized the use of "deviation IQs" as standard scores of IQ tests rather than the "quotient IQs" ("mental age" divided by "chronological age") then used for the Stanford–Binet test. He devoted a whole chapter in his book The Measurement of Adult Intelligence to the topic of IQ classification and proposed different category names from those used by Lewis Terman. Wechsler also criticized the practice of earlier authors who published IQ classification tables without specifying which IQ test was used to obtain the scores reported in the tables.

Wechsler–Bellevue 1939 IQ classification

IQ Range ("deviation IQ")	IQ Classification	Percent Included
128 and over	Very Superior	2.2
120–127	Superior	6.7
111–119	Bright Normal	16.1
91–110	Average	50.0
80–90	Dull normal	16.1
66–79	Borderline	6.7
65 and below	Defective	2.2

In 1958, Wechsler published another edition of his book Measurement and Appraisal of Adult Intelligence. He revised his chapter on the topic of IQ classification and commented that "mental age" scores were not a more valid way to score intelligence tests than IQ scores. He continued to use the same classification terms.

Wechsler Adult Intelligence Scales 1958 Classification

IQ Range ("deviation IQ")	IQ Classification	(Theoretical) Percent Included
128 and over	Very Superior	2.2
120–127	Superior	6.7
111–119	Bright Normal	16.1
91–110	Average	50.0
80–90	Dull normal	16.1
66–79	Borderline	6.7
65 and below	Defective	2.2

The third revision (Form L-M) in 1960 of the Stanford–Binet IQ test used the deviation scoring pioneered by David Wechsler. For rough comparability of scores between the second and third revision of the Stanford–Binet test, scoring table author Samuel Pinneau set 100 for the median standard score level and 16 standard score points for each standard deviation above or below that level. The highest score obtainable by direct look-up from the standard scoring tables (based on norms from the 1930s) was IQ 171 at various chronological ages from three years six months (with a test raw score "mental age" of six years and two months) up to age six years and three months (with a test raw score "mental age" of ten years and three months). The classification for Stanford–Binet L-M scores does not include terms such as "exceptionally gifted" and "profoundly gifted" in the test manual itself. David Freides, reviewing the Stanford–Binet Third Revision in 1970 for the Buros Seventh Mental Measurements Yearbook (published in 1972), commented that the test was obsolete by that year.

Terman's Stanford–Binet Third Revision (Form L-M) classification

IQ Range ("deviation IQ")	IQ Classification
140 and over	Very superior
120–139	Superior
110–119	High average
90–109	Normal or average
80–89	Low average
70–79	Borderline defective
Below 70	Mentally defective

The first edition of the Woodcock–Johnson Tests of Cognitive Abilities was published by Riverside in 1977. The classifications used by the WJ-R Cog were "modern in that they describe levels of performance as opposed to offering a diagnosis."

Woodcock–Johnson R

IQ Score	WJ-R Cog 1977 Classification
131 and above	Very superior
121 to 130	Superior
111 to 120	High Average
90 to 110	Average
80 to 89	Low Average
70 to 79	Low
69 and below	Very Low

The revised version of the Wechsler Adult Intelligence Scale (the WAIS-R) was developed by David Wechsler and published by Psychological Corporation in 1981. Wechsler changed a few of the boundaries for classification categories and a few of their names compared to the 1958 version of the test. The test's manual included information about how the actual percentage of persons in the norming sample scoring at various levels compared to theoretical expectations.

Wechsler Adult Intelligence Scales 1981 Classification

IQ Range ("deviation IQ")	IQ Classification	Actual Percent Included	Theoretical Percent Included
130+	Very Superior	2.6	2.2
120–129	Superior	6.9	6.7
110–119	High Average	16.6	16.1
90–109	Average	49.1	50.0
80–89	Low Average	16.1	16.1
70–79	Borderline	6.4	6.7
below 70	Mentally Retarded	2.3	2.2

The Kaufman Assessment Battery for Children (K-ABC) was developed by Alan S. Kaufman and Nadeen L. Kaufman and published in 1983 by American Guidance Service.

K-ABC 1983 Ability Classifications

Range of Standard Scores	Name of Category	Percent of Norm Sample	Theoretical Percent Included
130+	Upper Extreme	2.3	2.2
120–129	Well Above Average	7.4	6.7
110–119	Above Average	16.7	16.1
90–109	Average	49.5	50.0
80–89	Below Average	16.1	16.1
70–79	Well Below Average	6.1	6.7
below 70	Lower Extreme	2.1	2.2

The fourth revision of the Stanford–Binet scales (S-B IV) was developed by Thorndike, Hagen, and Sattler and published by Riverside Publishing in 1986. It retained the deviation scoring of the third revision with each standard deviation from the median being defined as a 16 IQ point difference. The S-B IV adopted new classification terminology. After this test was published, psychologist Nathan Brody lamented that IQ tests had still not caught up with advances in research on human intelligence during the twentieth century.

Stanford–Binet Intelligence Scale, Fourth Edition (S-B IV) 1986 classification

IQ Range ("deviation IQ")	IQ Classification
132 and above	Very superior
121–131	Superior
111–120	High average
89–110	Average
79–88	Low average
68–78	Slow learner
67 or below	Mentally retarded

The third edition of the Wechsler Adult Intelligence Scale (WAIS-III) used different classification terminology from the earliest versions of Wechsler tests.

Wechsler (WAIS–III) 1997 IQ test classification

IQ Range ("deviation IQ")	IQ Classification
130 and above	Very superior
120–129	Superior
110–119	High average
90–109	Average
80–89	Low average
70–79	Borderline
69 and below	Extremely low

Classification of low IQ

Main article: Intellectual disability

See also: Borderline intellectual functioning

The earliest terms for classifying individuals of low intelligence were medical or legal terms that preceded the development of IQ testing. The legal system recognized a concept of some individuals being so cognitively impaired that they were not responsible for criminal behavior. Medical doctors sometimes encountered adult patients who could not live independently, being unable to take care of their own daily living needs. Various terms were used to attempt to classify individuals with varying degrees of intellectual disability. Many of the earliest terms are now considered extremely offensive.

In current medical diagnosis, IQ scores alone are not conclusive for a finding of intellectual disability. Recently adopted diagnostic standards place the major emphasis on the adaptive behavior of each individual, with IQ score just being one factor in diagnosis in addition to adaptive behavior scales, and no category of intellectual disability being defined primarily by IQ scores. Psychologists point out that evidence from IQ testing should always be used with other assessment evidence in mind: "In the end, any and all interpretations of test performance gain diagnostic meaning when they are corroborated by other data sources and when they are empirically or logically related to the area or areas of difficulty specified in the referral."

In the United States, the Supreme Court ruled in the case Atkins v. Virginia, 536 U.S. 304 (2002) that states could not impose capital punishment on persons with "mental retardation", defined in subsequent cases as persons with IQ scores below 70. This legal standard continues to be actively litigated in capital cases.

Historical

Historically, terms for intellectual disability eventually become perceived as an insult, in a process commonly known as the euphemism treadmill. The terms mental retardation and mentally retarded became popular in the middle of the 20th century to replace the previous set of terms, which included "imbecile", "idiot", "feeble-minded", and "moron", among others, and are now considered offensive, often extremely so. By the end of the 20th century, retardation and retard became widely seen as disparaging and politically incorrect, although they are still used in some clinical contexts.

The American Association for the Study of the Feeble-minded divided adults with intellectual deficits into three categories. Idiot indicated the greatest degree of intellectual disability in which a person's mental age is below three years. Imbecile indicated an intellectual disability less severe than idiocy and a mental age between three and seven years. Moron was defined as someone a mental age between eight and twelve. Alternative definitions of these terms based on IQ were also used.

The term cretin dates to 1770–80 and comes from a dialectal French word for Christian. The implication was that people with significant intellectual or developmental disabilities were "still human" (or "still Christian") and deserved to be treated with basic human dignity. Although cretin is no longer in use, the term cretinism is still used to refer to the mental and physical disability resulting from untreated congenital hypothyroidism.

Mongolism and Mongoloid idiot were terms used to identify someone with Down syndrome, as the doctor who first described the syndrome, John Langdon Down, believed that children with Down syndrome shared facial similarities with the now-obsolete category of "Mongolian race". The Mongolian People's Republic requested that the medical community cease the use of the term; in 1960, the World Health Organization agreed the term should cease being used.

Retarded comes from the Latin retardare, "to make slow, delay, keep back, or hinder", so mental retardation meant the same as mentally delayed. The first record of retarded in relation to being mentally slow was in 1895. The term mentally retarded was used to replace terms like idiot, moron, and imbecile because retarded was not then a derogatory term. By the 1960s, however, the term had taken on a partially derogatory meaning. The noun retard is particularly seen as pejorative; a BBC survey in 2003 ranked it as the most offensive disability-related word. The terms mentally retarded and mental retardation are still fairly common, but organizations such as the Special Olympics and Best Buddies are striving to eliminate their use and often refer to retard and its variants as the "r-word". These efforts resulted in U.S. federal legislation, known as Rosa's Law, which replaced the term mentally retarded with the term intellectual disability in federal law.

Classification of high IQ

Genius

Main article: Genius

 

Galton in his later years

Francis Galton (1822–1911) was a pioneer in investigating both eminent human achievement and mental testing. In his book Hereditary Genius, writing before the development of IQ testing, he proposed that hereditary influences on eminent achievement are strong, and that eminence is rare in the general population. Lewis Terman chose "'near' genius or genius" as the classification label for the highest classification on his 1916 version of the Stanford–Binet test. By 1926, Terman began publishing about a longitudinal study of California schoolchildren who were referred for IQ testing by their schoolteachers, called Genetic Studies of Genius, which he conducted for the rest of his life. Catherine M. Cox, a colleague of Terman's, wrote a whole book, The Early Mental Traits of 300 Geniuses, published as volume 2 of The Genetic Studies of Genius book series, in which she analyzed biographical data about historic geniuses. Although her estimates of childhood IQ scores of historical figures who never took IQ tests have been criticized on methodological grounds, Cox's study was thorough in finding out what else matters besides IQ in becoming a genius. By the 1937 second revision of the Stanford–Binet test, Terman no longer used the term "genius" as an IQ classification, nor has any subsequent IQ test. In 1939, Wechsler wrote "we are rather hesitant about calling a person a genius on the basis of a single intelligence test score."

The Terman longitudinal study in California eventually provided historical evidence on how genius is related to IQ scores. Many California pupils were recommended for the study by schoolteachers. Two pupils who were tested but rejected for inclusion in the study because of IQ scores too low for the study grew up to be Nobel Prize winners in physics: William Shockley and Luis Walter Alvarez. Based on the historical findings of the Terman study and on biographical examples such as Richard Feynman, who had an IQ of 125 and went on to win the Nobel Prize in physics and become widely known as a genius, the current view of psychologists and other scholars of genius is that a minimum IQ, about 125, is strictly necessary for genius, but that IQ is sufficient for the development of genius only when combined with the other influences identified by Cox's biographical study: an opportunity for talent development along with the characteristics of drive and persistence. Charles Spearman, bearing in mind the influential theory that he originated—that intelligence comprises both a "general factor" and "special factors" more specific to particular mental tasks—, wrote in 1927, "Every normal man, woman, and child is, then, a genius at something, as well as an idiot at something."

Giftedness

Main article: Intellectual giftedness

A major point of consensus among all scholars of intellectual giftedness is that there is no generally agreed upon definition of giftedness. Although there is no scholarly agreement about identifying gifted learners, there is a de facto reliance on IQ scores for identifying participants in school gifted education programs. In practice, many school districts in the United States use an IQ score of 130, including roughly the upper 2 to 3 percent of the national population as a cut-off score for inclusion in school gifted programs.

Five levels of giftedness have been suggested to differentiate the vast difference in abilities that exists between children on varying ends of the gifted spectrum. Although there is no strong consensus on the validity of these quantifiers, they are accepted by many experts of gifted children.

Levels of Giftedness (M.U. Gross)

Classification	IQ Range	σ	Prevalence
Mildly gifted	115–129	+1.00–+1.99	1:6
Moderately gifted	130–144	+2.00–+2.99	1:44
Highly gifted	145–159	+3.00–+3.99	1:1,000
Exceptionally gifted	160–179	+4.00–+5.33	1:10,000
Profoundly gifted	180–	+5.33–	< 1:1,000,000

As long ago as 1937, Lewis Terman pointed out that error of estimation in IQ scoring increases as IQ score increases, so that there is less and less certainty about assigning a test-taker to one band of scores or another as one looks at higher bands. Current IQ tests also have large error bands for high IQ scores. As an underlying reality, such distinctions as those between "exceptionally gifted" and "profoundly gifted" have never been well established. All longitudinal studies of IQ have shown that test-takers can bounce up and down in score, and thus switch up and down in rank order as compared to one another, over the course of childhood. Some test-givers claim that IQ classification categories such as "profoundly gifted" are meaningful, but those are based on the obsolete Stanford–Binet Third Revision (Form L-M) test. The highest reported standard score for most IQ tests is IQ 160, approximately the 99.997th percentile (leaving aside the issue of the considerable error in measurement at that level of IQ on any IQ test). IQ scores above this level are dubious as there are insufficient normative cases upon which to base a statistically justified rank-ordering. Moreover, there has never been any validation of the Stanford–Binet L-M on adult populations, and there is no trace of such terminology in the writings of Lewis Terman. Although two current tests attempt to provide "extended norms" that allow for classification of different levels of giftedness, those norms are not based on well validated data.

Energy security

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Energy_security 

 

A U.S. Navy F/A-18 Super Hornet displaying an "Energy Security" logo.

Energy security is the association between national security and the availability of natural resources for energy consumption. Access to (relatively) cheap energy has become essential to the functioning of modern economies. However, the uneven distribution of energy supplies among countries has led to significant vulnerabilities. International energy relations have contributed to the globalization of the world leading to energy security and energy vulnerability at the same time.

Renewable resources exist worldwide across every biome except the North and South Poles (only nuclear (and wind in the winter) is feasible), in contrast to fossil fuels, which are concentrated in a limited number of countries.

Nations don't switch from unpredictable fossil fuels to renewables overnight. It is a long, continuous process.

Rapid deployment of renewable energy, increased energy efficiency, and diversification of energy sources, energy stores, and types of energy machines can use all result in significant energy security and economic benefits.

Threats

The modern world relies on a vast energy supply to fuel everything from transportation to communication, to security and health delivery systems. Perhaps most alarmingly, peak oil expert Michael Ruppert has claimed that for every kilocalorie of food produced in the industrial world, 10 kilocalories of oil and gas energy are invested in the forms of fertilizer, pesticide, packaging, transportation, and running farm equipment. Energy plays an important role in the national security of any given country as a fuel to power the economic engine. Some sectors rely on energy more heavily than others; for example, the Department of Defense relies on petroleum for approximately 77% of its energy needs. Not every sector is as critical as the others. Some have greater importance to energy security.

Threats to a nation's energy security include

• Political/Domestic instability of major energy-producing countries (e.g. change in leadership's environmental values, or regime change)
• Reliance on foreign countries for oil
  • Foreign in-state conflict (e.g. religious civil wars)
  • Foreign exporters' interests (e.g. Quid Pro Quo/blackmail/extortion)
  • Foreign non-state actors targeting the supply and transportation of oil resources (e.g. theft)
• Manipulation of energy supplies (e.g. mega-corporation or state-backed racketeering)
• Competition over energy sources (e.g. biofuel(biodiesel, bioethanol) vs oil(crude, distilled fuel) vs coal vs natural gas vs nuclear vs wind vs solar vs hydro(dam, pumped))
• Unreliable energy stores (e.g. long time to spin a turbine to create power, or Li-ion battery grid explosion, or pumped hydro dam becoming clogged)
• Attacks on supply infrastructure (e.g. hackers stopping flow pumps inside a pipeline or intentionally surging an electrical grid to over/underload it)
  • Terrorism (e.g. napalming oil and/or fuel reserves)
• Accidents (e.g. shoddy weld causing debris buildup in a pipeline)
  • Natural disasters (e.g. wind turbine collapsing from a major earthquake)

The political and economic instability caused by war or other factors such as strike action can also prevent the proper functioning of the energy industry in a supplier country. For example, the nationalization of oil in Venezuela has triggered strikes and protests in which Venezuela's oil production rates have yet to recover. Exporters may have political or economic incentive to limit their foreign sales or cause disruptions in the supply chain. Since Venezuela's nationalization of oil, anti-American Hugo Chávez threatened to cut off supplies to the United States more than once. The 1973 oil embargo against the United States is an historical example in which oil supplies were cut off to the United States due to U.S. support of Israel during the Yom Kippur War. This has been done to apply pressure during economic negotiations—such as during the 2007 Russia–Belarus energy dispute. Terrorist attacks targeting oil facilities, pipelines, tankers, refineries, and oil fields are so common they are referred to as "industry risks".  Infrastructure for producing the resource is extremely vulnerable to sabotage. One of the worst risks to oil transportation is the exposure of the five ocean chokepoints, like the Iranian-controlled Strait of Hormuz. Anthony Cordesman, a scholar at the Center for Strategic and International Studies in Washington, D.C., warns, "It may take only one asymmetric or conventional attack on a Ghawar Saudi oil field or tankers in the Strait of Hormuz to throw the market into a spiral." 

New threats to energy security have emerged in the form of the increased world competition for energy resources due to the increased pace of industrialization in countries such as India and China, as well as due to the increasing consequences of climate change.  Although still a minority concern, the possibility of price rises resulting from the peaking of world oil production is also starting to attract the attention of at least the French government.  Increased competition over energy resources may also lead to the formation of security compacts to enable an equitable distribution of oil and gas between major powers. However, this may happen at the expense of less developed economies. The Group of Five, precursors to the G8, first met in 1975 to coordinate economic and energy policies in the wake of the 1973 Arab oil embargo, a rise in inflation and a global economic slowdown.  NATO leaders meeting in Bucharest Romania, in April 2008, may discuss the possibility of using the military alliance "as an instrument of energy security". One of the possibilities include placing troops in the Caucasus region to police oil and gas pipelines.

Long-term security

Long-term measures to increase energy security center on reducing dependence on any one source of imported energy, increasing the number of suppliers, exploiting native fossil fuel or renewable energy resources, and reducing overall demand through energy conservation measures. It can also involve entering into international agreements to underpin international energy trading relationships, such as the Energy Charter Treaty in Europe. All the concern coming from security threats on oil sources' long term security measures will help reduce the future cost of importing and exporting fuel into and out of countries without having to worry about harm coming to the goods being transported.

The impact of the 1973 oil crisis and the emergence of the OPEC cartel was a particular milestone that prompted some countries to increase their energy security. Japan, almost totally dependent on imported oil, steadily introduced the use of natural gas, nuclear power, high-speed mass transit systems, and implemented energy conservation measures. The United Kingdom began exploiting North Sea oil and gas reserves, and became a net exporter of energy into the 2000s.

In countries other than the UK, energy security has historically been a lower priority. The United States, for example, has continued to increase its dependency on imported oil although, following the oil price increases since 2003, the development of biofuels has been suggested as a means of addressing this.

Increasing energy security is also one of the reasons behind a block on the development of natural gas imports in Sweden. Greater investment in native renewable energy technologies and energy conservation is envisaged instead. India is carrying out a major hunt for domestic oil to decrease its dependency on OPEC, while Iceland is well advanced in its plans to become energy independent by 2050 through deploying 100% renewable energy.

Short-term security

Petroleum

A map of world oil reserves according to OPEC, 2013

Petroleum, otherwise known as "crude oil", has become the resource most used by countries all around the world including Russia, China (actually, China is mostly dependent on coal (70.5% in 2010, 58% in 2019)) and the United States of America. With all the oil wells located around the world energy security has become a main issue to ensure the safety of the petroleum that is being harvested. In the middle east oil fields become main targets for sabotage because of how heavily countries rely on oil. Many countries hold strategic petroleum reserves as a buffer against the economic and political impacts of an energy crisis. For example, all 31 members of the International Energy Agency hold a minimum of 90 days of their oil imports. These countries also committed to passing legislation to develop an emergency response plan in the case of oil supply shocks and other short-term threats to energy security. 

The value of such reserves was demonstrated by the relative lack of disruption caused by the 2007 Russia-Belarus energy dispute, when Russia indirectly cut exports to several countries in the European Union.

Due to the theories in peak oil and need to curb demand, the United States military and Department of Defense had made significant cuts, and have been making a number of attempts to come up with more efficient ways to use oil.

Natural gas

Countries by natural gas proven reserves, based on data from The World Factbook, 2014

Compared to petroleum, reliance on imported natural gas creates significant short-term vulnerabilities. The gas conflicts between Ukraine and Russia of 2006 and 2009 serve as vivid examples of this. Many European countries saw an immediate drop in supply when Russian gas supplies were halted during the Russia-Ukraine gas dispute in 2006.

Natural gas has been a viable source of energy in the world. Consisting of mostly methane, natural gas is produced using two methods: biogenic and thermogenic. Biogenic gas comes from methanogenic organisms located in marshes and landfills, whereas thermogenic gas comes from the anaerobic decay of organic matter deep under the Earth's surface. Russia is one of the three current leading country in production of natural gas alongside USA and Saudi Arabia.

One of the biggest problems currently facing natural gas providers is the ability to store and transport it. With its low density, it is difficult to build enough pipelines in North America to transport sufficient natural gas to match demand. These pipelines are reaching near capacity and even at full capacity do not produce the amount of gas needed.

In the European Union, security of gas supply is protected by Regulation 2017/1938 of 25 October 2017, which concerns "measures to safeguard the security of gas supply" and took the place of the previous regulation 994/2010 on the same subject. EU policy operates on a number of regional groupings, a network of common gas security risk assessments, and a "solidarity mechanism", which would be activated in the event of a significant gas supply crisis.

A bilateral solidarity agreement was signed between Germany and Denmark on 14 December 2020.

The proposed UK-EU Trade and Cooperation Agreement "provides for a new set of arrangements for extensive technical cooperation ... particularly with regard to security of supply".

Nuclear power

Sources of uranium delivered to EU utilities in 2007, from the 2007 Annual report of the Euratom Supply Agency

Uranium for nuclear power is mined and enriched in diverse and "stable" countries. These include Canada (23% of the world's total in 2007), Australia (21%), Kazakhstan (16%) and more than 10 other countries. Uranium is mined and fuel is manufactured significantly in advance of need. Nuclear fuel is considered by some to be a relatively reliable power source, being more common in the Earth's crust than tin, mercury or silver, though a debate over the timing of peak uranium does exist.

Nuclear power reduces carbon emissions. Although a very viable resource, nuclear power is controversial due to the risks associated with it. Another factor in the debate with nuclear power is that many people or companies simply do not want any nuclear energy plant or radioactive waste near them.

Currently, nuclear power provides 13% of the world's total electricity. The most notable use of nuclear power within the United States is in U.S. Navy aircraft carriers and submarines, which have been exclusively nuclear-powered for several decades. These classes of ship provide the core of the Navy's power, and as such are the single most noteworthy application of nuclear power in the United States.

Renewable energy

Main article: Renewable energy

The deployment of renewable fuels

• Increases the diversity of electricity sources, reducing strangleholds of one fuel type
• Increases backup energy via biofuel reserves
• Increases backup electricity stores via batteries that can produce and/or store electricity
• Contributes to the flexibility of the rigid electrical grid via local generation (independent of easily targeted centralized power distributors) 
• Increases resistance to threats to energy security

For countries where growing dependence on imported gas is a significant energy security issue, renewable technologies can provide alternative sources of electric power as well as possibly displacing electricity demand through direct heat production (e.g. geothermal and burning fuels for heat and electricity). Renewable biofuels for transport represent a key source of diversification from petroleum products. As the finite resources that have been so crucial to survival in the world decline day by day, countries will begin to realize that the need for renewable fuel sources will be more vital than ever before.

With greater production of renewable energy, less overall energy production is on-demand. The electrical grid does not store energy. The grid only distributes electricity on-demand. Lack of control with regards to timing of energy production necessitates very large batteries. Before renewables, fuel-fired turbines could be spun up whenever needed, day or night, rain or shine. Solar panels can't be told to turn on at night, so energy needs to stored from what is captured during the day, so that the energy can be released at night. Wind power fluctuates uncontrollably, so it too needs storage capacity. Nuclear can be operational whenever needed, so it does not need storage capacity. Basically, if a method of power generation absolutely cannot function 24/7, or there is more electricity generated than being used at any point in time, batteries are needed to collect and provide a controlled release of electricity.

Renewable energy is not the same as clean energy. Renewable energy comes from solar, geothermal, hydro-electric, biofuel (optimally crude oil from algae and ethanol from switchgrass), and wind power. Clean energy is all those methods of energy production, but also nuclear (nuclear resources, like coal, oil, and natural gas, are very finite and not quickly renewable). In sixty minutes there is enough solar energy hitting Earth to power the world for one year. With the addition of solar panels, wind turbines, and diverse types of batteries all around the world, a little pressure is taken off the need to produce more oil.

Geothermal (renewable and clean energy) can indirectly reduce the need for other sources of fuel. By using the heat from the outer core of the Earth to heat water, steam created from the heated water can not only power electricity-generating turbines, but also eliminate the need for consuming electricity to create hot water for showers, washing machines, dishwashers, sterilizers, and more; geothermal is one of the cleanest and most efficient options, needing fuel to dig deep holes, hot water pumps, and tubing to distribute the hot water. Geothermal not only helps energy security, but also food security via year-round heated greenhouses.  Hydroelectric, already incorporated into many dams around the world, produces a lot of energy, usually on demand, and is very easy to produce energy as the dams control the gravity-fed water allowed through gates which spin up turbines located inside of the dam. Biofuels have been researched relatively thoroughly, using several different sources such as sugary corn (very inefficient) and cellulose-rich switchgrass (more efficient) to produce ethanol, and fat-rich algae to produce a synthetic crude oil (or algae-derived ethanol, which is very, very inefficient), these options are substantially cleaner than the consumption of petroleum. "Most life cycle analysis results for perennial and ligno-cellulosic crops conclude that biofuels can supplement anthropogenic energy demands and mitigate green house gas emissions to the atmosphere". Using net-carbon-positive oil to fuel transportation is a major source of green house gases, any one of these developments could replace the energy we derive from oil. Traditional fossil fuel exporters (e.g. Russia) who built their country's wealth from memorialized plant remains (fossil fuels) and have not yet diversified their energy portfolio to include renewable energy have greater national energy insecurity.

In 2021, global renewable energy capacity made record-breaking growth, increasing by 295 gigawatts (295 billion Watts, equivalent to 295,000,000,000 Watts, or a third of a trillion Watts) despite supply chain issues and high raw material prices. The European Union was especially impactful -- its annual additions increased nearly 30% to 36 gigawatts in 2021.

The International Energy Agency's 2022 Renewable Energy Market Update predicts that the global capacity of renewables would increase an additional 320 gigawatts. For context, that would almost entirely cover the electricity demand of Germany. However, the report cautioned that current public policies are a threat to future renewable energy growth: "the amount of renewable power capacity added worldwide is expected to plateau in 2023, as continued progress for solar is offset by a 40% decline in hydropower expansion and little change in wind additions."