Real coordinate space

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Real_coordinate_space 

 

Cartesian coordinates identify points of the Euclidean plane with pairs of real numbers

In mathematics, the real coordinate space of dimension n, denoted Rⁿ (/ɑːrˈɛn/ ar-EN) or ${\displaystyle \mathbb {R} ^{n}}$, is the set of the n-tuples of real numbers, that is the set of all sequences of n real numbers. With component-wise addition and scalar multiplication, it is a real vector space, and its elements are called coordinate vectors.

The coordinates over any basis of the elements of a real vector space form a real coordinate space of the same dimension as that of the vector space. Similarly, the Cartesian coordinates of the points of a Euclidean space of dimension n form a real coordinate space of dimension n.

These one to one correspondences between vectors, points and coordinate vectors explain the names of coordinate space and coordinate vector. It allows using geometric terms and methods for studying real coordinate spaces, and, conversely, to use methods of calculus in geometry. This approach of geometry was introduced by René Descartes in the 17th century. It is widely used, as it allows locating points in Euclidean spaces, and computing with them.

Definition and structures

For any natural number n, the set Rⁿ consists of all n-tuples of real numbers (R). It is called the "n-dimensional real space" or the "real n-space".

An element of Rⁿ is thus a n-tuple, and is written

$${\displaystyle (x_{1},x_{2},\ldots ,x_{n})}$$

where each x_i is a real number. So, in multivariable calculus, the domain of a function of several real variables and the codomain of a real vector valued function are subsets of Rⁿ for some n.

The real n-space has several further properties, notably:

• With componentwise addition and scalar multiplication, it is a real vector space. Every n-dimensional real vector space is isomorphic to it.
• With the dot product (sum of the term by term product of the components), it is an inner product space. Every n-dimensional real inner product space is isomorphic to it.
• As every inner product space, it is a topological space, and a topological vector space.
• It is a Euclidean space and a real affine space, and every Euclidean or affine space is isomorphic to it.
• It is an analytic manifold, and can be considered as the prototype of all manifolds, as, by definition, a manifold is, near each point, isomorphic to an open subset of Rⁿ.
• It is an algebraic variety, and every real algebraic variety is a subset of Rⁿ.

These properties and structures of Rⁿ make it fundamental in almost all areas of mathematics and their application domains, such as statistics, probability theory, and many parts of physics.

The domain of a function of several variables

Main articles: Multivariable calculus and Real multivariable function

Any function f(x₁, x₂, ..., x_n) of n real variables can be considered as a function on Rⁿ (that is, with Rⁿ as its domain). The use of the real n-space, instead of several variables considered separately, can simplify notation and suggest reasonable definitions. Consider, for n = 2, a function composition of the following form:

$${\displaystyle F(t)=f(g_{1}(t),g_{2}(t)),}$$

where functions g₁ and g₂ are continuous. If

• ∀x₁ ∈ R : f(x₁, ·) is continuous (by x₂)
• ∀x₂ ∈ R : f(·, x₂) is continuous (by x₁)

then F is not necessarily continuous. Continuity is a stronger condition: the continuity of f in the natural R² topology (discussed below), also called multivariable continuity, which is sufficient for continuity of the composition F.

Vector space

The coordinate space Rⁿ forms an n-dimensional vector space over the field of real numbers with the addition of the structure of linearity, and is often still denoted Rⁿ. The operations on Rⁿ as a vector space are typically defined by

$${\displaystyle \mathbf {x} +\mathbf {y} =(x_{1}+y_{1},x_{2}+y_{2},\ldots ,x_{n}+y_{n})}$$

$${\displaystyle \alpha \mathbf {x} =(\alpha x_{1},\alpha x_{2},\ldots ,\alpha x_{n}).}$$

The zero vector is given by

$${\displaystyle \mathbf {0} =(0,0,\ldots ,0)}$$

and the additive inverse of the vector x is given by

$${\displaystyle -\mathbf {x} =(-x_{1},-x_{2},\ldots ,-x_{n}).}$$

This structure is important because any n-dimensional real vector space is isomorphic to the vector space Rⁿ.

Matrix notation

Main article: Matrix (mathematics)

In standard matrix notation, each element of Rⁿ is typically written as a column vector

$${\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}}}$$

and sometimes as a row vector:

$${\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}.}$$

The coordinate space Rⁿ may then be interpreted as the space of all n × 1 column vectors, or all 1 × n row vectors with the ordinary matrix operations of addition and scalar multiplication.

Linear transformations from Rⁿ to R^m may then be written as m × n matrices which act on the elements of Rⁿ via left multiplication (when the elements of Rⁿ are column vectors) and on elements of R^m via right multiplication (when they are row vectors). The formula for left multiplication, a special case of matrix multiplication, is:

$${\displaystyle (A{\mathbf {x} })_{k}=\sum _{l=1}^{n}A_{kl}x_{l}}$$

Any linear transformation is a continuous function (see below). Also, a matrix defines an open map from Rⁿ to R^m if and only if the rank of the matrix equals to m.

Standard basis

Main article: Standard basis

The coordinate space Rⁿ comes with a standard basis:

$${\displaystyle {\begin{aligned}\mathbf {e} _{1}&=(1,0,\ldots ,0)\\\mathbf {e} _{2}&=(0,1,\ldots ,0)\\&{}\;\;\vdots \\\mathbf {e} _{n}&=(0,0,\ldots ,1)\end{aligned}}}$$

To see that this is a basis, note that an arbitrary vector in Rⁿ can be written uniquely in the form

$${\displaystyle \mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}.}$$

Geometric properties and uses

Orientation

The fact that real numbers, unlike many other fields, constitute an ordered field yields an orientation structure on Rⁿ. Any full-rank linear map of Rⁿ to itself either preserves or reverses orientation of the space depending on the sign of the determinant of its matrix. If one permutes coordinates (or, in other words, elements of the basis), the resulting orientation will depend on the parity of the permutation.

Diffeomorphisms of Rⁿ or domains in it, by their virtue to avoid zero Jacobian, are also classified to orientation-preserving and orientation-reversing. It has important consequences for the theory of differential forms, whose applications include electrodynamics.

Another manifestation of this structure is that the point reflection in Rⁿ has different properties depending on evenness of n. For even n it preserves orientation, while for odd n it is reversed (see also improper rotation).

Affine space

Further information: Affine space

Rⁿ understood as an affine space is the same space, where Rⁿ as a vector space acts by translations. Conversely, a vector has to be understood as a "difference between two points", usually illustrated by a directed line segment connecting two points. The distinction says that there is no canonical choice of where the origin should go in an affine n-space, because it can be translated anywhere.

Convexity

The n-simplex (see below) is the standard convex set, that maps to every polytope, and is the intersection of the standard (n + 1) affine hyperplane (standard affine space) and the standard (n + 1) orthant (standard cone).

 

Further information: Convex analysis

In a real vector space, such as Rⁿ, one can define a convex cone, which contains all non-negative linear combinations of its vectors. Corresponding concept in an affine space is a convex set, which allows only convex combinations (non-negative linear combinations that sum to 1).

In the language of universal algebra, a vector space is an algebra over the universal vector space R^∞ of finite sequences of coefficients, corresponding to finite sums of vectors, while an affine space is an algebra over the universal affine hyperplane in this space (of finite sequences summing to 1), a cone is an algebra over the universal orthant (of finite sequences of nonnegative numbers), and a convex set is an algebra over the universal simplex (of finite sequences of nonnegative numbers summing to 1). This geometrizes the axioms in terms of "sums with (possible) restrictions on the coordinates".

Another concept from convex analysis is a convex function from Rⁿ to real numbers, which is defined through an inequality between its value on a convex combination of points and sum of values in those points with the same coefficients.

Euclidean space

Main articles: Euclidean space and Cartesian coordinate system

The dot product

$${\displaystyle \mathbf {x} \cdot \mathbf {y} =\sum _{i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+x_{2}y_{2}+\cdots +x_{n}y_{n}}$$

defines the norm |x| = √x ⋅ x on the vector space Rⁿ. If every vector has its Euclidean norm, then for any pair of points the distance

$${\displaystyle d(\mathbf {x} ,\mathbf {y} )=\|\mathbf {x} -\mathbf {y} \|={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}}$$

is defined, providing a metric space structure on Rⁿ in addition to its affine structure.

As for vector space structure, the dot product and Euclidean distance usually are assumed to exist in Rⁿ without special explanations. However, the real n-space and a Euclidean n-space are distinct objects, strictly speaking. Any Euclidean n-space has a coordinate system where the dot product and Euclidean distance have the form shown above, called Cartesian. But there are many Cartesian coordinate systems on a Euclidean space.

Conversely, the above formula for the Euclidean metric defines the standard Euclidean structure on Rⁿ, but it is not the only possible one. Actually, any positive-definite quadratic form q defines its own "distance" √q(x − y), but it is not very different from the Euclidean one in the sense that

$${\displaystyle \exists C_{1}>0,\ \exists C_{2}>0,\ \forall \mathbf {x} ,\mathbf {y} \in \mathbb {R} ^{n}:C_{1}d(\mathbf {x} ,\mathbf {y} )\leq {\sqrt {q(\mathbf {x} -\mathbf {y} )}}\leq C_{2}d(\mathbf {x} ,\mathbf {y} ).}$$

Such a change of the metric preserves some of its properties, for example the property of being a complete metric space. This also implies that any full-rank linear transformation of Rⁿ, or its affine transformation, does not magnify distances more than by some fixed C₂, and does not make distances smaller than 1 / C₁ times, a fixed finite number times smaller.

The aforementioned equivalence of metric functions remains valid if √q(x − y) is replaced with M(x − y), where M is any convex positive homogeneous function of degree 1, i.e. a vector norm (see Minkowski distance for useful examples). Because of this fact that any "natural" metric on Rⁿ is not especially different from the Euclidean metric, Rⁿ is not always distinguished from a Euclidean n-space even in professional mathematical works.

In algebraic and differential geometry

Although the definition of a manifold does not require that its model space should be Rⁿ, this choice is the most common, and almost exclusive one in differential geometry.

On the other hand, Whitney embedding theorems state that any real differentiable m-dimensional manifold can be embedded into R^2m.

Other appearances

Other structures considered on Rⁿ include the one of a pseudo-Euclidean space, symplectic structure (even n), and contact structure (odd n). All these structures, although can be defined in a coordinate-free manner, admit standard (and reasonably simple) forms in coordinates.

Rⁿ is also a real vector subspace of Cⁿ which is invariant to complex conjugation; see also complexification.

Polytopes in Rⁿ

See also: Linear programming and Convex polytope

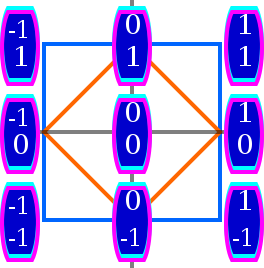
There are three families of polytopes which have simple representations in Rⁿ spaces, for any n, and can be used to visualize any affine coordinate system in a real n-space. Vertices of a hypercube have coordinates (x₁, x₂, ..., x_n) where each x_k takes on one of only two values, typically 0 or 1. However, any two numbers can be chosen instead of 0 and 1, for example −1 and 1. An n-hypercube can be thought of as the Cartesian product of n identical intervals (such as the unit interval [0,1]) on the real line. As an n-dimensional subset it can be described with a system of 2n inequalities:

$${\displaystyle {\begin{matrix}0\leq x_{1}\leq 1\\\vdots \\0\leq x_{n}\leq 1\end{matrix}}}$$

for [0,1], and

$${\displaystyle {\begin{matrix}|x_{1}|\leq 1\\\vdots \\|x_{n}|\leq 1\end{matrix}}}$$

for [−1,1].

Each vertex of the cross-polytope has, for some k, the x_k coordinate equal to ±1 and all other coordinates equal to 0 (such that it is the kth standard basis vector up to sign). This is a dual polytope of hypercube. As an n-dimensional subset it can be described with a single inequality which uses the absolute value operation:

$${\displaystyle \sum _{k=1}^{n}|x_{k}|\leq 1\,,}$$

but this can be expressed with a system of 2ⁿ linear inequalities as well.

The third polytope with simply enumerable coordinates is the standard simplex, whose vertices are n standard basis vectors and the origin (0, 0, ..., 0). As an n-dimensional subset it is described with a system of n + 1 linear inequalities:

$${\displaystyle {\begin{matrix}0\leq x_{1}\\\vdots \\0\leq x_{n}\\\sum \limits _{k=1}^{n}x_{k}\leq 1\end{matrix}}}$$

Replacement of all "≤" with "<" gives interiors of these polytopes.

Topological properties

The topological structure of Rⁿ (called standard topology, Euclidean topology, or usual topology) can be obtained not only from Cartesian product. It is also identical to the natural topology induced by Euclidean metric discussed above: a set is open in the Euclidean topology if and only if it contains an open ball around each of its points. Also, Rⁿ is a linear topological space (see continuity of linear maps above), and there is only one possible (non-trivial) topology compatible with its linear structure. As there are many open linear maps from Rⁿ to itself which are not isometries, there can be many Euclidean structures on Rⁿ which correspond to the same topology. Actually, it does not depend much even on the linear structure: there are many non-linear diffeomorphisms (and other homeomorphisms) of Rⁿ onto itself, or its parts such as a Euclidean open ball or the interior of a hypercube).

Rⁿ has the topological dimension n. An important result on the topology of Rⁿ, that is far from superficial, is Brouwer's invariance of domain. Any subset of Rⁿ (with its subspace topology) that is homeomorphic to another open subset of Rⁿ is itself open. An immediate consequence of this is that R^m is not homeomorphic to Rⁿ if m ≠ n – an intuitively "obvious" result which is nonetheless difficult to prove.

Despite the difference in topological dimension, and contrary to a naïve perception, it is possible to map a lesser-dimensional^{[clarification needed]} real space continuously and surjectively onto Rⁿ. A continuous (although not smooth) space-filling curve (an image of R¹) is possible.^{[clarification needed]}

Examples

Empty column vector, the only element of R0

R1

n ≤ 1

Cases of 0 ≤ n ≤ 1 do not offer anything new: R¹ is the real line, whereas R⁰ (the space containing the empty column vector) is a singleton, understood as a zero vector space. However, it is useful to include these as trivial cases of theories that describe different n.

n = 2

Both hypercube and cross-polytope in R² are squares, but coordinates of vertices are arranged differently

Further information: Two-dimensional space

Further information: Cartesian plane

See also: SL2(R)

n = 3

Cube (the hypercube) and octahedron (the cross-polytope) of R³. Coordinates are not shown

 

Main article: Three-dimensional space

n = 4

 

Further information: Four-dimensional space

R⁴ can be imagined using the fact that 16 points (x₁, x₂, x₃, x₄), where each x_k is either 0 or 1, are vertices of a tesseract (pictured), the 4-hypercube (see above).

The first major use of R⁴ is a spacetime model: three spatial coordinates plus one temporal. This is usually associated with theory of relativity, although four dimensions were used for such models since Galilei. The choice of theory leads to different structure, though: in Galilean relativity the t coordinate is privileged, but in Einsteinian relativity it is not. Special relativity is set in Minkowski space. General relativity uses curved spaces, which may be thought of as R⁴ with a curved metric for most practical purposes. None of these structures provide a (positive-definite) metric on R⁴.

Euclidean R⁴ also attracts the attention of mathematicians, for example due to its relation to quaternions, a 4-dimensional real algebra themselves. See rotations in 4-dimensional Euclidean space for some information.

In differential geometry, n = 4 is the only case where Rⁿ admits a non-standard differential structure: see exotic R⁴.

Norms on Rⁿ

One could define many norms on the vector space Rⁿ. Some common examples are

• the p-norm, defined by ${\textstyle \|\mathbf {x} \|_{p}:={\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}}$ for all ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$ where ${\displaystyle p}$ is a positive integer. The case ${\displaystyle p=2}$ is very important, because it is exactly the Euclidean norm.
• the ${\displaystyle \infty }$-norm or maximum norm, defined by ${\displaystyle \|\mathbf {x} \|_{\infty }:=\max\{x_{1},\dots ,x_{n}\}}$ for all ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$. This is the limit of all the p-norms: ${\textstyle \|\mathbf {x} \|_{\infty }=\lim _{p\to \infty }{\sqrt[{p}]{\sum _{i=1}^{n}|x_{i}|^{p}}}}$.

A really surprising and helpful result is that every norm defined on Rⁿ is equivalent. This means for two arbitrary norms ${\displaystyle \|\cdot \|}$ and ${\displaystyle \|\cdot \|'}$ on Rⁿ you can always find positive real numbers ${\displaystyle \alpha ,\beta >0}$, such that

$${\displaystyle \alpha \cdot \|\mathbf {x} \|\leq \|\mathbf {x} \|'\leq \beta \cdot \|\mathbf {x} \|}$$

for all ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$.

This defines an equivalence relation on the set of all norms on Rⁿ. With this result you can check that a sequence of vectors in Rⁿ converges with ${\displaystyle \|\cdot \|}$ if and only if it converges with ${\displaystyle \|\cdot \|'}$.

Here is a sketch of what a proof of this result may look like:

Because of the equivalence relation it is enough to show that every norm on Rⁿ is equivalent to the Euclidean norm ${\displaystyle \|\cdot \|_{2}}$. Let ${\displaystyle \|\cdot \|}$ be an arbitrary norm on Rⁿ. The proof is divided in two steps:

• We show that there exists a ${\displaystyle \beta >0}$, such that ${\displaystyle \|\mathbf {x} \|\leq \beta \cdot \|\mathbf {x} \|_{2}}$ for all ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$. In this step you use the fact that every ${\displaystyle \mathbf {x} =(x_{1},\dots ,x_{n})\in \mathbb {R} ^{n}}$ can be represented as a linear combination of the standard basis: ${\textstyle \mathbf {x} =\sum _{i=1}^{n}e_{i}\cdot x_{i}}$. Then with the Cauchy–Schwarz inequality
  $${\displaystyle \|\mathbf {x} \|=\left\|\sum _{i=1}^{n}e_{i}\cdot x_{i}\right\|\leq \sum _{i=1}^{n}\|e_{i}\|\cdot |x_{i}|\leq {\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}}}\cdot {\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}=\beta \cdot \|\mathbf {x} \|_{2},}$$

  
  where ${\textstyle \beta :={\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}}}}$.
• Now we have to find an ${\displaystyle \alpha >0}$, such that ${\displaystyle \alpha \cdot \|\mathbf {x} \|_{2}\leq \|\mathbf {x} \|}$ for all ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$. Assume there is no such ${\displaystyle \alpha }$. Then there exists for every ${\displaystyle k\in \mathbb {N} }$ a ${\displaystyle \mathbf {x} _{k}\in \mathbb {R} ^{n}}$, such that ${\displaystyle \|\mathbf {x} _{k}\|_{2}>k\cdot \|\mathbf {x} _{k}\|}$. Define a second sequence ${\displaystyle ({\tilde {\mathbf {x} }}_{k})_{k\in \mathbb {N} }}$ by ${\textstyle {\tilde {\mathbf {x} }}_{k}:={\frac {\mathbf {x} _{k}}{\|\mathbf {x} _{k}\|_{2}}}}$. This sequence is bounded because ${\displaystyle \|{\tilde {\mathbf {x} }}_{k}\|_{2}=1}$. So because of the Bolzano–Weierstrass theorem there exists a convergent subsequence ${\displaystyle ({\tilde {\mathbf {x} }}_{k_{j}})_{j\in \mathbb {N} }}$ with limit ${\displaystyle \mathbf {a} \in }$ Rⁿ. Now we show that ${\displaystyle \|\mathbf {a} \|_{2}=1}$ but ${\displaystyle \mathbf {a} =\mathbf {0} }$, which is a contradiction. It is
  $${\displaystyle \|\mathbf {a} \|\leq \left\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\|+\left\|{\tilde {\mathbf {x} }}_{k_{j}}\right\|\leq \beta \cdot \left\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}+{\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\ {\overset {j\to \infty }{\longrightarrow }}\ 0,}$$

  
  because ${\displaystyle \|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\|\to 0}$ and ${\displaystyle 0\leq {\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}<{\frac {1}{k_{j}}}}$, so ${\displaystyle {\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\to 0}$. This implies ${\displaystyle \|\mathbf {a} \|=0}$, so ${\displaystyle \mathbf {a} =\mathbf {0} }$. On the other hand ${\displaystyle \|\mathbf {a} \|_{2}=1}$, because ${\displaystyle \|\mathbf {a} \|_{2}=\left\|\lim _{j\to \infty }{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}=\lim _{j\to \infty }\left\|{\tilde {\mathbf {x} }}_{k_{j}}\right\|_{2}=1}$. This can not ever be true, so the assumption was false and there exists such a ${\displaystyle \alpha >0}$.

Space sustainability

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Space_sustainability 

 

A computer-generated animation by the European Space Agency representing space debris in low earth orbit at the current rate of growth compared to mitigation measures being taken.

Space sustainability aims to maintain the safety and health of the space environment.

Similar to sustainability initiatives on Earth, space sustainability seeks to use the environment of space to meet the current needs of society without compromising the needs of future generations. It usually focuses on space closest to Earth, Low Earth Orbit (LEO), since this environment is the one most used and therefore most relevant to humans. It also considers Geostationary Equatorial Orbit (GEO) as this orbit is another popular choice for Earth-orbiting mission designs.

The issue of space sustainability is a new phenomenon that is gaining more attention in recent years as the launching of satellites and other space objects has increased. These launches have resulted in more space debris orbiting Earth, hindering the ability of nations to operate in the space environment while increasing the risk of a future launch-related accident that could disrupt its proper use. Space weather also acts as an outstanding factor for spacecraft failure. The current protocol for spacecraft disposal at end-of-life has, at large, not been followed in mission designs and demands extraneous amounts of time for disposal.

Precedent created through prior policy initiatives has facilitated initial mitigation of space pollution and created a foundation for space sustainability efforts. To further mitigation, international and transdisciplinary consortia have stepped forward to analyze existing operations, develop standards, and incentivize future procedures to prioritize a sustainable approach. A shift towards sustainable interactions with the space environment is growing in urgency due to the implications of climate change and increasing risk to spacecraft as time presses on.

Fundamentals

Space sustainability requires all space participants to have three consensuses. The space field should be used peacefully, jointly protect the space field from harm, and maximize space utilization through environmental, economic, and security exploration of space. These consensuses also clarify the relationship between space sustainability and international security, that states and individuals explore space for various purposes. Their reliance on space needs to be guided by rules, order, and policies and obtain more benefits without negatively affecting the space environment and space activities.

However, striking an agreement remains challenging even with such demands in place. In the discussions between countries on long-term sustainability, technical improvements are given more importance than introducing and applying new legal regimes. Specifically, technical approaches to space debris have been proposed, such as debris removal. Specific data on space debris is also being explored to help study its impact on sustainability and promote further cooperation between countries.

Current state

Space sustainability comes into play to address the pressing current state of near-Earth orbits and its high amounts of orbital debris. Spacecraft collisions with orbital debris, space weather, overcrowding in low earth orbit (LEO) makes spacecraft susceptible to higher rates of failure. The current end-of-life protocol for spacecraft exacerbates the space sustainability crisis; many spacecraft are not properly disposed, which increasing the likelihood of further collisions.

Orbital debris

Orbital debris is defined as unmanned, inoperate objects that exist in space. This orbital debris breaks down further as time progresses as a result of naturally occurring events, such as high-velocity collisions with micrometeoroids, and forced events, such as a controlled release of a launch vehicle. In LEO, these collisions can take place at speeds anywhere between an average velocity of 9 kilometers per second (km/s) and 14 km/s relative to the debris and spacecraft. In GEO, however, these high-speed collisions are a much lower risk as the average relative velocity between the debris and spacecraft is typically between 0 km/s and 2.5 km/s. As of 2012, the United States Joint Space Operations Center tracked 21,000 pieces of orbital debris larger than 10 cm in Earth’s nearby orbits (LEO, GEO, and sun-synchronous), where 16,000 of these pieces are catalogued. Space debris can be categorized into three categories: small, medium, and large. Small debris is for pieces that are less than 10 centimeters (cm). Medium-sized debris is for pieces larger than 10 cm, but not an entire spacecraft. Large-sized debris has no official classification, but typically refers to entire spacecraft, such as an out of use satellite or launch vehicle. It is difficult to track small-sized debris in LEO, and challenging to track small and medium-sized debris in GEO. Yet this statement is not to discount the abilities of LEO and GEO tracking capabilities, the smallest piece of tracked debris can weigh as low as ten grams. If the size of the debris prohibits it from being tracked, it also cannot be avoided by the spacecraft and does not allow the spacecraft to lower its risk of collisions. The likelihood of the Kessler syndrome, which essentially states that each collision produces more debris, grows larger as the amount of orbital debris multiplies, increasing the amount of further collisions until space cannot be used entirely.

Space weather

Space weather poses a risk to satellite health, consequently, resulting in greater amounts of orbital debris. Space weather impacts satellite health in a variety of ways. Firstly, surface charging from the sun’s surface facilitates electrical discharges, damaging on-orbit electronics, posing a threat to mission failure. Single Event Upsets (SEUs) can also damage electronics. Dielectric charging and bulk charging can also occur, causing energy problems within the spacecraft. Additionally, at altitudes less than one thousand kilometers, atmospheric drag can increase during solar storms by increasing the altitude of the spacecraft, only adding more drag onto the spacecraft. These factors degrade performance over the spacecraft’s lifetime, leaving the spacecraft more susceptible to further system and mission failures.

Overcrowding

There has been a dramatic increase in the use of LEO and GEO orbits over the last sixty years since the first satellite launch in 1957. To date, there have been approximately ten thousand satellite launches, whereas only approximately 2000 are still active. These satellites can be used for a variety of purposes, which are telecommunications, navigation, weather monitoring, and exploration. Within the coming decade, companies like SpaceX are predicted to launch an additional fifteen thousand satellites into LEO and GEO orbits. Microsatellites built by universities or research organizations have also increased in popularity, contributing to the overcrowding of near earth orbits. This overcrowding of LEO and GEO orbits increases the likelihood of potential collisions among satellites and orbital debris, contributing further to the large amount of orbital debris present in space.

End of life protocol

The current end of life protocol is that at the end of mission, spacecraft are either added to the graveyard orbit or at a low enough altitude that drag will allow the spacecraft to burn up upon reentry and fall back to Earth. Approximately twenty satellites are put into the graveyard orbit each year, but this rate is expected to increase to one thousand satellites per year by 2050. There is no current process to return satellites to Earth after entering the graveyard orbit. The process of a spacecraft returning to Earth via drag can take between ten to one hundred years. This protocol is critical to reduce overcrowding in near-Earth orbits.

Mega constellation and space debris

The impact of constellations on the space environment has also been studied, such as the probability of collisions of mega constellations in the presence of large amounts of space debris. Although studies have shown that the predictors of mega constellations are highly variable, specific information related to mega constellations is not transparent.

But any catastrophic collision, as in the case of Kessler syndrome, has consequences for people and the environment. Putting this thinking into mega constellations, mega constellations existence may have potential benefits, but it will not bring adequate help to the governance of space debris. At the same time, the space debris situation cannot be underestimated or ignored because of the existence of mega constellations.

Concern

The existence of orbital debris has caused great trouble to the conduct of space activities. The development of space sustainability has not given sufficient political attention, although some warnings and discussions have made this abundantly clear. Debris management is still voluntary on the part of the state, and there are no laws mandating debris management practices, including the amount of debris to be managed. Although the UN Space Debris Mitigation Guidelines were promulgated in 2007 as an initial measure of space debris governance, there is still no broad consensus or action on further limits on space debris after that.

The difficulties for individuals wishing to participate in debris management initiatives cannot be ignored. Any individual or sector desiring to participate in space debris operations needs to obtain permission from the launching state, which is difficult for the launching state to do. This is because the process of space debris management inevitably has a negative impact on other space objects, and there is a lot of subsequent liability in terms of financial consumption. Therefore, the launching state would argue that space debris management requires the joint efforts of all states. However, it is difficult to determine what actions can be taken to gain acceptance between countries.

Regulations

Current space sustainability efforts rely heavily on the precedent set by regulatory agreements and conventions of the twentieth century. Much of this precedent is included in or is related to the Outer Space Treaty of 1963, which represented one of the initial major efforts by the United Nations to create legal frameworks for the operation of nations in space.

Pre-Outer Space Treaty

The international community has had concerns about space contamination since the 1950’s prior to the launch of Sputnik I. These concerns stemmed from the idea that increasing rates of exploration into further areas of outer space could lead to contamination capable of damaging other planetary bodies, resulting in limitations to human exploration on these bodies and potential harm to the Earth. Efforts to combat these concerns began in 1956 with the International Astronautical Federation (IAF) and the United Nations Committee on the Peaceful Uses of Outer Space (COPUOUS). These efforts continued to 1957 through the National Academy of Sciences and International Council for Science (ICSU). Each of these organizations aimed to study space contamination and develop strategies for how to best address its potential consequences. The ICSU went on to create the Committee on Contamination by Extraterrestrial Exploration (CETEX) that put forward recommendations leading to the establishment of the Committee on Space Research (COSPAR). COSPAR continues to address outer space research on an international scale today [cite cospar].

Outer Space Treaty

Relevant regulations of international space law to sustainability in space can be found in the Outer Space Treaty, which was adopted by the UN General Assembly in 1963. The Outer Space Treaty contains seventeen articles designed to create a basic framework for how international law can be applied in outer space. Basic principles of the Outer Space Treaty include the provision in Article IX that parties should "avoid harmful contamination of space and celestial bodies;"  definitions of "harmful contamination" are not provided. Other articles of relevance to space sustainability include articles I, II, and III that concern the fair and inclusive international use of space in a manner free from sovereignty, ownership, or occupation by any nation. In addition, articles VII and VIII protect ownership by their respective countries of any objects launched to space while attributing responsibility for any damages to the property or personnel of other countries by those objects to said countries. Descriptions or definitions for what these damages may entail are not provided.

COSPAR Planetary Protection Policy

Principles of Article IX provided the basis for the Committee of Space Research (COSPAR) Planetary Protection Policy guidelines, which are generally well-regarded among scientific experts. Such guidelines, however, are non-binding and often described as "soft-law," as they lack legal mandate. The Planetary Protection Policy is primarily concerned with providing information regarding best practices to avoid contamination of the space environment during space exploration missions. COSPAR believes that the prevention of such contamination is in the best interest of humanity as it may impede scientific progress, exploration, and the mission of a search for life. In addition, the argument is made that cross-contamination of the Earth can be potentially harmful to its environment due to the largely unknown nature of potential space contaminants.

Other relevant regulations

Regulatory clarifications concerning the Outer Space Treaty of 1963 of relevance to space sustainability were made in subsequent years. The 1967 Return Agreement relates mainly to the return of lost astronauts to their appropriate nations, but also requires Outer Space Treaty signing nations to assist other nations with the return of objects that return to Earth from orbit to their proper owners The 1972 Liability Convention attributes liability for damages from space objects to the nation that launched the object, regardless of whether that damage occurred in space or on Earth. Other clarifications include the 1975 registration convention that attempted to create mechanisms for nations to identify space objects, and the 1979 Moon Agreement that established protections for the environments of the Moon and other nearby planetary bodies. These agreements and conventions represented attempts to improve the initial Outer Space Treaty as space exploration continued to grow in importance throughout the 20th century.

Attitudes

Countries and major international institutions

Both the state and space agencies are working to improve the laws and regulations that facilitate the long-term sustainability of space. For example, the European Code of Conduct for Space Debris Mitigation signed by France, the UK and other countries in 2016. China, Brazil, Mexico and others have legal background and methodological measures under long-term space sustainability. However, the main problem is that until the concept of space sustainability is agreed between countries, inter-regional efforts are not working well.

Currently, the Committee on the Peaceful Uses of Outer Space (COPUOS) encourages states to incorporate the space debris mitigation guidelines developed by bodies such as the Inter-Agency Space Debris Coordination (IADC) into their national legislation, thereby regulating state behavior. Some countries have responded positively to this, such as Switzerland, the Netherlands and Spain. However, there are still some countries that do not consider debris management approaches in their national legislation, such as Japan and Australia. Many delegates at the COPUOS meeting expressed their reasons for doing so, arguing that space debris management is closely linked to technology and funding. Technology is dynamic and constantly evolving. Therefore, the incorporation of debris governance guidelines into national law is not an immediate priority at this time.

Scientific attitudes

A study outlined rationale for governance that regulates the current free externalization of true costs and risks, treating orbital space around the Earth as an "additional ecosystem" or a common "part of the human environment" which should be subject to the same concerns and regulations like e.g. oceans on Earth. While scientists may not have the means to make and enforce global laws themselves, the study concluded in 2022 that it needs "new policies, rules and regulations at national and international level".

Mitigation

Sustainability mitigation efforts include but are not limited to design specifications, policy change, removal of space debris, and restoration of orbiting semi-functional technologies. Efforts begin by regulating the debris released during normal operations and post-mission breakups. Due to the increased awareness of high-velocity collisions and orbital debris in the previous decades, missions have adapted design specifications to account for these risks. For example, the RADARSAT program implemented 17 kilograms of shielding to their spacecraft, which increased the program’s predicted success rate to 87% from 50%. Another effort in mitigation is restoring semi-functional satellites, which allows a spacecraft classified as “debris” to “functional.”  Space debris mitigation focuses on limiting debris release during normal operations, collisions and intentional destruction. Mitigation also includes reducing the possibility for post-mission breakups due to stored energy and/or operations phases, as well as addressing procedure for end of mission disposal for spacecraft.

Space Sustainability Rating

One example leading the regulatory sustainability measures is the Space Sustainability Rating (SSR), which is an instigator for industry competitors to incorporate sustainability into spacecraft design. The Space Sustainability Rating was first conceptualized at the World Economic Forum Global Future Council on Space Technologies designed by international and transdisciplinary consortia. The four leading organizations are the European Space Agency, Massachusetts Institute of Technology, University of Texas at Austin, and BryceTech with the goal to define the technical and programmatic aspects of the SSR. The SSR represents an innovative approach to combating orbital debris through incentivizing the industry to prioritize sustainable and responsible operations. This response entails the consideration of potential harm to the space environment and other spacecraft, all while maintaining mission objectives and high-quality service. The rating takes inspiration from other standards, like leadership in energy and environmental design (LEED) for the building sector. Several of the factors emphasized in the rating were extracted from LEED design considerations like the incorporation of feedback and public comments, or the rating’s advocacy to influence policy, such as orbit fragmentation risks, collision avoidance capabilities, trackability, and adoption of international standards.

Tracking

Tracking is one of the main Space Sustainability Rating modules’ efforts. The module "Detectability, Identification and Tracking" (DIT) consists of standardizing the comparison of satellite missions to encourage satellite operators to improve their satellite design and operational approaches for the observer to detect, identify, and track the satellites. Tracking presents challenges when the observer seeks to monitor and predict the spacecraft behavior over time. While the observer may know the name, owner, and instantaneous location of the satellite, the operator controls the full knowledge of the orbital parameters. The Space Situational Awareness (SSA) is one the tools geared towards solving the challenges presented when tracking orbiting satellites and debris. The SSA continuously tracks objects using ground-based radar and optical stations so the orbital paths of debris can be predicted and operations avoid collisions. It feeds data to 30 different systems like satellites, optical telescopes, radar systems, and supercomputers to predict risk of collision days in advance. Other efforts in tracking orbital debris are made by the US Space Surveillance Network (SSN).

Removal

Under the "External Services" module of the SSR, the rating offers commitment to use or demonstration of use of end-of-life removal services. Space debris mitigation measures are found to be inadequate to stabilize debris environments with an actual current compliance of approximately sixty percent. Moreover, a low compliance rate of approximately thirty percent of the 103 spacecraft that reached end of life between 1997 and 2003 were disposed of in a graveyard orbit. Since policy has not caught up to ensure the longevity of LEO for future generations, actions like Active Debris Removal (ADR) are being considered to stabilize the future of LEO environment. Most famous removal concepts are based on directed energy, momentum exchange or electrodynamics, aerodynamic drag augmentation, solar sails, auxiliary propulsion units, retarding surfaces and on-orbit capture. As ADR consists of an external disposal method to remove obsolete satellites or spacecraft fragments. Since large-sized debris objects in orbit provide a potential source for tens of thousands of fragments in the future, ADR efforts focus on objects with high mass and large cross-sectional areas, in densely populated regions, and at high altitudes; in this instance, retired satellites and rocket bodies are a priority. Other practical advancements toward space debris removal include missions like RemoveDEBRIS and End-of-Life Service (ELS-d).

Growing urgency

The growth of all tracked objects in space over time

The previous reduced state of regulation and mitigation on space debris and rocket fuel emissions is aggravating the Earth’s stratosphere through collisions and ozone depletion, increasing the risk for spacecraft health through its lifetime.

Inaccessibility to LEO

Due to the increase of satellites being launched and the growing amount of orbital debris in LEO, the risk of LEO becoming inaccessible over time (in accordance with the Kessler syndrome) is increasing in likelihood. The mitigation policies for creating space debris fall under an area of voluntary codes by the states, although it has been disputed whether the Article I Outer Space Treaty or the Article IX Outer Space Treaty protects the space environment from deliberate harm, which has yet to be upheld. In 2007, an inactive Chinese satellite was purposefully destroyed by the Chinese government as a part of their anti-satellite weapon test (ASAT), spreading nearly 2800 objects of space debris five centimeters or larger into LEO. An analysis concluded that about eighty percent of the debris will remain in LEO nine years after this destruction. In addition, the destruction increased the collision likelihood for three Italian satellites that launched the same year as the Fengyun-1C destruction. The increase in collision ranged between ten and sixty percent. However, there were no legal consequences against the Chinese government.

Rocket fuel emissions

When rockets are launched into space, parts of their fuel enter the stratosphere of the Earth. Rocket fuel emissions are made up of carbon dioxide, water, hydrochloric acid, alumina and soot particles. The most concerning emissions from rocket fuel are chlorine and alumina particles from solid rocket motors (SRMs) and soot from kerosene fueled engines. When the hydrochloric acid from the engine exhaust dissociates, the free chlorine roams freely in the stratosphere. The chemical reaction between these chlorine and alumina causes ozone depletion. In addition, the soot particles form over a black umbrella over the stratosphere which can cause the temperature of the Earth’s surface to lower and further depleting the ozone layer, an unintentional form of geoengineering. The nature of geoengineering has been disputed as a form of mitigating global warming and has the possibility of being banned and holding rockets accountable for the soot particles they distribute to the stratosphere. New types of engines and fuels are emerging, mainly the liquid oxygen (LOX) and monomethylhydrazine engine, but there is minimal research on their impact on the environment besides their emission of hydroxide and nitrogen oxide compounds, two molecules that have significant impact on the ozone layer. Currently, rocket fuel emissions have been deemed insignificant when it comes to their consequences to Earth’s environment and LEO. However, emissions will increase in the coming years, making rocket fuel’s contribution to global warming much more significant.

Beyond LEO

Space sustainability concepts and mindsets tend to stay in Low Earth Orbit (LEO). One reason that cannot be ignored is that it is easier to discuss the problem at hand than to speculate on the unknown. There are also examples to prove that since Apollo 17 completed its mission and stayed in Low Earth orbit in 1972, human-crewed space missions in Low Earth orbit have ceased to exist. In this way, it is a reasonable assumption that the closer Moon could be the next object to be explored when the gaze is not limited to LEO. Both lunar orbit and LEO are part of the space environment. In the context of the presence of space debris in LEO, it is normal to speculate that lunar orbit also possesses the nuisance of debris. Space debris measures similar to those in LEO related to space sustainability would be taken.

Not only has the Moon been the subject of study, but other bodies have also been taken into account. Elon Musk, the chief executive of SpaceX at the International Astronautical Congress in 2016, explained the ambitious goal of exploring Mars in the 22nd century. But complicated issues remain, such as the technical aspects of achieving long-distance space flight and the rules and legal aspects associated with the technology, all of which need to be considered.