Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations.
Given a structured object X of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This can occur in many ways; for example, if X is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups. If the object X is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (i.e., an isometry).
In general, every kind of structure in mathematics will have its own kind of symmetry, many of which are listed in the given points mentioned above.
Symmetry in geometry
The types of symmetry considered in basic geometry include reflectional symmetry, rotation symmetry, translational symmetry and glide reflection symmetry, which are described more fully in the main article Symmetry (geometry).
Symmetry in calculus
Even and odd functions
Even functions
Let f(x) be a real-valued function of a real variable, then f is even if the following equation holds for all x and -x in the domain of f:
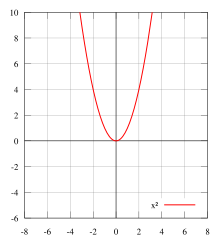
Geometrically speaking, the graph face of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis. Examples of even functions include |x|, x2, x4, cos(x), and cosh(x).
Odd functions
Again, let f(x) be a real-valued function of a real variable, then f is odd if the following equation holds for all x and -x in the domain of f:
That is,
Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin. Examples of odd functions are x, x3, sin(x), sinh(x), and erf(x).
Integrating
The integral of an odd function from −A to +A is zero, provided that A is finite and that the function is integrable (e.g., has no vertical asymptotes between −A and A).
The integral of an even function from −A to +A is twice the integral from 0 to +A, provided that A is finite and the function is integrable (e.g., has no vertical asymptotes between −A and A). This also holds true when A is infinite, but only if the integral converges.
Series
- The Maclaurin series of an even function includes only even powers.
- The Maclaurin series of an odd function includes only odd powers.
- The Fourier series of a periodic even function includes only cosine terms.
- The Fourier series of a periodic odd function includes only sine terms.
Symmetry in linear algebra
Symmetry in matrices
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose (i.e., it is invariant under matrix transposition). Formally, matrix A is symmetric if
By the definition of matrix equality, which requires that the entries in all corresponding positions be equal, equal matrices must have the same dimensions (as matrices of different sizes or shapes cannot be equal). Consequently, only square matrices can be symmetric.
The entries of a symmetric matrix are symmetric with respect to the main diagonal. So if the entries are written as A = (aij), then aij = aji, for all indices i and j.
For example, the following 3×3 matrix is symmetric:
Every square diagonal matrix is symmetric, since all off-diagonal entries are zero. Similarly, each diagonal element of a skew-symmetric matrix must be zero, since each is its own negative.
In linear algebra, a real symmetric matrix represents a self-adjoint operator over a real inner product space. The corresponding object for a complex inner product space is a Hermitian matrix with complex-valued entries, which is equal to its conjugate transpose. Therefore, in linear algebra over the complex numbers, it is often assumed that a symmetric matrix refers to one which has real-valued entries. Symmetric matrices appear naturally in a variety of applications, and typical numerical linear algebra software makes special accommodations for them.
Symmetry in abstract algebra
Symmetric groups
The symmetric group Sn (on a finite set of n symbols) is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself. Since there are n! (n factorial) possible permutations of a set of n symbols, it follows that the order (i.e., the number of elements) of the symmetric group Sn is n!.
Symmetric polynomials
A symmetric polynomial is a polynomial P(X1, X2, ..., Xn) in n variables, such that if any of the variables are interchanged, one obtains the same polynomial. Formally, P is a symmetric polynomial if for any permutation σ of the subscripts 1, 2, ..., n, one has P(Xσ(1), Xσ(2), ..., Xσ(n)) = P(X1, X2, ..., Xn).
Symmetric polynomials arise naturally in the study of the relation between the roots of a polynomial in one variable and its coefficients, since the coefficients can be given by polynomial expressions in the roots, and all roots play a similar role in this setting. From this point of view, the elementary symmetric polynomials are the most fundamental symmetric polynomials. A theorem states that any symmetric polynomial can be expressed in terms of elementary symmetric polynomials, which implies that every symmetric polynomial expression in the roots of a monic polynomial can alternatively be given as a polynomial expression in the coefficients of the polynomial.
Examples
In two variables X1 and X2, one has symmetric polynomials such as:
and in three variables X1, X2 and X3, one has as a symmetric polynomial:
Symmetric tensors
In mathematics, a symmetric tensor is tensor that is invariant under a permutation of its vector arguments:
for every permutation σ of the symbols {1,2,...,r}. Alternatively, an rth order symmetric tensor represented in coordinates as a quantity with r indices satisfies
The space of symmetric tensors of rank r on a finite-dimensional vector space is naturally isomorphic to the dual of the space of homogeneous polynomials of degree r on V. Over fields of characteristic zero, the graded vector space of all symmetric tensors can be naturally identified with the symmetric algebra on V. A related concept is that of the antisymmetric tensor or alternating form. Symmetric tensors occur widely in engineering, physics and mathematics.
Galois theory
Given a polynomial, it may be that some of the roots are connected by various algebraic equations. For example, it may be that for two of the roots, say A and B, that A2 + 5B3 = 7. The central idea of Galois theory is to consider those permutations (or rearrangements) of the roots having the property that any algebraic equation satisfied by the roots is still satisfied after the roots have been permuted. An important proviso is that we restrict ourselves to algebraic equations whose coefficients are rational numbers. Thus, Galois theory studies the symmetries inherent in algebraic equations.
Automorphisms of algebraic objects
In abstract algebra, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.
Examples
- In set theory, an arbitrary permutation of the elements of a set X is an automorphism. The automorphism group of X is also called the symmetric group on X.
- In elementary arithmetic, the set of integers, Z, considered as a group under addition, has a unique nontrivial automorphism: negation. Considered as a ring, however, it has only the trivial automorphism. Generally speaking, negation is an automorphism of any abelian group, but not of a ring or field.
- A group automorphism is a group isomorphism from a group to itself. Informally, it is a permutation of the group elements such that the structure remains unchanged. For every group G there is a natural group homomorphism G → Aut(G) whose image is the group Inn(G) of inner automorphisms and whose kernel is the center of G. Thus, if G has trivial center it can be embedded into its own automorphism group.
- In linear algebra, an endomorphism of a vector space V is a linear operator V → V. An automorphism is an invertible linear operator on V. When the vector space is finite-dimensional, the automorphism group of V is the same as the general linear group, GL(V).
- A field automorphism is a bijective ring homomorphism from a field to itself. In the cases of the rational numbers (Q) and the real numbers (R) there are no nontrivial field automorphisms. Some subfields of R have nontrivial field automorphisms, which however do not extend to all of R (because they cannot preserve the property of a number having a square root in R). In the case of the complex numbers, C, there is a unique nontrivial automorphism that sends R into R: complex conjugation, but there are infinitely (uncountably) many "wild" automorphisms (assuming the axiom of choice).[6] Field automorphisms are important to the theory of field extensions, in particular Galois extensions. In the case of a Galois extension L/K the subgroup of all automorphisms of L fixing K pointwise is called the Galois group of the extension.
Symmetry in representation theory
Symmetry in quantum mechanics: bosons and fermions
In quantum mechanics, bosons have representatives that are symmetric under permutation operators, and fermions have antisymmetric representatives.
This implies the Pauli exclusion principle for fermions. In fact, the Pauli exclusion principle with a single-valued many-particle wavefunction is equivalent to requiring the wavefunction to be antisymmetric. An antisymmetric two-particle state is represented as a sum of states in which one particle is in state and the other in state :
and antisymmetry under exchange means that A(x,y) = −A(y,x). This implies that A(x,x) = 0, which is Pauli exclusion. It is true in any basis, since unitary changes of basis keep antisymmetric matrices antisymmetric, although strictly speaking, the quantity A(x,y) is not a matrix but an antisymmetric rank-two tensor.
Conversely, if the diagonal quantities A(x,x) are zero in every basis, then the wavefunction component:
is necessarily antisymmetric. To prove it, consider the matrix element:
This is zero, because the two particles have zero probability to both be in the superposition state . But this is equal to
The first and last terms on the right hand side are diagonal elements and are zero, and the whole sum is equal to zero. So the wavefunction matrix elements obey:
- .
or
Symmetry in set theory
Symmetric relation
We call a relation symmetric if every time the relation stands from A to B, it stands too from B to A. Note that symmetry is not the exact opposite of antisymmetry.
Symmetry in metric spaces
Isometries of a space
An isometry is a distance-preserving map between metric spaces. Given a metric space, or a set and scheme for assigning distances between elements of the set, an isometry is a transformation which maps elements to another metric space such that the distance between the elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional space, two geometric figures are congruent if they are related by an isometry: related by either a rigid motion, or a composition of a rigid motion and a reflection. Up to a relation by a rigid motion, they are equal if related by a direct isometry.
Isometries have been used to unify the working definition of symmetry in geometry and for functions, probability distributions, matrices, strings, graphs, etc.
Symmetries of differential equations
A symmetry of a differential equation is a transformation that leaves the differential equation invariant. Knowledge of such symmetries may help solve the differential equation.
A Line symmetry of a system of differential equations is a continuous symmetry of the system of differential equations. Knowledge of a Line symmetry can be used to simplify an ordinary differential equation through reduction of order.
For ordinary differential equations, knowledge of an appropriate set of Lie symmetries allows one to explicitly calculate a set of first integrals, yielding a complete solution without integration.
Symmetries may be found by solving a related set of ordinary differential equations. Solving these equations is often much simpler than solving the original differential equations.
Symmetry in probability
In the case of a finite number of possible outcomes, symmetry with respect to permutations (relabelings) implies a discrete uniform distribution.
In the case of a real interval of possible outcomes, symmetry with respect to interchanging sub-intervals of equal length corresponds to a continuous uniform distribution.
In other cases, such as "taking a random integer" or "taking a random real number", there are no probability distributions at all symmetric with respect to relabellings or to exchange of equally long subintervals. Other reasonable symmetries do not single out one particular distribution, or in other words, there is not a unique probability distribution providing maximum symmetry.
There is one type of isometry in one dimension that may leave the probability distribution unchanged, that is reflection in a point, for example zero.
A possible symmetry for randomness with positive outcomes is that the former applies for the logarithm, i.e., the outcome and its reciprocal have the same distribution. However this symmetry does not single out any particular distribution uniquely.
For a "random point" in a plane or in space, one can choose an origin, and consider a probability distribution with circular or spherical symmetry, respectively.