Finite-state machine

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Finite-state_machine 

Classes of automata

A finite-state machine (FSM) or finite-state automaton (FSA, plural: automata), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. A deterministic finite-state machine can be constructed equivalent to any non-deterministic one.

The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are vending machines, which dispense products when the proper combination of coins is deposited, elevators, whose sequence of stops is determined by the floors requested by riders, traffic lights, which change sequence when cars are waiting, and combination locks, which require the input of a sequence of numbers in the proper order.

The finite-state machine has less computational power than some other models of computation such as the Turing machine. The computational power distinction means there are computational tasks that a Turing machine can do but an FSM cannot. This is because an FSM's memory is limited by the number of states it has. A finite-state machine has the same computational power as a Turing machine that is restricted such that its head may only perform "read" operations, and always has to move from left to right. FSMs are studied in the more general field of automata theory.

Example: coin-operated turnstile

State diagram for a turnstile

 

A turnstile

An example of a simple mechanism that can be modeled by a state machine is a turnstile. A turnstile, used to control access to subways and amusement park rides, is a gate with three rotating arms at waist height, one across the entryway. Initially the arms are locked, blocking the entry, preventing patrons from passing through. Depositing a coin or token in a slot on the turnstile unlocks the arms, allowing a single customer to push through. After the customer passes through, the arms are locked again until another coin is inserted.

Considered as a state machine, the turnstile has two possible states: Locked and Unlocked. There are two possible inputs that affect its state: putting a coin in the slot (coin) and pushing the arm (push). In the locked state, pushing on the arm has no effect; no matter how many times the input push is given, it stays in the locked state. Putting a coin in – that is, giving the machine a coin input – shifts the state from Locked to Unlocked. In the unlocked state, putting additional coins in has no effect; that is, giving additional coin inputs does not change the state. However, a customer pushing through the arms, giving a push input, shifts the state back to Locked.

The turnstile state machine can be represented by a state-transition table, showing for each possible state, the transitions between them (based upon the inputs given to the machine) and the outputs resulting from each input:

Current State	Input	Next State	Output
Locked	coin	Unlocked	Unlocks the turnstile so that the customer can push through.
	push	Locked	None
Unlocked	coin	Unlocked	None
	push	Locked	When the customer has pushed through, locks the turnstile.

The turnstile state machine can also be represented by a directed graph called a state diagram (above). Each state is represented by a node (circle). Edges (arrows) show the transitions from one state to another. Each arrow is labeled with the input that triggers that transition. An input that doesn't cause a change of state (such as a coin input in the Unlocked state) is represented by a circular arrow returning to the original state. The arrow into the Locked node from the black dot indicates it is the initial state.

Concepts and terminology

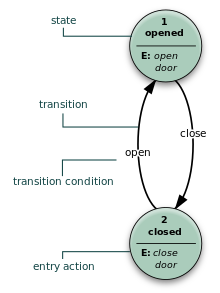
A state is a description of the status of a system that is waiting to execute a transition. A transition is a set of actions to be executed when a condition is fulfilled or when an event is received. For example, when using an audio system to listen to the radio (the system is in the "radio" state), receiving a "next" stimulus results in moving to the next station. When the system is in the "CD" state, the "next" stimulus results in moving to the next track. Identical stimuli trigger different actions depending on the current state.

In some finite-state machine representations, it is also possible to associate actions with a state:

• an entry action: performed when entering the state, and
• an exit action: performed when exiting the state.

Representations

Fig. 1 UML state chart example (a toaster oven)

 

Fig. 2 SDL state machine example

 

Fig. 3 Example of a simple finite-state machine

 

For an introduction, see State diagram.

State/Event table

Several state-transition table types are used. The most common representation is shown below: the combination of current state (e.g. B) and input (e.g. Y) shows the next state (e.g. C). The complete action's information is not directly described in the table and can only be added using footnotes. An FSM definition including the full action's information is possible using state tables (see also virtual finite-state machine).

State-transition table

Current state Input	State A	State B	State C
Input X	...	...	...
Input Y	...	State C	...
Input Z	...	...	...

UML state machines

The Unified Modeling Language has a notation for describing state machines. UML state machines overcome the limitations of traditional finite-state machines while retaining their main benefits. UML state machines introduce the new concepts of hierarchically nested states and orthogonal regions, while extending the notion of actions. UML state machines have the characteristics of both Mealy machines and Moore machines. They support actions that depend on both the state of the system and the triggering event, as in Mealy machines, as well as entry and exit actions, which are associated with states rather than transitions, as in Moore machines.

SDL state machines

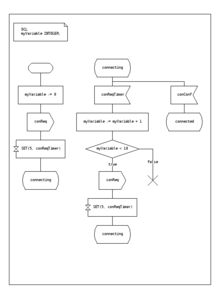
The Specification and Description Language is a standard from ITU that includes graphical symbols to describe actions in the transition:

• send an event
• receive an event
• start a timer
• cancel a timer
• start another concurrent state machine
• decision

SDL embeds basic data types called "Abstract Data Types", an action language, and an execution semantic in order to make the finite-state machine executable.

Other state diagrams

There are a large number of variants to represent an FSM such as the one in figure 3.

Usage

In addition to their use in modeling reactive systems presented here, finite-state machines are significant in many different areas, including electrical engineering, linguistics, computer science, philosophy, biology, mathematics, video game programming, and logic. Finite-state machines are a class of automata studied in automata theory and the theory of computation. In computer science, finite-state machines are widely used in modeling of application behavior (control theory), design of hardware digital systems, software engineering, compilers, network protocols, and computational linguistics.

Classification

Finite-state machines can be subdivided into acceptors, classifiers, transducers and sequencers.

Acceptors

Fig. 4: Acceptor FSM: parsing the string "nice".

 

Fig. 5: Representation of an acceptor; this example shows one that determines whether a binary number has an even number of 0s, where S₁ is an accepting state and S₂ is a non accepting state.

Acceptors (also called detectors or recognizers) produce binary output, indicating whether or not the received input is accepted. Each state of an acceptor is either accepting or non accepting. Once all input has been received, if the current state is an accepting state, the input is accepted; otherwise it is rejected. As a rule, input is a sequence of symbols (characters); actions are not used. The start state can also be an accepting state, in which case the acceptor accepts the empty string. The example in figure 4 shows an acceptor that accepts the string "nice". In this acceptor, the only accepting state is state 7.

A (possibly infinite) set of symbol sequences, called a formal language, is a regular language if there is some acceptor that accepts exactly that set. For example, the set of binary strings with an even number of zeroes is a regular language (cf. Fig. 5), while the set of all strings whose length is a prime number is not.

An acceptor could also be described as defining a language that would contain every string accepted by the acceptor but none of the rejected ones; that language is accepted by the acceptor. By definition, the languages accepted by acceptors are the regular languages.

The problem of determining the language accepted by a given acceptor is an instance of the algebraic path problem—itself a generalization of the shortest path problem to graphs with edges weighted by the elements of an (arbitrary) semiring.

An example of an accepting state appears in Fig. 5: a deterministic finite automaton (DFA) that detects whether the binary input string contains an even number of 0s.

S₁ (which is also the start state) indicates the state at which an even number of 0s has been input. S₁ is therefore an accepting state. This acceptor will finish in an accept state, if the binary string contains an even number of 0s (including any binary string containing no 0s). Examples of strings accepted by this acceptor are ε (the empty string), 1, 11, 11..., 00, 010, 1010, 10110, etc.

Classifiers

Classifiers are a generalization of acceptors that produce n-ary output where n is strictly greater than two.

Transducers

Main article: Finite-state transducer

 

Fig. 6 Transducer FSM: Moore model example

 

Fig. 7 Transducer FSM: Mealy model example

Transducers produce output based on a given input and/or a state using actions. They are used for control applications and in the field of computational linguistics.

In control applications, two types are distinguished:

Moore machine

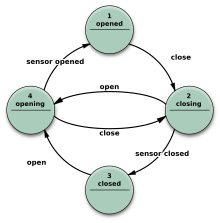
The FSM uses only entry actions, i.e., output depends only on state. The advantage of the Moore model is a simplification of the behaviour. Consider an elevator door. The state machine recognizes two commands: "command_open" and "command_close", which trigger state changes. The entry action (E:) in state "Opening" starts a motor opening the door, the entry action in state "Closing" starts a motor in the other direction closing the door. States "Opened" and "Closed" stop the motor when fully opened or closed. They signal to the outside world (e.g., to other state machines) the situation: "door is open" or "door is closed".

Mealy machine

The FSM also uses input actions, i.e., output depends on input and state. The use of a Mealy FSM leads often to a reduction of the number of states. The example in figure 7 shows a Mealy FSM implementing the same behaviour as in the Moore example (the behaviour depends on the implemented FSM execution model and will work, e.g., for virtual FSM but not for event-driven FSM). There are two input actions (I:): "start motor to close the door if command_close arrives" and "start motor in the other direction to open the door if command_open arrives". The "opening" and "closing" intermediate states are not shown.

Sequencers

Sequencers (also called generators) are a subclass of acceptors and transducers that have a single-letter input alphabet. They produce only one sequence, which can be seen as an output sequence of acceptor or transducer outputs.

Determinism

A further distinction is between deterministic (DFA) and non-deterministic (NFA, GNFA) automata. In a deterministic automaton, every state has exactly one transition for each possible input. In a non-deterministic automaton, an input can lead to one, more than one, or no transition for a given state. The powerset construction algorithm can transform any nondeterministic automaton into a (usually more complex) deterministic automaton with identical functionality.

A finite-state machine with only one state is called a "combinatorial FSM". It only allows actions upon transition into a state. This concept is useful in cases where a number of finite-state machines are required to work together, and when it is convenient to consider a purely combinatorial part as a form of FSM to suit the design tools.

Alternative semantics

There are other sets of semantics available to represent state machines. For example, there are tools for modeling and designing logic for embedded controllers. They combine hierarchical state machines (which usually have more than one current state), flow graphs, and truth tables into one language, resulting in a different formalism and set of semantics. These charts, like Harel's original state machines, support hierarchically nested states, orthogonal regions, state actions, and transition actions.

Mathematical model

In accordance with the general classification, the following formal definitions are found.

A deterministic finite-state machine or deterministic finite-state acceptor is a quintuple ${\displaystyle (\Sigma ,S,s_{0},\delta ,F)}$, where:

• ${\displaystyle \Sigma }$ is the input alphabet (a finite non-empty set of symbols);
• ${\displaystyle S}$ is a finite non-empty set of states;
• ${\displaystyle s_{0}}$ is an initial state, an element of ${\displaystyle S}$;
• ${\displaystyle \delta }$ is the state-transition function: ${\displaystyle \delta :S\times \Sigma \rightarrow S}$ (in a nondeterministic finite automaton it would be ${\displaystyle \delta :S\times \Sigma \rightarrow {\mathcal {P}}(S)}$, i.e. ${\displaystyle \delta }$ would return a set of states);
• ${\displaystyle F}$ is the set of final states, a (possibly empty) subset of ${\displaystyle S}$.

For both deterministic and non-deterministic FSMs, it is conventional to allow ${\displaystyle \delta }$ to be a partial function, i.e. ${\displaystyle \delta (s,x)}$ does not have to be defined for every combination of ${\displaystyle s\in S}$ and ${\displaystyle x\in \Sigma }$. If an FSM ${\displaystyle M}$ is in a state ${\displaystyle s}$, the next symbol is ${\displaystyle x}$ and ${\displaystyle \delta (s,x)}$ is not defined, then ${\displaystyle M}$ can announce an error (i.e. reject the input). This is useful in definitions of general state machines, but less useful when transforming the machine. Some algorithms in their default form may require total functions.

A finite-state machine has the same computational power as a Turing machine that is restricted such that its head may only perform "read" operations, and always has to move from left to right. That is, each formal language accepted by a finite-state machine is accepted by such a kind of restricted Turing machine, and vice versa.

A finite-state transducer is a sextuple ${\displaystyle (\Sigma ,\Gamma ,S,s_{0},\delta ,\omega )}$, where:

• ${\displaystyle \Sigma }$ is the input alphabet (a finite non-empty set of symbols);
• ${\displaystyle \Gamma }$ is the output alphabet (a finite non-empty set of symbols);
• ${\displaystyle S}$ is a finite non-empty set of states;
• ${\displaystyle s_{0}}$ is the initial state, an element of ${\displaystyle S}$;
• ${\displaystyle \delta }$ is the state-transition function: ${\displaystyle \delta :S\times \Sigma \rightarrow S}$;
• ${\displaystyle \omega }$ is the output function.

If the output function depends on the state and input symbol (${\displaystyle \omega :S\times \Sigma \rightarrow \Gamma }$) that definition corresponds to the Mealy model, and can be modelled as a Mealy machine. If the output function depends only on the state (${\displaystyle \omega :S\rightarrow \Gamma }$) that definition corresponds to the Moore model, and can be modelled as a Moore machine. A finite-state machine with no output function at all is known as a semiautomaton or transition system.

If we disregard the first output symbol of a Moore machine, ${\displaystyle \omega (s_{0})}$, then it can be readily converted to an output-equivalent Mealy machine by setting the output function of every Mealy transition (i.e. labeling every edge) with the output symbol given of the destination Moore state. The converse transformation is less straightforward because a Mealy machine state may have different output labels on its incoming transitions (edges). Every such state needs to be split in multiple Moore machine states, one for every incident output symbol.

Optimization

Main article: DFA minimization

Optimizing an FSM means finding a machine with the minimum number of states that performs the same function. The fastest known algorithm doing this is the Hopcroft minimization algorithm. Other techniques include using an implication table, or the Moore reduction procedure. Additionally, acyclic FSAs can be minimized in linear time.

Implementation

Hardware applications

Fig. 9 The circuit diagram for a 4-bit TTL counter, a type of state machine

In a digital circuit, an FSM may be built using a programmable logic device, a programmable logic controller, logic gates and flip flops or relays. More specifically, a hardware implementation requires a register to store state variables, a block of combinational logic that determines the state transition, and a second block of combinational logic that determines the output of an FSM. One of the classic hardware implementations is the Richards controller.

In a Medvedev machine, the output is directly connected to the state flip-flops minimizing the time delay between flip-flops and output.

Through state encoding for low power state machines may be optimized to minimize power consumption.

Software applications

The following concepts are commonly used to build software applications with finite-state machines:

• Automata-based programming
• Event-driven finite-state machine
• Virtual finite-state machine
• State design pattern

Finite-state machines and compilers

Finite automata are often used in the frontend of programming language compilers. Such a frontend may comprise several finite-state machines that implement a lexical analyzer and a parser. Starting from a sequence of characters, the lexical analyzer builds a sequence of language tokens (such as reserved words, literals, and identifiers) from which the parser builds a syntax tree. The lexical analyzer and the parser handle the regular and context-free parts of the programming language's grammar.

Chakra

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Chakra 

Sapta Chakra, an 1899 manuscript (above) illustrates the esoteric correspondence(s) between subtle energy and Tibetan psycho-physiology.

Chakras (UK: /ˈtʃʌkrəz/, US: /ˈtʃɑːkrəz/ CHUK-rəz, CHAH-krəz; Sanskrit: चक्र, romanized: cakra, lit. 'wheel, circle'; Pali: cakka) are various focal points used in a variety of ancient meditation practices, collectively denominated as Tantra, or the esoteric or inner traditions of Hinduism.

The concept of the chakra arose in the early traditions of Hinduism. Beliefs differ between the Indian religions, with many Buddhist texts consistently mentioning five chakras, while Hindu sources reference six or seven. Early Sanskrit texts speak of them both as meditative visualizations combining flowers and mantras and as physical entities in the body. Within Kundalini yoga, the techniques of breathing exercises, visualizations, mudras, bandhas, kriyas, and mantras are focused on manipulating the flow of subtle energy through chakras.

The modern Western chakra system arose from multiple sources, starting in the 1880s, followed by Sir John Woodroffe's 1919 book The Serpent Power, and Charles W. Leadbeater's 1927 book The Chakras, which introduced the Seven rainbow colours for the chakras. Psychological and other attributes, and a wide range of supposed correspondences with other systems such as alchemy, astrology, gemstones, homeopathy, Kabbalah and Tarot were added later.

Etymology

See also: Yantra and Mandala

Lexically, chakra is the Indic reflex of an ancestral Indo-European form *kʷékʷlos, whence also "wheel" and "cycle" (Ancient Greek: κύκλος, romanized: kýklos). It has both literal and metaphorical uses, as in the "wheel of time" or "wheel of dharma", such as in Rigveda hymn verse 1.164.11, pervasive in the earliest Vedic texts.

In Buddhism, especially in Theravada, the Pali noun cakka connotes "wheel". Within the central "Tripitaka", the Buddha variously refers the "dhammacakka", or "wheel of dharma", connoting that this dharma, universal in its advocacy, should bear the marks characteristic of any temporal dispensation. The Buddha spoke of freedom from cycles in and of themselves, whether karmic, reincarnative, liberative, cognitive or emotional.

In Jainism, the term chakra also means "wheel" and appears in various contexts in its ancient literature. As in other Indian religions, chakra in esoteric theories in Jainism such as those by Buddhisagarsuri means a yogic energy center.

Ancient history

See also: Yoga and Nadi (yoga)

The term chakra appears to first emerge within the Hindu Vedas, though not precisely in the sense of psychic energy centers, rather as chakravartin or the king who "turns the wheel of his empire" in all directions from a center, representing his influence and power. The iconography popular in representing the Chakras, states the scholar David Gordon White, traces back to the five symbols of yajna, the Vedic fire altar: "square, circle, triangle, half moon and dumpling".

The hymn 10.136 of the Rigveda mentions a renunciate yogi with a female named kunamnama. Literally, it means "she who is bent, coiled", representing both a minor goddess and one of many embedded enigmas and esoteric riddles within the Rigveda. Some scholars, such as D.G. White and Georg Feuerstein, have suggested that she may be a reference to kundalini shakti and a precursor to the terminology associated with the chakras in later tantric traditions.

Breath channels (nāḍi) are mentioned in the classical Upanishads of Hinduism from the 1st millennium BCE, but not psychic-energy chakra theories. Three classical Nadis are Ida, Pingala and Sushumna in which the central channel Sushumna is said to be foremost as per Kṣurikā-Upaniṣhad. The latter, states David Gordon White, were introduced about 8th-century CE in Buddhist texts as hierarchies of inner energy centers, such as in the Hevajra Tantra and Caryāgiti. These are called by various terms such as cakka, padma (lotus) or pitha (mound). These medieval Buddhist texts mention only four chakras, while later Hindu texts such as the Kubjikāmata and Kaulajñānanirnaya expanded the list to many more.

In contrast to White, according to Feuerstein, early Upanishads of Hinduism do mention chakras in the sense of "psychospiritual vortices", along with other terms found in tantra: prana or vayu (life energy) along with nadi (energy carrying arteries). According to Gavin Flood, the ancient texts do not present chakra and kundalini-style yoga theories although these words appear in the earliest Vedic literature in many contexts. The chakra in the sense of four or more vital energy centers appear in the medieval era Hindu and Buddhist texts.

Overview

An illustration of a Saiva Nath chakra system, folio 2 from the Nath Charit, 1823. Mehrangarh Museum Trust.

Chakra and divine energies

Shining, she holds
the noose made of the energy of will,
the hook which is energy of knowledge,
the bow and arrows made of energy of action.
Split into support and supported,
divided into eight, bearer of weapons,
arising from the chakra with eight points,
she has the ninefold chakra as a throne.

—Yoginihrdaya 53–54
(Translator: Andre Padoux)

The Chakras are part of esoteric medieval-era beliefs about physiology and psychic centers that emerged across Indian traditions. The belief held that human life simultaneously exists in two parallel dimensions, one "physical body" (sthula sarira) and other "psychological, emotional, mind, non-physical" it is called the "subtle body" (sukshma sarira). This subtle body is energy, while the physical body is mass. The psyche or mind plane corresponds to and interacts with the body plane, and the belief holds that the body and the mind mutually affect each other. The subtle body consists of nadi (energy channels) connected by nodes of psychic energy called chakra. The belief grew into extensive elaboration, with some suggesting 88,000 chakras throughout the subtle body. The number of major chakras varied between various traditions, but they typically ranged between four and seven. Nyingmapa Vajrayana Buddhist teachings mention eight chakras and there is a complete yogic system for each of them.

The important chakras are stated in Hindu and Buddhist texts to be arranged in a column along the spinal cord, from its base to the top of the head, connected by vertical channels. The tantric traditions sought to master them, awaken and energize them through various breathing exercises or with assistance of a teacher. These chakras were also symbolically mapped to specific human physiological capacity, seed syllables (bija), sounds, subtle elements (tanmatra), in some cases deities, colors and other motifs.

Belief in the chakra system of Hinduism and Buddhism differs from the historic Chinese system of meridians in acupuncture. Unlike the latter, the chakra relates to subtle body, wherein it has a position but no definite nervous node or precise physical connection. The tantric systems envision it as continually present, highly relevant and a means to psychic and emotional energy. It is useful in a type of yogic rituals and meditative discovery of radiant inner energy (prana flows) and mind-body connections. The meditation is aided by extensive symbology, mantras, diagrams, models (deity and mandala). The practitioner proceeds step by step from perceptible models, to increasingly abstract models where deity and external mandala are abandoned, inner self and internal mandalas are awakened.

These ideas are not unique to Hindu and Buddhist traditions. Similar and overlapping concepts emerged in other cultures in the East and the West, and these are variously called by other names such as subtle body, spirit body, esoteric anatomy, sidereal body and etheric body. According to Geoffrey Samuel and Jay Johnston, professors of Religious studies known for their studies on Yoga and esoteric traditions:

Ideas and practices involving so-called 'subtle bodies' have existed for many centuries in many parts of the world. (...) Virtually all human cultures known to us have some kind of concept of mind, spirit or soul as distinct from the physical body, if only to explain experiences such as sleep and dreaming. (...) An important subset of subtle-body practices, found particularly in Indian and Tibetan Tantric traditions, and in similar Chinese practices, involves the idea of an internal 'subtle physiology' of the body (or rather of the body-mind complex) made up of channels through which substances of some kind flow, and points of intersection at which these channels come together. In the Indian tradition the channels are known as nadi and the points of intersection as cakra.

— Geoffrey Samuel and Jay Johnston, Religion and the Subtle Body in Asia and the West: Between Mind and Body

Contrast with classical yoga

Chakra and related beliefs have been important to the esoteric traditions, but they are not directly related to mainstream yoga. According to the Indologist Edwin Bryant and other scholars, the goals of classical yoga such as spiritual liberation (freedom, self-knowledge, moksha) is "attained entirely differently in classical yoga, and the cakra / nadi / kundalini physiology is completely peripheral to it."

Classical traditions

In meditation, chakras are often visualised in different ways, such as a lotus flower, or a disc containing a particular deity.

The classical eastern traditions, particularly those that developed in India during the 1st millennium AD, primarily describe nadi and chakra in a "subtle body" context. To them, they are in same dimension as of the psyche-mind reality that is invisible yet real. In the nadi and cakra flow the prana (breath, life energy). The concept of "life energy" varies between the texts, ranging from simple inhalation-exhalation to far more complex association with breath-mind-emotions-sexual energy. This prana or essence is what vanishes when a person dies, leaving a gross body. Some of this concept states this subtle body is what withdraws within, when one sleeps. All of it is believed to be reachable, awake-able and important for an individual's body-mind health, and how one relates to other people in one's life. This subtle body network of nadi and chakra is, according to some later Indian theories and many new age speculations, closely associated with emotions.

Hindu Tantra

Main article: Kundalini energy

Esoteric traditions in Hinduism mention numerous numbers and arrangements of chakras, of which a classical system of six-plus-one, the last being the Sahasrara, is most prevalent. This seven-part system, central to the core texts of hatha yoga, is one among many systems found in Hindu tantric literature. Hindu Tantra associates six Yoginis with six places in the subtle body, corresponding to the six chakras of the six-plus-one system.

Association of six Yoginis with chakra locations in the Rudrayamala Tantra

Place in subtle body	Yogini
1. Muladhara	Dakini
2. Svadhisthana	Rakini
3. Manipura	Lakini
4. Anahata	Kakini
5. Vishuddhi	Shakini
6. Ajna	Hakini

The Chakra methodology is extensively developed in the goddess tradition of Hinduism called Shaktism. It is an important concept along with yantras, mandalas and kundalini yoga in its practice. Chakra in Shakta tantrism means circle, an "energy center" within, as well as being a term for group rituals such as in chakra-puja (worship within a circle) which may or may not involve tantra practice. The cakra-based system is a part of the meditative exercises that came to be known as yoga.

Buddhist Tantra

Main article: Vajrayana

 

A Tibetan illustration of the subtle body showing the central channel and two side channels as well as five chakras.

 

A Tibetan thangka with a diagram showing six chakras—a root chakra, a chakra at the sex organs, one at the navel, one at the heart, another at the throat and the last one located at the crown.

The esoteric traditions in Buddhism generally teach four chakras. In some early Buddhist sources, these chakras are identified as: manipura (navel), anahata (heart), vishuddha (throat) and ushnisha kamala (crown). In one development within the Nyingma lineage of the Mantrayana of Tibetan Buddhism a popular conceptualization of chakras in increasing subtlety and increasing order is as follows: Nirmanakaya (gross self), Sambhogakaya (subtle self), Dharmakaya (causal self), and Mahasukhakaya (non-dual self), each vaguely and indirectly corresponding to the categories within the Shaiva Mantramarga universe, i.e., Svadhisthana, Anahata, Visuddha, Sahasrara, etc. However, depending on the meditational tradition, these vary between three and six. The chakras are considered psycho-spiritual constituents, each bearing meaningful correspondences to cosmic processes and their postulated Buddha counterpart.

A system of five chakras is common among the Mother class of Tantras and these five chakras along with their correspondences are:

• Basal chakra (Element: Earth, Buddha: Amoghasiddhi, Bija mantra: LAM)
• Abdominal chakra (Element: Water, Buddha: Ratnasambhava, Bija mantra: VAM)
• Heart chakra (Element: Fire, Buddha: Akshobhya, Bija mantra: RAM)
• Throat chakra (Element: Wind, Buddha: Amitabha, Bija mantra: YAM)
• Crown chakra (Element: Space, Buddha: Vairochana, Bija mantra: KHAM)

Chakras clearly play a key role in Tibetan Buddhism, and are considered to be the pivotal providence of Tantric thinking. And, the precise use of the chakras across the gamut of tantric sadhanas gives little space to doubt the primary efficacy of Tibetan Buddhism as distinct religious agency, that being that precise revelation that, without Tantra there would be no Chakras, but more importantly, without Chakras, there is no Tibetan Buddhism. The highest practices in Tibetan Buddhism point to the ability to bring the subtle pranas of an entity into alignment with the central channel, and to thus penetrate the realisation of the ultimate unity, namely, the "organic harmony" of one's individual consciousness of Wisdom with the co-attainment of All-embracing Love, thus synthesizing a direct cognition of absolute Buddhahood.

According to Samuel, the buddhist esoteric systems developed cakra and nadi as "central to their soteriological process". The theories were sometimes, but not always, coupled with a unique system of physical exercises, called yantra yoga or 'phrul 'khor.

Chakras, according to the Bon tradition, enable the gestalt of experience, with each of the five major chakras, being psychologically linked with the five experiential qualities of unenlightened consciousness, the six realms of woe.

The tsa lung practice embodied in the Trul khor lineage, unbaffles the primary channels, thus activating and circulating liberating prana. Yoga awakens the deep mind, thus bringing forth positive attributes, inherent gestalts, and virtuous qualities. In a computer analogy, the screen of one's consciousness is slated and an attribute-bearing file is called up that contains necessary positive or negative, supportive qualities.

Tantric practice is said to eventually transform all experience into clear light. The practice aims to liberate from all negative conditioning, and the deep cognitive salvation of freedom from control and unity of perception and cognition.

The seven chakra system

One widely popular schema of seven chakras is as follows, from bottom to top: 1. Muladhara 2. Svadhisthana 3. Nabhi-Manipura 4. Anahata 5. Vishuddhi 6. Ajna 7. Sahasrara. The colours are modern.

The more common and most studied chakra system incorporates six major chakras along with a seventh center generally not regarded as a chakra. These points are arranged vertically along the axial channel (sushumna nadi in Hindu texts, Avadhuti in some Buddhist texts). According to Gavin Flood, this system of six chakras plus the sahasrara "center" at the crown first appears in the Kubjikāmata-tantra, an 11th-century Kaula work.

It was this chakra system that was translated in the early 20th century by Sir John Woodroffe (also called Arthur Avalon) in the text The Serpent Power. Avalon translated the Hindu text Ṣaṭ-Cakra-Nirūpaṇa meaning the examination (nirūpaṇa) of the seven (ṣaṭ) chakras (cakra).

The Chakras are traditionally considered meditation aids. The yogi progresses from lower chakras to the highest chakra blossoming in the crown of the head, internalizing the journey of spiritual ascent. In both the Hindu kundalini and Buddhist candali traditions, the chakras are pierced by a dormant energy residing near or in the lowest chakra. In Hindu texts she is known as Kundalini, while in Buddhist texts she is called Candali or Tummo (Tibetan: gtum mo, "fierce one").

Below are the common new age description of these six chakras and the seventh point known as sahasrara. This new age version incorporates the Newtonian colors of the rainbow not found in any ancient Indian system.

Image of chakra	Name	Sanskrit (Translation)	Location	No. of petals	Modern colour	Seed syllable	Description
	Sahasrara	सहस्रार "Thousand-petaled"	Crown	1000	Multi or violet	—	Highest spiritual centre, pure consciousness, containing neither object nor subject. When the feminine Kundalini Shakti rises to this point, it unites with the masculine Shiva, giving self-realization and samadhi. In esoteric Buddhism, it is called Mahasukha, the petal lotus of "Great Bliss" corresponding to the fourth state of Four Noble Truths.
	Ajna or Agya	आज्ञा "Command"	Between eyebrows	2	Indigo	—	Guru chakra, or in New Age usage third-eye chakra, the subtle center of energy, where the tantra guru touches the seeker during the initiation ritual. He or she commands the awakened kundalini to pass through this centre.
	Vishuddha	विशुद्ध "Purest"	Throat	16	Blue	Ham (space)	16 petals covered with the sixteen Sanskrit vowels. Associated with the element of space (akasha). The residing deity is Panchavaktra shiva, with 5 heads and 4 arms, and the Shakti is Shakini. In esoteric Buddhism, it is called Sambhoga and is generally considered to be the petal lotus of "Enjoyment" corresponding to the third state of Four Noble Truths.
	Anahata	अनाहत "Unstruck"	Heart	12	Green	Yam (air)	Within it is a yantra of two intersecting triangles, forming a hexagram, symbolising a union of the male and female, and the element of air (vayu). The presiding deity is Ishana Rudra Shiva, and the Shakti is Kakini. In esoteric Buddhism, this Chakra is called Dharma and is generally considered to be the petal lotus of "Essential nature" and corresponding to the second state of Four Noble Truths.
	Manipura	मणिपूर "Jewel city"	Navel	10	Yellow	Ram (fire)	For the Nath yogi meditation system, this is described as the Madhyama-Shakti or the intermediate stage of self-discovery. This chakra is represented as a downward pointing triangle representing fire in the middle of a lotus with ten petals. The presiding deity is Braddha Rudra, with Lakini as the Shakti.
	Svadhishthana	स्वाधिष्ठान "Where the self is established"	Root of sexual organs	6	Orange	Vam (water)	Svadhisthana is represented with a lotus within which is a crescent moon symbolizing the water element. The presiding deity is Brahma, with the Shakti being Rakini (or Chakini). In esoteric Buddhism, it is called Nirmana, the petal lotus of "Creation" and corresponding to the first state of Four Noble Truths.
	Muladhara	मूलाधार "Root"	Base of spine	4	Red	Lam (earth)	Dormant Kundalini is often said to be resting here, wrapped three and a half, or seven or twelve times. Sometimes she is wrapped around the black Svayambhu linga, the lowest of three obstructions to her full rising (also known as knots or granthis). It is symbolised as a four-petaled lotus with a yellow square at its center representing the element of earth. The seed syllable is Lam for the earth element. All sounds, words and mantras in their dormant form rest in the muladhara chakra, where Ganesha resides, while the Shakti is Dakini. The associated animal is the elephant.

Western chakra system

Main article: Esotericism

History

Chakra positions in supposed relation to nervous plexuses, from Charles W. Leadbeater's 1927 book The Chakras

Kurt Leland, for the Theosophical Society in America, concluded that the western chakra system was produced by an "unintentional collaboration" of many groups of people: esotericists and clairvoyants, often theosophical; Indologists; the scholar of myth, Joseph Campbell; the founders of the Esalen Institute and the psychological tradition of Carl Jung; the colour system of Charles W. Leadbeater's 1927 book The Chakras, treated as traditional lore by some modern Indian yogis; and energy healers such as Barbara Brennan. Leland states that far from being traditional, the two main elements of the modern system, the rainbow colours and the list of qualities, first appeared together only in 1977.

The concept of a set of seven chakras came to the West in the 1880s; at that time each chakra was associated with a nerve plexus. In 1918, Sir John Woodroffe, alias Arthur Avalon, translated two Indian texts, the Ṣaṭ-Cakra-Nirūpaṇa and the Pādukā-Pañcaka, and in his book The Serpent Power drew Western attention to the seven chakra theory.

In the 1920s, each of the seven chakras was associated with an endocrine gland, a tradition that has persisted. More recently, the lower six chakras have been linked to both nerve plexuses and glands. The seven rainbow colours were added by Leadbeater in 1927; a variant system in the 1930s proposed six colours plus white. Leadbeater's theory was influenced by Johann Georg Gichtel's 1696 book Theosophia Practica, which mentioned inner "force centres".

Psychological and other attributes such as layers of the aura, developmental stages, associated diseases, Aristotelian elements, emotions, and states of consciousness were added still later. A wide range of supposed correspondences such as with alchemical metals, astrological signs and planets, foods, herbs, gemstones, homeopathic remedies, Kabbalistic spheres, musical notes, totem animals, and Tarot cards have also been proposed.

New Age

Further information: New Age

In Anatomy of the Spirit (1996), Caroline Myss described the function of chakras as follows: "Every thought and experience you've ever had in your life gets filtered through these chakra databases. Each event is recorded into your cells...". The chakras are described as being aligned in an ascending column from the base of the spine to the top of the head. New Age practices often associate each chakra with a certain colour. In various traditions, chakras are associated with multiple physiological functions, an aspect of consciousness, a classical element, and other distinguishing characteristics; these do not correspond to those used in ancient Indian systems. The chakras are visualised as lotuses or flowers with a different number of petals in every chakra.

The chakras are thought to vitalise the physical body and to be associated with interactions of a physical, emotional and mental nature. They are considered loci of life energy or prana (which New Age belief equates with shakti, qi in Chinese, ki in Japanese, koach-ha-guf in Hebrew, bios in Greek, and aether in both Greek and English), which is thought to flow among them along pathways called nadi. The function of the chakras is to spin and draw in this energy to keep the spiritual, mental, emotional and physical health of the body in balance.

Rudolf Steiner considered the chakra system to be dynamic and evolving. He suggested that this system has become different for modern people than it was in ancient times and that it will, in turn, be radically different in future times. Steiner described a sequence of development that begins with the upper chakras and moves down, rather than moving in the opposite direction. He gave suggestions on how to develop the chakras through disciplining thoughts, feelings, and will. According to Florin Lowndes, a "spiritual student" can further develop and deepen or elevate thinking consciousness when taking the step from the "ancient path" of schooling to the "new path" represented by Steiner's The Philosophy of Freedom.

Skeptical response

Further information: Scientific skepticism

The not-for-profit Edinburgh Skeptics Society states that despite their popularity, "there has never been any evidence for these meridian lines or chakras". It adds that while practitioners sometimes cite "scientific evidence" for their claims, such evidence is often "incredibly shaky".

Physiology

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Physiology 

Oil painting depicting Claude Bernard, the father of modern physiology, with his pupils

Physiology (/ˌfɪziˈɒlədʒi/; from Ancient Greek φύσις (phúsis) 'nature, origin', and -λογία (-logía) 'study of') is the scientific study of functions and mechanisms in a living system. As a sub-discipline of biology, physiology focuses on how organisms, organ systems, individual organs, cells, and biomolecules carry out the chemical and physical functions in a living system. According to the classes of organisms, the field can be divided into medical physiology, animal physiology, plant physiology, cell physiology, and comparative physiology.

Central to physiological functioning are biophysical and biochemical processes, homeostatic control mechanisms, and communication between cells. Physiological state is the condition of normal function, while pathological state refers to abnormal conditions, including human diseases.

The Nobel Prize in Physiology or Medicine is awarded by the Royal Swedish Academy of Sciences for exceptional scientific achievements in physiology related to the field of medicine.

Foundations

Cells

Main article: Cell physiology

Although there are differences between animal, plant, and microbial cells, the basic physiological functions of cells can be divided into the processes of cell division, cell signaling, cell growth, and cell metabolism.

Plants

Main article: Plant physiology

Plant physiology is a subdiscipline of botany concerned with the functioning of plants. Closely related fields include plant morphology, plant ecology, phytochemistry, cell biology, genetics, biophysics, and molecular biology. Fundamental processes of plant physiology include photosynthesis, respiration, plant nutrition, tropisms, nastic movements, photoperiodism, photomorphogenesis, circadian rhythms, seed germination, dormancy, and stomata function and transpiration. Absorption of water by roots, production of food in the leaves, and growth of shoots towards light are examples of plant physiology.

Animals

Main article: Biology § Animal form and function

Humans

Main article: Human body § Physiology

Human physiology seeks to understand the mechanisms that work to keep the human body alive and functioning, through scientific enquiry into the nature of mechanical, physical, and biochemical functions of humans, their organs, and the cells of which they are composed. The principal level of focus of physiology is at the level of organs and systems within systems. The endocrine and nervous systems play major roles in the reception and transmission of signals that integrate function in animals. Homeostasis is a major aspect with regard to such interactions within plants as well as animals. The biological basis of the study of physiology, integration refers to the overlap of many functions of the systems of the human body, as well as its accompanied form. It is achieved through communication that occurs in a variety of ways, both electrical and chemical.

Changes in physiology can impact the mental functions of individuals. Examples of this would be the effects of certain medications or toxic levels of substances. Change in behavior as a result of these substances is often used to assess the health of individuals.

Much of the foundation of knowledge in human physiology was provided by animal experimentation. Due to the frequent connection between form and function, physiology and anatomy are intrinsically linked and are studied in tandem as part of a medical curriculum.

Comparative physiology

Main article: Comparative physiology

Involving evolutionary physiology and environmental physiology, comparative physiology considers the diversity of functional characteristics across organisms.

History

The classical era

The study of human physiology as a medical field originates in classical Greece, at the time of Hippocrates (late 5th century BC). Outside of Western tradition, early forms of physiology or anatomy can be reconstructed as having been present at around the same time in China, India and elsewhere. Hippocrates incorporated the theory of humorism, which consisted of four basic substances: earth, water, air and fire. Each substance is known for having a corresponding humor: black bile, phlegm, blood, and yellow bile, respectively. Hippocrates also noted some emotional connections to the four humors, on which Galen would later expand. The critical thinking of Aristotle and his emphasis on the relationship between structure and function marked the beginning of physiology in Ancient Greece. Like Hippocrates, Aristotle took to the humoral theory of disease, which also consisted of four primary qualities in life: hot, cold, wet and dry. Galen (c. 130–200 AD) was the first to use experiments to probe the functions of the body. Unlike Hippocrates, Galen argued that humoral imbalances can be located in specific organs, including the entire body. His modification of this theory better equipped doctors to make more precise diagnoses. Galen also played off of Hippocrates' idea that emotions were also tied to the humors, and added the notion of temperaments: sanguine corresponds with blood; phlegmatic is tied to phlegm; yellow bile is connected to choleric; and black bile corresponds with melancholy. Galen also saw the human body consisting of three connected systems: the brain and nerves, which are responsible for thoughts and sensations; the heart and arteries, which give life; and the liver and veins, which can be attributed to nutrition and growth. Galen was also the founder of experimental physiology. And for the next 1,400 years, Galenic physiology was a powerful and influential tool in medicine.

Early modern period

Jean Fernel (1497–1558), a French physician, introduced the term "physiology". Galen, Ibn al-Nafis, Michael Servetus, Realdo Colombo, Amato Lusitano and William Harvey, are credited as making important discoveries in the circulation of the blood.^[20] Santorio Santorio in 1610s was the first to use a device to measure the pulse rate (the pulsilogium), and a thermoscope to measure temperature.

In 1791 Luigi Galvani described the role of electricity in nerves of dissected frogs. In 1811, César Julien Jean Legallois studied respiration in animal dissection and lesions and found the center of respiration in the medulla oblongata. In the same year, Charles Bell finished work on what would later become known as the Bell-Magendie law, which compared functional differences between dorsal and ventral roots of the spinal cord. In 1824, François Magendie described the sensory roots and produced the first evidence of the cerebellum's role in equilibration to complete the Bell-Magendie law.

In the 1820s, the French physiologist Henri Milne-Edwards introduced the notion of physiological division of labor, which allowed to "compare and study living things as if they were machines created by the industry of man." Inspired in the work of Adam Smith, Milne-Edwards wrote that the "body of all living beings, whether animal or plant, resembles a factory ... where the organs, comparable to workers, work incessantly to produce the phenomena that constitute the life of the individual." In more differentiated organisms, the functional labor could be apportioned between different instruments or systems (called by him as appareils).

In 1858, Joseph Lister studied the cause of blood coagulation and inflammation that resulted after previous injuries and surgical wounds. He later discovered and implemented antiseptics in the operating room, and as a result, decreased death rate from surgery by a substantial amount.

The Physiological Society was founded in London in 1876 as a dining club. The American Physiological Society (APS) is a nonprofit organization that was founded in 1887. The Society is, "devoted to fostering education, scientific research, and dissemination of information in the physiological sciences."

In 1891, Ivan Pavlov performed research on "conditional responses" that involved dogs' saliva production in response to a bell and visual stimuli.

In the 19th century, physiological knowledge began to accumulate at a rapid rate, in particular with the 1838 appearance of the Cell theory of Matthias Schleiden and Theodor Schwann. It radically stated that organisms are made up of units called cells. Claude Bernard's (1813–1878) further discoveries ultimately led to his concept of milieu interieur (internal environment), which would later be taken up and championed as "homeostasis" by American physiologist Walter B. Cannon in 1929. By homeostasis, Cannon meant "the maintenance of steady states in the body and the physiological processes through which they are regulated." In other words, the body's ability to regulate its internal environment. William Beaumont was the first American to utilize the practical application of physiology.

Nineteenth-century physiologists such as Michael Foster, Max Verworn, and Alfred Binet, based on Haeckel's ideas, elaborated what came to be called "general physiology", a unified science of life based on the cell actions, later renamed in the 20th century as cell biology.

Late modern period

In the 20th century, biologists became interested in how organisms other than human beings function, eventually spawning the fields of comparative physiology and ecophysiology. Major figures in these fields include Knut Schmidt-Nielsen and George Bartholomew. Most recently, evolutionary physiology has become a distinct subdiscipline.

In 1920, August Krogh won the Nobel Prize for discovering how, in capillaries, blood flow is regulated.

In 1954, Andrew Huxley and Hugh Huxley, alongside their research team, discovered the sliding filaments in skeletal muscle, known today as the sliding filament theory.

Recently, there have been intense debates about the vitality of physiology as a discipline (Is it dead or alive?). If physiology is perhaps less visible nowadays than during the golden age of the 19th century, it is in large part because the field has given birth to some of the most active domains of today's biological sciences, such as neuroscience, endocrinology, and immunology. Furthermore, physiology is still often seen as an integrative discipline, which can put together into a coherent framework data coming from various different domains.

Notable physiologists

Main article: List of physiologists

Women in physiology

Initially, women were largely excluded from official involvement in any physiological society. The American Physiological Society, for example, was founded in 1887 and included only men in its ranks. In 1902, the American Physiological Society elected Ida Hyde as the first female member of the society. Hyde, a representative of the American Association of University Women and a global advocate for gender equality in education, attempted to promote gender equality in every aspect of science and medicine.

Soon thereafter, in 1913, J.S. Haldane proposed that women be allowed to formally join The Physiological Society, which had been founded in 1876. On 3 July 1915, six women were officially admitted: Florence Buchanan, Winifred Cullis, Ruth C. Skelton, Sarah C. M. Sowton, Constance Leetham Terry, and Enid M. Tribe. The centenary of the election of women was celebrated in 2015 with the publication of the book "Women Physiologists: Centenary Celebrations And Beyond For The Physiological Society." (ISBN 978-0-9933410-0-7)

Prominent women physiologists include:

• Bodil Schmidt-Nielsen, the first woman president of the American Physiological Society in 1975.
• Gerty Cori, along with husband Carl Cori, received the Nobel Prize in Physiology or Medicine in 1947 for their discovery of the phosphate-containing form of glucose known as glycogen, as well as its function within eukaryotic metabolic mechanisms for energy production. Moreover, they discovered the Cori cycle, also known as the Lactic acid cycle, which describes how muscle tissue converts glycogen into lactic acid via lactic acid fermentation.
• Barbara McClintock was rewarded the 1983 Nobel Prize in Physiology or Medicine for the discovery of genetic transposition. McClintock is the only female recipient who has won an unshared Nobel Prize.
• Gertrude Elion, along with George Hitchings and Sir James Black, received the Nobel Prize for Physiology or Medicine in 1988 for their development of drugs employed in the treatment of several major diseases, such as leukemia, some autoimmune disorders, gout, malaria, and viral herpes.
• Linda B. Buck, along with Richard Axel, received the Nobel Prize in Physiology or Medicine in 2004 for their discovery of odorant receptors and the complex organization of the olfactory system.
• Françoise Barré-Sinoussi, along with Luc Montagnier, received the Nobel Prize in Physiology or Medicine in 2008 for their work on the identification of the Human Immunodeficiency Virus (HIV), the cause of Acquired Immunodeficiency Syndrome (AIDS).
• Elizabeth Blackburn, along with Carol W. Greider and Jack W. Szostak, was awarded the 2009 Nobel Prize for Physiology or Medicine for the discovery of the genetic composition and function of telomeres and the enzyme called telomerase.

Subdisciplines

There are many ways to categorize the subdisciplines of physiology:

• based on the taxa studied: human physiology, animal physiology, plant physiology, microbial physiology, viral physiology
• based on the level of organization: cell physiology, molecular physiology, systems physiology, organismal physiology, ecological physiology, integrative physiology
• based on the process that causes physiological variation: developmental physiology, environmental physiology, evolutionary physiology
• based on the ultimate goals of the research: applied physiology (e.g., medical physiology), non-applied (e.g., comparative physiology)

Physiological societies

Transnational physiological societies include:

• American Physiological Society
• International Union of Physiological Sciences
• The Physiological Society

National physiological societies include:

• Brazilian Society of Physiology