Factorial

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Factorial

Selected factorials; values in scientific notation are rounded

${\displaystyle n}$	${\displaystyle n!}$
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	1.551121004×1025
50	3.041409320×1064
70	1.197857167×10100
100	9.332621544×10157
450	1.733368733×101000
1000	4.023872601×102567
3249	6.412337688×1010000
10000	2.846259681×1035659
25206	1.205703438×10100000
100000	2.824229408×10456573
205023	2.503898932×101000004
1000000	8.263931688×105565708
10100	1010101.9981097754820

In mathematics, the factorial of a non-negative integer ${\displaystyle n}$, denoted by ${\displaystyle n!}$, is the product of all positive integers less than or equal to ${\displaystyle n}$. The factorial of ${\displaystyle n}$ also equals the product of ${\displaystyle n}$ with the next smaller factorial:

$${\displaystyle {\begin{aligned}n!&=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 3\times 2\times 1\\&=n\times (n-1)!\\\end{aligned}}}$$

For example,

$${\displaystyle 5!=5\times 4\times 3\times 2\times 1=5\times 24=120.}$$

The value of 0! is 1, according to the convention for an empty product.

Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book Sefer Yetzirah. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of ${\displaystyle n}$ distinct objects: there are ${\displaystyle n!}$. In mathematical analysis, factorials are used in power series for the exponential function and other functions, and they also have applications in algebra, number theory, probability theory, and computer science.

Much of the mathematics of the factorial function was developed beginning in the late 18th and early 19th centuries. Stirling's approximation provides an accurate approximation to the factorial of large numbers, showing that it grows more quickly than exponential growth. Legendre's formula describes the exponents of the prime numbers in a prime factorization of the factorials, and can be used to count the trailing zeros of the factorials. Daniel Bernoulli and Leonhard Euler interpolated the factorial function to a continuous function of complex numbers, except at the negative integers, the (offset) gamma function.

Many other notable functions and number sequences are closely related to the factorials, including the binomial coefficients, double factorials, falling factorials, primorials, and subfactorials. Implementations of the factorial function are commonly used as an example of different computer programming styles, and are included in scientific calculators and scientific computing software libraries. Although directly computing large factorials using the product formula or recurrence is not efficient, faster algorithms are known, matching to within a constant factor the time for fast multiplication algorithms for numbers with the same number of digits.

History

The concept of factorials has arisen independently in many cultures:

• In Indian mathematics, one of the earliest known descriptions of factorials comes from the Anuyogadvāra-sūtra, one of the canonical works of Jain literature, which has been assigned dates varying from 300 BCE to 400 CE. It separates out the sorted and reversed order of a set of items from the other ("mixed") orders, evaluating the number of mixed orders by subtracting two from the usual product formula for the factorial. The product rule for permutations was also described by 6th-century CE Jain monk Jinabhadra. Hindu scholars have been using factorial formulas since at least 1150, when Bhāskara II mentioned factorials in his work Līlāvatī, in connection with a problem of how many ways Vishnu could hold his four characteristic objects (a conch shell, discus, mace, and lotus flower) in his four hands, and a similar problem for a ten-handed god.
• In the mathematics of the Middle East, the Hebrew mystic book of creation Sefer Yetzirah, from the Talmudic period (200 to 500 CE), lists factorials up to 7! as part of an investigation into the number of words that can be formed from the Hebrew alphabet. Factorials were also studied for similar reasons by 8th-century Arab grammarian Al-Khalil ibn Ahmad al-Farahidi. Arab mathematician Ibn al-Haytham (also known as Alhazen, c. 965 – c. 1040) was the first to formulate Wilson's theorem connecting the factorials with the prime numbers.
• In Europe, although Greek mathematics included some combinatorics, and Plato famously used 5040 (a factorial) as the population of an ideal community, in part because of its divisibility properties, there is no direct evidence of ancient Greek study of factorials. Instead, the first work on factorials in Europe was by Jewish scholars such as Shabbethai Donnolo, explicating the Sefer Yetzirah passage. In 1677, British author Fabian Stedman described the application of factorials to change ringing, a musical art involving the ringing of several tuned bells.

From the late 15th century onward, factorials became the subject of study by western mathematicians. In a 1494 treatise, Italian mathematician Luca Pacioli calculated factorials up to 11!, in connection with a problem of dining table arrangements. Christopher Clavius discussed factorials in a 1603 commentary on the work of Johannes de Sacrobosco, and in the 1640s, French polymath Marin Mersenne published large (but not entirely correct) tables of factorials, up to 64!, based on the work of Clavius. The power series for the exponential function, with the reciprocals of factorials for its coefficients, was first formulated in 1676 by Isaac Newton in a letter to Gottfried Wilhelm Leibniz. Other important works of early European mathematics on factorials include extensive coverage in a 1685 treatise by John Wallis, a study of their approximate values for large values of ${\displaystyle n}$ by Abraham de Moivre in 1721, a 1729 letter from James Stirling to de Moivre stating what became known as Stirling's approximation, and work at the same time by Daniel Bernoulli and Leonhard Euler formulating the continuous extension of the factorial function to the gamma function. Adrien-Marie Legendre included Legendre's formula, describing the exponents in the factorization of factorials into prime powers, in an 1808 text on number theory.

The notation ${\displaystyle n!}$ for factorials was introduced by the French mathematician Christian Kramp in 1808. Many other notations have also been used. Another later notation, in which the argument of the factorial was half-enclosed by the left and bottom sides of a box, was popular for some time in Britain and America but fell out of use, perhaps because it is difficult to typeset. The word "factorial" (originally French: factorielle) was first used in 1800 by Louis François Antoine Arbogast, in the first work on Faà di Bruno's formula, but referring to a more general concept of products of arithmetic progressions. The "factors" that this name refers to are the terms of the product formula for the factorial.

Definition

The factorial function of a positive integer ${\displaystyle n}$ is defined by the product of all positive integers not greater than ${\displaystyle n}$

$${\displaystyle n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n.}$$

This may be written more concisely in product notation as

$${\displaystyle n!=\prod _{i=1}^{n}i.}$$

If this product formula is changed to keep all but the last term, it would define a product of the same form, for a smaller factorial. This leads to a recurrence relation, according to which each value of the factorial function can be obtained by multiplying the previous value by ${\displaystyle n}$:

$${\displaystyle n!=n\cdot (n-1)!.}$$

For example, ${\displaystyle 5!=5\cdot 4!=5\cdot 24=120}$.

Factorial of zero

The factorial of ${\displaystyle 0}$ is ${\displaystyle 1}$, or in symbols, ${\displaystyle 0!=1}$. There are several motivations for this definition:

• For ${\displaystyle n=0}$, the definition of ${\displaystyle n!}$ as a product involves the product of no numbers at all, and so is an example of the broader convention that the empty product, a product of no factors, is equal to the multiplicative identity.
• There is exactly one permutation of zero objects: with nothing to permute, the only rearrangement is to do nothing.
• This convention makes many identities in combinatorics valid for all valid choices of their parameters. For instance, the number of ways to choose all ${\displaystyle n}$ elements from a set of ${\displaystyle n}$ is ${\textstyle {\tbinom {n}{n}}={\tfrac {n!}{n!0!}}=1,}$ a binomial coefficient identity that would only be valid with ${\displaystyle 0!=1}$.
• With ${\displaystyle 0!=1}$, the recurrence relation for the factorial remains valid at ${\displaystyle n=1}$. Therefore, with this convention, a recursive computation of the factorial needs to have only the value for zero as a base case, simplifying the computation and avoiding the need for additional special cases.
• Setting ${\displaystyle 0!=1}$ allows for the compact expression of many formulae, such as the exponential function, as a power series: ${\textstyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$
• This choice matches the gamma function ${\displaystyle 0!=\Gamma (0+1)=1}$, and the gamma function must have this value to be a continuous function.

Applications

The earliest uses of the factorial function involve counting permutations: there are ${\displaystyle n!}$ different ways of arranging ${\displaystyle n}$ distinct objects into a sequence. Factorials appear more broadly in many formulas in combinatorics, to account for different orderings of objects. For instance the binomial coefficients ${\displaystyle {\tbinom {n}{k}}}$ count the ${\displaystyle k}$-element combinations (subsets of ${\displaystyle k}$ elements) from a set with ${\displaystyle n}$ elements, and can be computed from factorials using the formula

$${\displaystyle {\binom {n}{k}}={\frac {n!}{k!(n-k)!}}.}$$

The Stirling numbers of the first kind sum to the factorials, and count the permutations of ${\displaystyle n}$ grouped into subsets with the same numbers of cycles. Another combinatorial application is in counting derangements, permutations that do not leave any element in its original position; the number of derangements of ${\displaystyle n}$ items is the nearest integer to ${\displaystyle n!/e}$.

In algebra, the factorials arise through the binomial theorem, which uses binomial coefficients to expand powers of sums. They also occur in the coefficients used to relate certain families of polynomials to each other, for instance in Newton's identities for symmetric polynomials. Their use in counting permutations can also be restated algebraically: the factorials are the orders of finite symmetric groups. In calculus, factorials occur in Faà di Bruno's formula for chaining higher derivatives. In mathematical analysis, factorials frequently appear in the denominators of power series, most notably in the series for the exponential function,

$${\displaystyle e^{x}=1+{\frac {x}{1}}+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots =\sum _{i=0}^{\infty }{\frac {x^{i}}{i!}},}$$

and in the coefficients of other Taylor series (in particular those of the trigonometric and hyperbolic functions), where they cancel factors of ${\displaystyle n!}$ coming from the ${\displaystyle n}$th derivative of ${\displaystyle x^{n}}$. This usage of factorials in power series connects back to analytic combinatorics through the exponential generating function, which for a combinatorial class with ${\displaystyle n_{i}}$ elements of size ${\displaystyle i}$ is defined as the power series

$${\displaystyle \sum _{i=0}^{\infty }{\frac {x^{i}n_{i}}{i!}}.}$$

In number theory, the most salient property of factorials is the divisibility of ${\displaystyle n!}$ by all positive integers up to ${\displaystyle n}$, described more precisely for prime factors by Legendre's formula. It follows that arbitrarily large prime numbers can be found as the prime factors of the numbers ${\displaystyle n!\pm 1}$, leading to a proof of Euclid's theorem that the number of primes is infinite. When ${\displaystyle n!\pm 1}$ is itself prime it is called a factorial prime; relatedly, Brocard's problem, also posed by Srinivasa Ramanujan, concerns the existence of square numbers of the form ${\displaystyle n!+1}$. In contrast, the numbers ${\displaystyle n!+2,n!+3,\dots n!+n}$ must all be composite, proving the existence of arbitrarily large prime gaps. An elementary proof of Bertrand's postulate on the existence of a prime in any interval of the form ${\displaystyle [n,2n]}$, one of the first results of Paul Erdős, was based on the divisibility properties of factorials. The factorial number system is a mixed radix notation for numbers in which the place values of each digit are factorials.

Factorials are used extensively in probability theory, for instance in the Poisson distribution and in the probabilities of random permutations. In computer science, beyond appearing in the analysis of brute-force searches over permutations, factorials arise in the lower bound of ${\displaystyle \log _{2}n!=n\log _{2}n-O(n)}$ on the number of comparisons needed to comparison sort a set of ${\displaystyle n}$ items, and in the analysis of chained hash tables, where the distribution of keys per cell can be accurately approximated by a Poisson distribution. Moreover, factorials naturally appear in formulae from quantum and statistical physics, where one often considers all the possible permutations of a set of particles. In statistical mechanics, calculations of entropy such as Boltzmann's entropy formula or the Sackur–Tetrode equation must correct the count of microstates by dividing by the factorials of the numbers of each type of indistinguishable particle to avoid the Gibbs paradox. Quantum physics provides the underlying reason for why these corrections are necessary.

Properties

Growth and approximation

Comparison of the factorial, Stirling's approximation, and the simpler approximation ${\displaystyle (n/e)^{n}}$, on a doubly logarithmic scale

 

Relative error in a truncated Stirling series vs. number of terms

 

Main article: Stirling's approximation

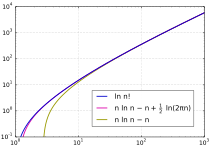
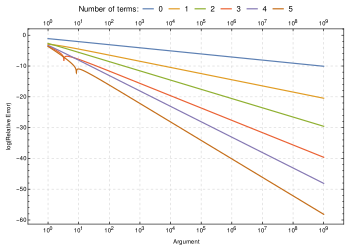
As a function of ${\displaystyle n}$, the factorial has faster than exponential growth, but grows more slowly than a double exponential function. Its growth rate is similar to ${\displaystyle n^{n}}$, but slower by an exponential factor. One way of approaching this result is by taking the natural logarithm of the factorial, which turns its product formula into a sum, and then estimating the sum by an integral:

$${\displaystyle \ln n!=\sum _{x=1}^{n}\ln x\approx \int _{1}^{n}\ln x\,dx=n\ln n-n+1.}$$

Exponentiating the result (and ignoring the negligible ${\displaystyle +1}$ term) approximates ${\displaystyle n!}$ as ${\displaystyle (n/e)^{n}}$. More carefully bounding the sum both above and below by an integral, using the trapezoid rule, shows that this estimate needs a correction term proportional to ${\displaystyle {\sqrt {n}}}$. The constant of proportionality for this correction can be found from the Wallis product, which expresses ${\displaystyle \pi }$ as a limiting ratio of factorials and powers of two. The result of these corrections is Stirling's approximation:

$${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\,.}$$

Here, the ${\displaystyle \sim }$ symbol means that, as ${\displaystyle n}$ goes to infinity, the ratio between the left and right sides approaches one in the limit. Stirling's formula provides the first term in an asymptotic series that becomes even more accurate when taken to greater numbers of terms:

$${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \right).}$$

An alternative version uses only odd exponents in the correction terms:

$${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n}}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}}+\cdots \right).}$$

Many other variations of these formulas have also been developed, by Srinivasa Ramanujan, Bill Gosper, and others.

The binary logarithm of the factorial, used to analyze comparison sorting, can be very accurately estimated using Stirling's approximation. In the formula below, the ${\displaystyle O(1)}$ term invokes big O notation.

$${\displaystyle \log _{2}n!=n\log _{2}n-(\log _{2}e)n+{\frac {1}{2}}\log _{2}n+O(1).}$$

Divisibility and digits

Main article: Legendre's formula

The product formula for the factorial implies that ${\displaystyle n!}$ is divisible by all prime numbers that are at most ${\displaystyle n}$, and by no larger prime numbers. More precise information about its divisibility is given by Legendre's formula, which gives the exponent of each prime ${\displaystyle p}$ in the prime factorization of ${\displaystyle n!}$ as

$${\displaystyle \sum _{i=1}^{\infty }\left\lfloor {\frac {n}{p^{i}}}\right\rfloor ={\frac {n-s_{p}(n)}{p-1}}.}$$

Here ${\displaystyle s_{p}(n)}$ denotes the sum of the base-${\displaystyle p}$ digits of ${\displaystyle n}$, and the exponent given by this formula can also be interpreted in advanced mathematics as the p-adic valuation of the factorial. Applying Legendre's formula to the product formula for binomial coefficients produces Kummer's theorem, a similar result on the exponent of each prime in the factorization of a binomial coefficient. Grouping the prime factors of the factorial into prime powers in different ways produces the multiplicative partitions of factorials.

The special case of Legendre's formula for ${\displaystyle p=5}$ gives the number of trailing zeros in the decimal representation of the factorials. According to this formula, the number of zeros can be obtained by subtracting the base-5 digits of ${\displaystyle n}$ from ${\displaystyle n}$, and dividing the result by four. Legendre's formula implies that the exponent of the prime ${\displaystyle p=2}$ is always larger than the exponent for ${\displaystyle p=5}$, so each factor of five can be paired with a factor of two to produce one of these trailing zeros. The leading digits of the factorials are distributed according to Benford's law. Every sequence of digits, in any base, is the sequence of initial digits of some factorial number in that base.

Another result on divisibility of factorials, Wilson's theorem, states that ${\displaystyle (n-1)!+1}$ is divisible by ${\displaystyle n}$ if and only if ${\displaystyle n}$ is a prime number. For any given integer ${\displaystyle x}$, the Kempner function of ${\displaystyle x}$ is given by the smallest ${\displaystyle n}$ for which ${\displaystyle x}$ divides ${\displaystyle n!}$. For almost all numbers (all but a subset of exceptions with asymptotic density zero), it coincides with the largest prime factor of ${\displaystyle x}$.

The product of two factorials, ${\displaystyle m!\cdot n!}$, always evenly divides ${\displaystyle (m+n)!}$. There are infinitely many factorials that equal the product of other factorials: if ${\displaystyle n}$ is itself any product of factorials, then ${\displaystyle n!}$ equals that same product multiplied by one more factorial, ${\displaystyle (n-1)!}$. The only known examples of factorials that are products of other factorials but are not of this "trivial" form are ${\displaystyle 9!=7!\cdot 3!\cdot 3!\cdot 2!}$, ${\displaystyle 10!=7!\cdot 6!=7!\cdot 5!\cdot 3!}$, and ${\displaystyle 16!=14!\cdot 5!\cdot 2!}$. It would follow from the abc conjecture that there are only finitely many nontrivial examples.

The greatest common divisor of the values of a primitive polynomial of degree ${\displaystyle d}$ over the integers evenly divides ${\displaystyle d!}$.

Continuous interpolation and non-integer generalization

The gamma function (shifted one unit left to match the factorials) continuously interpolates the factorial to non-integer values

 

Absolute values of the complex gamma function, showing poles at non-positive integers

 

Main article: Gamma function

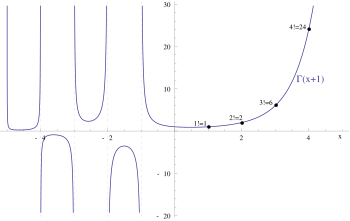
There are infinitely many ways to extend the factorials to a continuous function. The most widely used of these uses the gamma function, which can be defined for positive real numbers as the integral

$${\displaystyle \Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx.}$$

The resulting function is related to the factorial of a non-negative integer ${\displaystyle n}$ by the equation

$${\displaystyle n!=\Gamma (n+1),}$$

which can be used as a definition of the factorial for non-integer arguments. At all values ${\displaystyle x}$ for which both ${\displaystyle \Gamma (x)}$ and ${\displaystyle \Gamma (x-1)}$ are defined, the gamma function obeys the functional equation

$${\displaystyle \Gamma (n)=(n-1)\Gamma (n-1),}$$

generalizing the recurrence relation for the factorials.

The same integral converges more generally for any complex number ${\displaystyle z}$ whose real part is positive. It can be extended to the non-integer points in the rest of the complex plane by solving for Euler's reflection formula

$${\displaystyle \Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}.}$$

However, this formula cannot be used at integers because, for them, the ${\displaystyle \sin \pi z}$ term would produce a division by zero. The result of this extension process is an analytic function, the analytic continuation of the integral formula for the gamma function. It has a nonzero value at all complex numbers, except for the non-positive integers where it has simple poles. Correspondingly, this provides a definition for the factorial at all complex numbers other than the negative integers. One property of the gamma function, distinguishing it from other continuous interpolations of the factorials, is given by the Bohr–Mollerup theorem, which states that the gamma function (offset by one) is the only log-convex function on the positive real numbers that interpolates the factorials and obeys the same functional equation. A related uniqueness theorem of Helmut Wielandt states that the complex gamma function and its scalar multiples are the only holomorphic functions on the positive complex half-plane that obey the functional equation and remain bounded for complex numbers with real part between 1 and 2.

Other complex functions that interpolate the factorial values include Hadamard's gamma function, which is an entire function over all the complex numbers, including the non-positive integers. In the p-adic numbers, it is not possible to continuously interpolate the factorial function directly, because the factorials of large integers (a dense subset of the p-adics) converge to zero according to Legendre's formula, forcing any continuous function that is close to their values to be zero everywhere. Instead, the p-adic gamma function provides a continuous interpolation of a modified form of the factorial, omitting the factors in the factorial that are divisible by p.

The digamma function is the logarithmic derivative of the gamma function. Just as the gamma function provides a continuous interpolation of the factorials, offset by one, the digamma function provides a continuous interpolation of the harmonic numbers, offset by the Euler–Mascheroni constant.

Computation

TI SR-50A, a 1975 calculator with a factorial key (third row, center right)

The factorial function is a common feature in scientific calculators. It is also included in scientific programming libraries such as the Python mathematical functions module and the Boost C++ library. If efficiency is not a concern, computing factorials is trivial: just successively multiply a variable initialized to ${\displaystyle 1}$ by the integers up to ${\displaystyle n}$. The simplicity of this computation makes it a common example in the use of different computer programming styles and methods.

The computation of ${\displaystyle n!}$ can be expressed in pseudocode using iteration as

define factorial(n):
  f := 1
  for i := 1, 2, 3, ..., n:
    f := f × i
  return f

or using recursion based on its recurrence relation as

define factorial(n):
  if n = 0 return 1
  return n × factorial(n − 1)

Other methods suitable for its computation include memoization, dynamic programming, and functional programming. The computational complexity of these algorithms may be analyzed using the unit-cost random-access machine model of computation, in which each arithmetic operation takes constant time and each number uses a constant amount of storage space. In this model, these methods can compute ${\displaystyle n!}$ in time ${\displaystyle O(n)}$, and the iterative version uses space ${\displaystyle O(1)}$. Unless optimized for tail recursion, the recursive version takes linear space to store its call stack. However, this model of computation is only suitable when ${\displaystyle n}$ is small enough to allow ${\displaystyle n!}$ to fit into a machine word. The values 12! and 20! are the largest factorials that can be stored in, respectively, the 32-bit and 64-bit integers. Floating point can represent larger factorials, but approximately rather than exactly, and will still overflow for factorials larger than ${\displaystyle 170!}$.

The exact computation of larger factorials involves arbitrary-precision arithmetic, because of fast growth and integer overflow. Time of computation can be analyzed as a function of the number of digits or bits in the result. By Stirling's formula, ${\displaystyle n!}$ has ${\displaystyle b=O(n\log n)}$ bits. The Schönhage–Strassen algorithm can produce a ${\displaystyle b}$-bit product in time ${\displaystyle O(b\log b\log \log b)}$, and faster multiplication algorithms taking time ${\displaystyle O(b\log b)}$ are known. However, computing the factorial involves repeated products, rather than a single multiplication, so these time bounds do not apply directly. In this setting, computing ${\displaystyle n!}$ by multiplying the numbers from 1 to ${\displaystyle n}$ in sequence is inefficient, because it involves ${\displaystyle n}$ multiplications, a constant fraction of which take time ${\displaystyle O(n\log ^{2}n)}$ each, giving total time ${\displaystyle O(n^{2}\log ^{2}n)}$. A better approach is to perform the multiplications as a divide-and-conquer algorithm that multiplies a sequence of ${\displaystyle i}$ numbers by splitting it into two subsequences of ${\displaystyle i/2}$ numbers, multiplies each subsequence, and combines the results with one last multiplication. This approach to the factorial takes total time ${\displaystyle O(n\log ^{3}n)}$: one logarithm comes from the number of bits in the factorial, a second comes from the multiplication algorithm, and a third comes from the divide and conquer.

Even better efficiency is obtained by computing n! from its prime factorization, based on the principle that exponentiation by squaring is faster than expanding an exponent into a product. An algorithm for this by Arnold Schönhage begins by finding the list of the primes up to ${\displaystyle n}$, for instance using the sieve of Eratosthenes, and uses Legendre's formula to compute the exponent for each prime. Then it computes the product of the prime powers with these exponents, using a recursive algorithm, as follows:

• Use divide and conquer to compute the product of the primes whose exponents are odd
• Divide all of the exponents by two (rounding down to an integer), recursively compute the product of the prime powers with these smaller exponents, and square the result
• Multiply together the results of the two previous steps

The product of all primes up to ${\displaystyle n}$ is an ${\displaystyle O(n)}$-bit number, by the prime number theorem, so the time for the first step is ${\displaystyle O(n\log ^{2}n)}$, with one logarithm coming from the divide and conquer and another coming from the multiplication algorithm. In the recursive calls to the algorithm, the prime number theorem can again be invoked to prove that the numbers of bits in the corresponding products decrease by a constant factor at each level of recursion, so the total time for these steps at all levels of recursion adds in a geometric series to ${\displaystyle O(n\log ^{2}n)}$. The time for the squaring in the second step and the multiplication in the third step are again ${\displaystyle O(n\log ^{2}n)}$, because each is a single multiplication of a number with ${\displaystyle O(n\log n)}$ bits. Again, at each level of recursion the numbers involved have a constant fraction as many bits (because otherwise repeatedly squaring them would produce too large a final result) so again the amounts of time for these steps in the recursive calls add in a geometric series to ${\displaystyle O(n\log ^{2}n)}$. Consequentially, the whole algorithm takes time ${\displaystyle O(n\log ^{2}n)}$, proportional to a single multiplication with the same number of bits in its result.

Related sequences and functions

Main article: List of factorial and binomial topics

Several other integer sequences are similar to or related to the factorials:

Alternating factorial

The alternating factorial is the absolute value of the alternating sum of the first ${\displaystyle n}$ factorials, ${\textstyle \sum _{i=1}^{n}(-1)^{n-i}i!}$. These have mainly been studied in connection with their primality; only finitely many of them can be prime, but a complete list of primes of this form is not known.

Bhargava factorial

The Bhargava factorials are a family of integer sequences defined by Manjul Bhargava with similar number-theoretic properties to the factorials, including the factorials themselves as a special case.

Double factorial

The product of all the odd integers up to some odd positive integer ${\displaystyle n}$ is called the double factorial of ${\displaystyle n}$, and denoted by ${\displaystyle n!!}$. That is,

$${\displaystyle (2k-1)!!=\prod _{i=1}^{k}(2i-1)={\frac {(2k)!}{2^{k}k!}}.}$$

For example, 9!! = 1 × 3 × 5 × 7 × 9 = 945. Double factorials are used in trigonometric integrals, in expressions for the gamma function at half-integers and the volumes of hyperspheres, and in counting binary trees and perfect matchings.

Exponential factorial

Just as triangular numbers sum the numbers from ${\displaystyle 1}$ to ${\displaystyle n}$, and factorials take their product, the exponential factorial exponentiates. The exponential factorial of ${\displaystyle n}$, denoted as ${\displaystyle n\$}$, is defined recursively as ${\displaystyle n^{(n-1)\$}}$, with the base case ${\displaystyle 0\$=1}$. For example,

$${\displaystyle 4\$=4^{3^{2^{1}}}=262144.}$$

These numbers grow much more quickly than regular factorials.

Falling factorial

The notations ${\displaystyle (x)_{n}}$ or ${\displaystyle x^{\underline {n}}}$ are sometimes used to represent the product of the ${\displaystyle n}$ integers counting up to and including ${\displaystyle x}$, equal to ${\displaystyle x!/(x-n)!}$. This is also known as a falling factorial or backward factorial, and the ${\displaystyle (x)_{n}}$ notation is a Pochhammer symbol. Falling factorials count the number of different sequences of ${\displaystyle n}$ distinct items that can be drawn from a universe of ${\displaystyle x}$ items. They occur as coefficients in the higher derivatives of polynomials, and in the factorial moments of random variables.

Hyperfactorials

The hyperfactorial of ${\displaystyle n}$ is the product ${\displaystyle 1^{1}\cdot 2^{2}\cdots n^{n}}$. These numbers form the discriminants of Hermite polynomials. They can be continuously interpolated by the K-function, and obey analogues to Stirling's formula and Wilson's theorem.

Jordan–Pólya numbers

The Jordan–Pólya numbers are the products of factorials, allowing repetitions. Every tree has a symmetry group whose number of symmetries is a Jordan–Pólya number, and every Jordan–Pólya number counts the symmetries of some tree.

Primorial

The primorial ${\displaystyle n\#}$ is the product of prime numbers less than or equal to ${\displaystyle n}$; this construction gives them some similar divisibility properties to factorials, but unlike factorials they are squarefree. As with the factorial primes ${\displaystyle n!\pm 1}$, researchers have studied primorial primes ${\displaystyle n\#\pm 1}$.

Subfactorial

The subfactorial yields the number of derangements of a set of ${\displaystyle n}$ objects. It is sometimes denoted ${\displaystyle !n}$, and equals the closest integer to ${\displaystyle n!/e}$.

Superfactorial

The superfactorial of ${\displaystyle n}$ is the product of the first ${\displaystyle n}$ factorials. The superfactorials are continuously interpolated by the Barnes G-function.

Von Neumann architecture

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Von_Neumann_architecture 

A von Neumann architecture scheme

The von Neumann architecture — also known as the von Neumann model or Princeton architecture — is a computer architecture based on a 1945 description by John von Neumann, and by others, in the First Draft of a Report on the EDVAC. The document describes a design architecture for an electronic digital computer with these components:

• A processing unit with both an arithmetic logic unit and processor registers
• A control unit that includes an instruction register and a program counter
• Memory that stores data and instructions
• External mass storage
• Input and output mechanisms

The term "von Neumann architecture" has evolved to refer to any stored-program computer in which an instruction fetch and a data operation cannot occur at the same time (since they share a common bus). This is referred to as the von Neumann bottleneck, which often limits the performance of the corresponding system.

The design of a von Neumann architecture machine is simpler than in a Harvard architecture machine—which is also a stored-program system, yet has one dedicated set of address and data buses for reading and writing to memory, and another set of address and data buses to fetch instructions.

A stored-program digital computer keeps both program instructions and data in read–write, random-access memory (RAM). Stored-program computers were an advancement over the program-controlled computers of the 1940s, such as the Colossus and the ENIAC. Those were programmed by setting switches and inserting patch cables to route data and control signals between various functional units. The vast majority of modern computers use the same memory for both data and program instructions, but have caches between the CPU and memory, and, for the caches closest to the CPU, have separate caches for instructions and data, so that most instruction and data fetches use separate buses (split cache architecture).

History

The earliest computing machines had fixed programs. Some very simple computers still use this design, either for simplicity or training purposes. For example, a desk calculator (in principle) is a fixed program computer. It can do basic mathematics, but it cannot run a word processor or games. Changing the program of a fixed-program machine requires rewiring, restructuring, or redesigning the machine. The earliest computers were not so much "programmed" as "designed" for a particular task. "Reprogramming" – when possible at all – was a laborious process that started with flowcharts and paper notes, followed by detailed engineering designs, and then the often-arduous process of physically rewiring and rebuilding the machine. It could take three weeks to set up and debug a program on ENIAC.

With the proposal of the stored-program computer, this changed. A stored-program computer includes, by design, an instruction set, and can store in memory a set of instructions (a program) that details the computation.

A stored-program design also allows for self-modifying code. One early motivation for such a facility was the need for a program to increment or otherwise modify the address portion of instructions, which operators had to do manually in early designs. This became less important when index registers and indirect addressing became usual features of machine architecture. Another use was to embed frequently used data in the instruction stream using immediate addressing. Self-modifying code has largely fallen out of favor, since it is usually hard to understand and debug, as well as being inefficient under modern processor pipelining and caching schemes.

Capabilities

On a large scale, the ability to treat instructions as data is what makes assemblers, compilers, linkers, loaders, and other automated programming tools possible. It makes "programs that write programs" possible. This has made a sophisticated self-hosting computing ecosystem flourish around von Neumann architecture machines.

Some high level languages leverage the von Neumann architecture by providing an abstract, machine-independent way to manipulate executable code at runtime (e.g., LISP), or by using runtime information to tune just-in-time compilation (e.g. languages hosted on the Java virtual machine, or languages embedded in web browsers).

On a smaller scale, some repetitive operations such as BITBLT or pixel and vertex shaders can be accelerated on general purpose processors with just-in-time compilation techniques. This is one use of self-modifying code that has remained popular.

Development of the stored-program concept

The mathematician Alan Turing, who had been alerted to a problem of mathematical logic by the lectures of Max Newman at the University of Cambridge, wrote a paper in 1936 entitled On Computable Numbers, with an Application to the Entscheidungsproblem, which was published in the Proceedings of the London Mathematical Society. In it he described a hypothetical machine he called a universal computing machine, now known as the "Universal Turing machine". The hypothetical machine had an infinite store (memory in today's terminology) that contained both instructions and data. John von Neumann became acquainted with Turing while he was a visiting professor at Cambridge in 1935, and also during Turing's PhD year at the Institute for Advanced Study in Princeton, New Jersey during 1936–1937. Whether he knew of Turing's paper of 1936 at that time is not clear.

In 1936, Konrad Zuse also anticipated, in two patent applications, that machine instructions could be stored in the same storage used for data.

Independently, J. Presper Eckert and John Mauchly, who were developing the ENIAC at the Moore School of Electrical Engineering of the University of Pennsylvania, wrote about the stored-program concept in December 1943. In planning a new machine, EDVAC, Eckert wrote in January 1944 that they would store data and programs in a new addressable memory device, a mercury metal delay-line memory. This was the first time the construction of a practical stored-program machine was proposed. At that time, he and Mauchly were not aware of Turing's work.

Von Neumann was involved in the Manhattan Project at the Los Alamos National Laboratory. It required huge amounts of calculation, and thus drew him to the ENIAC project, during the summer of 1944. There he joined the ongoing discussions on the design of this stored-program computer, the EDVAC. As part of that group, he wrote up a description titled First Draft of a Report on the EDVAC based on the work of Eckert and Mauchly. It was unfinished when his colleague Herman Goldstine circulated it, and bore only von Neumann's name (to the consternation of Eckert and Mauchly). The paper was read by dozens of von Neumann's colleagues in America and Europe, and influenced the next round of computer designs.

Jack Copeland considers that it is "historically inappropriate to refer to electronic stored-program digital computers as 'von Neumann machines'". His Los Alamos colleague Stan Frankel said of von Neumann's regard for Turing's ideas

I know that in or about 1943 or '44 von Neumann was well aware of the fundamental importance of Turing's paper of 1936…. Von Neumann introduced me to that paper and at his urging I studied it with care. Many people have acclaimed von Neumann as the "father of the computer" (in a modern sense of the term) but I am sure that he would never have made that mistake himself. He might well be called the midwife, perhaps, but he firmly emphasized to me, and to others I am sure, that the fundamental conception is owing to Turing— in so far as not anticipated by Babbage…. Both Turing and von Neumann, of course, also made substantial contributions to the "reduction to practice" of these concepts but I would not regard these as comparable in importance with the introduction and explication of the concept of a computer able to store in its memory its program of activities and of modifying that program in the course of these activities.

At the time that the "First Draft" report was circulated, Turing was producing a report entitled Proposed Electronic Calculator. It described in engineering and programming detail, his idea of a machine he called the Automatic Computing Engine (ACE). He presented this to the executive committee of the British National Physical Laboratory on February 19, 1946. Although Turing knew from his wartime experience at Bletchley Park that what he proposed was feasible, the secrecy surrounding Colossus, that was subsequently maintained for several decades, prevented him from saying so. Various successful implementations of the ACE design were produced.

Both von Neumann's and Turing's papers described stored-program computers, but von Neumann's earlier paper achieved greater circulation and the computer architecture it outlined became known as the "von Neumann architecture". In the 1953 publication Faster than Thought: A Symposium on Digital Computing Machines (edited by B. V. Bowden), a section in the chapter on Computers in America reads as follows:

The Machine of the Institute For Advanced Studies, Princeton

In 1945, Professor J. von Neumann, who was then working at the Moore School of Engineering in Philadelphia, where the E.N.I.A.C. had been built, issued on behalf of a group of his co-workers, a report on the logical design of digital computers. The report contained a detailed proposal for the design of the machine that has since become known as the E.D.V.A.C. (electronic discrete variable automatic computer). This machine has only recently been completed in America, but the von Neumann report inspired the construction of the E.D.S.A.C. (electronic delay-storage automatic calculator) in Cambridge (see page 130).

In 1947, Burks, Goldstine and von Neumann published another report that outlined the design of another type of machine (a parallel machine this time) that would be exceedingly fast, capable perhaps of 20,000 operations per second. They pointed out that the outstanding problem in constructing such a machine was the development of suitable memory with instantaneously accessible contents. At first they suggested using a special vacuum tube—called the "Selectron"—which the Princeton Laboratories of RCA had invented. These tubes were expensive and difficult to make, so von Neumann subsequently decided to build a machine based on the Williams memory. This machine—completed in June, 1952 in Princeton—has become popularly known as the Maniac. The design of this machine inspired at least half a dozen machines now being built in America, all known affectionately as "Johniacs".

In the same book, the first two paragraphs of a chapter on ACE read as follows:

Automatic Computation at the National Physical Laboratory

One of the most modern digital computers which embodies developments and improvements in the technique of automatic electronic computing was recently demonstrated at the National Physical Laboratory, Teddington, where it has been designed and built by a small team of mathematicians and electronics research engineers on the staff of the Laboratory, assisted by a number of production engineers from the English Electric Company, Limited. The equipment so far erected at the Laboratory is only the pilot model of a much larger installation which will be known as the Automatic Computing Engine, but although comparatively small in bulk and containing only about 800 thermionic valves, as can be judged from Plates XII, XIII and XIV, it is an extremely rapid and versatile calculating machine.

The basic concepts and abstract principles of computation by a machine were formulated by Dr. A. M. Turing, F.R.S., in a paper¹. read before the London Mathematical Society in 1936, but work on such machines in Britain was delayed by the war. In 1945, however, an examination of the problems was made at the National Physical Laboratory by Mr. J. R. Womersley, then superintendent of the Mathematics Division of the Laboratory. He was joined by Dr. Turing and a small staff of specialists, and, by 1947, the preliminary planning was sufficiently advanced to warrant the establishment of the special group already mentioned. In April, 1948, the latter became the Electronics Section of the Laboratory, under the charge of Mr. F. M. Colebrook.

Early von Neumann-architecture computers

The First Draft described a design that was used by many universities and corporations to construct their computers. Among these various computers, only ILLIAC and ORDVAC had compatible instruction sets.

• ARC2 (Birkbeck, University of London) officially came online on May 12, 1948.
• Manchester Baby (Victoria University of Manchester, England) made its first successful run of a stored program on June 21, 1948.
• EDSAC (University of Cambridge, England) was the first practical stored-program electronic computer (May 1949)
• Manchester Mark 1 (University of Manchester, England) Developed from the Baby (June 1949)
• CSIRAC (Council for Scientific and Industrial Research) Australia (November 1949)
• MESM in Kyiv, Ukraine (November 1950)
• EDVAC (Ballistic Research Laboratory, Computing Laboratory at Aberdeen Proving Ground 1951)
• ORDVAC (U-Illinois) at Aberdeen Proving Ground, Maryland (completed November 1951)
• IAS machine at Princeton University (January 1952)
• MANIAC I at Los Alamos Scientific Laboratory (March 1952)
• ILLIAC at the University of Illinois, (September 1952)
• BESM-1 in Moscow (1952)
• AVIDAC at Argonne National Laboratory (1953)
• ORACLE at Oak Ridge National Laboratory (June 1953)
• BESK in Stockholm (1953)
• JOHNNIAC at RAND Corporation (January 1954)
• DASK in Denmark (1955)
• WEIZAC at the Weizmann Institute of Science in Rehovot, Israel (1955)
• PERM in Munich (1956)
• SILLIAC in Sydney (1956)

Early stored-program computers

The date information in the following chronology is difficult to put into proper order. Some dates are for first running a test program, some dates are the first time the computer was demonstrated or completed, and some dates are for the first delivery or installation.

• The IBM SSEC had the ability to treat instructions as data, and was publicly demonstrated on January 27, 1948. This ability was claimed in a US patent. However it was partially electromechanical, not fully electronic. In practice, instructions were read from paper tape due to its limited memory.
• The ARC2 developed by Andrew Booth and Kathleen Booth at Birkbeck, University of London officially came online on May 12, 1948. It featured the first rotating drum storage device.
• The Manchester Baby was the first fully electronic computer to run a stored program. It ran a factoring program for 52 minutes on June 21, 1948, after running a simple division program and a program to show that two numbers were relatively prime.
• The ENIAC was modified to run as a primitive read-only stored-program computer (using the Function Tables for program ROM) and was demonstrated as such on September 16, 1948, running a program by Adele Goldstine for von Neumann.
• The BINAC ran some test programs in February, March, and April 1949, although was not completed until September 1949.
• The Manchester Mark 1 developed from the Baby project. An intermediate version of the Mark 1 was available to run programs in April 1949, but was not completed until October 1949.
• The EDSAC ran its first program on May 6, 1949.
• The EDVAC was delivered in August 1949, but it had problems that kept it from being put into regular operation until 1951.
• The CSIR Mk I ran its first program in November 1949.
• The SEAC was demonstrated in April 1950.
• The Pilot ACE ran its first program on May 10, 1950, and was demonstrated in December 1950.
• The SWAC was completed in July 1950.
• The Whirlwind was completed in December 1950 and was in actual use in April 1951.
• The first ERA Atlas (later the commercial ERA 1101/UNIVAC 1101) was installed in December 1950.

Evolution

Single system bus evolution of the architecture

Through the decades of the 1960s and 1970s computers generally became both smaller and faster, which led to evolutions in their architecture. For example, memory-mapped I/O lets input and output devices be treated the same as memory. A single system bus could be used to provide a modular system with lower cost. This is sometimes called a "streamlining" of the architecture. In subsequent decades, simple microcontrollers would sometimes omit features of the model to lower cost and size. Larger computers added features for higher performance.

Design limitations

Von Neumann bottleneck

The shared bus between the program memory and data memory leads to the von Neumann bottleneck, the limited throughput (data transfer rate) between the central processing unit (CPU) and memory compared to the amount of memory. Because the single bus can only access one of the two classes of memory at a time, throughput is lower than the rate at which the CPU can work. This seriously limits the effective processing speed when the CPU is required to perform minimal processing on large amounts of data. The CPU is continually forced to wait for needed data to move to or from memory. Since CPU speed and memory size have increased much faster than the throughput between them, the bottleneck has become more of a problem, a problem whose severity increases with every new generation of CPU.

The von Neumann bottleneck was described by John Backus in his 1977 ACM Turing Award lecture. According to Backus:

Surely there must be a less primitive way of making big changes in the store than by pushing vast numbers of words back and forth through the von Neumann bottleneck. Not only is this tube a literal bottleneck for the data traffic of a problem, but, more importantly, it is an intellectual bottleneck that has kept us tied to word-at-a-time thinking instead of encouraging us to think in terms of the larger conceptual units of the task at hand. Thus programming is basically planning and detailing the enormous traffic of words through the von Neumann bottleneck, and much of that traffic concerns not significant data itself, but where to find it.

Mitigations

There are several known methods for mitigating the Von Neumann performance bottleneck. For example, the following all can improve performance:

• Providing a cache between the CPU and the main memory
• providing separate caches or separate access paths for data and instructions (the so-called Modified Harvard architecture)
• using branch predictor algorithms and logic
• providing a limited CPU stack or other on-chip scratchpad memory to reduce memory access
• Implementing the CPU and the memory hierarchy as a system on chip, providing greater locality of reference and thus reducing latency and increasing throughput between processor registers and main memory

The problem can also be sidestepped somewhat by using parallel computing, using for example the non-uniform memory access (NUMA) architecture—this approach is commonly employed by supercomputers. It is less clear whether the intellectual bottleneck that Backus criticized has changed much since 1977. Backus's proposed solution has not had a major influence. Modern functional programming and object-oriented programming are much less geared towards "pushing vast numbers of words back and forth" than earlier languages like FORTRAN were, but internally, that is still what computers spend much of their time doing, even highly parallel supercomputers.

As of 1996, a database benchmark study found that three out of four CPU cycles were spent waiting for memory. Researchers expect that increasing the number of simultaneous instruction streams with multithreading or single-chip multiprocessing will make this bottleneck even worse. In the context of multi-core processors, additional overhead is required to maintain cache coherence between processors and threads.

Self-modifying code

Main article: Self-modifying code

Aside from the von Neumann bottleneck, program modifications can be quite harmful, either by accident or design. In some simple stored-program computer designs, a malfunctioning program can damage itself, other programs, or the operating system, possibly leading to a computer crash. Memory protection and other forms of access control can usually protect against both accidental and malicious program changes.

Viral phenomenon

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Viral_phenomenon

Viral phenomena are objects or patterns that are able to replicate themselves or convert other objects into copies of themselves when these objects are exposed to them. Analogous to the way in which viruses propagate, the term viral pertains to a video, image, or written content spreading to numerous online users within a short time period. This concept has become a common way to describe how thoughts, information, and trends move into and through a human population.

The popularity of viral media has been fueled by the rapid rise of social network sites, wherein audiences—who are metaphorically described as experiencing "infection" and "contamination"—play as passive carriers rather than an active role to 'spread' content, making such content "go viral". The term viral media differs from spreadable media as the latter refers to the potential of content to become viral. Memes are one known example of informational viral patterns.

History

Terminology

Meme

The word meme was coined by Richard Dawkins in his 1976 book The Selfish Gene as an attempt to explain memetics; or, how ideas replicate, mutate, and evolve. When asked to assess this comparison, Lauren Ancel Meyers, a biology professor at the University of Texas, stated that "memes spread through online social networks similarly to the way diseases do through offline populations." This dispersion of cultural movements is shown through the spread of memes online, especially when seemingly innocuous or trivial trends spread and die in rapid fashion.

Viral

The term viral pertains to a video, image, or written content spreading to numerous online users within a short time period. If something goes viral, many people discuss it. Accordingly, Tony D. Sampson defines viral phenomena as spreadable accumulations of events, objects, and affects that are overall content built up by popular discourses surrounding network culture. There is also a relationship to the biological notion of disease spread and epidemiology. In this context, "going viral" is similar to an epidemic spread, which occurs if more than one person is infected by a disease for every person infected. Thus, if a piece of content is shared with more than one person every time it is seen, then this will result in viral growth.

In Understanding Media (1964), philosopher Marshall McLuhan describes photography in particular, and technology in general, as having a potentially "virulent nature." In Jean Baudrillard's 1981 treatise Simulacra and Simulation, the philosopher describes An American Family, arguably the first "reality" television series, as a marker of a new age in which the medium of television has a "viral, endemic, chronic, alarming presence."

Another formulation of the 'viral' concept includes the term media virus, or viral media, coined by Douglas Rushkoff, who defines it as a type of Trojan horse: "People are duped into passing a hidden agenda while circulating compelling content." Mosotho South-African media theorist Thomas Mofolo uses Rushkoff's idea to define viral as a type of virtual collective consciousness that primarily manifests via digital media networks and evolves into offline actions to produce a new social reality. Mofolo bases this definition on a study about how internet users involved in the Tunisian Arab Spring perceived the value of Facebook towards their revolution. Mofolo's understanding of the viral was first developed in a study on Global Citizen's #TogetherAtHome campaign and used to formulate a new theoretical framework called Hivemind Impact. Hivemind impact is a specific type of virality that is simulated via digital media networks with the goal of harnessing the virtual collective consciousness to take action on a social issue. For Mofolo, the viral eventually evolves into McLuhan's 'global village' when the virtual collective consciousness reaches a point of noogenesis that then becomes the noosphere.

Content sharing

See also: Content sharing

Early history

A page from Martin Luther's Ninety-five Theses, which was widely and rapidly distributed in 1517

Before writing and while most people were illiterate, the dominant means of spreading memes was oral culture like folk tales, folk songs, and oral poetry, which mutated over time as each retelling presented an opportunity for change. The printing press provided an easy way to copy written texts instead of handwritten manuscripts. In particular, pamphlets could be published in only a day or two, unlike books which took longer. For example, Martin Luther's Ninety-five Theses took only two months to spread throughout Europe. A study of United States newspapers in the 1800s found human-interest, "news you can use" stories and list-focused articles circulated nationally as local papers mailed copies to each other and selected content for reprinting. Chain letters spread by postal mail throughout the 1900s.

Urban legends also began as word-of-mouth memes. Like hoaxes, they are examples of falsehoods that people swallow, and, like them, often achieve broad public notoriety.

CompuServe

Beyond vocal sharing, the 20th century made huge strides in the World Wide Web and the ability to content share. In 1979, dial-up internet service provided by the company CompuServ was a key player in online communications and how information began spreading beyond the print. Those with access to a computer in the earliest of stages could not comprehend the full effect that public access to the internet could or would create. It is hard to remember the times of newspapers being delivered to households across the country in order to receive their news for the day, and it was when The Columbus Dispatch out of Columbus, Ohio broke barriers when it was first to publish in online format. The success that was predicted by CompuServe and the Associated Press led to some of the largest newspapers to become part of the movement to publish the news via online format. Content sharing in the journalism world brings new advances to viral aspects of how news is spread in a matter of seconds.

Internet memes

Main article: Internet meme

The creation of the Internet enabled users to select and share content with each other electronically, providing new, faster, and more decentralized controlled channels for spreading memes. Email forwards are essentially text memes, often including jokes, hoaxes, email scams, written versions of urban legends, political messages, and digital chain letters; if widely forwarded they might be called 'viral emails'. User-friendly consumer photo editing tools like Photoshop and image-editing websites have facilitated the creation of the genre of the image macro, where a popular image is overlaid with different humorous text phrases. These memes are typically created with Impact font. The growth of video-sharing websites like YouTube made viral videos possible.

It is sometimes difficult to predict which images and videos will "go viral"; sometimes the creation of a new Internet celebrity is a sudden surprise. One of the first documented viral videos is "Numa Numa", a webcam video of then-19-year-old Gary Brolsma lip-syncing and dancing to the Romanian pop song "Dragostea Din Tei".

The sharing of text, images, videos, or links to this content have been greatly facilitated by social media such as Facebook and Twitter. Other mimicry memes carried by Internet media include hashtags, language variations like intentional misspellings, and fads like planking. The popularity and widespread distribution of Internet memes have gotten the attention of advertisers, creating the field of viral marketing. A person, group, or company desiring much fast, cheap publicity might create a hashtag, image, or video designed to go viral; many such attempts are unsuccessful, but the few posts that "go viral" generate much publicity.

Types of viral phenomena

Viral videos

Main article: Viral video

Viral videos are among the most common type of viral phenomena. A viral video is any clip of animation or film that is spread rapidly through online sharing. Viral videos can receive millions of views as they are shared on social media sites, reposted to blogs, sent in emails and so on. When a video goes viral it has become very popular. Its exposure on the Internet grows exponentially as more and more people discover it and share it with others. An article or an image can also become viral.

The classification is probably assigned more as a result of intensive activity and the rate of growth among users in a relatively short amount of time than of simply how many hits something receives. Most viral videos contain humor and fall into broad categories:

• Unintentional: Videos that the creators never intended to go viral. These videos may have been posted by the creator or shared with friends, who then spread the content.
• Humorous: Videos that have been created specifically to entertain people. If a video is funny enough, it will spread.
• Promotional: Videos that are designed to go viral with a marketing message to raise brand awareness. Promotional viral videos fall under viral marketing practices. For instance, one of the newest viral commercial video – Extra Gum commercial.
• Charity: Videos created and spread in order to collect donations. For instance, Ice Bucket challenge was a hit on social networks in the summer of 2014.
• Art performances: a video created by artists to raise the problem, express ideas and the freedom of creativity.
• Political: Viral videos are powerful tools for politicians to boost their popularity. Barack Obama campaign launched Yes We Can slogan as a viral video on YouTube. "The Obama campaign posted almost 800 videos on YouTube, and the McCain campaign posted just over 100. The pro-Obama video "Yes we can" went viral after being uploaded to YouTube in February 2008." Other political viral videos served not as a promotion but as an agent for support and unification. Social media was actively employed in the Arab Spring. "The Tunisian uprising had special resonance in Egypt because it was prompted by incidents of police corruption and viral social media condemnation of them."

YouTube effect

With the creation of YouTube, a video-sharing website, there has been a huge surge in the number of viral videos on the Internet. This is primarily due to the ease of access to these videos and the ease of sharing them via social media websites. The ability to share videos from one person to another with ease means there are many cases of 'overnight' viral videos. "YouTube, which makes it easy to embed its content elsewhere have the freedom and mobility once ascribed to papyrus, enabling their rapid circulation across a range of social networks." YouTube has overtaken television in terms of the size of audience. As one example, American Idol was the most viewable TV show in 2009 in the U.S. while "a video of Scottish woman Susan Boyle auditioning for Britain's Got Talent with her singing was viewed more than 77 million times on YouTube". The capacity to attract an enormous audience on a user-friendly platform is one of the leading factors why YouTube generates viral videos. YouTube contributes to viral phenomenon spreadability since the idea of the platform is based on sharing and contribution. "Sites such as YouTube, eBay, Facebook, Flickr, Craigslist, and Wikipedia, only exist and have value because people use and contribute to them, and they are clearly better the more people are using and contributing to them. This is the essence of Web 2.0."

An example of one of the most prolific viral YouTube videos that fall into the promotional viral videos category is Kony 2012. On March 5, 2012, the charity organization Invisible Children Inc. posted a short film about the atrocities committed in Uganda by Joseph Kony and his rebel army. Artists use YouTube as their one of the main branding and communication platform to spread videos and make them viral. For instance, after her time off, Adele released her most-viewed song "Hello". "Hello" crossed 100 million views in just five days, making it the fastest video to reach it in 2015. YouTube viral videos make stars. As an example, Justin Bieber who was discovered since his video on YouTube Chris Brown's song "With You" went viral. Since its launch in 2005, YouTube has become a hub for aspiring singers and musicians. Talent managers look to it to find budding pop stars.

According to Visible Measures, the original "Kony 2012" video documentary, and the hundreds of excerpts and responses uploaded by audiences across the Web, collectively garnered 100 million views in a record six days. This example of how quickly the video spread emphasizes how YouTube acts as a catalyst in the spread of viral media. YouTube is considered as "multiple existing forms of participatory culture" and that trend is useful for the sake of business. "The discourse of Web 2.0 its power has been its erasure of this larger history of participatory practices, with companies acting as if they were "bestowing" agency onto audiences, making their creative output meaningful by valuing it within the logics of commodity culture."

Viral marketing

Main article: Viral marketing

Viral marketing is the phenomenon in which people actively assess media or content and decide to spread to others such as making a word-of-mouth recommendation, passing content through social media, posting a video to YouTube. The term was first popularized in 1995, after Hotmail spreading their service offer "Get your free web-base email at Hotmail." Viral marketing has become important in the business field in building brand recognition, with companies trying to get their customers and other audiences involved in circulating and sharing their content on social media both in voluntary and involuntary ways. Many brands undertake guerrilla marketing or buzz marketing to gain public attention. Some marketing campaigns seek to engage an audience to unwittingly pass along their campaign message.

The use of viral marketing is shifting from the concept that the content drives its own attention to the intended attempt to draw the attention. The companies are worried about making their content 'go viral' and how their customers' communication has the potential to circulate it widely. There has been much discussion about morality in doing viral marketing. Iain Short (2010) points out that many applications on Twitter and Facebook generates automated marketing message and update it on the audience's personal timelines without users personally pass it along.

Stacy Wood from North Carolina State University has conducted research and found that the value of recommendations from 'everyday people' has a potential impact on the brands. Consumers have been bombarded by thousands of messages every day which makes authenticity and credibility of marketing message been questioned; word of mouth from 'everyday people' therefore becomes an incredibly important source of credible information. If a company sees that the word-of-mouth from "the average person" is crucial for the greater opportunity for influencing others, many questions remain. "What implicit contracts exist between brands and those recommenders? What moral codes and guidelines should brands respect when encouraging, soliciting, or reacting to comments from those audiences they wish to reach? What types of compensation, if any, do audience members deserve for their promotional labor when they provide a testimonial."

An example of effective viral marketing can be the unprecedented boost in sales of the Popeyes chicken sandwich. After the Twitter account for Chick-fil-A attempted to undercut Popeyes by suggesting that Popeyes' chicken sandwich wasn't the "original chicken sandwich", Popeyes responded with a tweet that would end up going viral. After the response had amassed 85,000 retweets and 300,000 likes, Popeyes chains began to sell many more sandwiches to the point where many locations sold all of their stock of chicken sandwiches. This prompted other chicken chains to tweet about their chicken sandwiches, but none of these efforts became as widespread as it was for Popeyes.

Financial contagion

Main article: Financial contagion

In macroeconomics, "financial contagion" is a proposed socially-viral phenomenon wherein disturbances quickly spread across global financial markets.

Evaluation by commentators

Some social commentators have a negative view of "viral" content, though others are neutral or celebrate the democratization of content as compared to the gatekeepers of older media. According to the authors of Spreadable Media: Creating Value and Meaning in a Networked Culture: "Ideas are transmitted, often without critical assessment, across a broad array of minds and this uncoordinated flow of information is associated with "bad ideas" or "ruinous fads and foolish fashions." Science fiction sometimes discusses 'viral' content "describing (generally bad) ideas that spread like germs." For example, the 1992 novel Snow Crash explores the implications of an ancient memetic meta-virus and its modern-day computer virus equivalent:

We are all susceptible to the pull of viral ideas. Like mass hysteria. Or a tune that gets into your head that you keep on humming all day until you spread it to someone else. Jokes. Urban legends. Crackpot religions. No matter how smart we get, there is always this deep irrational part that makes us potential hosts for self-replicating information.

— Snow Crash (1992)

The spread of viral phenomena is also regarded as part of the cultural politics of network culture or the virality of the age of networks. Network culture enables the audience to create and spread viral content. "Audiences play an active role in 'spreading' content rather than serving as passive carriers of viral media: their choices, investments, agendas, and actions determine what gets valued." Various authors have pointed to the intensification in connectivity brought about by network technologies as a possible trigger for increased chances of infection from wide-ranging social, cultural, political, and economic contagions. For example, the social scientist Jan van Dijk warns of new vulnerabilities that arise when network society encounters "too much connectivity." The proliferation of global transport networks makes this model of society susceptible to the spreading of biological diseases. Digital networks become volatile under the destructive potential of computer viruses and worms. Enhanced by the rapidity and extensiveness of technological networks, the spread of social conformity, political rumor, fads, fashions, gossip, and hype threatens to destabilize established political order.

Links between viral phenomena that spread on digital networks and the early sociological theories of Gabriel Tarde have been made in digital media theory by Tony D Sampson (2012; 2016). In this context, Tarde's social imitation thesis is used to argue against the biological deterministic theories of cultural contagion forwarded in memetics. In its place, Sampson proposes a Tarde-inspired somnambulist media theory of the viral.