Biosynthesis

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Biosynthesis 

Biosynthesis is a multi-step, enzyme-catalyzed process where substrates are converted into more complex products in living organisms. In biosynthesis, simple compounds are modified, converted into other compounds, or joined to form macromolecules. This process often consists of metabolic pathways. Some of these biosynthetic pathways are located within a single cellular organelle, while others involve enzymes that are located within multiple cellular organelles. Examples of these biosynthetic pathways include the production of lipid membrane components and nucleotides. Biosynthesis is usually synonymous with anabolism.

The prerequisite elements for biosynthesis include: precursor compounds, chemical energy (e.g. ATP), and catalytic enzymes which may require coenzymes (e.g.NADH, NADPH). These elements create monomers, the building blocks for macromolecules. Some important biological macromolecules include: proteins, which are composed of amino acid monomers joined via peptide bonds, and DNA molecules, which are composed of nucleotides joined via phosphodiester bonds.

Properties of chemical reactions

Biosynthesis occurs due to a series of chemical reactions. For these reactions to take place, the following elements are necessary:

• Precursor compounds: these compounds are the starting molecules or substrates in a reaction. These may also be viewed as the reactants in a given chemical process.
• Chemical energy: chemical energy can be found in the form of high energy molecules. These molecules are required for energetically unfavorable reactions. Furthermore, the hydrolysis of these compounds drives a reaction forward. High energy molecules, such as ATP, have three phosphates. Often, the terminal phosphate is split off during hydrolysis and transferred to another molecule.
• Catalytic enzymes: these molecules are special proteins that catalyze a reaction by increasing the rate of the reaction and lowering the activation energy.
• Coenzymes or cofactors: cofactors are molecules that assist in chemical reactions. These may be metal ions, vitamin derivatives such as NADH and acetyl CoA, or non-vitamin derivatives such as ATP. In the case of NADH, the molecule transfers a hydrogen, whereas acetyl CoA transfers an acetyl group, and ATP transfers a phosphate.

In the simplest sense, the reactions that occur in biosynthesis have the following format:

${\displaystyle {\ce {Reactant ->[][enzyme] Product}}}$

Some variations of this basic equation which will be discussed later in more detail are:

1. Simple compounds which are converted into other compounds, usually as part of a multiple step reaction pathway. Two examples of this type of reaction occur during the formation of nucleic acids and the charging of tRNA prior to translation. For some of these steps, chemical energy is required:

   ${\displaystyle {\ce {{Precursor~molecule}+ATP<=>{product~AMP}+PP_{i}}}}$

2. Simple compounds that are converted into other compounds with the assistance of cofactors. For example, the synthesis of phospholipids requires acetyl CoA, while the synthesis of another membrane component, sphingolipids, requires NADH and FADH for the formation the sphingosine backbone. The general equation for these examples is:

   ${\displaystyle {\ce {{Precursor~molecule}+Cofactor->[][enzyme]macromolecule}}}$

3. Simple compounds that join to create a macromolecule. For example, fatty acids join to form phospholipids. In turn, phospholipids and cholesterol interact noncovalently in order to form the lipid bilayer. This reaction may be depicted as follows:

   ${\displaystyle {\ce {{Molecule~1}+Molecule~2->macromolecule}}}$

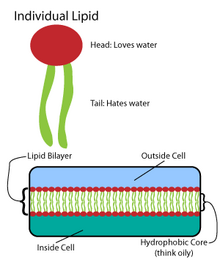
Lipid

Lipid membrane bilayer

Many intricate macromolecules are synthesized in a pattern of simple, repeated structures. For example, the simplest structures of lipids are fatty acids. Fatty acids are hydrocarbon derivatives; they contain a carboxyl group "head" and a hydrocarbon chain "tail". These fatty acids create larger components, which in turn incorporate noncovalent interactions to form the lipid bilayer. Fatty acid chains are found in two major components of membrane lipids: phospholipids and sphingolipids. A third major membrane component, cholesterol, does not contain these fatty acid units.

Phospholipids

The foundation of all biomembranes consists of a bilayer structure of phospholipids. The phospholipid molecule is amphipathic; it contains a hydrophilic polar head and a hydrophobic nonpolar tail. The phospholipid heads interact with each other and aqueous media, while the hydrocarbon tails orient themselves in the center, away from water. These latter interactions drive the bilayer structure that acts as a barrier for ions and molecules.

There are various types of phospholipids; consequently, their synthesis pathways differ. However, the first step in phospholipid synthesis involves the formation of phosphatidate or diacylglycerol 3-phosphate at the endoplasmic reticulum and outer mitochondrial membrane. The synthesis pathway is found below:

The pathway starts with glycerol 3-phosphate, which gets converted to lysophosphatidate via the addition of a fatty acid chain provided by acyl coenzyme A. Then, lysophosphatidate is converted to phosphatidate via the addition of another fatty acid chain contributed by a second acyl CoA; all of these steps are catalyzed by the glycerol phosphate acyltransferase enzyme. Phospholipid synthesis continues in the endoplasmic reticulum, and the biosynthesis pathway diverges depending on the components of the particular phospholipid.

Sphingolipids

Like phospholipids, these fatty acid derivatives have a polar head and nonpolar tails. Unlike phospholipids, sphingolipids have a sphingosine backbone. Sphingolipids exist in eukaryotic cells and are particularly abundant in the central nervous system. For example, sphingomyelin is part of the myelin sheath of nerve fibers.

Sphingolipids are formed from ceramides that consist of a fatty acid chain attached to the amino group of a sphingosine backbone. These ceramides are synthesized from the acylation of sphingosine. The biosynthetic pathway for sphingosine is found below:

As the image denotes, during sphingosine synthesis, palmitoyl CoA and serine undergo a condensation reaction which results in the formation of dehydrosphingosine. This product is then reduced to form dihydrospingosine, which is converted to sphingosine via the oxidation reaction by FAD.

Cholesterol

This lipid belongs to a class of molecules called sterols. Sterols have four fused rings and a hydroxyl group. Cholesterol is a particularly important molecule. Not only does it serve as a component of lipid membranes, it is also a precursor to several steroid hormones, including cortisol, testosterone, and estrogen.

Cholesterol is synthesized from acetyl CoA. The pathway is shown below:

More generally, this synthesis occurs in three stages, with the first stage taking place in the cytoplasm and the second and third stages occurring in the endoplasmic reticulum. The stages are as follows:

1. The synthesis of isopentenyl pyrophosphate, the "building block" of cholesterol

2. The formation of squalene via the condensation of six molecules of isopentenyl phosphate

3. The conversion of squalene into cholesterol via several enzymatic reactions

Nucleotides

The biosynthesis of nucleotides involves enzyme-catalyzed reactions that convert substrates into more complex products. Nucleotides are the building blocks of DNA and RNA. Nucleotides are composed of a five-membered ring formed from ribose sugar in RNA, and deoxyribose sugar in DNA; these sugars are linked to a purine or pyrimidine base with a glycosidic bond and a phosphate group at the 5' location of the sugar.

Purine nucleotides

The synthesis of IMP.

The DNA nucleotides adenosine and guanosine consist of a purine base attached to a ribose sugar with a glycosidic bond. In the case of RNA nucleotides deoxyadenosine and deoxyguanosine, the purine bases are attached to a deoxyribose sugar with a glycosidic bond. The purine bases on DNA and RNA nucleotides are synthesized in a twelve-step reaction mechanism present in most single-celled organisms. Higher eukaryotes employ a similar reaction mechanism in ten reaction steps. Purine bases are synthesized by converting phosphoribosyl pyrophosphate (PRPP) to inosine monophosphate (IMP), which is the first key intermediate in purine base biosynthesis. Further enzymatic modification of IMP produces the adenosine and guanosine bases of nucleotides.

1. The first step in purine biosynthesis is a condensation reaction, performed by glutamine-PRPP amidotransferase. This enzyme transfers the amino group from glutamine to PRPP, forming 5-phosphoribosylamine. The following step requires the activation of glycine by the addition of a phosphate group from ATP.
2. GAR synthetase performs the condensation of activated glycine onto PRPP, forming glycineamide ribonucleotide (GAR).
3. GAR transformylase adds a formyl group onto the amino group of GAR, forming formylglycinamide ribonucleotide (FGAR).
4. FGAR amidotransferase catalyzes the addition of a nitrogen group to FGAR, forming formylglycinamidine ribonucleotide (FGAM).
5. FGAM cyclase catalyzes ring closure, which involves removal of a water molecule, forming the 5-membered imidazole ring 5-aminoimidazole ribonucleotide (AIR).
6. N5-CAIR synthetase transfers a carboxyl group, forming the intermediate N5-carboxyaminoimidazole ribonucleotide (N5-CAIR).
7. N5-CAIR mutase rearranges the carboxyl functional group and transfers it onto the imidazole ring, forming carboxyamino- imidazole ribonucleotide (CAIR). The two step mechanism of CAIR formation from AIR is mostly found in single celled organisms. Higher eukaryotes contain the enzyme AIR carboxylase, which transfers a carboxyl group directly to AIR imidazole ring, forming CAIR.
8. SAICAR synthetase forms a peptide bond between aspartate and the added carboxyl group of the imidazole ring, forming N-succinyl-5-aminoimidazole-4-carboxamide ribonucleotide (SAICAR).
9. SAICAR lyase removes the carbon skeleton of the added aspartate, leaving the amino group and forming 5-aminoimidazole-4-carboxamide ribonucleotide (AICAR).
10. AICAR transformylase transfers a carbonyl group to AICAR, forming N-formylaminoimidazole- 4-carboxamide ribonucleotide (FAICAR).
11. The final step involves the enzyme IMP synthase, which performs the purine ring closure and forms the inosine monophosphate intermediate.

Pyrimidine nucleotides

Uridine monophosphate (UMP) biosynthesis

Other DNA and RNA nucleotide bases that are linked to the ribose sugar via a glycosidic bond are thymine, cytosine and uracil (which is only found in RNA). Uridine monophosphate biosynthesis involves an enzyme that is located in the mitochondrial inner membrane and multifunctional enzymes that are located in the cytosol.

1. The first step involves the enzyme carbamoyl phosphate synthase combining glutamine with CO₂ in an ATP dependent reaction to form carbamoyl phosphate.
2. Aspartate carbamoyltransferase condenses carbamoyl phosphate with aspartate to form uridosuccinate.
3. Dihydroorotase performs ring closure, a reaction that loses water, to form dihydroorotate.
4. Dihydroorotate dehydrogenase, located within the mitochondrial inner membrane, oxidizes dihydroorotate to orotate.
5. Orotate phosphoribosyl hydrolase (OMP pyrophosphorylase) condenses orotate with PRPP to form orotidine-5'-phosphate.
6. OMP decarboxylase catalyzes the conversion of orotidine-5'-phosphate to UMP.

After the uridine nucleotide base is synthesized, the other bases, cytosine and thymine are synthesized. Cytosine biosynthesis is a two-step reaction which involves the conversion of UMP to UTP. Phosphate addition to UMP is catalyzed by a kinase enzyme. The enzyme CTP synthase catalyzes the next reaction step: the conversion of UTP to CTP by transferring an amino group from glutamine to uridine; this forms the cytosine base of CTP. The mechanism, which depicts the reaction UTP + ATP + glutamine ⇔ CTP + ADP + glutamate, is below:

Cytosine is a nucleotide that is present in both DNA and RNA. However, uracil is only found in RNA. Therefore, after UTP is synthesized, it is must be converted into a deoxy form to be incorporated into DNA. This conversion involves the enzyme ribonucleoside triphosphate reductase. This reaction that removes the 2'-OH of the ribose sugar to generate deoxyribose is not affected by the bases attached to the sugar. This non-specificity allows ribonucleoside triphosphate reductase to convert all nucleotide triphosphates to deoxyribonucleotide by a similar mechanism.

In contrast to uracil, thymine bases are found mostly in DNA, not RNA. Cells do not normally contain thymine bases that are linked to ribose sugars in RNA, thus indicating that cells only synthesize deoxyribose-linked thymine. The enzyme thymidylate synthetase is responsible for synthesizing thymine residues from dUMP to dTMP. This reaction transfers a methyl group onto the uracil base of dUMP to generate dTMP. The thymidylate synthase reaction, dUMP + 5,10-methylenetetrahydrofolate ⇔ dTMP + dihydrofolate, is shown to the right.

DNA

As DNA polymerase moves in a 3' to 5' direction along the template strand, it synthesizes a new strand in the 5' to 3' direction

Although there are differences between eukaryotic and prokaryotic DNA synthesis, the following section denotes key characteristics of DNA replication shared by both organisms.

DNA is composed of nucleotides that are joined by phosphodiester bonds. DNA synthesis, which takes place in the nucleus, is a semiconservative process, which means that the resulting DNA molecule contains an original strand from the parent structure and a new strand. DNA synthesis is catalyzed by a family of DNA polymerases that require four deoxynucleoside triphosphates, a template strand, and a primer with a free 3'OH in which to incorporate nucleotides.

In order for DNA replication to occur, a replication fork is created by enzymes called helicases which unwind the DNA helix. Topoisomerases at the replication fork remove supercoils caused by DNA unwinding, and single-stranded DNA binding proteins maintain the two single-stranded DNA templates stabilized prior to replication.

DNA synthesis is initiated by the RNA polymerase primase, which makes an RNA primer with a free 3'OH. This primer is attached to the single-stranded DNA template, and DNA polymerase elongates the chain by incorporating nucleotides; DNA polymerase also proofreads the newly synthesized DNA strand.

During the polymerization reaction catalyzed by DNA polymerase, a nucleophilic attack occurs by the 3'OH of the growing chain on the innermost phosphorus atom of a deoxynucleoside triphosphate; this yields the formation of a phosphodiester bridge that attaches a new nucleotide and releases pyrophosphate.

Two types of strands are created simultaneously during replication: the leading strand, which is synthesized continuously and grows towards the replication fork, and the lagging strand, which is made discontinuously in Okazaki fragments and grows away from the replication fork. Okazaki fragments are covalently joined by DNA ligase to form a continuous strand. Then, to complete DNA replication, RNA primers are removed, and the resulting gaps are replaced with DNA and joined via DNA ligase.

Amino acids

Main article: Amino acid synthesis

A protein is a polymer that is composed from amino acids that are linked by peptide bonds. There are more than 300 amino acids found in nature of which only twenty, known as the standard amino acids, are the building blocks for protein. Only green plants and most microbes are able to synthesize all of the 20 standard amino acids that are needed by all living species. Mammals can only synthesize ten of the twenty standard amino acids. The other amino acids, valine, methionine, leucine, isoleucine, phenylalanine, lysine, threonine and tryptophan for adults and histidine, and arginine for babies are obtained through diet.

Amino acid basic structure

L-amino acid

The general structure of the standard amino acids includes a primary amino group, a carboxyl group and the functional group attached to the α-carbon. The different amino acids are identified by the functional group. As a result of the three different groups attached to the α-carbon, amino acids are asymmetrical molecules. For all standard amino acids, except glycine, the α-carbon is a chiral center. In the case of glycine, the α-carbon has two hydrogen atoms, thus adding symmetry to this molecule. With the exception of proline, all of the amino acids found in life have the L-isoform conformation. Proline has a functional group on the α-carbon that forms a ring with the amino group.

Nitrogen source

One major step in amino acid biosynthesis involves incorporating a nitrogen group onto the α-carbon. In cells, there are two major pathways of incorporating nitrogen groups. One pathway involves the enzyme glutamine oxoglutarate aminotransferase (GOGAT) which removes the amide amino group of glutamine and transfers it onto 2-oxoglutarate, producing two glutamate molecules. In this catalysis reaction, glutamine serves as the nitrogen source. An image illustrating this reaction is found to the right.

The other pathway for incorporating nitrogen onto the α-carbon of amino acids involves the enzyme glutamate dehydrogenase (GDH). GDH is able to transfer ammonia onto 2-oxoglutarate and form glutamate. Furthermore, the enzyme glutamine synthetase (GS) is able to transfer ammonia onto glutamate and synthesize glutamine, replenishing glutamine.

The glutamate family of amino acids

The glutamate family of amino acids includes the amino acids that derive from the amino acid glutamate. This family includes: glutamate, glutamine, proline, and arginine. This family also includes the amino acid lysine, which is derived from α-ketoglutarate.

The biosynthesis of glutamate and glutamine is a key step in the nitrogen assimilation discussed above. The enzymes GOGAT and GDH catalyze the nitrogen assimilation reactions.

In bacteria, the enzyme glutamate 5-kinase initiates the biosynthesis of proline by transferring a phosphate group from ATP onto glutamate. The next reaction is catalyzed by the enzyme pyrroline-5-carboxylate synthase (P5CS), which catalyzes the reduction of the ϒ-carboxyl group of L-glutamate 5-phosphate. This results in the formation of glutamate semialdehyde, which spontaneously cyclizes to pyrroline-5-carboxylate. Pyrroline-5-carboxylate is further reduced by the enzyme pyrroline-5-carboxylate reductase (P5CR) to yield a proline amino acid.

In the first step of arginine biosynthesis in bacteria, glutamate is acetylated by transferring the acetyl group from acetyl-CoA at the N-α position; this prevents spontaneous cyclization. The enzyme N-acetylglutamate synthase (glutamate N-acetyltransferase) is responsible for catalyzing the acetylation step. Subsequent steps are catalyzed by the enzymes N-acetylglutamate kinase, N-acetyl-gamma-glutamyl-phosphate reductase, and acetylornithine/succinyldiamino pimelate aminotransferase and yield the N-acetyl-L-ornithine. The acetyl group of acetylornithine is removed by the enzyme acetylornithinase (AO) or ornithine acetyltransferase (OAT), and this yields ornithine. Then, the enzymes citrulline and argininosuccinate convert ornithine to arginine.

The diaminopimelic acid pathway

There are two distinct lysine biosynthetic pathways: the diaminopimelic acid pathway and the α-aminoadipate pathway. The most common of the two synthetic pathways is the diaminopimelic acid pathway; it consists of several enzymatic reactions that add carbon groups to aspartate to yield lysine:

1. Aspartate kinase initiates the diaminopimelic acid pathway by phosphorylating aspartate and producing aspartyl phosphate.
2. Aspartate semialdehyde dehydrogenase catalyzes the NADPH-dependent reduction of aspartyl phosphate to yield aspartate semialdehyde.
3. 4-hydroxy-tetrahydrodipicolinate synthase adds a pyruvate group to the β-aspartyl-4-semialdehyde, and a water molecule is removed. This causes cyclization and gives rise to (2S,4S)-4-hydroxy-2,3,4,5-tetrahydrodipicolinate.
4. 4-hydroxy-tetrahydrodipicolinate reductase catalyzes the reduction of (2S,4S)-4-hydroxy-2,3,4,5-tetrahydrodipicolinate by NADPH to yield Δ'-piperideine-2,6-dicarboxylate (2,3,4,5-tetrahydrodipicolinate) and H₂O.
5. Tetrahydrodipicolinate acyltransferase catalyzes the acetylation reaction that results in ring opening and yields N-acetyl α-amino-ε-ketopimelate.
6. N-succinyl-α-amino-ε-ketopimelate-glutamate aminotransaminase catalyzes the transamination reaction that removes the keto group of N-acetyl α-amino-ε-ketopimelate and replaces it with an amino group to yield N-succinyl-L-diaminopimelate.
7. N-acyldiaminopimelate deacylase catalyzes the deacylation of N-succinyl-L-diaminopimelate to yield L,L-diaminopimelate.
8. DAP epimerase catalyzes the conversion of L,L-diaminopimelate to the meso form of L,L-diaminopimelate.
9. DAP decarboxylase catalyzes the removal of the carboxyl group, yielding L-lysine.

The serine family of amino acids

The serine family of amino acid includes: serine, cysteine, and glycine. Most microorganisms and plants obtain the sulfur for synthesizing methionine from the amino acid cysteine. Furthermore, the conversion of serine to glycine provides the carbons needed for the biosynthesis of the methionine and histidine.

During serine biosynthesis, the enzyme phosphoglycerate dehydrogenase catalyzes the initial reaction that oxidizes 3-phospho-D-glycerate to yield 3-phosphonooxypyruvate. The following reaction is catalyzed by the enzyme phosphoserine aminotransferase, which transfers an amino group from glutamate onto 3-phosphonooxypyruvate to yield L-phosphoserine. The final step is catalyzed by the enzyme phosphoserine phosphatase, which dephosphorylates L-phosphoserine to yield L-serine.

There are two known pathways for the biosynthesis of glycine. Organisms that use ethanol and acetate as the major carbon source utilize the glyconeogenic pathway to synthesize glycine. The other pathway of glycine biosynthesis is known as the glycolytic pathway. This pathway converts serine synthesized from the intermediates of glycolysis to glycine. In the glycolytic pathway, the enzyme serine hydroxymethyltransferase catalyzes the cleavage of serine to yield glycine and transfers the cleaved carbon group of serine onto tetrahydrofolate, forming 5,10-methylene-tetrahydrofolate.

Cysteine biosynthesis is a two-step reaction that involves the incorporation of inorganic sulfur. In microorganisms and plants, the enzyme serine acetyltransferase catalyzes the transfer of acetyl group from acetyl-CoA onto L-serine to yield O-acetyl-L-serine. The following reaction step, catalyzed by the enzyme O-acetyl serine (thiol) lyase, replaces the acetyl group of O-acetyl-L-serine with sulfide to yield cysteine.

The aspartate family of amino acids

The aspartate family of amino acids includes: threonine, lysine, methionine, isoleucine, and aspartate. Lysine and isoleucine are considered part of the aspartate family even though part of their carbon skeleton is derived from pyruvate. In the case of methionine, the methyl carbon is derived from serine and the sulfur group, but in most organisms, it is derived from cysteine.

The biosynthesis of aspartate is a one step reaction that is catalyzed by a single enzyme. The enzyme aspartate aminotransferase catalyzes the transfer of an amino group from aspartate onto α-ketoglutarate to yield glutamate and oxaloacetate. Asparagine is synthesized by an ATP-dependent addition of an amino group onto aspartate; asparagine synthetase catalyzes the addition of nitrogen from glutamine or soluble ammonia to aspartate to yield asparagine.

The diaminopimelic acid lysine biosynthetic pathway

The diaminopimelic acid biosynthetic pathway of lysine belongs to the aspartate family of amino acids. This pathway involves nine enzyme-catalyzed reactions that convert aspartate to lysine.

1. Aspartate kinase catalyzes the initial step in the diaminopimelic acid pathway by transferring a phosphoryl from ATP onto the carboxylate group of aspartate, which yields aspartyl-β-phosphate.
2. Aspartate-semialdehyde dehydrogenase catalyzes the reduction reaction by dephosphorylation of aspartyl-β-phosphate to yield aspartate-β-semialdehyde.
3. Dihydrodipicolinate synthase catalyzes the condensation reaction of aspartate-β-semialdehyde with pyruvate to yield dihydrodipicolinic acid.
4. 4-hydroxy-tetrahydrodipicolinate reductase catalyzes the reduction of dihydrodipicolinic acid to yield tetrahydrodipicolinic acid.
5. Tetrahydrodipicolinate N-succinyltransferase catalyzes the transfer of a succinyl group from succinyl-CoA on to tetrahydrodipicolinic acid to yield N-succinyl-L-2,6-diaminoheptanedioate.
6. N-succinyldiaminopimelate aminotransferase catalyzes the transfer of an amino group from glutamate onto N-succinyl-L-2,6-diaminoheptanedioate to yield N-succinyl-L,L-diaminopimelic acid.
7. Succinyl-diaminopimelate desuccinylase catalyzes the removal of acyl group from N-succinyl-L,L-diaminopimelic acid to yield L,L-diaminopimelic acid.
8. Diaminopimelate epimerase catalyzes the inversion of the α-carbon of L,L-diaminopimelic acid to yield meso-diaminopimelic acid.
9. Siaminopimelate decarboxylase catalyzes the final step in lysine biosynthesis that removes the carbon dioxide group from meso-diaminopimelic acid to yield L-lysine.

Proteins

The tRNA anticodon interacts with the mRNA codon in order to bind an amino acid to growing polypeptide chain.

 

The process of tRNA charging

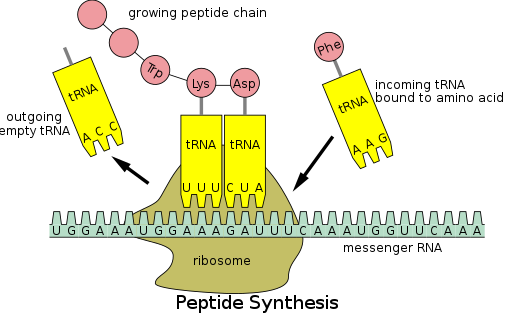
Protein synthesis occurs via a process called translation. During translation, genetic material called mRNA is read by ribosomes to generate a protein polypeptide chain. This process requires transfer RNA (tRNA) which serves as an adaptor by binding amino acids on one end and interacting with mRNA at the other end; the latter pairing between the tRNA and mRNA ensures that the correct amino acid is added to the chain. Protein synthesis occurs in three phases: initiation, elongation, and termination. Prokaryotic (archaeal and bacterial) translation differs from eukaryotic translation; however, this section will mostly focus on the commonalities between the two organisms.

Additional background

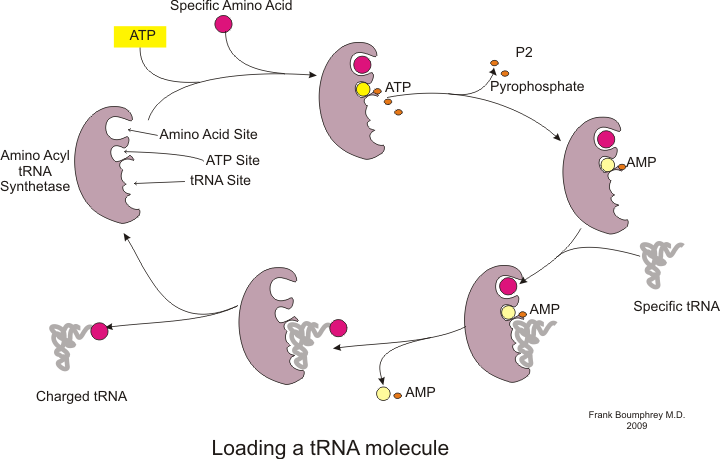
Before translation can begin, the process of binding a specific amino acid to its corresponding tRNA must occur. This reaction, called tRNA charging, is catalyzed by aminoacyl tRNA synthetase. A specific tRNA synthetase is responsible for recognizing and charging a particular amino acid. Furthermore, this enzyme has special discriminator regions to ensure the correct binding between tRNA and its cognate amino acid. The first step for joining an amino acid to its corresponding tRNA is the formation of aminoacyl-AMP:

${\displaystyle {\ce {{Amino~acid}+ATP<=>{aminoacyl-AMP}+PP_{i}}}}$

This is followed by the transfer of the aminoacyl group from aminoacyl-AMP to a tRNA molecule. The resulting molecule is aminoacyl-tRNA:

${\displaystyle {\ce {{Aminoacyl-AMP}+ tRNA <=> {aminoacyl-tRNA}+ AMP}}}$

The combination of these two steps, both of which are catalyzed by aminoacyl tRNA synthetase, produces a charged tRNA that is ready to add amino acids to the growing polypeptide chain.

In addition to binding an amino acid, tRNA has a three nucleotide unit called an anticodon that base pairs with specific nucleotide triplets on the mRNA called codons; codons encode a specific amino acid. This interaction is possible thanks to the ribosome, which serves as the site for protein synthesis. The ribosome possesses three tRNA binding sites: the aminoacyl site (A site), the peptidyl site (P site), and the exit site (E site).

There are numerous codons within an mRNA transcript, and it is very common for an amino acid to be specified by more than one codon; this phenomenon is called degeneracy. In all, there are 64 codons, 61 of each code for one of the 20 amino acids, while the remaining codons specify chain termination.

Translation in steps

As previously mentioned, translation occurs in three phases: initiation, elongation, and termination.

Translation

Step 1: Initiation

The completion of the initiation phase is dependent on the following three events:

1. The recruitment of the ribosome to mRNA

2. The binding of a charged initiator tRNA into the P site of the ribosome

3. The proper alignment of the ribosome with mRNA's start codon

Step 2: Elongation

Following initiation, the polypeptide chain is extended via anticodon:codon interactions, with the ribosome adding amino acids to the polypeptide chain one at a time. The following steps must occur to ensure the correct addition of amino acids:

1. The binding of the correct tRNA into the A site of the ribosome

2. The formation of a peptide bond between the tRNA in the A site and the polypeptide chain attached to the tRNA in the P site

3. Translocation or advancement of the tRNA-mRNA complex by three nucleotides

Translocation "kicks off" the tRNA at the E site and shifts the tRNA from the A site into the P site, leaving the A site free for an incoming tRNA to add another amino acid.

Step 3: Termination

The last stage of translation occurs when a stop codon enters the A site. Then, the following steps occur:

1. The recognition of codons by release factors, which causes the hydrolysis of the polypeptide chain from the tRNA located in the P site

2. The release of the polypeptide chain

3. The dissociation and "recycling" of the ribosome for future translation processes

A summary table of the key players in translation is found below:

Key players in Translation	Translation Stage	Purpose
tRNA synthetase	before initiation	Responsible for tRNA charging
mRNA	initiation, elongation, termination	Template for protein synthesis; contains regions named codons which encode amino acids
tRNA	initiation, elongation, termination	Binds ribosomes sites A, P, E; anticodon base pairs with mRNA codon to ensure that the correct amino acid is incorporated into the growing polypeptide chain
ribosome	initiation, elongation, termination	Directs protein synthesis and catalyzes the formation of the peptide bond

Diseases associated with macromolecule deficiency

Familial hypercholesterolemia causes cholesterol deposits

Errors in biosynthetic pathways can have deleterious consequences including the malformation of macromolecules or the underproduction of functional molecules. Below are examples that illustrate the disruptions that occur due to these inefficiencies.

• Familial hypercholesterolemia: this disorder is characterized by the absence of functional receptors for LDL. Deficiencies in the formation of LDL receptors may cause faulty receptors which disrupt the endocytic pathway, inhibiting the entry of LDL into the liver and other cells. This causes a buildup of LDL in the blood plasma, which results in atherosclerotic plaques that narrow arteries and increase the risk of heart attacks.
• Lesch–Nyhan syndrome: this genetic disease is characterized by self- mutilation, mental deficiency, and gout. It is caused by the absence of hypoxanthine-guanine phosphoribosyltransferase, which is a necessary enzyme for purine nucleotide formation. The lack of enzyme reduces the level of necessary nucleotides and causes the accumulation of biosynthesis intermediates, which results in the aforementioned unusual behavior.
• Severe combined immunodeficiency (SCID): SCID is characterized by a loss of T cells. Shortage of these immune system components increases the susceptibility to infectious agents because the affected individuals cannot develop immunological memory. This immunological disorder results from a deficiency in adenosine deanimase activity, which causes a buildup of dATP. These dATP molecules then inhibit ribonucleotide reductase, which prevents of DNA synthesis.
• Huntington's disease: this neurological disease is caused from errors that occur during DNA synthesis. These errors or mutations lead to the expression of a mutant huntingtin protein, which contains repetitive glutamine residues that are encoded by expanding CAG trinucleotide repeats in the gene. Huntington's disease is characterized by neuronal loss and gliosis. Symptoms of the disease include: movement disorder, cognitive decline, and behavioral disorder.

Combinatorics

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Combinatorics

Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.

Combinatorics is well known for the breadth of the problems it tackles. Combinatorial problems arise in many areas of pure mathematics, notably in algebra, probability theory, topology, and geometry, as well as in its many application areas. Many combinatorial questions have historically been considered in isolation, giving an ad hoc solution to a problem arising in some mathematical context. In the later twentieth century, however, powerful and general theoretical methods were developed, making combinatorics into an independent branch of mathematics in its own right. One of the oldest and most accessible parts of combinatorics is graph theory, which by itself has numerous natural connections to other areas. Combinatorics is used frequently in computer science to obtain formulas and estimates in the analysis of algorithms.

A mathematician who studies combinatorics is called a combinatorialist.

Definition

The full scope of combinatorics is not universally agreed upon. According to H.J. Ryser, a definition of the subject is difficult because it crosses so many mathematical subdivisions. Insofar as an area can be described by the types of problems it addresses, combinatorics is involved with:

• the enumeration (counting) of specified structures, sometimes referred to as arrangements or configurations in a very general sense, associated with finite systems,
• the existence of such structures that satisfy certain given criteria,
• the construction of these structures, perhaps in many ways, and
• optimization: finding the "best" structure or solution among several possibilities, be it the "largest", "smallest" or satisfying some other optimality criterion.

Leon Mirsky has said: "combinatorics is a range of linked studies which have something in common and yet diverge widely in their objectives, their methods, and the degree of coherence they have attained." One way to define combinatorics is, perhaps, to describe its subdivisions with their problems and techniques. This is the approach that is used below. However, there are also purely historical reasons for including or not including some topics under the combinatorics umbrella. Although primarily concerned with finite systems, some combinatorial questions and techniques can be extended to an infinite (specifically, countable) but discrete setting.

History

An example of change ringing (with six bells), one of the earliest nontrivial results in graph theory.

 

Main article: History of combinatorics

Basic combinatorial concepts and enumerative results appeared throughout the ancient world. In the 6th century BCE, ancient Indian physician Sushruta asserts in Sushruta Samhita that 63 combinations can be made out of 6 different tastes, taken one at a time, two at a time, etc., thus computing all 2⁶ − 1 possibilities. Greek historian Plutarch discusses an argument between Chrysippus (3rd century BCE) and Hipparchus (2nd century BCE) of a rather delicate enumerative problem, which was later shown to be related to Schröder–Hipparchus numbers. Earlier, in the Ostomachion, Archimedes (3rd century BCE) may have considered the number of configurations of a tiling puzzle, while combinatorial interests possibly were present in lost works by Apollonius.

In the Middle Ages, combinatorics continued to be studied, largely outside of the European civilization. The Indian mathematician Mahāvīra (c. 850) provided formulae for the number of permutations and combinations, and these formulas may have been familiar to Indian mathematicians as early as the 6th century CE. The philosopher and astronomer Rabbi Abraham ibn Ezra (c. 1140) established the symmetry of binomial coefficients, while a closed formula was obtained later by the talmudist and mathematician Levi ben Gerson (better known as Gersonides), in 1321. The arithmetical triangle—a graphical diagram showing relationships among the binomial coefficients—was presented by mathematicians in treatises dating as far back as the 10th century, and would eventually become known as Pascal's triangle. Later, in Medieval England, campanology provided examples of what is now known as Hamiltonian cycles in certain Cayley graphs on permutations.

During the Renaissance, together with the rest of mathematics and the sciences, combinatorics enjoyed a rebirth. Works of Pascal, Newton, Jacob Bernoulli and Euler became foundational in the emerging field. In modern times, the works of J.J. Sylvester (late 19th century) and Percy MacMahon (early 20th century) helped lay the foundation for enumerative and algebraic combinatorics. Graph theory also enjoyed an increase of interest at the same time, especially in connection with the four color problem.

In the second half of the 20th century, combinatorics enjoyed a rapid growth, which led to establishment of dozens of new journals and conferences in the subject. In part, the growth was spurred by new connections and applications to other fields, ranging from algebra to probability, from functional analysis to number theory, etc. These connections shed the boundaries between combinatorics and parts of mathematics and theoretical computer science, but at the same time led to a partial fragmentation of the field.

Approaches and subfields of combinatorics

Enumerative combinatorics

Five binary trees on three vertices, an example of Catalan numbers.

 

Main article: Enumerative combinatorics

Enumerative combinatorics is the most classical area of combinatorics and concentrates on counting the number of certain combinatorial objects. Although counting the number of elements in a set is a rather broad mathematical problem, many of the problems that arise in applications have a relatively simple combinatorial description. Fibonacci numbers is the basic example of a problem in enumerative combinatorics. The twelvefold way provides a unified framework for counting permutations, combinations and partitions.

Analytic combinatorics

Main article: Analytic combinatorics

Analytic combinatorics concerns the enumeration of combinatorial structures using tools from complex analysis and probability theory. In contrast with enumerative combinatorics, which uses explicit combinatorial formulae and generating functions to describe the results, analytic combinatorics aims at obtaining asymptotic formulae.

Partition theory

A plane partition.

 

Main article: Partition theory

Partition theory studies various enumeration and asymptotic problems related to integer partitions, and is closely related to q-series, special functions and orthogonal polynomials. Originally a part of number theory and analysis, it is now considered a part of combinatorics or an independent field. It incorporates the bijective approach and various tools in analysis and analytic number theory and has connections with statistical mechanics. Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representation theory in general.

Graph theory

Petersen graph.

 

Main article: Graph theory

Graphs are fundamental objects in combinatorics. Considerations of graph theory range from enumeration (e.g., the number of graphs on n vertices with k edges) to existing structures (e.g., Hamiltonian cycles) to algebraic representations (e.g., given a graph G and two numbers x and y, does the Tutte polynomial T_G(x,y) have a combinatorial interpretation?). Although there are very strong connections between graph theory and combinatorics, they are sometimes thought of as separate subjects. While combinatorial methods apply to many graph theory problems, the two disciplines are generally used to seek solutions to different types of problems.

Design theory

Main article: Combinatorial design

Design theory is a study of combinatorial designs, which are collections of subsets with certain intersection properties. Block designs are combinatorial designs of a special type. This area is one of the oldest parts of combinatorics, such as in Kirkman's schoolgirl problem proposed in 1850. The solution of the problem is a special case of a Steiner system, which systems play an important role in the classification of finite simple groups. The area has further connections to coding theory and geometric combinatorics.

Combinatorial design theory can be applied to the area of design of experiments. Some of the basic theory of combinatorial designs originated in the statistician Ronald Fisher's work on the design of biological experiments. Modern applications are also found in a wide gamut of areas including finite geometry, tournament scheduling, lotteries, mathematical chemistry, mathematical biology, algorithm design and analysis, networking, group testing and cryptography.

Finite geometry

Main article: Finite geometry

Finite geometry is the study of geometric systems having only a finite number of points. Structures analogous to those found in continuous geometries (Euclidean plane, real projective space, etc.) but defined combinatorially are the main items studied. This area provides a rich source of examples for design theory. It should not be confused with discrete geometry (combinatorial geometry).

Order theory

Hasse diagram of the powerset of {x,y,z} ordered by inclusion.

 

Main article: Order theory

Order theory is the study of partially ordered sets, both finite and infinite. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". Various examples of partial orders appear in algebra, geometry, number theory and throughout combinatorics and graph theory. Notable classes and examples of partial orders include lattices and Boolean algebras.

Matroid theory

Main article: Matroid theory

Matroid theory abstracts part of geometry. It studies the properties of sets (usually, finite sets) of vectors in a vector space that do not depend on the particular coefficients in a linear dependence relation. Not only the structure but also enumerative properties belong to matroid theory. Matroid theory was introduced by Hassler Whitney and studied as a part of order theory. It is now an independent field of study with a number of connections with other parts of combinatorics.

Extremal combinatorics

Main article: Extremal combinatorics

Extremal combinatorics studies how large or how small a collection of finite objects (numbers, graphs, vectors, sets, etc.) can be, if it has to satisfy certain restrictions. Much of extremal combinatorics concerns classes of set systems; this is called extremal set theory. For instance, in an n-element set, what is the largest number of k-element subsets that can pairwise intersect one another? What is the largest number of subsets of which none contains any other? The latter question is answered by Sperner's theorem, which gave rise to much of extremal set theory.

The types of questions addressed in this case are about the largest possible graph which satisfies certain properties. For example, the largest triangle-free graph on 2n vertices is a complete bipartite graph K_n,n. Often it is too hard even to find the extremal answer f(n) exactly and one can only give an asymptotic estimate.

Ramsey theory is another part of extremal combinatorics. It states that any sufficiently large configuration will contain some sort of order. It is an advanced generalization of the pigeonhole principle.

Probabilistic combinatorics

Self-avoiding walk in a square grid graph.

 

Main article: Probabilistic method

In probabilistic combinatorics, the questions are of the following type: what is the probability of a certain property for a random discrete object, such as a random graph? For instance, what is the average number of triangles in a random graph? Probabilistic methods are also used to determine the existence of combinatorial objects with certain prescribed properties (for which explicit examples might be difficult to find), simply by observing that the probability of randomly selecting an object with those properties is greater than 0. This approach (often referred to as the probabilistic method) proved highly effective in applications to extremal combinatorics and graph theory. A closely related area is the study of finite Markov chains, especially on combinatorial objects. Here again probabilistic tools are used to estimate the mixing time.

Often associated with Paul Erdős, who did the pioneering work on the subject, probabilistic combinatorics was traditionally viewed as a set of tools to study problems in other parts of combinatorics. However, with the growth of applications to analyze algorithms in computer science, as well as classical probability, additive number theory, and probabilistic number theory, the area recently grew to become an independent field of combinatorics.

Algebraic combinatorics

Young diagram of a partition (5,4,1).

 

Main article: Algebraic combinatorics

Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra. Algebraic combinatorics has come to be seen more expansively as an area of mathematics where the interaction of combinatorial and algebraic methods is particularly strong and significant. Thus the combinatorial topics may be enumerative in nature or involve matroids, polytopes, partially ordered sets, or finite geometries. On the algebraic side, besides group and representation theory, lattice theory and commutative algebra are common.

Combinatorics on words

Construction of a Thue–Morse infinite word.

 

Main article: Combinatorics on words

Combinatorics on words deals with formal languages. It arose independently within several branches of mathematics, including number theory, group theory and probability. It has applications to enumerative combinatorics, fractal analysis, theoretical computer science, automata theory, and linguistics. While many applications are new, the classical Chomsky–Schützenberger hierarchy of classes of formal grammars is perhaps the best-known result in the field.

Geometric combinatorics

An icosahedron.

 

Main article: Geometric combinatorics

Geometric combinatorics is related to convex and discrete geometry. It asks, for example, how many faces of each dimension a convex polytope can have. Metric properties of polytopes play an important role as well, e.g. the Cauchy theorem on the rigidity of convex polytopes. Special polytopes are also considered, such as permutohedra, associahedra and Birkhoff polytopes. Combinatorial geometry is a historical name for discrete geometry.

It includes a number of subareas such as polyhedral combinatorics (the study of faces of convex polyhedra), convex geometry (the study of convex sets, in particular combinatorics of their intersections), and discrete geometry, which in turn has many applications to computational geometry. The study of regular polytopes, Archimedean solids, and kissing numbers is also a part of geometric combinatorics. Special polytopes are also considered, such as the permutohedron, associahedron and Birkhoff polytope.

Topological combinatorics

Splitting a necklace with two cuts.

 

Main article: Topological combinatorics

Combinatorial analogs of concepts and methods in topology are used to study graph coloring, fair division, partitions, partially ordered sets, decision trees, necklace problems and discrete Morse theory. It should not be confused with combinatorial topology which is an older name for algebraic topology.

Arithmetic combinatorics

Main article: Arithmetic combinatorics

Arithmetic combinatorics arose out of the interplay between number theory, combinatorics, ergodic theory, and harmonic analysis. It is about combinatorial estimates associated with arithmetic operations (addition, subtraction, multiplication, and division). Additive number theory (sometimes also called additive combinatorics) refers to the special case when only the operations of addition and subtraction are involved. One important technique in arithmetic combinatorics is the ergodic theory of dynamical systems.

Infinitary combinatorics

Main article: Infinitary combinatorics

Infinitary combinatorics, or combinatorial set theory, is an extension of ideas in combinatorics to infinite sets. It is a part of set theory, an area of mathematical logic, but uses tools and ideas from both set theory and extremal combinatorics. Some of the things studied include continuous graphs and trees, extensions of Ramsey's theorem, and Martin's axiom. Recent developments concern combinatorics of the continuum and combinatorics on successors of singular cardinals.

Gian-Carlo Rota used the name continuous combinatorics to describe geometric probability, since there are many analogies between counting and measure.

Related fields

Kissing spheres are connected to both coding theory and discrete geometry.

Combinatorial optimization

Combinatorial optimization is the study of optimization on discrete and combinatorial objects. It started as a part of combinatorics and graph theory, but is now viewed as a branch of applied mathematics and computer science, related to operations research, algorithm theory and computational complexity theory.

Coding theory

Coding theory started as a part of design theory with early combinatorial constructions of error-correcting codes. The main idea of the subject is to design efficient and reliable methods of data transmission. It is now a large field of study, part of information theory.

Discrete and computational geometry

Discrete geometry (also called combinatorial geometry) also began as a part of combinatorics, with early results on convex polytopes and kissing numbers. With the emergence of applications of discrete geometry to computational geometry, these two fields partially merged and became a separate field of study. There remain many connections with geometric and topological combinatorics, which themselves can be viewed as outgrowths of the early discrete geometry.

Combinatorics and dynamical systems

Combinatorial aspects of dynamical systems is another emerging field. Here dynamical systems can be defined on combinatorial objects. See for example graph dynamical system.

Combinatorics and physics

There are increasing interactions between combinatorics and physics, particularly statistical physics. Examples include an exact solution of the Ising model, and a connection between the Potts model on one hand, and the chromatic and Tutte polynomials on the other hand.