From Wikipedia, the free encyclopedia
A Fourier series () is a sum that represents a periodic function as a sum of sine and cosine waves. The frequency of each wave in the sum, or harmonic, is an integer multiple of the periodic function's fundamental frequency. Each harmonic's phase and amplitude can be determined using harmonic analysis. A Fourier series may potentially contain an infinite
number of harmonics. Summing part of but not all the harmonics in a
function's Fourier series produces an approximation to that function.
For example, using the first few harmonics of the Fourier series for a square wave yields an approximation of a square wave.
A square wave (represented as the blue dot) is approximated by its
sixth partial sum (represented as the purple dot), formed by summing the
first six terms (represented as arrows) of the square wave's Fourier
series. Each arrow starts at the vertical sum of all the arrows to its
left (i.e. the previous partial sum).
The first four partial sums of the Fourier series for a square wave. As more harmonics are added, the partial sums converge to (become more and more like) the square wave.
Function  (in red) is a Fourier series sum of 6 harmonically related sine waves (in blue). Its Fourier transform
(in red) is a Fourier series sum of 6 harmonically related sine waves (in blue). Its Fourier transform  is a frequency-domain representation that reveals the amplitudes of the summed sine waves.
is a frequency-domain representation that reveals the amplitudes of the summed sine waves.
Almost any periodic function can be represented by a Fourier series that converges. Convergence of Fourier series means that as more and more harmonics from the series are summed, each successive partial Fourier series sum will better approximate the function, and will equal the function with a potentially infinite number of harmonics. The mathematical proofs for this may be collectively referred to as the Fourier Theorem (see § Convergence).
Fourier series can only represent functions that are periodic.
However, non-periodic functions can be handled using an extension of the
Fourier Series called the Fourier transform which treats non-periodic functions as periodic with infinite period. This transform thus can generate frequency domain representations of non-periodic functions as well as periodic functions, allowing a waveform to be converted between its time domain representation and its frequency domain representation.
Since Fourier's
time, many different approaches to defining and understanding the
concept of Fourier series have been discovered, all of which are
consistent with one another, but each of which emphasizes different
aspects of the topic. Some of the more powerful and elegant approaches
are based on mathematical ideas and tools that were not available in
Fourier's time. Fourier originally defined the Fourier series for real-valued functions of real arguments, and used the sine and cosine functions as the basis set for the decomposition. Many other Fourier-related transforms have since been defined, extending his initial idea to many applications and birthing an area of mathematics called Fourier analysis.
Definition
The Fourier series  represents a synthesis of a periodic function
represents a synthesis of a periodic function  by summing harmonically related sinusoids (called harmonics) whose coefficients are determined by harmonic analysis.
by summing harmonically related sinusoids (called harmonics) whose coefficients are determined by harmonic analysis.
Common forms
The Fourier series can be represented in different forms. The amplitude-phase form, sine-cosine form, and exponential form are commonly used and are expressed here for a real-valued function  . (See § Complex-valued functions and § Other common notations for alternative forms).
. (See § Complex-valued functions and § Other common notations for alternative forms).
The number of terms summed,  , is a potentially infinite integer. Even so, the series might not converge or exactly equate to
, is a potentially infinite integer. Even so, the series might not converge or exactly equate to  at all values of
at all values of  (such as a single-point discontinuity) in the analysis interval. For the well-behaved functions typical of physical processes, equality is customarily assumed, and the Dirichlet conditions provide sufficient conditions.
(such as a single-point discontinuity) in the analysis interval. For the well-behaved functions typical of physical processes, equality is customarily assumed, and the Dirichlet conditions provide sufficient conditions.
The integer index,  , is also the number of cycles the
, is also the number of cycles the  harmonic makes in the function's period
harmonic makes in the function's period  . Therefore:
. Therefore:
- The
 harmonic's wavelength is
harmonic's wavelength is  and in units of
and in units of  .
. - The
 harmonic's frequency is
harmonic's frequency is  and in reciprocal units of
and in reciprocal units of  .
.
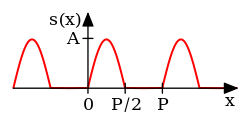
Fig 1. The top graph shows a non-periodic function s(x) in blue defined only over the red interval from 0 to P.
The function can be analyzed over this interval to produce the Fourier
series in the bottom graph. The Fourier series is always a periodic
function, even if original function s(x) wasn't.
Amplitude-phase form
The Fourier series in amplitude-phase form is:
Fourier series, amplitude-phase form
 |
|
(Eq.1)
|
- Its
 harmonic is
harmonic is  .
.  is the
is the  harmonic's amplitude and
harmonic's amplitude and  is its phase shift.
is its phase shift.- The fundamental frequency of
 is the term for when
is the term for when  equals 1, and can be referred to as the
equals 1, and can be referred to as the  harmonic.
harmonic.  is sometimes called the
is sometimes called the  harmonic or DC component. It is the mean value of
harmonic or DC component. It is the mean value of  .
.
Clearly Eq.1
can represent functions that are just a sum of one or more of the
harmonic frequencies. The remarkable thing, for those not yet familiar
with this concept, is that it can also represent the intermediate
frequencies and/or non-sinusoidal functions because of the potentially
infinite number of terms ( ).
).
Fig
2. The blue curve is the cross-correlation of a square wave and a
cosine function, as the phase lag of the cosine varies over one cycle.
The amplitude and phase lag at the maximum value are the polar
coordinates of one harmonic in the Fourier series expansion of the
square wave. The corresponding Cartesian coordinates can be determined
by evaluating the cross-correlation at just two phase lags separated by
90º.
The coefficients  and
and  can be determined by a harmonic analysis process. Consider a real-valued function
can be determined by a harmonic analysis process. Consider a real-valued function  that is integrable on an interval that starts at any
that is integrable on an interval that starts at any  and has length
and has length  . The cross-correlation function:
. The cross-correlation function:
![{\displaystyle \mathrm {X} _{f}(\tau )={\tfrac {2}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\cdot \cos \left(2\pi f(x-\tau )\right)\,dx;\quad \tau \in \left[0,{\tfrac {2\pi }{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5240eaa70571932d715193314ccebab98f25b305) |
|
(Eq.2)
|
is essentially a matched filter, with template  . The maximum of
. The maximum of  is a measure of the amplitude
is a measure of the amplitude  of frequency
of frequency  in the function
in the function  , and the value of
, and the value of  at the maximum determines the phase
at the maximum determines the phase  of that frequency. Figure 2 is an example, where
of that frequency. Figure 2 is an example, where  is a square wave (not shown), and frequency
is a square wave (not shown), and frequency  is the
is the  harmonic.
harmonic.
Rather than computationally intensive cross-correlation which requires evaluating every phase, Fourier analysis exploits a trigonometric identity:
Equivalence of polar and Cartesian forms
 |
|
(Eq.3)
|
Substituting this into Eq.2 gives:
![{\displaystyle {\begin{aligned}\mathrm {X} _{n}(\varphi )&={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left({\tfrac {2\pi }{P}}nx-\varphi \right)\,dx;\quad \varphi \in [0,2\pi ]\\&=\cos(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left({\tfrac {2\pi }{P}}nx\right)\,dx} _{\triangleq \ a_{n}}+\sin(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \sin \left({\tfrac {2\pi }{P}}nx\right)\,dx} _{\triangleq \ b_{n}}\\&=\cos(\varphi )\cdot a_{n}+\sin(\varphi )\cdot b_{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b65590f785d22d6b81e65752068b5555a7af90a)
Note the definitions of  and
and  , and that
, and that  and
and  can be simplified:
can be simplified:

The derivative of

is zero at the phase of maximum correlation.

And the correlation peak value is:

 and
and  are the Cartesian coordinates of a vector with polar coordinates
are the Cartesian coordinates of a vector with polar coordinates  and
and  Figure 2 is an example of these relationships.
Figure 2 is an example of these relationships.
Sine-cosine form
Substituting Eq.3 into Eq.1 gives:
![{\displaystyle {\displaystyle s_{\scriptscriptstyle N}(x)={\frac {A_{0}}{2}}+\sum _{n=1}^{N}\left[A_{n}\cos(\varphi _{n})\cdot \cos \left({\tfrac {2\pi }{P}}nx\right)+A_{n}\sin(\varphi _{n})\cdot \sin \left({\tfrac {2\pi }{P}}nx\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e904306df1ed48e64053b1f579c8bfab5508157)
In terms of the readily computed quantities,  and
and  , recall that:
, recall that:



Therefore an alternative form of the Fourier series, using the Cartesian coordinates, is the sine-cosine form:
Fourier series, sine-cosine form
 |
|
(Eq.4)
|
Exponential form
Another applicable identity is Euler's formula:
![{\displaystyle {\begin{aligned}\cos \left({\tfrac {2\pi }{P}}nx-\varphi _{n}\right)&{}\equiv {\tfrac {1}{2}}e^{i\left(2\pi nx/P-\varphi _{n}\right)}+{\tfrac {1}{2}}e^{-i\left(2\pi nx/P-\varphi _{n}\right)}\\[6pt]&=\left({\tfrac {1}{2}}e^{-i\varphi _{n}}\right)\cdot e^{i2\pi (+n)x/P}+\left({\tfrac {1}{2}}e^{-i\varphi _{n}}\right)^{*}\cdot e^{i2\pi (-n)x/P}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ccce1b987630c62705a4a1c8750077d2cd2ade7)
(Note: the ∗ denotes complex conjugation.)
Therefore, with definitions:

the final result is:
Fourier series, exponential form
 |
|
(Eq.5)
|
This is the customary form for generalizing to § Complex-valued functions. Negative values of  correspond to negative frequency (explained in Fourier transform § Use of complex sinusoids to represent real sinusoids).
correspond to negative frequency (explained in Fourier transform § Use of complex sinusoids to represent real sinusoids).
Example
Plot of the
sawtooth wave, a periodic continuation of the linear function

on the interval
![(-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)
Animated plot of the first five successive partial Fourier series
Consider a sawtooth function:


In this case, the Fourier coefficients are given by
![{\displaystyle {\begin{aligned}a_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0.\\[4pt]b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd645b661c531998472837b4709b23bf2d2c939)
It can be shown that the Fourier series converges to  at every point
at every point  where
where  is differentiable, and therefore:
is differentiable, and therefore:
-
![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c051045100b8d31eada1c7fcfd414759404ed25b)
|
|
(Eq.6)
|
When  , the Fourier series converges to 0, which is the half-sum of the left- and right-limit of s at
, the Fourier series converges to 0, which is the half-sum of the left- and right-limit of s at  . This is a particular instance of the Dirichlet theorem for Fourier series.
. This is a particular instance of the Dirichlet theorem for Fourier series.
This example leads to a solution of the Basel problem.
Convergence
A proof that a Fourier series is a valid representation of any periodic function (that satisfies the Dirichlet conditions) is overviewed in § Fourier theorem proving convergence of Fourier series.
In engineering
applications, the Fourier series is generally presumed to converge
almost everywhere (the exceptions being at discrete discontinuities)
since the functions encountered in engineering are better-behaved than
the functions that mathematicians can provide as counter-examples to
this presumption. In particular, if  is continuous and the derivative of
is continuous and the derivative of  (which may not exist everywhere) is square integrable, then the Fourier series of
(which may not exist everywhere) is square integrable, then the Fourier series of  converges absolutely and uniformly to
converges absolutely and uniformly to  .[3] If a function is square-integrable on the interval
.[3] If a function is square-integrable on the interval ![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba) , then the Fourier series converges to the function at almost every point.
It is possible to define Fourier coefficients for more general
functions or distributions, in such cases convergence in norm or weak convergence is usually of interest.
, then the Fourier series converges to the function at almost every point.
It is possible to define Fourier coefficients for more general
functions or distributions, in such cases convergence in norm or weak convergence is usually of interest.
Four partial sums (Fourier series) of lengths 1, 2, 3, and 4 terms,
showing how the approximation to a square wave improves as the number of
terms increases (animation)
Four partial sums (Fourier series) of lengths 1, 2, 3, and 4 terms,
showing how the approximation to a sawtooth wave improves as the number
of terms increases (animation)
Example of convergence to a somewhat arbitrary function. Note the development of the "ringing" (Gibbs phenomenon) at the transitions to/from the vertical sections.
Complex-valued functions
If  is a complex-valued function of a real variable
is a complex-valued function of a real variable  both components (real and imaginary part) are real-valued functions
that can be represented by a Fourier series. The two sets of
coefficients and the partial sum are given by:
both components (real and imaginary part) are real-valued functions
that can be represented by a Fourier series. The two sets of
coefficients and the partial sum are given by:
 and
and 

Defining  yields:
yields:
 |
|
(Eq.7)
|
This is identical to Eq.5 except  and
and  are no longer complex conjugates. The formula for
are no longer complex conjugates. The formula for  is also unchanged:
is also unchanged:
![{\displaystyle {\begin{aligned}c_{n}&={\tfrac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\frac {2\pi }{P}}nx}\ dx+i\cdot {\tfrac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\\[4pt]&={\tfrac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\ =\ {\tfrac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2f3a7cab08bd95f922c1fbc2f921addb4edfcd3)
Other common notations
The notation  is inadequate for discussing the Fourier coefficients of several
different functions. Therefore, it is customarily replaced by a modified
form of the function (
is inadequate for discussing the Fourier coefficients of several
different functions. Therefore, it is customarily replaced by a modified
form of the function ( , in this case), such as
, in this case), such as ![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea) or
or ![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586) , and functional notation often replaces subscripting:
, and functional notation often replaces subscripting:
![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}[n]\cdot e^{i\,2\pi nx/P}\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}&&\scriptstyle {\mathsf {common\ engineering\ notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1a1ac253b5d7a763eff884963eb5efbc5dd0879)
In engineering, particularly when the variable  represents time, the coefficient sequence is called a frequency domain representation. Square brackets are often used to emphasize that the domain of this function is a discrete set of frequencies.
represents time, the coefficient sequence is called a frequency domain representation. Square brackets are often used to emphasize that the domain of this function is a discrete set of frequencies.
Another commonly used frequency domain representation uses the Fourier series coefficients to modulate a Dirac comb:
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)
where  represents a continuous frequency domain. When variable
represents a continuous frequency domain. When variable  has units of seconds,
has units of seconds,  has units of hertz. The "teeth" of the comb are spaced at multiples (i.e. harmonics) of
has units of hertz. The "teeth" of the comb are spaced at multiples (i.e. harmonics) of  , which is called the fundamental frequency.
, which is called the fundamental frequency.  can be recovered from this representation by an inverse Fourier transform:
can be recovered from this representation by an inverse Fourier transform:
![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)
The constructed function  is therefore commonly referred to as a Fourier transform, even though the Fourier integral of a periodic function is not convergent at the harmonic frequencies.
is therefore commonly referred to as a Fourier transform, even though the Fourier integral of a periodic function is not convergent at the harmonic frequencies.
History
The Fourier series is named in honor of Jean-Baptiste Joseph Fourier (1768–1830), who made important contributions to the study of trigonometric series, after preliminary investigations by Leonhard Euler, Jean le Rond d'Alembert, and Daniel Bernoulli. Fourier introduced the series for the purpose of solving the heat equation in a metal plate, publishing his initial results in his 1807 Mémoire sur la propagation de la chaleur dans les corps solides (Treatise on the propagation of heat in solid bodies), and publishing his Théorie analytique de la chaleur (Analytical theory of heat) in 1822. The Mémoire
introduced Fourier analysis, specifically Fourier series. Through
Fourier's research the fact was established that an arbitrary (at first,
continuous and later generalized to any piecewise-smooth)
function can be represented by a trigonometric series. The first
announcement of this great discovery was made by Fourier in 1807, before
the French Academy.
Early ideas of decomposing a periodic function into the sum of simple
oscillating functions date back to the 3rd century BC, when ancient
astronomers proposed an empiric model of planetary motions, based on deferents and epicycles.
The heat equation is a partial differential equation.
Prior to Fourier's work, no solution to the heat equation was known in
the general case, although particular solutions were known if the heat
source behaved in a simple way, in particular, if the heat source was a sine or cosine wave. These simple solutions are now sometimes called eigensolutions. Fourier's idea was to model a complicated heat source as a superposition (or linear combination) of simple sine and cosine waves, and to write the solution as a superposition of the corresponding eigensolutions. This superposition or linear combination is called the Fourier series.
From a modern point of view, Fourier's results are somewhat informal, due to the lack of a precise notion of function and integral in the early nineteenth century. Later, Peter Gustav Lejeune Dirichlet and Bernhard Riemann expressed Fourier's results with greater precision and formality.
Although the original motivation was to solve the heat equation,
it later became obvious that the same techniques could be applied to a
wide array of mathematical and physical problems, and especially those
involving linear differential equations with constant coefficients, for
which the eigensolutions are sinusoids. The Fourier series has many such applications in electrical engineering, vibration analysis, acoustics, optics, signal processing, image processing, quantum mechanics, econometrics, shell theory, etc.
Beginnings
Joseph Fourier wrote:

Multiplying both sides by  , and then integrating from
, and then integrating from  to
to  yields:
yields:

This immediately gives any coefficient ak of the trigonometrical series for φ(y)
for any function which has such an expansion. It works because if φ has
such an expansion, then (under suitable convergence assumptions) the
integral

can be carried out term-by-term. But all terms involving

for
j ≠ k vanish when integrated from −1 to 1, leaving only the

term.
In these few lines, which are close to the modern formalism
used in Fourier series, Fourier revolutionized both mathematics and
physics. Although similar trigonometric series were previously used by Euler, d'Alembert, Daniel Bernoulli and Gauss,
Fourier believed that such trigonometric series could represent any
arbitrary function. In what sense that is actually true is a somewhat
subtle issue and the attempts over many years to clarify this idea have
led to important discoveries in the theories of convergence, function spaces, and harmonic analysis.
When Fourier submitted a later competition essay in 1811, the committee (which included Lagrange, Laplace, Malus and Legendre, among others) concluded: ...the
manner in which the author arrives at these equations is not exempt of
difficulties and...his analysis to integrate them still leaves something
to be desired on the score of generality and even rigour.
Fourier's motivation
Heat distribution in a metal plate, using Fourier's method
The Fourier series expansion of the sawtooth function (above) looks more complicated than the simple formula  ,
so it is not immediately apparent why one would need the Fourier
series. While there are many applications, Fourier's motivation was in
solving the heat equation. For example, consider a metal plate in the shape of a square whose sides measure
,
so it is not immediately apparent why one would need the Fourier
series. While there are many applications, Fourier's motivation was in
solving the heat equation. For example, consider a metal plate in the shape of a square whose sides measure  meters, with coordinates
meters, with coordinates ![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610) .
If there is no heat source within the plate, and if three of the four
sides are held at 0 degrees Celsius, while the fourth side, given by
.
If there is no heat source within the plate, and if three of the four
sides are held at 0 degrees Celsius, while the fourth side, given by  , is maintained at the temperature gradient
, is maintained at the temperature gradient  degrees Celsius, for
degrees Celsius, for  in
in  ,
then one can show that the stationary heat distribution (or the heat
distribution after a long period of time has elapsed) is given by
,
then one can show that the stationary heat distribution (or the heat
distribution after a long period of time has elapsed) is given by

Here, sinh is the hyperbolic sine function. This solution of the heat equation is obtained by multiplying each term of Eq.6 by  . While our example function
. While our example function  seems to have a needlessly complicated Fourier series, the heat distribution
seems to have a needlessly complicated Fourier series, the heat distribution  is nontrivial. The function
is nontrivial. The function  cannot be written as a closed-form expression. This method of solving the heat problem was made possible by Fourier's work.
cannot be written as a closed-form expression. This method of solving the heat problem was made possible by Fourier's work.
Complex Fourier series animation
An example of the ability of the complex Fourier series to trace any
two dimensional closed figure is shown in the adjacent animation of the
complex Fourier series tracing the letter 'e' (for exponential). Note
that the animation uses the variable 't' to parameterize the letter 'e'
in the complex plane, which is equivalent to using the parameter 'x' in
this article's subsection on complex valued functions.
In the animation's back plane, the rotating vectors are
aggregated in an order that alternates between a vector rotating in the
positive (counter clockwise) direction and a vector rotating at the same
frequency but in the negative (clockwise) direction, resulting in a
single tracing arm with lots of zigzags. This perspective shows how the
addition of each pair of rotating vectors (one rotating in the positive
direction and one rotating in the negative direction) nudges the
previous trace (shown as a light gray dotted line) closer to the shape
of the letter 'e'.
In the animation's front plane, the rotating vectors are
aggregated into two sets, the set of all the positive rotating vectors
and the set of all the negative rotating vectors (the non-rotating
component is evenly split between the two), resulting in two tracing
arms rotating in opposite directions. The animation's small circle
denotes the midpoint between the two arms and also the midpoint between
the origin and the current tracing point denoted by '+'. This
perspective shows how the complex Fourier series is an extension (the
addition of an arm) of the complex geometric series which has just one
arm. It also shows how the two arms coordinate with each other. For
example, as the tracing point is rotating in the positive direction, the
negative direction arm stays parked. Similarly, when the tracing point
is rotating in the negative direction, the positive direction arm stays
parked.
In between the animation's back and front planes are rotating
trapezoids whose areas represent the values of the complex Fourier
series terms. This perspective shows the amplitude, frequency, and phase
of the individual terms of the complex Fourier series in relation to
the series sum spatially converging to the letter 'e' in the back and
front planes. The audio track's left and right channels correspond
respectively to the real and imaginary components of the current tracing
point '+' but increased in frequency by a factor of 3536 so that the
animation's fundamental frequency (n=1) is a 220 Hz tone (A220).
Other applications
The discrete-time Fourier transform is an example of a Fourier series.
Another application is to solve the Basel problem by using Parseval's theorem. The example generalizes and one may compute ζ(2n), for any positive integern.
Table of common Fourier series
Some common pairs of periodic functions and their Fourier Series coefficients are shown in the table below.
 designates a periodic function defined on
designates a periodic function defined on  .
. designate the Fourier Series coefficients (sine-cosine form) of the periodic function
designate the Fourier Series coefficients (sine-cosine form) of the periodic function  .
.
Time domain

|
Plot
|
Frequency domain (sine-cosine form)

|
Remarks
|

|
|

|
Full-wave rectified sine
|

|
|

|
Half-wave rectified sine
|

|
|

|

|

|
|

|
|

|
|

|
|

|
|

|
|
Table of basic properties
This
table shows some mathematical operations in the time domain and the
corresponding effect in the Fourier series coefficients. Notation:
- Complex conjugation is denoted by an asterisk.
 designate
designate  -periodic functions or functions defined only for
-periodic functions or functions defined only for ![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f) designate the Fourier series coefficients (exponential form) of
designate the Fourier series coefficients (exponential form) of  and
and 
| Property
|
Time domain
|
Frequency domain (exponential form)
|
Remarks
|
| Linearity
|

|
![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)
|

|
| Time reversal / Frequency reversal
|

|
![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)
|
|
| Time conjugation
|

|
![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)
|
|
| Time reversal & conjugation
|

|
![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)
|
|
| Real part in time
|

|
![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)
|
|
| Imaginary part in time
|

|
![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)
|
|
| Real part in frequency
|

|
![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)
|
|
| Imaginary part in frequency
|

|
![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)
|
|
| Shift in time / Modulation in frequency
|

|
![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb7150e991a2642dc0c62cdee40602d99227420)
|

|
| Shift in frequency / Modulation in time
|

|
![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)
|

|
Symmetry properties
When the real and imaginary parts of a complex function are decomposed into their even and odd parts,
there are four components, denoted below by the subscripts RE, RO, IE,
and IO. And there is a one-to-one mapping between the four components of
a complex time function and the four components of its complex
frequency transform:

From this, various relationships are apparent, for example:
- The transform of a real-valued function (sRE + sRO) is the even symmetric function SRE + i SIO. Conversely, an even-symmetric transform implies a real-valued time-domain.
- The transform of an imaginary-valued function (i sIE + i sIO) is the odd symmetric function SRO + i SIE, and the converse is true.
- The transform of an even-symmetric function (sRE + i sIO) is the real-valued function SRE + SRO, and the converse is true.
- The transform of an odd-symmetric function (sRO + i sIE) is the imaginary-valued function i SIE + i SIO, and the converse is true.
Other properties
Riemann–Lebesgue lemma
If  is integrable,
is integrable, ![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5) ,
,  and
and  This result is known as the Riemann–Lebesgue lemma.
This result is known as the Riemann–Lebesgue lemma.
If  belongs to
belongs to  (an interval of length
(an interval of length  ) then:
) then: ![{\textstyle \sum _{n=-\infty }^{\infty }{\Bigl |}S[n]{\Bigr |}^{2}={\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45449c99cf90bed698c4b3797561759081fc2e5)
If  are coefficients and
are coefficients and  then there is a unique function
then there is a unique function  such that
such that ![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140) for every
for every  .
.
Convolution theorems
Given  -periodic functions,
-periodic functions,  and
and  with Fourier series coefficients
with Fourier series coefficients ![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586) and
and ![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)

- The pointwise product:

 -periodic, and its Fourier series coefficients are given by the discrete convolution of the
-periodic, and its Fourier series coefficients are given by the discrete convolution of the  and
and  sequences:
sequences: ![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)
- The periodic convolution:

 -periodic, with Fourier series coefficients:
-periodic, with Fourier series coefficients: ![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)
- A doubly infinite sequence
 in
in  is the sequence of Fourier coefficients of a function in
is the sequence of Fourier coefficients of a function in ![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8) if and only if it is a convolution of two sequences in
if and only if it is a convolution of two sequences in  .
.
Derivative property
We say that  belongs to
belongs to
 if
if  is a 2π-periodic function on
is a 2π-periodic function on  which is
which is  times differentiable, and its
times differentiable, and its  derivative is continuous.
derivative is continuous.
- If
 , then the Fourier coefficients
, then the Fourier coefficients ![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed) of the derivative
of the derivative  can be expressed in terms of the Fourier coefficients
can be expressed in terms of the Fourier coefficients ![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b) of the function
of the function  , via the formula
, via the formula ![{\displaystyle {\widehat {s'}}[n]=in{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6) .
. - If
 , then
, then ![{\displaystyle {\widehat {s^{(k)}}}[n]=(in)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20) . In particular, since for a fixed
. In particular, since for a fixed  we have
we have ![{\displaystyle {\widehat {s^{(k)}}}[n]\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1) as
as  , it follows that
, it follows that ![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c) tends to zero, which means that the Fourier coefficients converge to zero faster than the kth power of n for any
tends to zero, which means that the Fourier coefficients converge to zero faster than the kth power of n for any  .
.
Compact groups
One of the interesting properties of the Fourier transform which we
have mentioned, is that it carries convolutions to pointwise products.
If that is the property which we seek to preserve, one can produce
Fourier series on any compact group. Typical examples include those classical groups that are compact. This generalizes the Fourier transform to all spaces of the form L2(G), where G is a compact group, in such a way that the Fourier transform carries convolutions to pointwise products. The Fourier series exists and converges in similar ways to the [−π,π] case.
An alternative extension to compact groups is the Peter–Weyl theorem, which proves results about representations of compact groups analogous to those about finite groups.
Riemannian manifolds
If the domain is not a group, then there is no intrinsically defined convolution. However, if  is a compact Riemannian manifold, it has a Laplace–Beltrami operator. The Laplace–Beltrami operator is the differential operator that corresponds to Laplace operator for the Riemannian manifold
is a compact Riemannian manifold, it has a Laplace–Beltrami operator. The Laplace–Beltrami operator is the differential operator that corresponds to Laplace operator for the Riemannian manifold  . Then, by analogy, one can consider heat equations on
. Then, by analogy, one can consider heat equations on  .
Since Fourier arrived at his basis by attempting to solve the heat
equation, the natural generalization is to use the eigensolutions of the
Laplace–Beltrami operator as a basis. This generalizes Fourier series
to spaces of the type
.
Since Fourier arrived at his basis by attempting to solve the heat
equation, the natural generalization is to use the eigensolutions of the
Laplace–Beltrami operator as a basis. This generalizes Fourier series
to spaces of the type  , where
, where  is a Riemannian manifold. The Fourier series converges in ways similar to the
is a Riemannian manifold. The Fourier series converges in ways similar to the ![[-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) case. A typical example is to take
case. A typical example is to take  to be the sphere with the usual metric, in which case the Fourier basis consists of spherical harmonics.
to be the sphere with the usual metric, in which case the Fourier basis consists of spherical harmonics.
Locally compact Abelian groups
The generalization to compact groups discussed above does not generalize to noncompact, nonabelian groups. However, there is a straightforward generalization to Locally Compact Abelian (LCA) groups.
This generalizes the Fourier transform to  or
or  , where
, where  is an LCA group. If
is an LCA group. If  is compact, one also obtains a Fourier series, which converges similarly to the
is compact, one also obtains a Fourier series, which converges similarly to the ![[-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) case, but if
case, but if  is noncompact, one obtains instead a Fourier integral. This generalization yields the usual Fourier transform when the underlying locally compact Abelian group is
is noncompact, one obtains instead a Fourier integral. This generalization yields the usual Fourier transform when the underlying locally compact Abelian group is  .
.
Extensions
Fourier series on a square
We can also define the Fourier series for functions of two variables  and
and  in the square
in the square ![{\displaystyle [-\pi ,\pi ]\times [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb) :
:
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\\[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)
Aside from being useful for solving partial differential
equations such as the heat equation, one notable application of Fourier
series on the square is in image compression. In particular, the jpeg image compression standard uses the two-dimensional discrete cosine transform, a discrete form of the Fourier cosine transform, which uses only cosine as the basis function.
For two-dimensional arrays with a staggered appearance, half of
the Fourier series coefficients disappear, due to additional symmetry.
Fourier series of Bravais-lattice-periodic-function
A three-dimensional Bravais lattice is defined as the set of vectors of the form:

where

are integers and

are three linearly independent vectors. Assuming we have some function,

, such that it obeys the condition of periodicity for any Bravais lattice vector

,

,
we could make a Fourier series of it. This kind of function can be, for
example, the effective potential that one electron "feels" inside a
periodic crystal. It is useful to make the Fourier series of the
potential when applying
Bloch's theorem. First, we may write any arbitrary position vector

in the coordinate-system of the lattice:

where

meaning that

is defined to be the magnitude of

, so

is the unit vector directed along

.
Thus we can define a new function,

This new function,  , is now a function of three-variables, each of which has periodicity
, is now a function of three-variables, each of which has periodicity  ,
,  , and
, and  respectively:
respectively:

This enables us to build up a set of Fourier coefficients, each being indexed by three independent integers  .
In what follows, we use function notation to denote these coefficients,
where previously we used subscripts. If we write a series for
.
In what follows, we use function notation to denote these coefficients,
where previously we used subscripts. If we write a series for  on the interval
on the interval ![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac) for
for  , we can define the following:
, we can define the following:

And then we can write:

Further defining:
![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&\triangleq {\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)
We can write  once again as:
once again as:

Finally applying the same for the third coordinate, we define:
![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&\triangleq {\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)
We write  as:
as:

Re-arranging:

Now, every reciprocal lattice vector can be written (but does not mean that it is the only way of writing) as  , where
, where  are integers and
are integers and  are reciprocal lattice vectors to satisfy
are reciprocal lattice vectors to satisfy  (
( for
for  , and
, and  for
for  ). Then for any arbitrary reciprocal lattice vector
). Then for any arbitrary reciprocal lattice vector  and arbitrary position vector
and arbitrary position vector  in the original Bravais lattice space, their scalar product is:
in the original Bravais lattice space, their scalar product is:

So it is clear that in our expansion of  , the sum is actually over reciprocal lattice vectors:
, the sum is actually over reciprocal lattice vectors:

where

Assuming

we can solve this system of three linear equations for

,

, and

in terms of

,

and

in order to calculate the volume element in the original cartesian coordinate system. Once we have

,

, and

in terms of

,

and

, we can calculate the
Jacobian determinant:
![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)
which after some calculation and applying some non-trivial cross-product identities can be shown to be equal to:

(it may be advantageous for the sake of simplifying
calculations, to work in such a Cartesian coordinate system, in which it
just so happens that  is parallel to the x axis,
is parallel to the x axis,  lies in the xy-plane, and
lies in the xy-plane, and  has components of all three axes). The denominator is exactly the
volume of the primitive unit cell which is enclosed by the three
primitive-vectors
has components of all three axes). The denominator is exactly the
volume of the primitive unit cell which is enclosed by the three
primitive-vectors  ,
,  and
and  . In particular, we now know that
. In particular, we now know that

We can write now  as an integral with the traditional coordinate system over the volume of the primitive cell, instead of with the
as an integral with the traditional coordinate system over the volume of the primitive cell, instead of with the  ,
,  and
and  variables:
variables:

writing

for the volume element

; and where

is the primitive unit cell, thus,

is the volume of the primitive unit cell.
Hilbert space interpretation
In the language of Hilbert spaces, the set of functions  is an orthonormal basis for the space
is an orthonormal basis for the space ![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) of square-integrable functions on
of square-integrable functions on ![[-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) . This space is actually a Hilbert space with an inner product given for any two elements
. This space is actually a Hilbert space with an inner product given for any two elements  and
and  by:
by:
 where
where  is the complex conjugate of
is the complex conjugate of 
The basic Fourier series result for Hilbert spaces can be written as

Sines
and cosines form an orthonormal set, as illustrated above. The integral
of sine, cosine and their product is zero (green and red areas are
equal, and cancel out) when

,

or the functions are different, and π only if

and

are equal, and the function used is the same.
This corresponds exactly to the complex exponential formulation given
above. The version with sines and cosines is also justified with the
Hilbert space interpretation. Indeed, the sines and cosines form an orthogonal set:


(where
δmn is the
Kronecker delta), and

furthermore, the sines and cosines are orthogonal to the constant function

. An
orthonormal basis for
![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)
consisting of real functions is formed by the functions

and

,

with
n= 1,2,.... The density of their span is a consequence of the
Stone–Weierstrass theorem, but follows also from the properties of classical kernels like the
Fejér kernel.
Fourier theorem proving convergence of Fourier series
These theorems, and informal variations of them that don't specify
the convergence conditions, are sometimes referred to generically as Fourier's theorem or the Fourier theorem.[22][23][24][25]
The earlier Eq.7
![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i{\tfrac {2\pi }{P}}nx},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b030eaf773387de3787b4a003ef7599624be959)
is a
trigonometric polynomial of degree

that can be generally expressed as:
![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i{\tfrac {2\pi }{P}}nx}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a29c02020f3c186b790b680deabe8e985ebcd700)
Least squares property
Parseval's theorem implies that:
Convergence theorems
Because of the least squares property, and because of the
completeness of the Fourier basis, we obtain an elementary convergence
result.
We have already mentioned that if  is continuously differentiable, then
is continuously differentiable, then ![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762) is the
is the  Fourier coefficient of the derivative
Fourier coefficient of the derivative  . It follows, essentially from the Cauchy–Schwarz inequality, that
. It follows, essentially from the Cauchy–Schwarz inequality, that  is absolutely summable. The sum of this series is a continuous function, equal to
is absolutely summable. The sum of this series is a continuous function, equal to  , since the Fourier series converges in the mean to
, since the Fourier series converges in the mean to  :
:
This result can be proven easily if  is further assumed to be
is further assumed to be  , since in that case
, since in that case ![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d) tends to zero as
tends to zero as  . More generally, the Fourier series is absolutely summable, thus converges uniformly to
. More generally, the Fourier series is absolutely summable, thus converges uniformly to  , provided that
, provided that  satisfies a Hölder condition of order
satisfies a Hölder condition of order  . In the absolutely summable case, the inequality:
. In the absolutely summable case, the inequality:
![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)
proves uniform convergence.
Many other results concerning the convergence of Fourier series are known, ranging from the moderately simple result that the series converges at  if
if  is differentiable at
is differentiable at  , to Lennart Carleson's much more sophisticated result that the Fourier series of an
, to Lennart Carleson's much more sophisticated result that the Fourier series of an  function actually converges almost everywhere.
function actually converges almost everywhere.
Divergence
Since
Fourier series have such good convergence properties, many are often
surprised by some of the negative results. For example, the Fourier
series of a continuous T-periodic function need not converge pointwise. The uniform boundedness principle yields a simple non-constructive proof of this fact.
In 1922, Andrey Kolmogorov published an article titled Une série de Fourier-Lebesgue divergente presque partout
in which he gave an example of a Lebesgue-integrable function whose
Fourier series diverges almost everywhere. He later constructed an
example of an integrable function whose Fourier series diverges
everywhere (Katznelson 1976).
























![{\displaystyle \mathrm {X} _{f}(\tau )={\tfrac {2}{P}}\int _{x_{0}}^{x_{0}+P}s(x)\cdot \cos \left(2\pi f(x-\tau )\right)\,dx;\quad \tau \in \left[0,{\tfrac {2\pi }{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5240eaa70571932d715193314ccebab98f25b305)








![{\displaystyle {\begin{aligned}\mathrm {X} _{n}(\varphi )&={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left({\tfrac {2\pi }{P}}nx-\varphi \right)\,dx;\quad \varphi \in [0,2\pi ]\\&=\cos(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left({\tfrac {2\pi }{P}}nx\right)\,dx} _{\triangleq \ a_{n}}+\sin(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \sin \left({\tfrac {2\pi }{P}}nx\right)\,dx} _{\triangleq \ b_{n}}\\&=\cos(\varphi )\cdot a_{n}+\sin(\varphi )\cdot b_{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b65590f785d22d6b81e65752068b5555a7af90a)









![{\displaystyle {\displaystyle s_{\scriptscriptstyle N}(x)={\frac {A_{0}}{2}}+\sum _{n=1}^{N}\left[A_{n}\cos(\varphi _{n})\cdot \cos \left({\tfrac {2\pi }{P}}nx\right)+A_{n}\sin(\varphi _{n})\cdot \sin \left({\tfrac {2\pi }{P}}nx\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e904306df1ed48e64053b1f579c8bfab5508157)




![{\displaystyle {\begin{aligned}\cos \left({\tfrac {2\pi }{P}}nx-\varphi _{n}\right)&{}\equiv {\tfrac {1}{2}}e^{i\left(2\pi nx/P-\varphi _{n}\right)}+{\tfrac {1}{2}}e^{-i\left(2\pi nx/P-\varphi _{n}\right)}\\[6pt]&=\left({\tfrac {1}{2}}e^{-i\varphi _{n}}\right)\cdot e^{i2\pi (+n)x/P}+\left({\tfrac {1}{2}}e^{-i\varphi _{n}}\right)^{*}\cdot e^{i2\pi (-n)x/P}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ccce1b987630c62705a4a1c8750077d2cd2ade7)




![(-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



![{\displaystyle {\begin{aligned}a_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0.\\[4pt]b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd645b661c531998472837b4709b23bf2d2c939)

![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c051045100b8d31eada1c7fcfd414759404ed25b)

![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
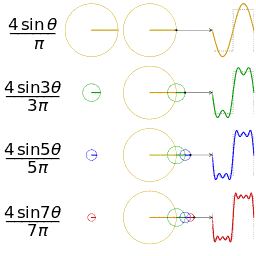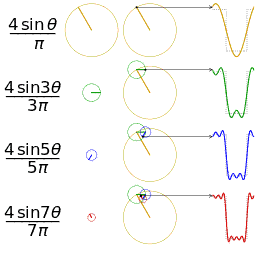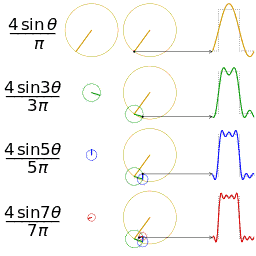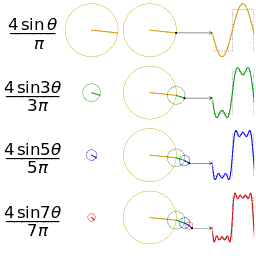










![{\displaystyle {\begin{aligned}c_{n}&={\tfrac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\frac {2\pi }{P}}nx}\ dx+i\cdot {\tfrac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\\[4pt]&={\tfrac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\ =\ {\tfrac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2f3a7cab08bd95f922c1fbc2f921addb4edfcd3)
![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}[n]\cdot e^{i\,2\pi nx/P}\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}&&\scriptstyle {\mathsf {common\ engineering\ notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1a1ac253b5d7a763eff884963eb5efbc5dd0879)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)











![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)




















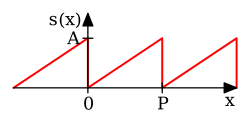








![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb7150e991a2642dc0c62cdee40602d99227420)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)



![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\textstyle \sum _{n=-\infty }^{\infty }{\Bigl |}S[n]{\Bigr |}^{2}={\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45449c99cf90bed698c4b3797561759081fc2e5)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)


![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed)

![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s'}}[n]=in{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6)

![{\displaystyle {\widehat {s^{(k)}}}[n]=(in)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20)

![{\displaystyle {\widehat {s^{(k)}}}[n]\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)



![[-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [-\pi ,\pi ]\times [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\\[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)



















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)



![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&\triangleq {\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)

![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&\triangleq {\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)



















![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)












![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)












![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i{\tfrac {2\pi }{P}}nx},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b030eaf773387de3787b4a003ef7599624be959)
![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i{\tfrac {2\pi }{P}}nx}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a29c02020f3c186b790b680deabe8e985ebcd700)







![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)

![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)


![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)

